Using Machine Learning in the Prediction of the Influence of Atmospheric Parameters on Health
Abstract
:1. Introduction
- Methodological contribution in the proposed novel model for prediction based on ensemble algorithm of machine learning;
- Technological contribution in this model based on the implementation of contemporary, modern EIT, which the authors will describe in detail in a section in which they will present results obtained on a case study of this paper, each in an appropriate, separate subsection.
1.1. Literature Review
1.2. State of the Art and Research Gaps
- Less-developed regions in the world, including the countries of the Western Balkans, along with the least developed countries in Africa, South America, and some countries in Central and South-East Asia, are less covered by the research, so the subject research conducted in the Republic of Serbia indeed represents the filling of a type of research gaps related to regional topology and economic power, which is the basis for enabling such research [57].
- Additionally, today, at the beginning of the third millennium, in a dominantly information-based human society, the subject research is the most frequently considered disease that affects the health of humanity, and the most prevalent investigations are related to heart diseases and viral epidemics. The number deals with non-accidental mortality in general, which is the case that is covered by this paper [58].
- Most of the research related to the described in the paper deal with the influence of specific groups and individual atmospheric factors—heat, air pollution, etc., on human health, and a minimal number of works are related to the study of the influence of all atmospheric parameters on human health; so is the research of this paper to fill the research gap, and in that sense [59].
- Remind of the ensemble method, to put it simply as a supervised meta-algorithm that combines multiple learning algorithms, has the most used taxonomy, which recognizes three types of this methodology; of boosting algorithms primarily reduce bias, but also variance in supervised learning through one iterative process; and bagging algorithms, which primarily improve the accuracy and stability of machine learning algorithms applied in regression and classification through expanding the basis training set of data and averaging algorithms, in which is made the process of creating multiple models and their combination to produce one model as the desired output [60].
- State it can be found in world literature that for different purposes, an ideal ensemble method should work on the principle of achieving six essential characteristics: accuracy, scalability, computational cost, usability, compactness, and speed of classification [61].
- Find in world literature that the state-of-the-art algorithms may differ from what applications are used [62].
- Remark that the success of an ensemble model is a function of the included member algorithms of the ensemble from one site and the nature of the data from another location. In this way, an ensemble works when it uses good characteristics of each member algorithm, enabling some degree of diversity [63].
- Notice that today there exist more auto machine learning frameworks that enable easy to use and achieve state-of-the-art predictive accuracy by utilizing state-of-the-art deep learning techniques without expertise from the existing dataset [64].
2. Materials and Methods
2.1. Methods
2.1.1. Emergent Intelligence Technique
2.1.2. Classification Methodology of Machine Learning
- Point (0,1) represents a perfect prediction, where all samples are classified correctly;
- Point (1,1) represents a classification that classifies all cases as positive;
- Point (1,0) represents a classification that classifies all samples incorrectly.
- Selection of classifiers for applying the classification algorithm;
- Selecting class attribute (output variable);
- Splitting the data set into two parts: training and test set;
- Training the classifier on the training code set when the values of the class attribute are known;
- Testing the classifier on the test set where they are hidden class attribute values.
Naive Bayes
LogitBoost
Decisions Trees
PART
SMO
Logistic Regression
2.1.3. Future Selection Techniques of Machine Learning
2.1.4. Machine Learning Ensemble Method for Predicting the Impact of Atmospheric Factors on Health
| Algorithm 1: Obtaining predictors of health hazards caused by atmospheric factors referent (number of attributes) = ni, i = 1, referent = n1 = 27 |
|
2.2. Materials
3. Results
Application of Proposed Algorithm of Ensemble Learning in the Case Study
- (1)
- InformationGain attribute evaluation(IG);
- (2)
- GainRatio attribute evaluation (GR);
- (3)
- SymmetricalUncert attribute evaluation (SU).
- Airpressureat7oclockmbar,
- Airpressureat14oclockmbar,
- Airpressureat21oclockmbar,
- Meandailyairpressurembar,
- DailytemperatureamplitudeC,
- Cloudinessat7oclockintenthsofthesky,
- Cloudinessat14oclockintenthsofthesky,
- Cloudinessat21oclockintenthsofthesky,
- Meandailycloudinessintenthsofthesky,
- Rainfallmm,
- The most critical parameter model was determined to be Watervapoursaturationat7oclockmbar, then Meandailywatervapoursaturationmbar, and so on: Watervapoursaturationat21oclockmbar, MaximumdailytemperatureC, MeandailytemperatureC, MinimumdailytemperatureC, Temperatureat21oclockC, and Temperatureat7oclockC.
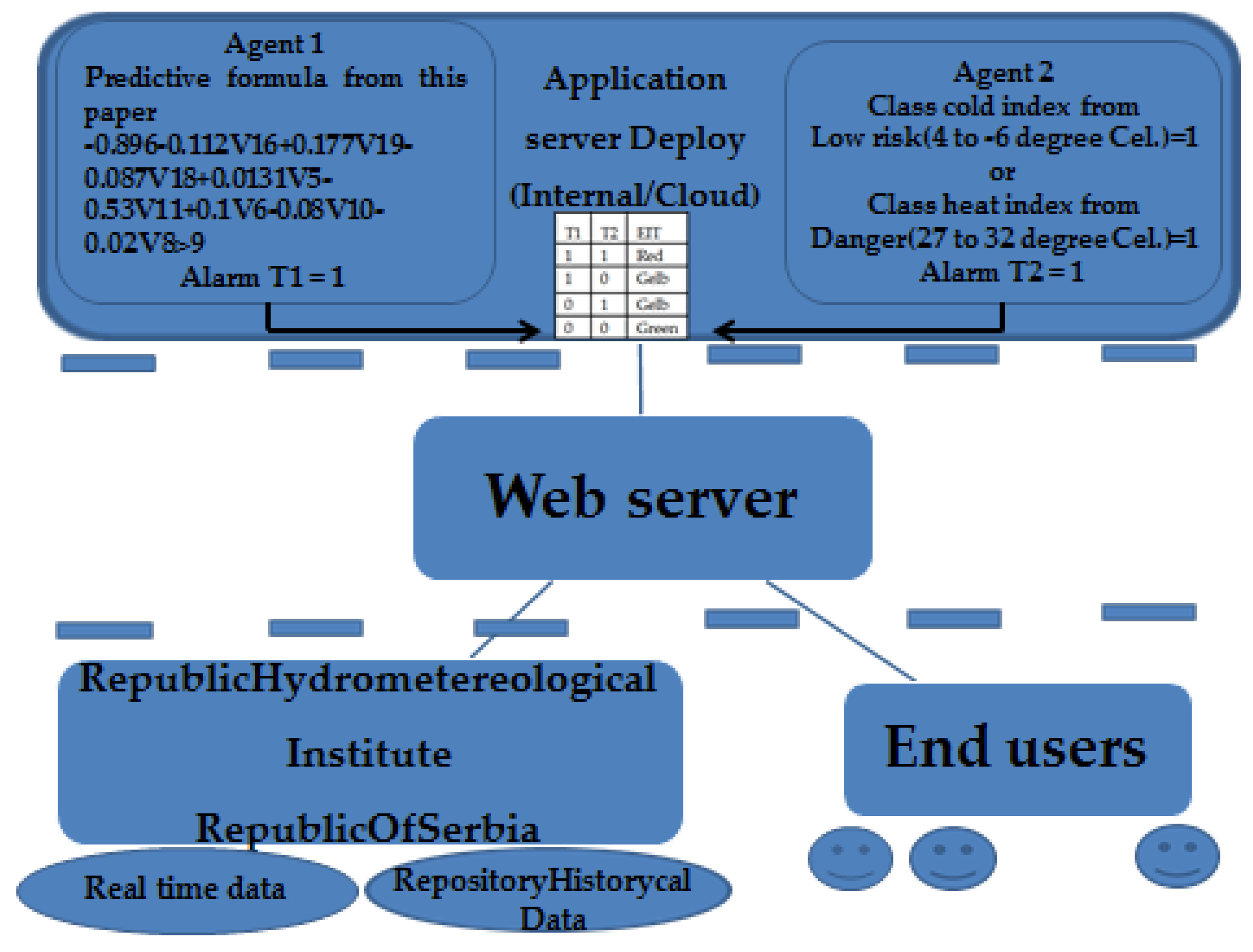
- Predictive formula is as follows:−0.896 − 0.112V16 + 0.177V19 − 0.087V18 + 0.031V5 − 0.53V11 + 0.1V6 − 0.08V10 − 0.02V8i.e., −0.896 − 0.112 ∗ Watervapoursaturationat7oclockmbar + 0.177 ∗ Meandailywatervapoursaturationmbar − 0.087 ∗ Watervapoursaturationat21oclockmbar + 0.031 ∗ MaximumdailytemperatureC − 0.53 ∗ MeandailytemperatureC + 0.10 ∗ MinimumdailytemperatureC − 0.08 ∗ Temperatureat21oclockC − 0.02 ∗ Temperatureat7oclock.
4. The Technical Solution of EIT as One Implementation of the Proposed Ensemble Method
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zheng, L.; Lin, R.; Wang, X.; Chen, W. The development and application of machine learning in atmospheric environment studies. Remote Sens. 2021, 13, 4839. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Haleh, H.; Ghaffari, A.; Meshkib, A.K. A combined model of MCDM and data mining for determining question weights in scientific exams. Appl. Math. Sci. 2012, 6, 173–196. [Google Scholar]
- Randjelovic, D.; Kuk, K.; Randjelovic, M. The application of the aggregation of several different approaches to weighting coefficients in determining the impact of weather conditions on public health. In Proceedings of the First American Academic Research Conference on Global Business, Economics, Finance and Social Sciences, New York, NY, USA, 27 May 2016. [Google Scholar]
- Dilaveris, P.; Synetos, A.; Giannopoulos, G.; Gialafos, E.; Pantazis, A.; Stefanadis, C. Climate impacts on myocardial infarction deaths in the Athens territory: The climate study. Heart 2006, 92, 1747–1751. [Google Scholar] [CrossRef] [PubMed]
- Randjelovic, D.; Cisar, P.; Kuk, K.; Bogdanovic, D.; Aksentijevic, V. E-service for early warning of citizens to wheather condi-tions and air pollution. J. Basic Appl. Res. Int. 2015, 10, 140–153. [Google Scholar]
- Trenchevski, A.; Kalendar, M.; Gjoreski, H.; Efnusheva, D. Prediction of air pollution concentration using weather data and regression models. In Proceedings of the 8th International Conference on Applied Innovations in IT, (ICAIIT), Köthen, Germany, 9 March 2020; pp. 55–61. [Google Scholar]
- Hoek, G.; Beelen, R.; De Hoogh, K.; Vienneau, D.; Gulliver, J.; Fischer, P.; Briggs, D. A review of land-use regression models to assess spatial variation of outdoor air pollution. Atmos. Environ. 2008, 42, 7561–7578. [Google Scholar] [CrossRef]
- Analitis, A.; Katsouyanni, K.; Biggeri, A.; Baccini, M.; Forsberg, B.; Bisanti, L.; Kirchmayer, U.; Ballester, F.; Cadum, E.; Goodman, P.G.; et al. Effects of cold weather on mortality: Results from 15 European cities within the PHEWE project. Am. J. Epidemiol. 2008, 168, 1397–1408. [Google Scholar] [CrossRef]
- Michelozzi, P.; Kirchmayer, U.; Katsouyanni, K.; Biggeri, A.; McGregor, G.; Menne, B.; Kassomenos, P.; Anderson, H.R.; Baccini, M.; Accetta, G.; et al. Assessment and prevention of acute health effects of weather conditions in Europe, the PHEWE project: Background, objectives, design. Environ. Health 2007, 6, 12. [Google Scholar] [CrossRef]
- Chiogna, M.; Gaetan, C.G. Mining epidemiological time series: An approach based on dynamic regression. Stat. Model. 2005, 5, 309–325. [Google Scholar] [CrossRef]
- Zanobetti, A.; Schwartz, J. Temperature and mortality in nine US cities. Epidemiology 2008, 1, 563–570. [Google Scholar] [CrossRef]
- Berko, J.; Ingram, D.; Saha, S.; Parker, J. Deaths Attributed to Heat, Cold, and Other Weather Events in the United States, 2006–2010; National Health Statistics Reports; U.S. Department of Health and Human Services: Washington, DC, USA, 2014. [Google Scholar]
- Vardoulakis, S.; Dear, K.; Hajat, S.; Heaviside, C.; Eggen, B.; McMichael, A.J. Comparative assessment of the effects of climate change on heat- and cold-related mortality in the United Kingdom and Australia. Environ. Health Perspect. 2014, 122, 1285–1292. [Google Scholar] [CrossRef] [PubMed]
- López, P.; Cativo-Calderon, E.H.; Otero, D.; Mahjabeen, R.; Atlas, S.; Rosendorff, C. The impact of environmental factors on the mortality of patients with chronic heart failure. Am. J. Cardiol. 2021, 146, 48–55. [Google Scholar] [CrossRef] [PubMed]
- Bogdanovic, D.; Milosevic, Z.; Lazarevic, K.; Dolicanin, Z.; Randjelovic, D.; Bogdanovic, S. The impact of the July 2007 heat wave on daily mortality in Belgrade, Serbia. Cent. Eur. J. Public Health 2013, 21, 140–145. [Google Scholar] [CrossRef] [PubMed]
- Dolicanin, Z.; Bogdanovic, D.; Lazarevic, K. Changes in stroke mortality trends and premature mortality due to stroke in Serbia, 1992–2013. Int J. Public Health 2016, 61, 131–137. [Google Scholar] [CrossRef]
- Bogdanović, D.; Doličanin, Ć.; Randjelović, D.; Milošević, Z.; Doličanin, D. An evaluation of health effects of precipitation using regression and one-way analysis of variance. In Proceedings of the Twentieth International Conference Ecological Truth, Zajecar, Srbija, 30 May–2 June 2012. [Google Scholar]
- Unkašević, M.; Tošić, I. Trends in extreme summer temperatures at Belgrade. Theor. Appl. Climatol. 2005, 82, 199–205. [Google Scholar] [CrossRef]
- Unkasevic, M.; Tosic, I. The maximum temperatures and heat waves in Serbia during the summer of 2007. Clim. Chang. 2011, 108, 207–223. [Google Scholar] [CrossRef]
- Kendrovski, T. The impact of ambient temperature on mortality among the urban population in Skopje, Macedonia during the period 1996–2000. BMC Public Health 2006, 6, 44. [Google Scholar] [CrossRef]
- Yang, J.; Liu, H.-Z.; Ou, C.-Q.; Lin, G.-Z.; Zhou, Q.; Shen, G.-C.; Chen, P.-Y.; Guo, Y. Global climate change: Impact of diurnal temperature range on mortality in Guangzhou, China. Environ. Pollut. 2013, 175, 131–136. [Google Scholar] [CrossRef]
- Bao, J.; Wang, Z.; Yu, C.; Li, X. The influence of temperature on mortality and its Lag effect: A study in four Chinese cities with different latitudes. BMC Public Health 2016, 16, 375. [Google Scholar] [CrossRef]
- Son, J.-Y.; Lee, J.-T.; Anderson, G.B.; Bell, M.L. Vulnerability to temperature-related mortality in Seoul, Korea. Environ. Res. Lett. 2011, 6, 034027. [Google Scholar] [CrossRef]
- Ou, C.Q.; Yang, J.; Ou, Q.; Liu, H.; Lin, G.; Chen, P.; Qian, J.; Guo, Y. The impact of relative humidity and atmospheric pressure on mortality in Guangzhou, China. Biomed. Environ. Sci. 2014, 27, 917–925. [Google Scholar] [CrossRef] [PubMed]
- Barreca, A.I.; Shimshack, J.P. Absolute humidity, temperature, and influenza mortality: 30 years of county-level evidence from the United States. Am. J. Epidemiol. 2012, 176, S114–S122. [Google Scholar] [CrossRef] [PubMed]
- Smith, R.; Davis, J.; Sacks, J.; Speckman, P. Regression models for air pollution and daily mortality: Analysis of data from Birmingham, Alabama. Environmetrics 2000, 11, 719–743. [Google Scholar] [CrossRef]
- Dominici, F.; Samet, J.M.; Zeger, S.L. Combining evidence on air pollution and daily mortality from the 20 largest US cities: A hierarchical modelling strategy. J. R. Stat. Soc. Ser. A (Stat. Soc.) 2000, 163, 263–302. [Google Scholar] [CrossRef]
- Song, W.; Jia, H.; Huang, J.; Zhang, Y. A satellite-based geographically weighted regression model for regional PM2.5 estimation over the Pearl River Delta region in China. Remote Sens. Environ. 2014, 154, 1–7. [Google Scholar] [CrossRef]
- Liu, W.; Li, X.; Chen, Z.; Zeng, G.; León, T.; Liang, J.; Huang, G.; Gao, Z.; Jiao, S.; He, X. Land use regression models coupled with meteorology to model spatial and temporal variability of NO2 and PM10 in Changsha, China. Atmos. Environ. 2015, 116, 272–280. [Google Scholar] [CrossRef]
- Wheeler, D.C.; Páez, A. Geographically weighted regression. In Handbook of Applied Spatial Analysis; Springer: Berlin/Heidelberg, Germany, 2010; pp. 461–486. [Google Scholar]
- Zuo, R.; Xiong, Y.; Wang, J.; Carranza, E.J.M. Deep learning and its application in geochemical mapping. Earth-Sci. Rev. 2019, 192, 1–14. [Google Scholar] [CrossRef]
- Deng, L.; Yu, D. Deep learning: Methods and applications. Found. Trends Signal Process. 2014, 7, 197–387. [Google Scholar] [CrossRef]
- Yuan, Q.; Shen, H.; Li, T.; Li, Z.; Li, S.; Jiang, Y.; Xu, H.; Tan, W.; Yang, Q.; Wang, J. Deep learning in environmental remote sensing: Achievements and challenges. Remote Sens. Environ. 2020, 241, 111716. [Google Scholar] [CrossRef]
- Yegnanarayana, B. Artificial Neural Networks; PHI Learning Pvt. Ltd.: New Delhi, India, 2009. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Pfaffhuber, K.A.; Berg, T.; Hirdman, D.; Stohl, A. Atmospheric mercury observations from Antarctica: Seasonal variation and source and sink region calculations. Atmos. Chem. Phys. 2012, 12, 3241–3251. [Google Scholar] [CrossRef]
- Baker, D.; Bösch, H.; Doney, S.; O’Brien, D.; Schimel, D. Carbon source/sink information provided by column CO2 measurements from the Orbiting Carbon Observatory. Atmos. Chem. Phys. 2010, 10, 4145–4165. [Google Scholar] [CrossRef]
- Bousiotis, D.; Brean, J.; Pope, F.D.; Dall’Osto, M.; Querol, X.; Alastuey, A.; Perez, N.; Petäjä, T.; Massling, A.; Nøjgaard, J.K. The effect of meteorological conditions and atmospheric composition in the occurrence and development of new particle formation (NPF) events in Europe. Atmos. Chem. Phys. 2021, 21, 3345–3370. [Google Scholar] [CrossRef]
- Lee, J.; Kim, K.Y. Analysis of source regions and meteorological factors for the variability of spring PM10 concentrations in Seoul, Korea. Atmos. Environ. 2018, 175, 199–209. [Google Scholar] [CrossRef]
- Zhao, H.; Li, X.; Zhang, Q.; Jiang, X.; Lin, J.; Peters, G.P.; Li, M.; Geng, G.; Zheng, B.; Huo, H. Effects of atmospheric transport and trade on air pollution mortality in China. Atmos. Chem. Phys. 2017, 17, 10367–10381. [Google Scholar] [CrossRef]
- Ma, Q.; Wu, Y.; Zhang, D.; Wang, X.; Xia, Y.; Liu, X.; Tian, P.; Han, Z.; Xia, X.; Wang, Y. Roles of regional transport and heterogeneous reactions in the PM2.5 increase during winter haze episodes in Beijing. Sci. Total Environ. 2017, 599, 246–253. [Google Scholar] [CrossRef]
- An, Z.; Huang, R.J.; Zhang, R.; Tie, X.; Li, G.; Cao, J.; Zhou, W.; Shi, Z.; Han, Y.; Gu, Z. Severe haze in northern China: A synergy of anthropogenic emissions and atmospheric processes. Proc. Natl. Acad. Sci. USA 2019, 116, 8657–8666. [Google Scholar] [CrossRef]
- Wu, R.; Xie, S. Spatial distribution of ozone formation in China derived from emissions of speciated volatile organic compounds. Environ. Sci. Technol. 2017, 51, 2574–2583. [Google Scholar] [CrossRef]
- Zhang, K.; Li, Y.; Schwartz, J.; O’Neill, M. What weather variables are important in predicting heat-related mortality? A new application of statistical learning methods. Environ. Res. 2014, 132, 350–359. [Google Scholar] [CrossRef]
- Lee, W.; Lim, Y.-H.; Ha, E.; Kim, Y.; Lee, W.K. Forecasting of non-accidental, cardiovascular, and respiratory mortality with environmental exposures adopting machine learning approaches. Environ. Sci. Pollut. Res. 2022, 9, 4069. [Google Scholar] [CrossRef]
- Liu, H.; Li, Q.; Yu, D.; Gu, Y. Air quality index and air pollutant concentration prediction based on machine learning algorithms. Appl. Sci. 2019, 9, 4069. [Google Scholar] [CrossRef]
- Pérez, P.; Trier, A.; Reyes, J. Prediction of PM2.5 concentrations several hours in advance using neural networks in Santiago, Chile. Atmos. Environ. 2000, 34, 1189–1196. [Google Scholar] [CrossRef]
- Corani, G. Air quality prediction in Milan: Feed-forward neural networks, pruned neural networks and lazy learning. Ecol. Model. 2005, 185, 513–529. [Google Scholar] [CrossRef]
- Biancofiore, F.; Busilacchio, M.; Verdecchia, M.; Tomassetti, B.; Aruffo, E.; Bianco, S.; Di Tommaso, S.; Colangeli, C.; Rosatelli, G.; Di Carlo, P. Recursive neural network model for analysis and forecast of PM10 and PM2.5. Atmos. Pollut. Res. 2017, 8, 652–659. [Google Scholar] [CrossRef]
- Fuller, G.W.; Carslaw, D.C.; Lodge, H.W. An empirical approach for the prediction of daily mean PM10 concentrations. Atmos. Environ. 2002, 36, 1431–1441. [Google Scholar] [CrossRef]
- Lepperod, A.J. Air Quality Prediction with Machine Learning. Master’s Thesis, Norwegian University of Science and Technology, Oslo, Norway, 2019. [Google Scholar]
- Dewi, K.C.; Mustika, W.F.; Murfi, H. Ensemble learning for predicting mortality rates affected by air quality. J. Phys. Conf. Ser. 2019, 1192, 012021. [Google Scholar] [CrossRef]
- Li, L.; Zhang, J.H.; Qiu, W.Y.; Wang, J.; Fang, Y. An ensemble spatiotemporal model for predicting PM2.5 concentrations. Int. J. Environ. Res. Public Health 2017, 14, 549. [Google Scholar] [CrossRef]
- Zhu, S.; Lian, X.; Liu, H.; Hu, J.; Wang, Y.; Che, J. Daily air quality index forecasting with Hybrid models. A case in China. Environ. Pollut. 2017, 231, 1232–1244. [Google Scholar] [CrossRef]
- Liang, Y.-C.; Maimury, Y.; Chen, A.H.-L.; Juarez, J.R.C. Machine learning-based prediction of air quality. Appl. Sci. 2020, 10, 9151. [Google Scholar] [CrossRef]
- Ncongwane, K.P.; Botai, J.O.; Sivakumar, V.; Botai, C.M. A literature review of the impacts of heat stress on human health across Africa. Sustainability 2021, 13, 5312. [Google Scholar] [CrossRef]
- Hadley, M.B.; Nalini, M.; Adhikari, S.; Szymonifka, J.; Etemadi, A.; Kamangar, F.; Khoshnia, M.; McChane, T.; Pourshams, A.; Poustchi, H.; et al. Spatial environmental factors predict cardiovascular and all-cause mortality: Results of the SPACE study. PLoS ONE 2022, 17, e0269650. [Google Scholar] [CrossRef] [PubMed]
- Mentzakis, E.; Delfino, D. Effects of air pollution and meteorological parameters on human health in the city of Athens, Greece. Int. J. Environ. Pollut. 2010, 40, 210–225. [Google Scholar] [CrossRef]
- Tsoumakas, G.; Partalas, I.; Vlahavas, I. A taxonomy and short review of ensemble selection. In Proceedings of the Workshop on Supervised and Unsupervised Ensemble Methods and Their Applications, ECAI 2008, Patras, Greece, 21–25 July 2008. [Google Scholar]
- Shahid, A.; Sreenivas, S.T.; Abdolhossein, S. Ensemble learning methods for decision making: Status and future prospects. In Proceedings of the International Conference on Machine Learning and Cybernetics, ICMLC 2015, Guangzhou, China, 12–15 July 2015; pp. 211–216. [Google Scholar] [CrossRef]
- Pintelas, P.; Livieris, I.E. Special issue on ensemble learning and applications. Algorithms 2020, 13, 140. [Google Scholar] [CrossRef]
- Lofstrom, T.; Johansson, U.; Bostrom, H. Ensemble member selection using multi-objective optimization. In Proceedings of the IEEE Symposium on Computational Intelligence and Data Mining, CIDM 2009, Part of the IEEE Symposium Series on Computational Intelligence 2009, Nashville, TN, USA, 30 March–2 April 2009; pp. 245–251. [Google Scholar] [CrossRef]
- Waring, J.; Lindvall, C.; Umeton, R. Automated machine learning: Review of the state-of-the-art and opportunities for healthcare. Artif. Intell. Med. 2020, 104, 101822. [Google Scholar] [CrossRef] [PubMed]
- Romero, C.; Ventura, S.; Espejo, P.; Hervas, C. Data mining algorithms to classify students. In Proceedings of the 1st IC on Educational Data Mining (EDM08), Montreal, QC, Canada, 20–21 June 2008. [Google Scholar]
- Fawcett, T. ROC Graphs: Notes and Practical Considerations for Data Mining Researchers; Technical Report HP Laboratories: Palo Alto, CA, USA, 2003. [Google Scholar]
- Vuk, M.; Curk, T. ROC curve, lift chart and calibration plot. Metodol. Zvezki 2006, 3, 89–108. [Google Scholar] [CrossRef]
- Dimić, G.; Prokin, D.; Kuk, K.; Micalović, M. Primena decision trees i naive bayes klasifikatora na skup podataka izdvojen iz moodle kursa. In Proceedings of the Conference INFOTEH, Jahorina, Bosnia and Herzegovina, 21–23 March 2012; Volume 11, pp. 877–882. [Google Scholar]
- Witten, H.; Eibe, F. Data Mining: Practical Machine Learning Tools and Techniques, 2nd ed.; Morgan Kaufmann Publishers: San Francisco, CA, USA, 2005. [Google Scholar]
- Benoît, G. Data mining. Ann. Rev. Inf. Sci. Technol. 2002, 36, 265–310. [Google Scholar] [CrossRef]
- Weka (University of Waikato: New Zealand). Available online: http://www.cs.waikato.ac.nz/ml/weka (accessed on 20 July 2022).
- Pearl, J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference; Morgan Kaufman Publishers: San Francisco, CA, USA, 1988. [Google Scholar]
- Harry, Z. The optimality of naive bayes. In Proceedings of the FLAIRS Conference, Miami Beach, FL, USA, 12–14 May 2004. [Google Scholar]
- Friedman, J.; Hastie, T.; Tibshirani, R. Additive logistic regression: A statistical view of boosting. Ann. Stat. 2000, 28, 337–407. [Google Scholar] [CrossRef]
- Rokach, L.; Maimon, O. Decision trees. In The Data Mining and Knowledge Discovery Handbook; Springer: Berlin/Heidelberg, Germany, 2005; pp. 165–192. [Google Scholar] [CrossRef]
- Xiaohu, W.; Lele, W.; Nianfeng, L. An application of decision tree based on ID3. Phys. Procedia 2012, 25, 1017–1021. [Google Scholar] [CrossRef]
- Quinlan, J.R. C4.5: Programs for Machine Learning; Morgan Kaufmann Publishers: San Francisco, CA, USA, 1993. [Google Scholar]
- Bella, A.; Ferri, C.; Hernández-Orallo, J.; Ramírez-Quintana, M.J. Calibration of machine learning models. In Handbook of Re-Search on Machine Learning Applications; IGI Global: Hershey, PA, USA, 2009. [Google Scholar]
- Zadrozny, B.; Elkan, C. Obtaining calibrated probability estimates from decision trees and naive Bayesian classifiers. In Proceedings of the Eighteenth International Conference on Machine Learning, San Francisco, CA, USA, 28 June–1 July 2001; Morgan Kaufmann Publishers, Inc.: San Francisco, CA, USA, 2001; pp. 609–616. [Google Scholar]
- Amin, N.; Habib, A. Comparison of Different Classification Techniques Using WEKA for Hematological Data. Am. J. Eng. Res. 2015, 4, 55–61. [Google Scholar]
- Ayu, M.A.; Ismail, S.A.; Matin, A.F.A.; Mantoro, T. A comparison study of classifier algorithms for mobile-phone’s accelerometer based activity recognition. Procedia Eng. 2012, 41, 224–229. [Google Scholar] [CrossRef]
- Liu, H.; Motoda, H. Feature Selection for Knowledge Discovery and Data Mining; Kluwer Academic Publishers: London, UK, 1998. [Google Scholar]
- Hall, M.A.; Smith, L.A. Practical feature subset selection for machine learning. In Proceedings of the 21st Australian Computer Science Conference, Perth, Australia, 4–6 February 1998; pp. 181–191. [Google Scholar]
- Moriwal, R.; Prakash, V. An efficient info-gain algorithm for finding frequent sequential traversal patterns from web logs based on dynamic weight constraint. In Proceedings of the CUBE International Information Technology Conference (CUBE ‘12), New York, NY, USA, 3–5 September 2012; ACM: New York, NY, USA, 2012; pp. 718–723. [Google Scholar]
- Sitorus, Z.; Saputra, K.; Sulistianingsih, I. C4.5 Algorithm Modeling For Decision Tree Classification Process Against Status UKM. Int. J. Sci. Technol. Res. 2018, 7, 63–65. [Google Scholar]
- Thakur, D.; Markandaiah, N.; Raj, D.S. Re optimization of ID3 and C4.5 decision tree. In Proceedings of the International Conference on Computer and Communication Technology (ICCCT), Allahabad, India, 17–19 September 2010; pp. 448–450. [Google Scholar]
- SPSS Statistics 17.0 Brief Guide. Available online: http://www.sussex.ac.uk/its/pdfs/SPSS_Statistics_Brief_Guide_17.0.pdf (accessed on 20 July 2022).
- Moore, S.; Notz, I.; Flinger, A. The Basic Practice of Statistics; W.H. Freeman: New York, NY, USA, 2013. [Google Scholar]
- Ilin, V. The Models for Identification and Quantification of the Determinants of ICT Adoption in Logistics Enterprises. Ph.D. Thesis, Faculty of Technical Sciences University Novi Sad, Novi Sad, Serbia, 2018. [Google Scholar]
- Hair, J.F.; Anderson, R.E.; Tatham, R.L.; Black, W.C. Multivariate Data Analysis; Prentice-Hall, Inc.: New York, NY, USA, 1998. [Google Scholar]
- Steadman, R.G. The assessment of sultriness. Part I: A temperature-humidity index based on human physiology and clothing science. J. Appl. Meteor. 1979, 18, 861–873. [Google Scholar] [CrossRef]
- Osczevski, R.; Bluestein, M. The New Wind Chill Equivalent Temperature Chart. Bull. Am. Meteorol. Soc. 2005, 86, 1453–1458. [Google Scholar] [CrossRef]




| Predicted Label | |||
|---|---|---|---|
| Positive | Negative | ||
| Actual label | Positive | TP | FN |
| Negative | FP | TN | |
| Variable-Serial Number and Notation | Atmospheric Parameter |
|---|---|
| 1-V1 | Airpressureat7oclockmbar |
| 2-V2 | Airpressureat14oclockmbar |
| 3-V3 | Airpressureat21oclockmbar |
| 4-V4 | Meandailyairpressurembar |
| 5-V5 | MaximumdailytemperatureC |
| 6-V6 | MinimumdailytemperatureC |
| 7-V7 | DailytemperatureamplitudeC |
| 8-V8 | Temperatureat7oclockC |
| 9-V9 | Temperatureat14oclockC |
| 10-V10 | Temperatureat21oclockC |
| 11-V11 | MeandailytemperatureC |
| 12-V12 | Relativehumidityat7oclockpercent |
| 13-V13 | Relativehumidityat14oclockpercent |
| 14-V14 | Relativehumidityat21oclockpercent |
| 15-V15 | Meandailyrelativehumiditypercent |
| 16-V16 | Watervapoursaturationat7oclockmbar |
| 17-V17 | Watervapoursaturationat14oclockmbar |
| 18-V18 | Watervapoursaturationat21oclockmbar |
| 19-V19 | Meandailywatervapoursaturationmbar |
| 20-V20 | Meandailywindspeedmsec |
| 21-V21 | Insolationh |
| 22-V22 | Cloudinessat7oclockintenthsofthesky |
| 23-V23 | Cloudinessat14oclockintenthsofthesky |
| 24-V24 | Cloudinessat21oclockintenthsofthesky |
| 25-V25 | Meandailycloudinessintenthsofthesky |
| 26-V26 | Snowfallcm |
| 27-V27 | Rainfallmm |
| 28-V28 | Emergency-daily mortality > 9 |
| B | S.E. | Wald | Df | Sig. | Exp (B) | ||||
|---|---|---|---|---|---|---|---|---|---|
| Airpressureat7oclockmbar | −0.043 | 0.020 | 4.535 | 1 | 0.033 | 0.958 | |||
| Airpressureat14oclockmbar | 0.060 | 0.033 | 3.332 | 1 | 0.068 | 1.061 | |||
| Airpressureat21oclockmbar | −0.038 | 0.020 | 3.802 | 1 | 0.051 | 0.962 | |||
| MaximumdailytemperatureC | 0.022 | 0.023 | 0.911 | 1 | 0.340 | 1.022 | |||
| MinimumdailytemperatureC | 0.040 | 0.026 | 2.354 | 1 | 0.125 | 1.040 | |||
| Temperatureat7oclockC | −0.745 | 0.256 | 8.453 | 1 | 0.004 | 0.475 | |||
| Temperatureat14oclockC | −0.646 | 0.255 | 6.439 | 1 | 0.011 | 0.524 | |||
| Temperatureat21oclockC | −1.48 | 0.509 | 8.459 | 1 | 0.004 | 0.227 | |||
| MeandailytemperatureC | 2.744 | 1.013 | 7.337 | 1 | 0.007 | 15.552 | |||
| Relativehumidityat7oclockpercent | −0.011 | 0.028 | 0.155 | 1 | 0.694 | 0.989 | |||
| Relativehumidityat14oclockpercent | 0.008 | 0.029 | 0.082 | 1 | 0.774 | 1.008 | |||
| Relativehumidityat21oclockpercent | −0.016 | 0.029 | 0.313 | 1 | 0.576 | 0.984 | |||
| Meandailyrelativehumiditypercent | 0.006 | 0.084 | 0.006 | 1 | 0.940 | 1.006 | |||
| Watervapoursaturationat7oclockmbar | −0.139 | 0.300 | 0.214 | 1 | 0.644 | 0.870 | |||
| Watervapoursaturationat14oclockmbar | −0.085 | 0.300 | 0.080 | 1 | 0.778 | 0.919 | |||
| Watervapoursaturationat21oclockmbar | −0.093 | 0.302 | 0.096 | 1 | 0.757 | 0.911 | |||
| Meandailywatervapoursaturationmbar | 0.348 | 0.893 | 0.152 | 1 | 0.697 | 1.416 | |||
| Meandailywindspeedmsec | −0.138 | 0.048 | 8.391 | 1 | 0.004 | 0.871 | |||
| Insolationh | 0.006 | 0.018 | 0.105 | 1 | 0.746 | 1.006 | |||
| Cloudinessat7oclockintenthsofthesky | −0.379 | 0.394 | 0.924 | 1 | 0.336 | 0.685 | |||
| Cloudinessat14oclockintenthsofthesky | −0.353 | 0.395 | 0.798 | 1 | 0.372 | 0.703 | |||
| Cloudinessat21oclockintenthsofthesky | −0.362 | 0.394 | 0.843 | 1 | 0.359 | 0.696 | |||
| Meandailycloudinessintenthsofthesky | 1.100 | 1.182 | 0.866 | 1 | 0.352 | 3.005 | |||
| Snowfallcm | 0.001 | 0.024 | 0.001 | 1 | 0.977 | 1.001 | |||
| Rainfallmm | −0.009 | 0.008 | 1.263 | 1 | 0.261 | 0.991 | |||
| Constant | 21.79 | 5.394 | 16.32 | 1 | 0.000 | 2.92 × 109 | |||
| Classification Table a,b | |||||||||
| Observed | Predicted | ||||||||
| Emergency-daily mortality > 9 | Percentage Correct | ||||||||
| 0 | 1 | ||||||||
| Step 0 | Emergency-daily mortality > 9 | 0 | 4984 | 0 | 100.0 | ||||
| 1 | 1500 | 0 | 0.0 | ||||||
| Overall Percentage | 76.9 | ||||||||
| Model Summary | |||||||||
| Step | −2 Log likelihood | Cox–Snell R Square | Nagelkerke R Square | ||||||
| 1 | 6859.654 c | 0.022 | 0.034 | ||||||
| Hosmer and Lemeshow Test | |||||||||
| Step | Chi-square | df | Sig. | ||||||
| 1 | 10.008 | 8 | 0.264 a | ||||||
| Accuracy | Recall | F1 Measure | ROC | |
|---|---|---|---|---|
| J48 | 0.649 | 0.759 | 0.672 | 0.56 |
| Naive Bayes | 0.679 | 0.63 | 0.65 | 0.578 |
| Logit Boost | 0.64 | 0.765 | 0.669 | 0.573 |
| PART | 0.688 | 0.769 | 0.67 | 0.571 |
| SMO | 0.592 | 0.769 | 0.669 | 0.5 |
| Atmospheric Parameter | IG | GR | SU |
|---|---|---|---|
| Airpressureat7oclockmbar | 27/0 | 27/0 | 27/0 |
| Airpressureat14oclockmbar | 20/0 | 18/0 | 18/0 |
| Airpressureat21oclockmbar | 18/0 | 20/0 | 19/0 |
| Meandailyairpressurembar | 19/0 | 19/0 | 20/0 |
| MaximumdailytemperatureC | 5/0.010 | 9/0.0089 | 7/0.0108 |
| MinimumdailytemperatureC | 7/0.0099 | 5/0.0102 | 5/0.0113 |
| DailytemperatureamplitudeC | 22/0 | 22/0 | 22/0 |
| Temperatureat7oclockC | 2/0.012 | 2/0.0112 | 1/0.013 |
| Temperatureat14oclockC | 10/0.008 | 8/0.0092 | 10/0.0101 |
| Temperatureat21oclockC | 1/0.013 | 10/0.007 | 8/0.0108 |
| MeandailytemperatureC | 8/0.0097 | 6/0.0097 | 6/0.0109 |
| Relativehumidityat7oclockpercent | 12/0.003 | 13/0.003 | 13/0.00345 |
| Relativehumidityat14oclockpercent | 14/0.0021 | 16/0.0022 | 15/0.0024 |
| Relativehumidityat21oclockpercent | 15/0.002 | 17/0.0021 | 16/0.0023 |
| Meandailyrelativehumiditypercent | 13/0.023 | 14/0.0027 | 14/0.0028 |
| Watervapoursaturationat7oclockmbar | 6/0.0104 | 4/0.0105 | 4/0.0118 |
| Watervapoursaturationat14oclockmbar | 9/0.0095 | 7/0.0096 | 9/0.0107 |
| Watervapoursaturationat21oclockmbar | 3/0.011 | 1/0.0114 | 2/0.0127 |
| Meandailywatervapoursaturationmbar | 4/0.0108 | 3/0.0109 | 3/0.0122 |
| Meandailywindspeedmsec | 17/0.014 | 15/0.0023 | 17/0.0020 |
| Insolationh | 11/0.0036 | 12/0.004 | 11/0.0044 |
| Cloudinessat7oclockintenthsofthesky | 23/0 | 23/0 | 23/0 |
| Cloudinessat14oclockintenthsofthesky | 26/0 | 26/0 | 26/0 |
| Cloudinessat21oclockintenthsofthesky | 25/0 | 25/0 | 25/0 |
| Meandailycloudinessintenthsofthesky | 24/0 | 24/0 | 24/0 |
| Snowfallcm | 16/0.01 | 11/0.006 | 12/0.00346 |
| Rainfallmm | 21/0 | 21/0 | 21/0 |
| B | S.E. | Wald | Df | Sig. | Exp(B) | ||||
|---|---|---|---|---|---|---|---|---|---|
| MaximumdailytemperatureC | 0.041 | 0.022 | 3.516 | 1 | 0.061 | 1.042 | |||
| MinimumdailytemperatureC | 0.025 | 0.025 | 0.970 | 1 | 0.325 | 1.025 | |||
| Temperatureat7oclockC | −0.741 | 0.256 | 8.415 | 1 | 0.004 | 0.477 | |||
| Temperatureat14oclockC | −0.696 | 0.254 | 7.511 | 1 | 0.006 | 0.499 | |||
| Temperatureat21oclockC | −1.484 | 0.508 | 8.528 | 1 | 0.003 | 0.227 | |||
| MeandailytemperatureC | 2.810 | 1.011 | 7.720 | 1 | 0.005 | 16.605 | |||
| Relativehumidityat7oclock | −0.014 | 0.027 | 0.246 | 1 | 0.620 | 0.987 | |||
| Relativehumidityat14oclock | 0.003 | 0.028 | 0.013 | 1 | 0.910 | 1.003 | |||
| Relativehumidityat21oclock | −0.017 | 0.028 | 0.369 | 1 | 0.543 | 0.983 | |||
| Meandailyrelativehumidity | 0.016 | 0.081 | 0.041 | 1 | 0.839 | 1.017 | |||
| Watervapoursaturationat7oclockmbar | −0.146 | 0.299 | 0.238 | 1 | 0.626 | 0.864 | |||
| Watervapoursaturationat14oclockmbar | −0.086 | 0.299 | 0.083 | 1 | 0.773 | 0.917 | |||
| Watervapoursaturationat21oclockmbar | −0.098 | 0.301 | 0.105 | 1 | 0.745 | 0.907 | |||
| Meandailywatervapoursaturationmbar | 0.343 | 0.891 | 0.149 | 1 | 0.700 | 1.410 | |||
| Meandailywindspeedmsec | −0.125 | 0.046 | 7.375 | 1 | 0.007 | 0.883 | |||
| Insolationh | −0.010 | 0.014 | 0.464 | 1 | 0.496 | 0.991 | |||
| Snowfallcm | 0.017 | 0.023 | 0.548 | 1 | 0.459 | 1.017 | |||
| Constant | 0.059 | 0.432 | 0.019 | 1 | 0.891 | 1.061 | |||
| Classification Table a,b | |||||||||
| Observed | Predicted | ||||||||
| Emergency-daily mortality > 9 | Percentage Correct | ||||||||
| 0 | 1 | ||||||||
| Step 0 | Emergency-daily mortality > 9 | 0 | 4985 | 0 | 100.0 | ||||
| 1 | 1501 | 0 | 0.0 | ||||||
| Overall Percentage | 76.9 | ||||||||
| Model Summary | |||||||||
| Step | −2 Log likelihood | Cox–Snell R Square | Nagelkerke R Square | ||||||
| 1 | 6885.229 c | 0.019 | 0.029 | ||||||
| Hosmer and Lemeshow Test | |||||||||
| Step | Chi-square | df | Sig. | ||||||
| 1 sa 17 | 12.921 | 8 | 0.115 | ||||||
| Accuracy 27/17 Parameters | Recall 27/17 Parameters | F1 Measure 27/17 Parameters | ROC 27/17 Parameters | |
|---|---|---|---|---|
| Naive Bayes | 0.679/0.681 | 0.63/0.636 | 0.65/0.654 | 0.578/0.578 |
| Logit Boost | 0.64/0.66 | 0.765/0.767 | 0.669/0.671 | 0.573/0.578 |
| Accuracy | Recall | F1 Measure | ROC | |
|---|---|---|---|---|
| Logit Boost/27 | 0.64 | 0.765 | 0.669 | 0.573 |
| Logit Boost/17 | 0.66 | 0.767 | 0.67 | 0.578 |
| Logit Boost/8 | 0.674 | 0.769 | 0.67 | 0.582 |
| B | S.E. | Wald | df | Sig. | Exp (B) | 95% C.I. for EXP (B) | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Lower | Upper | |||||||||
| MaximumdailytemperatureC | 0.031 | 0.022 | 2.084 | 1 | 0.149 | 1.032 | 0.989 | 1.076 | ||
| MinimumdailytemperatureC | 0.010 | 0.023 | 0.172 | 1 | 0.678 | 1.010 | 0.964 | 1.057 | ||
| Temperatureat7oclockC | −0.002 | 0.028 | 0.003 | 1 | 0.956 | 0.998 | 0.946 | 1.054 | ||
| Temperatureat21oclockC | −0.008 | 0.051 | 0.023 | 1 | 0.880 | 0.992 | 0.897 | 1.097 | ||
| MeandailytemperatureC | −0.053 | 0.088 | 0.370 | 1 | 0.543 | 0.948 | 0.798 | 1.126 | ||
| Watervapoursaturationat7oclockmbar | −0.112 | 0.040 | 7.912 | 1 | 0.005 | 0.894 | 0.826 | 0.966 | ||
| Watervapoursaturationat21oclockmbar | −0.087 | 0.042 | 4.260 | 1 | 0.039 | 0.917 | 0.844 | 0.996 | ||
| Meandailywatervapoursaturationmbar | 0.177 | 0.071 | 6.243 | 1 | 0.012 | 1.194 | 1.039 | 1.372 | ||
| Constant | −0.896 | 0.132 | 45.88 | 1 | 0.000 | 0.408 | ||||
| Classification Table a,b | ||||||||||
| Observed | Predicted | |||||||||
| Emergency-daily mortality > 9 | ||||||||||
| 0 | 1 | Percentage Correct | ||||||||
| Step 0 | Emergency-daily mortality >9 | 0 | 5057 | 0 | 100.0 | |||||
| 1 | 1518 | 0 | 0.0 | |||||||
| Overall Percentage | 76.9 | |||||||||
| Model Summary c | ||||||||||
| Step | −2 Log likelihood | Cox–Snell R Square | Nagelkerke R Square | |||||||
| 1 | 7000.920 c | 0.016 | 0.024 | |||||||
| Hosmer and Lemeshow Test | ||||||||||
| Step | Chi-square | df | Sig. | |||||||
| 1 | 18.207 | 8 | 0.020 | |||||||
| T1 | T2 | EIT |
|---|---|---|
| 1 | 1 | Red |
| 1 | 0 | Gelb |
| 0 | 1 | Gelb |
| 0 | 0 | Green |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ranđelović, D.; Ranđelović, M.; Čabarkapa, M. Using Machine Learning in the Prediction of the Influence of Atmospheric Parameters on Health. Mathematics 2022, 10, 3043. https://doi.org/10.3390/math10173043
Ranđelović D, Ranđelović M, Čabarkapa M. Using Machine Learning in the Prediction of the Influence of Atmospheric Parameters on Health. Mathematics. 2022; 10(17):3043. https://doi.org/10.3390/math10173043
Chicago/Turabian StyleRanđelović, Dragan, Milan Ranđelović, and Milan Čabarkapa. 2022. "Using Machine Learning in the Prediction of the Influence of Atmospheric Parameters on Health" Mathematics 10, no. 17: 3043. https://doi.org/10.3390/math10173043





