Reliability Sensibility Analysis of the PCB Assembly concerning Warpage during the Reflow Soldering Process
Abstract
:1. Introduction
2. Finite Element Simulation for PCB Assembly Warpage
2.1. Theoretical Model for Heat Transfer during the Reflow Soldering
2.2. Simulation and Discussion
2.2.1. Finite Element Model and the Loading Process
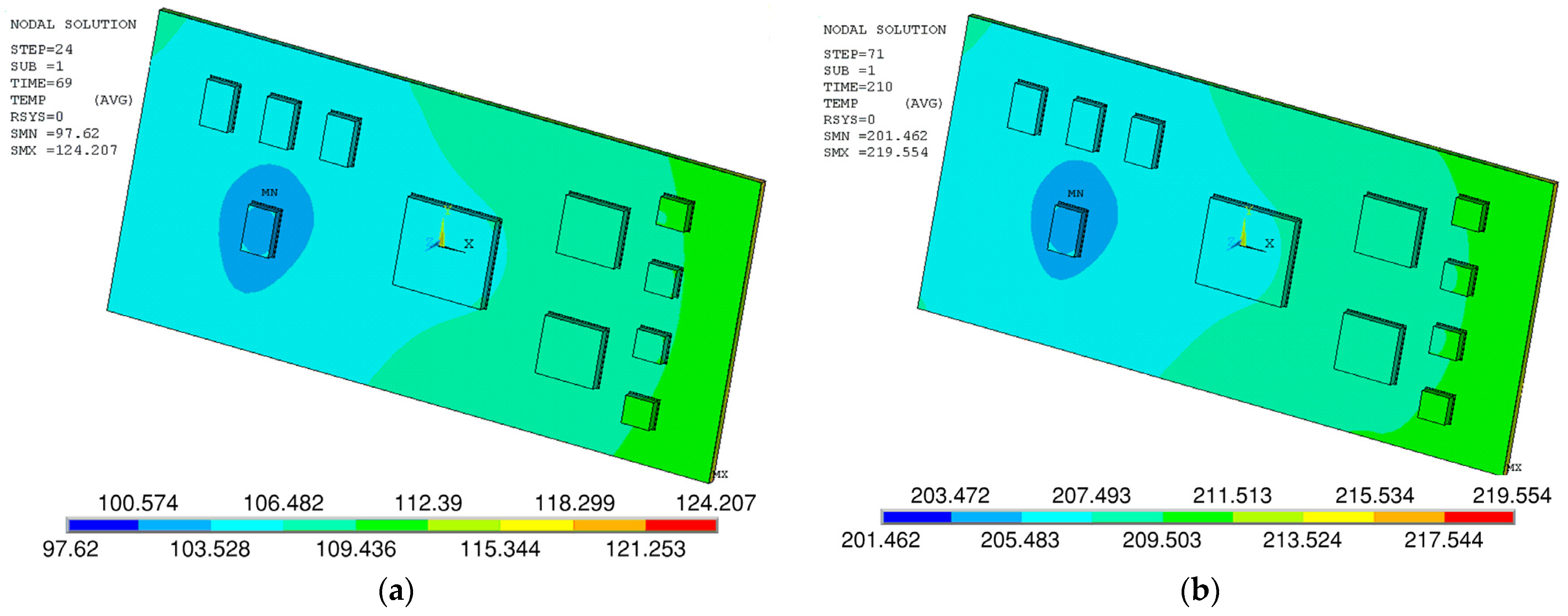
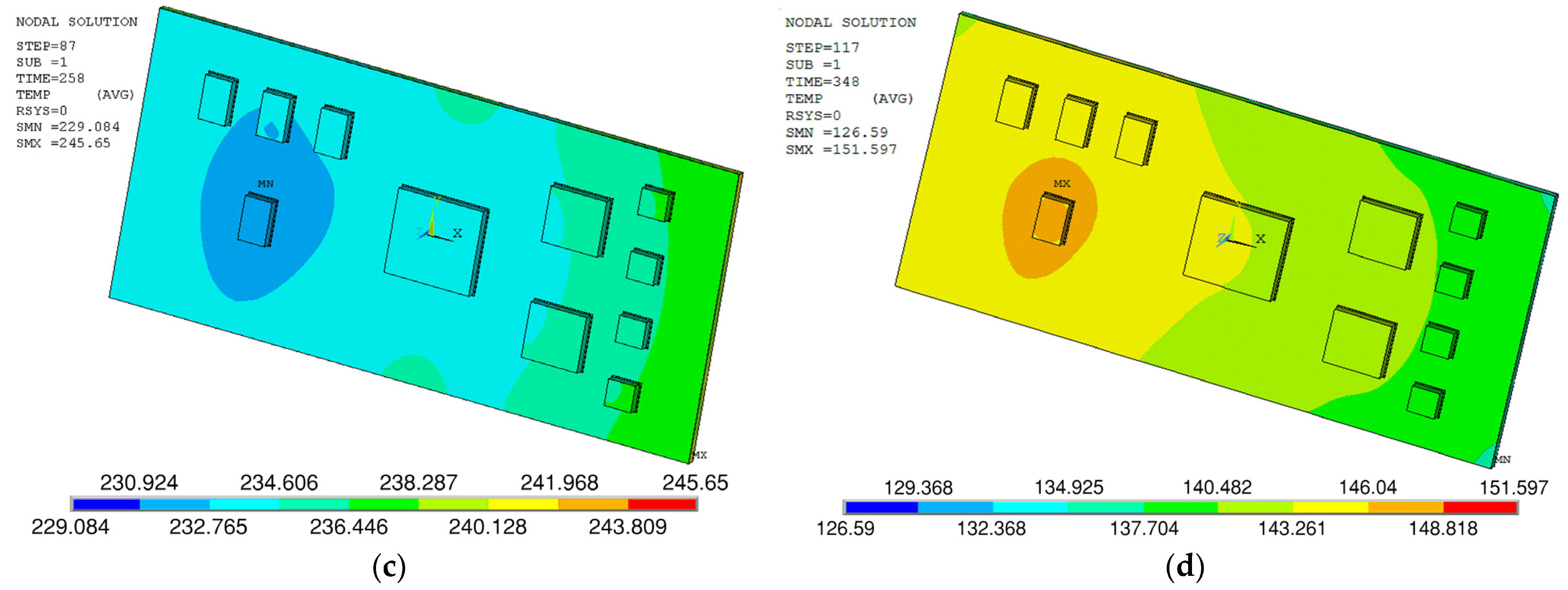
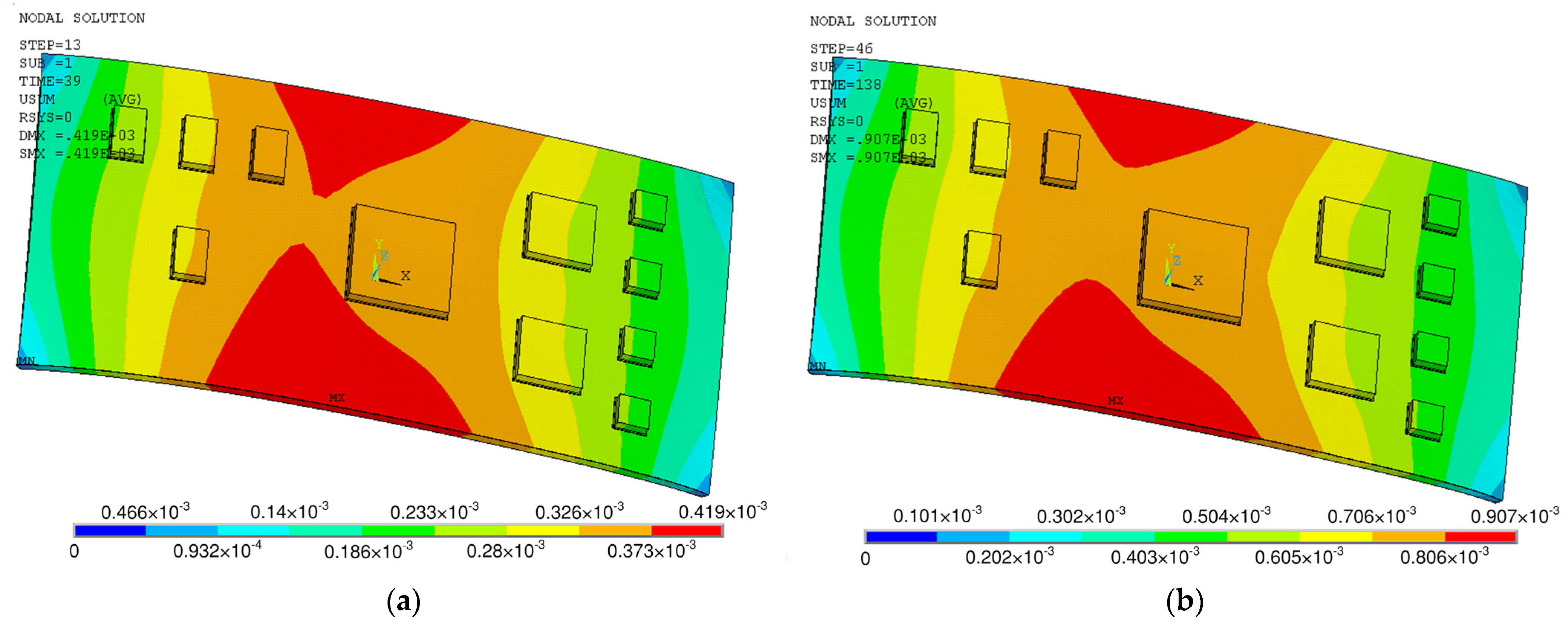
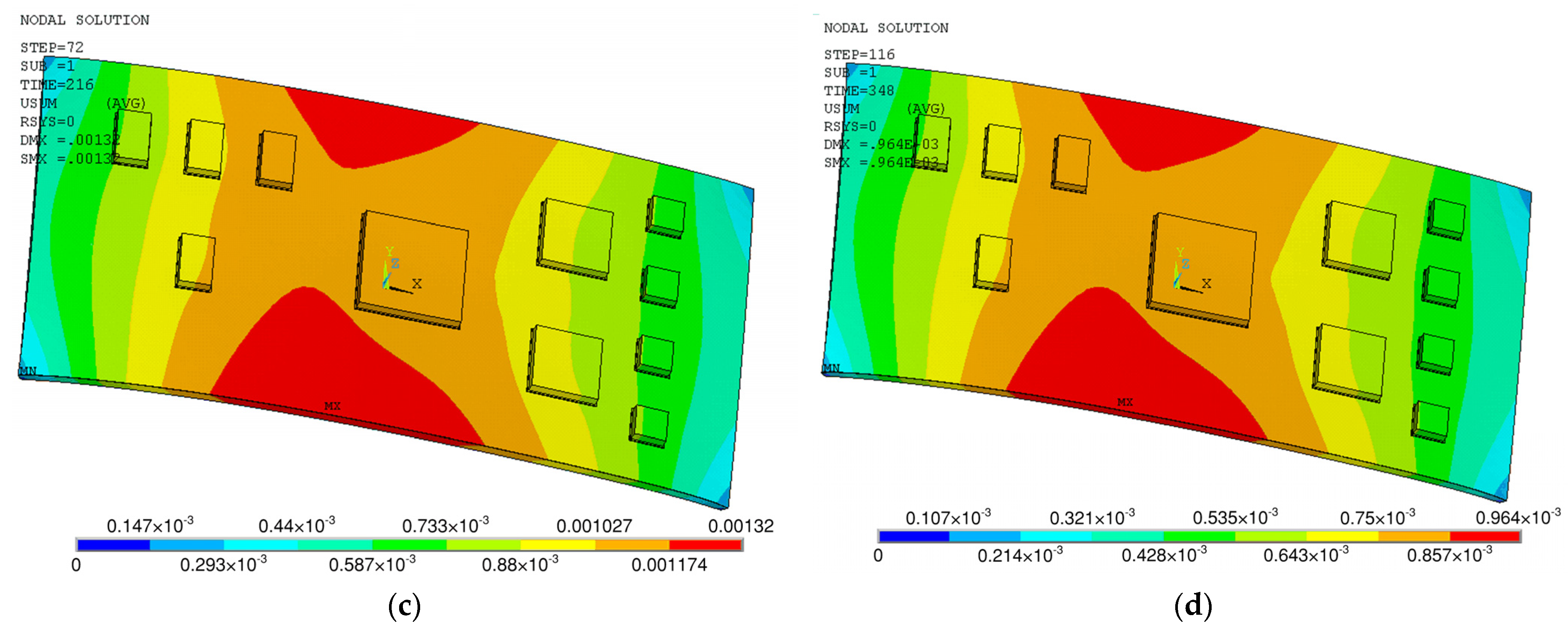
2.2.2. Discussion
2.2.3. Calculation of the Warpage Percentage for the PCB Assembly
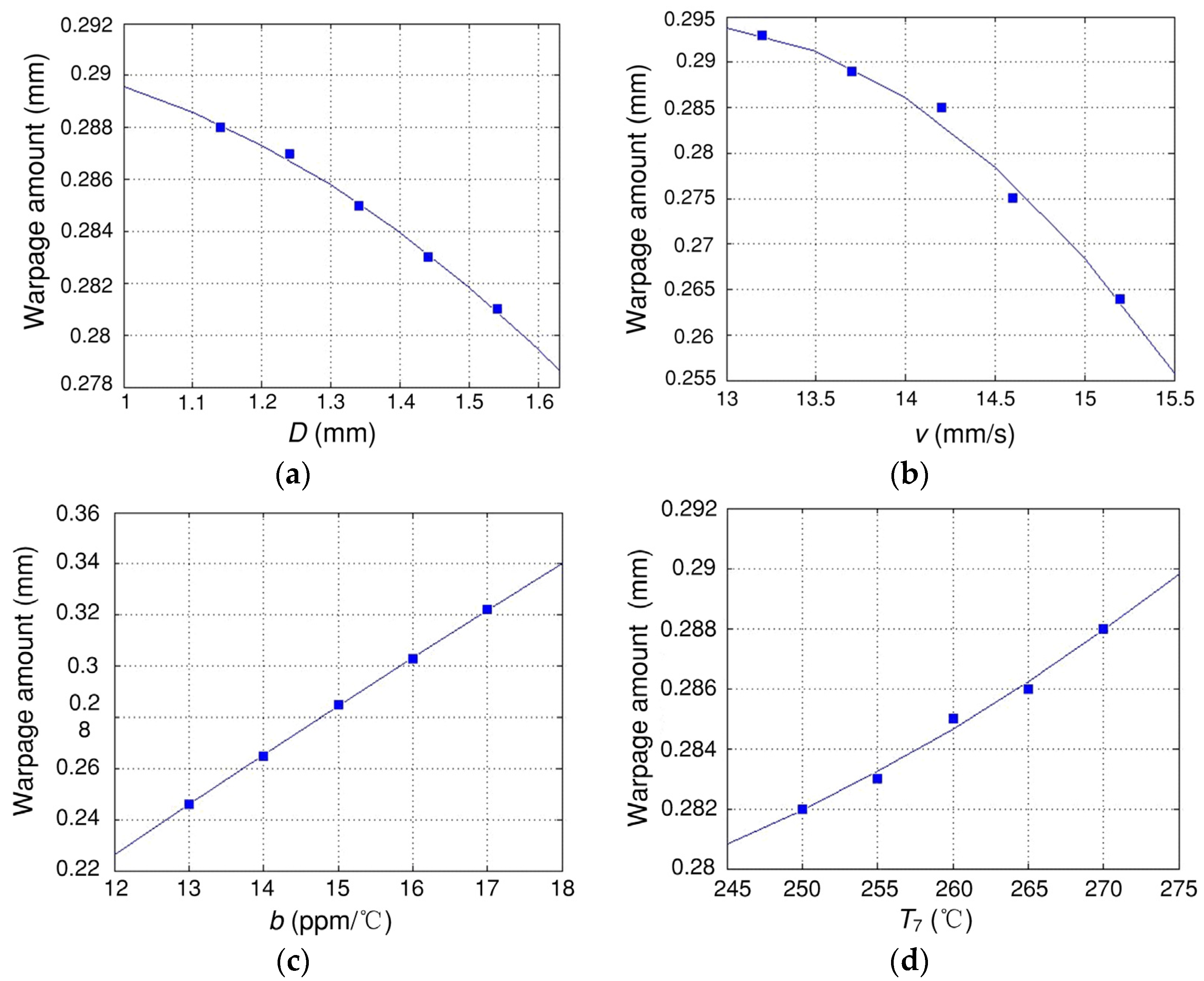
2.2.4. Analysis of the Factors Affecting Warpage
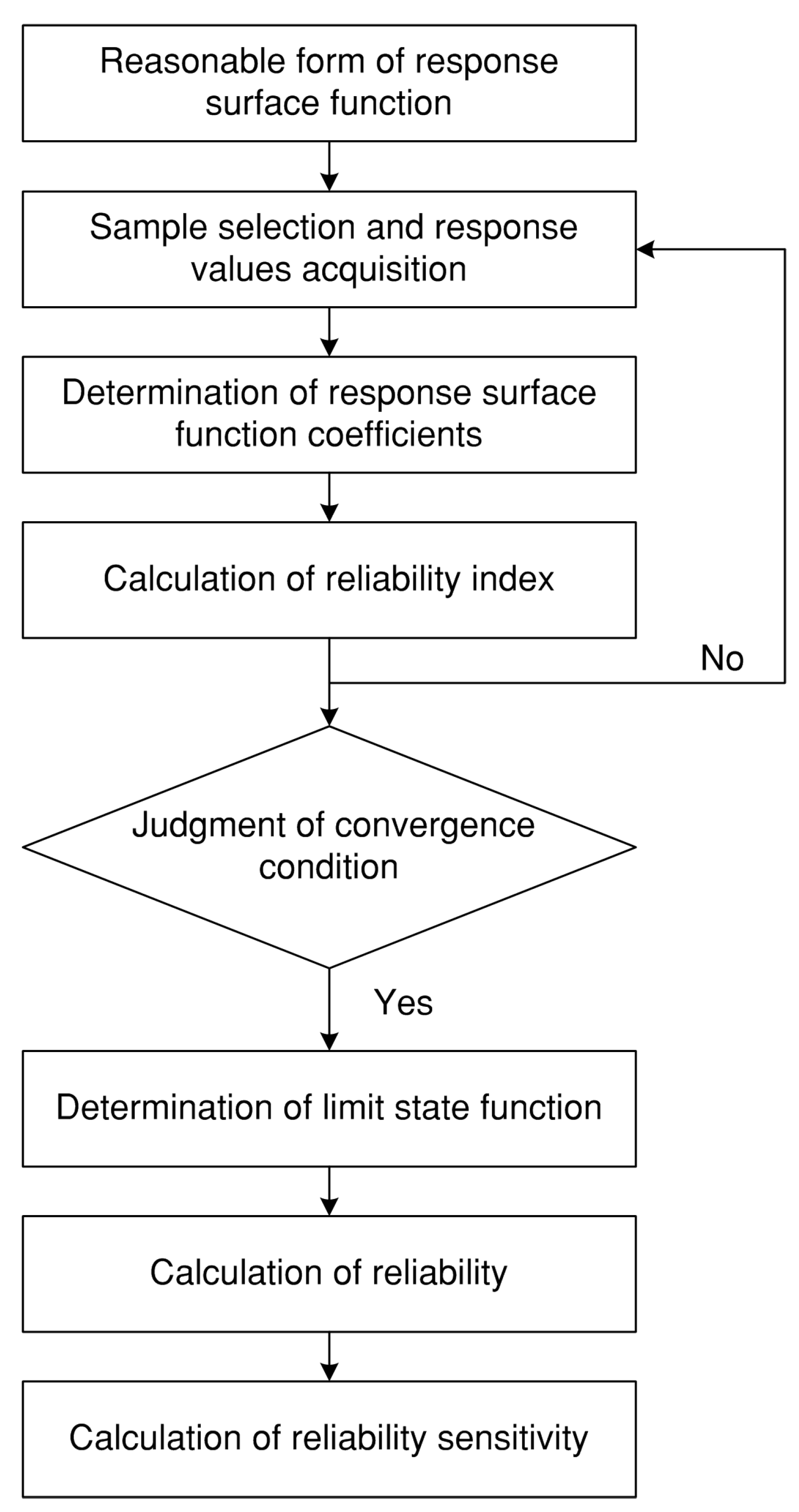
3. Reliability Sensitivity of the PCB Assembly concerning Warpage
3.1. Limit State Function Based on the RSM
3.2. Reliability Calculation
3.3. Calculation of Reliability Sensitivity
3.4. Case Study
4. Conclusions
- (1)
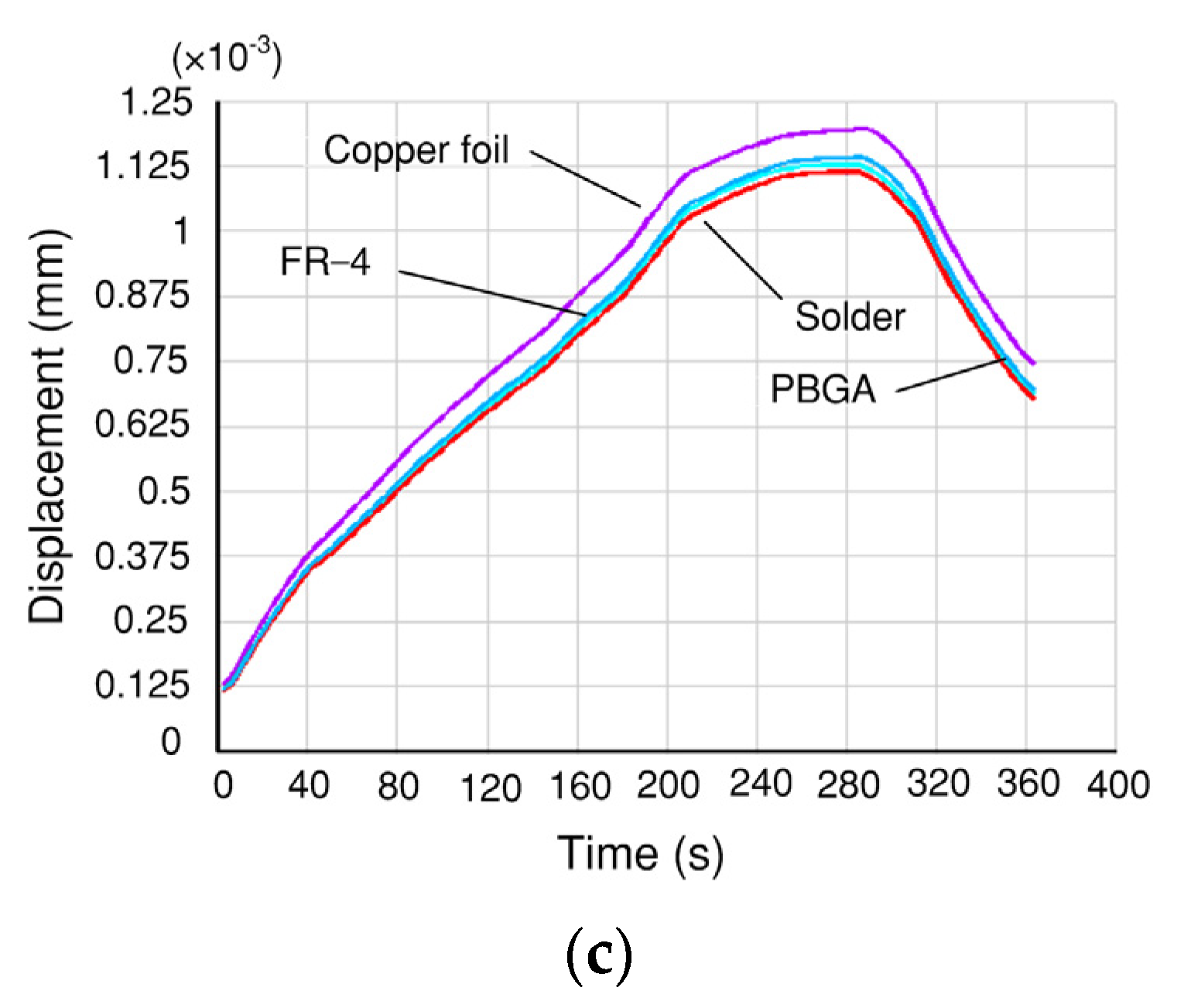
- The coupled thermal-mechanical FEM was applied to simulating the temperature change and warpage process during the reflow soldering on the PCB assembly. The results showed that the warpage had a similar trend to that of the temperature change. Specifically, the amount of warpage increased nonlinearly with the increase of PCB assembly temperature. There was a significant rise in the warpage rate with the increasing heating rate;
- (2)
- By means of the limit state function, the reliability on the PCB assembly concerning warpage with the influence of multiple factor random errors was 0.9907. The calculation method can provide a theoretical guidance for the limitation of the allowable error range of the material properties, the geometric dimensions and the process parameters, which are beneficial to reduce the possibility of warpage failure on the PCB assembly during the reflow soldering process;
- (3)
- The reliability sensitivity analysis of the PCB assembly showed that the mean and variance of each parameter had varying degrees of influence on the reliability. The reliability improved as the mean of PCB thickness and conveyor belt speed increased while it decreased as the mean of the CTE of the PCB and the temperature in the 7th oven zone increased. Among others, the PCB thickness had the greatest impact on reliability. Meanwhile, an increase in the variance of all parameters reduced the reliability.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lau, C.S.; Khor, C.Y.; Soares, D.; Teixeira, F.C.; Abdullah, M.Z. Thermo-mechanical challenges of reflowed lead-free solder joints in surface mount components: A review. Solder. Surf. Mt. Technol. 2016, 28, 41–62. [Google Scholar] [CrossRef]
- Chen, L.M.; Li, E.Y.; Wang, H. Time-based reflow soldering optimization by using adaptive Kriging-HDMR method. Solder. Surf. Mt. Technol. 2016, 28, 101–113. [Google Scholar] [CrossRef]
- Geczy, A.; Fejos, M.; Tersztyanszky, L.; Kemler, A.; Szabo, A. Investigating printed circuit board shrinkage during reflow soldering. In Proceedings of the 37th International Spring Seminar on Electronics Technology 2014, Dresden, Germany, 7–11 May 2014; pp. 219–224. [Google Scholar] [CrossRef]
- Geczy, A.; Fejos, M.; Tersztyanszky, L. Investigating and compensating printed circuit board shrinkage induced failures during reflow soldering. Solder. Surf. Mt. Technol. 2015, 27, 61–68. [Google Scholar] [CrossRef]
- Addagarla, A.; Prasad, N.S. Finite element analysis of flip–chip on board (FCOB) assembly during reflow soldering process. Solder. Surf. Mt. Technol. 2012, 24, 92–99. [Google Scholar] [CrossRef]
- Lau, C.S.; Tan, C.Y.; Le, C.K.; Ye, N. A numerical technique to evaluate warpage behavior of double sided rigid-flex board assemblies during reflow soldering process. In Proceedings of the 70th IEEE Electronic Components and Technology Conference, Orlando, FL, USA, 3–30 June 2020; pp. 554–560. [Google Scholar] [CrossRef]
- Kang, J.S. Parametric study of warpage in PBGA packages. Int. J. Adv. Manuf. Technol. 2020, 107, 4213–4219. [Google Scholar] [CrossRef]
- Liu, C.W.; Li, M.; Lu, J.C.; Gao, L.M. A new approach to minimize package warpage in reflow process. In Proceedings of the 18th International Conference on Electronic Packaging Technology, Harbin, China, 16–19 August 2017; pp. 988–991. [Google Scholar]
- Ding, H.; Ume, I.C.; Powell, R.E.; Hanna, C.R. Parametric study of warpage in printed wiring board assemblies. IEEE Trans. Compon. Packag. Technol. 2005, 28, 517–524. [Google Scholar] [CrossRef]
- Tan, W.; Ume, I.C. Application of lamination theory to study warpage across PWB and PWBA during convective reflow process. IEEE Trans. Compon. Pack. Manuf. Technol. 2012, 2, 217–223. [Google Scholar] [CrossRef]
- Wang, T.H.; Tsai, C.I.; Lee, C.C.; Lai, Y.S. Study of factors affecting warpage of HFCBGA subjected to reflow soldering-liked profile. Microelectron. Reliab. 2013, 53, 297–302. [Google Scholar] [CrossRef]
- Xia, W.S.; Xiao, M.; Chen, Y.H.; Wu, F.S.; Liu, Z.; Fu, H.Z. Thermal warpage analysis of PBGA mounted on PCB during reflow process by FEM and experimental measurement. Solder. Surf. Mt. Technol. 2014, 26, 162–171. [Google Scholar] [CrossRef]
- Chung, S.; Kwak, J.B. Realistic warpage evaluation of printed board assembly during reflow process. Solder. Surf. Mt. Technol. 2015, 27, 137–145. [Google Scholar] [CrossRef]
- Jafari-Asl, J.; Ohadi, S.; Ben Seghier, M.E.A.; Trung, N.-T. Accurate structural reliability analysis using an improved line-sampling-method-based slime mold algorithm. ASCE-ASME J. Risk. Uncertain. Eng. Syst. Part A-Civ. Eng. 2021, 7, 04021015. [Google Scholar] [CrossRef]
- Cornebize, T.; Legrand, A. Simulation-based optimization and sensibility analysis of MPI applications: Variability matters. J. Parallel Distrib. Comput. 2022, 166, 111–125. [Google Scholar] [CrossRef]
- Rashki, M.; Moghaddam, M.A.; Miri, M. System-level reliability sensitivity analysis by using weighted average simulation method. Qual. Reliab. Eng. Int. 2019, 35, 1826–1845. [Google Scholar] [CrossRef]
- Zhai, X.; Fei, C.W.; Zhai, Q.G.; Wang, J.J. Reliability and sensitivity analyses of HPT blade-tip radial running clearance using multiply response surface model. J. Cent. South Univ. 2014, 21, 4368–4377. [Google Scholar] [CrossRef]
- Guo, W.; Cui, W.M.; Yu, T.X.; Song, B.F. The reliability and sensibility analysis for an aircraft lock mechanism based on the surrogate models. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Houston, TX, USA, 13–19 November 2015; Volume 14, pp. 1–9. [Google Scholar] [CrossRef]
- Zhang, T.X.; Zhang, Y.M. A new model for reliability design and reliability sensitivity analysis of a hydraulic piston pump. Proc. Inst. Mech. Eng. Part O-J. Risk Reliab. 2017, 231, 11–24. [Google Scholar] [CrossRef]
- Lu, C.; Feng, Y.W.; Liem, R.P.; Fei, C.W. Improved Kriging with extremum response surface method for structural dynamic reliability and sensitivity analyses. Aerosp. Sci. Technol. 2018, 76, 164–175. [Google Scholar] [CrossRef]
- Maizia, A.; Hocine, A.; Dehmous, H.; Chapelle, D. Prediction of reliability analysis of composite tubular structure under hygro-thermo-mechanical loading. Mech. Adv. Mater. Struct. 2019, 26, 372–379. [Google Scholar] [CrossRef]
- Rad, M.J.G.; Ohadi, S.; Jafari-Asl, J.; Vatani, A.; Ahmadabadi, S.A.; Correia, J.A.F.O. GNDO-SVR: An efficient surrogate modeling approach for reliability-based design optimization of concrete dams. Structures 2022, 35, 722–733. [Google Scholar] [CrossRef]
- Illes, B. Measuring heat transfer coefficient in convection reflow ovens. Measurement 2010, 43, 1134–1141. [Google Scholar] [CrossRef]
- Xu, Y.Z.; Liu, Y.; Zhang, L. Effects of the solder phase transformation on the optimization of reflow soldering parameters and temperature profiles. Discrete Dyn. Nat. Soc. 2021, 2021, 9955967. [Google Scholar] [CrossRef]
- Srivalli, C.; Abdullah, M.Z.; Khor, C.Y. Numerical investigations on the effects of different cooling periods in reflow-soldering process. Heat Mass Transf. 2015, 51, 1413–1423. [Google Scholar] [CrossRef]
- Lei, Q.Y.; Zhang, Z.Y.; Zhuo, S.Y.; Lin, K.J. Research on furnace temperature curve based on heat convection and heat radiation. In Proceedings of the 2nd International Academic Exchange Conference on Science and Technology Innovation, Guangzhou, China, 18–20 December 2020; Volume 233, p. 04004. [Google Scholar] [CrossRef]
- Ma, G.; Huang, X.Q.; Liu, S.H. Heat transfer modeling and oven temperature curve optimization of integrated circuit board reflow soldering. IEEE Access 2021, 9, 141876–141889. [Google Scholar] [CrossRef]
- IPC-A-600G; Acceptability of Printed Boards. The Institute for Interconnecting and Packaging Electronic Circuits: Bannockburn, IL, USA, 2004.
- IPC-TM-650; Test Methods Manual. The Institute for Interconnecting and Packaging Electronic Circuits: Northbrook, IL, USA, 2020.
- Aziz, M.S.A.; Abdullah, M.Z.; Khor, C.Y.; Azid, I.A.; Jalar, A.; Ani, F.C. Influence of printed circuit board thickness in wave soldering. Sci. Iran. 2017, 24, 2963–2976. [Google Scholar] [CrossRef]
- Li, X.L.; Chen, G.H.; Cui, H.C.; Yang, D.X. Direct probability integral method for static and dynamic reliability analysis of structures with complicated performance functions. Comput. Meth. Appl. Mech. Eng. 2021, 374, 113583. [Google Scholar] [CrossRef]
- Li, P.; Li, H.Y.; Huang, Y.B.; Wang, K.F.; Xia, N. Quasi-sparse response surface constructing accurately and robustly for efficient simulation based optimization. Adv. Eng. Softw. 2017, 114, 325–336. [Google Scholar] [CrossRef]
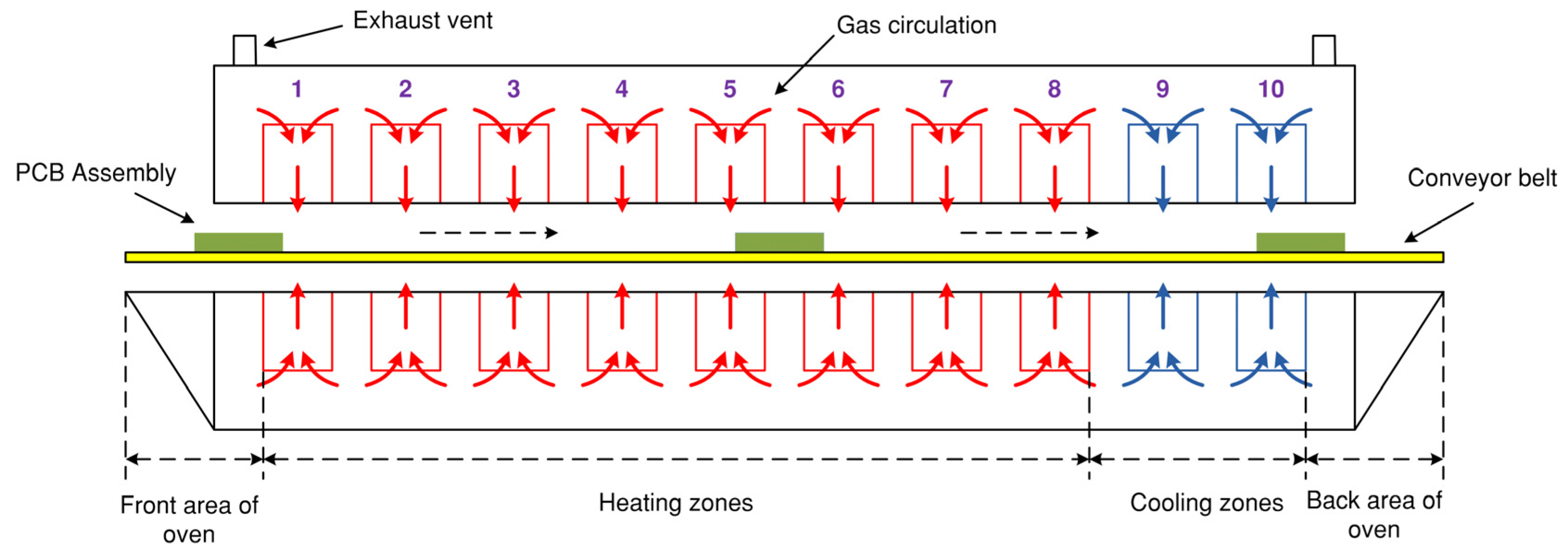
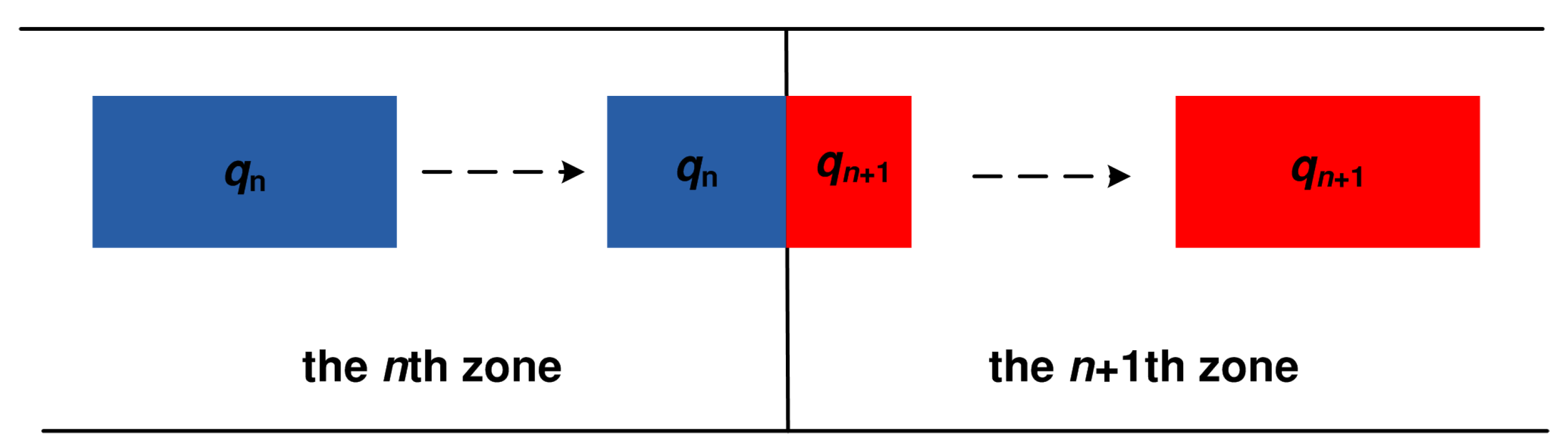


| Part | Material | Size (mm) | Quantity |
|---|---|---|---|
| PCB | FR-4 | 100 × 65 × 1.34 | 1 |
| Copper foil | 100 × 65 × 0.07 | 1 | |
| Solder | Sn-Ag-Cu | 5.5 × 5.5 × 0.15 | 4 |
| 5.5 × 8.5 × 0.15 | 4 | ||
| 10.5 × 10.5 × 0.15 | 2 | ||
| 15.5 × 15.5 × 0.15 | 1 | ||
| Component | Si | 5 × 5 × 1.5 | 4 |
| 5 × 8 × 1.5 | 4 | ||
| PBGA | 10 × 10 × 1.5 | 2 | |
| 15 × 15 × 1.5 | 1 |
| Material | Density (kg/m3) | Specific Heat (J/kg·K) | Thermal Conductivity (W/m·K) | Elastic Modulus (Gpa) | Poisson Ratio | CTE (ppm/°C) |
|---|---|---|---|---|---|---|
| FR-4 | 1820 | 840 | 0.29 | 30 °C: 22.4 95 °C: 20.68 150 °C: 17.92 | 0.39 | 27 °C: 13.62 37 °C: 14.19 47 °C: 14.77 57 °C: 16.38 130 °C: 31.62 220 °C: 73.6 |
| Copper foil | 8893 | 265.47 + 0.31T | 469.95 + 0.1761T | 76 | 0.35 | 17 |
| Solder | 7400 | 301 | 33 | 60.73 − 0.06T | 0.36 | 23.9 + 0.02 T |
| Silicon die | 2330 | 27 °C: 713 127 °C: 785 227 °C: 832 | 27 °C: 156 127 °C: 105 227 °C: 80 | 167 | 0.3 | 25 °C: 2.6 100 °C: 3.1 225 °C: 3.6 |
| BT substrate | 3000 | 1570 | 65 | 17.8 | 0.15 | <215 °C: 35.0 >215 °C: 140 |
| Zone | Preheating Zone | Soaking Zone | Reflow Zone | Cooling Zone | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| T1 | T2 | T3 | T4 | T5 | T6 | T7 | T8 | T9 | T10 | |
| Temperature (°C) | 160 | 165 | 180 | 185 | 205 | 240 | 260 | 230 | 60 | 20 |
| Variable | v (mm/s) | T7 (°C) | D (mm) | b (ppm/°C) |
|---|---|---|---|---|
| Mean | 14.2 | 260 | 1.34 | 15 |
| Standard deviation | 0.2 | 5 | 0.05 | 0.5 |
| No. | v (mm/s) | T7 (°C) | D (mm) | b (ppm/°C) | l (mm) | ||||
|---|---|---|---|---|---|---|---|---|---|
| Level | Value | Level | Value | Level | Value | Level | Value | ||
| 1 | p2 | 14.2 | p2 | 260 | p2 | 1.34 | p2 | 15 | 0.285 |
| 2 | p1 | 13.734 | p1 | 248.35 | p2 | 1.34 | p2 | 15 | 0.297 |
| 3 | p3 | 14.666 | p1 | 248.35 | p2 | 1.34 | p2 | 15 | 0.269 |
| 4 | p1 | 13.734 | p3 | 271.65 | p2 | 1.34 | p2 | 15 | 0.292 |
| 5 | p3 | 14.666 | p3 | 271.65 | p2 | 1.34 | p2 | 15 | 0.274 |
| 6 | p2 | 14.2 | p2 | 260 | p1 | 1.22 | p1 | 13.835 | 0.265 |
| 7 | p2 | 14.2 | p2 | 260 | p3 | 1.46 | p1 | 13.835 | 0.261 |
| 8 | p2 | 14.2 | p2 | 260 | p1 | 1.22 | p3 | 16.165 | 0.310 |
| 9 | p2 | 14.2 | p2 | 260 | p3 | 1.46 | p3 | 16.165 | 0.305 |
| 10 | p1 | 13.734 | p2 | 260 | p2 | 1.34 | p1 | 13.835 | 0.267 |
| 11 | p3 | 14.666 | p2 | 260 | p2 | 1.34 | p1 | 13.835 | 0.251 |
| 12 | p1 | 13.734 | p2 | 260 | p2 | 1.34 | p3 | 16.165 | 0.312 |
| 13 | p3 | 14.666 | p2 | 260 | p2 | 1.34 | p3 | 16.165 | 0.293 |
| 14 | p2 | 14.2 | p1 | 248.35 | p1 | 1.22 | p2 | 15 | 0.285 |
| 15 | p2 | 14.2 | p3 | 271.65 | p1 | 1.22 | p2 | 15 | 0.290 |
| 16 | p2 | 14.2 | p1 | 248.35 | p3 | 1.46 | p2 | 15 | 0.280 |
| 17 | p2 | 14.2 | p3 | 271.65 | p3 | 1.46 | p2 | 15 | 0.286 |
| 18 | p1 | 13.734 | p2 | 260 | p1 | 1.22 | p2 | 15 | 0.292 |
| 19 | p3 | 14.666 | p2 | 260 | p1 | 1.22 | p2 | 15 | 0.274 |
| 20 | p1 | 13.734 | p2 | 260 | p3 | 1.46 | p2 | 15 | 0.288 |
| 21 | p3 | 14.666 | p2 | 260 | p3 | 1.46 | p2 | 15 | 0.271 |
| 22 | p2 | 14.2 | p1 | 248.35 | p2 | 1.34 | p1 | 13.835 | 0.250 |
| 23 | p2 | 14.2 | p3 | 271.65 | p2 | 1.34 | p1 | 13.835 | 0.265 |
| 24 | p2 | 14.2 | p1 | 248.35 | p2 | 1.34 | p3 | 16.165 | 0.294 |
| 25 | p2 | 14.2 | p3 | 271.65 | p2 | 1.34 | p3 | 16.165 | 0.310 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Liu, M.; Yin, M.; Yan, Y. Reliability Sensibility Analysis of the PCB Assembly concerning Warpage during the Reflow Soldering Process. Mathematics 2022, 10, 3055. https://doi.org/10.3390/math10173055
Guo Y, Liu M, Yin M, Yan Y. Reliability Sensibility Analysis of the PCB Assembly concerning Warpage during the Reflow Soldering Process. Mathematics. 2022; 10(17):3055. https://doi.org/10.3390/math10173055
Chicago/Turabian StyleGuo, Yu, Minghe Liu, Mingang Yin, and Yutao Yan. 2022. "Reliability Sensibility Analysis of the PCB Assembly concerning Warpage during the Reflow Soldering Process" Mathematics 10, no. 17: 3055. https://doi.org/10.3390/math10173055
APA StyleGuo, Y., Liu, M., Yin, M., & Yan, Y. (2022). Reliability Sensibility Analysis of the PCB Assembly concerning Warpage during the Reflow Soldering Process. Mathematics, 10(17), 3055. https://doi.org/10.3390/math10173055





