A Finite Element Reduced-Dimension Method for Viscoelastic Wave Equation
Abstract
:1. Introduction
2. The CNFE Algorithm
3. The RDRCNFE Algorithm of the VW Equation
3.1. Generation of POD Bases
3.2. Establishment of RDRCNFE Algorithm
3.3. The Stability and Error Estimates for the RDRCNFE Solutions
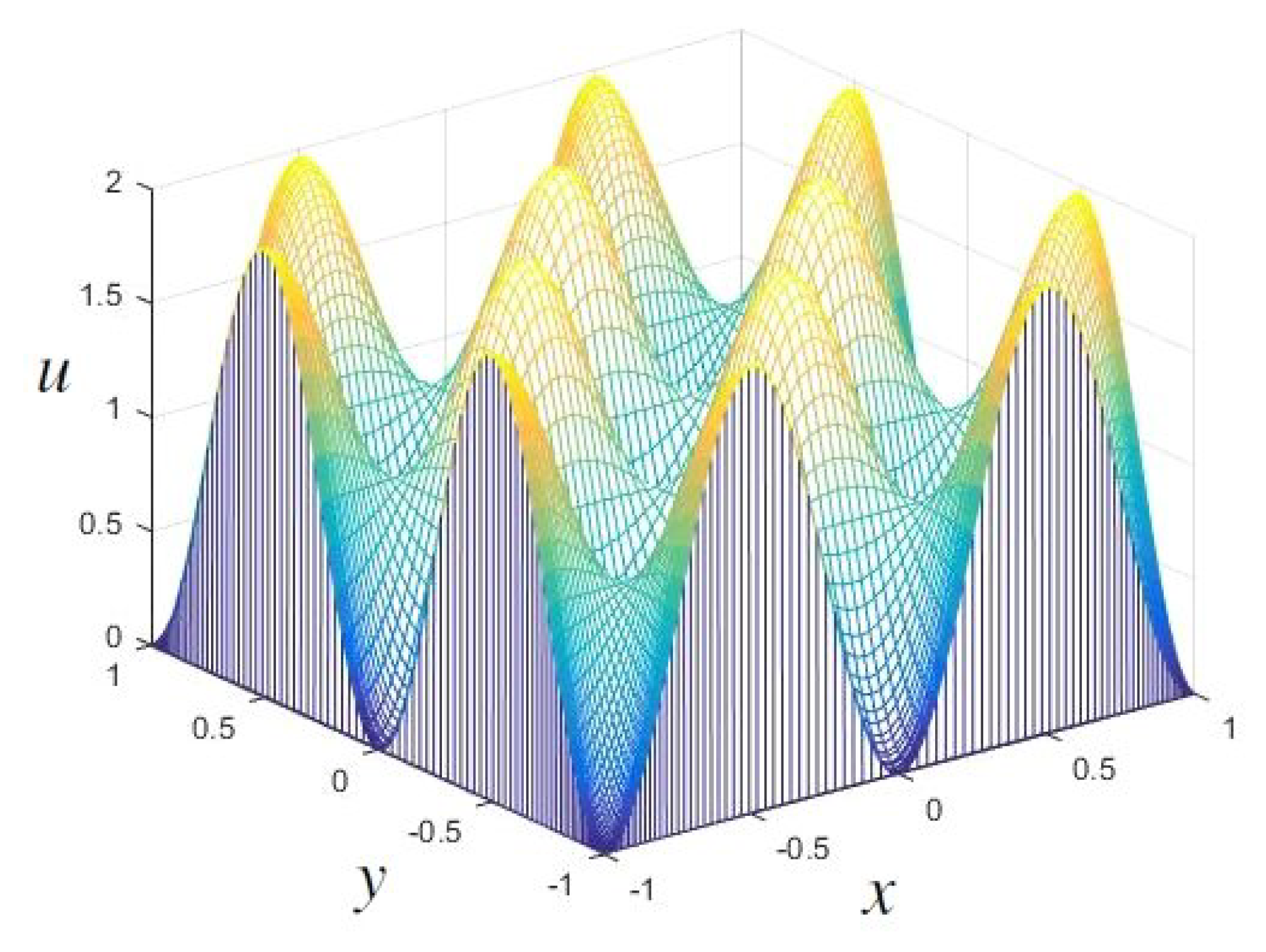
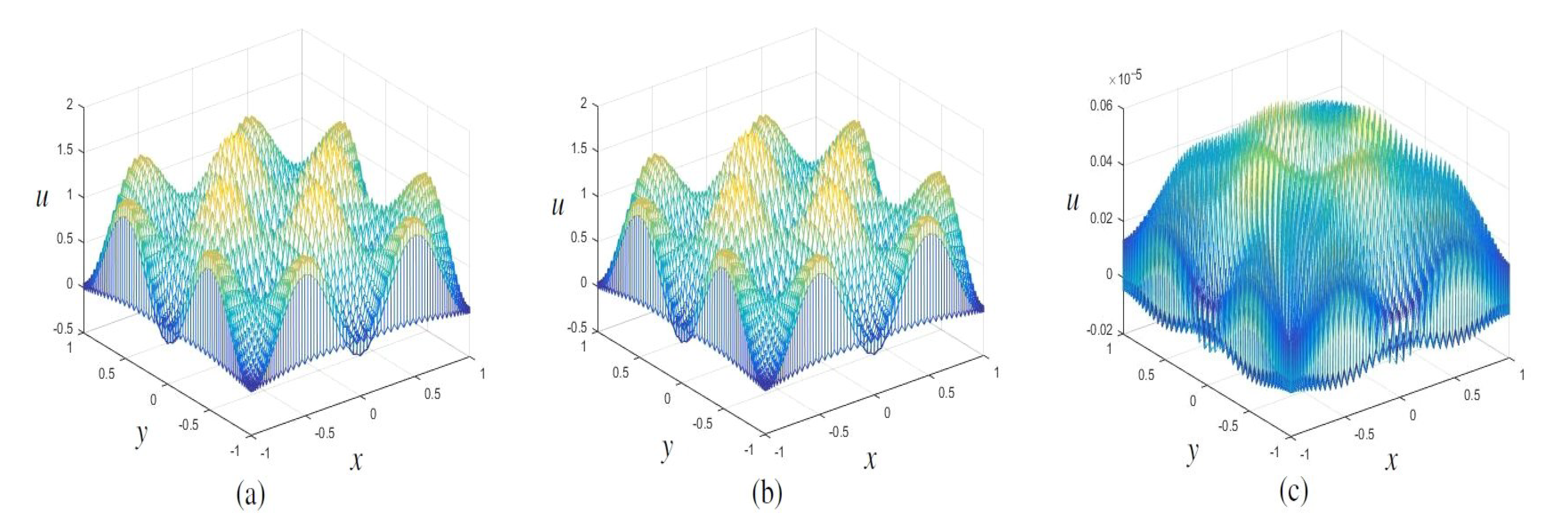
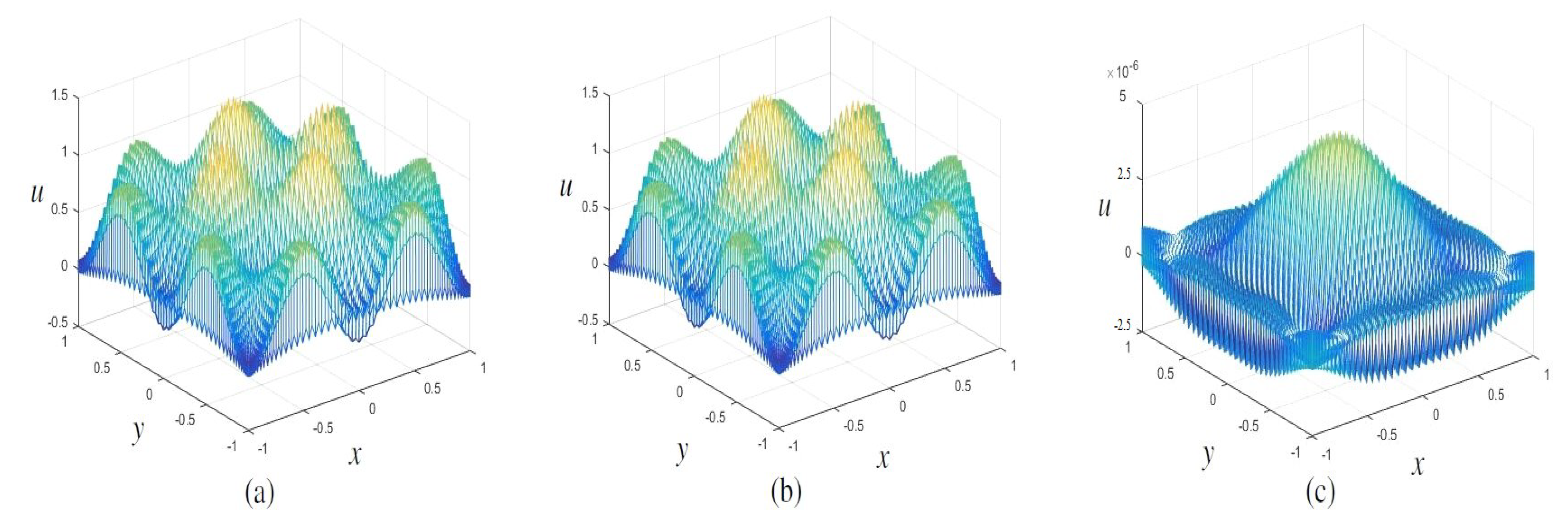
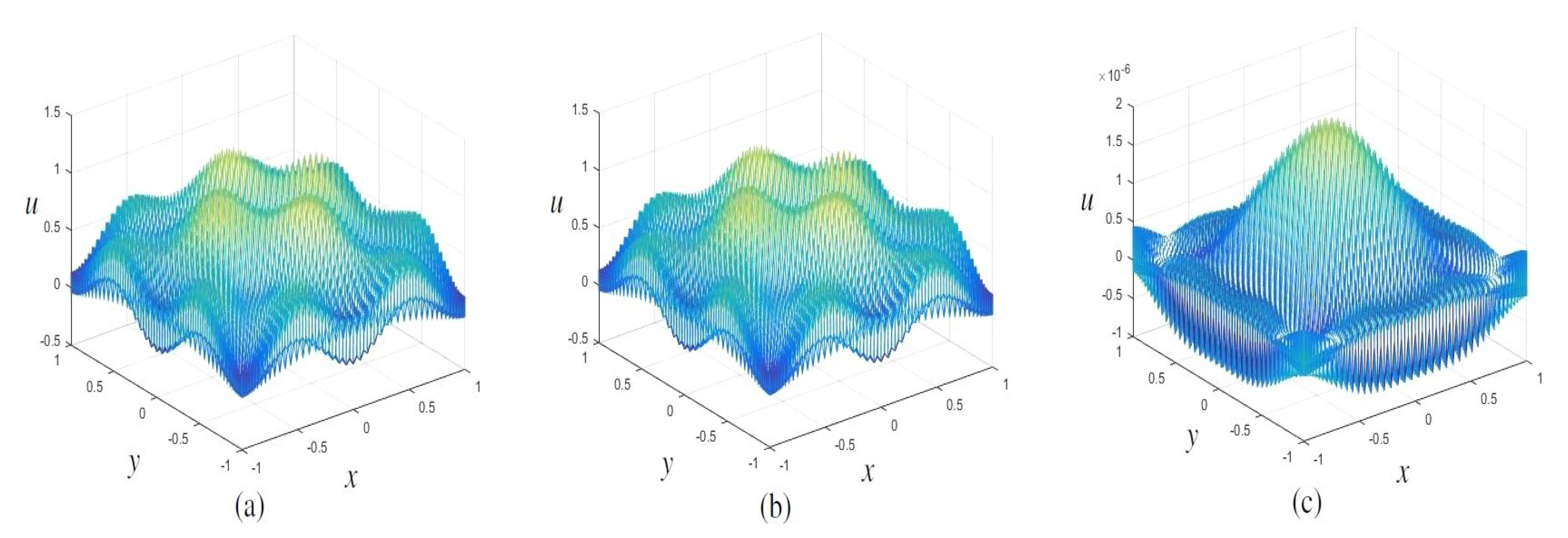
4. Some Numerical Experiments
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- de Saint-Venant, A.J.C. Théorie du mouvement non permanent des eaux, avec application auxcrues des rivers et a l’introduction des marées dans leur lit. Comptes Rendus De L’Académie Des Sci. 1871, 73, 147–154. [Google Scholar]
- Giovangigli, V.; Tran, B. Mathematical analysis of a Saint-Venant model with variable temperature. Math. Mod. Meth. Appl. Sci. 2010, 20, 1251–1297. [Google Scholar] [CrossRef]
- Li, H.; Zhao, Z.H.; Luo, Z.D. A space-time continuous finite element method for 2D viscoelastic wave equation. Bound. Value Probl. 2016, 2016, 53. [Google Scholar] [CrossRef]
- Luo, Z.D.; Chen, G. Proper Orthogonal Decomposition Methods for Partial Differential Equations; Academic Press of Elsevier: San Diego, CA, USA, 2018. [Google Scholar]
- Alekseev, A.K.; Bistrian, D.A.; Bondarev, A.E.; Navon, I.M. On linear and nonlinear aspects of dynamic mode decomposition. Int. J. Numer. Meth. Fluids 2016, 82, 348–371. [Google Scholar] [CrossRef]
- Deng, Q.X.; Luo, Z.D. A reduced-order extrapolated finite difference iterative scheme for uniform transmission line equation. Appl. Numer. Math. 2022, 172, 514–524. [Google Scholar] [CrossRef]
- Du, J.; Navon, I.M.; Zhu, J.; Fang, F.; Alekseev, A.K. Reduced order modeling based on POD of a parabolized Navier-Stokes equations model II Trust region POD 4D VAR data assimilation. Comput. Math. Appl. 2013, 65, 380–394. [Google Scholar] [CrossRef]
- Li, H.R.; Song, Z.Y. A reduced-order energy-stability-preserving finite difference iterative scheme based on POD for the Allen-Cahn equation. J. Math. Anal. Appl. 2020, 491, 124245. [Google Scholar] [CrossRef]
- Li, H.R.; Song, Z.Y. A reduced-order finite element method based on proper orthogonal decomposition for the Allen-Cahn model. J. Math. Anal. Appl. 2021, 500, 125103. [Google Scholar] [CrossRef]
- Luo, Z.D. The reduced-order extrapolating method about the Crank–Nicolson finite element solution coefficient vectors for parabolic type equation. Mathematics 2020, 8, 1261. [Google Scholar] [CrossRef]
- Luo, Z.D.; Jiang, W.R. A reduced-order extrapolated technique about the unknown coefficient vectors of solutions in the finite element method for hyperbolic type equation. Appl. Numer. Math. 2020, 158, 123–133. [Google Scholar] [CrossRef]
- Chaturantabut, S.; Sorensen, D.C. A state space error estimate for POD-DEIM nonlinear model reduction. SIAM J. Numer. Anal. 2012, 50, 46–63. [Google Scholar] [CrossRef]
- Sirovich, L. Turbulence and the dynamics of coherent structures part I–III. Quart. Appl. Math. 1987, 45, 561–590. [Google Scholar] [CrossRef]
- Song, Z.Y.; Li, H.R. Numerical simulation of the temperature field of the stadium building foundation in frozen areas based on the finite element method and proper orthogonal decomposition technique. Math. Method Appl. Sci. 2021, 44, 8528–8542. [Google Scholar] [CrossRef]
- Zhu, S.; Dede, L.; Quarteroni, A. Isogeometric analysis and proper orthogonal decomposition for parabolic problems. Numer. Math. 2017, 135, 333–370. [Google Scholar] [CrossRef]
- Kunisch, K.; Volkwein, S. Galerkin proper orthogonal decomposition methods for a general equation in fluid dynamischs. SIAM J. Numer. Anal. 2002, 40, 492–515. [Google Scholar] [CrossRef]
- Li, K.; Huang, T.Z.; Li, L.; Lanteri, S.; Xu, L.; Li, B. A Reduced-Order Discontinuous Galerkin Method Based on POD for Electromagnetic Simulation. IEEE Trans. Antennas Propag. 2018, 66, 242–254. [Google Scholar] [CrossRef]
- Luo, Z.D.; Wang, H. A highly efficient reduced-order extrapolated finite difference algorithm for time-space tempered fractional diffusion-wave equation. Appl. Math. Lett. 2020, 102, 106090. [Google Scholar] [CrossRef]
- Hinze, M.; Kunkel, M. Residual based sampling in POD model order reduction of drift-diffusion equations in parametrized electrical networks. J. Appl. Math. Mech. 2012, 92, 91–104. [Google Scholar] [CrossRef]
- Stefanescu, R.; Navon, I.M. POD/DEIM nonlinear model order reduction of an ADI implicit shallow water equations model. J. Comput. Phys. 2013, 237, 95–114. [Google Scholar] [CrossRef]
- Zokagoa, J.M.; Soulaïmani, A. A POD-based reduced-order model for free surface shallow water flows over real bathymetries for Monte-Carlo-type applications. Comput Methods Appl. Mech. Eng. 2012, 221–222, 1–23. [Google Scholar] [CrossRef]
- Baiges, J.; Codina, R.; Idelsohn, S. Explicit reduced-order models for the stabilized finite element approximation of the incompressible Navier-Stokes equations. Int. J. Numer. Methods Fluids 2013, 72, 1219–1243. [Google Scholar] [CrossRef]
- Luo, Z.D.; Jin, S.J. A reduced-order extrapolated Crank–Nicolson collocation spectral method based on POD for the 2D viscoelastic wave equations. Numer. Meth. Partial Differ. Equ. 2020, 36, 49–65. [Google Scholar] [CrossRef]
- Benner, P.; Cohen, A.; Ohlberger, M.; Willcox, A.K. Model Rduction and Approximation Theory and Algorithm; Computational Science & Engineering; SIAM: Philadelphia, PA, USA, 2017. [Google Scholar]
- Quarteroni, A.; Manzoni, A.; Negri, F. Reduced Basis Methods for Partial Differential Equations; Springer International Publishing: Manila, Philippines, 2016. [Google Scholar]
- Yang, J.; Luo, Z.D. Proper orthogonal decomposition reduced-order extrapolation continuous space-time finite element method for the two-dimensional unsteady Stokes equation. J. Math. Anal. Appl. 2019, 475, 123–138. [Google Scholar] [CrossRef]
- Zeng, Y.H.; Luo, Z.D. The reduced-dimension technique for the unknown solution coefficient vectors in the Crank–Nicolson finite element method for the Sobolev equation. J. Math. Anal. Appl. 2022, 513, 126207. [Google Scholar] [CrossRef]
- Luo, Z.D. The dimensionality reduction of Crank–Nicolson mixed finite element solution coefficient vectors for the unsteady Stokes equation. Mathematics 2022, 10, 2273. [Google Scholar] [CrossRef]
- Zhang, G.; Lin, Y. Notes on Functional Analysis; Peking University Press: Beijing, China, 1987. (In Chinese) [Google Scholar]
- Ghoreishy, M.H.R. Determination of the parameters of the Prony series in hyper-viscoelastic material models using the finite element method. Mater. Des. 2012, 35, 791–797. [Google Scholar] [CrossRef]
| t | n | CPU Runtime | CPU Runtime | ||
|---|---|---|---|---|---|
| 500 | 2.224293 | 88.897 s | 2.361843 | 2.478 s | |
| 1000 | 4.227492 | 187.957 s | 4.963873 | 3.692 s | |
| 1500 | 6.746293 | 273.375 s | 5.663234 | 4.323 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Z. A Finite Element Reduced-Dimension Method for Viscoelastic Wave Equation. Mathematics 2022, 10, 3066. https://doi.org/10.3390/math10173066
Luo Z. A Finite Element Reduced-Dimension Method for Viscoelastic Wave Equation. Mathematics. 2022; 10(17):3066. https://doi.org/10.3390/math10173066
Chicago/Turabian StyleLuo, Zhendong. 2022. "A Finite Element Reduced-Dimension Method for Viscoelastic Wave Equation" Mathematics 10, no. 17: 3066. https://doi.org/10.3390/math10173066
APA StyleLuo, Z. (2022). A Finite Element Reduced-Dimension Method for Viscoelastic Wave Equation. Mathematics, 10(17), 3066. https://doi.org/10.3390/math10173066






