Numerical Solutions of Fractional-Order Electrical RLC Circuit Equations via Three Numerical Techniques
Abstract
:1. Introduction
2. Fractional Perturbation Iteration Algorithm (FPIA)
3. Fractional Successive Differentiation Method (FSDM)
4. Fractional Novel Analytical Method (FNAM)
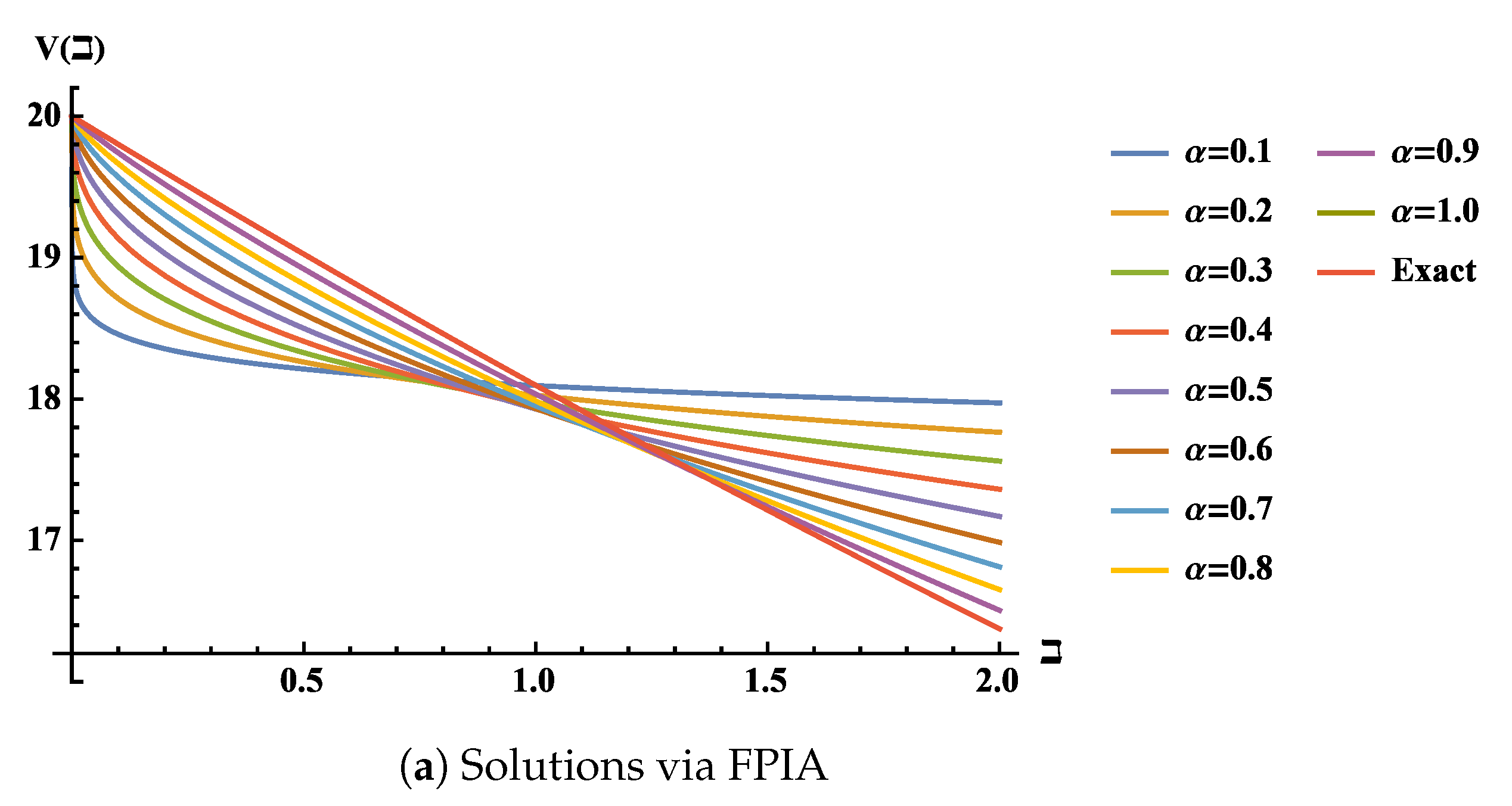
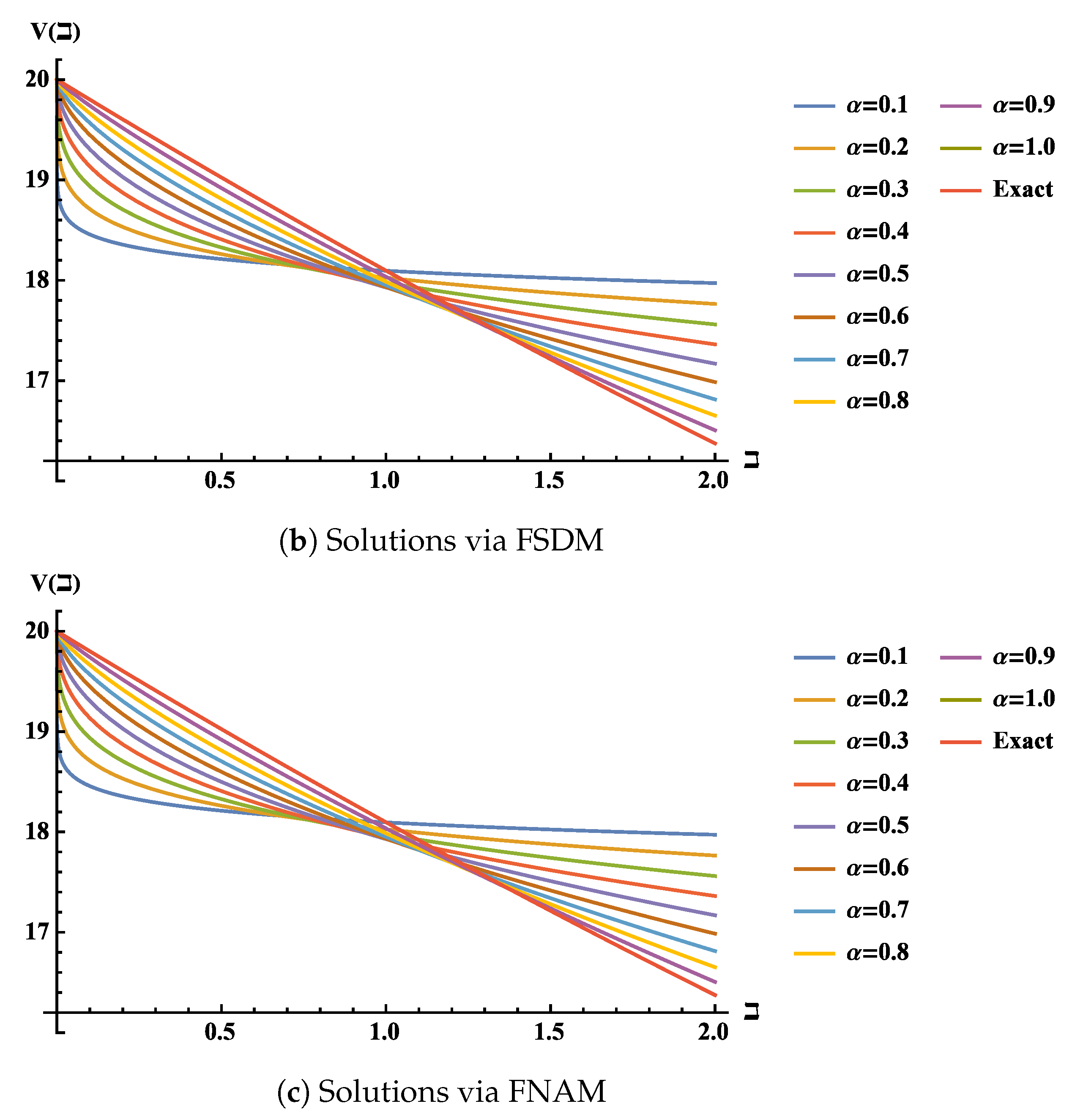
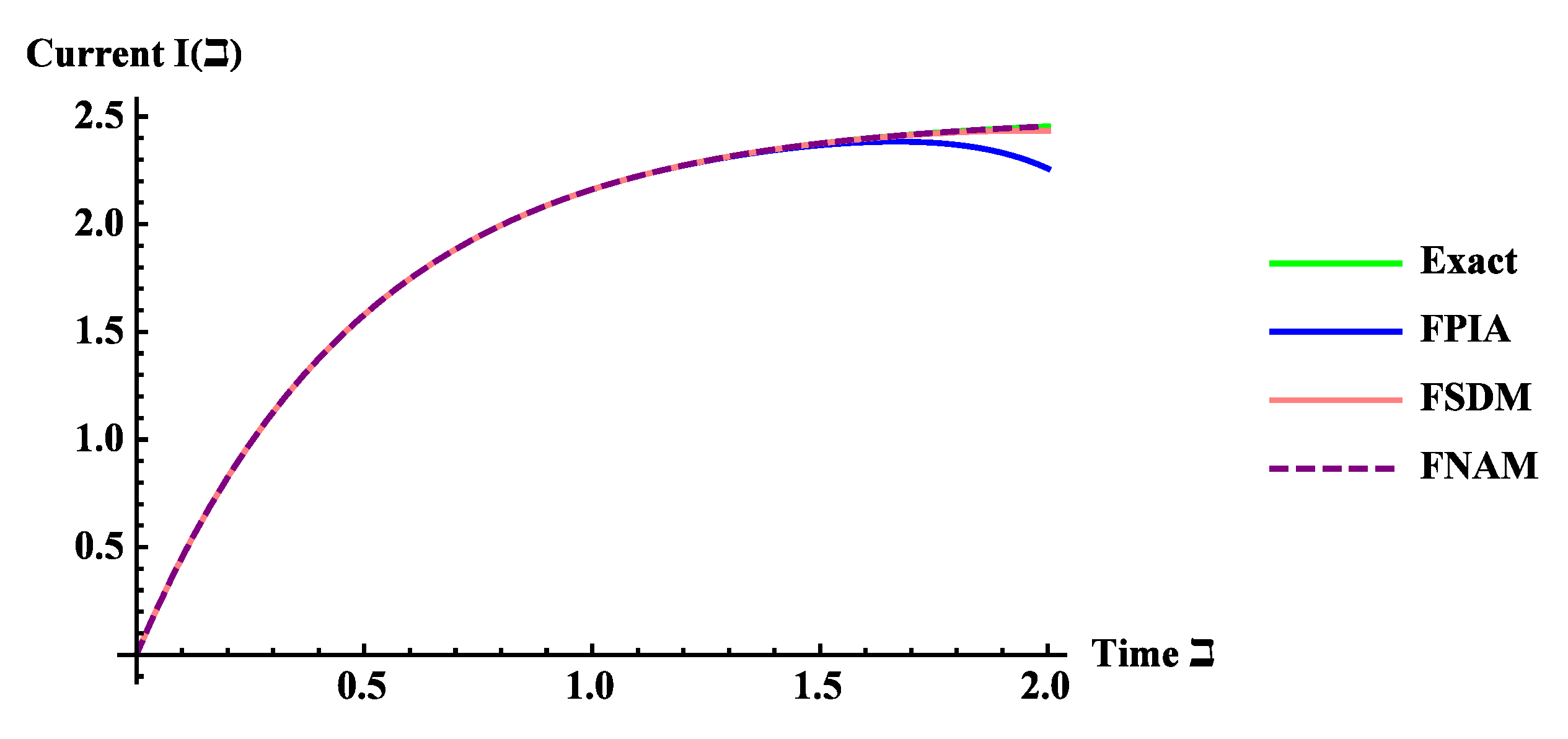
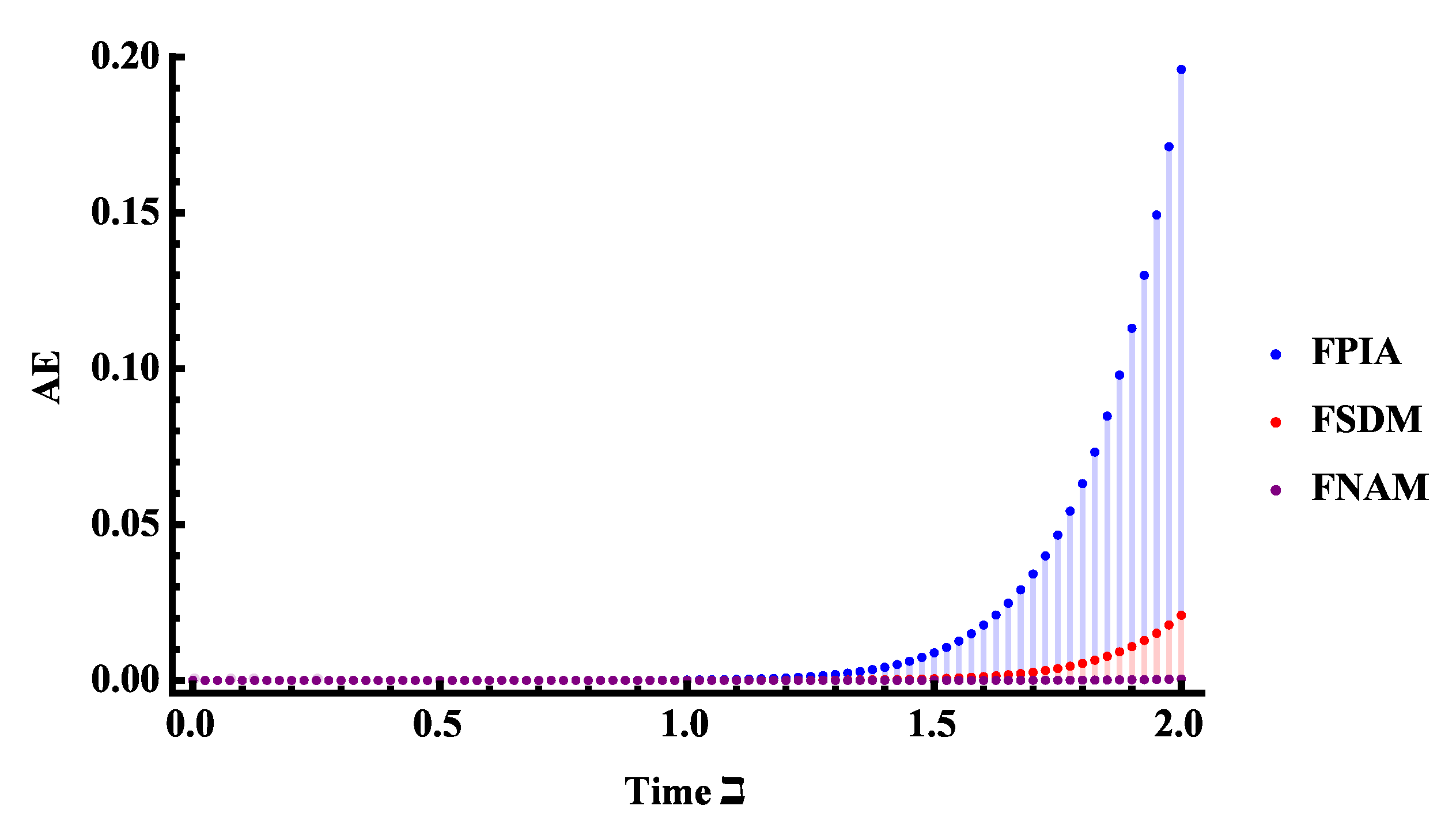
5. Application for RLC Circuits
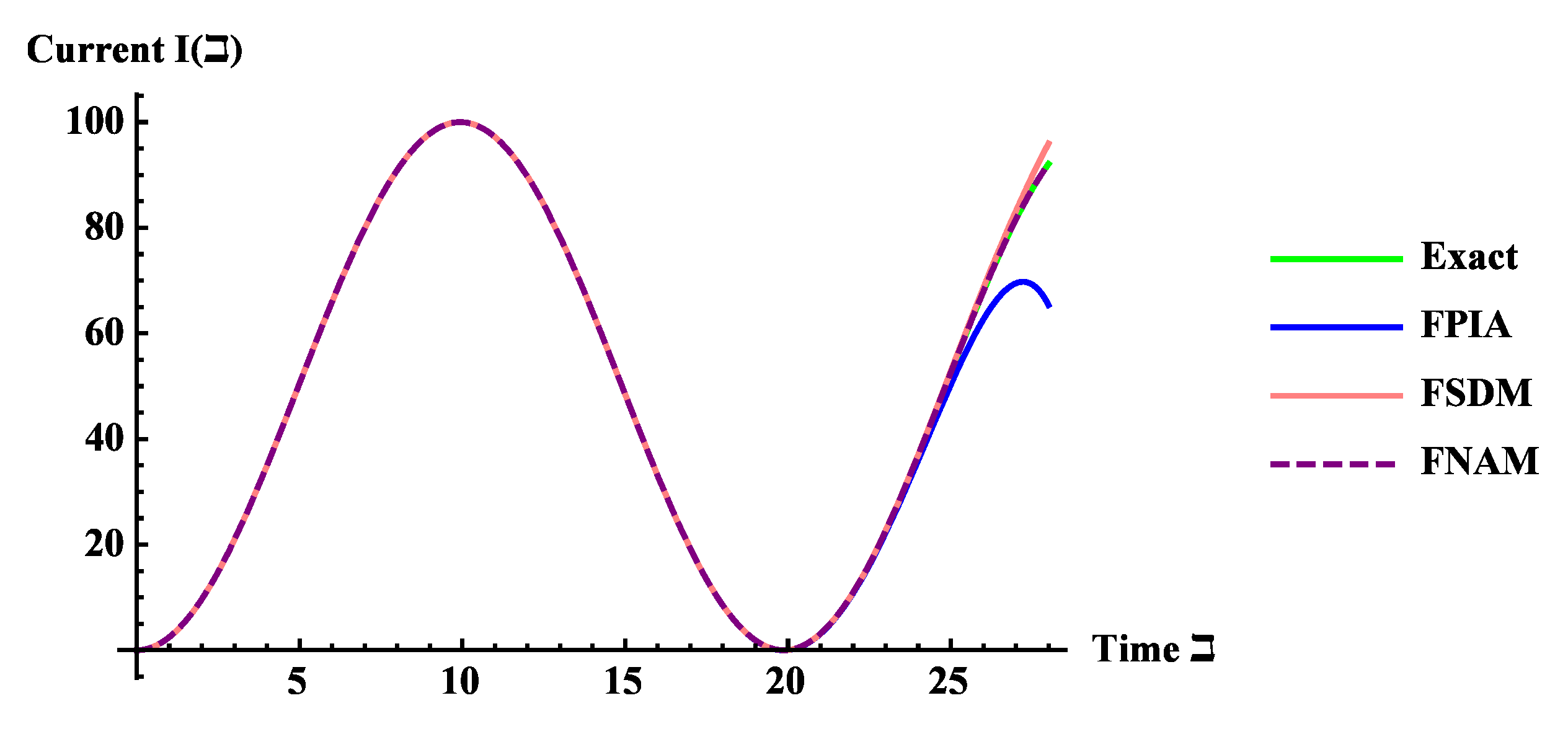
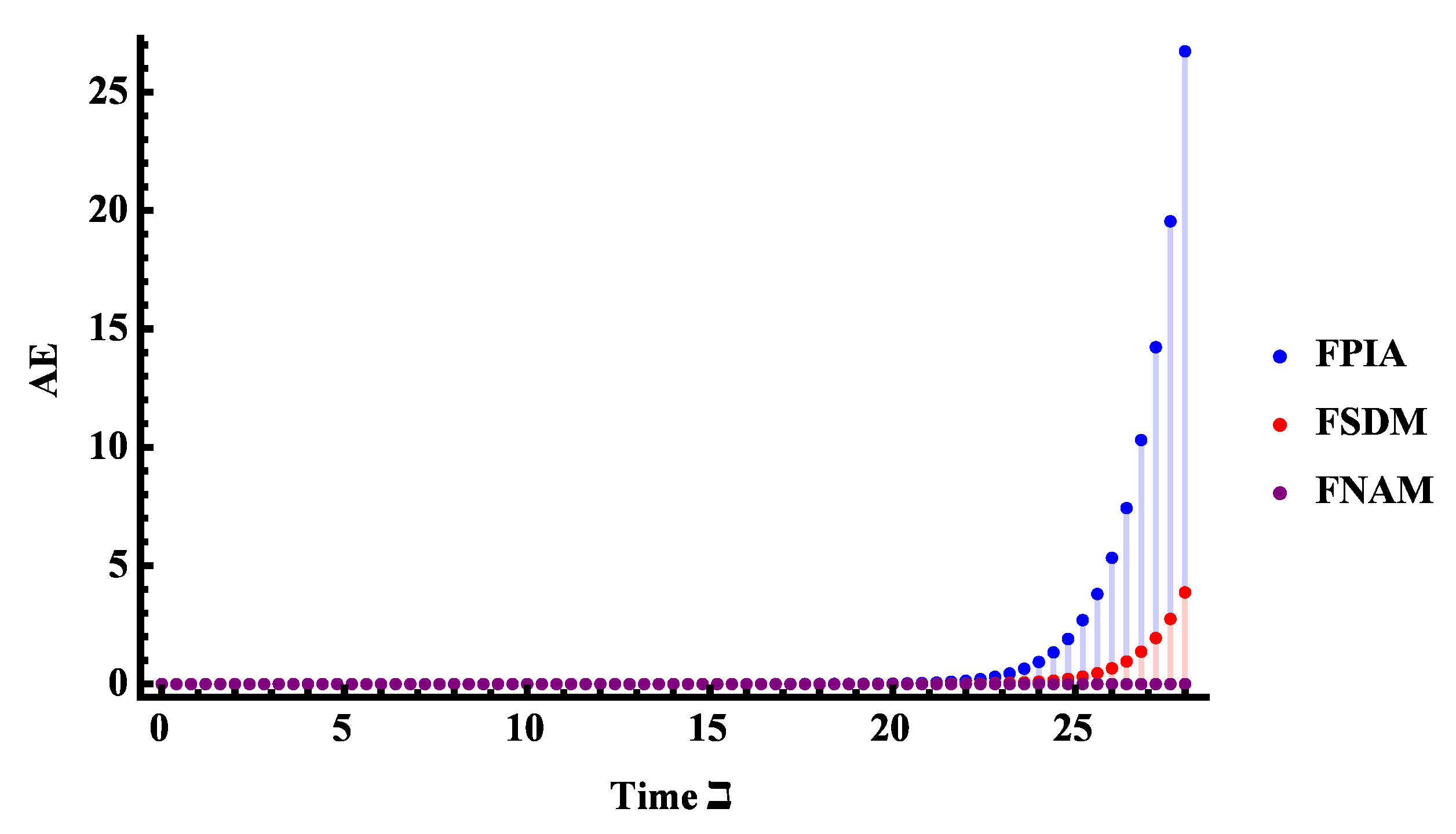
5.1. Inductor–Capacitor (LC) Circuit of Fractional Order
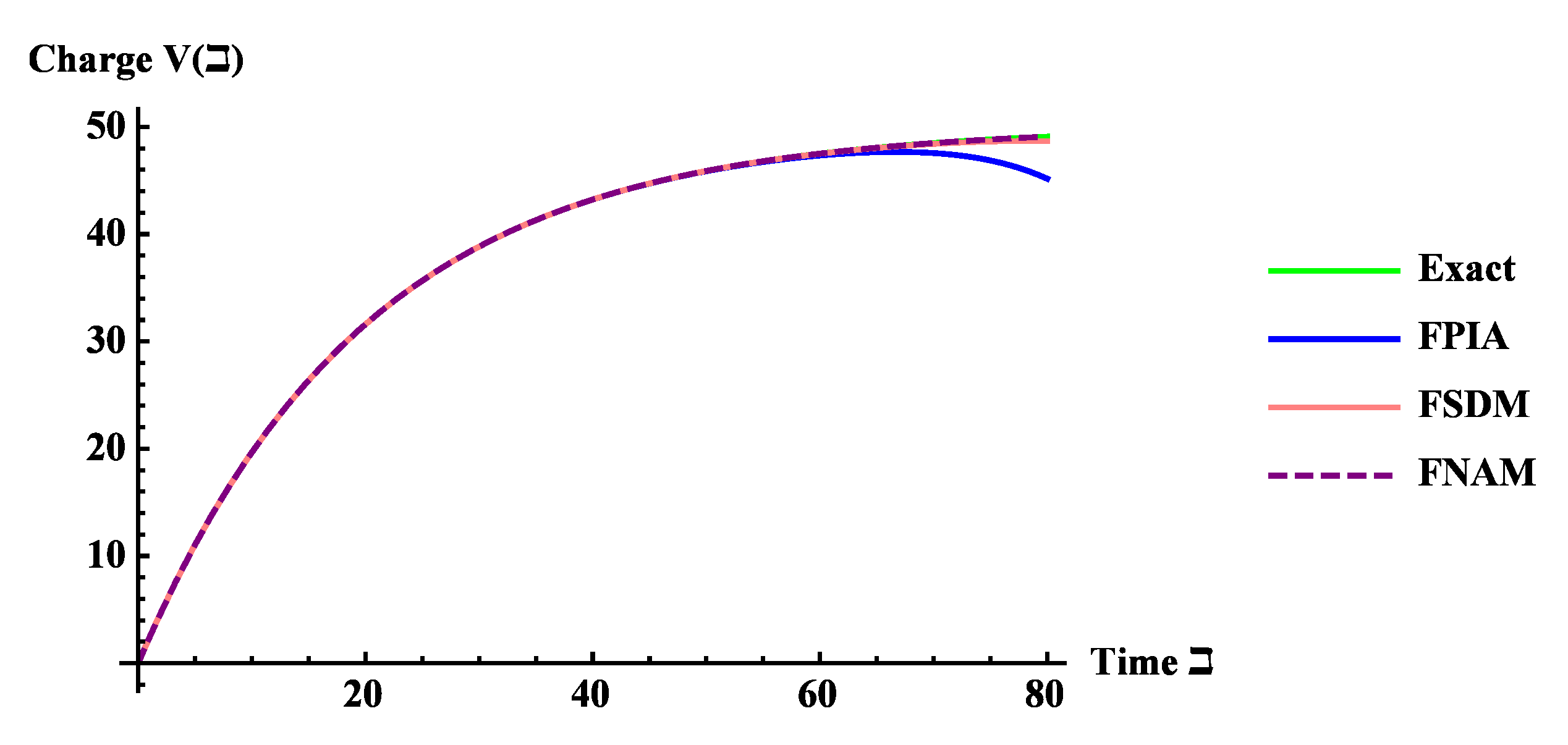
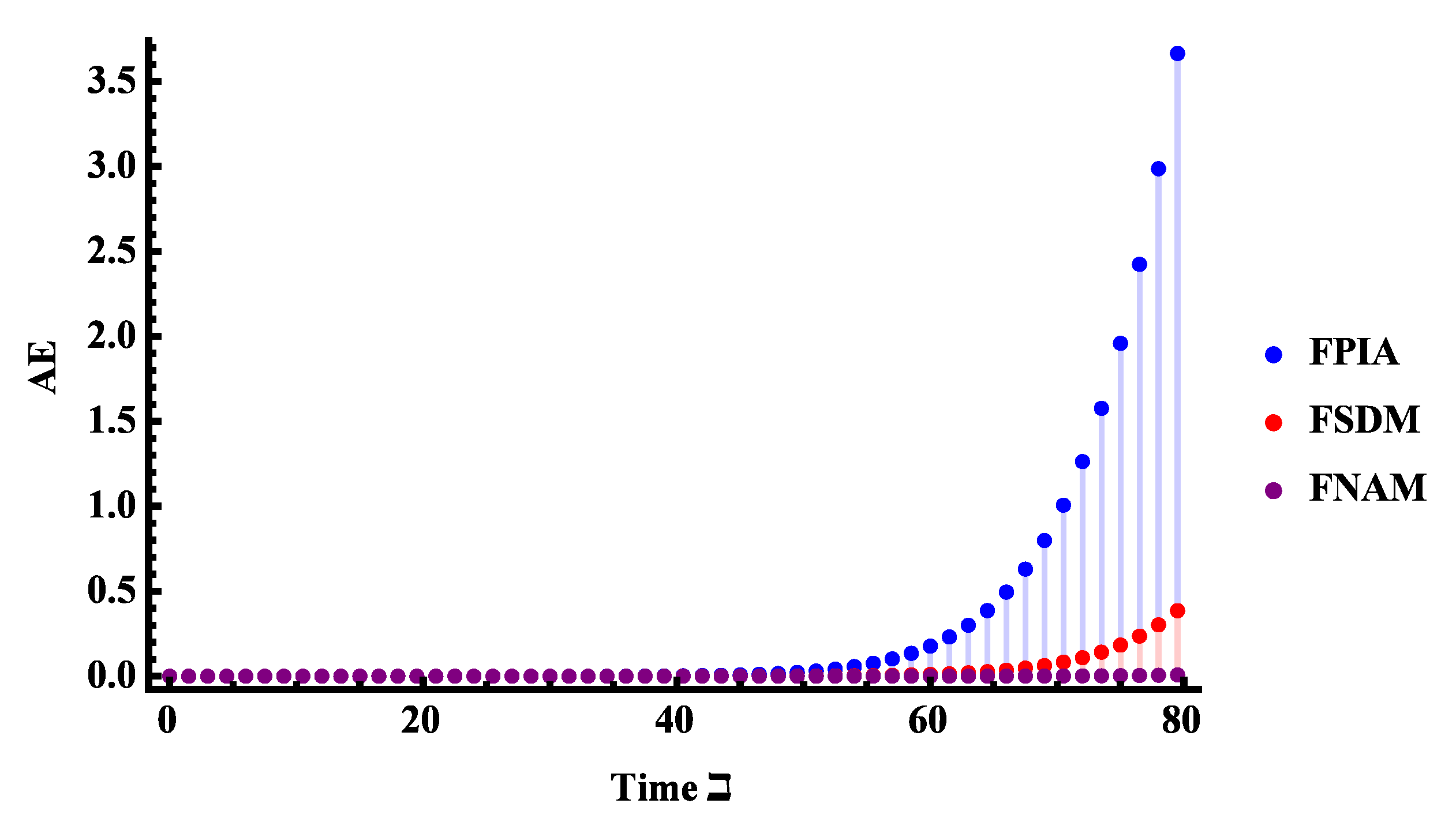
5.2. Resistor–Capacitor (RC) Circuit of Fractional Order
5.3. Inductor–Resistor (RL) Circuit of Fractional Order
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Abro, K.A.; Gomez-Aguilar, J.F. A comparison of heat and mass transfer on a Walter’s-B fluid via Caputo-Fabrizio versus Atangana-Baleanu fractional derivatives using the Fox-H function. Eur. Phys. J. Plus 2019, 134, 101. [Google Scholar] [CrossRef]
- Aguilar, J.F.G.; Baleanu, D. Fractional Transmission Line with Losses. Z. Nat. A 2014, 69, 539–546. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.F.; Escobar-Jiménez, R.F.; López-López, M.G.; Alvarado-Martínez, V.M. Atangana-Baleanu fractional derivative applied to electromagnetic waves in dielectric media. J. Electromagn. Waves Appl. 2016, 30, 1937–1952. [Google Scholar] [CrossRef]
- Atangana, A.; Aguilar, J.F.G. Fractional derivatives with noindex law property: Application to chaos and statistics. Chaos Solitons Fractals 2018, 114, 516–535. [Google Scholar] [CrossRef]
- Atangana, A.; Mekkaoui, T. Trinition the complex number with two imaginary parts: Fractal, chaos and fractional calculus. Chaos Solitons Fractals 2019, 128, 366–381. [Google Scholar] [CrossRef]
- Atangana, A.; Gómez-Aguilar, J.F. Decolonisation of fractional calculus rules: Breaking commutativity and associativity to capture more natural phenomena. Eur. Phys. J. Plus 2018, 133, 166. [Google Scholar] [CrossRef]
- Khan, H.; Jarad, F.; Abdeljawad, T.; Khan, A. A singular ABC fractional differential equation with p-Laplacian operator. Chaos Solitons Fractals 2019, 129, 56–61. [Google Scholar] [CrossRef]
- Owolabi, K.M. Numerical analysis and pattern formation process for space fractional super diffusive systems. Discret. Contin. Dyn. Syst.-S 2019, 12, 543–566. [Google Scholar] [CrossRef]
- Aguilar, J.F.G. Fundamental solutions to electrical circuits of non-integer order via fractional derivatives with and without singular kernels. Eur. Phys. J. Plus 2018, 133, 197. [Google Scholar] [CrossRef]
- Sabir, Z.; Saoud, S.; Raja, M.A.Z.; Hafiz Abdul Wahab, A.A. Heuristic computing technique for numerical solutions of nonlinear fourth order Emden–Fowler equation. Math. Comput. Simul. 2020, 178, 534–548. [Google Scholar] [CrossRef]
- Sabir, Z.; Raja, M.A.Z.; Arbi, A.; Altamirano, G.C.; Cao, J. Neuro–swarms intelligent computing using Gudermannian kernel for solving a class of second order Lane–Emden singular nonlinear model. AIMS Math. 2021, 6, 2468–2485. [Google Scholar] [CrossRef]
- Gomez-Aguilar, J.F.; Atangana, A. New insight in fractional differentiation: Power, exponential decay and Mittag-Leffler laws and applications. Eur. Phys. J. Plus 2017, 132, 1–23. [Google Scholar] [CrossRef]
- Sene, N.; Abdelmalek, K. Analysis of the fractional diffusion equations described by Atangana-Baleanu-Caputo fractional derivative. Chaos Solitons Fractals 2019, 127, 158–164. [Google Scholar] [CrossRef]
- Aguilar, J.F.G. Behavior characteristics of a cap-resistor, memcapacitor, and a memristor from the response obtained of RC and RL electrical circuits described by fractional differential equations. Turk. J. Electr. Eng. Comput. Sci. 2016, 24, 1421–1433. [Google Scholar] [CrossRef]
- Morales-Delgado, V.F.; Gomez-Aguilar, J.F.; Taneco-Hernandez, M.A.; Escobar-Jimenez, R.F. Fractional operator without singular kernel: Applications to linear electrical circuits. J. Cir. Theor. Appl. 2018, 46, 2394–2419. [Google Scholar] [CrossRef]
- Morales-Delgado, V.F.; Gomez-Aguilar, J.F.; Taneco-Hernandez, M.A. Analytical solutions of electrical circuits described by fractional conformable derivatives in Liouville-Caputo sense. AEU-Int. J. Electron. Commun. 2018, 85, 108–117. [Google Scholar] [CrossRef]
- Gomez-Aguilar, J.F.; Escobar-Jimenez, R.F.; Olivares-Peregrino, V.H.; Taneco-Hernandez, M.A.; Guerrero-Ramirez, G.V. Electrical circuits RC and RL involving fractional operators with bi-order. Adv. Mech. Eng. 2017, 9, 1687814017707132. [Google Scholar] [CrossRef]
- Gomez-Aguilar, J.F.; Atangana, A.; Morales-Delgado, V.F. Electrical circuits RC, LC, and RL described by Atangana Baleanu fractional derivatives. Int. J. Circ. Theor. Appl. 2017, 45, 1514–1533. [Google Scholar] [CrossRef]
- Radwan, A.G.; Salama, K.N. Fractional-order RC and RL circuits. Circuits Syst. Signal Process 2012, 31, 1901–1915. [Google Scholar] [CrossRef]
- Sene, N.; Gomez-Aguilar, J.F. Analytical solutions of electrical circuits considering certain generalized fractional derivatives. Eur. Phys. J. Plus 2019, 134, 260. [Google Scholar] [CrossRef]
- Sene, N. Fractional input stability for electrical circuits described by the Riemann-Liouville and the Caputo fractional derivatives. AIMS Math. 2019, 4, 147–165. [Google Scholar] [CrossRef]
- Gomez–Aguilar, J.F.; Cordova-Fraga, T.; Escalante-Martinez, J.E.; Calderon-Ramon, C.; Escobar-Jimenez, R.F. Electrical circuits described by a fractional derivative with regular Kernel. Rev. Mex. FíSica 2016, 62, 144–154. [Google Scholar]
- Gomez-Aguilar, J.F.; Juan, R.G.; Roberto, R.H.J.; Manuel, G.C. Fractional RC and LC Electrical Circuits. Investig. Tecnol. 2014, 15, 311–319. Available online: http://www.redalyc.org/articulo.oa?id=40430749013 (accessed on 25 July 2022).
- Ali, M.F.; Sharma, M.; Jain, R. An Application of Fractional Calculus in Electrical Engineering. Int. J. Adv. Eng. Technol. Appl. 2016, 5, 41–45. [Google Scholar] [CrossRef]
- Krantz, S.G.; Simmons, G.F. Differential Equations: Theory, Technique and Practice, 2nd ed.; McGraw-Hill: Boston, MA, USA, 2007. [Google Scholar]
- Atangana, A.; Nieto, J.J. Numerical solution for the model of RLC circuit via the fractional derivative without singular kernel. Adv. Mech. Eng. 2015, 7, 1687814015613758. [Google Scholar] [CrossRef]
- Atangana, A.; Alkahtani, B.S.T. Extension of the resistance, inductance, capacitance electrical circuit to fractional derivative without singular kernel. Adv. Mech. Eng. 2015, 7, 1687814015591937. [Google Scholar] [CrossRef]
- Kaczorek, T. Positive electrical circuits and their reachability. Arch. Electr. Eng. 2011, 60, 283–301. [Google Scholar] [CrossRef]
- Kaczorek, T.; Rogowski, K. Fractional Linear Systems and Electrical Circuits; Springer International Publishing: Basel, Switzerland, 2015. [Google Scholar]
- Almarri, B.; Ali, A.H.; Al-Ghafri, K.S.; Almutairi, A.; Bazighifan, O.; Awrejcewicz, J. Symmetric and Non-Oscillatory Characteristics of the Neutral Differential Equations Solutions Related to p-Laplacian Operators. Symmetry 2022, 14, 566. [Google Scholar] [CrossRef]
- Almarri, B.; Ali, A.H.; Lopes, A.M.; Bazighifan, O. Nonlinear Differential Equations with Distributed Delay: Some New Oscillatory Solutions. Mathematics 2022, 10, 995. [Google Scholar] [CrossRef]
- Almarri, B.; Janaki, S.; Ganesan, V.; Ali, A.H.; Nonlaopon, K.; Bazighifan, O. Novel Oscillation Theorems and Symmetric Properties of Nonlinear Delay Differential Equations of Fourth-Order with a Middle Term. Symmetry 2022, 14, 585. [Google Scholar] [CrossRef]
- Bazighifan, O.; Ali, A.H.; Mofarreh, F.; Raffoul, Y.N. Extended Approach to the Asymptotic Behavior and Symmetric Solutions of Advanced Differential Equations. Symmetry 2022, 14, 686. [Google Scholar] [CrossRef]
- Ali, A.H.; Meften, G.; Bazighifan, O.; Iqbal, M.; Elaskar, S.; Awrejcewicz, J. A Study of Continuous Dependence and Symmetric Properties of Double Diffusive Convection: Forchheimer Model. Symmetry 2022, 14, 682. [Google Scholar] [CrossRef]
- Abed Meften, G.; Ali, A.H.; Al-Ghafri, K.; Awrejcewicz, J.; Bazighifan, O. Nonlinear Stability and Linear Instability of Double-Diffusive Convection in a Rotating with LTNE Effects and Symmetric Properties: Brinkmann-Forchheimer Model. Symmetry 2022, 14, 565. [Google Scholar] [CrossRef]
- Qaraad, B.; Bazighifan, O.; Nofal, T.A.; Ali, A.H. Neutral differential equations with distribution deviating arguments: Oscillation conditions. J. Ocean. Eng. Sci. 2022. [Google Scholar] [CrossRef]
- Ali, A.H.; Jaber, A.S.; Yaseen, M.T.; Rasheed, M.; Bazighifan, O.; Nofal, T.A. A comparison of finite difference and finite volume methods with numerical simulations: Burgers equation model. Complexity 2022. [Google Scholar] [CrossRef]
- Bazighifan, O. An Approach for Studying Asymptotic Properties of Solutions of Neutral Differential Equations. Symmetry 2020, 12, 555. [Google Scholar] [CrossRef]
- Santra, S.S.; Ghosh, T.; Bazighifan, O. Explicit criteria for the oscillation of second-order differential equations with several sub-linear neutral coefficients. Adv. Differ. Equ. 2020, 2020, 643. [Google Scholar] [CrossRef]
- Bazighifan, O.; Kumam, P. Oscillation Theorems for Advanced Differential Equations with p-Laplacian Like Operators. Mathematics 2020, 8, 821. [Google Scholar] [CrossRef]
- Bazighifan, O.; Alotaibi, H.; Mousa, A.A.A. Neutral Delay Differential Equations: Oscillation Conditions for the Solutions. Symmetry 2021, 13, 101. [Google Scholar] [CrossRef]
- Moaaz, O.; El-Nabulsi, R.A.; Bazighifan, O. Oscillatory Behavior of Fourth-Order Differential Equations with Neutral Delay. Symmetry 2020, 12, 371. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations. In Mathematics in Science and Engineering; Academic Press: San Diego, CA, USA, 1999; Volume 198. [Google Scholar]
- Senol, M.; Dolapci, I.T. On the Perturbation–Iteration Algorithm for fractional differential equations. J. King Saud Univ. Sci. 2016, 28, 69–74. [Google Scholar] [CrossRef]
- Wazwaz, A.M. The successive differentiation method for solving Bratu equation and Bratu-Type equations. Rom. J. Phys. 2016, 61, 774–783. [Google Scholar]
- Sultana, M.; Arshad, U.; Alam, M.N.; Bazighifan, O.; Askar, S.; Awrejcewicz, J. New Results of the Time-Space Fractional Derivatives of Kortewege-De Vries Equations via Novel Analytic Method. Symmetry 2021, 13, 2296. [Google Scholar] [CrossRef]
- Sultana, M.; Arshad, U.; Ali, A.H.; Bazighifan, O.; Al–Moneef, A.A.; Nonlaopon, K. New Efficient Computations with Symmetrical and Dynamic Analysis for Solving Higher-Order Fractional Partial Differential Equations. Symmetry 2022, 14, 1653. [Google Scholar] [CrossRef]
- Qureshi, S.; Chang, M.M.; Shaikh, A.A. Analysis of series RL and RC circuits with time–invariant source using truncated M, Atangana beta and conformable derivatives. J. Ocean. Eng. Sci. 2021, 6, 217–227. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arshad, U.; Sultana, M.; Ali, A.H.; Bazighifan, O.; Al-moneef, A.A.; Nonlaopon, K. Numerical Solutions of Fractional-Order Electrical RLC Circuit Equations via Three Numerical Techniques. Mathematics 2022, 10, 3071. https://doi.org/10.3390/math10173071
Arshad U, Sultana M, Ali AH, Bazighifan O, Al-moneef AA, Nonlaopon K. Numerical Solutions of Fractional-Order Electrical RLC Circuit Equations via Three Numerical Techniques. Mathematics. 2022; 10(17):3071. https://doi.org/10.3390/math10173071
Chicago/Turabian StyleArshad, Uroosa, Mariam Sultana, Ali Hasan Ali, Omar Bazighifan, Areej A. Al-moneef, and Kamsing Nonlaopon. 2022. "Numerical Solutions of Fractional-Order Electrical RLC Circuit Equations via Three Numerical Techniques" Mathematics 10, no. 17: 3071. https://doi.org/10.3390/math10173071
APA StyleArshad, U., Sultana, M., Ali, A. H., Bazighifan, O., Al-moneef, A. A., & Nonlaopon, K. (2022). Numerical Solutions of Fractional-Order Electrical RLC Circuit Equations via Three Numerical Techniques. Mathematics, 10(17), 3071. https://doi.org/10.3390/math10173071









