Finite-Time Extended State Observer-Based Fixed-Time Attitude Control for Hypersonic Vehicles
Abstract
:1. Introduction
2. Problem Formulation
3. Controller Design and Stability Analysis
3.1. Finite-Time Extended State Observer Design
3.2. Tracking Differentiator Design
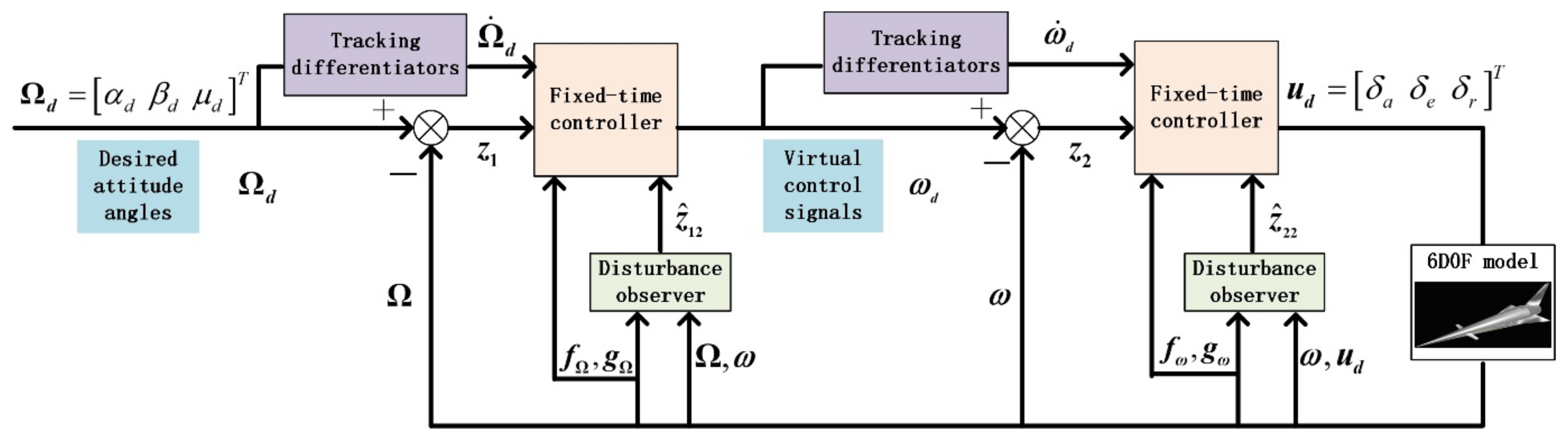
3.3. Fixed-Time Controller Design
3.3.1. Controller Design for the Attitude Angle Loop
3.3.2. Controller Design for the Attitude Angular Rate Loop
3.4. Stability Analysis
4. Simulations
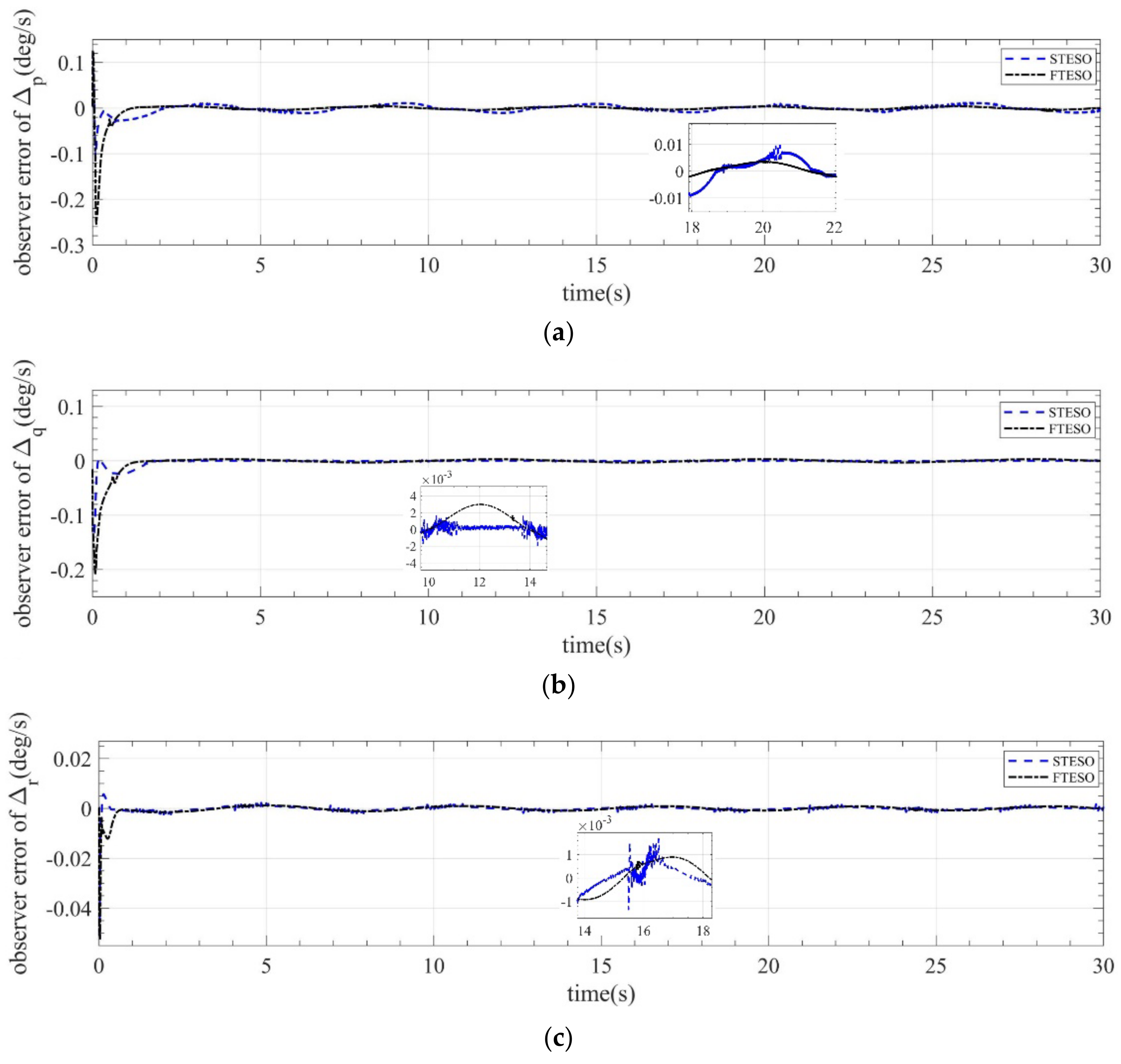
4.1. Comparison of the FTESO and STESO
4.2. Comparison of the FTBC and NBC Controllers
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ding, Y.; Yue, X.; Chen, G.; Si, J. Review of control and guidance technology on hypersonic vehicle. Chin. J. Aeronaut. 2022, 35, 1–18. [Google Scholar] [CrossRef]
- Shamma, J.S.; Cloutier, J.R. Gain-scheduled missile autopilot design using linear parameter varying transformations. J. Guid. Control Dyn. 1993, 16, 256–263. [Google Scholar] [CrossRef]
- Sigthorsson, D.O.; Jankovsky, P.; Serrani, A.; Yurkovich, S. Robust linear output feedback control of an airbreathing hypersonic vehicle. J. Guid. Control Dyn. 2008, 31, 1052–1066. [Google Scholar] [CrossRef]
- Hu, Q.; Meng, Y.; Wang, C.; Zhang, Y. Adaptive backstepping control for air-breathing hypersonic vehicles with input nonlinearities. Aerosp. Sci. Technol. 2018, 73, 289–299. [Google Scholar] [CrossRef]
- Bao, C.; Wang, P.; Tang, G. Integrated method of guidance, control and morphing for hypersonic morphing vehicle in glide phase. Chin. J. Aeronaut. 2021, 34, 535–553. [Google Scholar] [CrossRef]
- Zhang, R.; Dong, L.; Sun, C. Adaptive nonsingular terminal sliding mode control design for near space hypersonic vehicles. IEEE/CAA J. Autom. Sin. 2014, 1, 155–161. [Google Scholar] [CrossRef]
- Zhang, X.; Hu, W.; Wei, C.; Xu, T. Nonlinear disturbance observer based adaptive super-twisting sliding mode control for generic hypersonic vehicles with coupled multisource disturbances. Eur. J. Control 2021, 57, 253–262. [Google Scholar] [CrossRef]
- Tian, J.; Zhang, S.; Zhang, Y.; Li, T. Active disturbance rejection control based robust output feedback autopilot design for airbreathing hypersonic vehicles. ISA Trans. 2018, 74, 45–59. [Google Scholar] [CrossRef]
- Hu, C.; Wei, X.; Cao, L.; Tao, Y.; Gao, Z.; Hu, Y. Integrated fault-tolerant control system design based on continuous model predictive control for longitudinal manoeuvre of hypersonic vehicle with actuator faults. IET Control Theory Appl. 2020, 14, 1769–1784. [Google Scholar] [CrossRef]
- Zhang, C.; Ahn, C.; Jin, W.; Wei, H. Online-learning control with weakened saturation response to attitude tracking: A variable learning intensity approach. Aerosp. Sci. Technol. 2021, 117, 106981. [Google Scholar] [CrossRef]
- Xia, J.; Zhang, J.; Feng, J.; Wang, Z.; Zhuang, G. Command filter-based adaptive fuzzy control for nonlinear systems with unknown control directions. IEEE Trans. Syst. Man Cybern. 2019, 51, 1945–1953. [Google Scholar] [CrossRef]
- Farrell, J.; Polycarpou, M.; Sharma, M.; Dong, W. Command Filtered Backstepping. IEEE Trans. Automat. Contr. 2009, 54, 1391–1395. [Google Scholar] [CrossRef]
- Zhang, X.; Zong, Q.; Dou, L.; Tian, B.; Liu, W. Improved finite-time command filtered backstepping fault-tolerant control for flexible hypersonic vehicle. J. Frankl. Inst. 2020, 357, 8543–8565. [Google Scholar] [CrossRef]
- Yu, J.; Shi, P.; Zhao, L. Finite-time command filtered backstepping control for a class of nonlinear systems. Automatica 2018, 92, 173–180. [Google Scholar] [CrossRef]
- Han, T.; Shin, H.; Hu, Q.; Tsourdos, A.; Xin, M. Differentiator-based incremental three-dimensional terminal angle guidance with enhanced robustness. IEEE Trans. Aerosp. Electron. Syst. 2022, 1. [Google Scholar] [CrossRef]
- Bu, X.; Wu, X.; Zhang, R.; Ma, Z.; Huang, J. Tracking differentiator design for the robust backstepping control of a flexible air-breathing hypersonic vehicle. J. Frankl. Inst. 2015, 352, 1739–1765. [Google Scholar] [CrossRef]
- Wang, X.; Guo, J.; Tang, S.; Qi, S. Fixed-time disturbance observer based fixed-time back-stepping control for an air-breathing hypersonic vehicle. ISA Trans. 2019, 88, 233–245. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Song, S. Tracking control of hypersonic vehicles with input saturation based on fast terminal sliding mode. Int. J. Aeronaut. Space Sci. 2019, 20, 493–505. [Google Scholar] [CrossRef]
- Dong, C.; Liu, Y.; Wang, Q. Barrier Lyapunov function based adaptive finite-time control for hypersonic flight vehicles with state constraints. ISA Trans. 2020, 96, 163–176. [Google Scholar] [CrossRef]
- Zhang, D.; Ma, P.; Wang, S.; Chao, T. Multi-constraints adaptive finite-time integrated guidance and control design. Aerosp. Sci. Technol. 2020, 107, 106334. [Google Scholar] [CrossRef]
- Ding, Y.; Yue, X.; Liu, C.; Dai, H.; Chen, G. Finite-time controller design with adaptive fixed-time anti-saturation compensator for hypersonic vehicle. ISA Trans. 2022, 122, 96–113. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Li, C.; Guo, Y.; Wang, C.; Li, P. Adaptive fault tolerant control for hypersonic vehicle with input saturation and state constraints. Acta Astronaut. 2020, 167, 302–313. [Google Scholar] [CrossRef]
- Yu, C.; Jiang, J.; Zhen, Z.; Bhatia, A.; Wang, S. Adaptive backstepping control for air-breathing hypersonic vehicle subject to mismatched uncertainties. Aerosp. Sci. Technol. 2020, 107, 106224. [Google Scholar] [CrossRef]
- Yang, J.; Li, S.; Sun, C.; Guo, L. Nonlinear-disturbance-observer-based robust flight control for airbreathing hypersonic vehicles. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 1263–1275. [Google Scholar] [CrossRef]
- Wang, B.; Derbeli, M.; Barambones, O.; Yousefpour, A.; Jahanshahi, H. Experimental validation of disturbance observer-based adaptive terminal sliding mode control subject to control input limitations for SISO and MIMO systems. Eur. J. Control 2022, 63, 151–163. [Google Scholar] [CrossRef]
- Zhou, X.; Li, X. Trajectory tracking control for electro-optical tracking system based on fractional-order sliding mode controller with super-twisting extended state observer. ISA Trans. 2021, 117, 85–95. [Google Scholar] [CrossRef]
- Wu, T.; Wang, H.; Yu, Y.; Liu, Y.; Wu, J. Quantized fixed-time fault-tolerant attitude control for hypersonic reentry vehicles. Appl. Math. Model. 2021, 98, 143–160. [Google Scholar] [CrossRef]
- Hu, Q.; Jiang, B. Continuous finite-time attitude control for rigid spacecraft based on angular velocity observer. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 1082–1092. [Google Scholar] [CrossRef]
- Li, B.; Hu, Q.; Yang, Y.; Postolache, O. Finite-time disturbance observer based integral sliding mode control for attitude stabilization under actuator failure. IET Control Theory Appl. 2019, 13, 50–58. [Google Scholar] [CrossRef]
- Sun, J.; Yi, J.; Pu, Z.; Tan, X. Fixed-time sliding mode disturbance observer-based nonsmooth backstepping control for hypersonic vehicles. IEEE Trans. Syst. Man Cybern. 2020, 50, 4377–4386. [Google Scholar] [CrossRef]
- Basin, M.; Yu, P.; Shtessel, Y. Finite- and fixed-time differentiators utilising HOSM techniques. IET Control Theory Appl. 2017, 11, 1144–1152. [Google Scholar] [CrossRef]

















| Module | Parameters |
|---|---|
| FTESO (14) | |
| STESO (43) | |
| TD (27) | |
| FTBC controller (31) and (36) | |
| Estimation Error | FTESO | STESO |
|---|---|---|
| 0.0015° | 0.0043° | |
| 0.00086° | 0.00175° | |
| 0.00052° | 0.0003° | |
| 0.0064°/s | 0.011°/s | |
| 0.003°/s | 0.002°/s | |
| 0.0014°/s | 0.0024°/s |
| Module | Parameters |
|---|---|
| Finite-time backstepping controller (44) | |
| Non-linear, non-smooth first-order filters (45) | |
| Fourth-order fixed-time SMDOs (46) |
| Channels | FTBC | NBC | ||
|---|---|---|---|---|
| Tracking Error | Settling Time | Tracking Error | Settling Time | |
| 0.0026° | 0.65 s | 0.025° | 1.27 s | |
| 0.0012° | 0.34 s | 0.00026° | 1.62 s | |
| 0.0005° | 1.08 s | 0.01° | 1.43 s | |
| Channels | FTBC | NBC | ||
|---|---|---|---|---|
| Tracking Error | Settling Time | Tracking Error | Settling Time | |
| p | 0.0045°/s | 1.13 s | 0.0023°/s | 1.69 s |
| q | 0.0056°/s | 1.31 s | 0.0188°/s | 1.43 s |
| r | 0.0025°/s | 0.55 s | 0.0027°/s | 1.29 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Feng, D.; Cui, J.; Wang, X. Finite-Time Extended State Observer-Based Fixed-Time Attitude Control for Hypersonic Vehicles. Mathematics 2022, 10, 3162. https://doi.org/10.3390/math10173162
Zhao J, Feng D, Cui J, Wang X. Finite-Time Extended State Observer-Based Fixed-Time Attitude Control for Hypersonic Vehicles. Mathematics. 2022; 10(17):3162. https://doi.org/10.3390/math10173162
Chicago/Turabian StyleZhao, Jiaqi, Dongzhu Feng, Jiashan Cui, and Xin Wang. 2022. "Finite-Time Extended State Observer-Based Fixed-Time Attitude Control for Hypersonic Vehicles" Mathematics 10, no. 17: 3162. https://doi.org/10.3390/math10173162





