Characterization of Blast Wave Parameters in the Detonation Locus and Near Field for Shaped Charges
Abstract
:1. Introduction
2. Theory and Technical Context of Blast Shock Waves
3. Materials and Methods
3.1. Experimental Study
3.2. Numerical Study
Methodology
3.3. Convergence Criteria
4. Results and Discussion
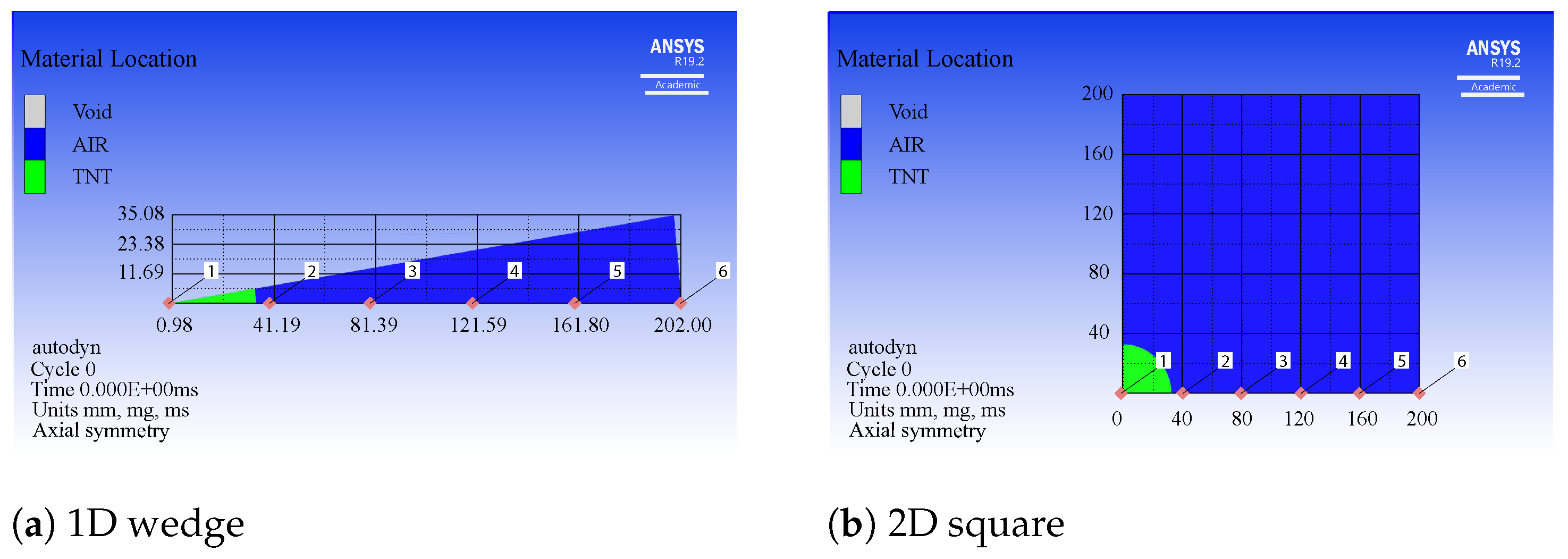
4.1. 1D Analysis for Spherical Charge
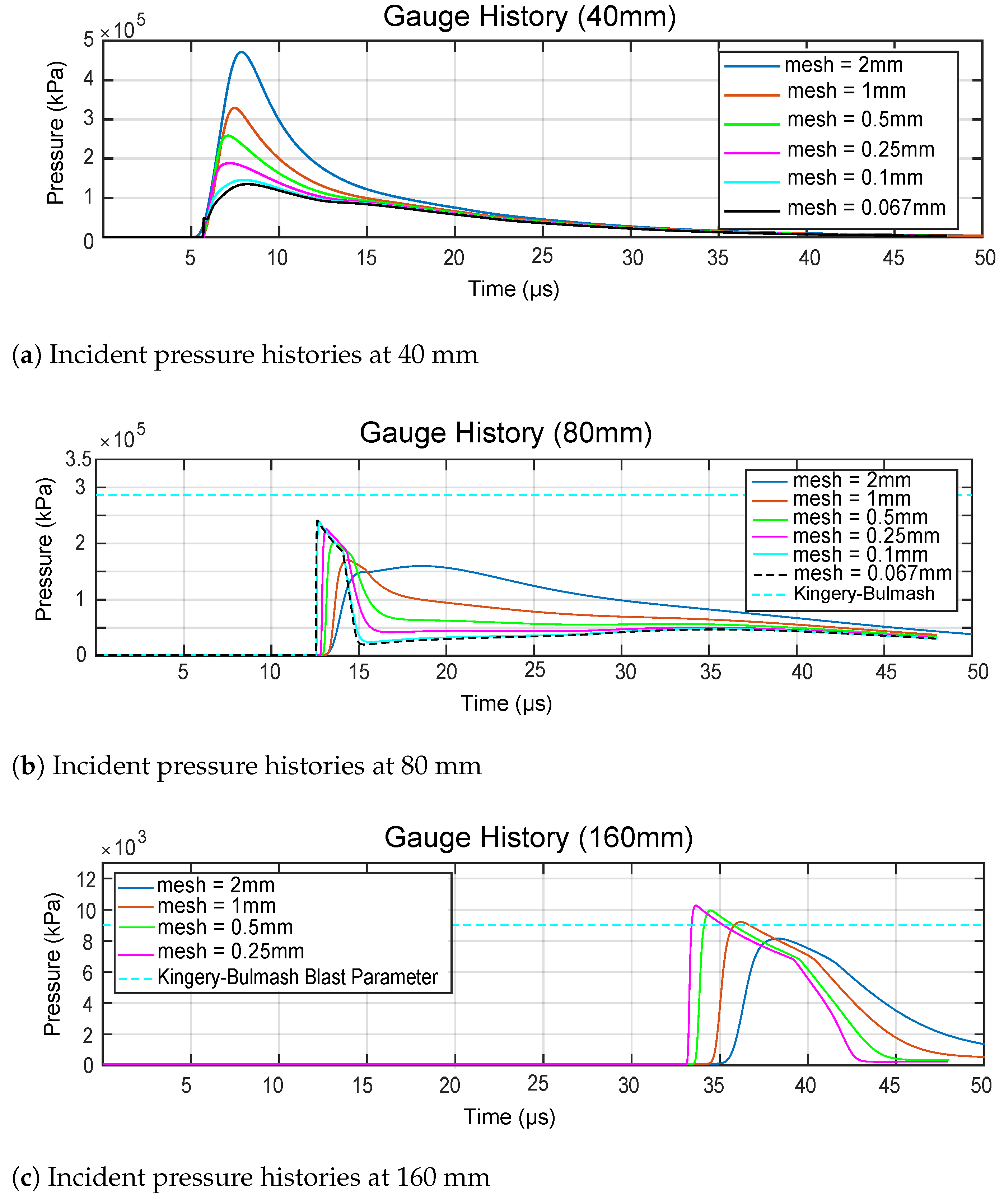
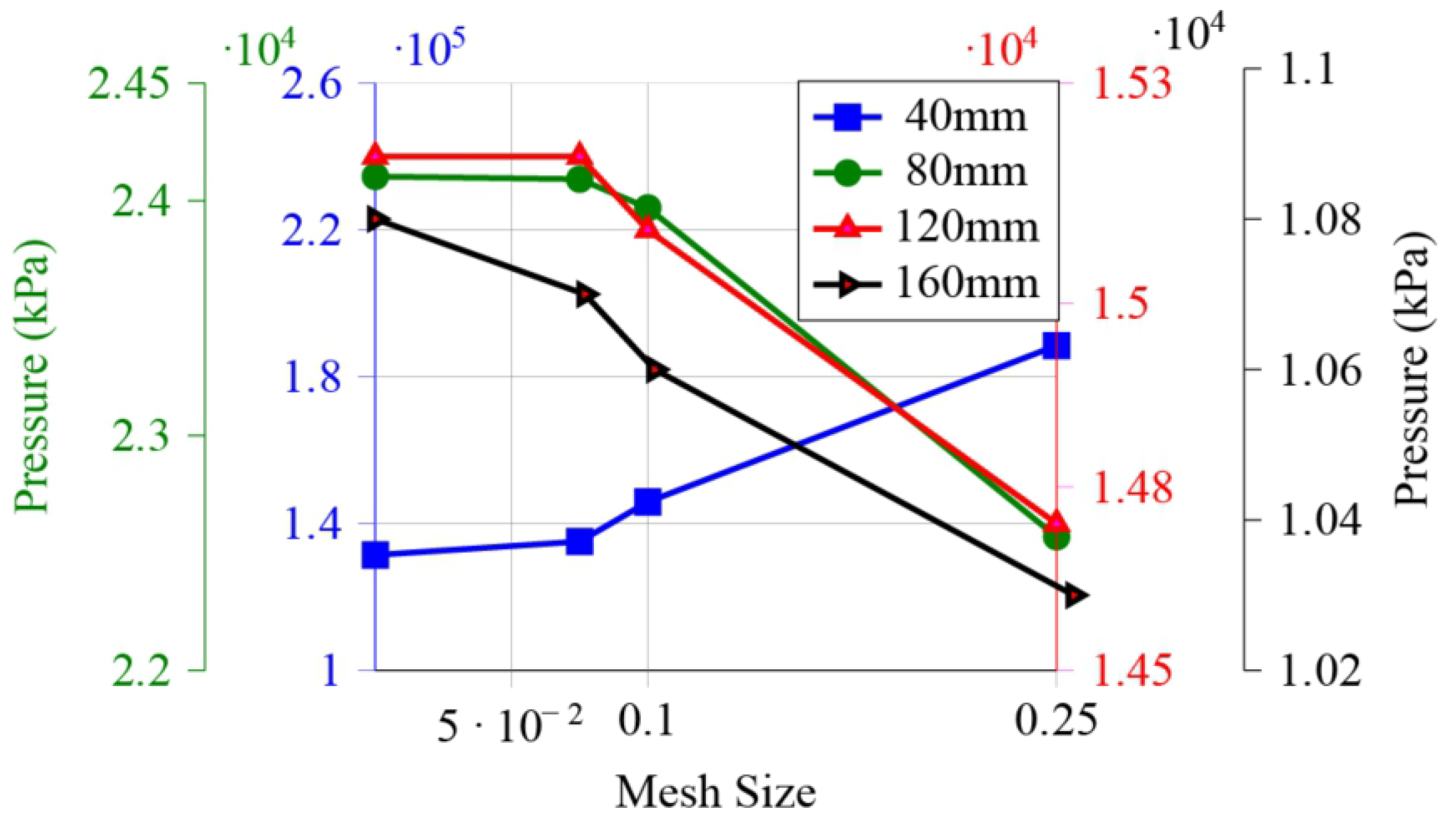
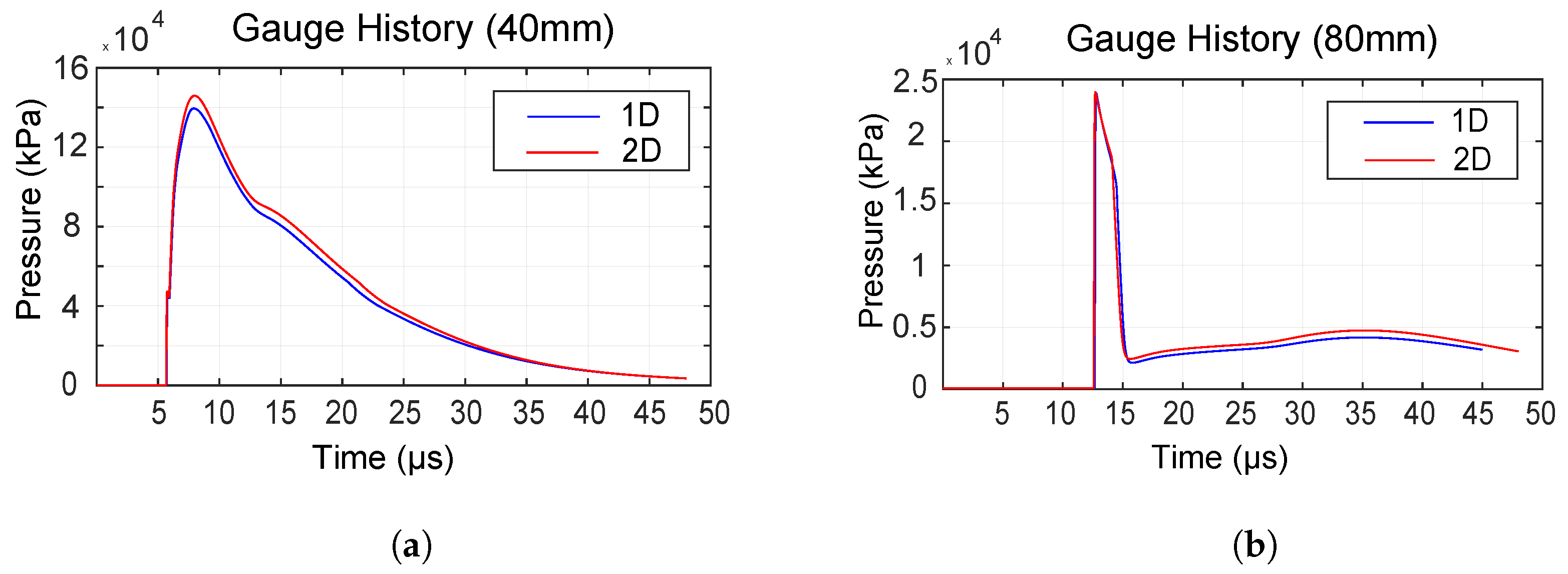
4.2. Convergence Criteria
4.3. 2D Analysis for Spherical Charge
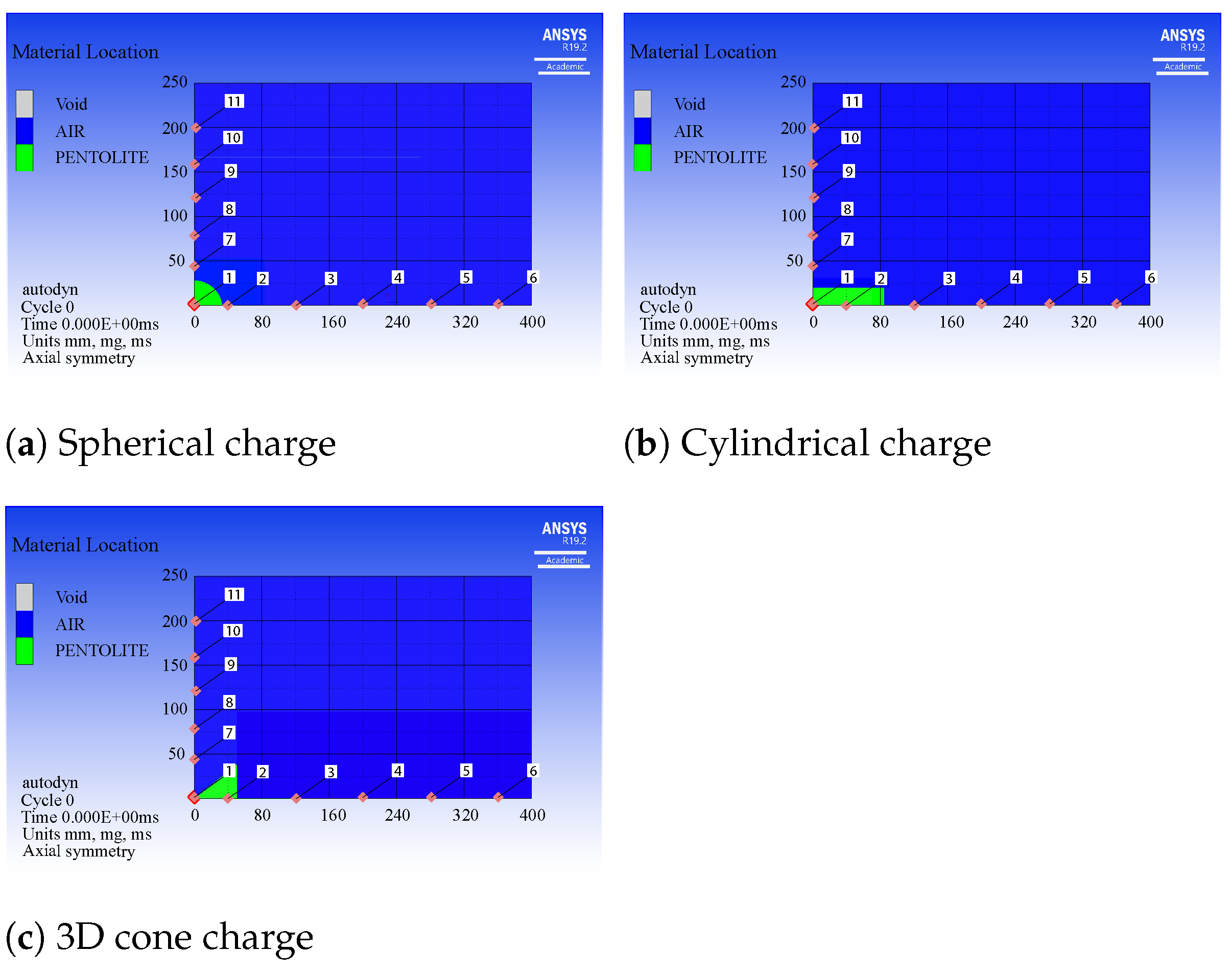
4.4. Shaped Charge Analysis
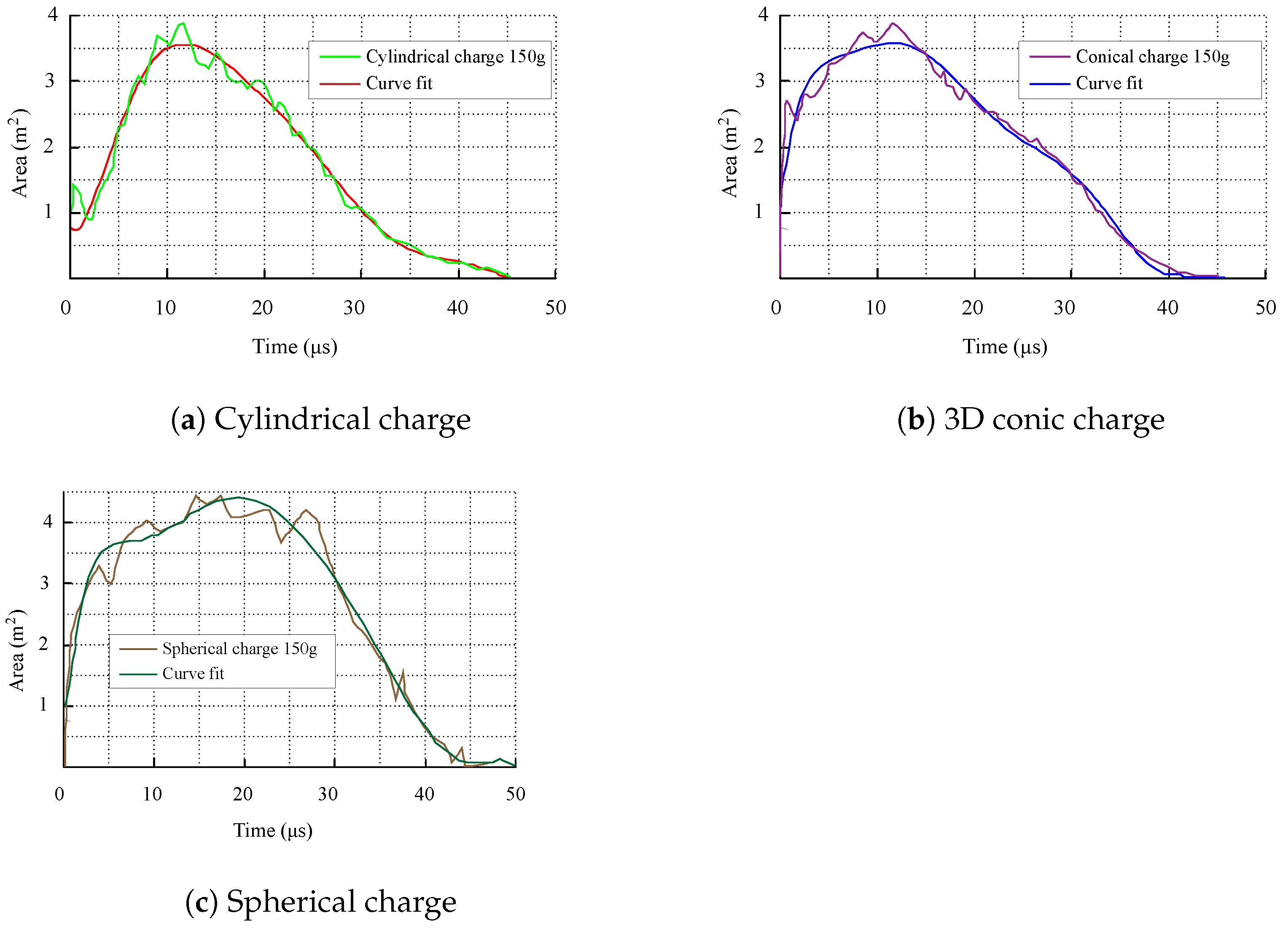
4.4.1. Spherical Charge
4.4.2. Cylindrical Charge
4.4.3. 3D Conic Charge
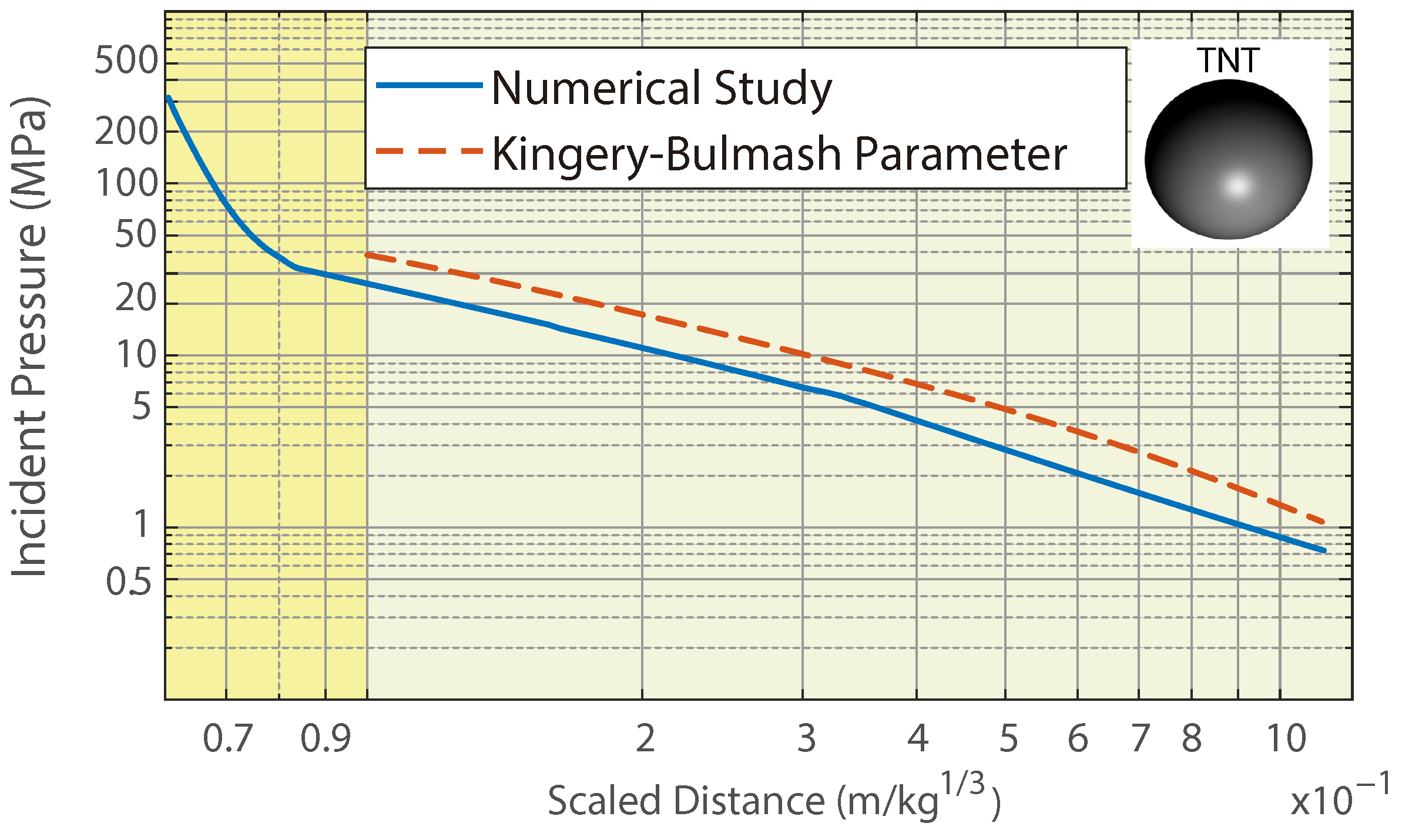
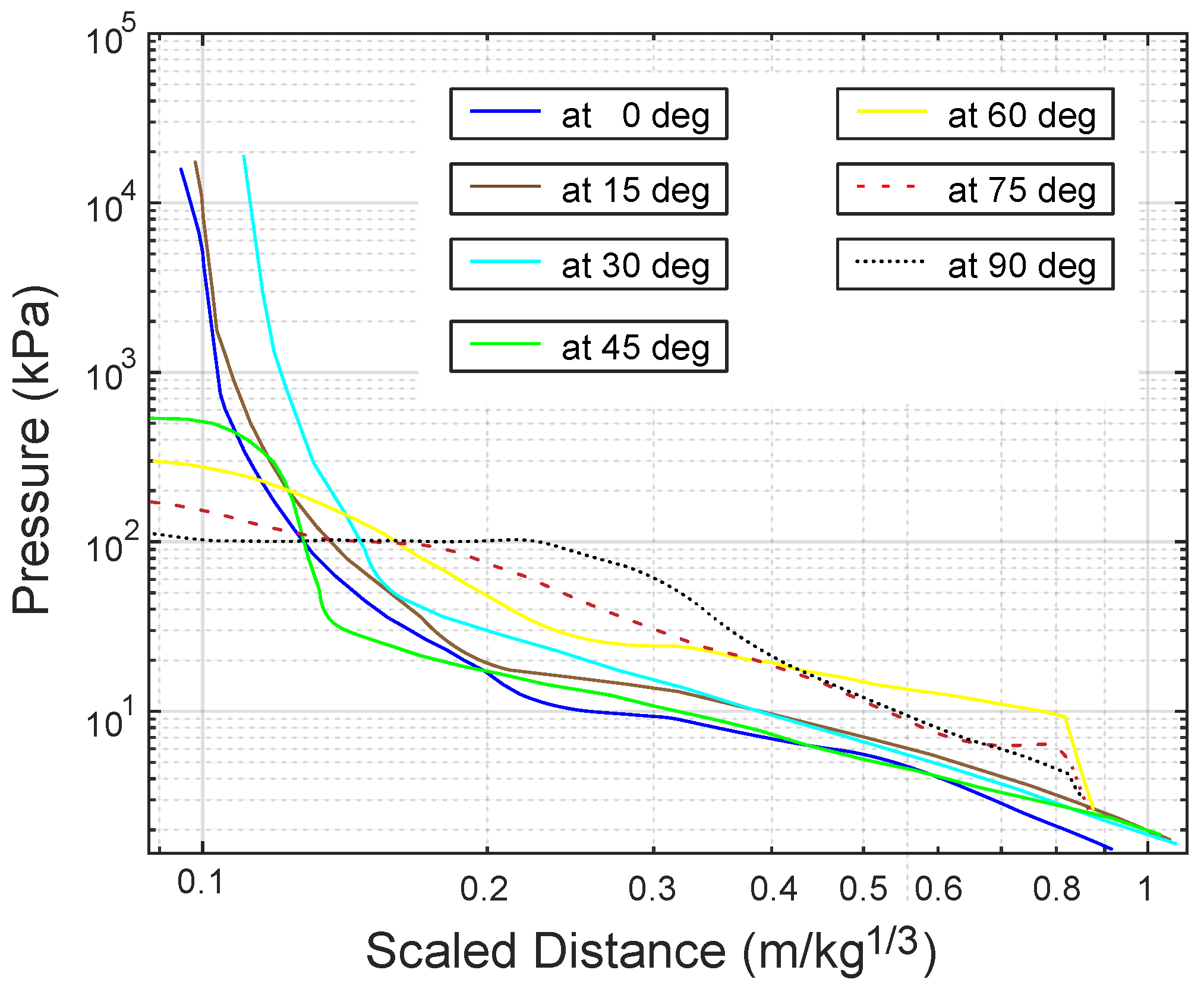
4.5. Blast Parameters for the Positive Phase
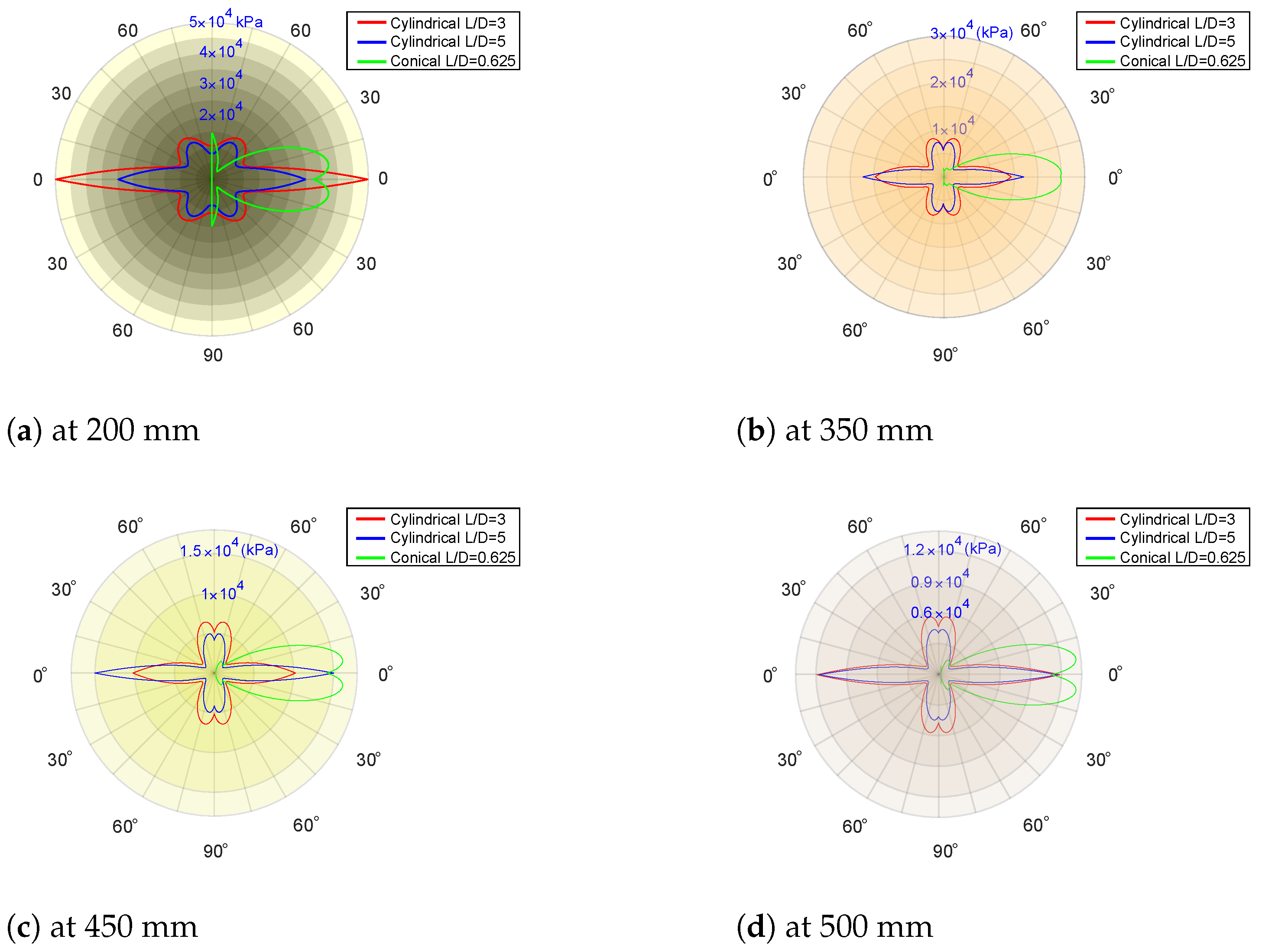
4.6. Influence of the L/D Aspect Ratio, Scaled Distance and Orientation
5. Conclusions
- The aspect ratio of the cylindrical and 3D cone-shaped charge have a significant effect on the inception, evolution, shape, propagation of the blast shock wave and incident peak pressure. As the aspect ratio decreases, more release energy is concentrated in the axial direction for a 3D cone-shaped charge, while as the aspect ratio increases, more release energy is concentrated in the radial direction for a cylindrical-shaped charge. The incident peak pressure follows the same previous analysis, but it decreases in the other direction. At an equivalent weight, the incident peak pressure caused by a 3D conic-shaped charge reaches higher values than a cylindrical charge. Therefore, the effect of a cylindrical-shaped charge could be considered for confined areas, while 3D conic shaped-charges could be considered for cutting purposes in the axial direction.
- From the experimental and numerical results, we realized that the orientation has less influence than the L/D aspect ratio on the incident pressure contours. However, it defines the vector-valued function of the radius of ashock wave in its early stage. The influence range on the incident pressure contours is from 0 to 5 degrees for cylindrical charges and from 0 to 30 degrees for 3D cone charges. In other words, cylindrical and 3D conic charges amplify their damage effect for such ranges, respectively.
- One of the challenges in the numerical simulation was to determine the effects caused by released energy in heat form. Typically, these data are simulated through an afterburn energy model which must be associated with chemistry. Unfortunately, this model is not available in the Autodyn hydrocode. Therefore, some non-linear effects caused by afterburn energy could not be simulated by numerical studies.
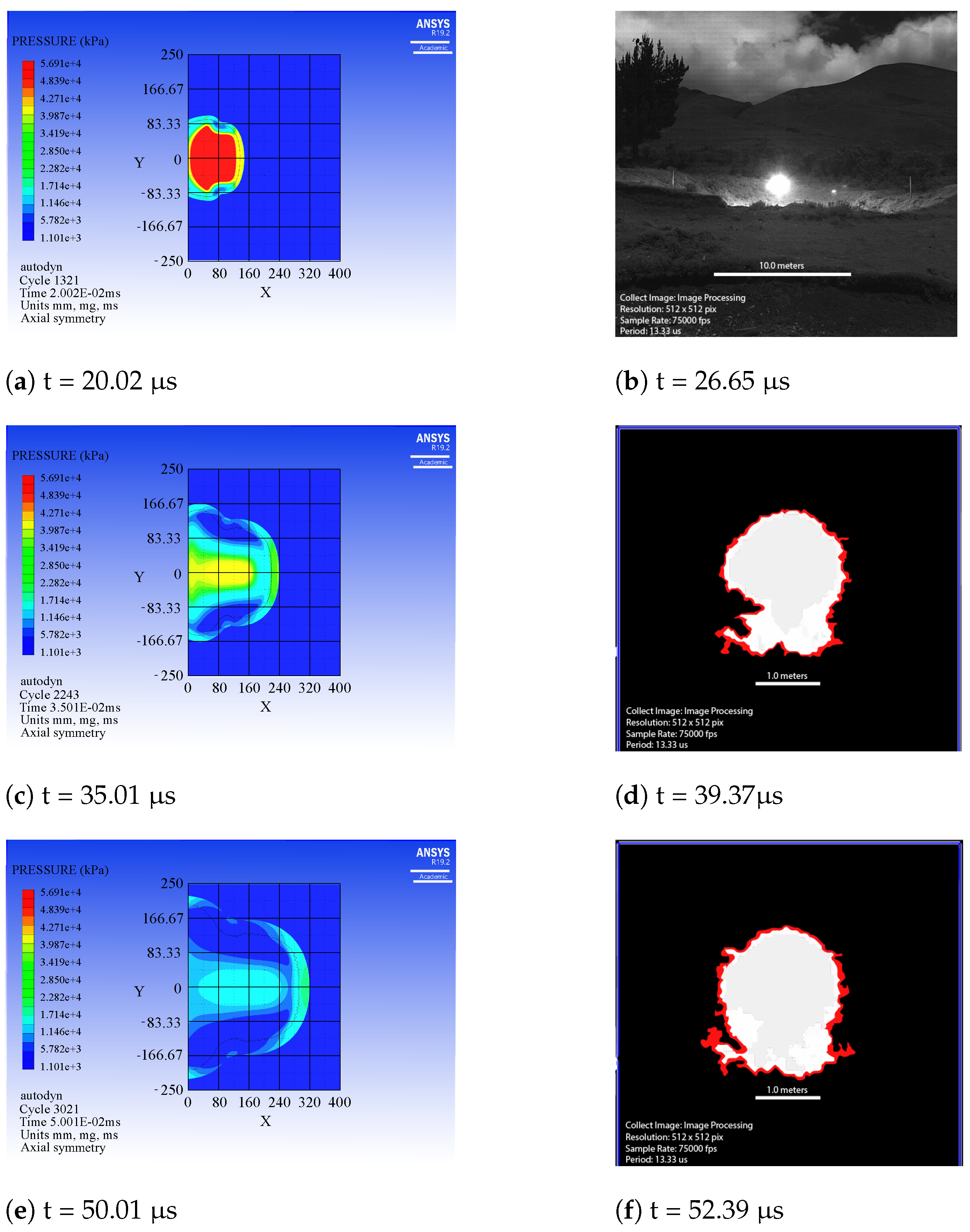
- The quantification of the magnitude of non-linear effects such as the reflection, refraction, and diffraction is an essential stage for providing full understanding of inception and evolution of a blast shock wave caused by cylindrical and 3D cone-shaped charges. Hereby, the results presented, which are mostly based on the hydrodynamic regime where radiation becomes less important, capture the superposition of waves. The image sequences indicate the presence of bridge waves which rarely emerge following a pattern. Subsequently, the results also yield the interaction between bridge waves and primary waves. It leads to a secondary shock wave. These facts allow the characterization of a blast shock wave for non-spherical charges significantly more complex than those by spherical charges. Therefore, compressible multiphase flows should be developed and incorporated into the Autodyn hydrocode in order to deal with discontinuous interfaces.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ataque Con Drones en la Penitenciaría de Guayaquil. Available online: https://www.expreso.ec/actualidad/explosiones-posible-drones-carcel-maxima-seguridad-guayaquil-111763.html (accessed on 13 September 2021).
- Reportan Ataque con Drones a cáRcel en Guayaquil, Ecuador. Available online: https://www.telesurtv.net/news/ecuador-reportan-ataque-drones-carcel-guayaquil-20210913-0016.html (accessed on 13 September 2021).
- Drones Atacan Penal de máXima Seguridad de Ecuador. Available online: https://www.vozdeamerica.com/a/drones-atacan-penal-maxima-seguridad-ecuador/6225705.html (accessed on 13 September 2021).
- Zhao, Y.; Cao, W.; Huang, F.; Han, Y.; Long, X. Evaluation of detonation performance and working capacity of explosives by optimized VLW EOS. Combust. Flame 2022, 235, 111734. [Google Scholar] [CrossRef]
- Mespoulet, J.; Plassard, F.; Hereil, P.; Lefrançois, A. Influence of HE shape on blast profile. In Proceedings of the 8th European LS-DYNA Users Conference, Strasbourg, France, 24 May 2011. [Google Scholar]
- Hryciow, Z.; Borkowski, W.; Rybak, P.; Wysockiois, Z. Influence of the shape of the explosive charge on blast profile. J. KONES 2014, 4, 169–176. [Google Scholar] [CrossRef]
- Castellano, A.; Caltagirone, J. TM5-1300, Structures to Resist Accidental Explosions. In Contents of Structures to Resist the Effects of Accidental Explosions (TM 5-1300, NAVFAC P-397, AFM 22); Department of Army Navy NAVFAC (Naval Facilities) P-397, Air Force Regulation 88-2; Department of Defense Explosives Safety Board: Alexandria, VA, USA, 1990; pp. 369–388. [Google Scholar]
- Castellano, A.; Caltagirone, J. Design and Analysis of Hardened Structures to Conventional Weapons Effects. In Contents of Structures to Resist the Effects of Accidental Explosions (TM 5-1300, NAVFAC P-397, AFM 22); U.S. Army Corps of Engineers, UNIFIED FACILITIES CRITERIA (UFC): Washington, DC, USA, 2002; pp. 254–268. [Google Scholar]
- Department of Army Navy. Structures to Resist the Effects of the Accidental Explosions. Int. J. Trend Sci. Res. Dev. 2019, 3, 6–8. [Google Scholar]
- Hyde, D. Fundamentals of Protective Design for Conventional Weapons. In User’s Guide for Microcomputer Programs ConWep and FunPro, Applications of TM 5-855-1; U.S. Army Corps of Engineers, UNIFIED FACILITIES CRITERIA (UFC): Washington, DC, USA, 1988. [Google Scholar]
- Selivanov, V.; Fedorov, S.; Babkin, A.; Bolotina, I. Using shaped charges with a “magnetic cut-off” for testing anti-meteoroid shields. Acta Astronaut. 2021, 180, 170–175. [Google Scholar] [CrossRef]
- Cole, R. Underwater Explosions; Princeton University Press: Princeton, NJ, USA, 1948; pp. 63–78. [Google Scholar]
- Stoner, R.; Richard, G.; Bleakney, W. The attenuation of spherical shock waves in air. J. Appl. Phys. 1948, 9, 670–678. [Google Scholar] [CrossRef]
- Knock, C.; Nigel, D. Predicting the peak pressure from the curved surface of detonating cylindrical charges. Propellants Explos. Pyrotech 2011, 3, 203–209. [Google Scholar] [CrossRef]
- Swisdak, M. Explosion effects in air. In Explosion Effects and Properties: Explosion Effects in Air; Naval Surface Weapons Center: Maryland, MD, USA, 1975; pp. 120–128. [Google Scholar]
- Plooster, M.N. Blast effects from cylindrical explosive charges: Experimental measurement. In Defense Technical Information Center; U.S. Departament of Defense: Washington, DC, USA, 1982. [Google Scholar]
- Fan, Y.; Chen, L.; Li, Z.; Xiang, X.; Fang, Q. Modeling the blast load induced by a close-in explosion considering cylindrical charge parameters. Def. Technol. 2022. [Google Scholar] [CrossRef]
- Gao, C.; Zhen, X.; Fang, Q.; Hong, J.; Wang, J. Numerical investigation on free air blast loads generated from center-initiated cylindrical charges with varied aspect ratio in arbitrary orientation. Def. Technol. 2021. [Google Scholar] [CrossRef]
- Rigby, S.; Osborne, C.; Langdon, L.; Cooke, S.; Pope, D. Spherical equivalence of cylindrical explosives: Effect of charge shape on deflection of blast-loaded plates. Int. J. Impact Eng. 2021, 155, 103892. [Google Scholar] [CrossRef]
- Yadav, H.; Gupta, N. Study of collapse of a free surface conical cavity due to a plane or spherical shock wave. Int. J. Impact Eng. 1985, 3, 217–232. [Google Scholar] [CrossRef]
- Xu, S.; Zheng, W.; Shao, X.; Cheng, W. Numerical method for predicting the blast wave in partially confined chamber. Math. Probl. Eng. 2018. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.; Liu, G.; Lam, K.; Zong, Z. Meshfree particle simulation of the detonation process for high explosives in shaped charge unlined cavity configurations. Shock Waves 2003, 6, 509–520. [Google Scholar] [CrossRef]
- Pka, D.; Bocian, A.; Bajkowski, M.; Magier, M. Numerical and experimental studies of the ŁK type shaped charge. Appl. Sci. 2020, 10, 6742. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, Z.; Jin, Y.; Zhen, J. The effect of cylindrical liner material on the jet formation and penetration capability of cylinder-cone-shaped charge. Materials 2022, 15, 3511. [Google Scholar] [CrossRef]
- Heuzé, O. General form of the Mie–Grüneisen equation of state. C. R. Mécanique 2012, 340, 679–687. [Google Scholar] [CrossRef]
- Shi, J.; Xiang, Z.; Zu, X.; Xiao, Q. Experimental and numerical investigation of jet performance based on Johnson-Cook model of liner material. Int. J. Impact Eng. 2022, 170, 104343. [Google Scholar] [CrossRef]
- Geum, Y. Numerical simulation of conical and linear-shaped charges using an Eulerian Elasto-Plastic Multi-Material Multi-Phase Flow model with detonation. Materials 2022, 15, 1700. [Google Scholar]
- Sherkar, P.; Shin, P.; Whittaker, A. Influence of Charge Shape and Point of Detonation on Blast-Resistant Design. J. Struct. Eng. 2015, 2, 04015109. [Google Scholar] [CrossRef]
- Hofreiter, L.; Berezutskyi, V.; Figuli, L. Soft Target Protection Theoretical Basis and Practical Measures. Soft Target Prot. 2015. [Google Scholar] [CrossRef]
- Hashemia, S.; Bradford, M. Numerical simulation of free-air explosion using LS-DYNA. Appl. Mech. Mater. 2014, 1, 780–785. [Google Scholar] [CrossRef]
- Wang, I. Simulation and experimental validation of the dynamic pressure of shock wave under free-field blast loading. J. Vibroeng. 2014, 7, 3547–3556. [Google Scholar]
- Sohaimi, A.; Arif, S.M.; Ishak, A. Using computational fluid dynamics (CFD) for blast wave propagation under structure. Procedia Comput. Sci. 2016, 1, 1202–1211. [Google Scholar] [CrossRef]
- Fedora, N.; Valge, S. Simulation of blast action on civil structures using ANSYS Autodyn. In Proceedings of the AIP Conference Proceedinge, Moscow, Russia, 3 July 2016. [Google Scholar]
- Xue, Q.; Li, S.; Xin, C.; Shi, L. Modeling of the whole process of shock wave overpressure of free-field air explosion. Def. Technol. 2016, 5, 815–820. [Google Scholar] [CrossRef]
- Dobratz, B.M. Physical properties. In Properties of Chemical Explosives and Explosive Simulants; Lawrence Livermore Laboratory: Livermore, CA, USA, 1972. [Google Scholar]
- Collins, G.; Imperial College London, London, UK. Applied Modelling and Computation Group. Personal communication, 2002. [Google Scholar]
- Chang, B.H.; Yin, J.P.; Cui, Z.; Liu, T. Numerical simulation of modified low-density jet penetrating shell charge. Def. Technol. 2015, 3, 426–437. [Google Scholar] [CrossRef]
- Meyers, M. Dynamic Behavior of Materials; John Wiley & Sons: Hoboken, NJ, USA, 1994; p. 240. [Google Scholar]
- Anderson, D.A.; Tannehill, J.C.; Pletcher, R.H. Mathematical procedure. In Computational Fluid Mechanics and Heat Transfer; Taylor & Francis: Abingdon, UK, 2020. [Google Scholar]
- Kwasniewski, L. Application of grid convergence index in FE computation. Bull. Pol. Acad. Sci. Tech. Sci. 2013, 1, 123–128. [Google Scholar] [CrossRef]
- Karimi, M.; Akdogan, G.; Dellimore, K.H.; Bradshaw, S.M. Quantification of numerical uncertainty in computational fluid dynamics modelling of hydrocyclones. Comput. Chem. Eng. 2012, 43, 45–54. [Google Scholar] [CrossRef]
- Roach, P. Quantification of Uncertainty in Computational Fluid Dynamics. Annu. Rev. Fluid Mech. 1997, 1, 123–1260. [Google Scholar] [CrossRef]
- Paudel, S.; Saenger, N. Grid refinement study for three dimensional CFD model involving incompressible free surface flow and rotating object. Comput. Fluids 2017, 143, 123–134. [Google Scholar] [CrossRef]
- Mejia, N.; Peralta, R.; Tapia, R.; Duran, R. Damage assessment of RC columns under the combined effects of contact explosion and axial loads by experimental and numerical investigations. Eng. Struct. 2022, 254, 113776. [Google Scholar] [CrossRef]







| Parameter | Unit | Pentolite 50/50 | TNT |
|---|---|---|---|
| Density | g/cm | 1.6 | 1.56 |
| Heat of Explosion | kcal/kg | 1300 | 1080 |
| Velocity of Detonation | m/s | 7418 | 6900 |
| Pressure of Detonation | kbar | 220 | 210 |
| Temperature of Explosion | K | 4497 | 3500 |
| Mesh | Pressure f [kPa] | ||||
|---|---|---|---|---|---|
| h | Gauge (2) | Gauge (3) | Gauge (4) | Gauge (5) | |
| [mm] | at 40 (mm) | at 80 (mm) | at 120 (mm) | at 160 (mm) | |
| 1 | 0.075 | 1.35 × 10 | 2.41 × 10 | 1.52 × 10 | 1.07 × 10 |
| 2 | 0.1 | 1.46 × 10 | 2.40 × 10 | 1.51 × 10 | 1.06 × 10 |
| 3 | 0.25 | 1.88 × 10 | 2.26 × 10 | 1.47 × 10 | 1.03 × 10 |
| 4 | 0.5 | 2.58 × 10 | 2.01 × 10 | 1.39 × 10 | 9.94 × 10 |
| 5 | 1 | 3.29 × 10 | 1.70 × 10 | 1.23 × 10 | 9.20 × 10 |
| 6 | 2 | 4.71 × 10 | 1.59 × 10 | 1.05 × 10 | 8.14 × 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mejía, N.; Mejía, R.; Toulkeridis, T. Characterization of Blast Wave Parameters in the Detonation Locus and Near Field for Shaped Charges. Mathematics 2022, 10, 3261. https://doi.org/10.3390/math10183261
Mejía N, Mejía R, Toulkeridis T. Characterization of Blast Wave Parameters in the Detonation Locus and Near Field for Shaped Charges. Mathematics. 2022; 10(18):3261. https://doi.org/10.3390/math10183261
Chicago/Turabian StyleMejía, Nestor, Rodrigo Mejía, and Theofilos Toulkeridis. 2022. "Characterization of Blast Wave Parameters in the Detonation Locus and Near Field for Shaped Charges" Mathematics 10, no. 18: 3261. https://doi.org/10.3390/math10183261
APA StyleMejía, N., Mejía, R., & Toulkeridis, T. (2022). Characterization of Blast Wave Parameters in the Detonation Locus and Near Field for Shaped Charges. Mathematics, 10(18), 3261. https://doi.org/10.3390/math10183261






