Research on Manufacturers’ Referral Strategy Considering Store Brand Retailers and Traditional Retailers
Abstract
:1. Introduction
2. Literature Review
2.1. Manufacturer Referral in the Supply Chain
2.2. Retailer Private Brands in the Supply Chain
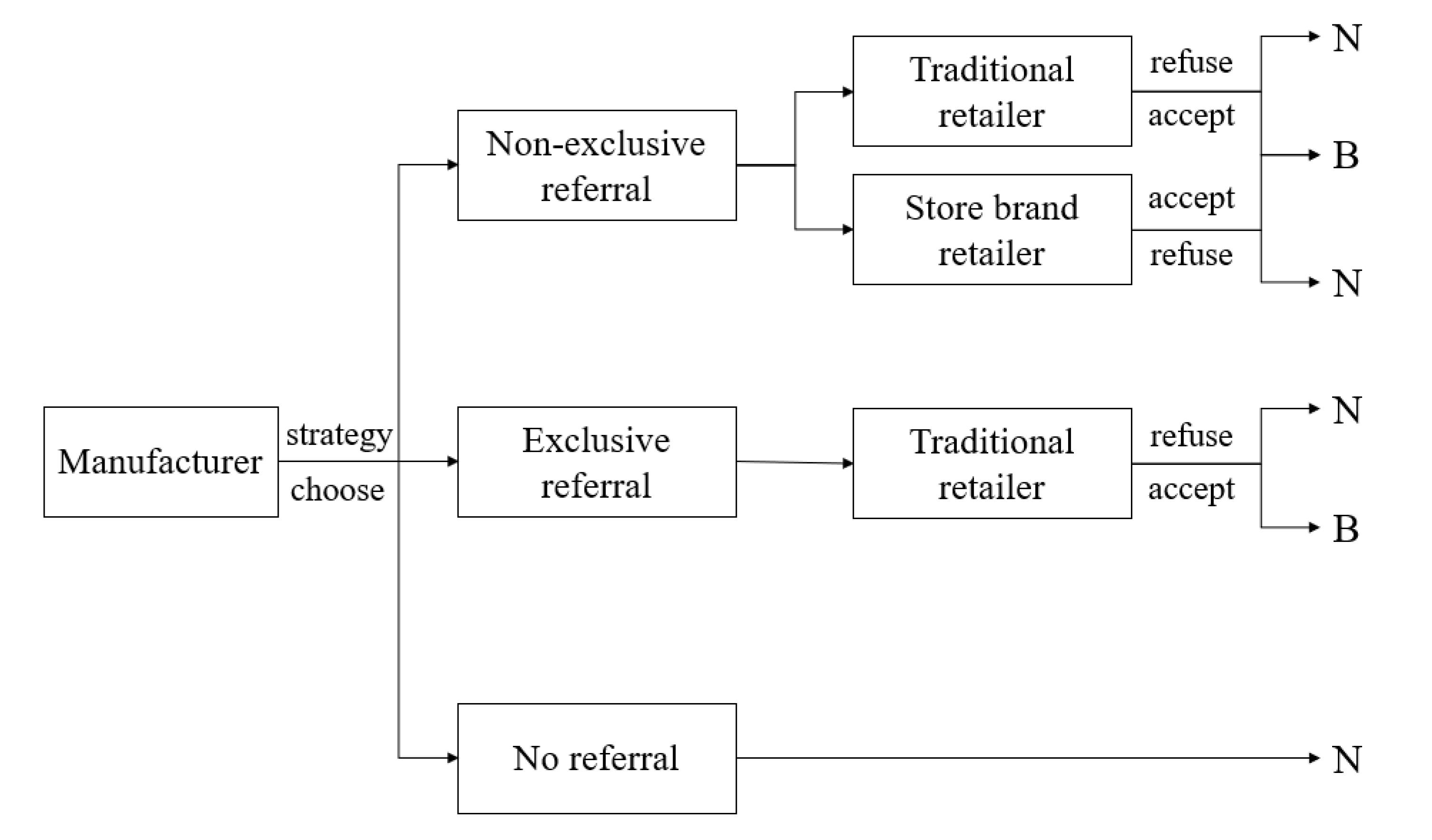
3. Model Description
3.1. No Referral (N)
3.2. Exclusive Referral to the Traditional Retailer (R)
3.3. Nonexclusive Referrals to Both Retailers (B)
4. Comparative Analysis of Order Quantity
5. Comparative Analysis of Member Cooperation
5.1. Analysis of the Manufacturer’s Referral Strategy
5.2. The Influence of Different Referral Strategies on the Traditional Retailer
5.3. The Influence of Different Referral Strategies on the Store Brand Retailer
6. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Athique, A. Integrated commodities in the digital economy. Media Cult. Soc. 2020, 42, 554–570. [Google Scholar] [CrossRef]
- Zhou, R.; Tang, D.; Da, D.; Chen, W.; Kong, L.; Boamah, V. Research on China’s Manufacturing Industry Moving towards the Middle and High-End of the GVC Driven by Digital Economy. Sustainability 2022, 14, 7717. [Google Scholar] [CrossRef]
- Tsay, A.A.; Agrawal, N. Channel conflict and coordination in the e-commerce age. Prod. Oper. Manag. 2004, 13, 93–110. [Google Scholar] [CrossRef]
- Han, F.; Li, L.; Lv, H.; Wang, H. Research on Brand Competition and Decisions in Supply Chains Under Manufacturer Information Referral. IEEE Access 2021, 9, 121414–121430. [Google Scholar] [CrossRef]
- Ennew, C.; Lockett, A.; Blackman, I.; Holland, C.P. Competition in Internet retail markets: The impact of links on web site traffic. Long Range Plan. 2005, 38, 359–372. [Google Scholar] [CrossRef]
- Wu, H.; Cai, G.; Chen, J.; Sheu, C. Online manufacturer referral to heterogeneous retailers. Prod. Oper. Manag. 2015, 24, 1768–1782. [Google Scholar] [CrossRef]
- Monteiro, R.C.P.A. How Can L’ Oréal Paris (Makeup) Be an Attractive Brand for Millennials in Portugal? Management from NOVA School of Business and Economics: Carcavelos, Portugal, 2017. [Google Scholar]
- Zhang, Y.; Hezarkhani, B. Competition in dual-channel supply chains: The manufacturers’ channel selection. Eur. J. Oper. Res. 2021, 291, 244–262. [Google Scholar] [CrossRef]
- Xu, L.X.; Xu, Q.; Liu, X. Wal-mart and carrefour′s supply chain management strategies in china. Int. J. Bus. Manag. 2014, 9, 155–161. [Google Scholar] [CrossRef]
- Neebe, K. Sustainability at Walmart: Success over the Long Haul. J. Appl. Corp. Financ. 2020, 32, 64–71. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Liu, Y.; Li, H. A coordination mechanism of supply chain with a retailer and two competitive suppliers. Complexity 2020, 2020, 2128497. [Google Scholar] [CrossRef]
- Zhang, N.; Huang, B. Research on Marketing Strategies of E-Commerce Enterprises on Suning E-Commerce under New External Conditions. For. Chem. Rev. 2022, 18, 157–165. [Google Scholar]
- Zhou, C.; Ma, N.; Cui, X.; Liu, Z. The impact of online referral on brand market strategies with consumer search and spillover effect. Soft Comput. 2020, 24, 2551–2565. [Google Scholar] [CrossRef]
- Masyita, D.A.; Yuliati, A.L. Pengaruh brand ambassador dian sastrowardoyo terhadap brand image produk makeup L’OREAL PARIS (studi pada konsumen L’OREAL kota BANDUNG). J. Ris. Akunt. Mercu Buana 2017, 3, 41–47. [Google Scholar] [CrossRef]
- Hussain, S.W.; Qureshi, J.A.; Mubeen, M.; Asrar, Z. Local players giving a run for the share to a global giant: A case study of Pampers brand of Proctor and Gamble Pakistan. Int. J. Exp. Learn. Case Stud. 2020, 5, 122–134. [Google Scholar]
- Tahirov, N.; Glock, C.H. Manufacturer encroachment and channel conflicts: A systematic review of the literature. Eur. J. Oper. Res. 2022, 302, 403–426. [Google Scholar] [CrossRef]
- Ghose, A.; Mukhopadhyay, T.; Rajan, U. The impact of Internet referral services on a supply chain. Inf. Syst. Res. 2007, 18, 300–319. [Google Scholar] [CrossRef]
- Wei, L.; Zhang, J.; Zhu, G. Incentive of retailer information sharing on manufacturer volume flexibility choice. Omega 2021, 100, 102210. [Google Scholar] [CrossRef]
- Li, W.; Chen, J.; Chen, B. Supply chain coordination with customer returns and retailer’s store brand product. Int. J. Prod. Econ. 2018, 203, 69–82. [Google Scholar] [CrossRef]
- Li, Z.L.; Guo, Q.; Nie, J.J. Dual-channel manufacturer’s referral strategies based on risk aversion. Chin. J. Manag. Sci. 2020, 28, 112–121. [Google Scholar]
- Karray, S.; Zaccour, G. Could co-op advertising be a manufacturer’s counter strategy to store brands? J. Bus. Res. 2009, 59, 1008–1015. [Google Scholar] [CrossRef]
- Amrouche, N.; Yan, R. National brand’s local advertising and wholesale-price incentive under prior versus no prior information. Ind. Mark. Manag. 2017, 64, 161–174. [Google Scholar] [CrossRef]
- Huang, J.; Liu, J.; Luo, S. Strategic Interactions between Manufacturer’s Direct Selling and Retailer’s Store Brand Introduction Decisions in Dual-Channel Supply Chain. In Proceedings of the 2009 International Conference on Management of e-Commerce and e-Government, Nanchang, China, 16–19 September 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 331–334. [Google Scholar]
- Ru, J.; Shi, R.; Zhang, J. Does a store brand always hurt the manufacturer of a competing national brand? Prod. Oper. Manag. 2015, 24, 272–286. [Google Scholar] [CrossRef]
- Kim, D.; Jung, G.O.; Park, H.H. Manufacturer’s retailer dependence: A private branding perspective. Ind. Mark. Manag. 2015, 49, 95–104. [Google Scholar] [CrossRef]
- Choi, S.C. Defensive strategy against a private label: Building brand premium for retailer cooperation. J. Retail. Consum. Serv. 2017, 34, 335–339. [Google Scholar] [CrossRef]
- Amrouche, N.; Yan, R. Implementing online store for national brand competing against private label. J. Bus. Res. 2012, 65, 325–332. [Google Scholar] [CrossRef]
- Hara, R.; Matsubayashi, N. Premium store brand: Product development collaboration between retailers and national brand manufacturers. Int. J. Prod. Econ. 2017, 185, 128–138. [Google Scholar] [CrossRef]
- Bauner, C.; Jaenicke, E.; Wang, E.; Wu, P.C. Couponing strategies in competition between a national brand and a private label product. J. Retail. 2019, 95, 57–66. [Google Scholar] [CrossRef]
- Huang, Z.; Feng, T. Money-back guarantee and pricing decision with retailer’s store brand. J. Retail. Consum. Serv. 2020, 52, 101897. [Google Scholar] [CrossRef]
- Luo, X.; Ge, L.; Chen, L.; Li, J. Online Channels and Store Brands: Strategic Interactions. J. Assoc. Inf. Syst. 2021, 22, 2. [Google Scholar] [CrossRef]
- Li, X.; Cai, X.; Chen, J. Quality and Private Label Encroachment Strategy. Prod. Oper. Manag. 2022, 31, 374–390. [Google Scholar] [CrossRef]
- Chen, Z.; Xu, H. Private labels and product quality under asymmetric information. J. Econ. Manag. Strategy 2021, 30, 743–759. [Google Scholar] [CrossRef]
- Nikolaeva, R.; Sriram, S. The moderating role of consumer and product characteristics on the value of customized on-line recommendations. Int. J. Electron. Commer. 2006, 11, 101–123. [Google Scholar] [CrossRef]
- Kumar, N.; Ruan, R. On manufacturers complementing the traditional retail channel with a direct online channel. Quant. Mark. Econ. 2006, 4, 289–323. [Google Scholar] [CrossRef]
- Cai, G.G.; Zhang, Z.G.; Zhang, M. Game theoretical perspectives on dual-channel supply chain competition with price discounts and pricing schemes. Int. J. Prod. Econ. 2009, 117, 80–96. [Google Scholar] [CrossRef]
- Cai, G.G.; Ying-Ju, C. In-store referrals on the internet. J. Retail. 2011, 87, 563–578. [Google Scholar] [CrossRef]
- Symeonidis, G. Comparing Cournot and Bertrand equilibria in a differentiated duopoly with product R&D. Int. J. Ind. Organ. 2003, 21, 39–55. [Google Scholar]
- Cai, G.; Dai, Y.; Zhou, S.X. Exclusive channels and revenue sharing in a complementary goods market. Mark. Sci. 2012, 31, 172–187. [Google Scholar] [CrossRef]
- Chen, J.X.; Liang, L.; Yao, D.Q.; Sun, S. Price and quality decisions in dual-channel supply chains. Eur. J. Oper. Res. 2017, 259, 935–948. [Google Scholar] [CrossRef]
- Chen, J.; Stanko, D. National and store brand advertising strategies. J. Oper. Res. Soc. 2015, 66, 1237–1249. [Google Scholar] [CrossRef]
- Yang, D.H.; Gao, X. Online retailer recommender systems: A competitive analysis. Int. J. Prod. Res. 2017, 55, 4089–4109. [Google Scholar] [CrossRef]
- Dekimpe, M.G.; Steenkamp, J.B.E.; Mellens, M.; Abeele, P.V. Decline and variability in brand loyalty. Int. J. Res. Mark. 1997, 14, 405–420. [Google Scholar] [CrossRef]
- Pi, Z.; Fang, W.; Zhang, B. Service and pricing strategies with competition and cooperation in a dual-channel supply chain with demand disruption. Comput. Ind. Eng. 2019, 138, 106130. [Google Scholar] [CrossRef]





| Parameter | Meaning |
|---|---|
| The consumer utility | |
| The market size of the traditional retailer | |
| The referral level of the manufacturer | |
| The intensity of market competition | |
| The wholesale price | |
| The consumer market loss rate of the manufacturer | |
| The retail price in Li (i = 1,2,3) | |
| The product sales in the original market | |
| The product sales in the referral market | |
| The profit of the manufacturer/traditional retailer/store brand retailer |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, F.; Wang, H.; Lv, H.; Li, B. Research on Manufacturers’ Referral Strategy Considering Store Brand Retailers and Traditional Retailers. Mathematics 2022, 10, 3326. https://doi.org/10.3390/math10183326
Han F, Wang H, Lv H, Li B. Research on Manufacturers’ Referral Strategy Considering Store Brand Retailers and Traditional Retailers. Mathematics. 2022; 10(18):3326. https://doi.org/10.3390/math10183326
Chicago/Turabian StyleHan, Feiyan, Herui Wang, Hongyu Lv, and Bo Li. 2022. "Research on Manufacturers’ Referral Strategy Considering Store Brand Retailers and Traditional Retailers" Mathematics 10, no. 18: 3326. https://doi.org/10.3390/math10183326
APA StyleHan, F., Wang, H., Lv, H., & Li, B. (2022). Research on Manufacturers’ Referral Strategy Considering Store Brand Retailers and Traditional Retailers. Mathematics, 10(18), 3326. https://doi.org/10.3390/math10183326





