Fractional-Order Multivariable Adaptive Control Based on a Nonlinear Scalar Update Law
Abstract
:1. Introduction
- we design a new FOMRAC scheme to handle the parameter uncertainty and to ensure the system error stability and closed-loop signal boundedness;
- using the proposed FOMRAC framework, only one parameter online update is needed such that the control scheme is computationally inexpensive;
- we conduct a complete theoretical analysis of the boundedness of all signals involved in this adaptive scheme and the convergence to zero of the mean value of the squared norm of the system error for the proposed control architecture;
- we verify the effectiveness of this control design by two illustrative numerical examples.
2. Preliminaries
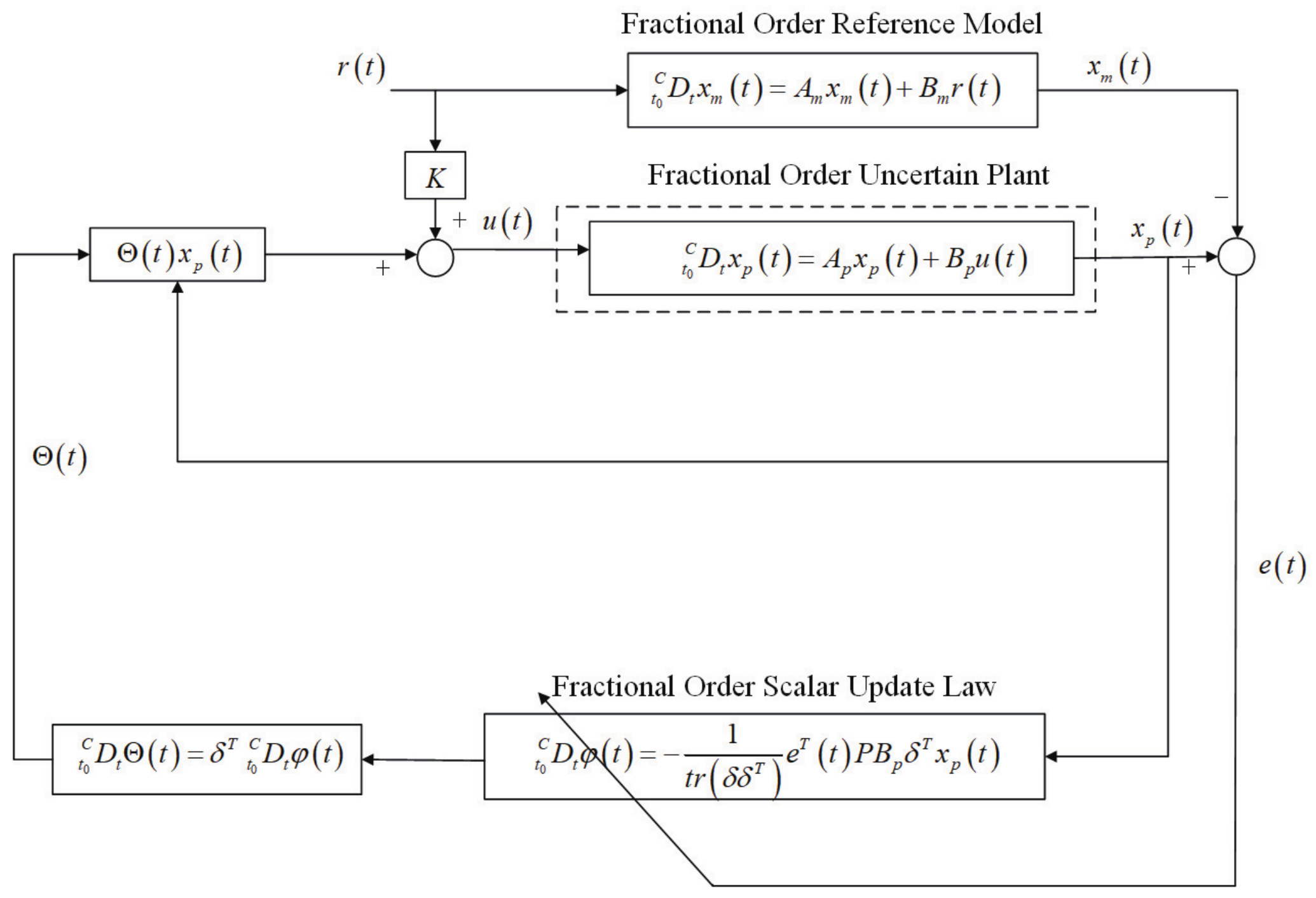
3. FOMRAC Problem
4. Main Results
- (i)
- The tracking error , the scalar function , the system state , the estimation error and parameter remain bounded for all ;
- (ii)
- The mean value of converges to zero when .
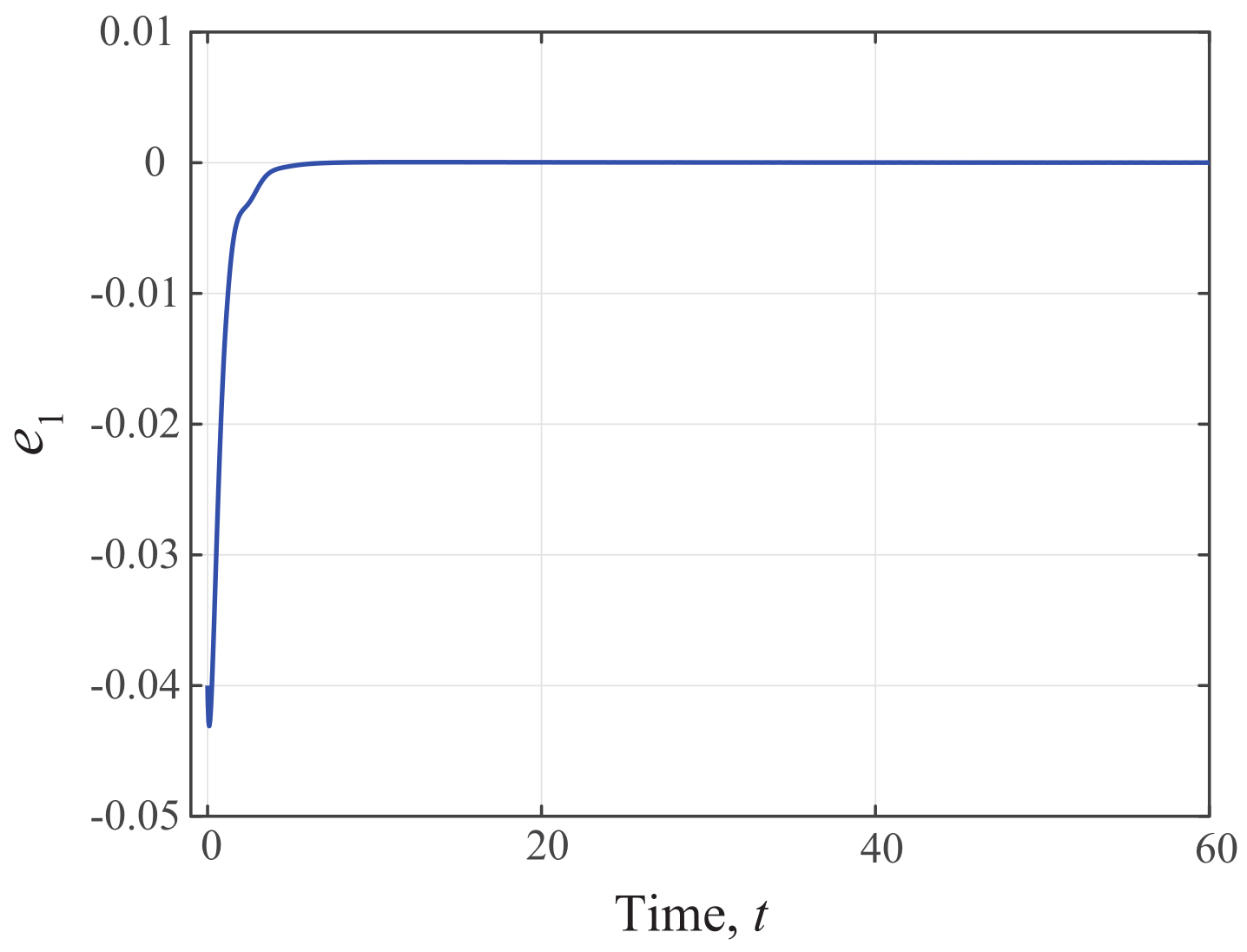
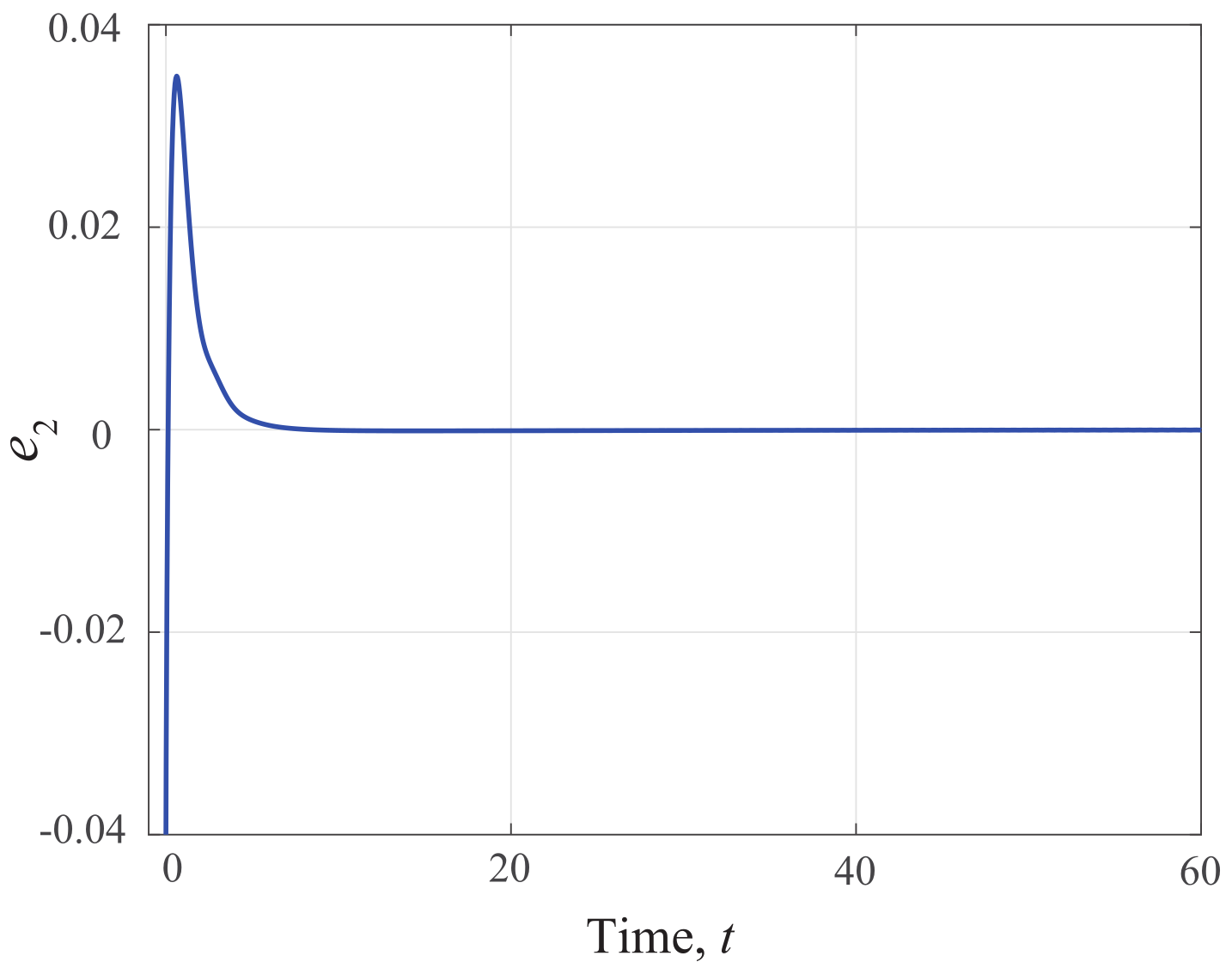
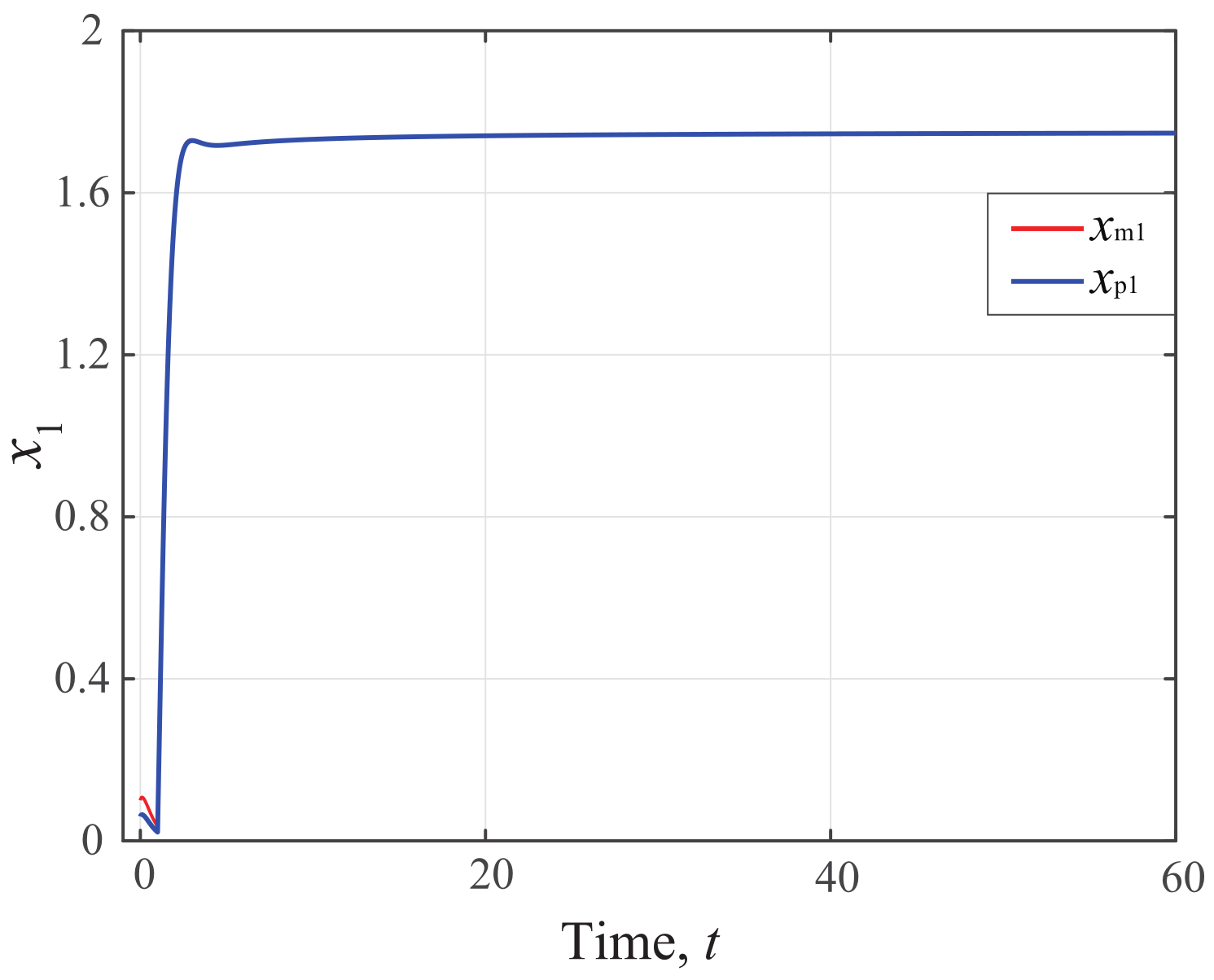
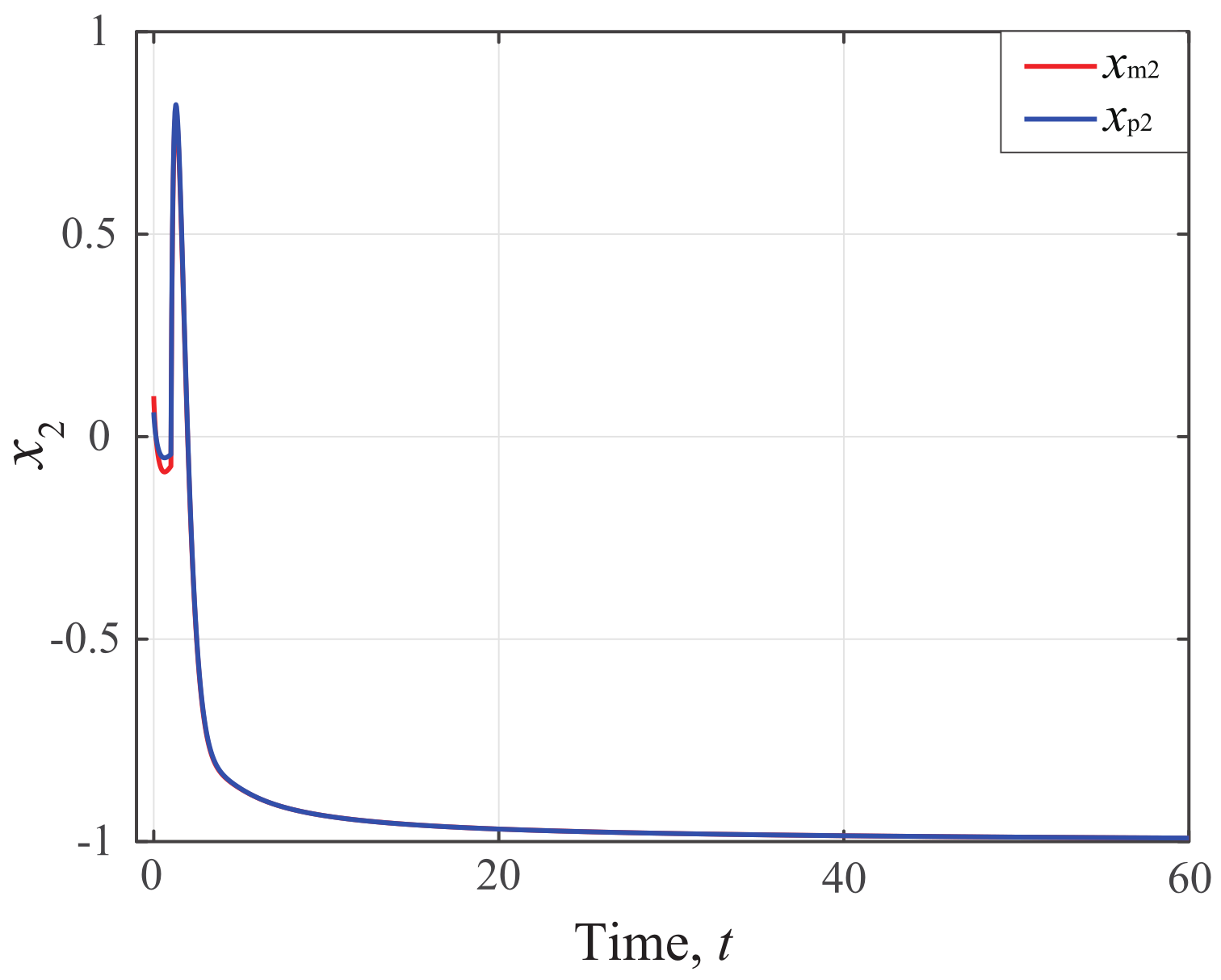
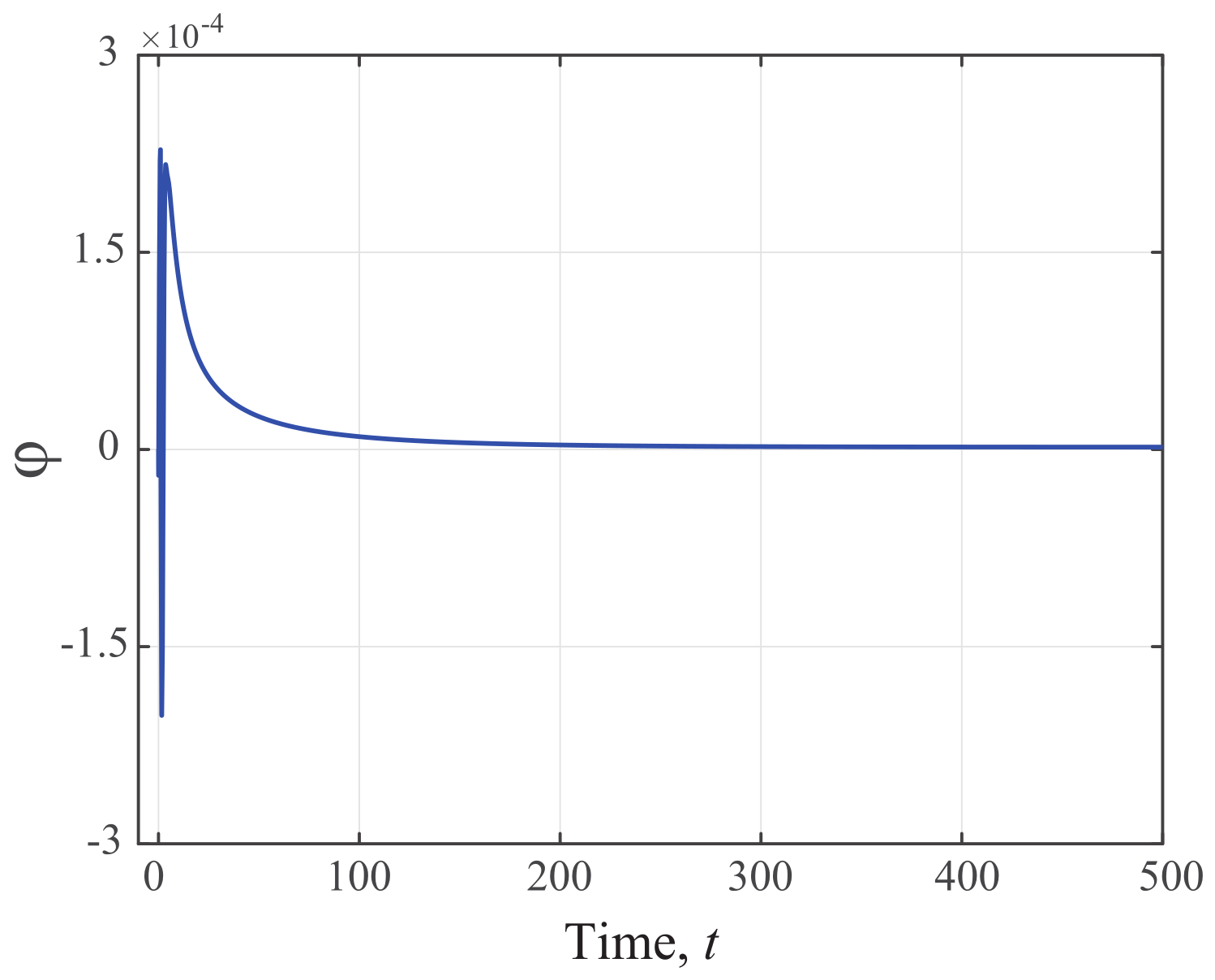
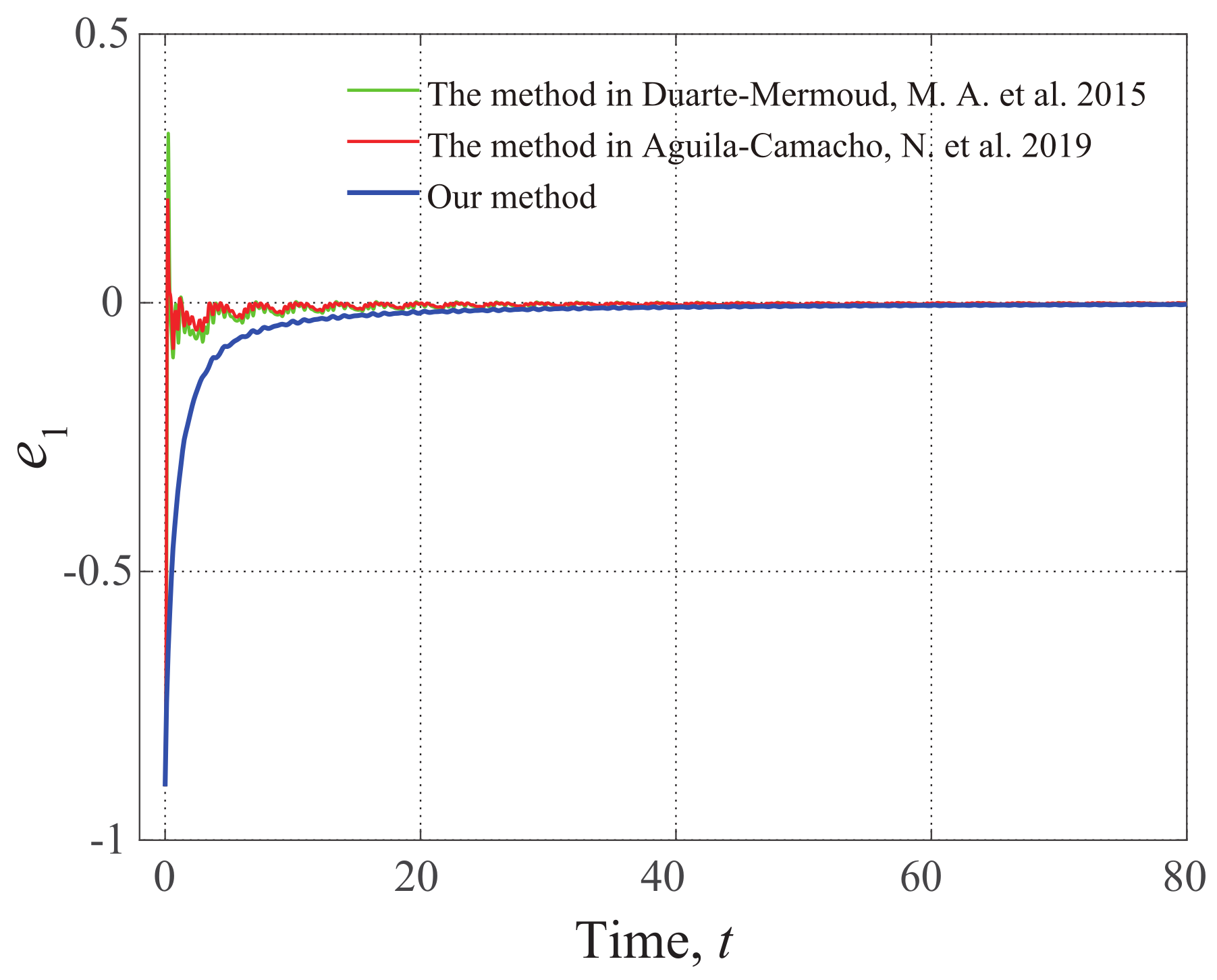
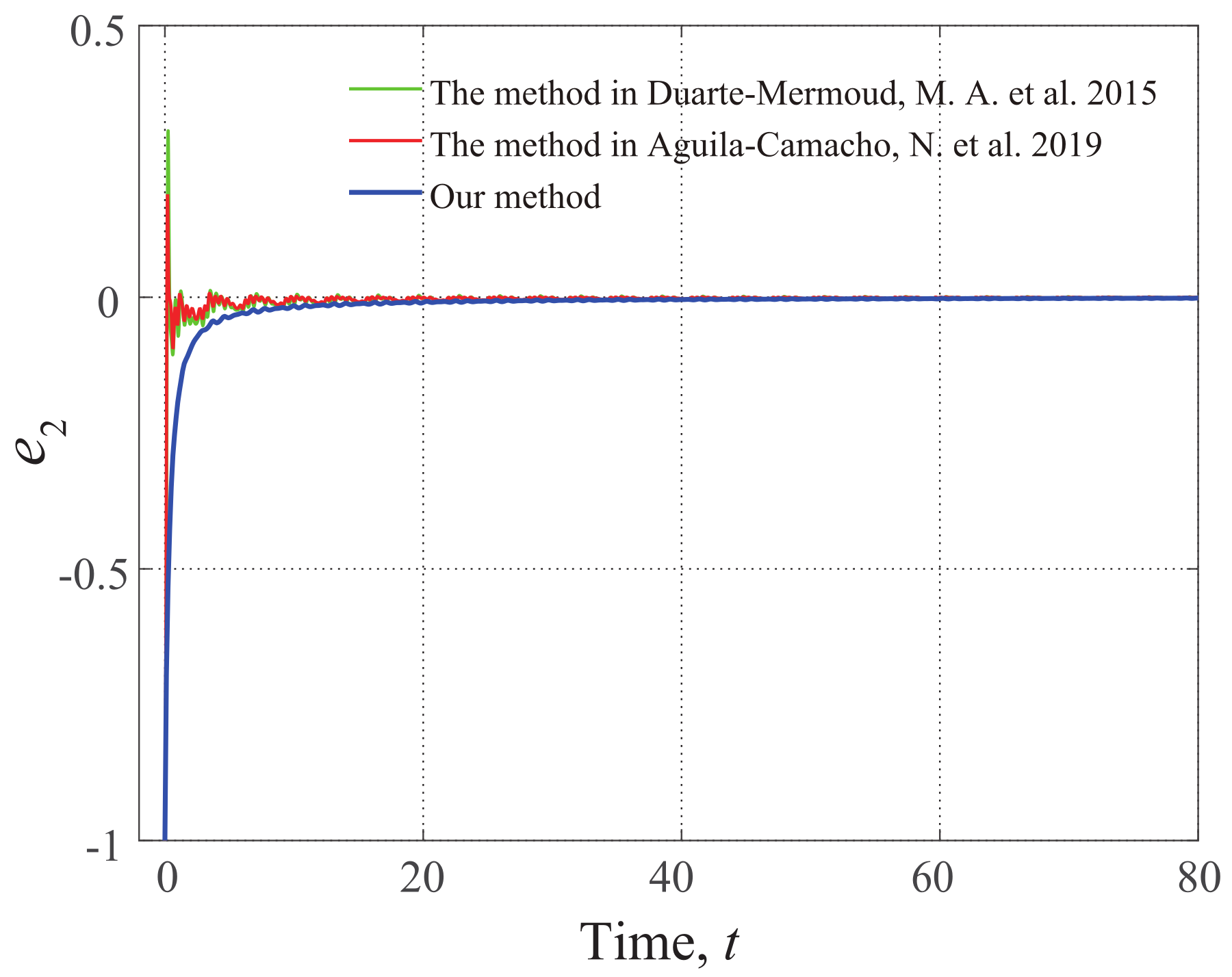
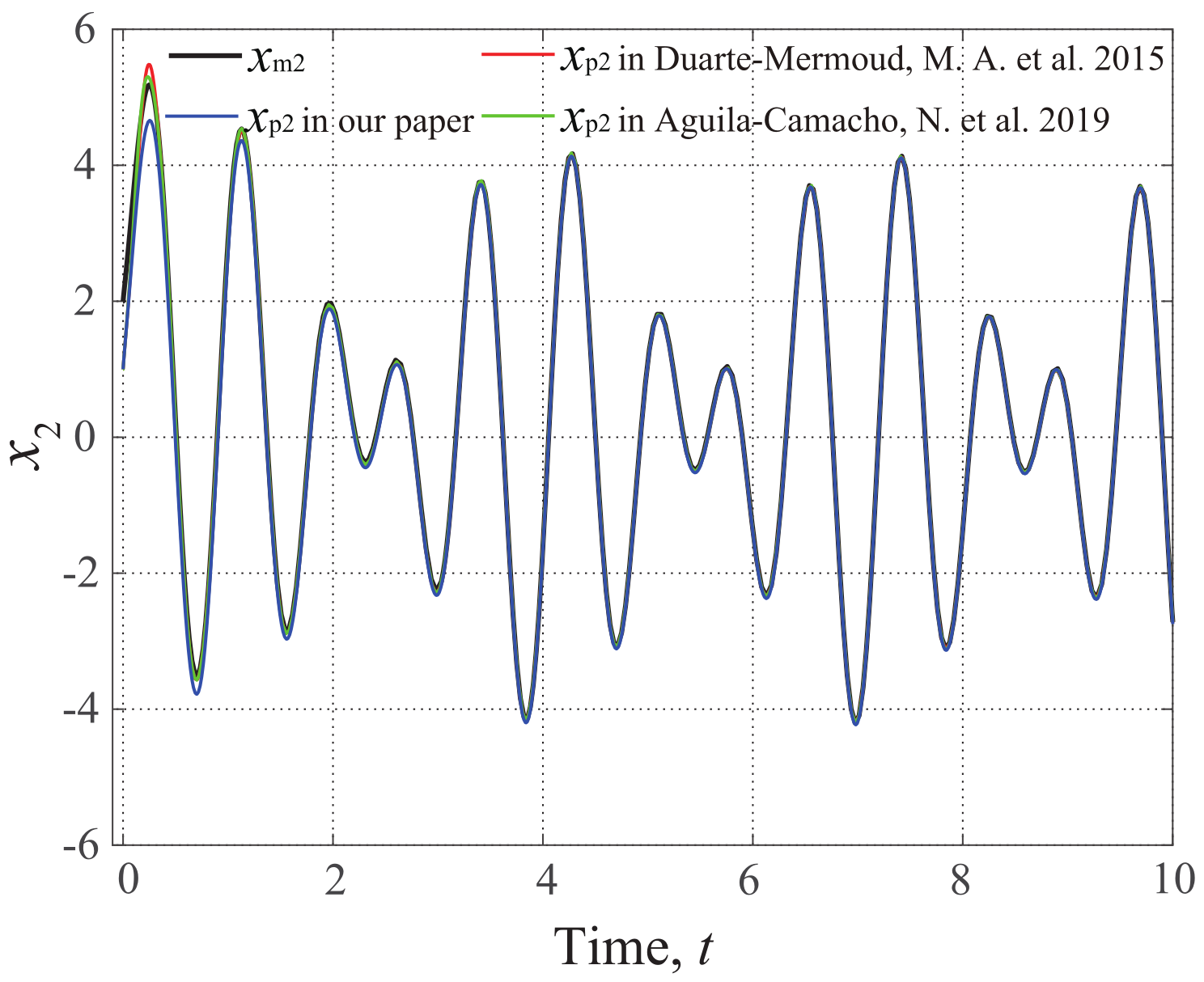
5. Simulation Example
External Disturbance
6. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ioannou, P.A.; Sun, J. Robust Adaptive Control; Prentice-Hall: Hoboken, NJ, USA, 1996. [Google Scholar]
- Nguyen, N.T. Model Reference Adaptive Control: A Primer; Springer: Belmont, CA, USA, 2018. [Google Scholar]
- Kahouli, O.; Jmal, A.; Naifar, O.; Nagy, A.M.; Ben Makhlouf, A. New Result for the Analysis of Katugampola Fractional-Order Systems-Application to Identification Problems. Mathematics 2022, 10, 1814. [Google Scholar] [CrossRef]
- Rapaic, M.R.; Pisano, A. Variable-order fractional operators for adaptive order and parameter estimation. IEEE Trans. Autom. Control 2014, 59, 798–803. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Feckan, M.; Danca, M.-F. Stability, Periodicity, and Related Problems in Fractional-Order Systems. Mathematics 2022, 10, 2040. [Google Scholar] [CrossRef]
- Aguila-Camacho, N.; Duarte-Mermoud, M.A. Fractional adaptive control for an automatic voltage regulator. ISA Trans. 2013, 52, 807–815. [Google Scholar] [CrossRef]
- Koszewnik, A.; Pawuszewicz, E.; Ostaszewski, M. Experimental Studies of the Fractional PID and TID Controllers for Industrial Process. Int. J. Control Autom. Syst. 2021, 19, 1847–1862. [Google Scholar] [CrossRef]
- Shakibjoo, A.D.; Moradzadeh, M.; Moussavi, S.Z.; Mohammadzadeh, A.; Vandevelde, L. Load frequency control for multi-area power systems: A new type-2 fuzzy approach based on Levenberg-Marquardt algorithm. ISA Trans. 2022, 121, 40–52. [Google Scholar] [CrossRef]
- Angel, L.; Viola, J. Fractional order PID for tracking control of a parallel robotic manipulator type delta. ISA Trans. 2018, 79, 172–188. [Google Scholar] [CrossRef]
- Djebbri, S.; Ladaci, S.; Metatla, A.; Balaska, H. Fractional-order model reference adaptive control of a multi-source renewable energy system with coupled DC/DC converters power compensation. Energy Syst. 2020, 11, 315–355. [Google Scholar] [CrossRef]
- Abuaisha, T.; Kertzscher, J. Fractional-order modelling and parameter identification of electrical coils. Fract. Calc. Appl. Anal. 2019, 22, 193–206. [Google Scholar] [CrossRef]
- Nikan, O.; Avazzadeh, Z.; Tenreiro Machado, J.A. Numerical approach for modeling fractional heat conduction in porous medium with the generalized Cattaneo model. Appl. Math. Model. 2021, 100, 107–124. [Google Scholar] [CrossRef]
- Nikan, O.; Avazzadeh, Z. Numerical simulation of fractional evolution model arising in viscoelastic mechanics. Appl. Numer. Math. 2021, 169, 303–320. [Google Scholar] [CrossRef]
- Nikan, O.; Molavi-Arabshai, S.M.; Jafari, H. Numerical simulation of the nonlinear fractional regularized long-wave model arising in ion acoustic plasma waves. Discret. Contin. Dyn. Syst. Ser. S 2018, 14, 3685. [Google Scholar] [CrossRef]
- Prasad, R.; Kumar, K.; Dohar, R. Caputo fractional order derivative model of Zika virus transmission dynamics. J. Math. Comput. Sci. 2023, 28, 145–157. [Google Scholar] [CrossRef]
- Akram, T.; Abbas, M.; Ali, A. A numerical study on time fractional Fisher equation using an extended cubic B-spline approximation. J. Math. Comput. Sci. 2021, 22, 85–96. [Google Scholar] [CrossRef]
- Nikan, O.; Avazzadeh, Z.; Tenreiro Machado, J.A. A local stabilized approach for approximating the modified time-fractional diffusion problem arising in heat and mass transfer. J. Adv. Res. 2021, 32, 45–60. [Google Scholar] [CrossRef]
- Shi, B.; Yuan, J.; Dong, C. On fractional model reference adaptive control. Sci. World J. 2014, 2014, 521625. [Google Scholar] [CrossRef]
- Cheng, S.S.; Wei, Y.H.; Chen, Y.Q.; Wang, Y.; Liang, Q. Fractional order multivariable composite model reference adaptive control. Int. J. Adapt. Control Signal Process. 2017, 31, 1467–1480. [Google Scholar] [CrossRef]
- Aguila-Camacho, N.; Duarte-Mermoud, M.A.; Gallegos, J.A. Lyapunov functions for fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2951–2957. [Google Scholar] [CrossRef]
- Aguila-Camacho, N.; Duarte-Mermoud, M.A. Boundedness of the solutions for certain classes of fractional differential equations with application to adaptive systems. ISA Trans. 2016, 60, 82–88. [Google Scholar] [CrossRef]
- Duarte-Mermoud, M.A.; Aguila-Camacho, N.; Gallegos, J.A.; Castro-Linares, R. Using general quadratic Lyapunov functions to prove Lyapunov uniform stability for fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 650–659. [Google Scholar] [CrossRef]
- Aguila-Camacho, N.; Gallegos, J.A.; Duarte-Mermoud, M.A. Analysis of fractional order error models in adaptive systems: Mixed order cases. Fract. Calc. Appl. Anal. 2019, 22, 1113–1132. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems; Prentice-Hall: Hoboken, NJ, USA, 1996. [Google Scholar]
- Haddad, W.M.; Chellaboina, V.S. Nonlinear Dynamical Systems and Control—A Lyapunov-Based Approach; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, F.; Hou, X.; Tian, T. Fractional-Order Multivariable Adaptive Control Based on a Nonlinear Scalar Update Law. Mathematics 2022, 10, 3385. https://doi.org/10.3390/math10183385
Yan F, Hou X, Tian T. Fractional-Order Multivariable Adaptive Control Based on a Nonlinear Scalar Update Law. Mathematics. 2022; 10(18):3385. https://doi.org/10.3390/math10183385
Chicago/Turabian StyleYan, Fang, Xiaorong Hou, and Tingting Tian. 2022. "Fractional-Order Multivariable Adaptive Control Based on a Nonlinear Scalar Update Law" Mathematics 10, no. 18: 3385. https://doi.org/10.3390/math10183385
APA StyleYan, F., Hou, X., & Tian, T. (2022). Fractional-Order Multivariable Adaptive Control Based on a Nonlinear Scalar Update Law. Mathematics, 10(18), 3385. https://doi.org/10.3390/math10183385






