On Some Properties of Addition Signed Cayley Graph
Abstract
1. Introduction
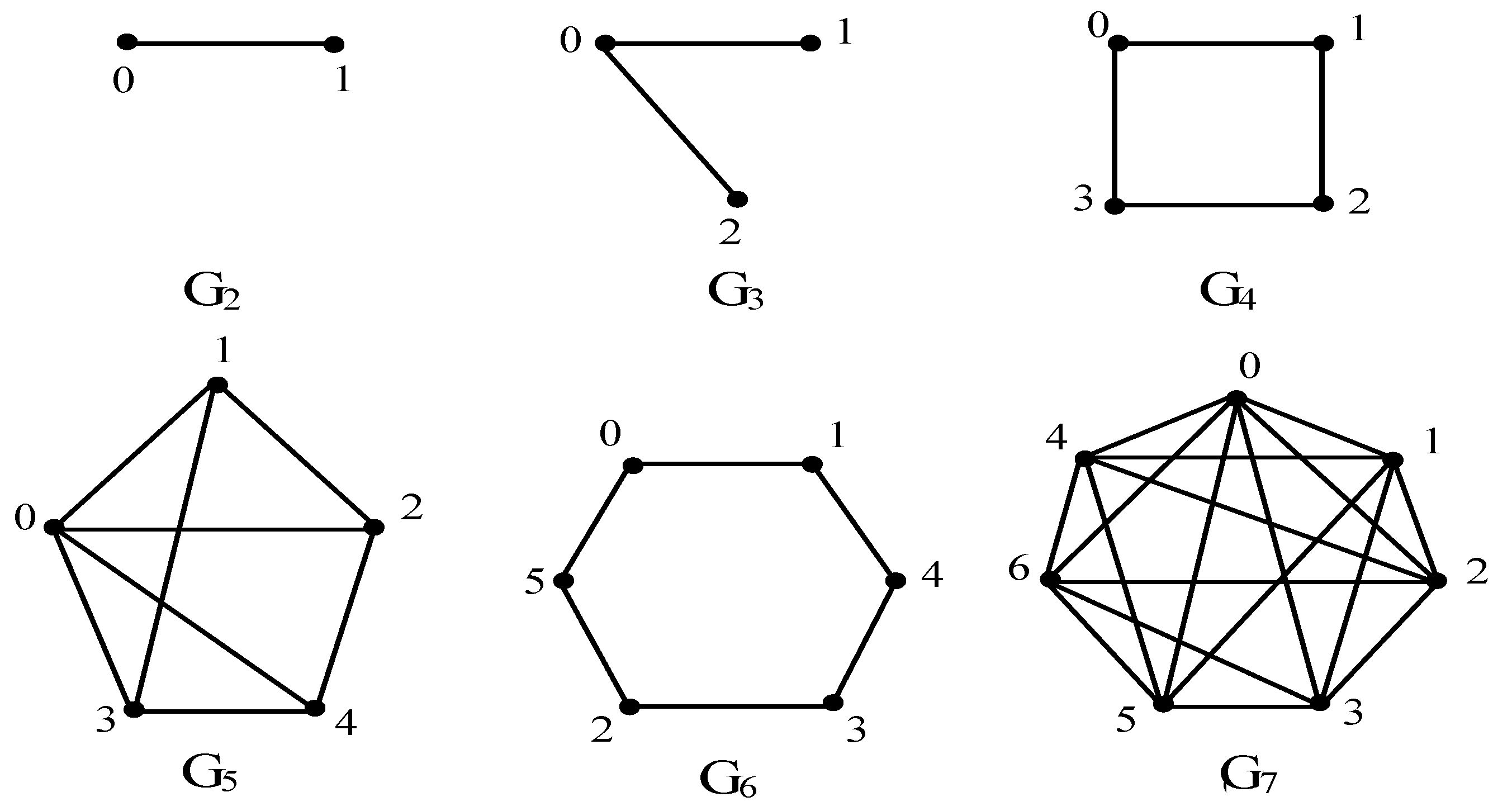
Addition Signed Cayley Graph
2. Some Properties of
2.1. Balancing in
- , .
- , .
- .
2.2. Clusterability in
2.3. Sign-Compatibility in
2.4. -Consistency of
3. Balance in Certain Derived Signed Graphs of
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Harary, F. Graph Theory; Addison-Wesley Publ. Comp.: Boston, MA, USA, 1969. [Google Scholar]
- West, D.B. Introduction to Graph Theory; Prentice-Hall of India Pvt. Ltd.: New Delhi, India, 1996. [Google Scholar]
- Zaslavsky, T. A mathematical bibliography of signed and gain graphs and allied areas. Electron. J. Combin. 2018, DS8. [Google Scholar] [CrossRef]
- Zaslavsky, T. Glossary of signed and gain graphs and allied areas. Electron. J. Combin. 1998, DS9. Available online: https://www.combinatorics.org/files/Surveys/ds9/ds9v1-1998.pdf (accessed on 11 July 2022).
- Harary, F. On the notion of balance of a signed graph. Mich. Math. 1953, 2, 143–146. [Google Scholar] [CrossRef]
- Sinha, D.; Wardak, O.; Dhama, A. On Some Properties of Signed Cayley Graph Sn. Mathematics 2022, 10, 2633. [Google Scholar] [CrossRef]
- Zaslavsky, T. Signed analogs of bipartite graphs. Discrete Math. 1998, 179, 205–216. [Google Scholar] [CrossRef]
- Davis, J.A. Clustering and structural balance in graphs. Hum. Relat. 1967, 20, 181–187. [Google Scholar] [CrossRef]
- Acharya, M.; Sinha, D. Common-edge sigraphs. AKCE Int. J. Graphs Comb. 2006, 3, 115–130. [Google Scholar]
- Behzad, M.; Chartrand, G.T. Line coloring of signed graphs. Elem. Math. 1969, 24, 49–52. [Google Scholar]
- Gill, M.K. Contribution to Some Topics in Graph Theory and It’s Applications. Ph.D. Thesis, Indian Institute of Technology, Bombay, India, 1969. [Google Scholar]
- Sharma, P.; Acharya, M. Balanced signed total graphs of commutative ring. Graphs Combin. 2016, 32, 1585–1597. [Google Scholar] [CrossRef]
- Sinha, D. New Frontiers in the Theory of Signed Graphs. Ph.D. Thesis, University of Delhi, New Delhi, India, 2005. [Google Scholar]
- Acharya, B.D. A characterization of consistent marked graphs. Nat. Acad. Sci. Lett. USA 1983, 6, 431–440. [Google Scholar]
- Sinha, D.; Acharya, M. Characterization of signed graphs whose iteratied line graphs are balanced and S-consistent. Bull. Malays. Math. Sci. Soc. 2016, 39, 297–306. [Google Scholar] [CrossRef]
- Zaslavsky, T. Consistency in the naturally vertex-signed line graph of a signed graph. Bull. Malays. Math. Sci. Soc. 2016, 39, 307–314. [Google Scholar] [CrossRef]
- Evans, A.B.; Fricke, G.H.; Maneri, C.C.; McKee, T.A.; Perkel, M. Representations of graphs modulo n. J. Graph Theory 1994, 18, 801–815. [Google Scholar] [CrossRef]
- Sinha, D.; Dhama, A. Unitary Cayley Meet Signed Graphs. Electron. Notes Discret. Math. 2017, 63, 425–434. [Google Scholar] [CrossRef]
- Sinha, D.; Garg, P. On the unitary Cayley signed graphs. Electron. J. Comb. 2011, 18, P229. [Google Scholar] [CrossRef]
- Sinha, D.; Garg, P.; Singh, A. Some properties of unitary addition Cayley graphs. Notes Number Theory Discret. Math. 2011, 17, 49–59. [Google Scholar]
- Sampathkumar, E. Point-signed and line-signed graphs. Natl. Acad. Sci. Lett. 1984, 7, 91–93. [Google Scholar]
- Sinha, D.; Dhama, A. Sign-Compatibility of common-edge signed graphs and 2-path signed graphs. Graph Theory Notes N.Y. 2013, 65, 55–61. [Google Scholar]
- Acharya, M.; Sinha, D. Characterizations of line sigraphs. Nat. Acad. Sci. Lett. 2005, 28, 31–34. [Google Scholar] [CrossRef]
- Acharya, M. ×-line sigraph of a sigraph. J. Combin. Math. Combin. Comput. 2009, 69, 103–111. [Google Scholar]
- Rose, H.E. A Course in Number Theory; Oxford Science Publications; Oxford University Press: Oxford, UK, 1988. [Google Scholar]
- Hoede, C. A characterization of consistent marked graphs. J. Graph Theory 1992, 16, 17–23. [Google Scholar] [CrossRef]
- Acharya, M.; Sinha, D. A Characterization of Sigraphs Whose Line Sigraphs and Jump Sigraphs are Switching Equivalent. Graph Theory Notes N. Y. 2003, 44, 30–34. [Google Scholar]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wardak, O.; Dhama, A.; Sinha, D.
On Some Properties of Addition Signed Cayley Graph
Wardak O, Dhama A, Sinha D.
On Some Properties of Addition Signed Cayley Graph
Wardak, Obaidullah, Ayushi Dhama, and Deepa Sinha.
2022. "On Some Properties of Addition Signed Cayley Graph
Wardak, O., Dhama, A., & Sinha, D.
(2022). On Some Properties of Addition Signed Cayley Graph






