Synthetic Data Generator for Solving Korean Arithmetic Word Problem
Abstract
:1. Introduction
2. Related Work
- A rule-based system is a method to derive an expression by matching the text of the problem to a manually created rule and schema pattern. Ref. [18] used four predefined schemas: change-in, change-out, combine, and compare. The text was transformed into suggested propositions, and the answer was obtained via simple reasoning. Furthermore, Ref. [19] developed a system that can solve multistep arithmetic problems by dividing the schema of [18] in more detail.
- A statistic-based method employs traditional machine learning to identify objects, variables, and operators within the text of a given problem, and the required answer is derived by adopting logical reasoning procedures. Ref. [20] used three classifiers to select problem-solving elements within a sentence. More specifically, the quantity pair classifier extracts the quantity associated with the derivation of an answer. The operator classifier then selects the operator with the highest probability for a given problem from among the basic operators (e.g., {+, −, ×, and /}). The order classifier is used for problems that require an operator (i.e., subtraction and division) related to the order of the operands. Ref. [21] proposed a logic template called Formula that analyzes text and selects key elements for equation inference to solve multistep math problems. The given problem is identified as the most probable equation using a log-linear model and converted into an arithmetic expression.
- Deep learning has attracted increasing attention owing to the activation of big data and the development of hardware and algorithms. The primary advantage of deep learning is that it can effectively learn the features of the large datasets without the need for human intervention. In [22], the Deep Neural Solver was proposed, which introduced deep learning solvers using seq2seq structures and equation templates. Subsequently, this influenced the emergence of various solvers with seq2seq structures structures [23,24]. Thereafter, a solver with other structures emerged with the advent of the Transformer. Ref. [25] used a Transformer to analyze the notations, namely prefix, infix, and postfix that resulted in enhanced performance when deriving arithmetic expressions. Additionally, Ref. [26] proposed an equation generation model that yielded mathematical expressions from the problem text without equation templates using expression tokens and operand-context pointers.
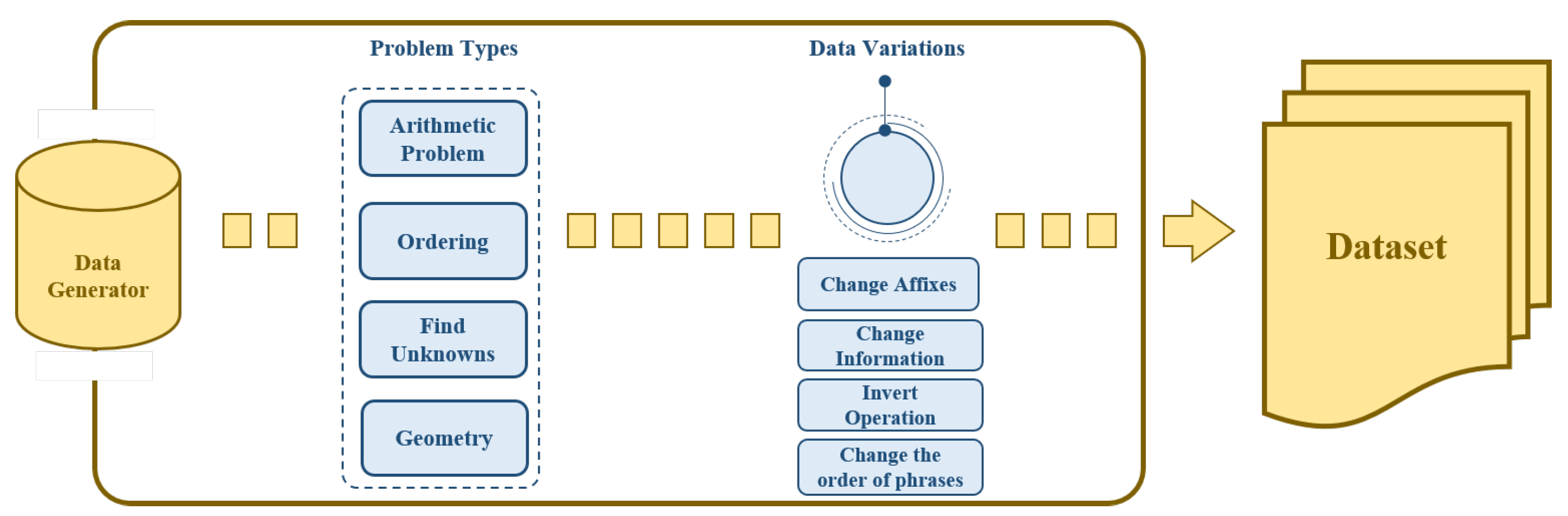
3. Data Generator
3.1. Types of Problems
3.2. Data Variations
3.3. Components of the Generated Data
3.4. Rule of Data
4. Materials and Methods
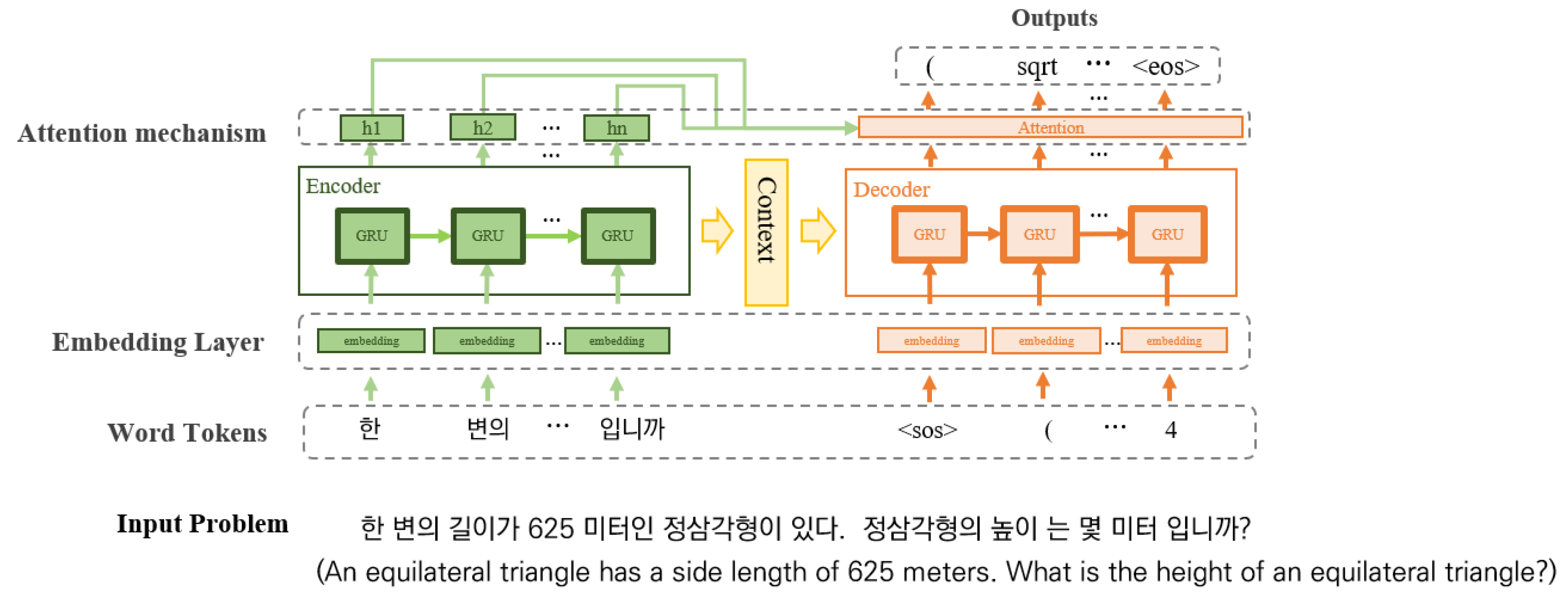
4.1. Architecture
4.1.1. Vanilla Seq2seq
4.1.2. Seq2Seq with Attention Mechanism
4.1.3. Transformer
4.2. Hyperparameters of Models
4.3. Word Embedding
- Skip-gram with negative sampling (SGNS) is a method of predicting the context word, which is the surrounding word of the target word. Vanilla skip-gram is very inefficient because it updates all word vectors during backpropagation. Therefore, negative sampling was proposed as a method to increase computational efficiency. First, this method randomly selects words to generate a subword set that is substantially smaller than the entire word set. Subsequently, this method performs positive and negative binary classification of whether the subset words are near the target word. This method updates only the word vectors that belong to the subset. In this manner, SGNS can perform vector computation efficiently [38].
- Global vectors for word representation (GloVe) is a method to compensate for the shortcomings of Word2Vec and latent semantic analysis (LSA). Because LSA is a count-based method, comprehensive statistical information can be obtained about words that appear together with a specific word. However, the performance of LSA is poor in the analogy task. By contrast, Word2Vec outperforms LSA in this task but cannot reflect statistical information because Word2Vec can only see context words. The GloVe is a method for using both embedding mechanisms [39].
- FastText uses an embedding learning mechanism identical to that of Word2Vec. However, Word2Vec treats words as indivisible units, whereas FastText treats each word as the sum of character unit n-grams (e.g., tri-gram, apple = app, ppl, ple). Owing to this characteristic, FastText has the advantage of being able to estimate the embedding of a word even if out-of-vocabulary problems or typos are present [40].
5. Result and Discussion
6. Conclusions
Future Research Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. In Proceedings of the NIPS 2014 Workshop on Deep Learning, Montreal, ON, Canada, 12 December 2014. [Google Scholar]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. In Advances in Neural Information Processing Systems 27 (NIPS 2014); MIT Press: Cambridge, MA, USA, 2014; Volume 27, pp. 3104–3112. [Google Scholar]
- Bahdanau, D.; Cho, K.H.; Bengio, Y. Neural machine translation by jointly learning to align and translate. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Luong, M.T.; Pham, H.; Manning, C.D. Effective Approaches to Attention-based Neural Machine Translation. In Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, Lisbon, Portugal, 17–21 September 2015; pp. 1412–1421. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Advances in Neural Information Processing Systems 30 (NIPS 2017); MIT Press: Cambridge, MA, USA, 2017; Volume 30. [Google Scholar]
- Kenton, J.D.M.W.C.; Toutanova, L.K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of the NAACL-HLT, Los Angeles, CA, USA, 2–7 June 2019; pp. 4171–4186. [Google Scholar]
- Brown, T.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.D.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language models are few-shot learners. In Advances in Neural Information Processing Systems 33 (NeurIPS 2020); MIT Press: Cambridge, MA, USA, 2020; Volume 33, pp. 1877–1901. [Google Scholar]
- Caldarini, G.; Jaf, S.; McGarry, K. A literature survey of recent advances in chatbots. Information 2022, 13, 41. [Google Scholar] [CrossRef]
- Dabre, R.; Chu, C.; Kunchukuttan, A. A survey of multilingual neural machine translation. ACM Comput. Surv. (CSUR) 2020, 53, 1–38. [Google Scholar] [CrossRef]
- Ramesh, A.; Pavlov, M.; Goh, G.; Gray, S.; Voss, C.; Radford, A.; Chen, M.; Sutskever, I. Zero-shot text-to-image generation. Proc. Mach. Learn. Res. 2021, 139, 8821–8831. [Google Scholar]
- Saharia, C.; Chan, W.; Saxena, S.; Li, L.; Whang, J.; Denton, E.; Ghasemipour, S.K.S.; Ayan, B.K.; Mahdavi, S.S.; Lopes, R.G.; et al. Photorealistic Text-to-Image Diffusion Models with Deep Language Understanding. arXiv 2022, arXiv:2205.11487. [Google Scholar]
- Boblow, D. Natural language input for a computer problem-solving system. Sem. Inform. Proc. 1968, 146–226. [Google Scholar]
- Charniak, E. Computer solution of calculus word problems. In Proceedings of the 1st International Joint Conference on Artificial Intelligence; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1969; pp. 303–316. [Google Scholar]
- Clark, P.; Etzioni, O. My computer is an honor student—but how intelligent is it? Standardized tests as a measure of AI. AI Mag. 2016, 37, 5–12. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, L.; Zhang, L.; Dai, B.T.; Shen, H.T. The gap of semantic parsing: A survey on automatic math word problem solvers. IEEE Trans. Patt. Anal. Mach. Intell. 2019, 42, 2287–2305. [Google Scholar] [CrossRef] [PubMed]
- Ki, K.S.; Lee, D.G.; Gweon, G. KoTAB: Korean template-based arithmetic solver with BERT. In Proceedings of the 2020 IEEE International Conference on Big Data and Smart Computing (BigComp), Busan, Korea, 19–22 February 2020; pp. 279–282. [Google Scholar]
- Fletcher, C.R. Understanding and solving arithmetic word problems: A computer simulation. Behav. Res. Methods Instrume. Comput. 1985, 17, 565–571. [Google Scholar] [CrossRef]
- Bakman, Y. Robust understanding of word problems with extraneous information. arXiv 2007, arXiv:math/0701393. [Google Scholar]
- Roy, S.; Vieira, T.; Roth, D. Reasoning about quantities in natural language. Trans. Assoc. Comput. Linguist. 2015, 3, 1–13. [Google Scholar] [CrossRef]
- Mitra, A.; Baral, C. Learning to use formulas to solve simple arithmetic problems. In Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), Berlin, Germany, 7–12 August 2016; pp. 2144–2153. [Google Scholar]
- Wang, Y.; Liu, X.; Shi, S. Deep neural solver for math word problems. In Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing, Copenhagen, Denmark, 7–11 September 2017; pp. 845–854. [Google Scholar]
- Wang, L.; Wang, Y.; Cai, D.; Zhang, D.; Liu, X. Translating a Math Word Problem to a Expression Tree. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, Brussels, Belgium, 31 October–4 November 2018; pp. 1064–1069. [Google Scholar]
- Chiang, T.R.; Chen, Y.N. Semantically-Aligned Equation Generation for Solving and Reasoning Math Word Problems. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), Minneapolis, MN, USA, 2–7 June 2019; pp. 2656–2668. [Google Scholar]
- Griffith, K.; Kalita, J. Solving arithmetic word problems automatically using transformer and unambiguous representations. In Proceedings of the 2019 International Conference on Computational Science and Computational Intelligence (CSCI), Las Vegas, NV, USA, 5–7 December 2019; pp. 526–532. [Google Scholar]
- Kim, B.; Ki, K.S.; Lee, D.; Gweon, G. Point to the expression: Solving algebraic word problems using the expression-pointer transformer model. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP), Online, 16–20 November 2020; pp. 3768–3779. [Google Scholar]
- Roy, S.; Roth, D. Solving General Arithmetic Word Problems. In Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, Lisbon, Portugal, 17–21 September 2015; pp. 1743–1752. [Google Scholar]
- Koncel-Kedziorski, R.; Roy, S.; Amini, A.; Kushman, N.; Hajishirzi, H. MAWPS: A math word problem repository. In Proceedings of the 2016 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, San Diego, CA, USA, 12–17 June 2016; pp. 1152–1157. [Google Scholar]
- Hosseini, M.J.; Hajishirzi, H.; Etzioni, O.; Kushman, N. Learning to solve arithmetic word problems with verb categorization. In Proceedings of the EMNLP, Doha, Qatar, 25–29 October 2014; pp. 523–533. [Google Scholar]
- Koncel-Kedziorski, R.; Hajishirzi, H.; Sabharwal, A.; Etzioni, O.; Ang, S.D. Parsing algebraic word problems into equations. Trans. Assoc. Comput. Linguist. 2015, 3, 585–597. [Google Scholar] [CrossRef]
- Kushman, N.; Artzi, Y.; Zettlemoyer, L.; Barzilay, R. Learning to automatically solve algebra word problems. In Proceedings of the 52nd Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), Baltimore, Maryland, 22–27 June 2014; pp. 271–281. [Google Scholar]
- Miao, S.Y.; Liang, C.C.; Su, K.Y. A Diverse Corpus for Evaluating and Developing English Math Word Problem Solvers. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, Online, 5–10 July 2020; pp. 975–984. [Google Scholar]
- Qin, J.; Lin, L.; Liang, X.; Zhang, R.; Lin, L. Semantically-Aligned Universal Tree-Structured Solver for Math Word Problems. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP), Online, 16–20 November 2020; pp. 3780–3789. [Google Scholar]
- Lin, X.; Shimotsuji, S.; Minoh, M.; Sakai, T. Efficient diagram understanding with characteristic pattern detection. Comput. Vis. Graph. Image Proc. 1985, 30, 84–106. [Google Scholar] [CrossRef]
- Seo, M.; Hajishirzi, H.; Farhadi, A.; Etzioni, O.; Malcolm, C. Solving geometry problems: Combining text and diagram interpretation. In Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, Lisbon, Portugal, 17–21 September 2015; pp. 1466–1476. [Google Scholar]
- Alvin, C.; Gulwani, S.; Majumdar, R.; Mukhopadhyay, S. Synthesis of problems for shaded area geometry reasoning. In Proceedings of the International Conference on Artificial Intelligence in Education; Springer: Berlin/Heidelberg, Germany, 2017; pp. 455–458. [Google Scholar]
- Graepel, T.; Obermayer, K. Large margin rank boundaries for ordinal regression. In Advances in Large Margin Classifiers; MIT Press: Cambridge, MA, USA, 2000; pp. 115–132. [Google Scholar]
- Mikolov, T.; Sutskever, I.; Chen, K.; Corrado, G.S.; Dean, J. Distributed representations of words and phrases and their compositionality. Adv. Neural Inform. Proc. Syst. 2013, 26, 3111–3119. [Google Scholar]
- Pennington, J.; Socher, R.; Manning, C.D. Glove: Global vectors for word representation. In Proceedings of the 2014 conference on empirical methods in natural language processing (EMNLP), Doha, Qatar, 25–29 October 2014; pp. 1532–1543. [Google Scholar]
- Bojanowski, P.; Grave, E.; Joulin, A.; Mikolov, T. Enriching word vectors with subword information. Trans. Assoc. Comput. Linguist. 2017, 5, 135–146. [Google Scholar] [CrossRef] [Green Version]
- Papineni, K.; Roukos, S.; Ward, T.; Zhu, W.J. Bleu: A method for automatic evaluation of machine translation. In Proceedings of the 40th annual meeting of the Association for Computational Linguistics, Philadelphia, PA, USA, 7–12 July 2002; pp. 311–318. [Google Scholar]


| Types of Problems | Descriptions/Example of Subtype Problems | ||
|---|---|---|---|
| Description | Finding an arithmetic expression and the desired answer for a specific situation | ||
| Example 1 | English | I was going to distribute the yuzu evenly to 59 people, but I accidentally gave it to 80 people. I gave 5 to each person and there were 43 left. If this yuzu is evenly distributed among 59 people, how many will be the maximum per person? | |
| Korean | 유자를 59명에게 똑같이 나누어 주어야 할 것을 잘못하여 80명에게 똑같이 나누어 주었더니, 한 사람당 5씩 주고 43개가 남았다. 이 유자를 59명에게 똑같이 나누어 주면 한 사람당 최대한 몇 개씩 가지게 되는지 구하시오. | ||
| Equation | ((80 × 5) + 43)/59 | ||
| Example 2 | English | Pil-Gyu gave 84 persimmons to Seong-Won and 22 to Yoon-Sang. Of the persimmons he had, 37 were left. Find out how many persimmons Pil-Gyu had at the beginning. | |
| Arithmetic Problem (12) | Korean | 필규는 감을 성원이에게 84 개를 주고 윤상이에게 22 개를 주었더니 가지고 있던 감중에서 37 개가 남았다. 처음에는 필규가 가지고 있던 감은 몇 개인지 구하여라. | |
| Equation | 84 + 22 + 37 | ||
| Example 3 | English | Find the sum of the odd numbers. The range is from 1 to 11. | |
| Korean | 홀수의 총합을 구하시오. 범위는 1부터 11까지이다. | ||
| Equation | 1 + 3 + 5 + 7 + 9 + 11 | ||
| Example 4 | English | The Japanese scores of Song-Woo, Dae-Yong, and Jong-Woo are 35, 70, and 54, respectively. Except for these three students, the average Japanese score was 54. If Song-Woo’s class has 81 students, what is the average Japanese score for the class? | |
| Korean | 송우, 대용이, 종우의 일본어 점수는 각각 35점, 70점, 54점이다. 이 3명을 제외한 나머지 학급의 일본어 점수 평균은 54점이다. 송우네 학급 인원수가 81명일 때, 학급 일본어 평균 점수는 몇 점인지 구하시오. | ||
| Equation | (54 × (81 − 3) + 35 + 70 + 54)/81 | ||
| Types of Problems | Descriptions/Example of Subtype Problems | ||
|---|---|---|---|
| Description | Finding the correct answer required in an ordered situation. | ||
| Example 1 | English | 47 male students are sitting in a row. If there are 32 boys behind Su-Jeong, how many boys are sitting in front of him? | |
| Korean | 47명의 남학생들이 한 줄로 줄을 앉아 있다. 수정이의 뒤에 32명의 남학생 있다면, 수정이의 앞에 앉아 있는 남학생은 몇 명이 있을까? | ||
| Equation | (47 − 1) − 32 | ||
| Ordering (7) | Example 2 | English | In the midterm exam, Yong-Hwan is placed 42nd and Doo-Hyeon is placed 40th. If Seong-Jae is ranked higher than Yong-Hwan and lower than Doo-Hyeon, what is Sung-Jae’s rank? |
| Korean | 중간고사 시험에서 용환이는 42위를 하였고, 두현이는 40위를 기록했다. 성재는 용환이보다 순위가 높고, 두현이보다는 순위가 낮다고 한다면 성재의 순위는? | ||
| Equation | (40 + 42)/2 | ||
| Example 3 | English | Twenty-four people are standing in a line in order from the tallest customer. Min-Jeong is standing 22nd from the front. If she lines up again in order of the shortest person, where is she standing? | |
| Korean | 키가 큰 손님부터 순서대로 24명이 한 줄로 서 있습니다. 민정이가 앞에서부터 스물 두 번째에 서 있습니다. 키가 작은 사람부터 순서대로 다시 줄을 서면 민정이는 몇 번째에 서 있습니까? | ||
| Equation | 24 − 22 + 1 | ||
| Types of Problems | Descriptions/Example of Subtype Problems | ||
|---|---|---|---|
| Finding Unknowns (11) | Description | (a) Finding the unknowns that satisfy the condition of an expression. (b) Finding the result from the correct operation given the situation, in which the operation is wrong. | |
| Example 1 (a) | English | Find the natural number corresponding to A in the addition expression of three-digit natural numbers ‘A5C + 1B5 = 960’ | |
| Korean | 세 자리 자연수의 덧셈식 ‘A5C + 1B5 = 960’에서 A에 해당하는 자연수를 구하여라. | ||
| Equation | (960//100) − (100//100) − (10 − 6 + 5 + (10 − ((960%10)% 10) + 5 − 1)//10 − 1)//10 | ||
| Example 2 (a) | English | A and B are natural three-digit numbers. 996 is 3 less than A and B is 92 less than 182. Find the sum of A and B. | |
| Korean | A, B는 자릿수가 세 개인 자연수이다. A보다 3 작은 수는 996이고, B는 182보다 92 작은 수이다. A와 B의 합을 구하여라. | ||
| Equation | (996 + 3) + (182 + 92) | ||
| Example 1 (b) | English | You get 90 when you subtract 19 from an unknown number. What is the result of subtracting 29 from the unknown number? | |
| Korean | 어떤 수에서 19를 뺐을 때 90가 되었습니다. 어떤 수에서 29를 빼면 얼마가 되는지 구하시오. | ||
| Equation | 90 + 19 − 29 | ||
| Example 2 (b) | English | If you multiply an unknown natural number by 18, subtract 30, add 16, and divide by 1 you get 526. What is the unknown natural number? | |
| Korean | 어떤 자연수에 18을 곱하고 나서 30을 빼고, 16을 더한 값을 1로 나눈다면 526이 된다고 합니다. 어떤 자연수를 구하시오. | ||
| Equation | (((526 × 1) − 16) + 30)/18 | ||
| Types of Problems | Descriptions/Example of Subtype Problems | ||
|---|---|---|---|
| Geometry (12) | Description | Finding the area, perimeter, or length of a side for a given geometric figure. | |
| Example 1 | English | If you have a circle of radius 21, what is the area of the circle? | |
| Korean | 반지름의 길이가 21인 원이 있다면, 원의 넓이는 얼마 인지 구하시오. | ||
| Equation | pi × 21 × 21 | ||
| Example 2 | English | If you have a square with a side length of 40 m, how many square meters is it? | |
| Korean | 한 변의 길이가 40m인 정사각형이 있다면, 정사각형의 넓이는 몇 ㎡입니까? | ||
| Equation | 40 × 40 | ||
| Example 3 | English | In math class, Jeongseok created a rectangle with yarn. There was no leftover yarn and he did not run out of thread. The total length of the yarn was 176 kilometers. If a rectangle is 58 kilometers wide, what is the vertical length? | |
| Korean | 수학시간에 정석이는 실로 직사각형을 만들었습니다. 사용한 실은 남지도 모자라지도 않았습니다. 실은 총 176 킬로미터 이고, 직사각형의 가로 길이는 58 킬로미터 라면, 세로 길이는 몇 킬로미터입니까? | ||
| Equation | (176 − (58 × 2))/2 | ||
| Example 4 | English | Na-Rae drew a rectangle with a perimeter of 80 km. If the width of the rectangle is three times the length, how many kilometers is the width? | |
| Korean | 나래는 둘레가 80km인 정사각형을 그렸습니다. 이 정사각형의 가로 길이가 세로 길이의 3배라고 하면, 가로 길이는 몇 km입니까? | ||
| Equation | ((80/2)/(3 + 1)) × 3 | ||
| Variation | Examples | ||
|---|---|---|---|
| Alternate Affixes | Original | English | Hyun-Woo collected 1 and 40, and Han-Gyul collected 25 and 59. Which child has a larger total? |
| Korean | 현우는 1와 40를 모았고, 한결은 25와 59를 모은 상태입니다. 어떤 아이의 총 수가 훨씬 클까요? | ||
| Variation | English | Hyun-Woo is collecting 1s and 40s. Han-Gyul gathered 25 and 59. Which child has a larger total? | |
| Korean | 현우는 1와 40를 모으고 있고. 한결은 25와 59를 모았습니다. 어떤 아이의 총 수가 훨씬 클까요? | ||
| Change Information | Original | English | Shin-Yeol picked two sequential numbers. When the sum of the two numbers drawn is 171, what is the greater of the two numbers Shin-Yeol picked? |
| Korean | 신열이는 연속된 두 수를 뽑았다. 뽑은 두 수의 합이 171이었을때, 신열이가 뽑은 두 수 중 큰 수는 몇인지 구하시오. | ||
| Variation | English | Joo-Hyung picked two sequential numbers. When the sum of the two numbers drawn is 171, what is the greater of the two numbers picked by Joo-Hyung?” | |
| Korean | 주형이는 연속된 두 수를 뽑았다. 뽑은 두 수의 합이 171이었을때, 주형이가 뽑은 두 수 중 큰 수는 몇인지 구하시오." | ||
| Replace Operator | Original | English | I subtracted 188 from an unknown number to get 833. Guess what value would be obtained if 248 was added to the unknown number. |
| Korean | 모르는 수에서 188를 뺐더니 833가 되었다. 그렇다면 모르는 수에서 248를 더했을 경우 어떤 값이 나올지 맞추어라. | ||
| Variation | English | If you add 188 to an unknown number, you get 833. Guess what value will be obtained if 248 is subtracted from the unknown number. | |
| Korean | 모르는 수에서 188를 더했더니 833가 되었다. 그렇다면 모르는 수에서 248를 뺄때 얼마가 될지 맞추어라. | ||
| Change the order of a phrases | Original | English | When I is divided by 129, the quotient is J, and the remainder is K. When I, J, and K are natural numbers, the quotient and the remainder are the same. Find the largest divisor of J. |
| Korean | I를 129로 나누었을 때 몫은 J이며, 나머지는 K가 됩니다. I,J, K는 자연수일 때, 몫과 나머지는 같습니다. 나누어지는 수 J 중 가장 큰 수를 구하시오. | ||
| Variation | English | I, J, and K are natural numbers. If you divide I by 129, the quotient is J and the remainder is K. Moreover, the quotient and the remainder are equal. Find the largest divisor of J. | |
| Korean | I, J, K는 자연수일 때, I를 129로 나누면 몫은 J이고, 나머지는 K가 됩니다. 또한, 식에서 몫과 나머지는 같습니다. 나누어지는 수 J 중 가장 큰 수를 구하시오. | ||
| Hyperparameters | Seq2seq | Seq2seq (with Attention) | Transformer | |||
|---|---|---|---|---|---|---|
| Word Embedding | FastText | FastText | FastText | GloVe | SGNS | Scratch |
| Embedding Size | [256] | [256] | [256, 384] | |||
| Hidden Size | [256] | [256] | [256, 384] | |||
| Number of Layers | [3, 4] | [3, 4] | [3, 4] | |||
| Learning Rate | [, ] | [, ] | [, , ] | |||
| Dropout | [0.1, 0.2, 0.4] | [0.1, 0.2, 0.4] | [0.1, 0.2, 0.4] | |||
| Batch Size | [1024] | [1024] | [256] | |||
| FFN Size | - | - | [512, 768] | |||
| Head | - | - | [4, 8] | |||
| # of Params | 5.8 M | 7.1 M | 7.4 M | |||
| Epochs | 300 | |||||
| Validation | Test | ||||
|---|---|---|---|---|---|
| Model | Embedding | BLEU Score (%) | Accuracy (%) | BLEU Score (%) | Accuracy (%) |
| Seq2seq | FastText | 93.54 | 82.11 | 93.33 | 82.06 |
| Seq2seq (with attention) | FastText | 97.15 | 89.56 | 97.04 | 89.39 |
| Transformer | Scratch | 85.66 | 79.92 | 85.17 | 79.63 |
| FastText | 93.61 | 89.05 | 93.33 | 89.08 | |
| SGNS | 94.94 | 90.27 | 94.76 | 90.38 | |
| GloVe | 94.71 | 90.93 | 94.75 | 90.97 | |
| Type of Predicted Equation | Input Problem | Correct Equation | Predicted Equation |
|---|---|---|---|
| There are 25 apples in a box. How many apples are in all 5 boxes? | 25 × 5 | 25 × 5 | |
| Predict the Correct Equation | There is a trapezoid with an upper side length of 25 cm, a lower side length of 34 cm, and a height of 12 cm. What is the area of the trapezoid? | (25 + 34) × 12/2 | (25 + 34) × 12/2 |
| There were 27 apples in the box. Five of them were discarded. If you put 18 more apples in this box, how many apples are in the box | 27 − 5 + 18 | 27 − 5 + 18 | |
| 1 dozen pencils are 12. How many are 6 dozen pencils in total? | 12 × 6 | 6 × 12 | |
| Change the Order | What is the perimeter of a parallelogram, the side of which is 18 cm long and the other side is 12 cm long? | (18 + 12) × 2 | 2 × (18 + 12) |
| There are machines that manufacture 900 toys per day. How many toys can the machine manufacture in 7 days without a break? | 900 × 7 | 7 × 900 | |
| What is the area of a triangle with a base of 13 m and a height of 8 m? | 13 × 8/2 | (13 × 8)/2 | |
| Add parentheses | I have a rectangular notebook with a perimeter of 46 cm and a height of 9 cm. How many cm is the width of this notebook? | (46 − 9 × 2/2) | (46 − (9 × 2))/2 |
| The sum of the four sides of a rectangle is 32 cm. If the width of this rectangle is 7 cm, how many cm is the length? | (32 − 7 × 2)/2 | (32 − (7 × 2))/2 |
| Actual Math Word Problem Dataset | |||
|---|---|---|---|
| Model | Embedding | BLEU Score(%) | Accuracy(%) |
| Seq2seq | FastText | 13.52 | 16.39 |
| Seq2seq (with attention) | FastText | 17.02 | 20.57 |
| Transformer | Scratch | 11.22 | 15.11 |
| GloVe | 15.94 | 24.43 | |
| SGNS | 19.99 | 27.00 | |
| FastText | 23.23 | 34.72 | |
| Input Problem | Correct Equation | Predicted Equation | |
|---|---|---|---|
| English | There are 268 fewer olives than quince, and there are 368 olives and quince in total. Find out how many quinces are there. | ((368 − 268)/2) + 268 | ((368 − 268)/2) + 268 |
| Korean | 올리브가 모과보다 268개 더 적고 올리브와 모과가 모두 합해서 368개 있다. 모과는 몇 개인지 구하여라. | ||
| English | We need to subtract 475 from an unknown number A, but the result of subtracting 214 by mistake is 911. What is the result of the original calculation? | 911 + 214 − 475 | 911 + 214 − 475 |
| Korean | 미지수 A에서 475를 빼야 하는데 실수로 214를 뺀 결과, 911가 나오게 되었다. 이때 원래대로 계산한 결과는 무엇일까요? | ||
| English | One box can hold 34 apples. How many apples can 4 boxes hold? | 34 × 4 | 34 × 4 |
| Korean | 사과를 한 상자에 34개씩 담을 수 있습니다. 사과 4상자에는 사과를 모두 몇 개 담을 수 있습니까? | ||
| English | A total of 808 friends are sitting in a row. 268 people are sitting in front of Chae-Yeon. How many friends are sitting behind her? | (808 − 1) − 268 | (808 − 1) − 268 |
| Korean | 808명의 친구들과 한 줄로 앉아 있습니다. 채연이의 앞에는 268명이 앉아 있다고 합니다. 채연이의 뒤에는 몇 명의 친구들이 앉아있을까요? | ||
| English | There are 4 comic books, 2 novels, and 2 textbooks on the bookshelf. How many books are on the bookshelf? | 4 + 2 + 2 | 4 × 2 |
| Korean | 책꽂이에 만화책 4권, 소설책 2권, 교과서 2권이 꽂혀 있습니다. 책꽂이에 꽂혀 있는 책은 모두 몇 권 인지 구하세요 | ||
| English | A triangle has a base of 17 cm and a height of 16 cm. What is the area of the triangle? | 17 × 16/2 | (17 × 16)/2 |
| Korean | 밑변이 17 cm이고 높이가 16 cm인 삼각형이 있습니다. 이 삼각형의 넓이는 몇 cm²입니까? | ||
| English | I have a rectangle with a width of 22 cm and a perimeter of 64 cm. What is the length of the rectangle in cm? | (64 − 22 × 2)/2 | (22 − (64 × 2))/2 |
| Korean | 가로의 길이가 22 cm이고 둘레는 64 cm인 직사각형이 있습니다. 이 직사각형의 세로는 몇 cm입니까? | ||
| English | I am trying to climb to the observatory of a certain building. If I have to climb 249 m and have reached 153 m, find out how much more I need to climb. | 249 − 153 | 153 + 249 − 153 |
| Korean | 어떤 건물의 전망대에 올라가려고 합니다. 전망대까지 249 m를 올라가야 하는데 153 m까지 올라왔다면 몇 m를 더 올라가야 할지 구하세요. | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, K.; Chun, C. Synthetic Data Generator for Solving Korean Arithmetic Word Problem. Mathematics 2022, 10, 3525. https://doi.org/10.3390/math10193525
Kim K, Chun C. Synthetic Data Generator for Solving Korean Arithmetic Word Problem. Mathematics. 2022; 10(19):3525. https://doi.org/10.3390/math10193525
Chicago/Turabian StyleKim, Kangmin, and Chanjun Chun. 2022. "Synthetic Data Generator for Solving Korean Arithmetic Word Problem" Mathematics 10, no. 19: 3525. https://doi.org/10.3390/math10193525
APA StyleKim, K., & Chun, C. (2022). Synthetic Data Generator for Solving Korean Arithmetic Word Problem. Mathematics, 10(19), 3525. https://doi.org/10.3390/math10193525







