Abstract
Friction has a vital role in studying materials’ and systems’ behavior. The friction between two objects and the inner friction of materials under the condition of vibration usually can present different characteristics. These characteristics are different from the conventional conditions. It is shown in practice that vibration can reduce the friction coefficient and friction force between two objects. Vibration can lighten abrasion of objects and reduce energy consumption. All of these can give great efficiency, but, until now, the vibration friction-reducing mechanism has not been fully revealed. In this manuscript, the friction-reducing mechanism of materials under arbitrary vibration forces is investigated. The results show that the effective friction coefficient of materials under arbitrary vibration forces is always the minimum. The relationship between the effective friction coefficient and the negative gradient is investigated in this research. When the vibration force direction projects are in the first and the third quadrants, the negative gradient of the effective friction coefficient gets larger slowly, and then it becomes stable. When the vibration force direction projects are in the second and the fourth quadrants, the negative gradient of the effective friction coefficient decays to zero at the initial stage and then increases rapidly.
MSC:
74H45
1. Introduction
Vibration is common in engineering practice and daily life, and it is the main content in the study of vibration friction mechanics. We are always in a vibration environment, such as the vibration of houses and bridges, the vibration of machine tools, the vibration of engines, and the vibration of road rollers and sinking and pulling machines. In the progress of science and engineering, a lot of mechanical equipment are moving towards high speed, high precision, and miniaturization [1,2]. Research on vibration is becoming more and more important. It is necessary to master vibration law and the transmission path of the interface so as to reasonably use or suppress vibration. One of the most important problems with vibration is the friction between interfaces. It is the key to improving the reliability and life of machinery and equipment, and its economic significance is very clear. In industry, generally in this case, the main reason leading to the failure of machines is not damage of the components of the machine itself but the wear of the contact interface of various parts under the action of fretting or sliding friction [3,4,5,6,7,8]. As one of the most fundamental physical phenomena, friction is the most common phenomenon, and vibration friction usually happens in mechanical systems [9,10,11,12]. Many researchers have focused on the relationships between vibration and friction. On the basis of oil film dynamic pressure lubrication and an elastic contact model of the asperities, Bao et al. set up a kinematic coupling model of the rotation-axial engagement process according to friction elements and gave the engagement characteristics of the multi-disc wet friction clutch [13]. Marques et al. studied several friction force models dealing with different friction phenomena in the research of multibody system dynamics [14]. To study the random stick-slip vibration of duffing systems of dry friction, a numerical approximate solution was performed by Jin et al. [15]. Some researchers performed experimental validation and investigations of vibration friction systems [16,17,18]. Sun et al. analyzed the friction coefficient based on the recurrence plots and proposed a new method to identify the running-in state of the friction pair [19,20]. Many nonlinear phenomena were presented in engineering of the discontinuities introduced by friction in the governing equations [21,22,23]. In engineering practice, friction between the contact bodies can cause lots of undesirable effects on the system, such as frictional chatter [24], wear in friction-induced vibrations [25,26], and reduction characteristics of silicon [27]. The natural frequencies and damped forced vibrations were investigated by Safaei for an improved and lightweight sandwich plate of a periodic load in a limited time [28]. Doan et al. analyzed the free vibration and static bucking of flexoelectric variable thickness nanoplates. To emphasize the affection of flexoelectricity in free vibration and static buckling of the nanoplates, a variety of parameter studies was conducted [29]. A nonlinear static bending study of microplates resting on imperfect Pasternak elastic foundations was carried out by Thai Dung et al. By the improved couple stress theory and finite element methods, the nonlinear finite element formulations were performed [30]. For illustration as a stationary process with white noise, the vibration response of beams in the condition of random load was studied by Nguyen et al. To predict the fundamental frequencies of the structures, the artificial neural network (ANN) model was presented [31]. The dynamic problem for the moment theory of elasticity related to the finite length crack in normal stress conditions on the banks was demoted to a series of displacement and rotation integral equations in [32], which were performed mathematically. Moreover, in [33], the dynamic problems related to micro-polar elastic bodies were carried out by an eigenvalues technique. Lai Thanh Tuan et al. devised and performed numerical and analytical solutions for problems in two dimensions, including the spreading of unsteady axisymmetric boundary disturbances of a “non-classical” elastic medium of spherical boundaries [34]. Recently, based on a serious of methodologies, many researchers have performed numerous studies on the computation of plate and shell structures. Many beneficial discoveries were made [35,36,37,38,39].
However, several problems for vibration friction in the case of arbitrary vibration working environments have not yet been sufficiently studied, including the effective coefficient of dynamic friction and the friction mechanism in arbitrary vibration of materials and the negative gradient of friction.
The purpose of this paper is to present the friction-reducing mechanism of materials under arbitrary vibration forces. Due to limitations associated with the negative gradient of the effective friction coefficient and the effective friction coefficient in arbitrary vibration working environments, the vibration friction characteristics of materials have not been thoroughly explained. Based on the effective coefficient of dynamic friction and the friction mechanism in arbitrary vibration of materials, the effective friction coefficient was deduced in this research, and the negative gradient of friction was also discussed.
The main body of this paper is split into four sections. The material model is presented in Section 2. The effective coefficient of friction is studied in Section 3. The negative gradient of the effective friction coefficient is given in Section 4. In Section 5, important conclusions are summarized.
2. Model of Material
It is a very common phenomenon that materials always vibrate under the vibration condition in engineering. In the last century, some researchers proposed the concept of effective friction coefficient from the perspective of breaking static conditions by using pure mechanical methods [14,17]. In this paper, the concept of effective friction coefficient is used to study the friction reduction effect of vibration under three conditions: that the vibration direction is parallel to the force, the vibration direction is parallel to the normal pressure, and the vibration direction is perpendicular to the force and the normal pressure. Then, on the basis of these three conditions, the effective friction coefficient formula of vibration in an arbitrary direction is further derived. It is proved that vibration can reduce friction. The influence and control of vibration parameters on friction reduction are explained by the change in effective friction coefficient reduction rate in this paper.
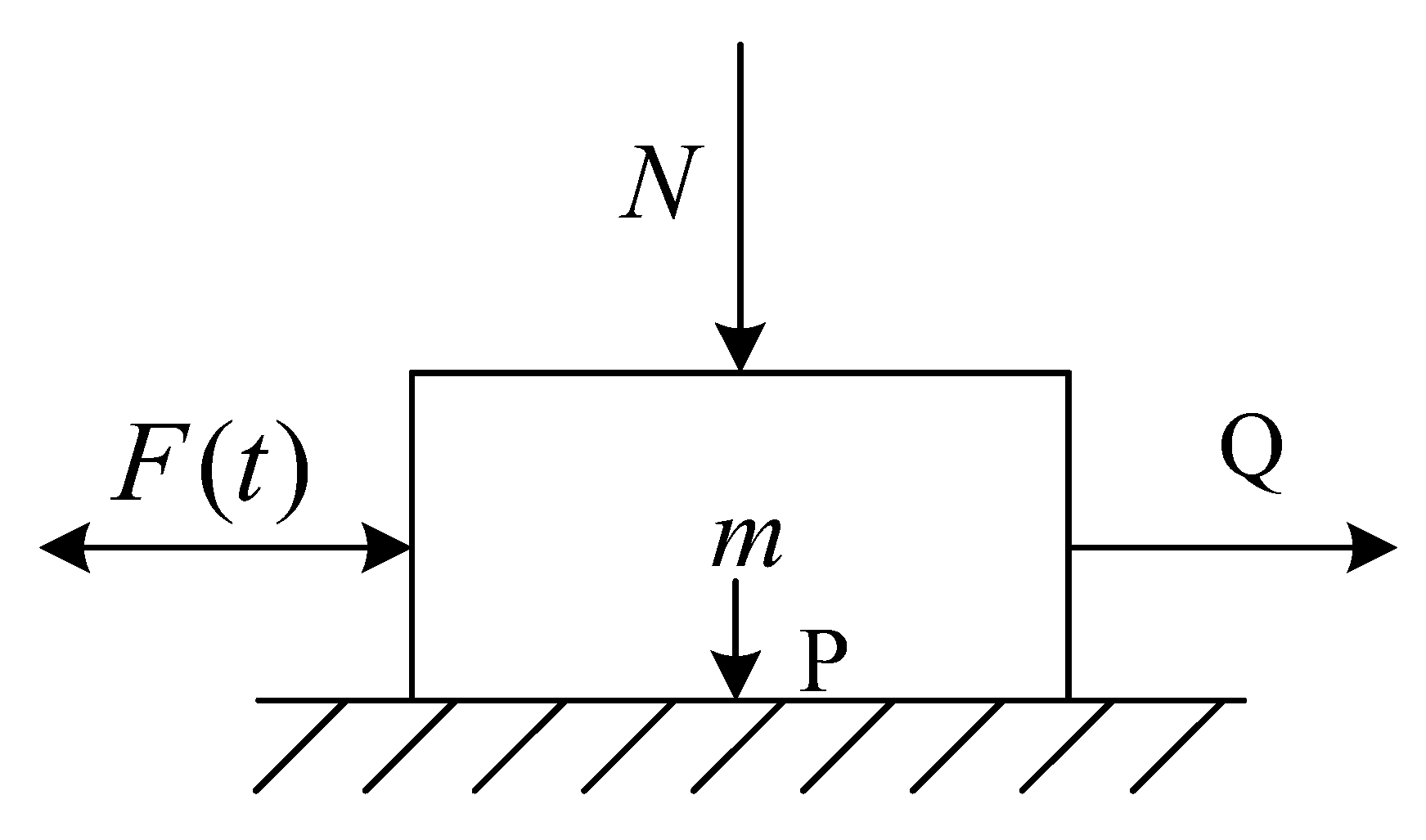
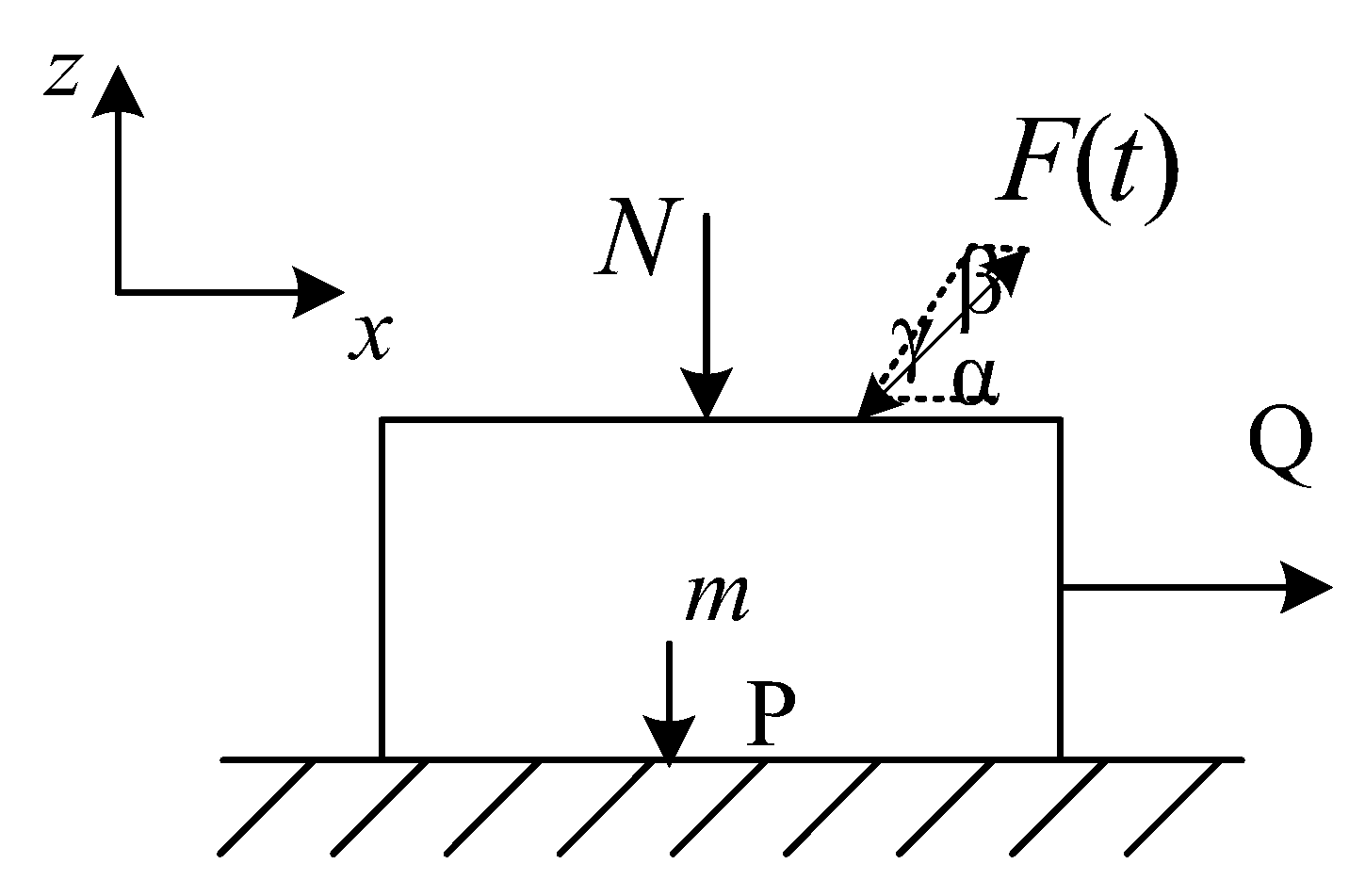
Firstly, the model is established in a Cartesian coordinate system. This is shown in Figure 1. The effective friction coefficient is ; is the coefficient of the maximum static friction between the material and the surface; is the normal compression force (opposite paralleled axis Z); is the tension force (paralleled axis ); is the amplitude of the force ; ; is the minimum force to move the material. P is the gravity force, P = mg.
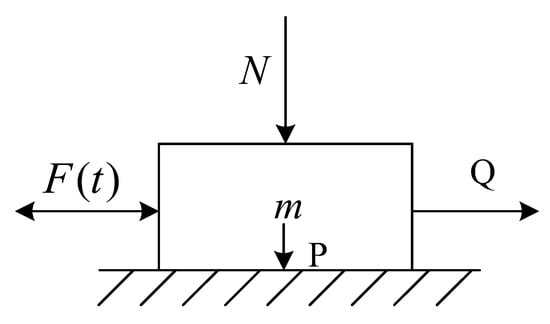
Figure 1.
The vibration model of parallel force.
This is the effective friction coefficient formula under the condition that the vibration and the force direction are parallel. Since > 0, the effective friction coefficient under vibration is less than the coefficient of the max static friction ; thus, the effective friction under vibration is reduced.
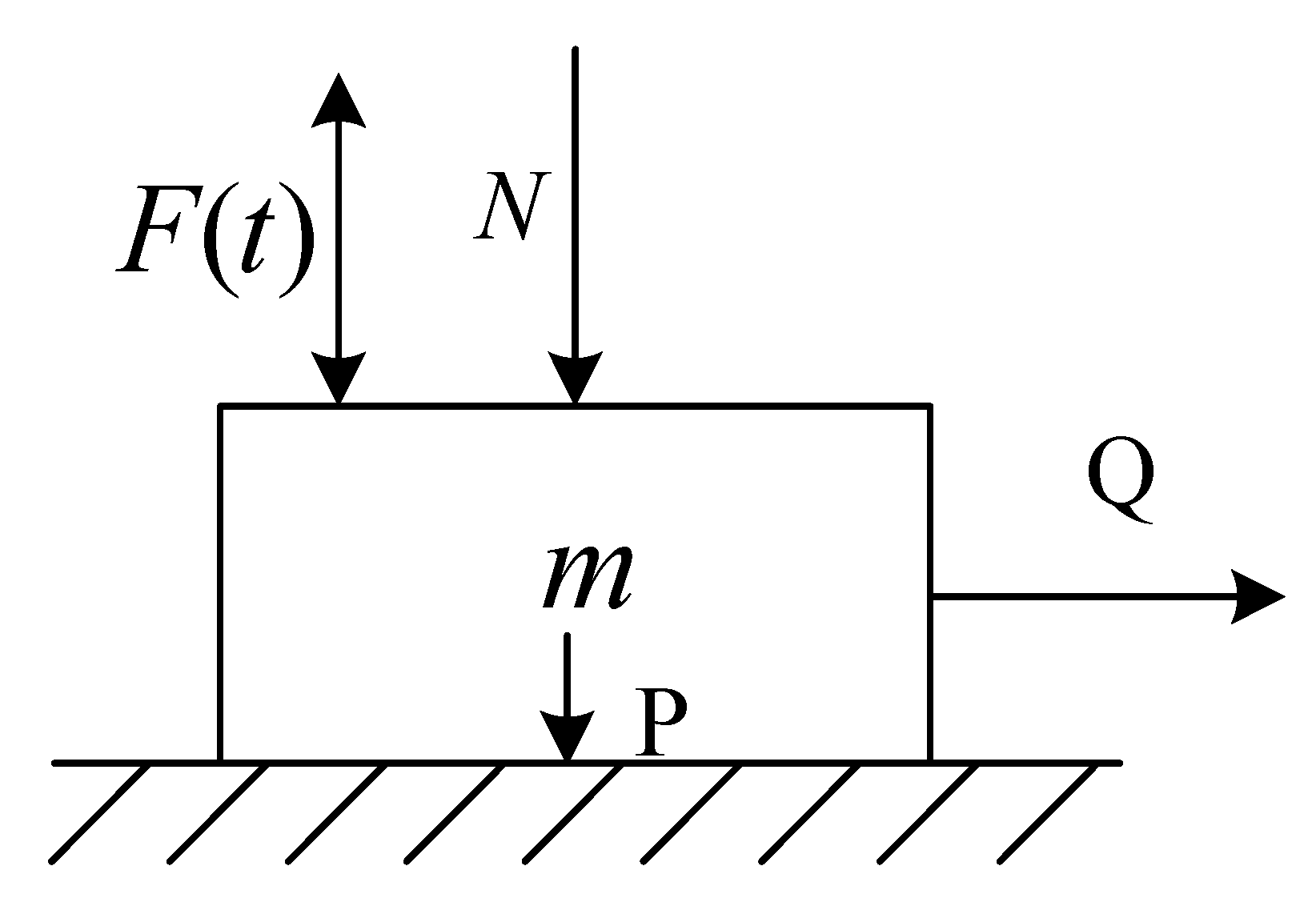
When the vibration direction is parallel to the normal pressure, the material model is shown in Figure 2.
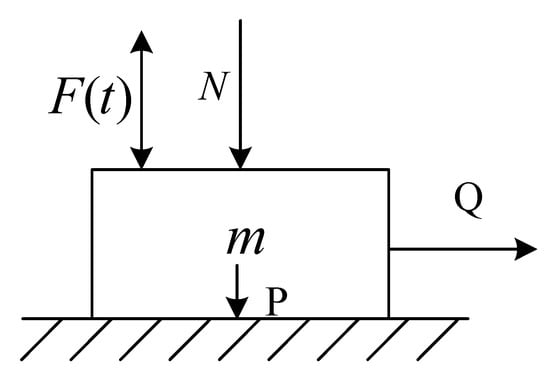
Figure 2.
The vibration model of vertical force.
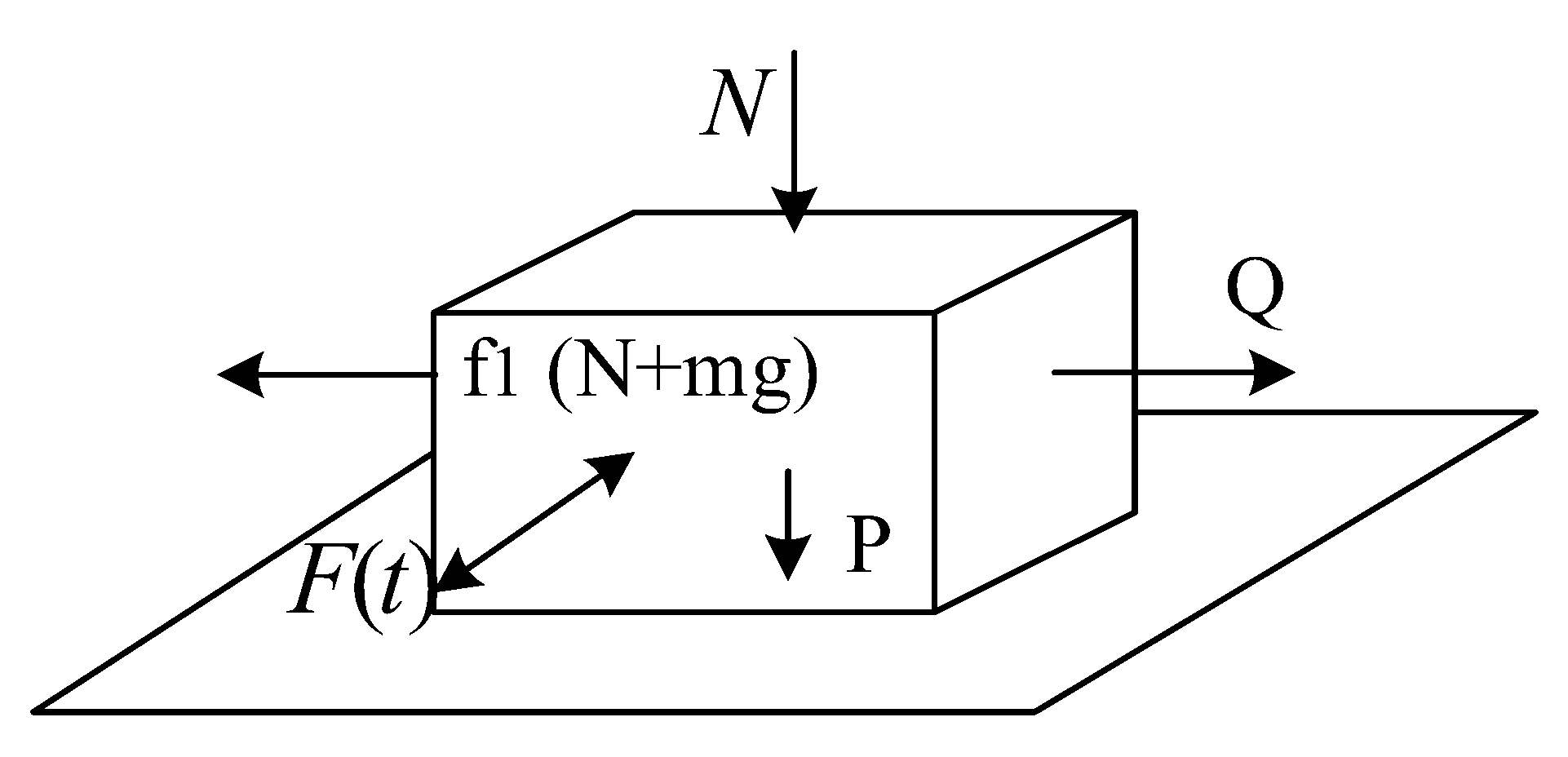
When the vibration direction is perpendicular to the force and the normal pressure, the material model is shown in Figure 3.
where A = , and P is the gravity force; P = mg.
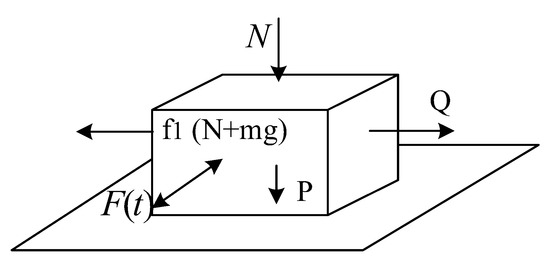
Figure 3.
The model of vibration vertical to the friction and the normal pressure.
Similarly, the effective friction under vibration is reduced in these conditions. Then, on the basis of these three conditions, the effective friction coefficient formula of vibration in an arbitrary direction is further derived. Arbitrary vibration force can be seen as three components, and the effective friction coefficient under the arbitrary time-varying external forces is one of the critical characters to show the nonlinear dynamic characteristics of the system. Herein, it is studied in different conditions, respectively.
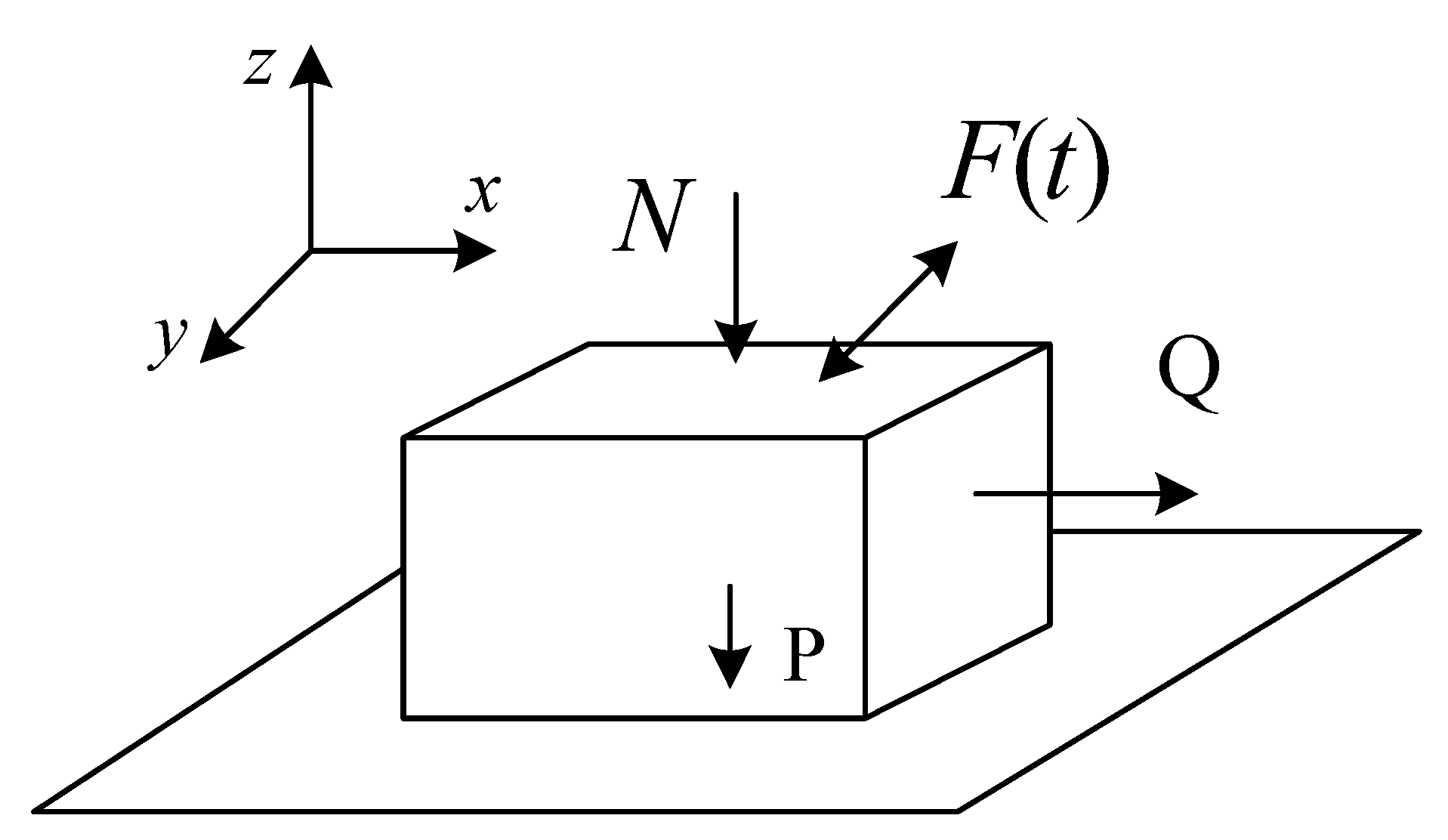
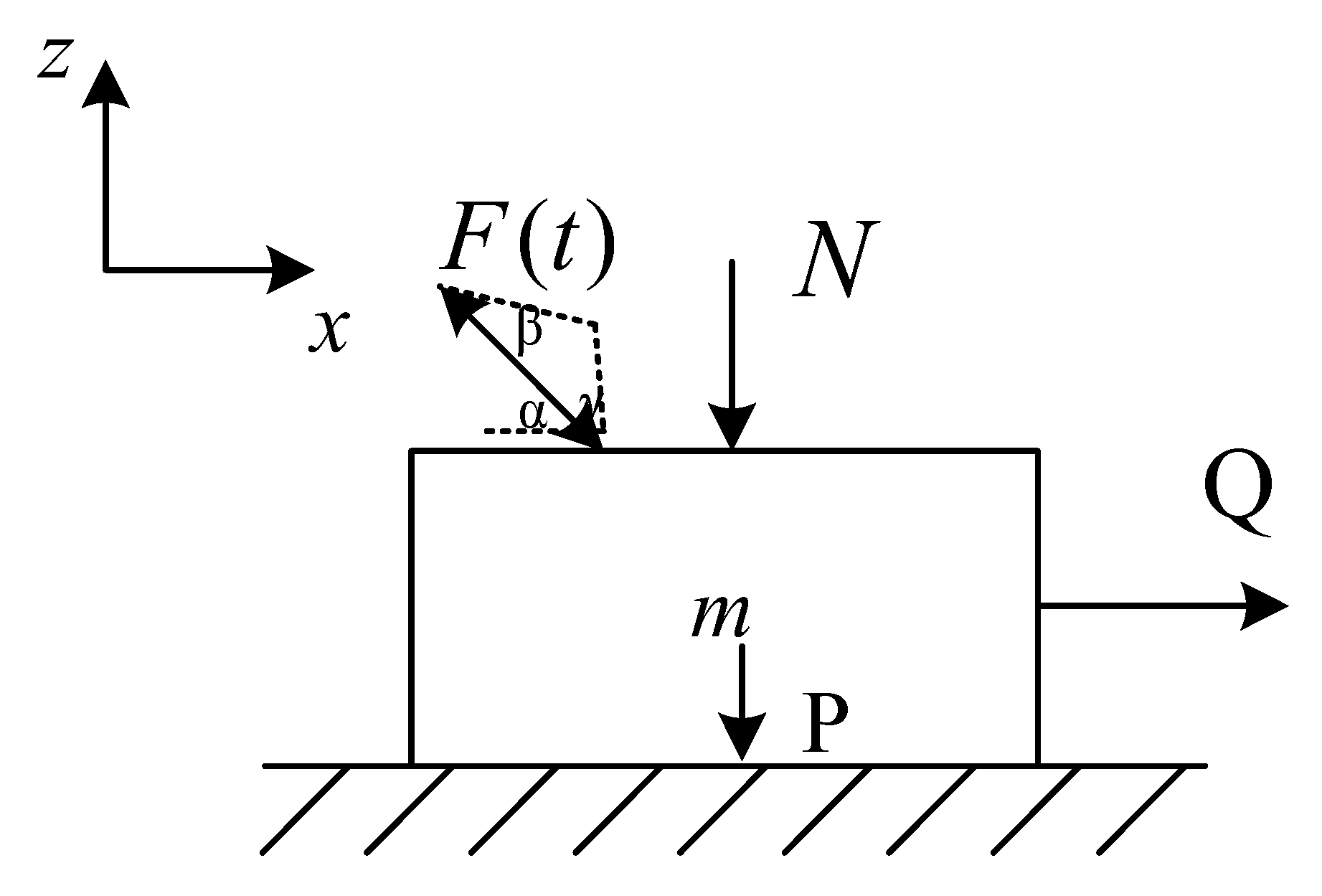
Firstly, the model is established in a Cartesian coordinate system, as shown in Figure 4. Next, m is the mass; is the coefficient of the maximum static friction between the material and the surface; is the normal compression force (opposite paralleled axis Z); is the tension force (paralleled axis ); is the amplitude of the force ; is the arbitrary time-varying external forces, and its vectors are . P is the gravity force, P = mg. Then, the arbitrary time-varying external forces in different conditions are discussed separately.
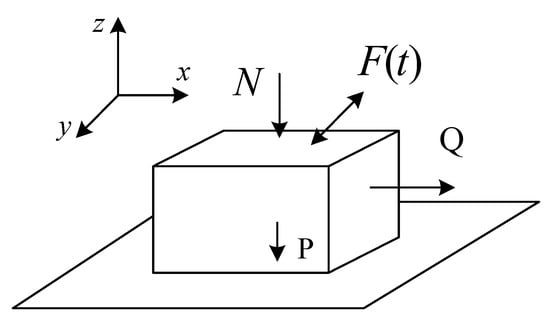
Figure 4.
Model of the vibratory material under arbitrary vibration.
3. Effective Coefficient of Friction
When the arbitrary time-varying external force projects are in the first and the third quadrants of the xz plane (including the limit boundary: projection in the axis z), the maximum synthetic tension and the minimum compression are obtained, as shown in Figure 5. Herein, the force comes to and yields
where is the minimum force to move the material.
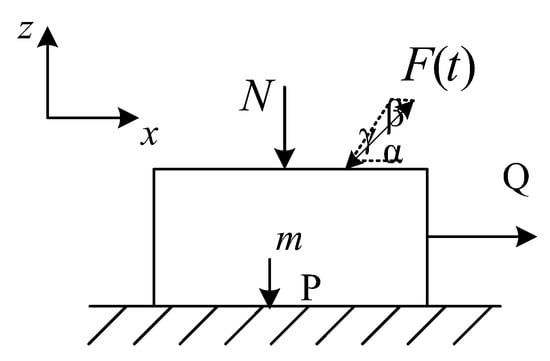
Figure 5.
Vibration force projects in the first and the third quadrants.
Then, there is
where is the effective coefficient of friction.
Here, supposing , there is
A = , then there is
there is .
For the above equation, when , , and at the same time, then the left could be equal to the right. However, , and so , , and cannot be all zero simultaneously. Hence, the supposition is not tenable. Therefore, there is .
When the vibration force projects are in the second and the fourth quadrants of the xz plane, the model is shown in Figure 6.
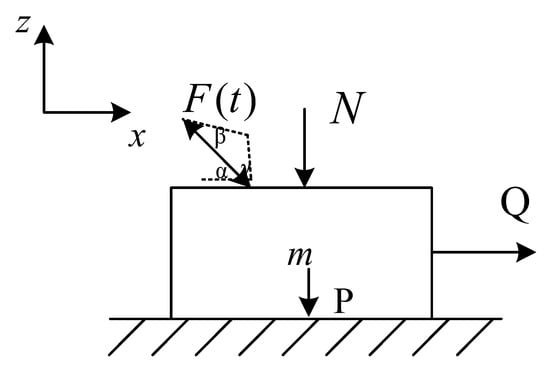
Figure 6.
Vibration force projects in the second and the fourth quadrants.
Assume and , there is,
Substituting into the above equation, there is
where is the effective coefficient of the friction when the vibration force project is in the second quadrant. Meanwhile, when the vibration force project is in the fourth quadrant, there is
where is the minimum force to move the material.
Simplifying the above expression yields
where is the effective coefficient of friction when the vibration force project is in the fourth quadrant.
Hence, the effective friction coefficient should be the minimum of the above, that is, .
Suppose , , , there is
Suppose , , , there is
When and , there is , ; when and , there is .
To sum up, the results show that when and , there is . Otherwise, there is always.
4. Negative Gradient of the Effective Friction Coefficient
In addition, the negative gradient of the effective friction coefficient is discussed in this paper. The negative gradient has a critical effect on the ratio of the effective friction coefficient to the friction coefficient. Suppose ,. When (in the first coordination), there is .
and , ; obtains the max value.
By deriving Equation (17), there is
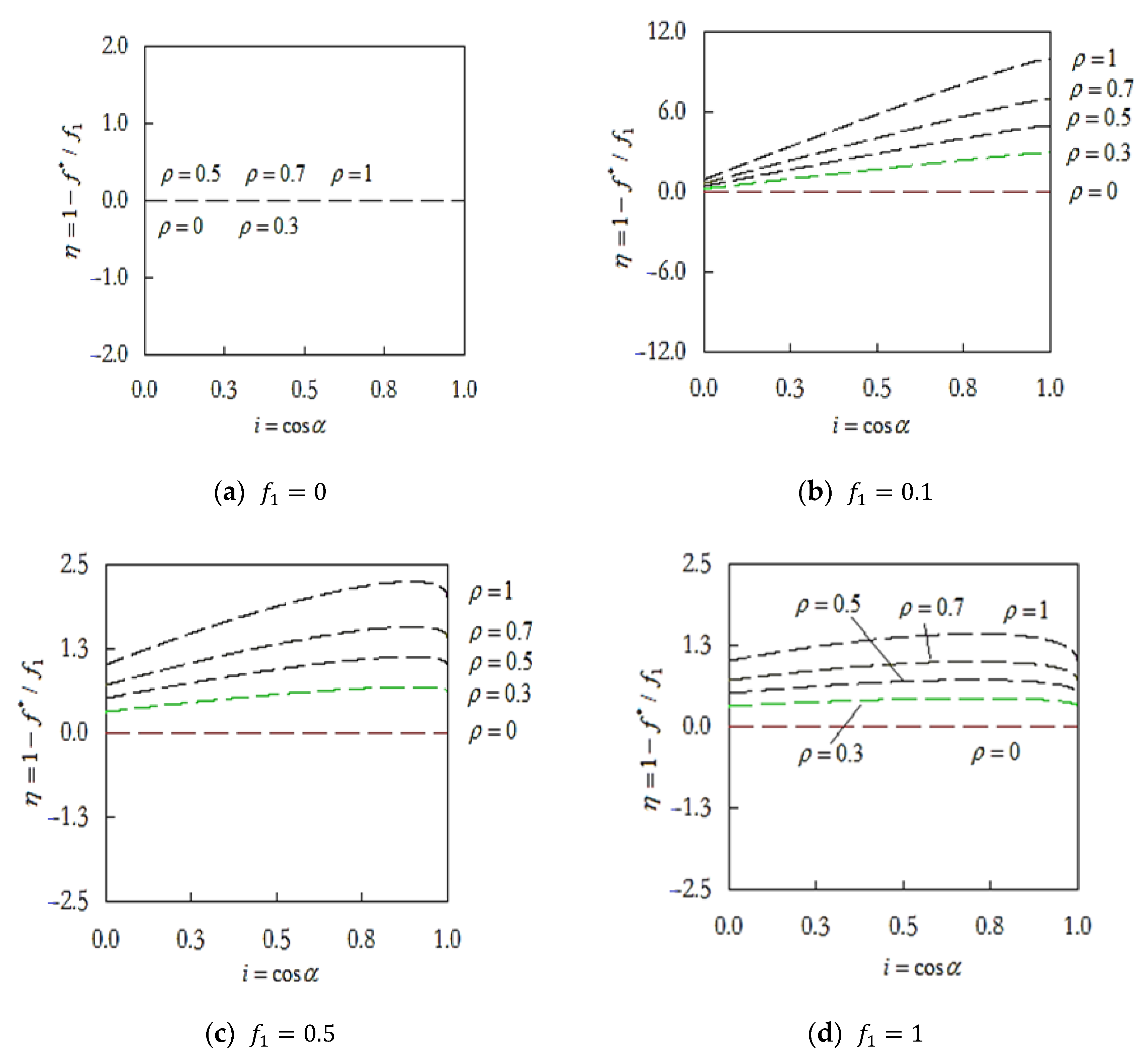
According to the values shown in Figure 7, there is no negative gradient at the stage. The curve is absolutely smooth, and the negative gradient is always zero in this stage. When , is increased with immediately, and the curve is much steeper. With the increase in , will be stable gradually. When will be flat.
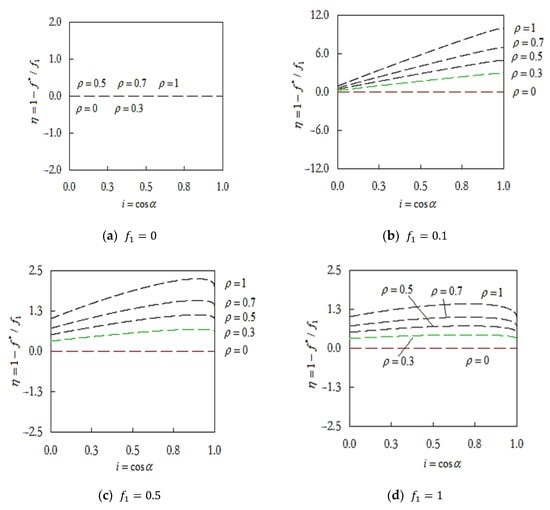
Figure 7.
The negative gradient of the effective friction coefficient .
According to , there is
Then, there is
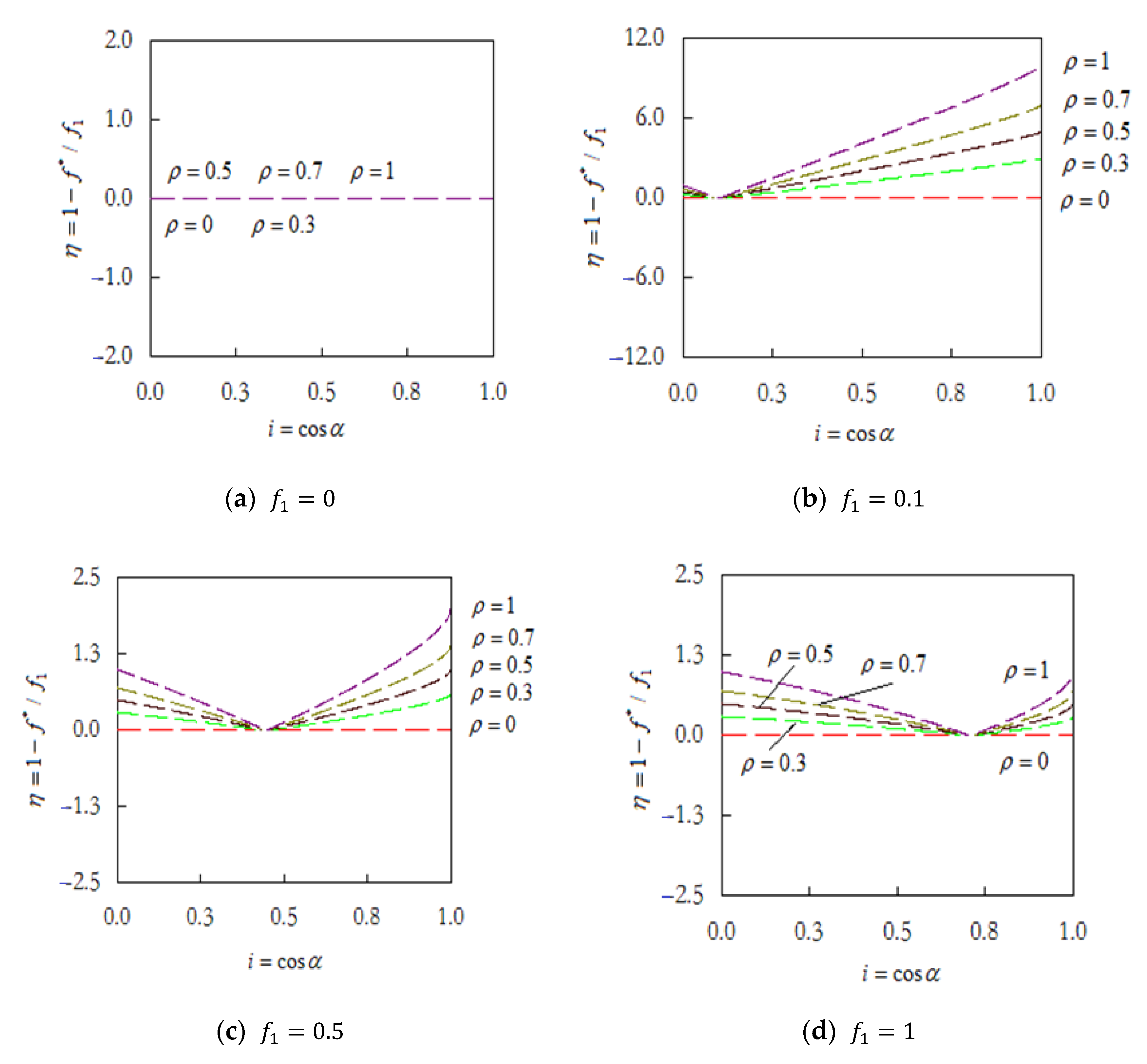
To sum up, according to the values shown in Figure 8, there is no negative gradient in the stage of . Obviously, there is no friction in this stage; is always zero with increasing . When , increases with obviously, and then the curve will be steeper. When , decreases with and decays to zero first, but then increases with gradually. In conclusion, the negative gradient of effective friction has a critical effect on friction. It was shown that the changes in the negative gradient of the effective friction coefficient changed the effective friction coefficient under the arbitrary time-varying external forces, which consequently reduced the friction. From a tribological perspective, the negative gradient of the effective friction coefficient plays a great role in the course of vibration affection on the friction. The rules concerning the negative gradient of the effective friction coefficient resulted in an effective friction coefficient, especially under the arbitrary time-varying external forces.
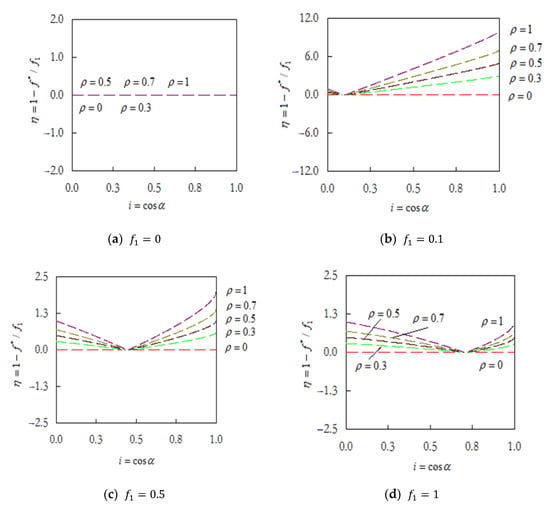
Figure 8.
The negative gradient of effective friction coefficient .
5. Conclusions
In conclusion, this paper investigated the effective coefficient of friction under arbitrary time-varying external forces. The results show the relationship of the effective friction coefficient and the negative gradient of friction.
(1) When the vibration force direction projects are in the first and the third quadrants, the negative gradient increases first, and then will be stable gradually. When the vibration force direction projects are in the second and the fourth quadrants, decreases but then increases gradually.
(2) From a tribological perspective, the negative gradient of the effective friction coefficient plays a great role in the course of vibration affection on the friction. The changes in the negative gradient of the effective friction coefficient resulted in an effective friction coefficient, especially under the arbitrary time-varying external forces. The effective friction coefficient was closely related to vibration properties and the influence and control on vibration systems with friction.
(3) It is shown that the numerical and analytical results of the rules concerning the negative gradient of the effective friction coefficient change the effective friction coefficient under the arbitrary time-varying external forces, which consequently reduce the friction in vibration.
Author Contributions
Q.W.: software, writing the original draft, investigation. Y.T.: formulation, approach, review and editing, supervision, formal analysis. L.X.: validation. B.W.: validation. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been supported by the National Natural Science Foundation of China NNSFC (Grant, No. 51305069).
Data Availability Statement
Some data, models, or code generated or used during the study are available from the corresponding author by request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pérez-Aracil, J.; Camacho-Gómez, C.; Pereira, E.; Vaziri, V.; Aphale, S.S.; Salcedo-Sanz, S. Eliminating Stick-Slip Vibrations in Drill-Strings witha Dual-Loop Control Strategy Optimised by the CRO-SL Algorithm. Mathmatics 2021, 9, 1526. [Google Scholar] [CrossRef]
- Sun, X.Q.; Wang, T.; Zhang, R.L.; Gu, F.S.; Ball, A.D. Numerical Modelling of Vibration Responses of Helical Gears under Progressive Tooth Wear for Condition Monitoring. Mathematics 2021, 9, 213. [Google Scholar] [CrossRef]
- Wu, J.T.; Yang, Y.; Yang, X.K.; Cheng, J.S. Fault feature analysis of cracked gear based on LOD and analytical-FE method. Mech. Syst. Signal Pr. 2018, 98, 951–967. [Google Scholar] [CrossRef]
- Sugiura, J.; Jones, S. Real-time stick-slip and vibration detection for 8 1/2”-hole-size rotary steerable tools in deeper wells and more aggressive drilling. In Proceedings of the AADE National Technical Conference, Houston, TX, USA, 10–12 April 2007. [Google Scholar]
- Robnett, E.; Hood, J.; Heisig, G.; Macpherson, J. Analysis of the stick-slip phenomenon using downhole drill string rotation data. In Proceedings of the SPE/IADC Drilling Conference, Amsterdam, The Netherlands, 9–11 March 1999. [Google Scholar]
- Baradaran-Nia, M.; Afizadeh, G.; Khanmohammadi, S.; Azar, B.F. Optimal sliding mode control of single degree-of-freedom hysteretic structural system. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4455–4466. [Google Scholar] [CrossRef]
- Fu, X.; Ai, H.; Li, C. Repetitive Learning Sliding Mode Stabilization Control for a Flexible-Base, Flexible-Link and Flexible-Joint Space Robot Capturing a Satellite. Appl. Sci. 2021, 11, 8077. [Google Scholar] [CrossRef]
- Kumar, V.C.; Hutchings, I.M. Reduction of the sliding friction of metals by the application of longitudinal or transverse ultrasonic vibration. Tribol. Int. 2004, 37, 833–840. [Google Scholar] [CrossRef]
- Adachi, K.; Kato, K.; Sasatani, Y. The micro-mechanism of friction drive with ultrasonic wave. Wear 1996, 194, 137–142. [Google Scholar] [CrossRef]
- Tucker, W.; Wang, C. On the effective control of torsional vibrations in drilling systems. J. Sound Vib. 1999, 224, 101–122. [Google Scholar] [CrossRef]
- Carducci, G.; Giannoccaro, N.I.; Messina, A.; Rollo, G. Identification of viscous friction coefficients for a pneumatic system model using optimization methods. Math. Comput. Simul. 2006, 71, 385–394. [Google Scholar] [CrossRef]
- Tsai, C.C.; Tseng, C.H. The effect of friction reduction in the presence of in-plane vibrations. Arch. Appl. Mech. 2006, 75, 164–176. [Google Scholar] [CrossRef]
- Bao, H.; Huang, W.; Lu, F. Investigation of engagement characteristics of a multi-disc wet friction clutch. Tribol. Int. 2021, 159, 106940. [Google Scholar]
- Jia, S.H. The effective friction coefficient under the vibration. J. Tsinghua Univ. 1959, 5, 165–170. [Google Scholar]
- Jin, X.; Xu, H.; Wang, Y.; Huang, Z. Approximately analytical procedure to evaluate random stick-slip vibration of Duffing system including dry friction. J. Sound Vib. 2019, 443, 520–536. [Google Scholar] [CrossRef]
- Marino, L.; Cicirello, A. Experimental investigation of a single-degree-of-freedom system with Coulomb friction. Nonlinear Dyn. 2020, 99, 1781–1799. [Google Scholar] [CrossRef]
- Wang, D.W.; Mo, J.L.; Wang, Z.G.; Chen, G.X.; Ouyang, H.; Zhou, Z.R. Numerical study of friction-induced vibration and noise on groove-textured surface. Tribol. Int. 2013, 64, 1–7. [Google Scholar] [CrossRef]
- Wang, X.C.; Huang, B.; Wang, R.L.; Mo, J.L.; Ouyang, H. Friction-induced stick-slip vibration and its experimental validation. Mech. Syst. Signal Process. 2020, 142, 106705. [Google Scholar] [CrossRef]
- Sun, G.D.; Zhu, H.; Ding, C. Using Recurrence Plots for Stability Analysis of Ring-on-Disc Tribopairs. Ind. Lubr. Tribol. 2019, 71, 532–539. [Google Scholar] [CrossRef]
- Sun, G.D.; Zhu, H.; Ding, C.; Jiang, Y.; Wei, C.L. On the Boundedness of Running-In Attractors Based on Recurrence Plot and Recurrence Qualification Analysis. Friction 2019, 7, 432–443. [Google Scholar] [CrossRef]
- Liu, Y.; Pavlovskaia, E.; Hendry, D.; Wiercigroch, M. Vibro-impact responses of capsule system with various friction models. Int. J. Mech. Sci. 2013, 72, 39–54. [Google Scholar] [CrossRef]
- Marques, F.; Flores, P.; Pimenta Claro, J.C.; Lankarani, H.M. A survey and comparison of several friction force models for dynamic analysis of multibody mechanical systems. Nonlinear Dyn. 2016, 86, 1407–1443. [Google Scholar] [CrossRef]
- Mostaghel, N. A non-standard analysis approach to systems involving friction. J. Sound Vib. 2005, 284, 583–595. [Google Scholar] [CrossRef]
- Rusinek, R.; Wiercigroch, M.; Wahi, P. Modelling of frictional chatter in metal cutting. Int. J. Mech. Sci. 2014, 89, 167–176. [Google Scholar] [CrossRef]
- Saha, A.; Wiercigroch, M.; Jankowski, K.; Wahi, P.; Stefański, A. Investigation of two different friction models from the perspective of friction-induced vibrations. Tribol. Int. 2015, 90, 185–197. [Google Scholar] [CrossRef]
- Yan, Y.; Liu, G.; Wiercigroch, M.; Xu, J. Safety estimation for a new model of regenerative and frictional cutting dynamics. Int. J. Mech. Sci. 2021, 201, 106468. [Google Scholar] [CrossRef]
- Yoo, S.S.; Kim, D.E. Effects of vibration frequency and amplitude on friction reduction and wear characteristics of silicon. Tribol. Int. 2016, 16, 198–206. [Google Scholar] [CrossRef]
- Safaei, B. Frequency-dependent damped vibrations of multifunctional foam plates sandwiched and integrated by composite faces. Eur. Phys. J. Plus 2021, 136, 646. [Google Scholar] [CrossRef]
- Duc, D.H.; Thom, D.V.; Cong, P.H.; Minh, P.V.; Nguyen, N.X. Vibration and static buckling behavior of variable thickness flexoelectric nanoplates. Mech. Based Des. Struct. Mach. 2022, 8, 1–29. [Google Scholar] [CrossRef]
- Dung, N.T.; Van Ke, T.; Huyen, T.T.H.; Van Minh, P. Nonlinear static bending analysis of microplates resting on imperfect two-parameter elastic foundations using modified couple stress theory. Comptes Rendus Mec. 2022, 350, 121–141. [Google Scholar] [CrossRef]
- Tho, N.C.; Ta, N.T.; Thom, D.V. New Numerical Results from Simulations of Beams and Space Frame Systems with a Tuned Mass Damper. Materials 2019, 12, 1329. [Google Scholar] [CrossRef] [PubMed]
- Han, S.Y.; Narasimhan, M.N.L.; Kennedy, T.C. Finite crack propagation in a micropolar elastic solid. KSME J. 1989, 3, 103. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, R.; Chadha, T.K. Eigen value approach to second dynamic problem of micropolar elastic solid. Indian J. Pure Appl. Math. 2003, 34, 743–754. [Google Scholar]
- Tuan, L.T.; Dung, N.T.; Van Thom, D.; Van Minh, P.; Zenkour, A.M. Propagation of non-stationary kinematic disturbances from a spherical cavity in the pseudo-elastic cosserat medium. Eur. Phys. J. Plus 2021, 136, 1199. [Google Scholar] [CrossRef]
- Tran, T.T.; Tran, V.K.; Le, P.B.; Phung, V.M.; Do, V.T.; Nguyen, H.N. Forced vibration analysis of laminated composite shells reinforced with graphene nanoplatelets using finite element method. Adv. Civ. Eng. 2020, 2020, 1471037. [Google Scholar] [CrossRef]
- Nam, V.H.; Nam, N.H.; Vinh, P.V.; Khoa, D.N.; Thom, D.V.; Minh, P.V. A new efficient modified first-order shear model for static bending and vibration behaviors of two-layer composite plate. Adv. Civ. Eng. 2019, 2019, 6814367. [Google Scholar] [CrossRef]
- van Thom, D.; Duc, D.H.; van Minh, P.; Tung, N.S. Finite element modelling for free vibration response of cracked stiffened fgm plates. Vietnam J. Sci. Technol. 2020, 58, 119. [Google Scholar] [CrossRef]
- Tho, N.C.; Thanh, N.T.; Tho, T.D.; van Minh, P.; Hoa, L.K. Modelling of the flexoelectric effect on rotating nanobeams with geometrical imperfection. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 510. [Google Scholar] [CrossRef]
- Dung, N.T.; van Minh, P.; Hung, H.M.; Tien, D.M. The third-order shear deformation theory for modelling the static bending and dynamic responses of piezoelectric bidirectional functionally graded plates. Adv. Mater. Sci. Eng. 2021, 2021, 5520240. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).