Error Propagation Model Using Jacobian-Torsor Model Weighting for Assembly Quality Analysis on Complex Product
Abstract
:1. Introduction
2. Preliminaries
2.1. Complex Network
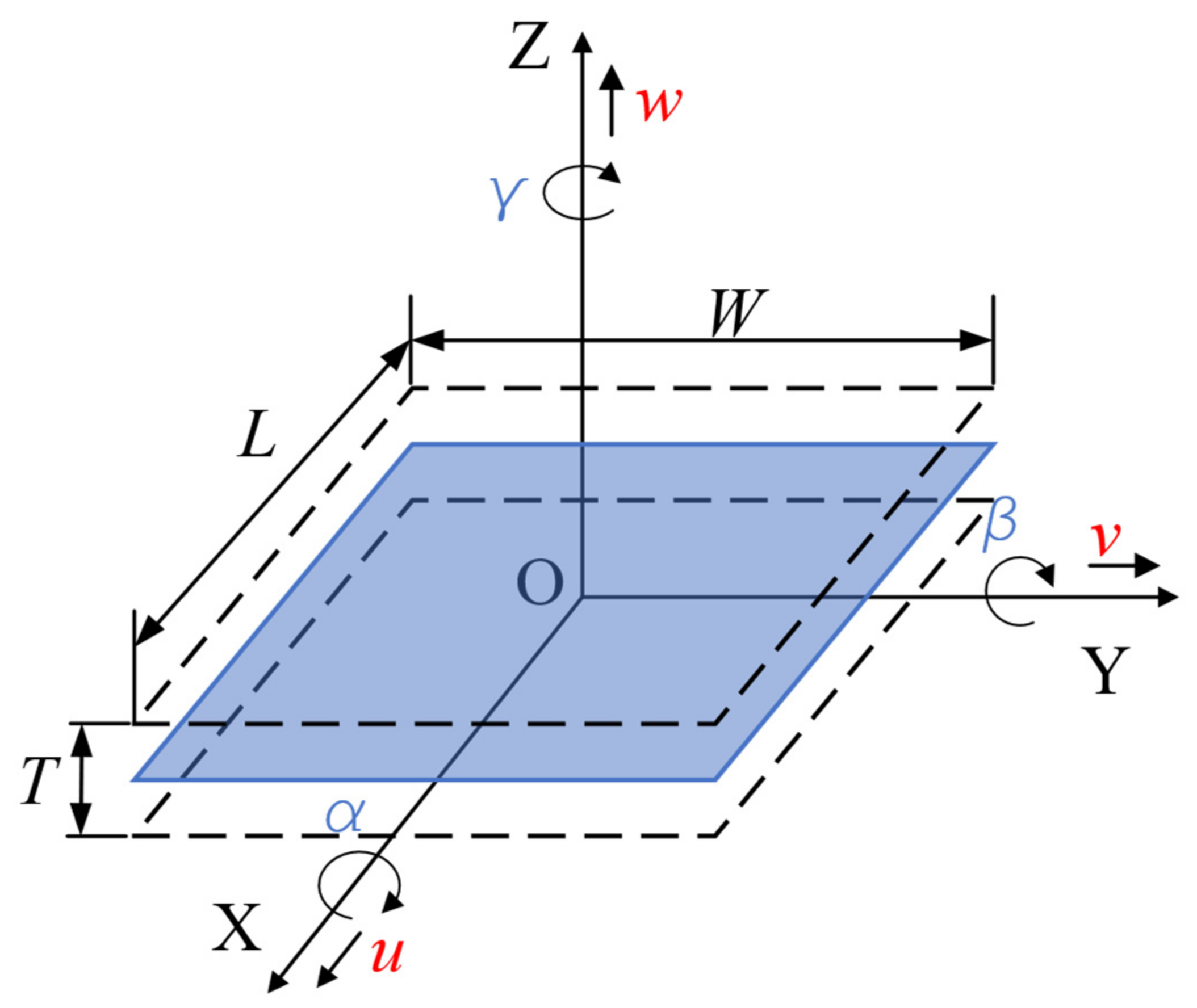
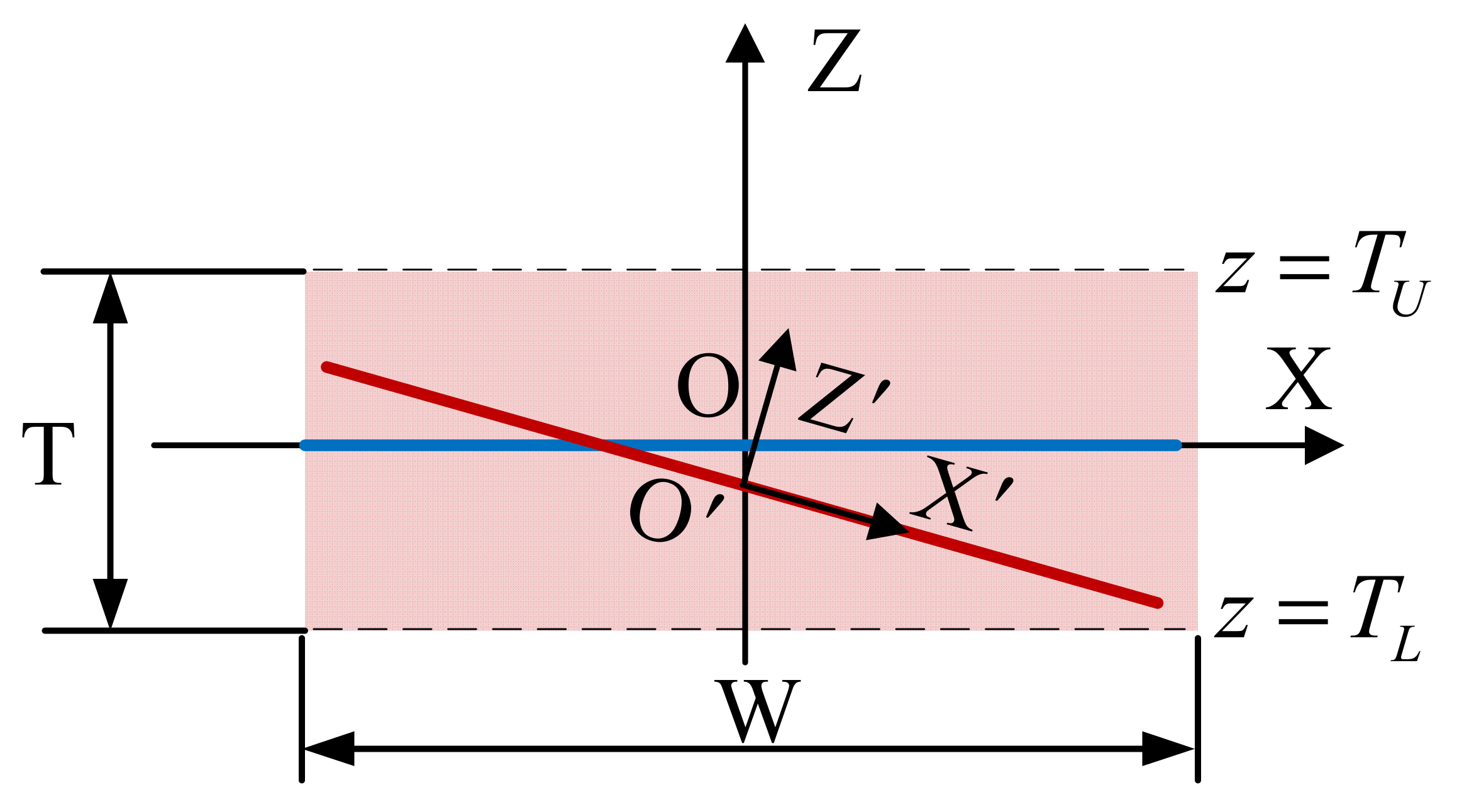
2.2. Jacobian-Torsor Model
3. Methodology
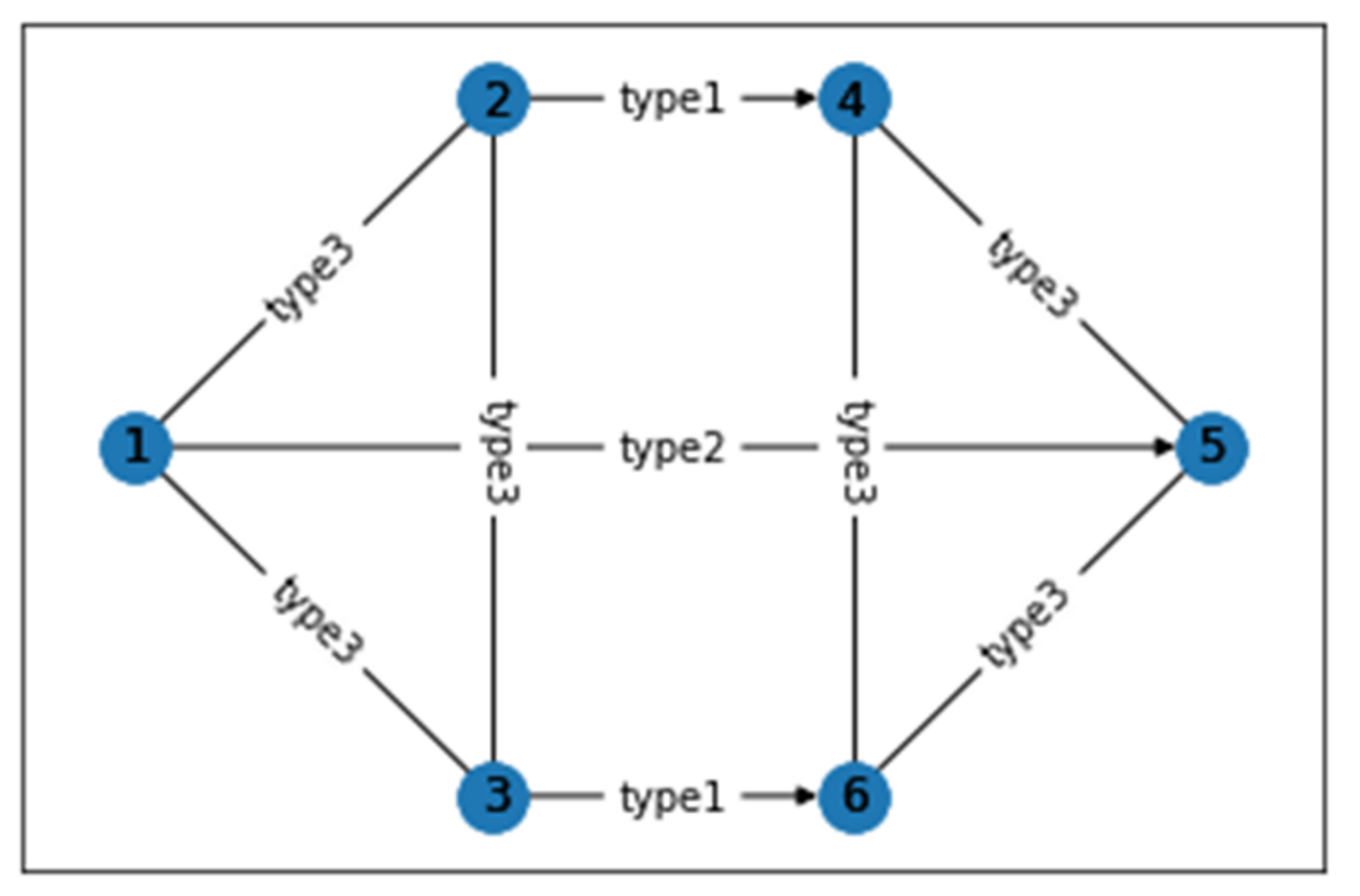
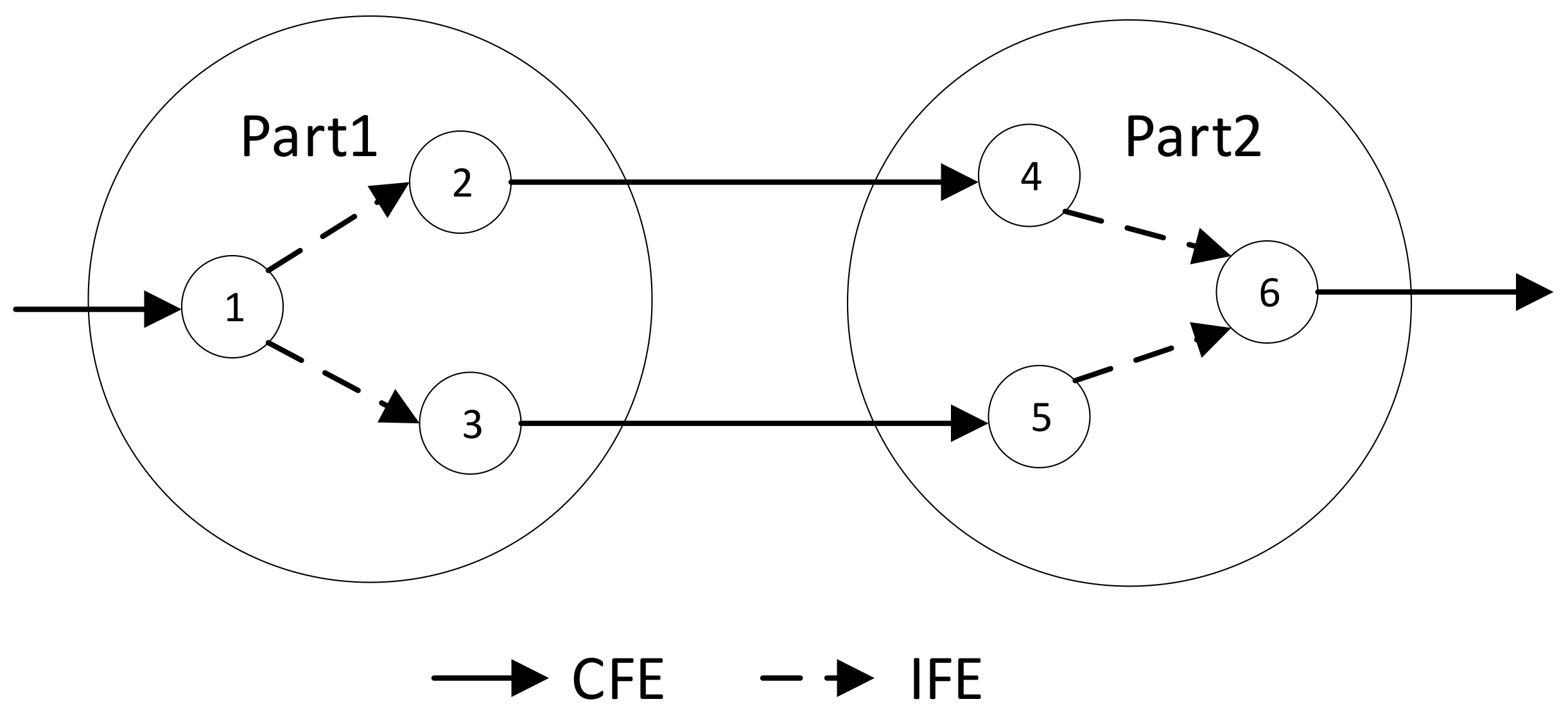
3.1. Complex Network Module for Assembly Quality Analysis
3.2. Assigning Weights to Edges Based on the J-T Model
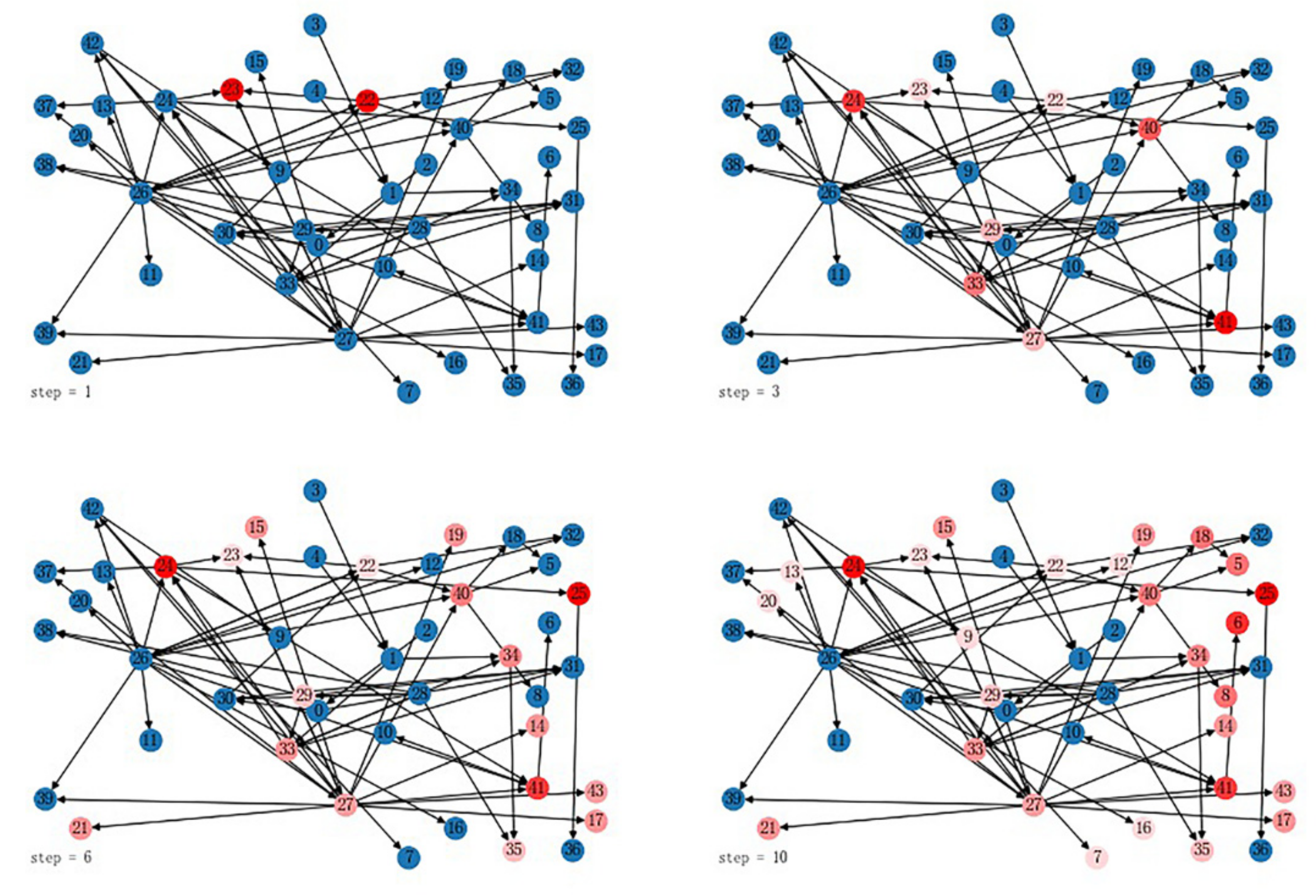
3.3. Key Node Identification Based on Probability Propagation Model
- (1)
- All feature nodes in the network model are initially in the normal state, represented by N, and initially carry an error of 0. Feature nodes affected by the propagation of the assembly error are transformed into the infected state, represented by .
- (2)
- The model runs in unit time as work steps, and in each work step, only the assembly feature nodes involved in that work step are capable of propagating the error.
- (3)
- The probability of propagation of the error from the infected node to the associated node is the variance of the weights of the edges between the two nodes.
- (4)
- In propagating the error, the error of the infected node is the sum of the error of the infected node and the weights of the connected edges.

4. Case Study
4.1. Approaches Implementation
4.2. Discussion
5. Conclusions
- (1)
- A method is identified for modeling and analyzing the assembly process of complex products based on complex networks in which the correlations and topologies between parts and features are expressed and analyzed using complex network models, allowing a preliminary understanding of the local characteristics of complex product parts through the statistical properties of complex networks.
- (2)
- A method of assigning weights to edges of the complex network is developed to objectively reflect the magnitude of the transmission error of the parts. The magnitude and direction of the error transmission between the assembly features are calculated using the Jacobian-Torsor model and expressed by the weights and directions of directed edges between nodes.
- (3)
- An error propagation model is designed to simulate the process of assembly quality deviation propagation and diffusion. The deviation transmission process is restored as much as possible based on the constructed assembly quality network. The important nodes in the network are obtained based on the statistical results of cumulative reception errors and the cumulative transmission errors of nodes. These nodes are divided into two categories, namely the assembly quality optimization control point and the assembly quality status monitoring point.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fei, C.-W.; Li, H.; Liu, H.-T.; Lu, C.; Keshtegar, B.; An, L.-Q. Multilevel Nested Reliability-Based Design Optimization with Hybrid Intelligent Regression for Operating Assembly Relationship. Aerosp. Sci. Technol. 2020, 103, 105906. [Google Scholar] [CrossRef]
- Villalonga, A.; Negri, E.; Biscardo, G.; Castano, F.; Haber, R.E.; Fumagalli, L.; Macchi, M. A Decision-Making Framework for Dynamic Scheduling of Cyber-Physical Production Systems Based on Digital Twins. Annu. Rev. Control 2021, 51, 357–373. [Google Scholar] [CrossRef]
- Jin, R.; Shi, J. Reconfigured Piecewise Linear Regression Tree for Multistage Manufacturing Process Control. IIE Trans. 2012, 44, 249–261. [Google Scholar] [CrossRef]
- Zhuang, C.; Gong, J.; Liu, J. Digital Twin-Based Assembly Data Management and Process Traceability for Complex Products. J. Manuf. Syst. 2021, 58, 118–131. [Google Scholar] [CrossRef]
- Zeng, W.; Rao, Y.; Wang, P.; Yi, W. A Solution of Worst-Case Tolerance Analysis for Partial Parallel Chains Based on the Unified Jacobian-Torsor Model. Precis. Eng. 2017, 47, 276–291. [Google Scholar] [CrossRef]
- Guo, F.; Liu, J.; Wang, Z.; Zou, F.; Zhao, X. Positioning Error Guarantee Method with Two-Stage Compensation Strategy for Aircraft Flexible Assembly Tooling. J. Manuf. Syst. 2020, 55, 285–301. [Google Scholar] [CrossRef]
- Sun, W.; Li, T.; Yang, D.; Sun, Q.; Huo, J. Dynamic Investigation of Aeroengine High Pressure Rotor System Considering Assembly Characteristics of Bolted Joints. Eng. Fail. Anal. 2020, 112, 104510. [Google Scholar] [CrossRef]
- Mir-Haidari, S.-E.; Behdinan, K. Nonlinear Effects of Bolted Flange Connections in Aeroengine Casing Assemblies. Mechanical Syst. Signal Process. 2022, 166, 108433. [Google Scholar] [CrossRef]
- Fei, C.; Liu, H.; Patricia Liem, R.; Choy, Y.; Han, L. Hierarchical Model Updating Strategy of Complex Assembled Structures with Uncorrelated Dynamic Modes. Chin. J. Aeronaut. 2021, 35, 281–296. [Google Scholar] [CrossRef]
- Hussain, T.; Yang, Z.; Popov, A.A.; McWilliam, S. Straight-Build Assembly Optimization: A Method to Minimize Stage-by-Stage Eccentricity Error in the Assembly of Axisymmetric Rigid Components (Two-Dimensional Case Study). J. Manuf. Sci. Eng. 2011, 133, 031014. [Google Scholar] [CrossRef]
- Jiali, Z.; Wei, G.; Zhanwen, N.; Hongbin, Y. Quality Stability of Multi-Stations Assembly Process Based on Stream of Variation. Chin. J. Mech. Eng. 2006, 42, 88–93. [Google Scholar]
- Hong, J. Assembly Accuracy Prediction and Adjustment Process Modeling of Precision Machine Tool Based on State Space Model. JME 2013, 49, 114. [Google Scholar] [CrossRef]
- Guo, J.; Li, B.; Hong, J.; Li, X. Assembly Adjustment Process Planning of Precision Machine Tools Based on Optimal Estimation of Variation Propagation. J. Mech. Eng. 2020, 56, 172–180. [Google Scholar]
- Beruvides, G.; Castaño, F.; Quiza, R.; Haber, R.E. Surface Roughness Modeling and Optimization of Tungsten–Copper Alloys in Micro-Milling Processes. Measurement 2016, 86, 246–252. [Google Scholar] [CrossRef]
- Shahi, V.J.; Masoumi, A.; Franciosa, P.; Ceglarek, D. Quality-Driven Optimization of Assembly Line Configuration for Multi-Station Assembly Systems with Compliant Non-Ideal Sheet Metal Parts. Procedia CIRP 2018, 75, 45–50. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, M.; Sun, C.; Hu, M.; Chen, D.; Liu, Z.; Tan, J. A Method to Minimize Stage-by-Stage Initial Unbalance in the Aero Engine Assembly of Multistage Rotors. Aerosp. Sci. Technol. 2019, 85, 270–276. [Google Scholar] [CrossRef]
- Zhou, T.; Gao, H.; Wang, X.; Li, L.; Liu, Q. Error Modeling and Compensating of a Novel 6-DOF Aeroengine Rotor Docking Equipment. Chin. J. Aeronaut. 2021, 35, 312–324. [Google Scholar] [CrossRef]
- Cai, J.; Liu, G.; Ouyang, B.; Cai, F. Research on Deflection Quality Assessment of Assembly Car Body Based on Deflection Measurement and Improved Principal Component Analysis Method. In Advances in Precision Instruments and Optical Engineering; Liu, G., Cen, F., Eds.; Springer: Singapore, 2022; pp. 193–201. [Google Scholar]
- Lafond, P.; Laperriere, L. Jacobian-Based Modeling of Dispersions Affecting Pre-Defined Functional Requirements of Mechanical Assemblies. In Proceedings of the 1999 IEEE International Symposium on Assembly and Task Planning (ISATP’99) (Cat. No.99TH8470), Porto, Portugal, 24–24 July 1999; pp. 20–25. [Google Scholar]
- Laperrière, L.; Ghie, W.; Desrochers, A. Statistical and Deterministic Tolerance Analysis and Synthesis Using a Unified Jacobian-Torsor Model. CIRP Ann. 2002, 51, 417–420. [Google Scholar] [CrossRef]
- Ghie, W.; Laperrière, L.; Desrochers, A. Statistical Tolerance Analysis Using the Unified Jacobian–Torsor Model. Int. J. Prod. Res. 2010, 48, 4609–4630. [Google Scholar] [CrossRef]
- Ding, S.; Jin, S.; Li, Z.; Chen, H. Multistage Rotational Optimization Using Unified Jacobian–Torsor Model in Aero-Engine Assembly. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2019, 233, 251–266. [Google Scholar] [CrossRef]
- Thornton, A.C. A Mathematical Framework for the Key Characteristic Process. Res. Eng. Des. 1999, 11, 145–157. [Google Scholar] [CrossRef]
- Whitney, D.E. The Role of Key Characteristics in the Design of Mechanical Assemblies. Assem. Autom. 2006, 26, 315–322. [Google Scholar] [CrossRef]
- Han, Z.; Mo, R.; Chang, Z.; Hao, L.; Niu, W. Key Assembly Structure Identification in Complex Mechanical Assembly Based on Multi-Source Information. Assem. Autom. 2017, 37, 208–218. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Z.; Zhong, X.; Zou, F. Identification of Influential Function Modules within Complex Products and Systems Based on Weighted and Directed Complex Networks. J. Intell. Manuf. 2019, 30, 2375–2390. [Google Scholar] [CrossRef]
- Liu, D.; Jiang, P. Fluctuation Analysis of Process Flow Based on Error Propagation Network. Chin. J. Mech. Eng. 2010, 46, 14–21. [Google Scholar] [CrossRef]
- Wang, P.; Wang, Y.; Wang, H.; Zheng, M. Quality Prediction of Multistage Machining Processes Based on Assigned Error Propagation Network. J. Mech. Eng. 2013, 49, 160–170. [Google Scholar] [CrossRef]
- Liu, Y.; Mei, Y.; Sun, C.; Li, R.; Wang, X.; Wang, H.; Tan, J.; Lu, Q. A Novel Cylindrical Profile Measurement Model and Errors Separation Method Applied to Stepped Shafts Precision Model Engineering. Measurement 2022, 188, 110486. [Google Scholar] [CrossRef]
- Zhu, P.; Yu, J.-b.; Zheng, X.-y.; Wang, Y.-s.; Sun, X.-w. Variation Propagation Network-Based Modeling and Error Tracing in Mechanical Assembling Process. J. Zhejiang Univ. (Eng. Sci.) 2019, 53, 1582–1593. [Google Scholar] [CrossRef]
- Hong, L.; Kun, C.; Xingwei, L.; Lili, L.; Jiakun, Z.; Hui, Y. Fluctuation Diffusion Network Modeling and Fluctuation Source Identification of Multi-Fluctuation-Source and Multi-Process Machining Processes. J. Xi’an Jiaotong Univ. 2021, 55, 73–83. [Google Scholar]
- Verna, E.; Genta, G.; Galetto, M.; Franceschini, F. Inspection Planning by Defect Prediction Models and Inspection Strategy Maps. Prod. Eng. Res. Devel. 2021, 15, 897–915. [Google Scholar] [CrossRef]
- Lou, H.; Chen, K.; Li, X.; Li, L.; Zhang, J.; Yu, H. Assembly Unit Partitioning Method of Complex Mechanical Products for Error Propagation. J. Xi’an Jiaotong Univ. 2021, 55, 86–94. [Google Scholar]
- Desrochers, A.; Clément, A. A Dimensioning and Tolerancing Assistance Model for CAD/CAM Systems. Int. J. Adv. Manuf. Technol. 1994, 9, 352–361. [Google Scholar] [CrossRef]
- Chen, H.; Jin, S.; Li, Z.; Lai, X. A Comprehensive Study of Three Dimensional Tolerance Analysis Methods. Comput.-Aided Des. 2014, 53, 1–13. [Google Scholar] [CrossRef]
- Laperrière, L.; Lafond, P. Modeling Tolerances and Dispersions of Mechanical Assemblies Using Virtual Joints. In Proceedings of the Volume 1: 25th Design Automation Conference; American Society of Mechanical Engineers: Las Vegas, NV, USA, 1999; pp. 933–942. [Google Scholar]
- Chen, H.; Jin, S.; Li, Z.; Lai, X. A Solution of Partial Parallel Connections for the Unified Jacobian–Torsor Model. Mechanism and Machine Theory 2015, 91, 39–49. [Google Scholar] [CrossRef]

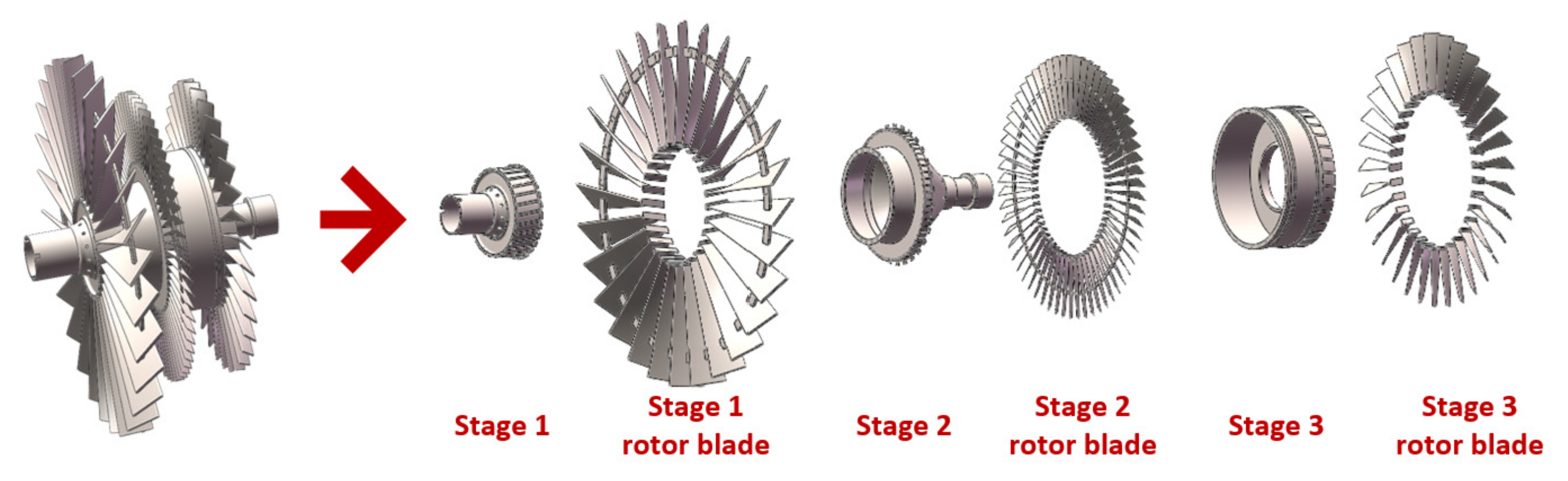
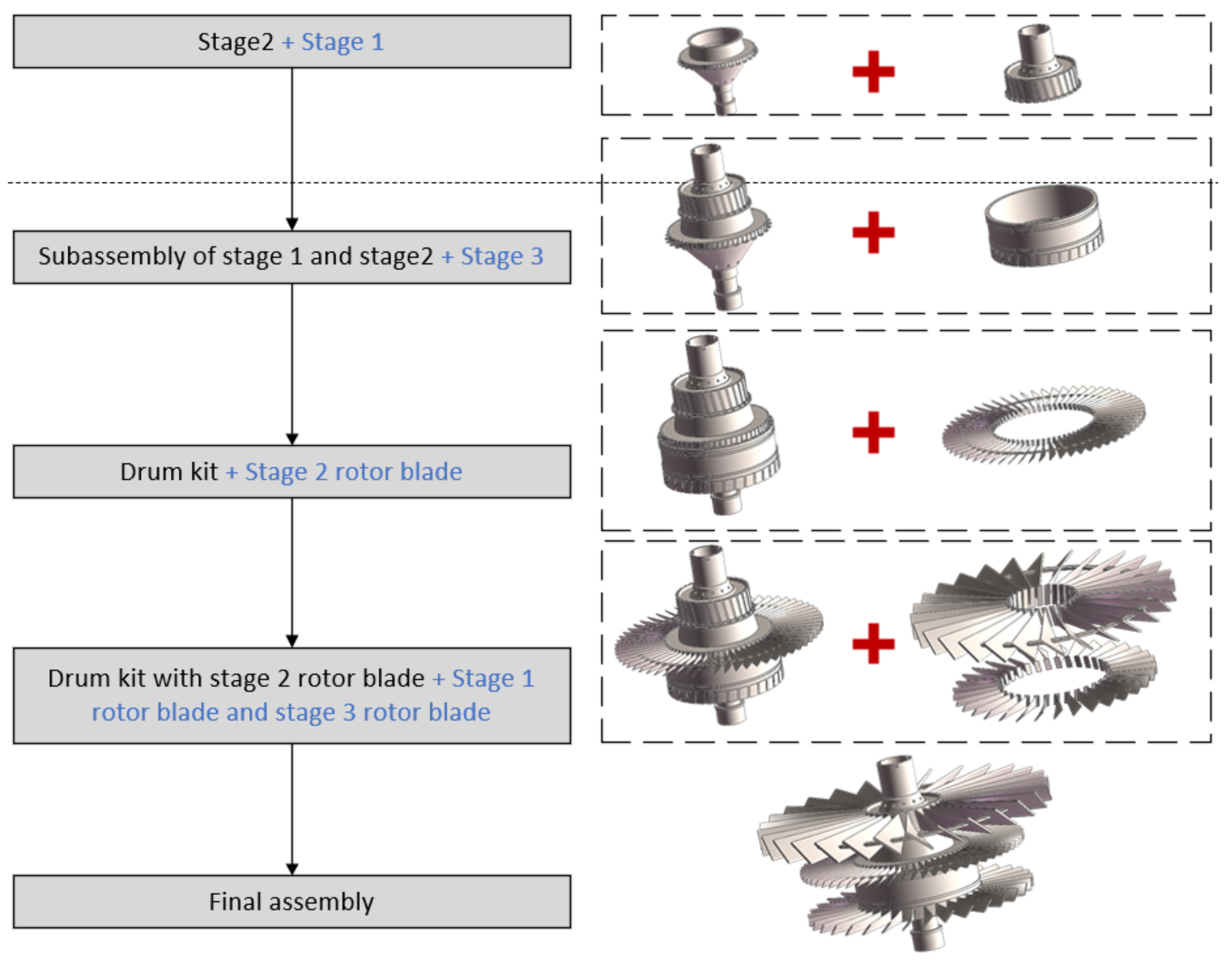
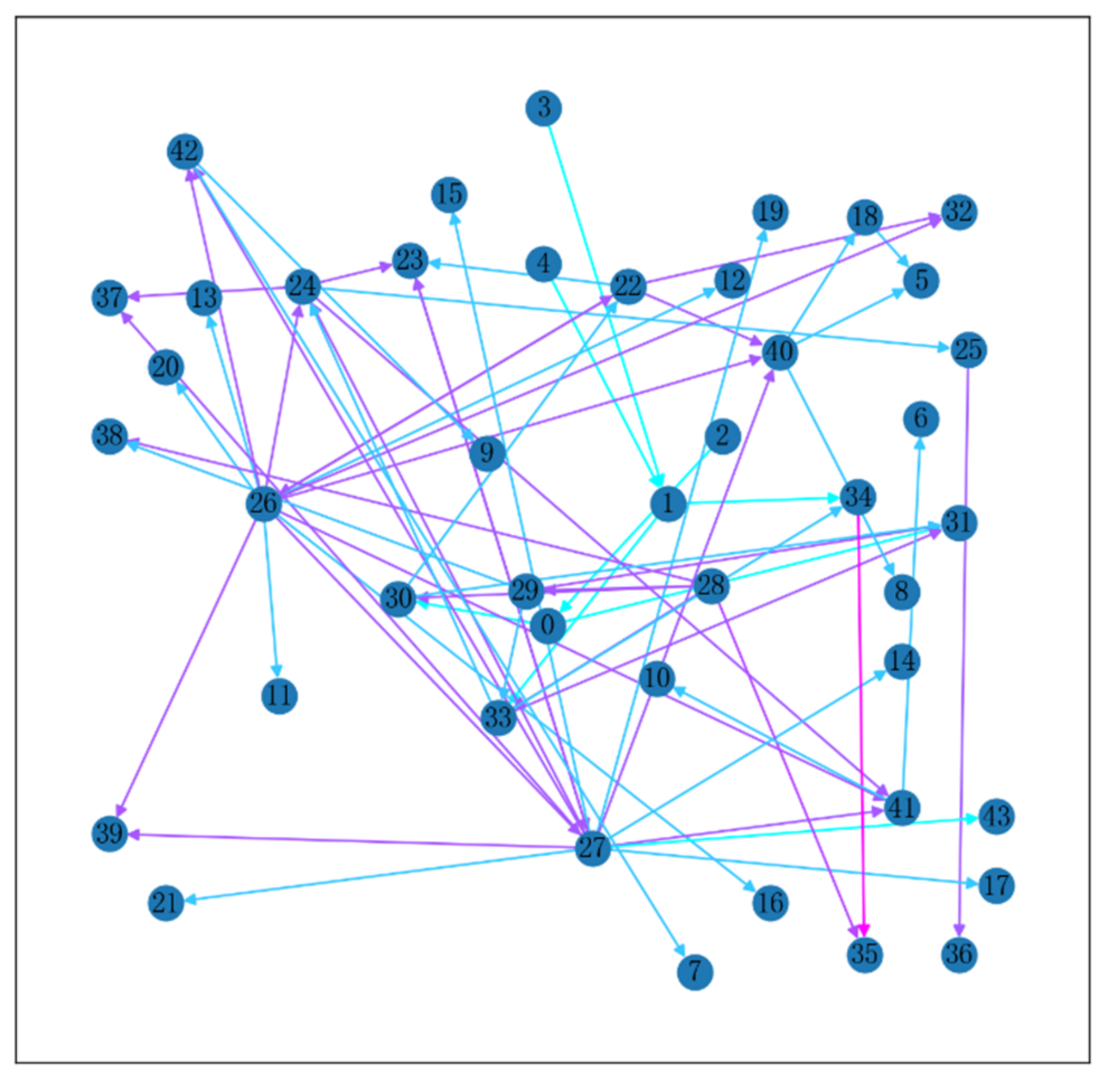
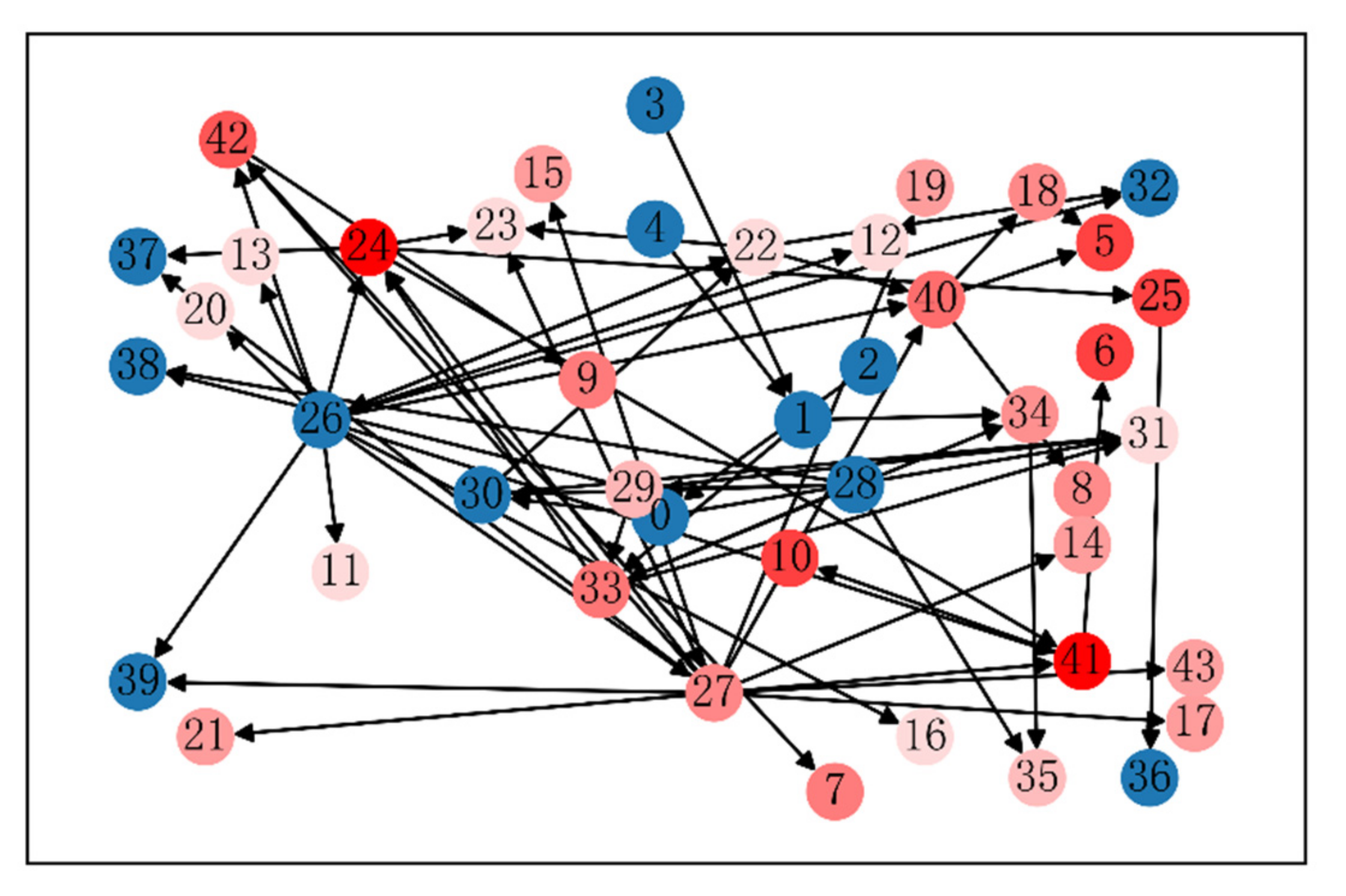

| Node | Feature | Node | Feature |
|---|---|---|---|
| 0 | Stage 1 rear bolt | 27 | Stage 2 disc journal outer circle |
| 1 | Stage 2 rear bolt | 28 | Stage 1 axial datum |
| 2 | Ten-angle self-locking nut 1 | 29 | Stage 2 axial reference |
| 3 | Ten-angle self-locking nut 2 | 30 | Stage 1 stop end face |
| 4 | Wire retaining ring | 31 | Stage 2 disc stop face |
| 5 | Stage 1 rotor blade | 32 | Stage 1 disk core hole |
| 6 | Stage 2 rotor blade | 33 | Stage 2 rear stop end face |
| 7 | Stage 3 rotor blade | 34 | Stage 3 front stop face |
| 8 | Stage 1 retaining ring assembly | 35 | Stage 3 rear face |
| … | … | … | … |
| 23 | Stage 2 inside diameter of the front stop | 40 | Stage 1 disc rim |
| 24 | Stage 2 inner diameter of rear stop | 41 | Stage 2 disc rim |
| 25 | Stage 3 inner diameter of the front stop | 42 | Stage 3 disc rim |
| 26 | Stage 1 disc journal outer circle | 43 | Pressing nut |
| Node | Degree Centrality | Node | Betweenness Centrality | Node | Closeness Centrality | Node | Eigenvector Centrality |
|---|---|---|---|---|---|---|---|
| 27 | 0.357143 | 27 | 0.075784 | 24 | 0.122449 | 41 | 0.323474 |
| 26 | 0.333333 | 24 | 0.065621 | 41 | 0.118347 | 23 | 0.323474 |
| 24 | 0.166667 | 22 | 0.06417 | 23 | 0.118227 | 37 | 0.323463 |
| 22 | 0.142857 | 23 | 0.055168 | 31 | 0.117216 | 5 | 0.244195 |
| 33 | 0.142857 | 26 | 0.051103 | 37 | 0.103175 | 27 | 0.244184 |
| 40 | 0.142857 | 33 | 0.048877 | 40 | 0.100595 | 6 | 0.244173 |
| 28 | 0.119048 | 30 | 0.04849 | 25 | 0.098142 | 10 | 0.244173 |
| 41 | 0.119048 | 40 | 0.022648 | 5 | 0.097403 | 40 | 0.184343 |
| 23 | 0.095238 | 0 | 0.019164 | 6 | 0.097222 | 24 | 0.184332 |
| 42 | 0.095238 | 1 | 0.015679 | 10 | 0.097222 | 42 | 0.184332 |
| Node | CTE | Node | CRE |
|---|---|---|---|
| 27 | 54.1609 | 41 | 64.9708 |
| 33 | 24.5601 | 5 | 60.6456 |
| 24 | 22.9293 | 23 | 54.8656 |
| 26 | 22.1153 | 10 | 49.9614 |
| 41 | 21.7522 | 6 | 47.7217 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xi, Y.; Gao, Z.; Chen, K.; Dai, H.; Liu, Z. Error Propagation Model Using Jacobian-Torsor Model Weighting for Assembly Quality Analysis on Complex Product. Mathematics 2022, 10, 3534. https://doi.org/10.3390/math10193534
Xi Y, Gao Z, Chen K, Dai H, Liu Z. Error Propagation Model Using Jacobian-Torsor Model Weighting for Assembly Quality Analysis on Complex Product. Mathematics. 2022; 10(19):3534. https://doi.org/10.3390/math10193534
Chicago/Turabian StyleXi, Yue, Zhiyong Gao, Kun Chen, Hongwei Dai, and Zhe Liu. 2022. "Error Propagation Model Using Jacobian-Torsor Model Weighting for Assembly Quality Analysis on Complex Product" Mathematics 10, no. 19: 3534. https://doi.org/10.3390/math10193534
APA StyleXi, Y., Gao, Z., Chen, K., Dai, H., & Liu, Z. (2022). Error Propagation Model Using Jacobian-Torsor Model Weighting for Assembly Quality Analysis on Complex Product. Mathematics, 10(19), 3534. https://doi.org/10.3390/math10193534





