Cross-Section Dimension Measurement of Construction Steel Pipe Based on Machine Vision
Abstract
:1. Introduction
1.1. Background and Significance of the Study
1.2. Technical Research Background
1.2.1. Visual Measurement Research Background
1.2.2. Background of Convolutional Neural Networks
2. Network Model
2.1. Improved RCF-Based Coarse Edge Detection Method
- Algorithm design
- (1)
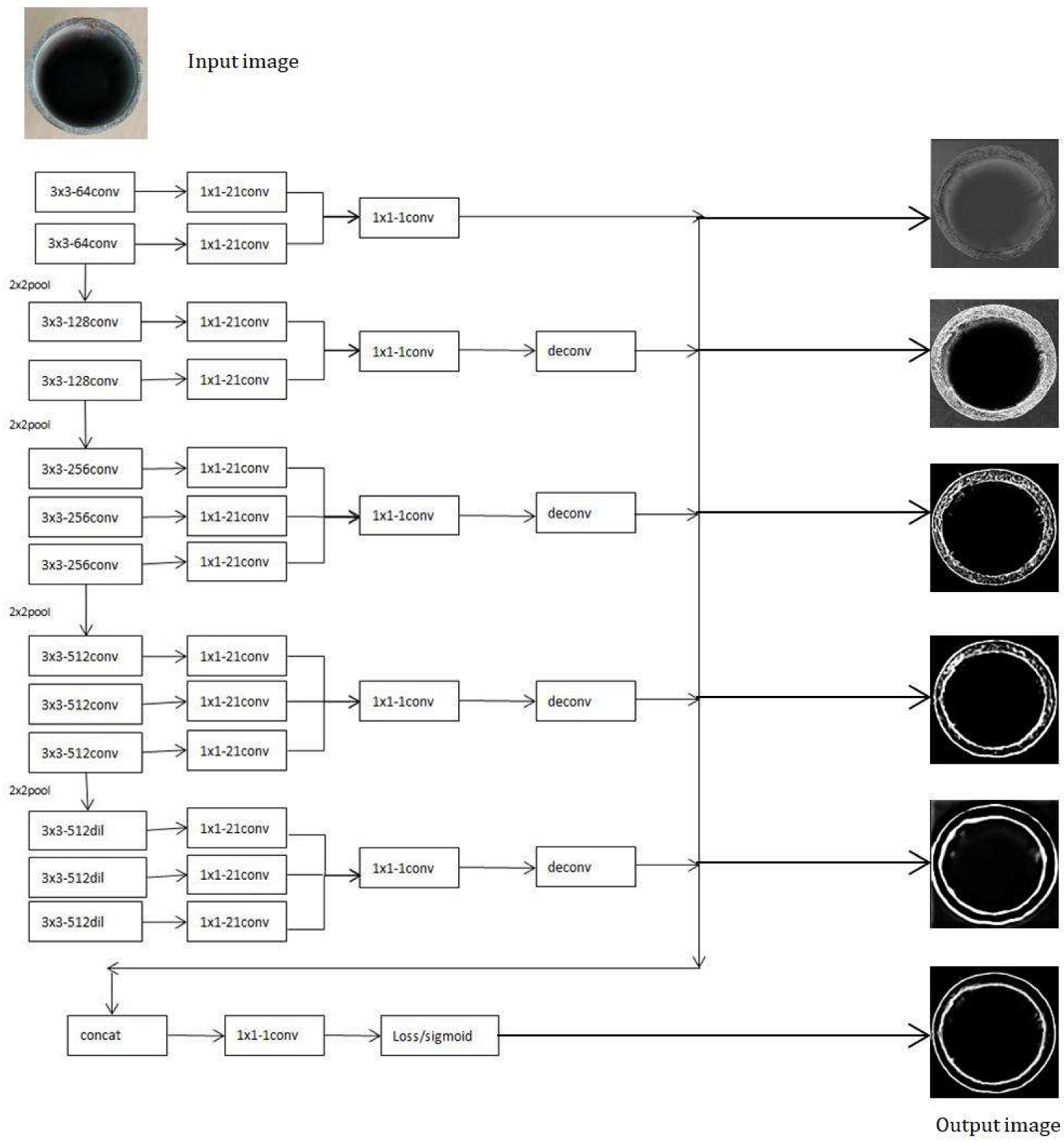
- The proposed model uses the dil (dilation convolution) module in the last stage, which adds voids to the standard convolution layer to increase the perceptual field. Compared with standard convolution, the dilation convolution has one more dilation parameter, which in this work is set to 2.
- (2)
- In the RCF model, a loss calculation function is added at the end of each stage, and a deconvolution layer is upsampled in each layer to map the image size to the original size. Finally, the output of each stage is superimposed on a 1 × 1 − 1 convolution to merge multiple channels and calculate the loss. Our model only uses it for loss calculation of the images after merging multiple channels, affording our model to detect edges more clearly and interfere with fewer contour lines than the original model. The network model of this paper is illustrated in Figure 3.
- Training sample set
2.2. Model Training and Detection
- (1)
- Choice of the loss function
- (2)
- Backward propagation parameters and activation functions
- (3)
- Training process
2.3. Experimental Analysis
3. Image Processing of Coarse Edges
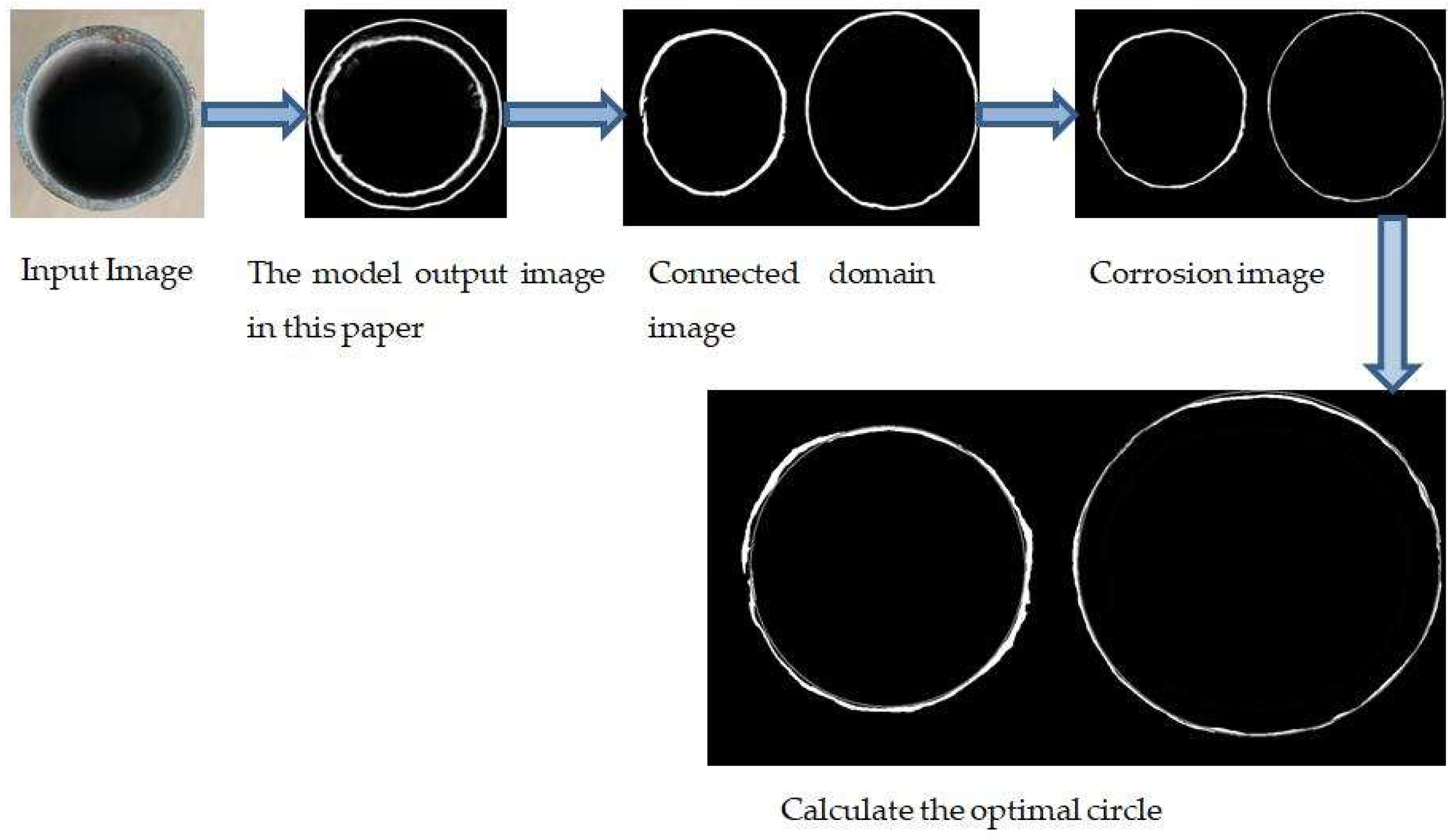
3.1. Connected Domain-Based Image Processing
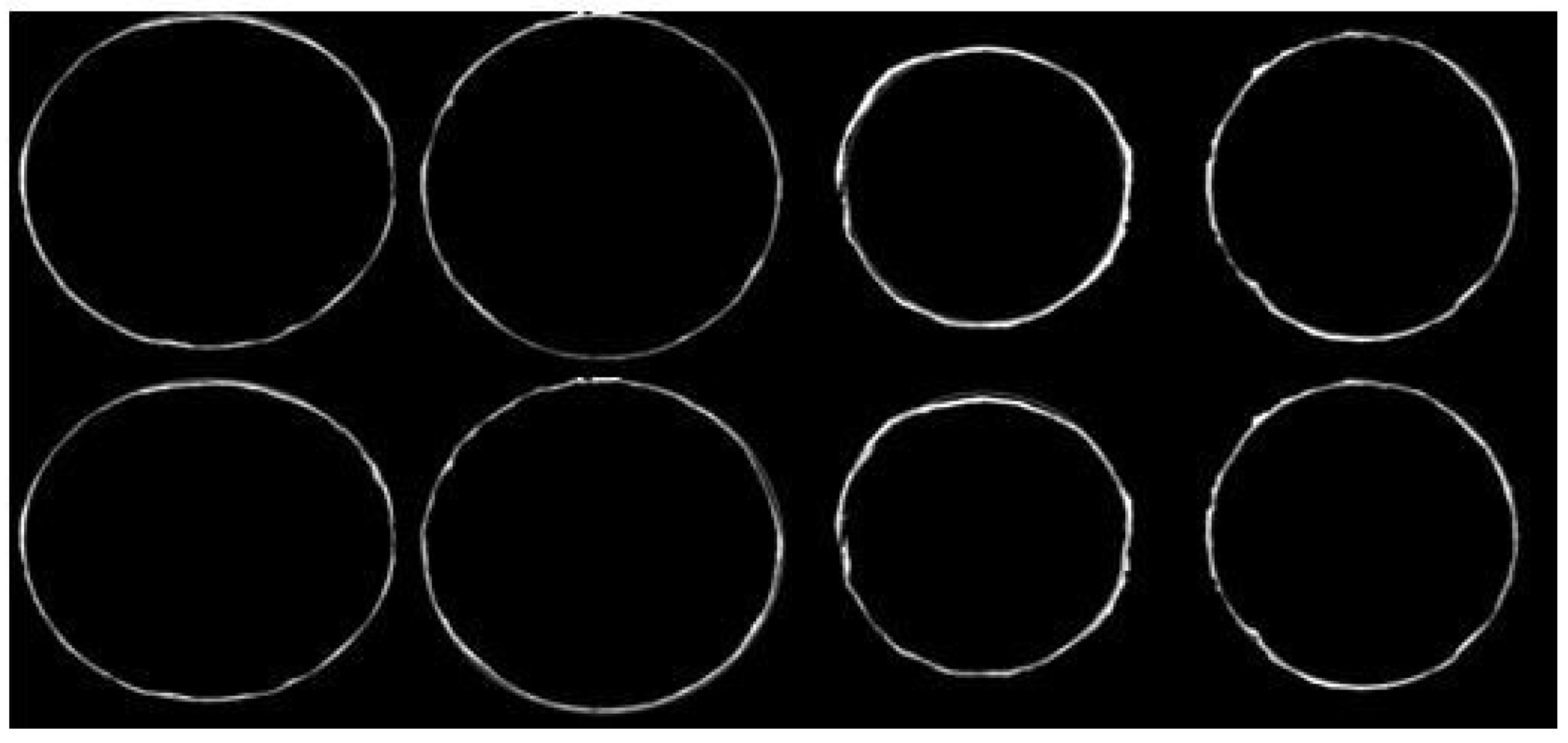
3.2. Accuracy of Circle Detection Based on Hough Transform
3.2.1. Hough Circle Detection
3.2.2. Radius Circle Centering Accuracy
- (1)
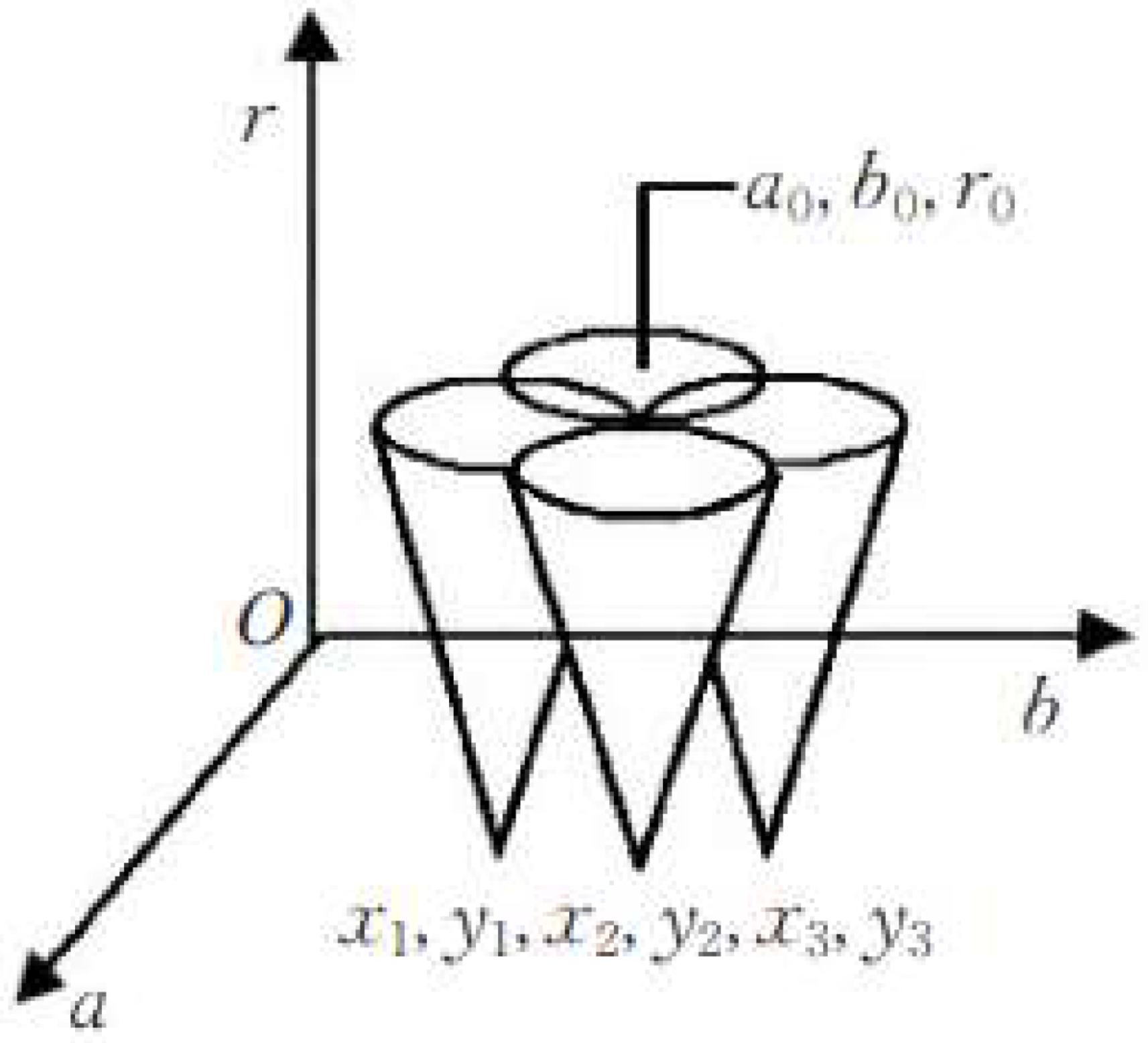
- Using the image of the connected domain, the approximate circle center, and coordinates of the circle in the picture are first detected using Hough circle detection.
- (2)
- Then, we determine the 8-neighborhood of the circle center based on the circle center that is found, and use the 8-neighborhood as the error circle center.
- (3)
- We calculate the distance from all the points on the image to the center of the eight circles and take the average as the radius.
- (4)
- We draw eight circles that are centered at the eight neighborhoods and the radius that is calculated in the previous step. Then, we calculate the overlap between these nine standard circles and the graph. The circle with the highest degree of overlap is the optimal circle.
3.3. Error Analysis
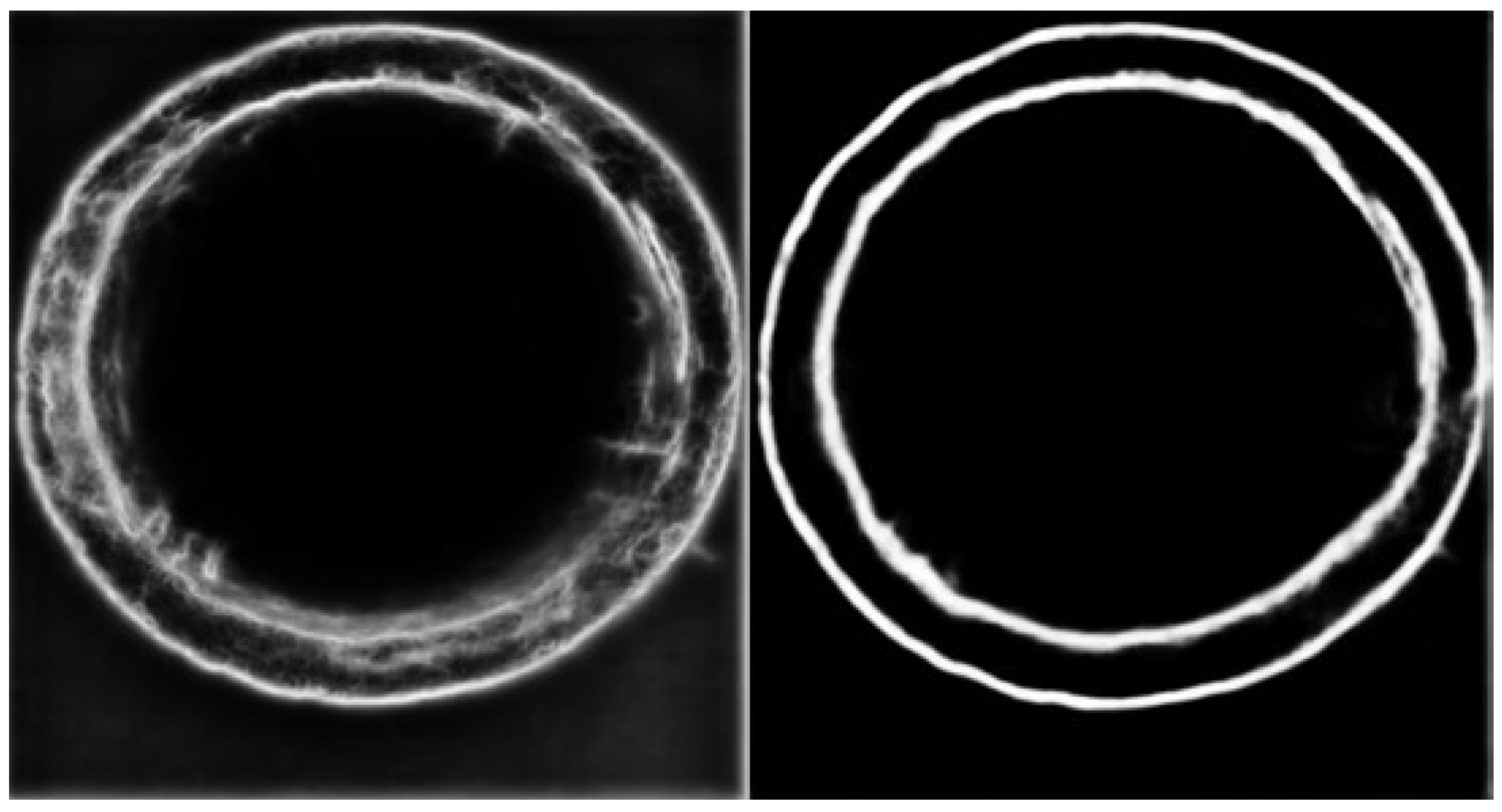
- Image clarity. Using CNNs does not require pre-processing the image and affords better robustness. However, to a certain extent, image clarity still impacts the extraction of coarse edges.
- Algorithm error. The coarse edge that is obtained by the optimized RCF model and binary image erosion, although as close as possible to the actual edge, still cannot accurately locate the actual edge.
4. Conclusions and Outlook
4.1. Summary
- A dimensional detection method for architectural steel tubes is proposed, which utilizes convolutional neural networks to extract edge features, solving the problem of the poor robustness of the traditional edge detection operator and improving practicality.
- Based on the problem of coarse edge size detection, this paper proposes an optimization algorithm for Hough circle detection based on the connected domain and binary image processing, making the Hough circle detection algorithm more applicable to engineering.
4.2. Outlook
- Optimize the coarse edge extraction model further so that the coarse edge image can be free of interference edge lines. This will improve the image processing rate and, thus, the speed of visual detection.
- Optimizing the fine edge algorithm based on coarse edge extraction to reduce the error between the refined edge and the actual edge.
- In this paper, only the cross-section size of the steel pipe is measured, and the length of the steel pipe can be further calculated using edge detection technology.
- Extending this technology to measure circular objects.
Author Contributions
Funding
Conflicts of Interest
References
- Cerruto, E.; Manetto, G.; Privitera, S.; Papa, R.; Longo, D. Effect of Image Segmentation Thresholding on Droplet Size Measurement. Agronomy 2022, 12, 1677. [Google Scholar] [CrossRef]
- Al-Haija, Q.A.; Gharaibeh, M.; Odeh, A. Detection in Adverse Weather Conditions for Autonomous Vehicles via Deep Learning. AI 2022, 3, 303–317. [Google Scholar] [CrossRef]
- Cavedo, F.; Norgia, M.; Pesatori, A.; Solari, G.E. Steel pipe measurement system based on laser rangefinder. IEEE Trans. Instrum. Meas. 2016, 65, 1472–1477. [Google Scholar] [CrossRef]
- Xin, R.; Zhang, J.; Shao, Y. Complex network classification with convolutional neural network. Tsinghua Sci. Technol. 2020, 25, 447–457. [Google Scholar] [CrossRef]
- Yang, J.; Yu, W.; Fang, H.-Y.; Huang, X.-Y.; Chen, S.-J. Detection of size of manufactured sand particles based on digital image processing. PLoS ONE 2018, 13, e0206135. [Google Scholar] [CrossRef] [PubMed]
- Rong, X.; Liao, Y.; Jiang, L. Size Measurement Based on Micro-Irregular Components. Sci. J. Intell. Syst. Res. 2021, 3. [Google Scholar]
- Kong, R. Machine Vision-based Measurement System of Rubber Hose Size. J. Image Signal Process. 2021, 10, 135–145. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, Q.; Sun, Q.; Feng, D.; Zhao, Y. Research on the size of mechanical parts based on image recognition. J. Vis. Commun. Image Represent. 2019, 59, 425–432. [Google Scholar] [CrossRef]
- Yu, W.; Zhu, X.; Mao, Z.; Liu, W. The Research on the Measurement System of Target Dimension Based on Digital Image. J. Phys. Conf. Ser. 2021, 1865, 042072. [Google Scholar] [CrossRef]
- Huang, Y.; Ye, Q.; Hao, M.; Jiao, J. Dimension Measuring System of Round Parts Based on Machine Vision. In Proceedings of the International Conference on Leading Edge Manufacturing in 21st Century, LEM21, Fukuoka, Japan, 7–9 November 2007; Volume 4, p. 9E532. [Google Scholar]
- Xu, Z.; Ji, X.; Wang, M.; Sun, X. Edge detection algorithm of medical image based on canny operator. J. Phys. Conf. Ser. 2021, 1955, 012080. [Google Scholar] [CrossRef]
- Hao, F.; Xu, D.; Chen, D.; Hu, Y.; Zhu, C. Sobel operator enhancement based on eight-directional convolution and entropy. Int. J. Inf. Technol. 2021, 13, 1823–1828. [Google Scholar] [CrossRef]
- Paik, J.K.; Katsaggelos, A.K. Edge detection using a neural network. In Proceedings of the International Conference on Acoustics, Speech, and Signal Processing, IEEE, Albuquerque, NM, USA, 3–6 April 1990; pp. 2145–2148. [Google Scholar]
- Meng, F.; Lin, W.; Wang, Z. Space edge detection based SVM algorithm. In Proceedings of the International Conference on Artificial Intelligence and Computational Intelligence, Taiyuan, China, 24–25 September 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 656–663. [Google Scholar]
- Ganin, Y.; Lempitsky, V. N4-Fields: Neural Network Nearest Neighbor Fields for Image Transforms. In Proceedings of the Asian Conference on Computer Vision, Singapore, 1–5 November 2014; Springer: Cham, Switzerland, 2014; pp. 536–551. [Google Scholar]
- Shen, W.; Wang, X.; Wang, Y.; Bai, X.; Zhang, Z. A deep convolutional feature learned by positive-sharing loss for contour detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3982–3991. [Google Scholar]
- Xie, S.; Tu, Z. Holistically-nested edge detection. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1395–1403. [Google Scholar]
- Liu, Y.; Lew, M.S. Learning relaxed deep supervision for better edge detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 231–240. [Google Scholar]
- Liu, Y.; Cheng, M.M.; Hu, X.; Wang, K.; Bai, X. Richer Convolutional Features for Edge Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3000–3009. [Google Scholar]
- Huan, L.; Xue, N.; Zheng, X.; He, W.; Gong, J.; Xia, G. Unmixing Convolutional Features for Crisp Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 6602–6609. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Tian, Y.; Wang, B.; Qi, Z.; Wang, Q. Bi-Directional Pyramid Network for Edge Detection. Electronics 2021, 10, 329. [Google Scholar] [CrossRef]
- Jiang, L. A fast and accurate circle detection algorithm based on random sampling. Future Gener. Comput. Syst. 2021, 123, 245–256. [Google Scholar] [CrossRef]
- Scitovski, R.; Sabo, K. A combination of k -means and DBSCAN algorithm for solving the multiple generalized circle detection problems. Adv. Data Anal. Classif. 2021, 15, 83–98. [Google Scholar] [CrossRef]
- Du, W.; Xi, Y.; Harada, K.; Zhang, Y.; Nagashima, K.; Qiao, Z. Improved Hough Transform and Total Variation Algorithms for Features Extraction of Wood. Forests 2021, 12, 466. [Google Scholar] [CrossRef]
- Liang, Y.; Zhang, D.; Nian, P.; Liang, X. Research on the application of binary-like coding and Hough circle detection technology in PCB traceability system. J. Ambient. Intell. Humaniz. Comput. 2021, 1–11. [Google Scholar] [CrossRef]
- Miao, H.; Teng, Z.; Kang, C.; Muhammadhaji, A. Stability analysis of a virus infection model with humoral immunity response and two time delays. Math. Methods Appl. Sci. 2016, 39, 3434–3449. [Google Scholar] [CrossRef]
- Zhang, F.; Li, J.; Zheng, C.; Wang, L. Dynamics of an HBV/HCV infection model with intracellular delay and cell proliferation. Commun. Nonlinear Sci. Numer. Simul. 2017, 42, 464–476. [Google Scholar] [CrossRef]








| ODS | OIS | |
|---|---|---|
| Canny | 0.519 | 0.519 |
| RCF | 0.648 | 0.660 |
| Model of this paper | 0.678 | 0.682 |
| Outer Circle 1 | Inner Circle 1 | Outer Circle 2 | Inner Circle 2 | |
|---|---|---|---|---|
| Hough Round overlap | 3504 | 2617 | 2381 | 878 |
| Algorithm overlap in this paper | 3504 | 1970 | 2742 | 2280 |
| Outer Circle 1 | Inner Circle 1 | Outer Circle 2 | Inner Circle 2 | |
|---|---|---|---|---|
| True value | 9.3 | 8.0 | 9.9 | 8.2 |
| Hough circle R | 9.374 | 8.205 | 9.910 | 8.072 |
| This paper tests the circle R | 9.374 | 8.180 | 9.893 | 8.287 |
| Hough circle error | 0.074 | 0.205 | 0.01 | 0.182 |
| Error in this article | 0.074 | 0.180 | 0.007 | 0.087 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, F.; Qin, Z.; Li, R.; Ji, Z. Cross-Section Dimension Measurement of Construction Steel Pipe Based on Machine Vision. Mathematics 2022, 10, 3535. https://doi.org/10.3390/math10193535
Yu F, Qin Z, Li R, Ji Z. Cross-Section Dimension Measurement of Construction Steel Pipe Based on Machine Vision. Mathematics. 2022; 10(19):3535. https://doi.org/10.3390/math10193535
Chicago/Turabian StyleYu, Fuxing, Zhihu Qin, Ruina Li, and Zhanlin Ji. 2022. "Cross-Section Dimension Measurement of Construction Steel Pipe Based on Machine Vision" Mathematics 10, no. 19: 3535. https://doi.org/10.3390/math10193535
APA StyleYu, F., Qin, Z., Li, R., & Ji, Z. (2022). Cross-Section Dimension Measurement of Construction Steel Pipe Based on Machine Vision. Mathematics, 10(19), 3535. https://doi.org/10.3390/math10193535








