A Novel Approach of Fuzzy Control Chart with Fuzzy Process Capability Indices Using Alpha Cut Triangular Fuzzy Number
Abstract
:1. Introduction
2. Methodology Development
2.1. Preliminaries
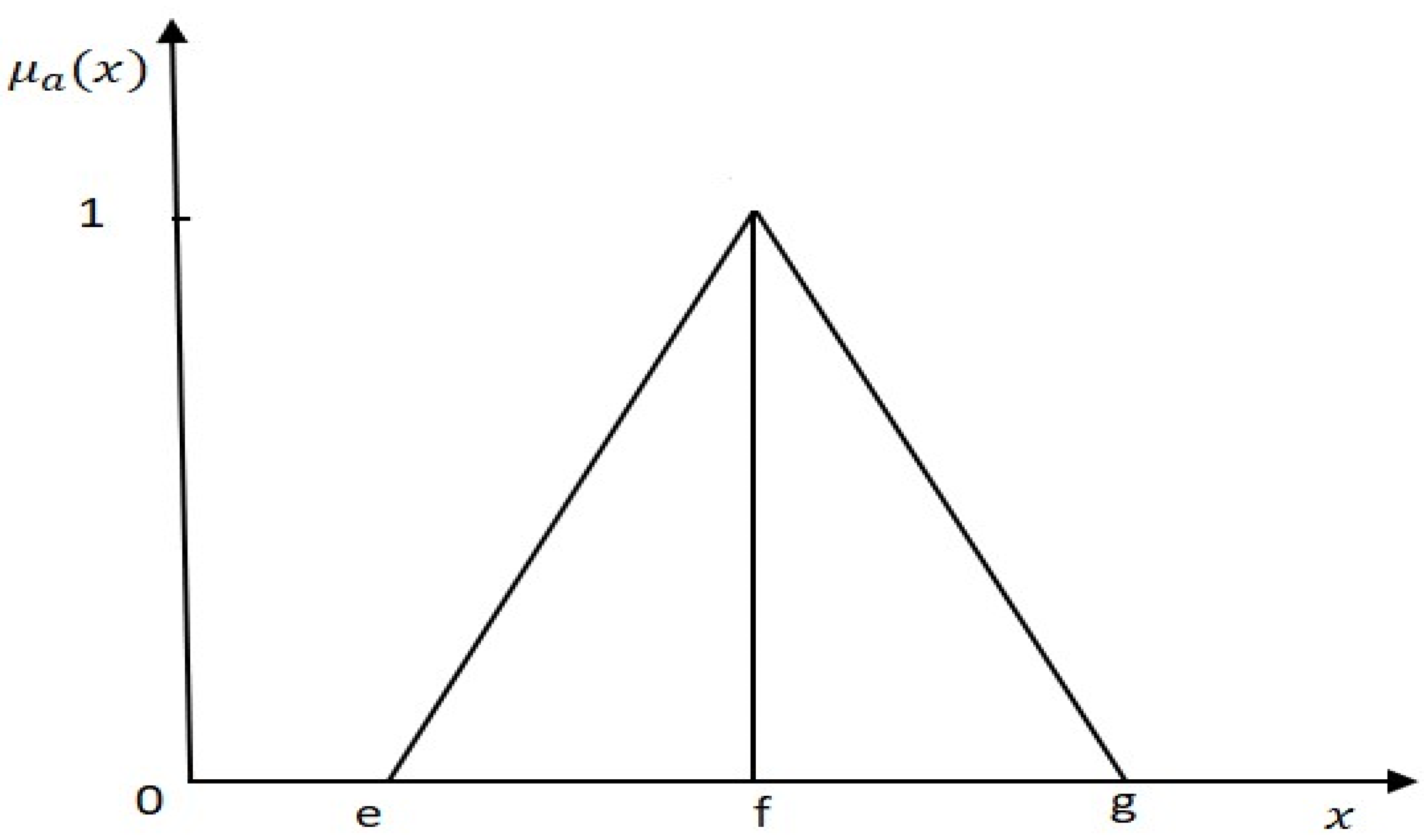
Triangular Fuzzy Number
2.2. Proposed Control Chart with and Values
3. Numerical Example and Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Montgomery, D.C. Statistical Quality Control; Wiley: New York, NY, USA, 2009; Volume 7. [Google Scholar]
- Ghoushchi, S.J.; Osgooei, E.; Haseli, G.; Tomaskova, H. A Novel Approach to Solve Fully Fuzzy Linear Programming Problems with Modified Triangular Fuzzy Numbers. Mathematics 2021, 9, 2937. [Google Scholar] [CrossRef]
- Yeh, C.T. On improving trapezoidal and triangular approximations of fuzzy numbers. Int. J. Approx. Reason. 2008, 48, 297–313. [Google Scholar] [CrossRef]
- Subramani, J.; Balamurali, S. Control charts for variables with specified process capabilities indices. Int. J. Probab. Stat. 2012, 1, 101–110. [Google Scholar] [CrossRef]
- Shafqat, A.; Huang, Z.; Aslam, M. Design of X-bar control chart based on Inverse Rayleigh Distribution under repetitive group sampling. Ain Shams Eng. J. 2021, 12, 943–953. [Google Scholar] [CrossRef]
- Lim, S.A.H.; Antony, J.; He, Z.; Arshed, N. Critical observations on the statistical process control implementation in the UK food industry: A survey. Int. J. Qual. Reliab. Manag. 2017, 34, 684–700. [Google Scholar] [CrossRef]
- Özdemir, A. Development of fuzzy − S control charts with unbalanced fuzzy data. Soft Comput. 2021, 25, 4015–4025. [Google Scholar] [CrossRef]
- Şentürk, S.; Erginel, N.; Kaya, İ.; Kahraman, C. Fuzzy exponentially weighted moving average control chart for univariate data with a real case application. Appl. Soft Comput. 2014, 22, 1–10. [Google Scholar] [CrossRef]
- Şentürk, S.; Erginel, N.; Kaya, I.; Kahraman, C. Design of fuzzy ũ control charts. J. Mult.-Valued Log. Soft Comput. 2011, 17, 459–473. [Google Scholar]
- Shu, M.H.; Dang, D.C.; Nguyen, T.L.; Hsu, B.M.; Phan, N.S. Fuzzy and control charts: A data-adaptability and human-acceptance approach. Complexity, 2017.Kane, V.E.: Process capability indices. J. Qual. Technol. 2017, 18, 41–52. [Google Scholar] [CrossRef]
- Kane, V.E. Process capability indices. J. Qual. Technol. 1986, 18, 41–52. [Google Scholar] [CrossRef]
- Kaya, İ.; Kahraman, C. Process capability analyses with fuzzy parameters. Expert Syst. Appl. 2011, 38, 11918–11927. [Google Scholar] [CrossRef]
- Alipour, H.; Noorossana, R. Fuzzy multivariate exponentially weighted moving average control chart. Int. J. Adv. Manuf. Technol. 2010, 48, 1001–1007. [Google Scholar] [CrossRef]
- Erginel, N.; Şentürk, S. Fuzzy EWMA and Fuzzy CUSUM Control Charts. In Fuzzy Statistical Decision-Making; Springer: Cham, Switzerland, 2016; pp. 281–295. [Google Scholar] [CrossRef]
- Erginel, N. Fuzzy rule-based and control charts. J. Intell. Fuzzy Syst. 2014, 27, 159–171. [Google Scholar] [CrossRef]
- Bradshaw, C.W., Jr. A fuzzy set theoretic interpretation of economic control limits. Eur. J. Oper. Res. 1983, 13, 403–408. [Google Scholar] [CrossRef]
- Wang, J.H.; Raz, T. On the construction of control charts using linguistic variables. Int. J. Prod. Res. 1990, 28, 477–487. [Google Scholar] [CrossRef]
- Kanagawa, A.; Tamaki, F.; Ohta, H. Control charts for process average and variability based on linguistic data. Int. J. Prod. Res. 1993, 31, 913–922. [Google Scholar] [CrossRef]
- Franceschini, F.; Romano, D. Control chart for linguistic variables: A method based on the use of linguistic quantifiers. Int. J. Prod. Res. 1999, 37, 3791–3801. [Google Scholar] [CrossRef]
- Taleb, H.; Limam, M. On fuzzy and probabilistic control charts. Int. J. Prod. Res. 2002, 40, 2849–2863. [Google Scholar] [CrossRef]
- Gülbay, M.; Kahraman, C.; Ruan, D. α-Cut fuzzy control charts for linguistic data. Int. J. Intell. Syst. 2004, 19, 1173–1195. [Google Scholar] [CrossRef]
- Gülbay, M.; Kahraman, C. An alternative approach to fuzzy control charts: Direct fuzzy approach. Inf. Sci. 2007, 177, 1463–1480. [Google Scholar] [CrossRef]
- Hou, S.; Wang, H.; Feng, S. Attribute control chart construction based on fuzzy score number. Symmetry 2016, 8, 139. [Google Scholar] [CrossRef]
- Fernández, M.N.P. Fuzzy theory and quality control charts. In Proceedings of the 2017 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Naples, Italy, 9–12 July 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Hesamian, G.; Akbari, M.G.; Yaghoobpoor, R. Quality control process based on fuzzy random variables. IEEE Trans. Fuzzy Syst. 2018, 27, 671–685. [Google Scholar] [CrossRef]
- Hryniewicz, O.; Kaczmarek-Majer, K.; Opara, K.R. Control charts based on fuzzy costs for monitoring short autocorrelated time series. Int. J. Approx. Reason. 2019, 114, 166–181. [Google Scholar] [CrossRef]
- Zohoori, B.; Verbraeck, A.; Bagherpour, M.; Khakdaman, M. Monitoring production time and cost performance by combining earned value analysis and adaptive fuzzy control. Comput. Ind. Eng. 2019, 127, 805–821. [Google Scholar] [CrossRef]
- Choi, Y.H.; Na, G.Y.; Yang, J. Fuzzy-inference-based decision-making method for the systematization of statistical process capability control. Comput. Ind. 2020, 123, 103296. [Google Scholar] [CrossRef]
- Faraz, A.; Moghadam, M.B. Fuzzy control chart a better alternative for Shewhart average chart. Qual. Quant. 2007, 41, 375–385. [Google Scholar] [CrossRef]
- Hryniewicz, O. Statistics with fuzzy data in statistical quality control. Soft Comput. 2008, 12, 229–234. [Google Scholar] [CrossRef]
- Amirzadeh, V.; Mashinchi, M.; Parchami, A. Construction of p-charts using degree of nonconformity. Inf. Sci. 2009, 179, 150–160. [Google Scholar] [CrossRef]
- Demirli, K.; Vijayakumar, S. Fuzzy logic based assignable cause diagnosis using control chart patterns. Inf. Sci. 2010, 180, 3258–3272. [Google Scholar] [CrossRef] [Green Version]
- Kaplan Göztok, K.; Uçurum, M.; Özdemir, A. Development of a fuzzy exponentially weighted moving average control chart with an α-level cut for monitoring a production process. Arab. J. Sci. Eng. 2021, 46, 1911–1924. [Google Scholar] [CrossRef]
- Khan, M.Z.; Khan, M.F.; Aslam, M.; Mughal, A.R. A study on average run length of fuzzy EWMA control chart. Soft Comput. 2022, 26, 1–8. [Google Scholar] [CrossRef]
- Alakoc, N.P. Fuzzy Xbar and S Control Charts Based on Confidence Intervals. J. Adv. Res. Nat. Appl. Sci. 2021, 7, 114–131. [Google Scholar] [CrossRef]
- Al-Refaie, A.; Abbasi, G.; Ghanim, D. Proposed α-cut CUSUM and EWMA control charts for fuzzy response observations. Int. J. Reliab. Qual. Saf. Eng. 2021, 28, 2150012. [Google Scholar] [CrossRef]


| Sample No. | |||||
|---|---|---|---|---|---|
| 1 | (38.077, 38.082, 38.087) | (38.07, 38.075, 38.08) | (38.08, 38.085, 38.09) | (38.051, 38.056, 38.061) | (38.061, 38.066, 38.071) |
| 2 | (38.05, 38.055, 38.06) | (38.078, 38.083, 38.088) | (38.058, 38.063, 38.068) | (38.081, 38.086, 38.091) | (38.074, 38.079, 38.084) |
| 3 | (38.063, 38.068, 38.073) | (38.038, 38.043, 38.048) | (38.084, 38.089, 38.094) | (38.064, 38.069, 38.074) | (38.062, 38.067, 38.072) |
| 4 | (38.061, 38.066, 38.071) | (38.05, 38.055, 38.06) | (38.076, 38.081, 38.086) | (38.059, 38.064, 38.069) | (38.053, 38.058, 38.063) |
| 5 | (38.076, 38.081, 38.086) | (38.068, 38.073, 38.078) | (38.081, 38.086, 38.091) | (38.079, 38.084, 38.089) | (38.071, 38.076, 38.081) |
| 6 | (38.045, 38.0538.055) | (38.084, 38.089, 38.094) | (38.067, 38.072, 38.077) | (38.053, 38.058, 38.063) | (38.056, 38.061, 38.066) |
| 7 | (38.072, 38.077, 38.082) | (38.044, 38.049, 38.054) | (38.052, 38.057, 38.062) | (38.076, 38.081, 38.086) | (38.056, 38.061, 38.066) |
| 8 | (38.069, 38.074, 38.079) | (38.081, 38.086, 38.091) | (38.065, 38.07, 38.075) | (38.062, 38.067, 38.072) | (38.065, 38.07, 38.075) |
| 9 | (38.062, 38.067, 38.072) | (38.081, 38.086, 38.091) | (38.076, 38.081, 38.086) | (38.049, 38.054, 38.059) | (38.056, 38.061, 38.066) |
| 10 | (38.079, 38.084, 38.089) | (38.075, 38.08, 38.085) | (38.074, 38.079, 38.084) | (38.056, 38.061, 38.066) | (38.068, 38.073, 38.078) |
| 11 | (38.088, 38.093, 38.098) | (38.073, 38.078, 38.083) | (38.08, 38.085, 38.09) | (38.075, 38.08, 38.085) | (38.06, 38.065, 38.07) |
| 12 | (38.047, 38.052, 38.057) | (38.048, 38.053, 38.058) | (38.078, 38.083, 38.088) | (38.063, 38.068, 38.073) | (38.075, 38.08, 38.085) |
| 13 | (38.07, 38.075, 38.08) | (38.06, 38.065, 38.07) | (38.049, 38.054, 38.059) | (38.073, 38.078, 38.083) | (38.065, 38.07, 38.075) |
| 14 | (38.069, 38.074, 38.079) | (38.047, 38.052, 38.057) | (38.081, 38.086, 38.091) | (38.078, 38.083, 38.088) | (38.073, 38.078, 38.083) |
| 15 | (38.063, 38.068, 38.073) | (38.073, 38.078, 38.083) | (38.065, 38.07, 38.075) | (38.055, 38.06, 38.065) | (38.056, 38.061, 38.066) |
| 16 | (38.075, 38.08, 38.085) | (38.051, 38.056, 38.061) | (38.079, 38.084, 38.089) | (38.048, 38.053, 38.058) | (38.066, 38.071, 38.076) |
| 17 | (38.076, 38.081, 38.086) | (38.066, 38.071, 38.076) | (38.062, 38.067, 38.072) | (38.069, 38.074, 38.079) | (38.058, 38.063, 38.068) |
| 18 | (38.058, 38.063, 38.068) | (38.072, 38.077, 38.082 | (38.052, 38.057, 38.062) | (38.063, 38.068, 38.073) | (38.059, 38.064, 38.069) |
| 19 | (38.06, 38.065, 38.07) | (38.064, 38.069, 38.074) | (38.065, 38.07, 38.075) | (38.057, 38.062, 38.067) | (38.051, 38.056, 38.061) |
| 20 | (38.057, 38.062, 38.067) | (38.048, 38.053, 38.058) | (38.064, 38.069, 38.074) | (38.06, 38.065, 38.07) | (38.05, 38.055, 38.06) |
| 21 | (38.089, 38.094, 38.099) | (38.048, 38.053, 38.058) | (38.065, 38.07, 38.075) | (38.069, 38.074, 38.079) | (38.069, 38.074, 38.079) |
| 22 | (38.068, 38.073, 38.078) | (38.082, 38.087, 38.092) | (38.066, 38.071, 38.076 | (38.072, 38.077, 38.082) | (38.064, 38.069, 38.074) |
| 23 | (38.056, 38.061, 38.066) | (38.08, 38.085, 38.09) | (38.075, 38.08, 38.085) | (38.069, 38.074, 38.079) | (38.059, 38.064, 38.069) |
| 24 | (38.07, 38.075, 38.08) | (38.043, 38.048, 38.053) | (38.074, 38.079, 38.084) | (38.054, 38.059, 38.064) | (38.056, 38.061, 38.066) |
| 25 | (38.049, 38.054, 38.059) | (38.049, 38.054, 38.059) | (38.074, 38.079, 38.084) | (38.061, 38.066, 38.071) | (38.055, 38.06, 38.065) |
| 38.0525 | 38.0550 | 38.5753 | 38.0673 | 38.0698 | 38.0723 | 38.0821 | 38.0845 | 38.0871 |
| 0 | 0 | 0 | 0.0265 | 0.0265 | 0.0265 | 0.0561 | 0.0561 | 0.0561 |
| 38.0525 | 38.0550 | 38.0575 | 38.0673 | 38.0698 | 38.0723 | 38.0821 | 38.0845 | 38.0871 |
| 0 | 0 | 0 | 0.0265 | 0.0265 | 0.0265 | 0.0561 | 0.0561 | 0.0561 |
| S.N. | In Control (✓) or Out of Control (×) | In Control (✓) or Out of Control (×) | In Control (✓) or Out of Control (×) | In Control (✓) or Out of Control (×) | In Control (✓) or Out of Control (×) | In Control (✓) or Out of Control (×) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 38.0678 | ✓ | 38.073 | ✓ | 38.0778 | ✓ | 0.029 | ✓ | 0.029 | ✓ | 0.029 | ✓ |
| 2 | 38.0682 | ✓ | 38.073 | ✓ | 38.0782 | ✓ | 0.031 | ✓ | 0.031 | ✓ | 0.031 | ✓ |
| 3 | 38.0622 | ✓ | 38.067 | ✓ | 38.0722 | ✓ | 0.046 | ✓ | 0.046 | ✓ | 0.046 | ✓ |
| 4 | 38.0598 | ✓ | 38.064 | ✓ | 38.0698 | ✓ | 0.026 | ✓ | 0.026 | ✓ | 0.026 | ✓ |
| 5 | 38.075 | ✓ | 38.08 | ✓ | 38.085 | ✓ | 0.013 | ✓ | 0.013 | ✓ | 0.013 | ✓ |
| 6 | 38.061 | ✓ | 38.066 | ✓ | 38.071 | ✓ | 0.039 | ✓ | 0.039 | ✓ | 0.039 | ✓ |
| 7 | 38.06 | ✓ | 38.065 | ✓ | 38.07 | ✓ | 0.032 | ✓ | 0.032 | ✓ | 0.032 | ✓ |
| 8 | 38.0684 | ✓ | 38.073 | ✓ | 38.0784 | ✓ | 0.019 | ✓ | 0.019 | ✓ | 0.019 | ✓ |
| 9 | 38.0648 | ✓ | 38.069 | ✓ | 38.0748 | ✓ | 0.032 | ✓ | 0.032 | ✓ | 0.032 | ✓ |
| 10 | 38.0704 | ✓ | 38.075 | ✓ | 38.0804 | ✓ | 0.023 | ✓ | 0.023 | ✓ | 0.023 | ✓ |
| 11 | 38.0752 | ✓ | 38.080 | ✓ | 38.0852 | ✓ | 0.028 | ✓ | 0.028 | ✓ | 0.028 | ✓ |
| 12 | 38.0622 | ✓ | 38.067 | ✓ | 38.0722 | ✓ | 0.031 | ✓ | 0.031 | ✓ | 0.031 | ✓ |
| 13 | 38.0634 | ✓ | 38.068 | ✓ | 38.0734 | ✓ | 0.024 | ✓ | 0.024 | ✓ | 0.024 | ✓ |
| 14 | 38.0696 | ✓ | 38.074 | ✓ | 38.0796 | ✓ | 0.034 | ✓ | 0.034 | ✓ | 0.034 | ✓ |
| 15 | 38.0624 | ✓ | 38.067 | ✓ | 38.0724 | ✓ | 0.018 | ✓ | 0.018 | ✓ | 0.018 | ✓ |
| 16 | 38.0638 | ✓ | 38.068 | ✓ | 38.0738 | ✓ | 0.031 | ✓ | 0.031 | ✓ | 0.031 | ✓ |
| 17 | 38.0662 | ✓ | 38.071 | ✓ | 38.0762 | ✓ | 0.018 | ✓ | 0.018 | ✓ | 0.018 | ✓ |
| 18 | 38.0608 | ✓ | 38.065 | ✓ | 38.0708 | ✓ | 0.02 | ✓ | 0.02 | ✓ | 0.02 | ✓ |
| 19 | 38.0594 | ✓ | 38.064 | ✓ | 38.0694 | ✓ | 0.014 | ✓ | 0.014 | ✓ | 0.014 | ✓ |
| 20 | 38.0558 | ✓ | 38.061 | ✓ | 38.0658 | ✓ | 0.016 | ✓ | 0.016 | ✓ | 0.016 | ✓ |
| 21 | 38.068 | ✓ | 38.073 | ✓ | 38.078 | ✓ | 0.041 | ✓ | 0.041 | ✓ | 0.041 | ✓ |
| 22 | 38.0704 | ✓ | 38.075 | ✓ | 38.0804 | ✓ | 0.018 | ✓ | 0.018 | ✓ | 0.018 | ✓ |
| 23 | 38.0678 | ✓ | 38.073 | ✓ | 38.0778 | ✓ | 0.024 | ✓ | 0.024 | ✓ | 0.024 | ✓ |
| 24 | 38.0594 | ✓ | 38.064 | ✓ | 38.0694 | ✓ | 0.031 | ✓ | 0.031 | ✓ | 0.031 | ✓ |
| 25 | 38.0576 | ✓ | 38.062 | ✓ | 38.0676 | ✓ | 0.025 | ✓ | 0.025 | ✓ | 0.025 | ✓ |
| S.N. | In Control (✓) or Out of Control (×) | In Control (✓) or Out of Control (×) | In Control (✓) or Out of Control (×) | In Control (✓) or Out of Control (×) | In Control (✓) or Out of Control (×) | In Control (✓) or Out of Control (×) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 38.0678 | ✓ | 38.0728 | ✓ | 38.0778 | ✓ | 0.029 | ✓ | 0.029 | ✓ | 0.029 | ✓ |
| 2 | 38.0682 | ✓ | 38.0732 | ✓ | 38.0782 | ✓ | 0.031 | ✓ | 0.031 | ✓ | 0.031 | ✓ |
| 3 | 38.0622 | ✓ | 38.0672 | ✓ | 38.0722 | ✓ | 0.046 | ✓ | 0.046 | ✓ | 0.046 | ✓ |
| 4 | 38.0598 | ✓ | 38.0648 | ✓ | 38.0698 | ✓ | 0.026 | ✓ | 0.026 | ✓ | 0.026 | ✓ |
| 5 | 38.075 | ✓ | 38.08 | ✓ | 38.085 | ✓ | 0.013 | ✓ | 0.013 | ✓ | 0.013 | ✓ |
| 6 | 38.061 | ✓ | 38.066 | ✓ | 38.071 | ✓ | 0.039 | ✓ | 0.039 | ✓ | 0.039 | ✓ |
| 7 | 38.06 | ✓ | 38.065 | ✓ | 38.07 | ✓ | 0.032 | ✓ | 0.032 | ✓ | 0.032 | ✓ |
| 8 | 38.0684 | ✓ | 38.0734 | ✓ | 38.0784 | ✓ | 0.019 | ✓ | 0.019 | ✓ | 0.019 | ✓ |
| 9 | 38.0648 | ✓ | 38.0698 | ✓ | 38.0748 | ✓ | 0.032 | ✓ | 0.032 | ✓ | 0.032 | ✓ |
| 10 | 38.0704 | ✓ | 38.0754 | ✓ | 38.0804 | ✓ | 0.023 | ✓ | 0.023 | ✓ | 0.023 | ✓ |
| 11 | 38.0752 | ✓ | 38.0802 | ✓ | 38.0852 | ✓ | 0.028 | ✓ | 0.028 | ✓ | 0.028 | ✓ |
| 12 | 38.0622 | ✓ | 38.0672 | ✓ | 38.0722 | ✓ | 0.031 | ✓ | 0.031 | ✓ | 0.031 | ✓ |
| 13 | 38.0634 | ✓ | 38.0684 | ✓ | 38.0734 | ✓ | 0.024 | ✓ | 0.024 | ✓ | 0.024 | ✓ |
| 14 | 38.0696 | ✓ | 38.0746 | ✓ | 38.0796 | ✓ | 0.034 | ✓ | 0.034 | ✓ | 0.034 | ✓ |
| 15 | 38.0624 | ✓ | 38.0674 | ✓ | 38.0724 | ✓ | 0.018 | ✓ | 0.018 | ✓ | 0.018 | ✓ |
| 16 | 38.0638 | ✓ | 38.0688 | ✓ | 38.0738 | ✓ | 0.031 | ✓ | 0.031 | ✓ | 0.031 | ✓ |
| 17 | 38.0662 | ✓ | 38.0712 | ✓ | 38.0762 | ✓ | 0.018 | ✓ | 0.018 | ✓ | 0.018 | ✓ |
| 18 | 38.0608 | ✓ | 38.0658 | ✓ | 38.0708 | ✓ | 0.02 | ✓ | 0.02 | ✓ | 0.02 | ✓ |
| 19 | 38.0594 | ✓ | 38.0644 | ✓ | 38.0694 | ✓ | 0.014 | ✓ | 0.014 | ✓ | 0.014 | ✓ |
| 20 | 38.0558 | ✓ | 38.0608 | ✓ | 38.0658 | ✓ | 0.016 | ✓ | 0.016 | ✓ | 0.016 | ✓ |
| 21 | 38.068 | ✓ | 38.073 | ✓ | 38.078 | ✓ | 0.041 | ✓ | 0.041 | ✓ | 0.041 | ✓ |
| 22 | 38.0704 | ✓ | 38.0754 | ✓ | 38.0804 | ✓ | 0.018 | ✓ | 0.018 | ✓ | 0.018 | ✓ |
| 23 | 38.0678 | ✓ | 38.0728 | ✓ | 38.0778 | ✓ | 0.024 | ✓ | 0.024 | ✓ | 0.024 | ✓ |
| 24 | 38.0594 | ✓ | 38.0644 | ✓ | 38.0694 | ✓ | 0.031 | ✓ | 0.031 | ✓ | 0.031 | ✓ |
| 25 | 38.0576 | ✓ | 38.0626 | ✓ | 38.0676 | ✓ | 0.025 | ✓ | 0.025 | ✓ | 0.025 | ✓ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, M.; Cheng, W. A Novel Approach of Fuzzy Control Chart with Fuzzy Process Capability Indices Using Alpha Cut Triangular Fuzzy Number. Mathematics 2022, 10, 3572. https://doi.org/10.3390/math10193572
Ahmad M, Cheng W. A Novel Approach of Fuzzy Control Chart with Fuzzy Process Capability Indices Using Alpha Cut Triangular Fuzzy Number. Mathematics. 2022; 10(19):3572. https://doi.org/10.3390/math10193572
Chicago/Turabian StyleAhmad, Mohammad, and Weihu Cheng. 2022. "A Novel Approach of Fuzzy Control Chart with Fuzzy Process Capability Indices Using Alpha Cut Triangular Fuzzy Number" Mathematics 10, no. 19: 3572. https://doi.org/10.3390/math10193572
APA StyleAhmad, M., & Cheng, W. (2022). A Novel Approach of Fuzzy Control Chart with Fuzzy Process Capability Indices Using Alpha Cut Triangular Fuzzy Number. Mathematics, 10(19), 3572. https://doi.org/10.3390/math10193572






