Approximation-Avoidance-Based Robust Quantitative Prescribed Performance Control of Unknown Strict-Feedback Systems
Abstract
:1. Introduction
2. Problem Statement and Preliminaries
2.1. System Model
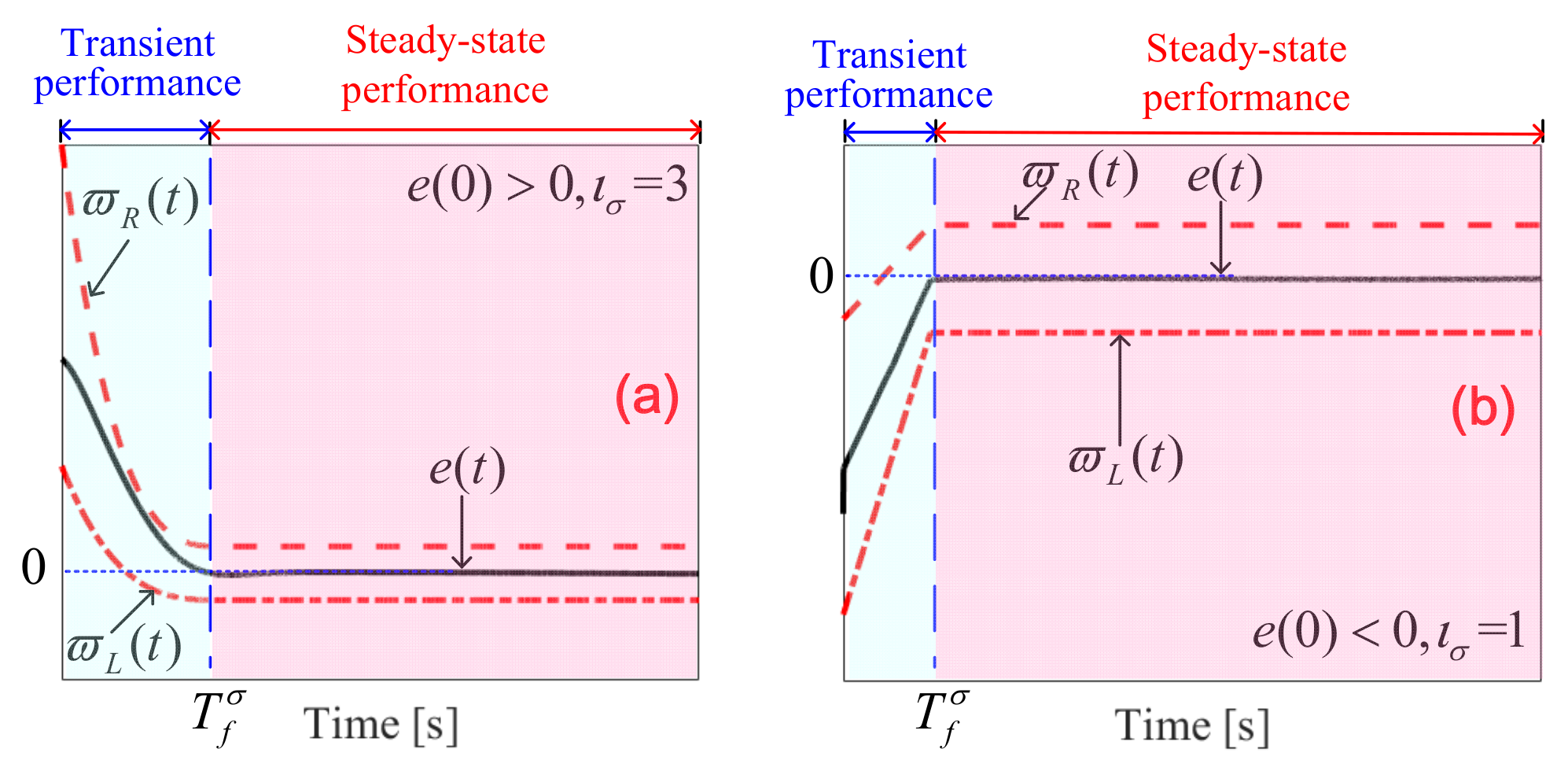
2.2. Quantitative Prescribed Performance
3. Main Results
3.1. Controller Design
3.2. Stability Analysis
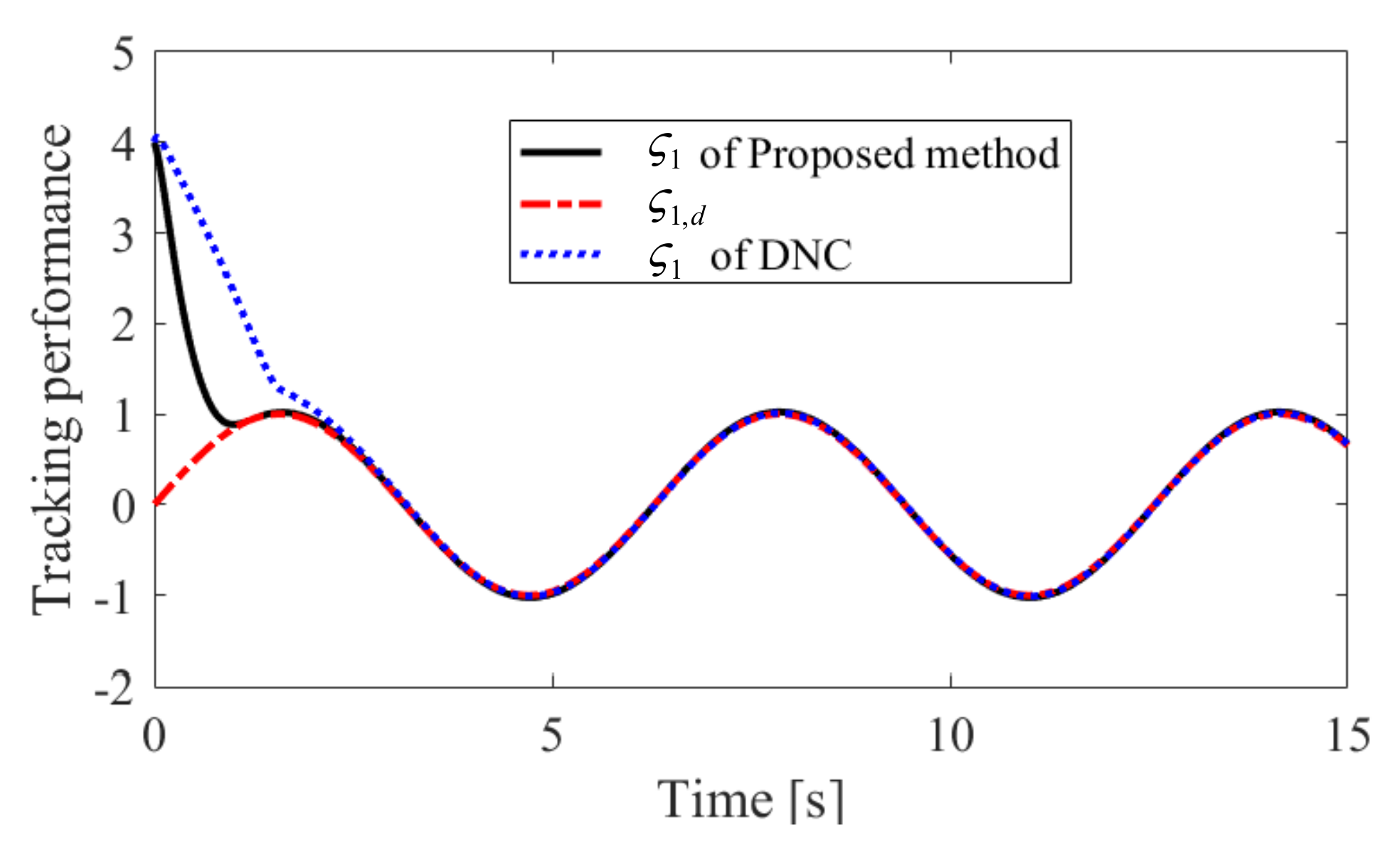
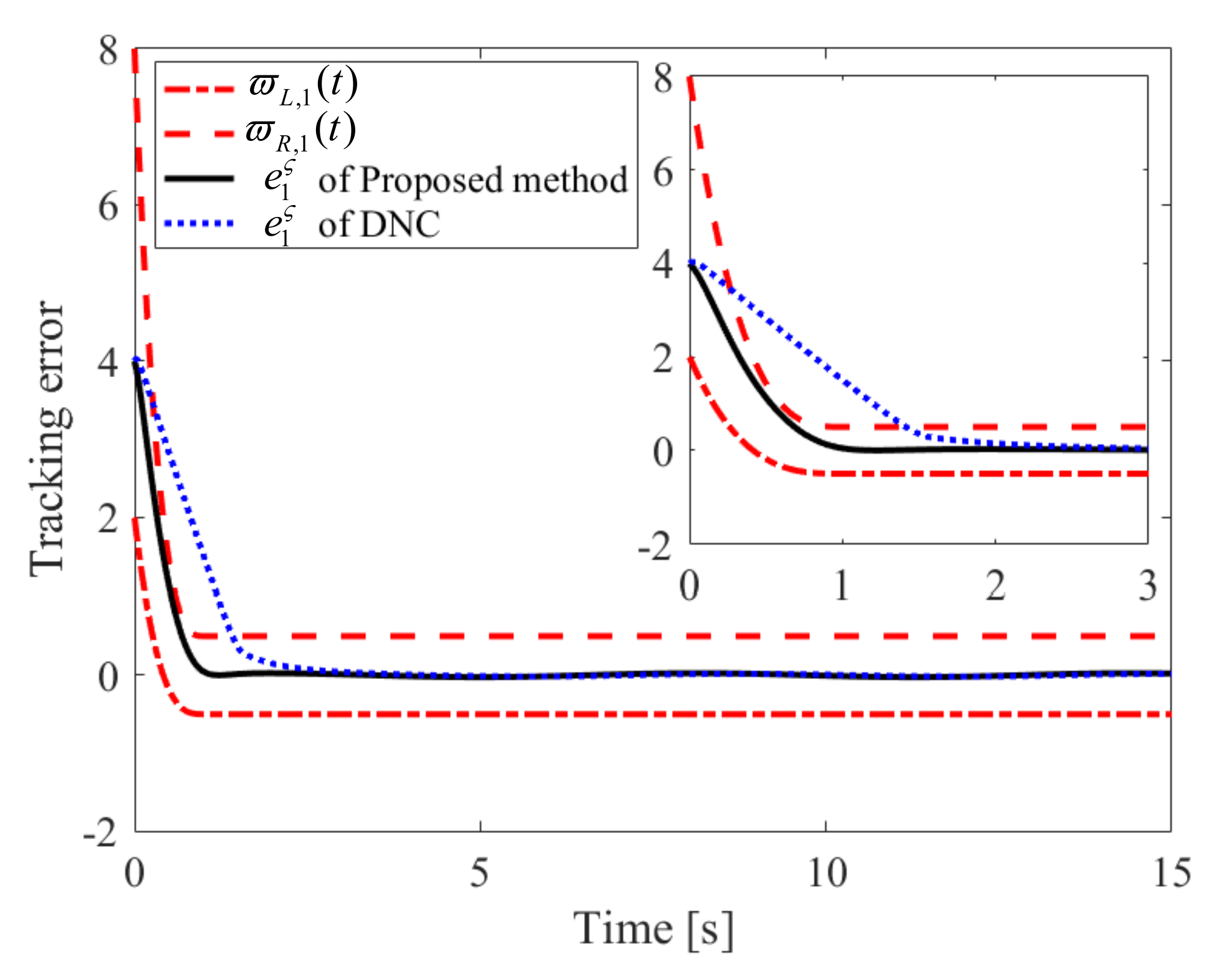
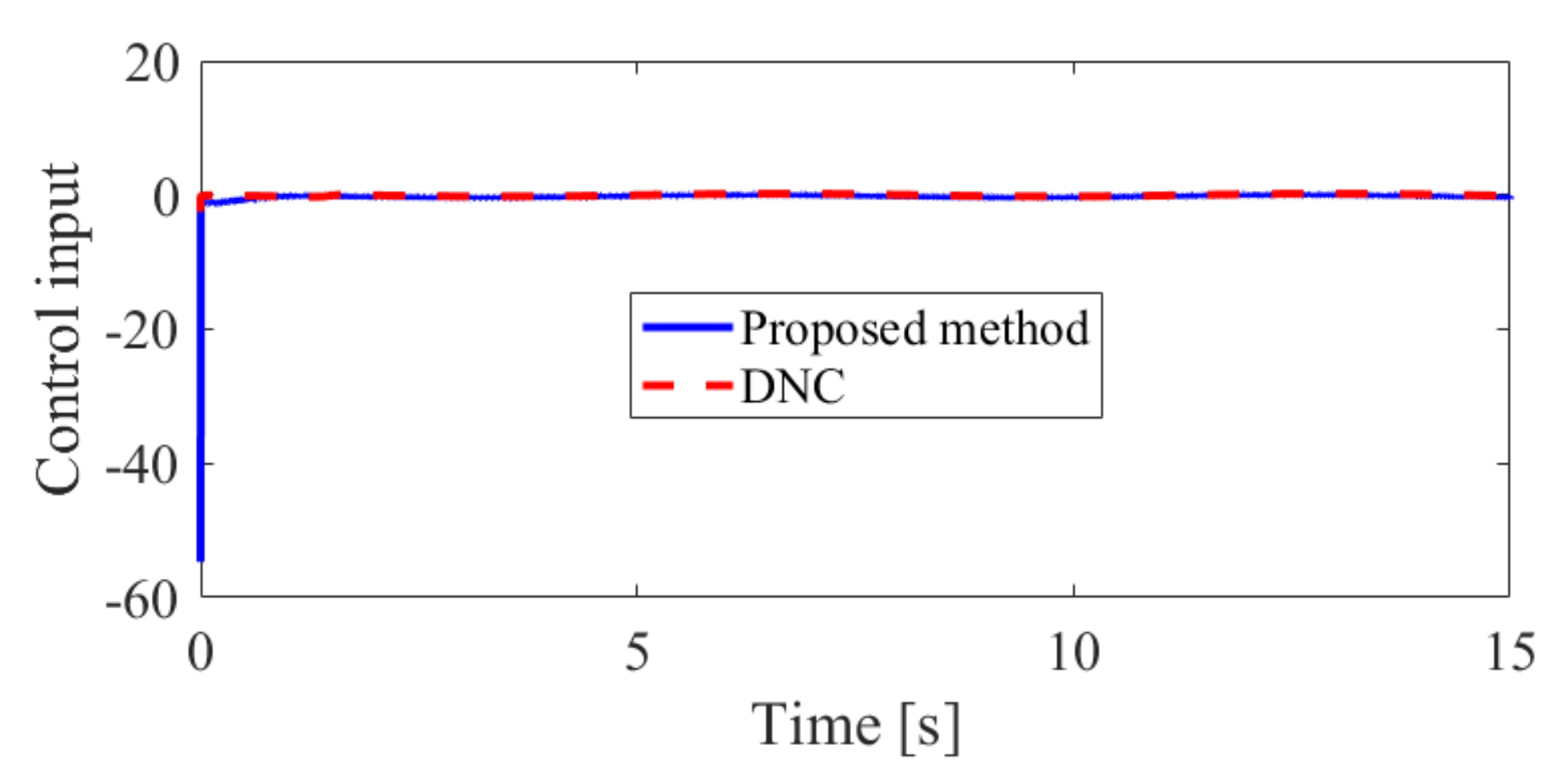
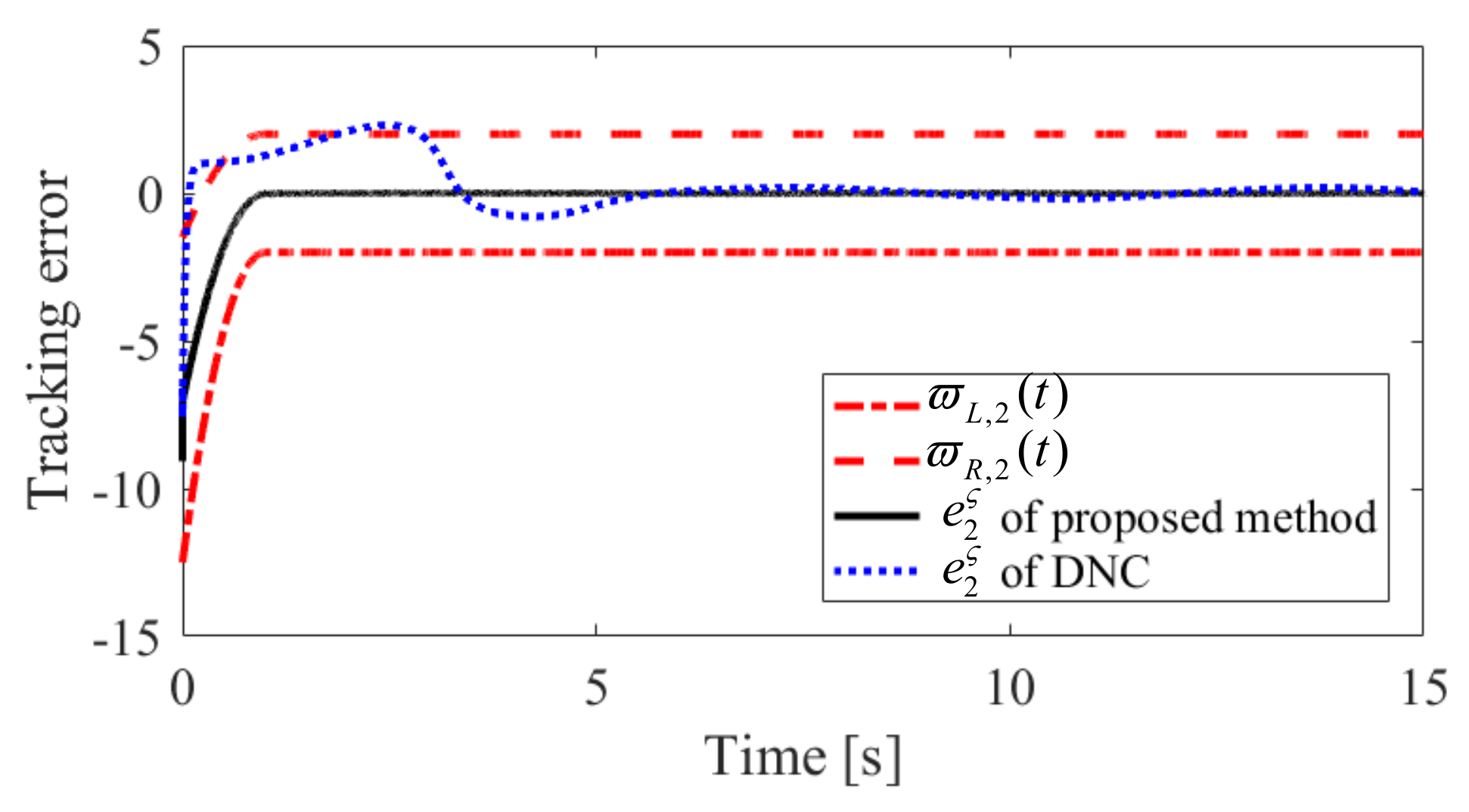
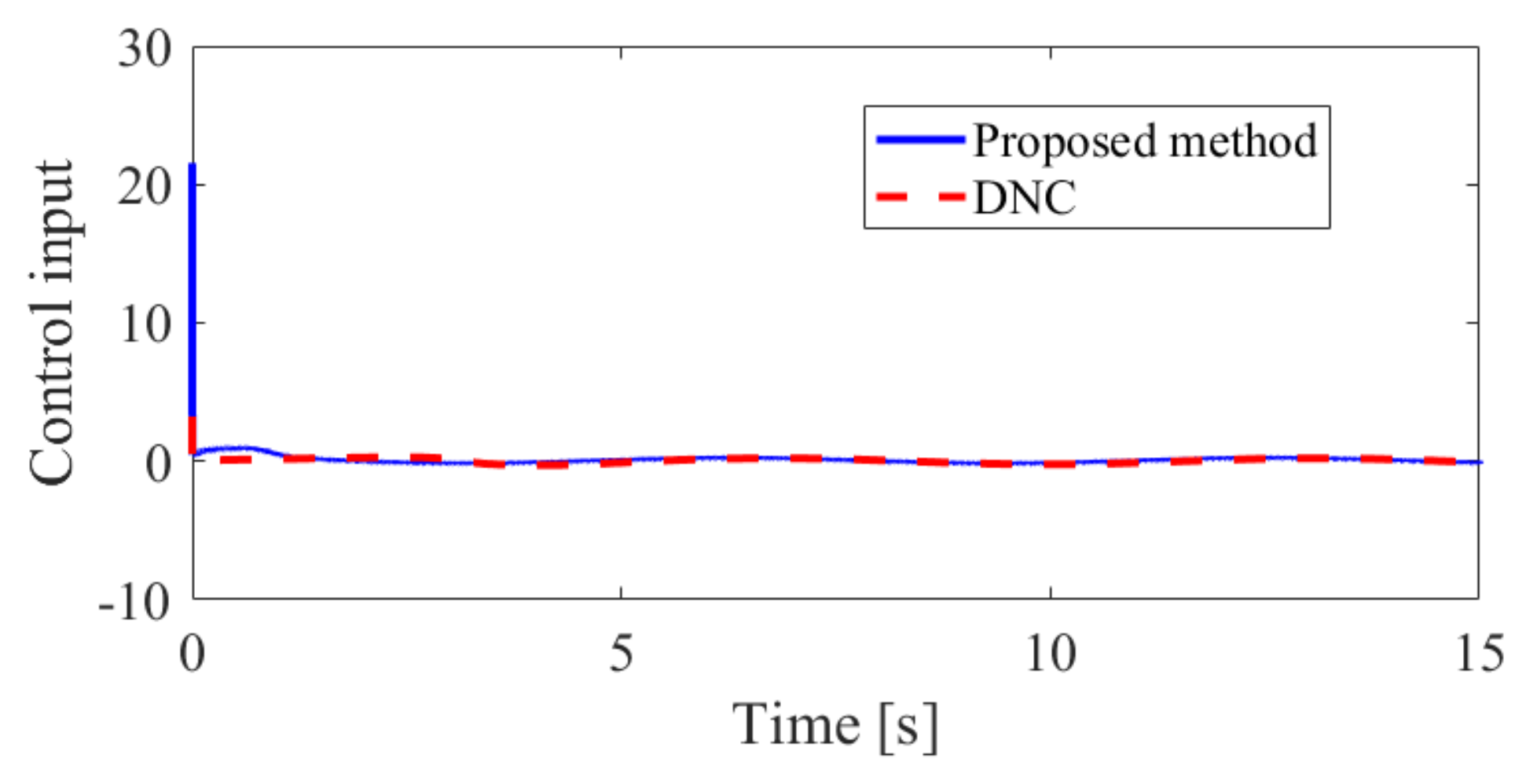
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bechlioulis, C.P.; Rovithakis, G.A. A low-complexity global approximation-free control scheme with prescribed performance for unknown pure feedback systems. Automatica 2014, 50, 1217–1226. [Google Scholar] [CrossRef]
- Bu, X.; Xiao, Y.; Lei, H. An Adaptive Critic Design-Based Fuzzy Neural Controller for Hypersonic Vehicles: Predefined Behavioral Nonaffine Control. IEEE/ASME Trans. Mechatron. 2019, 24, 1871–1881. [Google Scholar] [CrossRef]
- Bu, X.; Jiang, B.; Lei, H. Non-fragile Quantitative Prescribed Performance Control of Waverider Vehicles with Actuator Saturation. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 3538–3548. [Google Scholar] [CrossRef]
- Bu, X. Air-Breathing Hypersonic Vehicles Funnel Control Using Neural Approximation of Non-affine Dynamics. IEEE/ASME Trans. Mechatron. 2018, 23, 2099–2108. [Google Scholar] [CrossRef]
- Bu, X.; Qi, Q.; Jiang, B. A Simplified Finite-Time Fuzzy Neural Controller with Prescribed Performance Applied to Waverider Aircraft. IEEE Trans. Fuzzy Syst. 2021, 30, 2529–2537. [Google Scholar] [CrossRef]
- Bu, X.; Wu, X.; Zhu, F.; Huang, J.; Ma, Z.; Zhang, R. Novel prescribed performance neural control of a flexible air-breathing hypersonic vehicle with unknown initial errors. ISA Trans. 2015, 59, 149–159. [Google Scholar] [CrossRef]
- Liang, H.; Zhang, Y.; Huang, T.; Ma, H. Prescribed Performance Cooperative Control for Multiagent Systems with Input Quantization. IEEE Trans. Cybern. 2020, 50, 1810–1819. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Hu, J.; Li, J.; Liu, B. Improved prescribed performance control for nonaffine pure-feedback systems with input saturation. Int. J. Robust Nonlinear Control. 2019, 29, 1769–1788. [Google Scholar] [CrossRef]
- Li, Y.; Tong, S.; Li, T. Adaptive Fuzzy Output Feedback Dynamic Surface Control of Interconnected Nonlinear Pure-Feedback Systems. IEEE Trans. Cybern. 2015, 45, 138–149. [Google Scholar] [CrossRef]
- Li, Y.; Tong, S.; Li, T. Composite Adaptive Fuzzy Output Feedback Control Design for Uncertain Nonlinear Strict-Feedback Systems with Input Saturation. IEEE Trans. Cybern. 2015, 45, 2299–2308. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Liu, Z.; Zhang, Y.; Chen, C.L.P. Adaptive Fuzzy Control for a Class of Stochastic Pure-Feedback Nonlinear Systems with Unknown Hysteresis. IEEE Trans. Fuzzy Syst. 2016, 24, 140–152. [Google Scholar] [CrossRef]
- Sun, K.; Li, Y.; Tong, S. Fuzzy Adaptive Output Feedback Optimal Control Design for Strict-Feedback Nonlinear Systems. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 33–44. [Google Scholar] [CrossRef]
- Gao, T.; Liu, Y.; Liu, L.; Li, D. Adaptive Neural Network-Based Control for a Class of Nonlinear Pure-Feedback Systems with Time-Varying Full State Constraints. IEEE/CAA J. Autom. Sin. 2018, 5, 923–933. [Google Scholar] [CrossRef]
- Choi, Y.H.; Yoo, S.J. Filter-Driven-Approximation-Based Control for a Class of Pure-Feedback Systems with Unknown Nonlinearities by State and Output Feedback. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 161–176. [Google Scholar] [CrossRef]
- Zerari, N.; Chemachema, M.; Essounbouli, N. Neural Network Based Adaptive Tracking Control for a Class of Pure Feedback Nonlinear Systems with Input Saturation. IEEE/CAA J. Autom. Sin. 2019, 6, 278–290. [Google Scholar] [CrossRef]
- Wu, J.; Wu, Z.; Li, J.; Wang, G.; Zhao, H.; Chen, W. Practical Adaptive Fuzzy Control of Nonlinear Pure-Feedback Systems with Quantized Nonlinearity Input. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 638–648. [Google Scholar] [CrossRef]
- Tan, L.N. Distributed H∞ Optimal Tracking Control for Strict-Feedback Nonlinear Large-Scale Systems with Disturbances and Saturating Actuators. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 4719–4731. [Google Scholar] [CrossRef]
- Chen, Q.; Shi, H.; Sun, M. Echo State Network-Based Backstepping Adaptive Iterative Learning Control for Strict-Feedback Systems: An Error-Tracking Approach. IEEE Trans. Cybern. 2020, 50, 3009–3022. [Google Scholar] [CrossRef]
- Qiu, J.; Su, K.; Wang, T.; Gao, H. Observer-Based Fuzzy Adaptive Event-Triggered Control for Pure-Feedback Nonlinear Systems with Prescribed Performance. IEEE Trans. Fuzzy Syst. 2019, 27, 2152–2162. [Google Scholar] [CrossRef]
- Bu, X.; Qi, Q. Fuzzy optimal tracking control of hypersonic flight vehicles via single-network adaptive critic design. IEEE Trans. Fuzzy Syst. 2022, 30, 270–278. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, G. Fuzzy Adaptive Output Feedback Control of Uncertain Nonlinear Systems with Prescribed Performance. IEEE Trans. Cybern. 2018, 48, 1342–1354. [Google Scholar] [CrossRef]
- Yang, Z.; Zong, X.; Wang, G. Adaptive prescribed performance tracking control for uncertain strict-feedback Multiple Inputs and Multiple Outputs nonlinear systems based on generalized fuzzy hyperbolic model. Int. J. Adapt. Control. Signal Process. 2020, 34, 1847–1864. [Google Scholar] [CrossRef]
- Gao, S.; Dong, H.; Zheng, W. Robust resilient control for parametric strict feedback systems with prescribed output and virtual tracking errors. Int. J. Robust Nonlinear Control. 2019, 29, 6212–6226. [Google Scholar] [CrossRef]
- Bu, X.; Wei, D.; Wu, X.; Huang, J. Guaranteeing preselected tracking quality for air-breathing hypersonic non-affine models with an unknown control direction via concise neural control. J. Frankl. Inst. 2016, 353, 3207–3232. [Google Scholar] [CrossRef]
- Bu, X. Guaranteeing prescribed output tracking performance for air-breathing hypersonic vehicles via non-affine back-stepping control design. Nonlinear Dyn. 2018, 91, 525–538. [Google Scholar] [CrossRef]
- Liu, Z.; Dong, X.; Xue, J.; Li, H.; Chen, Y. Adaptive neural control for a class of pure-feedback nonlinear systems via dynamic surface technique. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1969–1975. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, J.; Wen, C.; Su, X. Distributed control of nonlinear systems with unknown time-varying control coefficients: A novel Nussbaum Function approach. IEEE Trans. Autom. Control. 2022. [Google Scholar] [CrossRef]
- Xu, B.; Huang, X.; Wang, D.; Sun, F. Dynamic surface control of constrained hypersonic flight models with parameter estimation and actuator compensation. Asian J. Control. 2014, 16, 162–174. [Google Scholar] [CrossRef]
- Bu, X.; Wu, X.; Ma, Z.; Zhang, R. Nonsingular direct neural control of air-breathing hypersonic vehicle via back-stepping. Neurocomputing 2015, 153, 164–173. [Google Scholar] [CrossRef]
- Park, J.; Kim, S.; Park, T. Output-Feedback Adaptive Neural Controller for Uncertain Pure-Feedback Nonlinear Systems Using a High-Order Sliding Mode Observer. IEEE Trans. Neural Networks Learn. Syst. 2019, 30, 1596–1601. [Google Scholar] [CrossRef]
- Bu, X.; He, G.; Wang, K. Tracking control of air-breathing hypersonic vehicles with non-affine dynamics via improved neural back-stepping design. ISA Trans. 2018, 75, 88–100. [Google Scholar] [CrossRef]
- Vu, V.; Pham, T.; Dao, P. Disturbance observer-based adaptive reinforcement learning for perturbed uncertain surface vessels. ISA Trans. 2022. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Y.; Bu, X. Approximation-Avoidance-Based Robust Quantitative Prescribed Performance Control of Unknown Strict-Feedback Systems. Mathematics 2022, 10, 3599. https://doi.org/10.3390/math10193599
Feng Y, Bu X. Approximation-Avoidance-Based Robust Quantitative Prescribed Performance Control of Unknown Strict-Feedback Systems. Mathematics. 2022; 10(19):3599. https://doi.org/10.3390/math10193599
Chicago/Turabian StyleFeng, Yin’an, and Xiangwei Bu. 2022. "Approximation-Avoidance-Based Robust Quantitative Prescribed Performance Control of Unknown Strict-Feedback Systems" Mathematics 10, no. 19: 3599. https://doi.org/10.3390/math10193599







