Multi-User Massive MIMO System with Adaptive Antenna Grouping for Beyond 5G Communication Network
Abstract
:1. Introduction
Motivation
- Sending error-free data with improved network performance and increased spectral efficiency for better use of a limited spectrum for communication networks of the next decade.
- To examine the proposed method on different deployment scenarios of the ITU-R M.2135 standard.
2. Background and Scope of the Study
2.1. Contribution
2.2. Organization
3. System Model and Problem Description
3.1. AAG-3M System Overview
Encoding
| Algorithm 1: Adaptive selection of antennas for grouping. |
| Step 1: Power gain calculation amongst ith transmitting antenna and all the received antennas j. Step 2: Reorganize the random variables in to ascending order. ‘l’ is the ordinal antenna number of the antenna correlated with P(l). The associated transmitting antenna is considered the best antenna among antennas. Step 3: Selection of the first two antennas The dual antennas, known as r and s, are identified by This implies the twin antennas are linked to each other. Step 4: Selection of the rest of the antenna Similarly, pick the next two antennas, the transmitting antennas, from the group. This process continues until all the transmission antennas are clustered. |
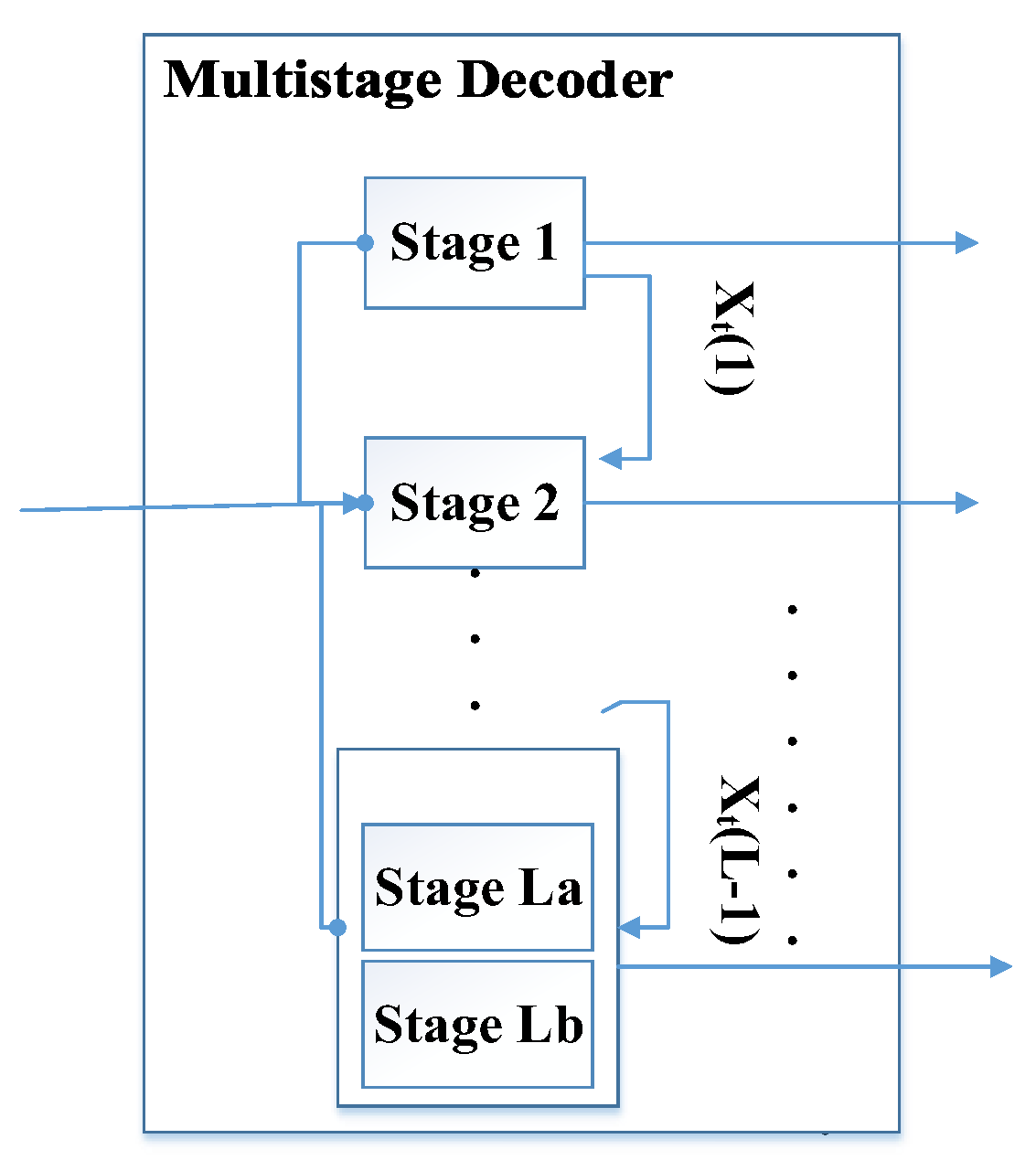
3.2. Decoding (ML)
3.3. Massive MIMO with Perfect CSI (System Model)
4. Simulation Parameters and Results
4.1. Comparison of Different Deployment Scenarios in AAG in Multilevel Massive MIMO (AAG-3M)
Effect of Multipath Propagation Scenario
- For the urban deployment scenario
- 2.
- For the sub-urban deployment scenario
- 3.
- For rural deployment scenario (high-speed deployment scenario)
4.2. Comparison of the Only AAG
4.3. Comparison of AAG-3M with Different Numbers of Users
4.4. Comparison of Spectral Efficiency AAG with and without Massive MIMO
5. Challenges and Future Scope
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Etzion, T.; Silberstein, N. Error-correcting codes in projective spaces via rank-metric codes and Ferrers diagrams. IEEE Trans. Inf. Theory 2009, 55, 2909–2919. [Google Scholar] [CrossRef] [Green Version]
- Ungerboeck, G. Channel coding with multilevel/phase signals. IEEE Trans. Inf. Theory 1982, 28, 55–67. [Google Scholar] [CrossRef]
- Sklar, B. Digital Communications; Prentice-Hall: Hoboken, NJ, USA, 2001; Volume 2. [Google Scholar]
- Cheng, J.-F.; Chuang, C.-H.; Lee, L.-S. Complexity-reduced multilevel coding with rate-compatible punctured convolutional codes. In Proceedings of the GLOBECOM’93 Global Telecommunications Conference, Houston, TX, USA, 29 November–2 December 1993; Including a Communications Theory Mini-Conference. Technical Program Conference Record. pp. 814–818. [Google Scholar]
- Kofman, Y.; Zehavi, E.; Shamai, S. Performance analysis of a multi-level coded modulation system. IEEE Trans. Commun. 1994, 42, 299–312. [Google Scholar] [CrossRef]
- Isaka, M.; Imai, H. On the iterative decoding of multilevel codes. IEEE J. Sel. Areas Commun. 2001, 19, 935–943. [Google Scholar] [CrossRef]
- Chopra, S.R.; Gupta, A. Error Analysis of Grouped Multilevel Space-Time Trellis Coding with the Combined Application of Massive MIMO and Cognitive Radio. Wirel. Pers. Commun. 2021, 117, 461–482. [Google Scholar] [CrossRef]
- Shahab, S.; Nosratinia, A. Antenna selection in MIMO systems. IEEE Commun. Mag. 2004, 42, 68–73. [Google Scholar]
- Marzetta, T.L. Noncooperative Cellular Wireless with Unlimited Numbers of Base Station Antennas. IEEE Trans. Wirel. Commun. 2010, 9, 3590–3600. [Google Scholar] [CrossRef]
- Alamouti, S.M. A simple Transmitter Diversity Scheme for Wireless Communications. IEEE J. Sel. Areas Commun. 1998, 16, 1451–1458. [Google Scholar] [CrossRef]
- Alamouti, S.; Tarokh, V.; Poon, P. Trellis coded Modulation and Transmit Diversity: Design Criteria & Performance evaluation. In Proceedings of the 1998 International Conference on Universal Personal Communications, Florence, Italy, 5–9 October 1998. [Google Scholar]
- Jafarkhani, H.; Seshadri, N. Super-orthogonal space-time trellis codes. IEEE Trans. Inf. Theory 2003, 49, 937–950. [Google Scholar] [CrossRef]
- Jafarkhani, H.; Hassanpour, N. Super-quasi-orthogonal space-time trellis codes for four transmit antennas. IEEE Trans. Wirel. Commun. 2005, 4, 215–227. [Google Scholar] [CrossRef] [Green Version]
- Ma, S.-C.; Lin, C.-H. Multilevel concatenated Space-time block codes. In Proceedings of the IEICE transactions on Fundamentals of Electronics, Communications, and Computer, Taipei, Taiwan, 1–3 July 2010; pp. 1845–1847. [Google Scholar]
- Gupta, A.; Jha, R.K. Power Optimization Using Massive MIMO and Small Cell Approach in Different Deployment Scenarios; Springer Science + Business Media: New York, NY, USA, 2016. [Google Scholar]
- Sharma, S.A.; Sharma, S. A Novel Cooperative Diversity Technique Based on Multilevel Pseudo Space–Time Trellis Coding. Wirel. Pers. Commun. 2017, 92, 1787–1800. [Google Scholar] [CrossRef]
- Tarokh, V.; Seshadri, N.; Calderbank, A.R. Space timecodes for high data rate wireless communication: Performance criterion and code construction. IEEE Trans. Inf. Theory 1998, 44, 744–765. [Google Scholar] [CrossRef] [Green Version]
- Mavares, D.; Torres, R.P. Spacetime code selection for transmits antenna diversity systems. In Proceedings of the First Mobile Computing and Wireless Communication International Conference, Amman, Jordan, 17–20 September 2006; pp. 83–87. [Google Scholar]
- Liu, L.; Jafarkhani, H. STtrellis codes based on channel-phase feedback. IEEE Trans. Commun. 2006, 54, 2186–2198. [Google Scholar] [CrossRef]
- Eksim, A.; Celebi, M.E. Received SNR-based code and antenna selection for limited feedback communication. In Proceedings of the 18th conference of IEEE Signal Processing and Communications Applications, Diyarbakir, Turkey, 22–24 April 2010; pp. 21–24. [Google Scholar]
- Wong, W.H.; Larsson, E. Orthogonal space-time block coding with antenna selection and power allocation. Electron. Lett. 2003, 39, 379–381. [Google Scholar] [CrossRef]
- Tao, M.; Li, Q.; Garg, H. Extended Space-Time Block Coding with Transmit Antenna Selection over Correlated Fading Channels. IEEE Trans. Wirel. Commun. 2007, 6, 3137–3141. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Vucetic, B.; Yuan, J. Space-time trellis codes with transmit antenna selection. Electron. Lett. 2003, 39, 854–855. [Google Scholar] [CrossRef]
- Tarokh, V.; Naguib, A.; Seshadri, N.; Calderbank, A.R. Combined array processing and Spacetime coding. IEEE Trans. Inf. Theory 1999, 45, 1121–1128. [Google Scholar] [CrossRef]
- Narasimhan, R. Spatial multiplexing with transmit antenna and constellation selection for correlated mimo fading channels. IEEE Trans. Signal Process. 2003, 51, 2829–2838. [Google Scholar] [CrossRef]
- Huang, Y.; Xu, D.; Yang, L. AAG for Space-time block coding and spatial multiplexing hybrid system. In Proceedings of the First Mobile Computing and Wireless Communication International Conference (MCWC 2006), Vancouver, BC, Canada, 3–6 July 2006; pp. 88–92. [Google Scholar]
- Li, Y.; Vucetic, B.; Santoso, A.; Chen, Z. Space-time trellis codes with adaptive weighting. Electron. Lett. 2003, 39, 1833–1834. [Google Scholar] [CrossRef]
- Santoso, A.; Li, Y.; Vucetic, B. Weighted space-time trellis codes. Electron. Lett. 2004, 40, 254–256. [Google Scholar] [CrossRef]
- Imai, H.; Hirakawa, S. A new multilevel coding method using error-correcting codes. IEEE Trans. Inf. Theory 1977, 23, 371–377. [Google Scholar] [CrossRef]
- Calderbank, A. ML codes and multistage decoding. IEEE Trans. Commun. 1989, 37, 222–229. [Google Scholar] [CrossRef]
- Waschmann, U.; Fischer, R.F.; Huber, J.B. ML codes: Theoretical concepts and practical design rules. IEEE Trans. On. Inf. Theory 1999, 45, 1361–1391. [Google Scholar] [CrossRef] [Green Version]
- Baghaie, A.M. Multilevel Space-Time Trellis Codes for Rayleigh Fading Channels. Master’s Thesis, University of Canterbury, Christchurch, New Zealand, 2008. [Google Scholar]
- Chen, Z.; Yuan, J.; Vucetic, B. An improved Space-time trellis coded modulation scheme on slow Rayleigh fading channels. In Proceedings of the IEEE International Conference on Communications, Helsinki, Finland, 11–14 June 2001; pp. 1110–1116. [Google Scholar]
- Sharma, S. A novel weighted multilevel Space-time trellis coding scheme. Comput. Math. Appl. 2012, 63, 280–287. [Google Scholar] [CrossRef] [Green Version]
- Jain, D.; Sharma, S. Adaptively Grouped Multilevel Space–Time Trellis Codes Combined with Beamforming and Component Code Selection. Wirel. Pers. Commun. 2014, 77, 2549–2563. [Google Scholar] [CrossRef]
- Jain, D.; Sharma, S. Performance Analysis of Adaptively Grouped Space-Time Trellis Coded Systems using Different Component Codes. Wirel. Pers. Commun. 2015, 82, 341–352. [Google Scholar] [CrossRef]
- Baghaie, M.; Martin, P.A.; Taylor, D.P. Grouped ML Space-Time Trellis Codes. IEEE Commun. Lett. 2010, 14, 232–234. [Google Scholar]
- Tran, T.X.; Teh, K.C. Error probability analysis of a novel adaptive beamforming receiver for large-scale multiple-input multiple-output communication system. IET Commun. 2015, 9, 291–299. [Google Scholar] [CrossRef]
- Abu-Ella, O.; Wang, X. Large-scale multiple-input multiple-output transceiver system. IET Commun. 2013, 7, 471–479. [Google Scholar] [CrossRef]
- Rusek, F.; Persson, D.; Lau, B.K.; Larsson, E.G.; Marzetta, T.L.; Tufvesson, F. Scaling Up MIMO: Opportunities and Challenges with Very Large Arrays. IEEE Signal Process. Mag. 2012, 30, 40–60. [Google Scholar] [CrossRef] [Green Version]
- Wagner, S.; Couillet, R.; Debbah, M.; Slock, D.T.M. Large System Analysis of Linear Precoding in Correlated MISO Broadcast Channels Under Limited Feedback. IEEE Trans. Inf. Theory 2012, 58, 4509–4537. [Google Scholar] [CrossRef] [Green Version]
- Karlsson, M.; Björnson, E.; Erik, G.L. Broadcasting in massive MIMO using OSTBC with reduced dimension. In Proceedings of the 2015 International Symposium on Wireless Communication Systems (ISWCS), Brussels, Belgium, 25–28 August 2015; pp. 386–390. [Google Scholar]
- Choudhury, P.K.; El-Nasr, M.A. Massive MIMO toward 5G. J. Electromagn. Waves Appl. 2020, 34, 1091–1094. [Google Scholar] [CrossRef]
- Ho, C.D.; Ngo, H.Q.; Matthaiou, M. Transmission Schemes and Power Allocation for Multiuser Massive MIMO Relaying. IEEE Trans. Veh. Technol. 2021, 70, 11469–11482. [Google Scholar] [CrossRef]
- Helmy, H.M.N.; El Daysti, S.; Shatila, H.; Aboul-Dahab, M. Performance Enhancement of Massive MIMO Using Deep Learning-Based Channel Estimation. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1051, 012029. [Google Scholar] [CrossRef]
- Larsson, E.G.; Edfors, O.; Tufvesson, F.; Marzetta, T.L. Massive MIMO for next generation wireless systems. IEEE Commun. Mag. 2014, 52, 186–195. [Google Scholar] [CrossRef] [Green Version]
- Luther, E. 5G Massive MIMO Testbed: From Theory to Reality; White Paper; National Instruments: Austin, TX, USA, 2014; pp. 1–11. [Google Scholar]
- Series, M. Guidelines for Evaluation of Radio Interface Technologies for IMT-Advanced; Report ITU 638; International Telecommunication Union: Geneva, Switzerland, 2009; pp. 1–72. [Google Scholar]
- Zhang, J.; Dong, W.; Gao, X.; Zhang, P.; Wu, Y. Cluster Identification and Properties of Outdoor Wideband MIMO Channel. In Proceedings of the 2007 IEEE 66th on Vehicular Technology Conference, 2007. VTC-2007 Fall, Baltimore, MD, USA, 30 September–3 October 2007; pp. 829–833. [Google Scholar]
- Lu, Y.; Zhang, J.; Gao, X.; Zhang, P.; Wu, Y. Outdoor-Indoor Propagation Characteristics of Peer-to-Peer System at 5.25 GHz. In Proceedings of the 2007 IEEE 66th on Vehicular Technology Conference, 2007. VTC-2007 Fall, Baltimore, MD, USA, 30 September–3 October 2007; pp. 869–873. [Google Scholar]
- Xu, D.; Zhang, J.; Gao, X.; Zhang, P.; Wu, Y. Indoor Office Propagation Measurements and Path Loss Models at 5.25 GHz. In Proceedings of the 2007 IEEE 66th on Vehicular Technology Conference, 2007. VTC-2007 Fall, Baltimore, MD, USA, 30 September–3 October 2007; pp. 844–848. [Google Scholar]
- Zhang, J.; Gao, X.; Zhang, P.; Yin, X. Propagation Characteristics of Wideband MIMO Channel in Hotspot Areas at 5.25 GHZ. In Proceedings of the IEEE 18th International Symposium on Personal, Indoor and Mobile Radio Communications, Athens, Greece, 3–7 September 2007; pp. 1–5. [Google Scholar] [CrossRef]
- Zhang, J.; Dong, D.; Liang, Y.; Nie, X.; Gao, X.; Zhang, Y.; Huang, C.; Liu, G. Propagation characteristics of wideband MIMO channel in urban micro- and macrocells. In Proceedings of the IEEE 19th International Symposium on Personal, Indoor and Mobile Radio Communications, Cannes, France, 15–18 September 2008; pp. 1–6. [Google Scholar] [CrossRef]
- Imoize, A.L.; Ibhaze, A.E.; Atayero, A.A.; Kavitha, K.V.N. Standard Propagation Channel Models for MIMO Communication Systems. Wirel. Commun. Mob. Comput. 2021, 2021, 8838792. [Google Scholar] [CrossRef]







| Ref. | Space–Time Coding Application | Methodology | Limitations/Contributions |
|---|---|---|---|
| [1] | Introduction of multilevel in error-correcting codes. | A new coding system called multilevel coding has been implemented that utilizes multiple error-correcting codes for signal transmission. | No antenna grouping/Massive MIMO/spectral efficiency based on multilevel in error-correcting codes. |
| [2] | Mapping by set partitioning in trellis code. | Signal constellation partitioning has been implemented and is referred to as set partitioning. Modulate and combine the mapped symbols to create complicated codes called multilevel codes. | No antenna grouping/Massive MIMO/spectral efficiency, but through mapping, create multilevel codes. |
| [4,5,6] | Multilevel codes in conjunction with iterative decoding of the block and convolutional code, and calculation of diversity and coding gain. | The multilevel coding scheme can deliver a preferred information transmission rate, error performance and coding, and diversity gain. | No antenna grouping/Massive MIMO/spectral efficiency. The major contributions are iterative decoding. |
| [10] | Multiple inputs and a single output are used with two transmitting and one receiving antenna and are applied with a diversity scheme in block coding. | A diversity scheme of two-branch simple transmission has been presented. The system uses two antennas for transmitting and one antenna for receiving. This has the same order of variety combined with one transmitting antenna and two receiving antennas as the max unit. With two transmitting antennas and the receiving M antennas, the scheme can be easily generalized to give a range of 2 M diversity. The novel idea does not need bandwidth expansion or input from the receiver to the transmitter, and the measurement complexity is close to the maximum combination of the receiver. | No antenna grouping/Massive MIMO/spectral efficiency. The key impact is the establishment of the diversity scheme. |
| [11] | Multiple inputs and a single output are used with two transmitting and one receive antenna and are applied with a diversity scheme in trellis coding. | The design procedure for choosing trellis codes with a simple transmit diversity scheme is described. Using this method, both diversity and coding gain can be achieved using two transmitting and one receiving antenna. | No antenna grouping/Massive MIMO/spectral efficiency, but the use of the diversity scheme in the trellis code, which benefits both coding and diversity, is a significant addition. |
| [12] | Multiple inputs and single output by optimal set partitioning are used with the designed multilevel super-orthogonal trellis coding. | A space–time code, known as space–time super-orthogonal trellis codes, with the new class, is presented. These codes symmetrically combine the allocated collection and modified space–time orthogonal codes to provide a better coding advantage and maximum diversity gain for the overall performance of previous STTCC codes. Moreover, the optimality of the parcel collection has been tested and the coding gain investigation has been evaluated. The perfect environment was used to schedule various quantities of states with codes running at different data rates up to a relatively high conceivable rate. | No Adaptive Antenna Grouping/Massive MIMO/spectral efficiency. The essential contribution is in trellis coding; the idea of orthogonality has been introduced. |
| [13] | Multiple inputs and a single output using four transmitting and one receiving antenna in terms of a cooperative diversity scheme are applied in orthogonal trellis coding. | In a cooperative diversity setting, a new family space–time trellis code is introduced, which extends the space–time super-orthogonal trellis codes intensively attributed to transmission antennas. A group of semi-orthogonal trellis codes is in use as building components in the new trellis codes. In space–time coding, multilevel coding will be further enhanced in its diversity plus coding gain. As a combination of MLC with STTCs, MLSTTCs are planned. MLSTTCs enhance the efficiency of the bandwidth, enhance diversity and coding gain and decrease decoding complexity, particularly for larger groups. | No Adaptive Antenna Grouping/Massive MIMO/spectral efficiency. However, the principle of super orthogonality has been introduced. |
| [14] | Multiple inputs and multiple outputs are used with four transmitting antennas and a different number of receiving antennas with Multilevel space-time trellis coding. | This paper presents a new code termed adaptively grouped MLSTTCs. This code is designed to perform better than traditional space-time trellis coding because it incorporates the advantages of MLC, STTC, antenna grouping, and CSIT simultaneously. | No Adaptive Antenna Grouping/Massive MIMO/Spectral efficiency. A noteworthy contribution is the introduction of antenna grouping. |
| [15] | Path-loss models in a standard. | Path-loss models have been standardized in this paper for different transmission models, such as the ITU-R M.2135 standard rural, suburban, and urban macro models. | No Adaptive Antenna Grouping major contribution works on path-loss model. |
| [16] | Multiple inputs and multiple outputs used two transmitting and two receiving antennas with multilevel pseudo-space–time trellis code. | In terms of its output difference with Shannon-bound sphere packing (a simple performance assessment tool), this paper shows that short block lengths of the code architecture show better results with convolution codes for point-to-point channels and the suggested MLPSTTCC. | No Massive MIMO. The main impact of cooperative diversity scheme implementation. |
| Ref. | Multi-Levelling | Antenna Grouping | AAG | Massive MIMO | Spectral Efficiency Analysis | Application in ITU-R M.2135 Standard |
|---|---|---|---|---|---|---|
| [1] | Yes | × | × | × | × | No |
| [2] | No | × | × | × | × | No |
| [6] | Yes | × | × | × | × | No |
| [11] | Yes | × | × | × | × | No |
| [13] | Yes | ✓ | × | × | × | No |
| [14] | Yes | ✓ | × | × | × | No |
| [16] | Yes | ✓ | ✓ | × | × | No |
| AAG-3M | Yes | ✓ | ✓ | ✓ | ✓ | Yes |
| Parameter | Values |
|---|---|
| Channel-specific bandwidth | 20 MHz |
| Sampling frequency | 30.72 MS/s |
| FFT size | 2048 |
| Utilized subcarriers in number | 1200 |
| Blocks of resources | 100 |
| OFDM symbol count per slot | 7 |
| Length of CyclicPrefix (samples) | 160 (first symbol) 144 (six following symbols) |
| Cell radius | 60 m (Indoor hotspot) 200 m (Ultra-Dense Urban) 500 m (Urban) 1299 m (Suburban) 1732 m (Rural) |
| Transmission bandwidth | 40 × 106 (Indoor hotspot) 20 × 106 (Others) |
| SNR (dB) | Spectral Efficiency (b/s/Hz) of AAG with Massive MIMO | Spectral Efficiency (b/s/Hz) of AAG without Massive MIMO | Diversity Gain |
|---|---|---|---|
| 2 | 2.6 | 1.87 | 0.73 |
| 4 | 2.8 | 1.92 | 0.88 |
| 6 | 2.95 | 1.98 | 0.97 |
| 8 | 3.1 | 1.99 | 1.11 |
| 10 | 3.2 | 1.995 | 1.205 |
| 12 | 3.3 | 1.998 | 1.302 |
| 14 | 3.35 | 1.999 | 1.351 |
| 16 | 3.37 | 1.999 | 1.371 |
| 18 | 3.38 | 2.00 | 1.38 |
| 20 | 3.38 | 2.00 | 1.38 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chopra, S.R.; Gupta, A.; Tanwar, S.; Safirescu, C.O.; Mihaltan, T.C.; Sharma, R. Multi-User Massive MIMO System with Adaptive Antenna Grouping for Beyond 5G Communication Network. Mathematics 2022, 10, 3621. https://doi.org/10.3390/math10193621
Chopra SR, Gupta A, Tanwar S, Safirescu CO, Mihaltan TC, Sharma R. Multi-User Massive MIMO System with Adaptive Antenna Grouping for Beyond 5G Communication Network. Mathematics. 2022; 10(19):3621. https://doi.org/10.3390/math10193621
Chicago/Turabian StyleChopra, Shakti Raj, Akhil Gupta, Sudeep Tanwar, Calin Ovidiu Safirescu, Traian Candin Mihaltan, and Ravi Sharma. 2022. "Multi-User Massive MIMO System with Adaptive Antenna Grouping for Beyond 5G Communication Network" Mathematics 10, no. 19: 3621. https://doi.org/10.3390/math10193621
APA StyleChopra, S. R., Gupta, A., Tanwar, S., Safirescu, C. O., Mihaltan, T. C., & Sharma, R. (2022). Multi-User Massive MIMO System with Adaptive Antenna Grouping for Beyond 5G Communication Network. Mathematics, 10(19), 3621. https://doi.org/10.3390/math10193621





