Identification of Nonlinear State-Space Systems via Sparse Bayesian and Stein Approximation Approach

Abstract

This paper is concerned with the parameter estimation of non-linear discrete-time systems from noisy state measurements in the state-space form. A novel sparse Bayesian convex optimisation algorithm is proposed for the parameter estimation and prediction. The method fully considers the approximation method, parameter prior and posterior, and adds Bayesian sparse learning and optimization for explicit modeling. Different from the previous identification methods, the main identification challenge resides in two aspects: first, a new objective function is obtained by our improved Stein approximation method in the convex optimization problem, so as to capture more information of particle approximation and convergence; second, another objective function is developed with L${}_1$-regularization, which is sparse method based on recursive least squares estimation. Compared with the previous study, the new objective function contains more information and can easily mine more important information from the raw data. Three simulation examples are given to demonstrate the proposed algorithm’s effectiveness. Furthermore, the performances of these approaches are analyzed, including parameter estimation of root mean squared error (RMSE), parameter sparsity and prediction of state and output result.

1. Introduction

In the actual world, non-linear systems are commonplace, such as social networks, industry systems, biological systems, finance, and chemical engineering. Identification of non-linear systems are widely acknowledged for its importance and difficulties [1,2], such as fractional order system [3,4,5], neural networks [6], non-linear ARMAX (NARMAX) [7], and Hammerstein–Wiener [8] models. The non-linear state-space model is a kind of expression for all these non-linear systems. A common method for identifying non-linear state-space models is to look for a concise description that is consistent with some non-linear terms (kernel functions) based on data [9,10]. Classic functional decomposition methods, such as Volterra expansion, Taylor polynomial expansion, or Fourier series [9,11], provide a few options for kernel functions. These methods are founded on the idea that there are a finite set of fundamental kernel functions whose linear combination can be utilized to describe the dynamics of a non-linear state-space system. However, under the condition of more kernel functions, the efficiency of this kind of method decreases rapidly. A promising way to identify non-linear state-space systems is probabilistic method [12,13,14,15], which has received a lot of attention over the past few years. Earlier non-linear state-space systems identification methods based on probabilistic method, such as regression method, maximum likelihood (ML) [16], expectation-maximization (EM) [17], mainly utilize gradient descent method while ignoring the parameter identification and approximation process information.

To further improve the efficiency of parameter identification, many identification techniques have been presented that combine the gradient descent technique and Bayesian approximation recently. In particular, those based on the variational inference method have attracted more attention due to their superior performance, such as variational inference in the Gaussian process (GP) [12], Gaussian-process state-space model (GP-SSM) [13], deep variational Bayes filters (DVBF) [14], optimistic inference control (OIC) [15]. Various approximation expectation-maximization (EM)-based techniques have also been studied. In [18], the authors have examined applying EM method to estimate the parameters of a non-linear state space model of the disease dynamics. In [19,20], both Bayesian and a ML estimation strategy are employed in addition to a competitive GP approximation method. For learning, Monte Carlo technique and EM method are utilized in [21], which also includes variational method using the same GP approximation.

Notably, none of these methods take into account the prediction’s resilience and all of them presuppose that the structure of non-linear state-space models is unknown. However, in reality, many parameters are missing precision due to reasons, such as slow convergence rate or falling into local optimum. In this article, we concentrate on the optimum problem since it is more difficult and has numerous real-world implications. For example, in a pilot plant PH process, Hammerstein–Wiener model is used in the prediction of the neutral liquid pH value [22]. In addition, the problem of non-linear state-space systems with missing precision is related to complexity of parameters. Sparse representation can be used in dealing with sparse solutions of linear regression equations, which can effectively reduce the complexity of parametric solutions. There are just a few papers that deal with the sparse representation identification issue and multiple constraints on the system’s parameters [23,24]. In [25], the convex constraint is added to the parameters sparse representation in the non-linear identification algorithm. These works of literature only consider the selection of sparse methods and do not consider conditional restrictions in the process of parameter approximation.

Unlike the previous work, our suggested framework, on the other hand, allows us to include more constraints on the corresponding model parameters, e.g., inequality constraint, priori information and Stein discrepancy constraints. The dynamical system discovery issue is reimagined in this paper from the perspectives of sparse regression [26,27,28], compressed sensing [29,30,31], Stein approximation theory [32], and convex optimization method [23]. The use of sparsity approaches is relatively new [33,34,35] in dynamical systems. We all know that most non-linear state-space systems have only a few important dynamics elements, resulting in sparse parameter set in a high-dimensional non-linear function space.

Although these efforts are focused on non-linear system identification using state-space models, they have some significant flaws. First, these methods carry out system identification in a two-stage way, that is, compute the posterior objective function with parameters, and then learning system parameter with noise. The computing posterior objective function and the learning system parameter are two different processes in these two-stage approaches, and their parameters cannot be modified together. System identification will perform worse as a result of this. The ideal relationship between these two processes would be one of complementarity. That is, learning system identification should contribute to computing posterior objective function, and the updated posterior objective function should contribute to learning system parameter with noise. For non-linear systems with state-space formulation, ref. [36] addresses the recursive joint inference and learning problem, and a reduced rank formulation of GP-SSMs is used to model the system as a Gaussian-process state space model (GP-SSM). In [37], a two-stage Bayesian optimization framework is introduced, which consists of representation of the objective function in low-dimensional parameter space and surrogate model selection in the reduced space. In this study, the only posterior objective function is considered, which can not achieve effective interactive learning, and may also compromise the optimization performance for system parameters.

To address the problems of existing identification methods for non-linear state-space systems, we propose non-linear state-space identification algorithm with Sparse Bayesian and Stein Approach (NSSI-SBSA), which is an optimization approach for improving the accuracy of system parameter identification and posterior distribution computing simultaneously in an integrated structure as opposed to the conventional two-stage method. In our new method, we select least absolute shrinkage and selection operator (LASSO) [26] as parameter sparsity algorithms. The sparse parameter is taken into posterior distribution, which reduced the complexity of posterior distribution. Compared with some sparse method of least angle regression (LARS) [38], sequentially thresholded least squares (STLS) [39], and basis pursuit denoising (BPDN) [40], LASSO is more suitable for high-dimensional data. In our article, the sparse model identification results strikes a natural balance between model sparsity and precision, and prevent the model from being overfit to the data.

From a statistical perspective, we will discuss how a Bayesian technology, optimization method, and Stein approximation strategy might mitigate the difficulties of large correlations in the state matrix. The following are some of the technical note’s most important contributions:

(1)

The NSSI-SBSA algorithm is proposed. In the algorithm, the sparse method is used for the parameter estimation and prediction. Parameter prior, Bayesian sparse learning, and optimisation are used in an integrated computing framework instead of the classical two-stage method. The sparse model identification results strikes a natural balance between model sparsity and precision, preventing the model from overfit to the data.

(2)

A nonconvex optimisation problem is constructed in the non-linear state-space system identification issue with additive noise. Compared with other related methods, we not only take the evidence maximisation as an objective function, but also consider the Stein discrepancy of parameters as another objective function in the non-convex optimization problem. The two functions are integrated into one objective function containing more information. It can captures more important information from the raw date and reduce the complexity of parametric solutions.

The rest of this paper is organized as follows. Section 2 describes problem statement and background. In Section 3, construct the model in Bayesian framework. In Section 4, non-convex optimisation with Stein constrain for identification is introduced. Three numerical illustration, including Narendra-Li Model, NARX model, Kernel state-space models (KSSM) are presented in Section 5. Finally, we give some closing remarks in Section 6.

2. Problem Statement and Background

We consider the following non-linear state-space model [25]

$$\begin{array}{cc}\hfill \pi \left({\mathbf{x}}_{ik}\right)& ={\mathbf{f}}_i\left({\mathbf{x}}_k,{\mathbf{u}}_k\right)+{\nu }_{ik}\hfill \\ \hfill & =\sum _{r=1}^N{\theta }_{ir}{f}_{ir}({\mathbf{x}}_k,{\mathbf{u}}_k)+{\nu }_{ik}\hfill \end{array}$$

(1)

$$o_{ik}={\mathbf{g}}_i\left({\mathbf{x}}_k,{\mathbf{u}}_k\right)+e_{ik},$$

where ${\mathbf{x}}_k=[x_{1k},\cdots x_{ik}\cdots x_{n_{\mathbf{x}},k}]$ is the state variable in time step k, and ${\mathbf{u}}_k$ is the external control input. When system is time continuous, $\pi \left(x_{ik}\right)={\dot{x}}_{ik}$; When system is time discrete, $\pi \left(x_{ik}\right)=x_{ik}$ or $x_{ik}-x_{i,k-1}$; ${\nu }_{ik}\sim \mathcal{N}\left(0,{\sigma }_{ik}^2\right)$ is noise (when $i\ne k,{\sigma }_{ik}=0$), which is set to be i.i.d. Gaussian distribution. $f_{ir}({\mathbf{x}}_k,{\mathbf{u}}_k):{\mathbb{R}}^{n_{\mathbf{x}}+n_{\mathbf{u}}}\to \mathbb{R}$ and ${\mathbf{g}}_i\left({\mathbf{x}}_k,{\mathbf{u}}_k\right)$$:{\mathbb{R}}^{n_{\mathbf{x}}+n_{\mathbf{u}}}\to \mathbb{R}$ is Lipschitz continuous function, and $n_{\mathbf{x}}$ and $n_{\mathbf{u}}$ are the dimensions of ${\mathbf{x}}_k$ and ${\mathbf{u}}_k$, respectively. ${\theta }_{ir}$ is the weight of basis functions. Together, ${\theta }_{ir}$ and $f_{ir}$ determine the dynamics. It is worth emphasizing that we make no assumptions about the non-linear functions on the right-hand side of (1).

If the system can provide M data samples that meet (1), the system in (1) can be represented as

$${\mathbf{Y}}_i={\mathbf{F}}_i{\theta }_i+{\nu }_i,i=1,\dots ,n_{\mathbf{x}},$$

(2)

where ${\mathbf{Y}}_i={\left[\pi \left(x_{i1}\right),\dots ,\pi \left(x_{iM}\right)\right]}^{\top }\in {\mathbb{R}}^{M\times 1},{\theta }_{i_T}\triangleq {\left[{\theta }_{i1},\dots ,{\theta }_{i{N}_i}\right]}^{\top }\in {\mathbb{R}}^{N_i\times 1},$${\nu }_i\triangleq {\left[{\nu }_{i0},\dots ,{\nu }_{i,M-1}\right]}^{\top }\in {\mathbb{R}}^{M\times 1}$, and ${\mathbf{F}}_i\in$${\mathbb{R}}^{M\times N_i}$ is called dictionary matrix. j-th column in ${\mathbf{F}}_i$ is described by

$${[{\mathbf{f}}_{ij}({\mathbf{x}}_0,{\mathbf{u}}_0),\dots ,{\mathbf{f}}_{ij}({\mathbf{x}}_{M-1},{\mathbf{u}}_{M-1})]}^{\top }.$$

In this article, the identification task is to estimate ${\theta }_i$ from the measured data of ${\mathbf{Y}}_i$. This leads to the solution of a linear regression issue, in which the least square (LS) method can be used if some of model’s non-linear part is understood, i.e., ${\mathbf{F}}_i$ is known. In (1), we merely discuss the identification problem, as we do in ${\mathbf{g}}_i\left({\mathbf{x}}_k,{\mathbf{u}}_k\right)$. Because of the potential non-relevant or independent columns in $F_i$, the solution ${\theta }_i$ in $\left(2\right)$ is often sparse, and a few frequently used non-linear dynamical models need to be considered. For the convenience of expression, we rewrite the linear regression issues in (2) into the following form

$$\mathbf{Y}=\mathbf{F}\theta +\nu$$

(3)

3. Constructing the Model in Bayesian Framework

All unknowns in Bayesian modeling are evaluated as they are random variables with specific distributions [41]. For $\mathbf{Y}=\mathbf{F}\theta +\nu$ in (3), noisy variables $\nu$ is Gaussian independently identically distribution (i.i.d.), i.e., $\nu \sim \mathcal{N}(\mathbf{0},\beta \mathbf{I}),\beta ={\sigma }^2$, identity matrix $\mathbf{I}$. We can obtain the likelihood of the data $P(\mathbf{Y}\mid \theta )=\mathcal{N}(\mathbf{Y}\mid \mathbf{F}\theta ,\beta \mathbf{I})\propto$$exp\{-\frac{1}{2\beta }\parallel \mathbf{Y}-\mathbf{F}\theta {\parallel }_2^2\}$. $P\left(\theta \right)$ is a prior distribution defined as $P\left(\theta \right)\propto exp\{-\frac{1}{2\alpha }{\theta }^T\theta \}={\prod }_{j}exp\{-\frac{1}{2\alpha }{\theta }_j^T{\theta }_j\}=$${\prod }_{j}P\left({\theta }_j\right)$, and $\alpha$ is hyper parameter. For the convenience of calculating sparse parameters $\theta$, $-\frac{1}{2\alpha }{\theta }^T\theta$ is selected as a concave non-decreasing function of $\left|{\theta }_j\right|$. The priors of $\theta$ includes Gaussian and t-distribution (see [42] for details).

The posterior $P(\theta \mid \mathbf{Y})$ is heavily linked and non-Gaussian, so computing the posterior mean $E(\theta \mid \mathbf{Y})$ is often difficult. To solve this problem, take $P(\theta \mid \mathbf{Y})$ as an approximation of Gaussian distribution. In [41], effective posterior computation algorithms are used in the computation.

Another method is to use super Gaussian priors, in which the priors $P\left({\theta }_j\right)$ is computed by the variational EM algorithms [42]. We define hyperparameters $\alpha \triangleq$${\left[{\alpha }_1,\dots ,{\alpha }_N\right]}^{\top }\in {\mathbb{R}}_{+}^N$. The priors of $\theta$ can be written as: $P\left(\theta \right)={\prod }_{j=1}^{n}P\left({\theta }_j\right)$, $P\left({\theta }_j\right)=\mathcal{N}\left({\theta }_j\mid 0,{\alpha }_j\right)\phi \left({\alpha }_j\right)$, where $\phi \left({\alpha }_j\right)$ is probability density function and $\phi \left({\alpha }_j\right)\ge 0$. $P(\theta ,\alpha )={\prod }_j\mathcal{N}\left({\theta }_j\mid 0,{\alpha }_j\right)\phi \left({\alpha }_j\right)=P(\theta \mid \alpha )P\left(\alpha \right)\le$ $P\left(\theta \right)$, where $P(\theta \mid \alpha )\triangleq {\prod }_j\mathcal{N}\left({\theta }_j\mid 0,{\alpha }_j\right),P\left(\alpha \right)\triangleq {\prod }_j\phi \left({\alpha }_j\right)$. Considering the data $\mathbf{Y}$, the posterior probability of $\theta$ can be represented as $P(\theta \mid \mathbf{Y},\alpha )=$$\frac{P(\mathbf{Y}\mid \theta )P(\theta ;\alpha )}{\int P(\mathbf{Y}\mid \theta )P(\theta ;\alpha )d\theta }=\mathcal{N}\left({\mathbf{m}}_{\theta },{\mathsf{\Sigma }}_{\theta }\right).$ From [43], the posterior mean ${\mathbf{m}}_{\theta }$ and covariance ${\mathsf{\Sigma }}_{\theta }$ are given by:

$$\begin{array}{cc}\hfill {\mathbf{m}}_{\theta }& =\mathsf{\Lambda }{\mathbf{F}}^{\top }{\left(\lambda \mathbf{I}+\mathbf{F}\mathsf{\Lambda }{\mathbf{F}}^{\top }\right)}^{-1}\mathbf{Y}\hfill \\ \hfill {\mathsf{\Sigma }}_{\theta }& =\mathsf{\Lambda }-\mathsf{\Lambda }{\mathbf{F}}^{\top }{\left(\lambda \mathbf{I}+\mathbf{F}\mathsf{\Lambda }{\mathbf{F}}^{\top }\right)}^{-1}\mathbf{F},\hfill \end{array}$$

(4)

where $\mathsf{\Lambda }$ is a diagonal matrix written as $diag\left[\alpha \right]$. It is obvious to maximize $P(\theta ,\alpha \mid \mathbf{Y}),$ the most important question is how to select the best $\widehat{\alpha }$. $P(\mathbf{Y}\mid \theta )$ and $P(\theta ;\alpha )$ are taken as prior information, so we need only consider $\int P(\mathbf{Y}\mid \theta )P(\theta ;\alpha )d\theta$. Using type-II ML [43], the marginal likelihood $\int P(\mathbf{Y}\mid \theta )P(\theta ;\alpha )d\theta$ can be maximised, and the selected $\widehat{\alpha }$ is written as

$$\widehat{\alpha }=\underset{\alpha \ge 0}{argmax}\int P(\mathbf{Y}\mid \theta )\prod _{j=1}^n\mathcal{N}\left({\theta }_j\mid 0,{\alpha }_j\right)\phi \left({\alpha }_j\right)d\theta .$$

(5)

After $\widehat{\alpha }$ is computed in (5), the estimation of $\theta$ can be obtained as $\widehat{\theta }=\mathbb{E}(\theta \mid \mathbf{Y};\widehat{\alpha })=$$\widehat{\mathsf{\Lambda }}{\mathbf{F}}^{\top }{\left(\lambda \mathbf{I}+\mathbf{F}\widehat{\mathsf{\Lambda }}{\mathbf{F}}^{\top }\right)}^{-1}\mathbf{Y}$, with $\widehat{\mathsf{\Lambda }}\triangleq diag\left[\widehat{\alpha }\right].$ It indicates that picking the most likely hyperparameters $\widehat{\alpha }$ is capable of explaining the data $\mathbf{Y}$.

4. Non-Convex Optimisation with Stein Method for Identification

4.1. Stein Operators Selection and Stein Constrain Design

The approach can be sketched as follows for a target distribution P with support Z. Find a suitable operator $\mathcal{B}:={\mathcal{B}}_P$ (referred to as the Stein operator) and a large class of functions ${\mathcal{F}}_{\mathcal{B}}=\mathcal{F}\left({\mathcal{B}}_P\right)$ (referred to as the Stein class) such that Z has distribution P, denoted $Z\sim P$, if, and only if, we have $f\in {\mathcal{F}}_{\mathcal{B}}$ for all functions

$$\mathbb{E}\left[\mathcal{B}f\right(Z\left)\right]=0.$$

A Stein operator can be designed in a variety of ways [32]. In our framework, Stein’s identity and kernelized Stein difference are crucial. $P\left(\theta \right)$ is probability density function, which is continuous and differentiable on $\theta$$\subseteq R^d$. According to Stein’s theory, suitable smooth and derivable function $\varphi \left(\theta \right)$ and $Q\left(\theta \right)$ are selected in (6), which are expressed as $\varphi \left(\theta \right)={\left[{\varphi }_1\left(\theta \right),\cdots ,{\varphi }_d\left(\theta \right)\right]}^{\top }$, $Q\left(\theta \right)={\left[Q_1\left(\theta \right),\cdots ,Q_d\left(\theta \right)\right]}^{\top }$.

$$E_{\theta \sim P}\left[{\mathcal{B}}_P\varphi \left(\theta \right)Q\left(\theta \right)\right]=0,$$

(6)

where

$${\mathcal{B}}_P\varphi \left(\theta \right)Q\left(\theta \right)=Q{\left(\theta \right)}^{{}^{\top }}\varphi {\left(\theta \right)}^{{}^{\top }}{\nabla }_{\theta }logP\left(\theta \right)$$

$$+{\nabla }_{\theta }\varphi \left(\theta \right)Q\left(\theta \right)+{\nabla }_{\theta }Q\left(\theta \right)\varphi \left(\theta \right).$$

The Stein operator ${\mathcal{B}}_P$ operates on the function $\varphi \left(\theta \right)Q\left(\theta \right)$ and produces a zero mean function ${\mathcal{B}}_P\varphi \left(\theta \right)Q\left(\theta \right)$ under $\theta \sim P$.

Assume mild zero boundary conditions on $\varphi \left(\theta \right)Q\left(\theta \right).$$\forall {\theta }_i$, when $\theta$ is compact, $\theta \subseteq R^d,$ $P\left(\theta \right)\varphi \left(\theta \right)Q\left(\theta \right)\approx 0$. The expectation of ${\mathcal{B}}_Q\varphi \left(\theta \right)Q\left(\theta \right)$ under $\theta \sim Q$ are no longer equal zero. The magnitude of ${\mathbb{E}}_{\theta \sim Q}\left[{\mathcal{B}}_P\varphi \left(\theta \right)Q\left(\theta \right)\right]$ is related with the difference between P and Q. The probability distances $S(Q,P)$ for $P\left(\theta \right)$ and $Q\left(\theta \right)$ in some proper function set ${\mathcal{F}}_{\mathcal{B}}$ are defined as

$$S(Q,P)=\underset{\varphi \in {\mathcal{F}}_{\mathcal{B}}}{max}\left\{{\left[{\mathbb{E}}_{\theta \sim Q}trace\left({\mathcal{B}}_P\varphi \left(\theta \right)Q\left(\theta \right)\right)\right]}^2\right\}.$$

(7)

The discriminative power and computational tractability of the Stein discrepancy are determined by the set ${\mathcal{F}}_{\mathcal{B}}$. ${\mathcal{F}}_{\mathcal{B}}$ includes sets of functions with bounded Lipschitz norms, each of which is a difficult and intractable functional optimization problem with special considerations. To tackle this trouble of calculation, $Q\left(\theta \right)$ and $\varphi \left(\theta \right)$ are selected in the unit sphere of a reproducing kernel Hilbert space (RKHS) [32]. Kernelized Stein discrepancy (KSD) between $P\left(\theta \right)$ and $Q\left(\theta \right)$ is described as

$$S(Q,P)=\underset{\varphi \in {\mathcal{H}}^d}{max}{\left[E_{x\sim Q}(trace\left({\mathcal{B}}_P\varphi \left(\theta \right)Q\left(\theta \right)\right))\right]}^2,$$

(8)

$${\mathrm{s}.\mathrm{t}.\left|\varphi \left(\theta \right)Q\left(\theta \right)\right|}_{{\mathcal{H}}^d}\le 1.$$

The optimal solution of (8) is $\psi \left(\theta \right)=\left[{\varphi }_{Q,P}^{\ast }\left(\theta \right)Q\left(\theta \right)\right]/{\left|{\varphi }_{Q,P}^{\ast }Q\left(\theta \right)\right|}_{{\mathcal{H}}^d}$ where

$${\psi }_{Q,P}^{\ast }(·)={\mathbb{E}}_{\theta \sim Q}\left[{\mathcal{B}}_P\mathbf{k}(\theta ,·)Q\left(\theta \right)\right].$$

(9)

A direct calculation shows that

$$S(Q,P)=|{\psi }_{Q,P}^{\ast 2}{|}_{{\mathcal{H}}^d}.$$

(10)

For any fixed ${\theta }^{\prime }$, kernel function $\mathbf{k}\left(\theta ,·\right)$ belongs to RKHS. $S(Q,P)$ =0, that is to say ${\psi }_{Q,P}^{\ast }\left(\theta \right)\equiv 0$ only if $P\left(\theta \right)=Q\left(\theta \right)$. The radial basis function $\left(\mathrm{RBF}\right)$ kernel $\mathbf{k}\left(\theta ,{\theta }^{\prime }\right)=exp\left(-\frac{1}{h}{∥\theta -{\theta }^{\prime }∥}_2^2\right)$ is purely positive definite in a strict sense. When ${\theta }^{\prime }$ approaches $\theta$, the $\mathrm{RBF}$ converges to 1. Then, $S(Q,P)$ contains the information of parameter approximation, which is an important factor affecting the accuracy of parameters $\theta$. For convenience, we define $T_j={\psi }_{Q,P}^{\ast }(·)$ and $K({\theta }_j,·)=\mathbf{k}({\theta }_j,·)Q\left({\theta }_j\right)$. $Q\left({\theta }_j\right)$ and $P\left({\theta }_j\right)$ are from the Gaussian distribution with different hyperparameters. $Q\left({\theta }_j\right)$ is defined as follows

$$Q\left({\theta }_j\right|{\tau }_j)\propto exp\left[-\frac{1}{2{\tau }_j}{\theta }_j^T{\theta }_j\right].$$

By subtracting $Q\left({\theta }_j\right|{\tau }_j)$ and $\mathbf{k}({\theta }_j,·)$ into $K({\theta }_j,·),$ we have

$$K({\theta }_j,·)\propto exp\left[-\frac{1}{h}{({\theta }_j-{\theta }_0)}^T({\theta }_j-{\theta }_0)\right].$$

Based on $K({\theta }_j,·)$, we have

$${\nabla }_{\theta }K({\theta }_j,·)\propto -\frac{2}{h}({\theta }_j-{\theta }_0)exp\left[-\frac{1}{h}{({\theta }_j-{\theta }_0)}^T({\theta }_j-{\theta }_0)\right].$$

According to the results, $T_j$ is written as

$$\begin{array}{cc}\hfill T_j& =K({\theta }_j,·)·{\nabla }_{{\theta }_j}logP\left({\theta }_j\right|{\alpha }_j)+{\nabla }_{\theta }K({\theta }_j,·)\hfill \\ \hfill & =-\frac{1}{{\alpha }_j}{\theta }_{j}exp\left[-\frac{1}{h}{({\theta }_j-{\theta }_0)}^T({\theta }_j-{\theta }_0)\right]\hfill \\ \hfill & -\frac{2}{h}({\theta }_j-{\theta }_0)exp\left[-\frac{1}{h}{({\theta }_j-{\theta }_0)}^T({\theta }_j-{\theta }_0)\right]\hfill \\ \hfill & \le -\frac{1}{{\alpha }_j}{\theta }_{j}exp\left[-\frac{1}{h}{\theta }_j{}^T{\theta }_j\right]-\frac{2}{h}{\theta }_{j}exp\left[-\frac{1}{h}{({\theta }_j-{\theta }_0)}^T({\theta }_j-{\theta }_0)\right]\hfill \\ \hfill & =-(\frac{1}{{\alpha }_j}+\frac{2}{h}){\theta }_{j}exp\left[-\frac{1}{h}{\theta }_j{}^T{\theta }_j\right].\hfill \end{array}$$

It is easy to derive the expectation of $T_j$

$$\begin{array}{cc}\hfill \mathbb{E}\left[T_j\right]& ={\displaystyle \int }-(\frac{1}{{\alpha }_j}+\frac{2}{h}){\theta }_{j}exp\left[-\frac{1}{h}{\theta }_j{}^T{\theta }_j\right]exp\left[-\frac{1}{2{\tau }_j}{\theta }_j^T{\theta }_j\right]d{\theta }_j\hfill \\ \hfill & ={\displaystyle \int }-(\frac{1}{{\alpha }_j}+\frac{2}{h}){\theta }_{j}exp\left[-(\frac{1}{h}+\frac{1}{2{\tau }_j}){\theta }_j{}^T{\theta }_j\right]d{\theta }_j\hfill \\ \hfill & =\frac{\frac{1}{{\alpha }_j}+\frac{2}{h}}{\frac{1}{{\tau }_j}+\frac{2}{h}}exp\left[-(\frac{1}{h}+\frac{1}{2{\tau }_j}){\theta }_j{}^T{\theta }_j\right].\hfill \end{array}$$

For convenience, let $\xi \left({\alpha }_j\right)=\frac{\frac{1}{{\alpha }_j}+\frac{2}{h}}{\frac{1}{{\tau }_j}+\frac{2}{h}}$, we have

$$\mathbb{E}\left[T_j\right]=\xi \left({\alpha }_j\right)exp\left[-(\frac{1}{h}+\frac{1}{2{\tau }_j}){\theta }_j{}^T{\theta }_j\right].$$

(11)

Putting every $\mathbb{E}\left[T_j\right]$ together, we obtain the following result:

$$\mathbb{E}\left[T\right]={\displaystyle \prod }\mathbb{E}\left[T_j\right].$$

Based on the (11), we see that $\mathbb{E}\left[T\right]$ is non-convex objective function in the $\alpha$-space. The optimisation problem is described as

$$\widehat{\alpha }=\underset{\alpha \ge 0}{argmin}\mathbb{E}\left[T\right].$$

(12)

Remark 1.

Stein method is improved and kernel function $\mathbf{k}\left(\theta ,{\theta }^{\prime }\right)$ is also from Stein class ${\mathcal{F}}_{\mathcal{B}}$, but the dynamic characteristics of proposed function $Q\left(\theta \right)$ is considered in the designing of ${\mathcal{B}}_P$ operator for the approximation of $P\left(\theta \right)$ in the unit sphere of RKHS. The new ${\mathcal{B}}_P$ operator can increase the chance to jump out of the local non-convex optimum. In the optimization problem, $\mathbb{E}\left[T\right]$ is a new objective function, which can accelerate approaching speed between $P\left(\theta \right)$ and $Q\left(\theta \right).$

4.2. Parameter Sparse Identification of Constraints from Data

In (12), $\mathbb{E}\left[T\right]$ is another objective function, which makes the parameter $\alpha$ less sensitive to noisy data and converges to true value. The problem of system identification with convex constraints is given by a sparse Bayesian formulation, which is then handled as a non-convex optimisation problem in this section. To obtain a better parameter $\alpha$, the new objective function is constructed as

$$\widehat{\alpha }\underset{\alpha \ge 0}{=argmax}(1/\mathbb{E}\left[T\right])\int P(\mathbf{Y}\mid \theta )\prod _{j=1}^n\mathcal{N}\left({\theta }_j\mid 0,{\alpha }_j\right)\phi \left({\alpha }_j\right)d\theta .$$

(13)

4.2.1. Objective Function in Parameter Identification

Theorem 1.

Use the notation ${\mathcal{J}}_{\alpha }\left(\alpha \right)$ as the objective function

$$\begin{array}{cc}\hfill {\mathcal{J}}_{\alpha }\left(\alpha \right)& =log\left|\lambda \mathbf{I}+\mathbf{F}\mathsf{\Lambda }{\mathbf{F}}^{\top }\right|\hfill \\ \hfill & +{\mathbf{Y}}^{\top }{\left(\lambda \mathbf{I}+\mathbf{F}\mathsf{\Lambda }{\mathbf{F}}^{\top }\right)}^{-1}\mathbf{Y}+\sum _{j=1}^{N}p\left({\alpha }_j\right)\hfill \\ \hfill & -2\sum _{j=1}^N(\frac{1}{h}+\frac{1}{2{\tau }_j}){\theta }_j^T{\theta }_j-2log\xi \left({\alpha }_j\right).\hfill \end{array}$$

(14)

By minimising ${\mathcal{J}}_{\alpha }\left(\alpha \right)$, the optimal hyperparameters $\widehat{\alpha }$ in (13) is derived, where $p\left({\alpha }_j\right)=-2log\phi \left({\alpha }_j\right)$. The mean of $\theta$ is calculated and represented as $\widehat{\theta }=\widehat{\mathsf{\Lambda }}{\mathbf{F}}^{\top }{\left(\lambda \mathbf{I}+\mathbf{F}\widehat{\mathsf{\Lambda }}{\mathbf{F}}^{\top }\right)}^{-1}\mathbf{Y}$.

Proof. 

Using the Woodbury inversion identity, re-express $m_{\theta }$ and ${\mathsf{\Sigma }}_{\theta }$ in (4):

$$\begin{array}{cc}\hfill {\mathrm{m}}_{\theta }& =\mathsf{\Lambda }{\mathbf{F}}^{\top }{\left(\lambda \mathrm{I}+\mathbf{F}\mathsf{\Lambda }{\mathbf{F}}^{\top }\right)}^{-1}\mathrm{Y}=\frac{1}{\lambda }{\mathsf{\Sigma }}_{\theta }^{\top }\mathbf{F}\mathrm{Y}\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill & {\mathsf{\Sigma }}_{\theta }=\mathsf{\Lambda }-\mathsf{\Lambda }{\mathbf{F}}^{\top }{\left(\lambda \mathrm{I}+\mathbf{F}\mathsf{\Lambda }{\mathbf{F}}^{\top }\right)}^{-1}\mathbf{F}\mathsf{\Lambda }\hfill \\ \hfill & ={\left({\mathsf{\Lambda }}^{-1}+\frac{1}{\lambda }{\mathbf{F}}^{\top }\mathbf{F}\right)}^{-1}.\hfill \end{array}$$

(16)

Since the data likelihood P$(\mathbf{Y}\mid \theta )$ is Gaussian, we can express the integral in (13) as follow:

$$(1/\mathbb{E}\left[T\right])\int \mathcal{N}(\mathbf{Y}\mid \mathbf{F}\theta ,\lambda \mathbf{I})\prod _{j=1}^N\mathcal{N}\left({\theta }_j\mid 0,{\alpha }_j\right)\phi \left({\alpha }_j\right)d\theta$$

(17)

$$=(1/\mathbb{E}\left[T\right]){\left(\frac{1}{2\pi \lambda }\right)}^{M/2}{\left(\frac{1}{2\pi }\right)}^{N/2}\int exp\{-E\left(\theta \right)\}d\theta \prod _{j=1}^N\frac{\phi \left({\alpha }_j\right)}{\sqrt{{\alpha }_j}},$$

where

$$\begin{array}{cc}\hfill E\left(\theta \right)& =\frac{1}{2\lambda }{\parallel \mathbf{Y}-\mathbf{F}\theta \parallel }^2+\frac{1}{2}{\theta }^{\top }{\mathsf{\Lambda }}^{-1}\theta \hfill \\ \hfill & =\frac{1}{2}{\left(\theta -{\mathbf{m}}_{\theta }\right)}^{\top }{\mathsf{\Sigma }}_{\theta }^{-1}\left(\theta -{\mathbf{m}}_{\theta }\right)+E\left(\mathbf{Y}\right).\hfill \end{array}$$

(18)

We obtain $E\left(\mathbf{Y}\right)$ using the Woodbury inversion identity.

$$\begin{array}{cc}\hfill E\left(\mathbf{Y}\right)& =\frac{1}{2}\left(\frac{1}{\lambda }{\mathbf{Y}}^{\top }\mathbf{Y}-\frac{1}{\lambda }{\mathbf{Y}}^{\top }\mathbf{F}{\mathsf{\Sigma }}_{\theta }{\mathsf{\Sigma }}_{\theta }^{-1}{\mathsf{\Sigma }}_{\theta }{\mathbf{F}}^{\top }\mathbf{Y}\frac{1}{\lambda }\right)\hfill \\ \hfill & =\frac{1}{2}{\mathbf{Y}}^{\top }{\left(\lambda \mathbf{I}+\mathbf{F}\mathsf{\Lambda }{\mathbf{F}}^{\top }\right)}^{-1}\mathbf{Y}.\hfill \end{array}$$

(19)

Just for the sake of calculation, we evaluate the integral of $exp\{-E(\theta \left)\right\}$ as follows

$$\int exp\{-E\left(\theta \right)\}d\theta =exp\{-E\left(\mathbf{Y}\right)\}{\left(2\pi \right)}^{N/2}{\left|{\mathsf{\Sigma }}_{\theta }\right|}^{1/2}.$$

Then, applying a $-2log(·)$ transformation to (17), we have

$$\begin{array}{cc}\hfill & -2log\int P(\mathbf{Y}\mid \theta )\prod _{j=1}^n\mathcal{N}\left({\theta }_j\mid 0,{\alpha }_j\right)\phi \left({\alpha }_j\right)d\theta -2log\mathbb{E}\left[T\right]\hfill \\ \hfill =& -log\left|{\mathsf{\Sigma }}_{\theta }\right|+Mlog2\pi \lambda +log\left|\mathsf{\Lambda }\right|+{\mathbf{Y}}^{\top }{\left(\lambda \mathbf{I}+\mathbf{F}\mathsf{\Lambda }{\mathbf{F}}^{\top }\right)}^{-1}\mathbf{Y}\hfill \\ \hfill & +\sum _{j=1}^{N}p\left({\alpha }_j\right)-2\sum _{j=1}^N(\frac{1}{h}+\frac{1}{2{\tau }_j}){\theta }_j^T{\theta }_j-2\sum _{j=1}^{N}log\xi \left({\alpha }_j\right)\hfill \\ \hfill =& log\left|\lambda \mathbf{I}+\mathbf{F}\mathsf{\Lambda }{\mathbf{F}}^{\top }\right|+Mlog2\pi +{\mathbf{Y}}^{\top }{\left(\lambda \mathbf{I}+\mathbf{F}\mathsf{\Lambda }{\mathbf{F}}^{\top }\right)}^{-1}\mathbf{Y}\hfill \\ \hfill & +\sum _{j=1}^{N}p\left({\alpha }_j\right)-2\sum _{j=1}^N(\frac{1}{h}+\frac{1}{2{\tau }_j}){\theta }_j^T{\theta }_j-2\sum _{j=1}^{N}log\xi \left({\alpha }_j\right),\hfill \end{array}$$

where $\left|{\mathsf{\Lambda }}^{-1}\parallel \lambda \mathbf{I}+\mathbf{F}\mathsf{\Lambda }{\mathbf{F}}^{\top }\right|=\left|\lambda \mathbf{I}\right|\left|{\mathsf{\Lambda }}^{-1}+\frac{1}{\lambda }{\mathbf{F}}^{\top }\mathbf{F}\right|$, $log\left|\lambda \mathrm{I}+\mathbf{F}\mathsf{\Lambda }{\mathbf{F}}^{\top }\right|=-log\left|{\mathsf{\Sigma }}_{\theta }\right|+Mlog\lambda +log\left|\mathsf{\Lambda }\right|.$ From (13), we then obtain

$$\begin{array}{cc}\hfill \widehat{\alpha }& =arg\underset{\alpha \ge 0}{min}(log\left|\lambda \mathbf{I}+\mathbf{F}\mathsf{\Lambda }{\mathbf{F}}^{\top }\right|+{\mathbf{Y}}^{\top }{\left(\lambda \mathbf{I}+\mathbf{F}\mathsf{\Lambda }{\mathbf{F}}^{\top }\right)}^{-1}\mathbf{Y}\hfill \\ \hfill & +\sum _{j=1}^{N}p\left({\alpha }_j\right)-2\sum _{j=1}^N(\frac{1}{h}+\frac{1}{2{\tau }_j}){\theta }_j^T{\theta }_j-2log{\xi }_j\left({\alpha }_j\right)).\hfill \end{array}$$

(20)

To acquire an approximation of $\theta$, we compute the posterior

mean $\theta :\widehat{\theta }=\mathbb{E}(\theta \mid \mathbf{Y};\widehat{\alpha })=\mathsf{\Lambda }{\mathbf{F}}^{\top }{\left(\lambda \mathrm{I}+\mathbf{F}\widehat{\mathsf{\Lambda }}{\mathbf{F}}^{\top }\right)}^{-1}\mathbf{Y}$.

Remark 2.

In (13), the objective function of recursive least squares estimation with L1-regularization is developed, which is integrated into the objective function of Stein approximation. The new one contains more information and can captures more important information from the raw date. We can obtain the relative good parameter probability distribution.

Lemma 1.

${\mathcal{J}}_{\alpha }\left(\alpha \right)$ in (14) is non-convex function.

Proof of Lemmma 1.

The data-dependent term ${\mathbf{Y}}^{\top }{\left(\lambda \mathbf{I}+\mathbf{F}\mathsf{\Lambda }{\mathbf{F}}^{\top }\right)}^{-1}\mathbf{Y}$ in (14) is studied. By (15) and (16), it can be transformed as

$$\begin{array}{cc}\hfill & {\mathbf{Y}}^{\top }{\left(\lambda \mathbf{I}+\mathbf{F}\mathsf{\Lambda }{\mathbf{F}}^{\top }\right)}^{-1}\mathbf{Y}\hfill \\ \hfill =& \frac{1}{\lambda }{\mathbf{Y}}^{\top }\mathbf{Y}-\frac{1}{\lambda }{\mathbf{Y}}^{\top }\mathbf{F}{\mathsf{\Sigma }}_{\theta }{\mathbf{F}}^{\top }\frac{1}{\lambda }\mathbf{Y}\hfill \\ \hfill =& \frac{1}{\lambda }{∥\mathbf{Y}-{\mathbf{Fm}}_{\theta }∥}_2^2+{\mathbf{m}}_{\theta }^{\top }{\mathsf{\Lambda }}^{-1}{\mathbf{m}}_{\theta }\hfill \\ \hfill =& \underset{\mathbf{x}}{min}\left\{\frac{1}{\lambda }{\parallel \mathbf{Y}-\mathbf{Fx}\parallel }_2^2+{\mathbf{x}}^{\top }{\mathsf{\Lambda }}^{-1}\mathbf{x}\right\}.\hfill \end{array}$$

(21)

The minimisation issue is simply demonstrated to be convex in $\theta$ and $\alpha$ dimensions. Define $\rho \left(\alpha \right)\triangleq log\left|\lambda \mathbf{I}+\mathbf{F}\mathsf{\Lambda }{\mathbf{F}}^{\top }\right|+{\sum }_{j=1}^{N}p\left({\alpha }_j\right)-2{\sum }_{j=1}^{N}log\xi \left({\alpha }_j\right)$. $log\left|x\right|$ is concave function. Furthermore, $\lambda \mathrm{I}+\mathbf{F}\mathsf{\Lambda }{\mathbf{F}}^{\top }$ is an affine function of $\alpha$. When $\alpha \ge 0,$ it is positive semi-definite. This means $log\left|\lambda \mathbf{I}+\mathbf{F}\mathsf{\Lambda }{\mathbf{F}}^{\top }\right|$ is a concave non-decreasing function of $\alpha$. We can see that $\rho \left(\alpha \right)$ is a concave function with respect to $\alpha$.

4.2.2. Modified Objective Function in $\theta$ Estimation

We use the modified objective function of $\theta$ with a penalty function. By analyzing the corresponding objective function of (14) in the $\alpha$ space, the analogous objective function is subsequently shown to be non-convex as well.

Theorem 2.

Solving the optimisation problem below yields the estimated value for θ given restrictions.

$$\underset{\theta }{min}{\parallel \mathbf{Y}-\mathbf{F}\theta \parallel }_2^2+\lambda r\left(\theta \right),$$

where penalty function $r\left(\theta \right)={min}_{\alpha \ge 0}{\theta }^{\top }{\mathsf{\Lambda }}^{-1}\theta +log\left|\lambda \mathbf{I}+\mathbf{F}\mathsf{\Lambda }{\mathbf{F}}^{\top }\right|+{\sum }_{j=1}^{N}p\left({\alpha }_j\right)-2{\sum }_{j=1}^N(\frac{1}{h}+\frac{1}{2{\alpha }_j}){\theta }_j^T{\theta }_j-2{\sum }_{j=1}^{N}log\xi \left({\alpha }_j\right)$.

Proof of Theorem 2.

Using the data-dependent term in $\left(21\right)$ and ${\mathcal{J}}_{\alpha }\left(\alpha \right)$ in (14), a stringent upper boundary auxiliary function can be created on ${\mathcal{J}}_{\alpha }\left(\alpha \right)$ as

$$\begin{array}{cc}\hfill {\mathcal{J}}_{\alpha ,\theta }(\alpha ,\theta )& =\frac{1}{\lambda }{\parallel \mathbf{Y}-\mathbf{F}\theta \parallel }_2^2+{\theta }^{\top }{\mathsf{\Lambda }}^{-1}\theta +log\left|\lambda \mathbf{I}+\mathbf{F}\mathsf{\Lambda }{\mathbf{F}}^{\top }\right|\hfill \\ \hfill & +\sum _{j=1}^{N}p\left({\alpha }_j\right)-2\sum _{j=1}^N(\frac{1}{h}+\frac{1}{2{\tau }_j}){\theta }_j^T{\theta }_j-2\sum _{j=1}^{N}log\xi \left({\alpha }_j\right).\hfill \end{array}$$

When we minimise ${\mathcal{J}}_{\alpha ,\theta }(\alpha ,\theta )$ over $\alpha$ and obtain

$$\begin{array}{cc}\hfill {\mathcal{J}}_{\theta }\left(\theta \right)& \triangleq \underset{\alpha \ge 0}{min}{\mathcal{J}}_{\alpha ,\theta }(\alpha ,\theta )\hfill \\ \hfill & =\frac{1}{\lambda }{\parallel \mathbf{Y}-\mathbf{F}\theta \parallel }_2^2+\underset{\alpha \ge 0}{min}({\theta }^{\top }{\mathsf{\Lambda }}^{-1}\theta +log\left|\lambda \mathbf{I}+\mathbf{F}\mathsf{\Lambda }{\mathbf{F}}^{\top }\right|\hfill \\ \hfill & +\sum _{j=1}^{N}p\left({\alpha }_j\right)-2\sum _{j=1}^N(\frac{1}{h}+\frac{1}{2{\tau }_j}){\theta }_j^T{\theta }_j-2\sum _{j=1}^{N}log\xi \left({\alpha }_j\right)).\hfill \end{array}$$

(22)

From the derivations in (21), we can see that the posterior mean ${\mathrm{m}}_{\theta }$ is the estimate of the parameter $\theta$.

Lemma 2.

In Theorem 2, the penalty function $r\left(\theta \right)$ promotes sparsity on the weights by being a non-decreasing concave function of θ.

Proof of Lemma 2.

It is obvious that $\rho \left(\alpha \right)$ in Lemma 1 is concave. Using the duality lemma (see Section 4.2 in [35]), $\rho \left(\alpha \right)$ is denoted as ${min}_{{\alpha }^{\ast }\ge 0}⟨{\alpha }^{\ast },\alpha ⟩-{\rho }^{\ast }\left({\alpha }^{\ast }\right)$, where ${\rho }^{\ast }\left({\alpha }^{\ast }\right)$ is defined as the concave conjugate of $\rho \left(\alpha \right)$ and ${\rho }^{\ast }\left({\alpha }^{\ast }\right)={min}_{\alpha \ge 0}⟨{\alpha }^{\ast },\alpha ⟩-\rho \left(\alpha \right)$. By (21), function ${\mathcal{J}}_{\alpha ,\theta }(\alpha ,\theta )$ can be re-written as

$$\begin{array}{cc}\hfill {\mathcal{J}}_{\alpha ,\theta }(\alpha ,\theta )& \triangleq ⟨{\alpha }^{\ast },\alpha ⟩-{\rho }^{\ast }\left({\alpha }^{\ast }\right)+{\mathbf{Y}}^{\top }{\left(\lambda \mathrm{I}+\mathbf{F}\mathsf{\Lambda }{\mathbf{F}}^{\top }\right)}^{-1}\mathbf{Y}\hfill \\ \hfill & =\frac{1}{\lambda }{\parallel \mathbf{Y}-\mathbf{F}\theta \parallel }_2^2+\sum _j\left(\frac{{\theta }_j^2}{{\alpha }_j-\frac{2}{h}-\frac{1}{{\tau }_j}}+{\alpha }_j^{\ast }{\alpha }_j\right)-{\rho }^{\ast }\left({\alpha }^{\ast }\right).\hfill \end{array}$$

(23)

$r\left(\theta \right)$ is re-expressed as

$$r\left(\theta \right)=\underset{\alpha ,\alpha \ast \ge 0}{min}\left\{\sum _j(\frac{{\theta }_j^2}{{\alpha }_j-\frac{2}{h}-\frac{1}{{\tau }_j}}+{\alpha }_j^{\ast }{\alpha }_j)-{\rho }^{\ast }\left({\alpha }^{\ast }\right)\right\}.$$

(24)

It is easy to see that when ${\alpha }_j=\frac{1}{2}\sqrt{{(\frac{2}{h}+\frac{1}{{\tau }_j})}^2+\frac{4{\theta }_j^2}{{\alpha }_j^{\ast }}}+(\frac{1}{h}+\frac{2}{{\tau }_j})$, $r\left(\theta \right)$ reaches the minimum over $\alpha$. Substitute ${\alpha }_j$ into $r\left(\theta \right)$

$$r\left(\theta \right)=\underset{\alpha \ast \ge 0}{min}\left\{\sum _{j}2\sqrt{\frac{{\alpha }_j}{{\alpha }_j-\frac{2}{h}-\frac{1}{{\tau }_j}}{\alpha }_j^{\ast }}\left|{\theta }_j\right|-{\rho }^{\ast }\left({\alpha }^{\ast }\right)\right\}.$$

(25)

When $r\left(\theta \right)$ is minimum, $\theta$ is much more sparse. From (26), $r\left(\theta \right)$ is non-decreasing concave function of $\theta$.

4.2.3. Parameter Estimation with Sparse Method

From (23), we can see that ${\rho }^{\ast }\left({\alpha }^{\ast }\right)$ does not affect the estimation of parameters $\alpha$, so ${\mathcal{J}}_{\alpha ,\theta }(\alpha ,\theta )$ is redefined as

$${\mathcal{J}}_{{\alpha }^{\ast }}(\alpha ,\theta )\triangleq \frac{1}{\lambda }{\parallel \mathbf{Y}-\mathbf{F}`\parallel }_2^2+\sum _j(\frac{{\theta }_j^2}{{\alpha }_j-\frac{2}{h}-\frac{1}{{\tau }_j}}+{\alpha }_j^{\ast }{\alpha }_j).$$

(26)

For a fixed ${\alpha }^{\ast }$, we notice that ${\mathcal{J}}_{{\alpha }^{\ast }}(\alpha ,\theta )$ is jointly convex in $\theta$ and $\alpha$. In (27), we can obtain $\frac{{\theta }_j^2}{{\alpha }_j-\frac{2}{h}-\frac{1}{{\tau }_j}}+{\alpha }_j^{\ast }{\alpha }_j\ge 2\sqrt{\frac{{\alpha }_j}{{\alpha }_j-\frac{2}{h}-\frac{1}{{\tau }_j}}{\alpha }_j^{\ast }}{\theta }_j$. When ${\alpha }_j=\frac{1}{2}\sqrt{{(\frac{2}{h}+\frac{1}{{\tau }_j})}^2+\frac{4{\theta }_j^2}{{\alpha }_j^{\ast }}}+(\frac{1}{h}+\frac{2}{{\tau }_j})$, ${\mathcal{J}}_{{\alpha }^{\ast }}(\alpha ,\theta )$ is minimized for any $\theta$. Substitute the ${\alpha }_j$ into ${\mathcal{J}}_{{\alpha }^{\ast }}(\alpha ,\theta )$, $\widehat{\theta }$ can be obtained as follows:

$$\widehat{\theta }=\underset{\theta }{argmin}\left\{{\parallel \mathbf{Y}-\mathbf{F}\theta \parallel }_2^2+2\lambda \sum _{j=1}^N\sqrt{\frac{{\alpha }_j}{{\alpha }_j-\frac{2}{h}-\frac{1}{{\tau }_j}}{\alpha }_j^{\ast }}\left|{\theta }_j\right|\right\}.$$

(27)

Due to the concavity of $r\left(\theta \right)$, the objective function in Theorem 2 can be optimised using a re-weighted $L_1$-minimisation in a similar kth way as was considered in (27).

In order to obtain more stable and accurate parameter $\widehat{\theta }$, the re-estimated method is put forward (Algorithm 1). At k-th iteration, the modified weight is then supplied by:

$$u_j^{\left(k\right)}\triangleq {\frac{\partial r\left(\theta \right)}{2\partial \left|{\theta }_j\right|}}_{\theta ={\theta }^{\left(k\right)}}={\eta }_j·\sqrt{{\alpha }_j^{\ast }},$$

(28)

where ${\eta }_j=\sqrt{\frac{{\alpha }_j}{{\alpha }_j-\frac{2}{h}-\frac{1}{{\tau }_j}}}.$ On the basis of the aforementioned, we can now describe how the parameters can be updated. To begin, we set the iteration count k to zero, $u_j^{\left(0\right)}=1$ and initialise

$${\eta }_j^{(k+1)}=\sqrt{\frac{{\alpha }_j^{\left(k\right)}}{{\alpha }_j^{\left(k\right)}-\frac{2}{h}-\frac{1}{{\tau }_j^{\left(k\right)}}}}.$$

(29)

Algorithm 1: Non-linear state-space identification algorithm with sparse Bayesian and Stein approach (NSSI-SBSA)

Input: 1: Generate time series data from the system of discrete-time dynamics characterized by (1) 2: Choose the dictionary functions that will be used to build the dictionary matrix   mentioned in Section 2;   $u_j^0=1$,${\alpha }_j^{\left(k\right)},h,{\tau }_j^{\left(k\right)},$ stopping threshold $\epsilon$ 3: for $k=0,1,\cdots$ do 4:   Solve the minimisation problem with L1-regularization and optimization method on $\theta$. $$\underset{\theta }{argmin}\left\{{\parallel \mathbf{Y}-\mathbf{F}\theta \parallel }_2^2+2\lambda \sum _{j=1}^N\sqrt{\frac{{\alpha }_j}{{\alpha }_j-\frac{2}{h}-\frac{1}{{\tau }_j}}{\alpha }_j^{\ast }}\left|{\theta }_j^{}\right|\right\}$$ 5:   Update parameter ${\eta }_j^{(k+1)}$ and $u_j^{(k+1)}$ in (28) and (29). 6:   $u_j^{(k+1)}\triangleq {\eta }_j^{(k+1)}·\sqrt{{\alpha }_j^{\ast (k+1)}}$ 7:   Update parameter ${\alpha }_j^{(k+1)}=\frac{1}{2}\sqrt{{(\frac{2}{h}+\frac{1}{{\tau }_j^{\left(k\right)}})}^2+\frac{4{({\theta }_j^{\left(k\right)})}^2}{{\alpha }_j^{\ast \left(k\right)}}}+(\frac{1}{h}+\frac{2}{{\tau }_j^{\left(k\right)}})$ 8: end for 9: if $|\theta -\widehat{\theta }|<\epsilon$ then 10:    Break 11: end if Output:      The sparse weight set of $\widehat{\theta }$.

We obtain $u_j^{\left(k\right)}={\eta }_j^{\left(k\right)}·\sqrt{{\alpha }_j^{\ast \left(k\right)}}$. ${\mathcal{J}}_{\alpha ,\theta }(\alpha ,\theta )$ is considered again. For any fixed $\alpha$ and $\theta$, the tightest bound can be obtained by minimising over ${\alpha }^{\ast }$. ${\alpha }^{\ast }$ is estimated, which equals the gradient of the function $\rho \left(\alpha \right)$ in Lemma 1. The estimation of ${\alpha }^{\ast }$ is computed as

$$\begin{array}{cc}\hfill {\widehat{\alpha }}^{\ast }& ={\nabla }_{\alpha }\rho \left(\alpha \right)\hfill \\ \hfill & =diag\left[{\mathbf{F}}^{\top }{\left(\lambda \mathbf{I}+\mathbf{F}\mathsf{\Lambda }{\mathbf{F}}^{\top }\right)}^{-1}\mathbf{F}\right]+p^{\prime }\left(\alpha \right)-2\zeta \left(\alpha \right),\hfill \end{array}$$

(30)

where $p^{\prime }\left(\alpha \right)=$${\left[p^{\prime }\left({\alpha }_1\right),\dots ,p^{\prime }\left({\alpha }_N\right)\right]}^{\top }$, $\zeta \left(\alpha \right)=$${\left[\frac{{\xi }^{\prime }\left({\alpha }_1\right)}{{\xi }^{\prime }\left({\alpha }_1\right)},\dots ,\frac{{\xi }^{\prime }\left({\alpha }_N\right)}{{\xi }^{\prime }\left({\alpha }_N\right)}\right]}^{\top }$. The optimal ${\alpha }^{\ast (k+1)}$ can then be replaced by ${\widehat{\alpha }}^{\ast (k+1)}=diag\left[{\mathbf{F}}^{\top }{\left(\lambda \mathrm{I}+\mathbf{F}{\mathsf{\Lambda }}^{\left(k\right)}{\mathbf{F}}^{\top }\right)}^{-1}\mathbf{F}\right]+$$p^{\prime }\left({\alpha }^{\left(k\right)}\right)-2\zeta \left(\alpha \right).$ After computing the estimation of

$${\alpha }_j=\frac{1}{2}\sqrt{{(\frac{2}{h}+\frac{1}{{\tau }_j})}^2+\frac{4{\theta }_j^2}{{\alpha }_j^{\ast }}}+(\frac{1}{h}+\frac{2}{{\tau }_j}),$$

(31)

we can compute ${\alpha }_j^{\ast (k+1)}$, which gives

$${\alpha }_j^{\ast (k+1)}={\mathbf{F}}_j^{\top }{\left(\lambda \mathbf{I}+{\mathbf{F}}_j{\mathsf{\Lambda }}^{\left(k\right)}{\mathbf{F}}_j^{\top }\right)}^{-1}{\mathbf{F}}_j+p^{\prime }\left({\alpha }_j^{\left(k\right)}\right)-2\zeta \left({\alpha }_j^{\left(k\right)}\right)$$

${\alpha }_j^{(k+1)}$ can be defined

$${\alpha }_j^{(k+1)}=\frac{1}{2}\sqrt{{(\frac{2}{h}+\frac{1}{{\tau }_j^{\left(k\right)}})}^2+\frac{4{({\theta }_j^{\left(k\right)})}^2}{{\alpha }_j^{\ast \left(k\right)}}}+(\frac{1}{h}+\frac{2}{{\tau }_j^{\left(k\right)}}).$$

Substitute ${\alpha }_j^{(k+1)}$ and ${\alpha }_j^{\ast (k+1)}$ into (27). Certain weights ${\eta }_j$ are estimated at each iteration k until $|\theta -\widehat{\theta }|<\epsilon$, where $\epsilon$ is stopping threshold. Algorithm 1 summarizes the above-mentioned procedure.

5. Numerical Example

All examples are conducted on a computer with an Intel Core i7-6500U CPU@2.50-GHz and 16 GB of RAM. CVX package is used to solve convex programs in MATLAB2016 platform. We will give three numerical examples: Narendra-Li Model [20], NARX model [25], and Kernel state-space models [44]. The utility and performance of Algorithm 1 is proven on three simulation cases in this section. The performance of Algorithm 1 on examples is then illustrated involving a well studied and challenging non-linear system. The root mean squared error (RMSE) criterion will be utilized to demonstrate the performance of the suggested identification approach against noise perturbation. The ith estimate of parameter $\theta$ is denoted by ${\widehat{\theta }}_i$ at the Monte Carlo experiment. The RMSE at the experiment is defined as

$$RMSE=\sqrt{\frac{{\sum }_{i=1}^n{({\widehat{\theta }}_i-{\theta }_i^{\ast })}^2}{n-1}}$$

where ${\theta }_i^{\ast }$ represents the true system parameter vector, and n is the trials. To validate the theoretical results, the identification of the structured state-space model in cases will be simulated in this part.

5.1. Example 1: Parameters Identification General Narendra-Li Model

Consider the state space representation of a non-linear system:

$$\begin{array}{cc}\hfill x_{t+1}^1=& \left(\frac{{\alpha }_1{x}_t^1}{1+{\left(x_t^1\right)}^2}+{\alpha }_2\right)sin\left(x_t^2\right)+{\xi }_1\left(t\right)\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill x_{t+1}^2=& {\beta }_1{x}_t^{2}cos\left(x_t^2\right)+{\beta }_2{x}_t^{1}exp\left(-\frac{{\left(x_t^1\right)}^2+{\left(x_t^2\right)}^2}{8}\right)\hfill \\ \hfill & +\frac{{\beta }_3{\left(u_t\right)}^3}{1+{\left(u_t\right)}^2+0.5cos\left(x_t^1+x_t^2\right)}+{\xi }_2\left(t\right)\hfill \\ \hfill y_t=& \frac{x_t^1}{1+0.5sin\left(x_t^2\right)}+\frac{x_t^2}{1+0.5sin\left(x_t^1\right)}\hfill \end{array}$$

(33)

where the state variable $x_t={\left[x_t^1,x_t^2\right]}^{\top }$. ${\xi }_i\left(t\right)$ is Gaussian white noise. To generate the estimation data, the system is excited with a uniformly distributed random input signal $u\left(t\right)\in [-2.5,2.5]$ with $1\le t\le 1000$. The validation dataset is generated with the input

$$u\left(t\right)=sin\frac{2\pi t}{10}+sin\frac{2\pi t}{25},t=1,\dots ,1000.$$

Let ${\mathsf{\Phi }}_1^t=\frac{x_t^1}{1+{\left(x_t^1\right)}^2}sin\left(x_t^2\right),{\mathsf{\Phi }}_2^t=sin\left(x_t^2\right),{\mathsf{\Phi }}_3^t=x_t^{2}cos\left(x_t^2\right),{\mathsf{\Phi }}_4^t=x_t^{1}exp\left(-\frac{{\left(x_t^1\right)}^2+{\left(x_t^2\right)}^2}{8}\right),$${\mathsf{\Phi }}_5^t=\frac{{\beta }_3{\left(u_t\right)}^3}{1+{\left(u_t\right)}^2+0.5cos\left(x_t^1+x_t^2\right)}.$ Because there are two state variables, the dictionary matrix $\mathsf{\Phi }$ can be built as follows:

$$\mathsf{\Phi }=\left[\begin{array}{ccccc}{\mathsf{\Phi }}_1^t& {\mathsf{\Phi }}_2^t& {\mathsf{\Phi }}_3^t& {\mathsf{\Phi }}_4^t& {\mathsf{\Phi }}_5^t\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ {\mathsf{\Phi }}_1^{t+M-1}& {\mathsf{\Phi }}_2^{t+M-1}& {\mathsf{\Phi }}_3^{t+M-1}& {\mathsf{\Phi }}_4^{t+M-1}& {\mathsf{\Phi }}_5^{t+M-1}\end{array}\right]$$

(34)

Then, the state set can be defined as

$${\mathbf{x}}_i\triangleq {\left[x_{t+1}^1,\dots ,x_{t+M}^1\right]}^{\top }\in {\mathbb{R}}^{M\times 1},i=1,2$$

Using the dictionary matrix $\mathsf{\Phi }$ in (34), the true value of parameter $\theta$ for the model in (32), (33) should be as follows:

$${\theta }_{true}=\left[{\theta }^{\left(1\right)},{\theta }^{\left(2\right)}\right]$$

$$=\left[\begin{array}{cc}{\alpha }_1(=4)& 0\\ {\alpha }_2(=3)& 0\\ 0& {\beta }_1(=1.4)\\ 0& {\beta }_2(=1.5)\\ 0& {\beta }_3(=1.6)\end{array}\right]$$

(35)

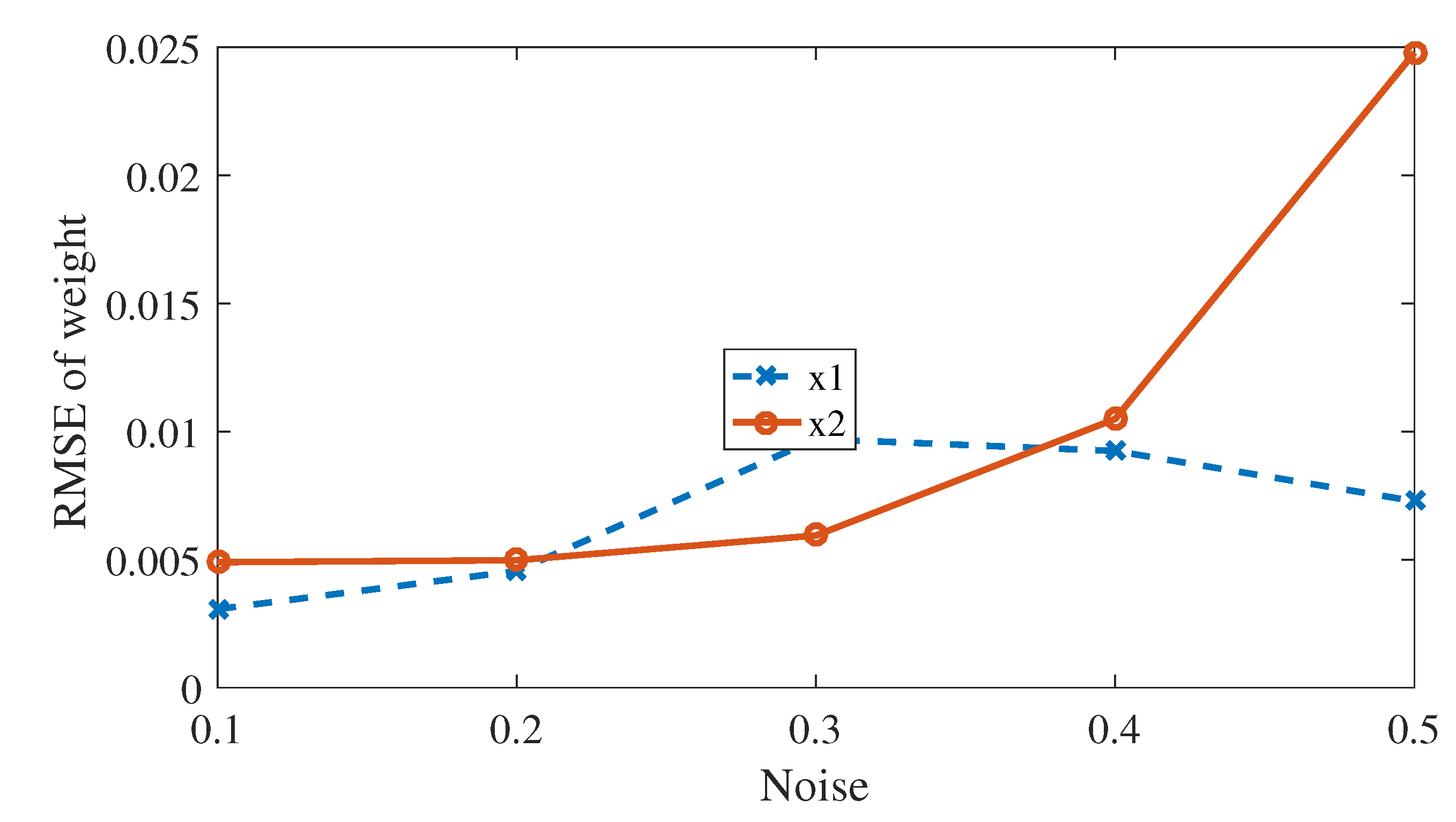
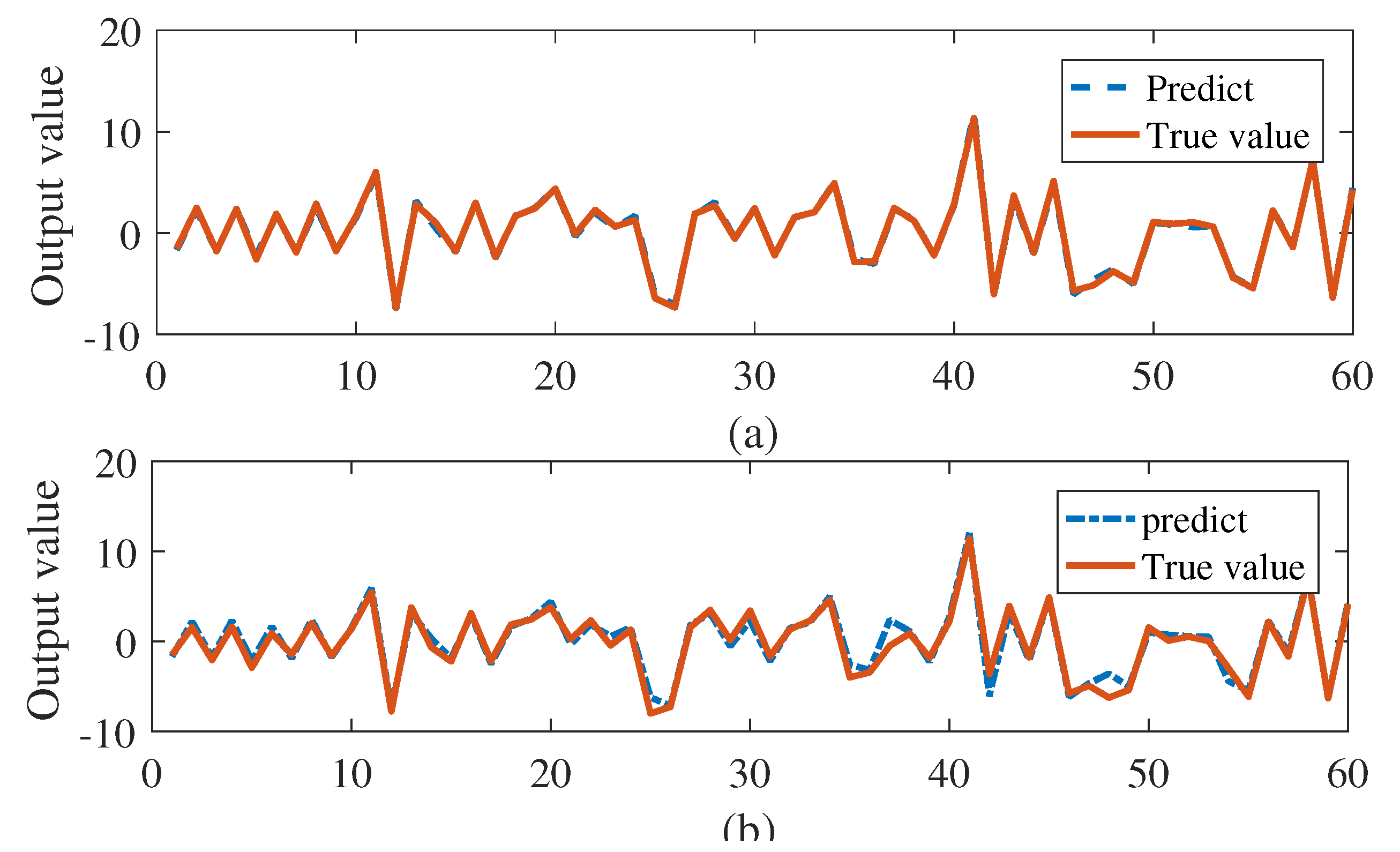
The parameters in bracket are true value. In our study, we use $T=1000$ samples for learning and add white Gaussian measurement noise of ${\xi }_i\left(t\right)=0.1$ to the training data. In (32) and (33), Algorithm 1 is used for identifying parameters. The coefficients ${\theta }^{\left(j\right)}$ is learned from prior data in (35). RMSE of $\theta$ is computed in the simulation, the result of which is $0.039$. When the noise ${\xi }_i\left(t\right)$ are 0.2, 0.3, 0.4, and 0.5, there is little change in the value of RMSE of $\theta$ in Figure 1. Despite using 2000 data points of [20], our method is substantially better than [20] in Table 1. Table 1 compares some previous results reported in the literature [45,46,47] with our method, we can also see that our method perform the best. In this experiment, we also examine how the method performs for various ${\xi }_i\left(t\right)=0.1,0.3$. The last 60 in generated data sequence is selected for testing and the predicting result is compared with the true value. When the Algorithm 1 is executed 8 times, the average of the RMSE of output $y_t$ is 0.06, and is not increased fast from Figure 2.

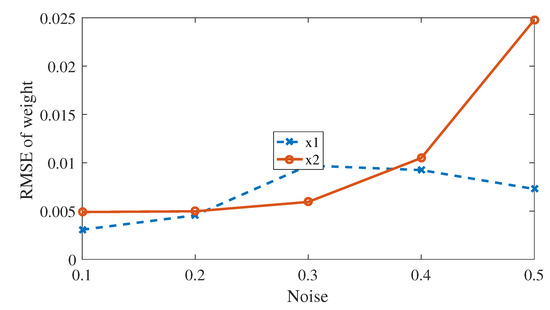
Figure 1. RMSE of state $x_1$ and $x_2$.

Table 1. Accuracy comparison of different methods (${\xi }_i=0.1$).

Method	RMSE	Data
Our paper	0.039	1000
Bayesian Learning [20]	0.06	2000
DWO [45]	$0.43$	50,000
MOD [46]	$0.46$	50,000
AHH [47]	$0.31$	2000
MARS [47]	$0.49$	2000

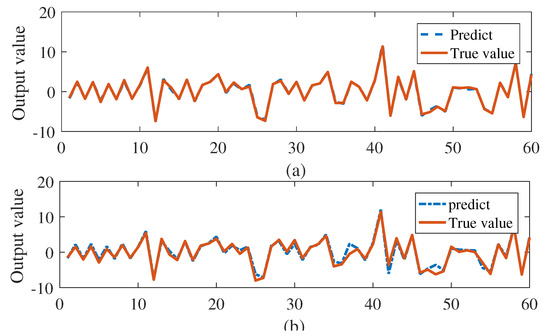
Figure 2. Output of the state mode for 60 testing data in example 1: (a) ${\xi }_i=0.1$ and (b) ${\xi }_i=0.3$.

In general, it is clear that the proposed model is capable enough to well describe the system behavior.

5.2. Example 2: Application to a NARX Model

We analyze the following polynomial terms model for a single-input single-output (SISO) non-linear autoregressive system with exogenous (NARX) input in this example [25].

$$y\left(t_{k+1}\right)=0.7y\left(t_{k-1}\right)-0.5y\left(t_{k-2}\right)+0.6u^2\left(t_{k-2}\right)-0.7y\left(t_{k-2}\right)u\left(t_{k-1}\right)+\xi \left(t_k\right)$$

(36)

with $y,u,\xi \in \mathbb{R}$. In expanded form, we may write (36) as:

$$\begin{array}{cc}\hfill y\left(t_{k+1}\right)& =w_1+w_{2}y\left(t_k\right)+\dots +w_{m_x+2}y\left(t_{k-m_z}\right)+\dots +w_N{y}^{d_x}\left(t_{k-m_z}\right)u^{d_u}\left(t_{k-m_u}\right)+\xi \left(t_k\right)\hfill \\ \hfill & ={\mathbf{w}}^{\top }\mathbf{f}\left(y\left(t_k\right),\dots ,y\left(t_{k-m_x}\right),u\left(t_k\right),\dots ,u\left(t_{k-m_u}\right)\right)+\xi \left(t_k\right)\hfill \end{array}$$

(37)

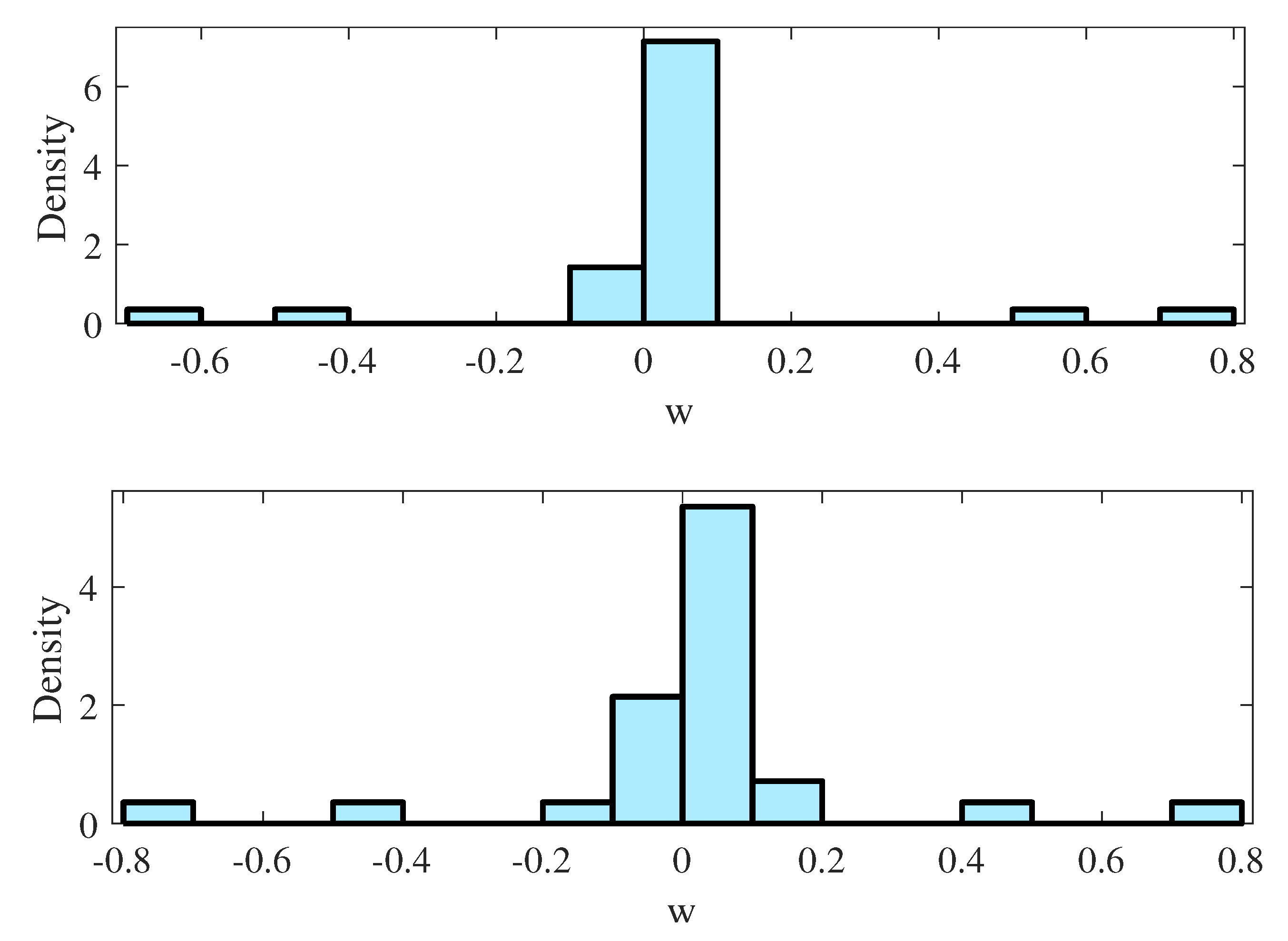
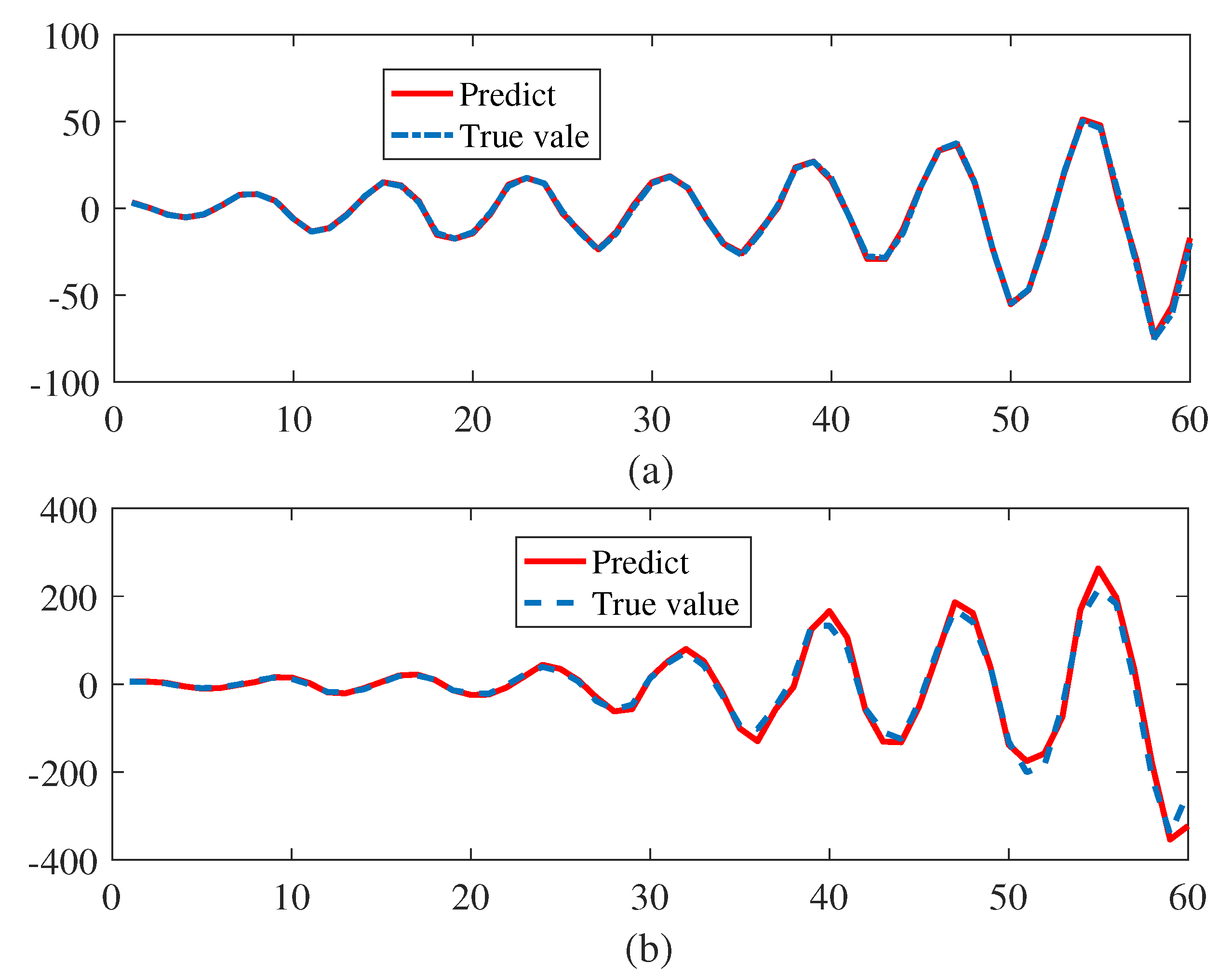
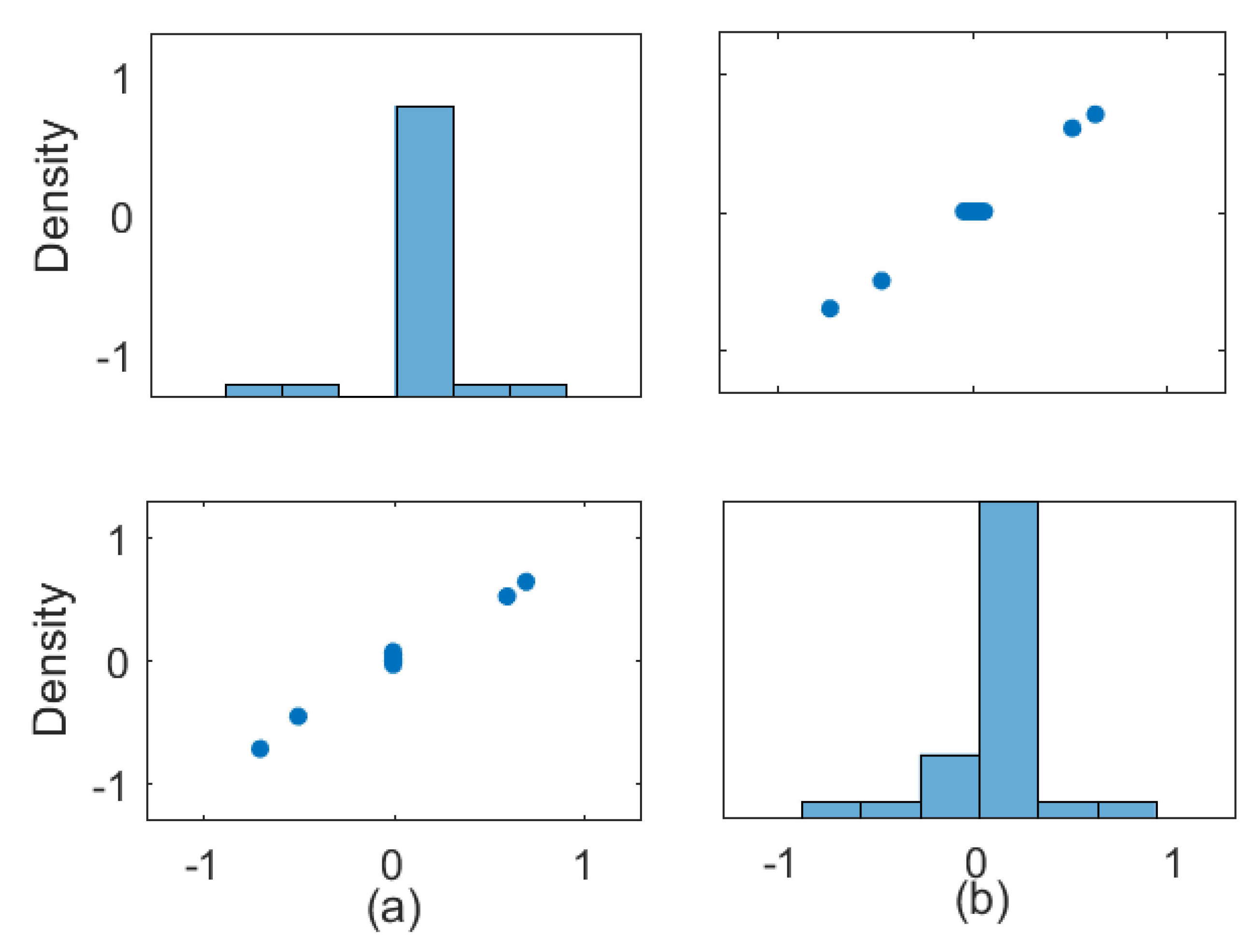
Model (36) is the general form of (37). $d_x$ and $d_u$ are the degree of the output and input; $m_y$ and $m_u$ is the given memory order of the output and input; ${\mathbf{w}}^{\top }=\left[w_1,\dots ,w_N\right]\in {\mathbb{R}}^N$ is the weight vector; and $\mathbf{f}\left(\mathbf{y}\left(t_k\right),\dots ,\mathbf{y}\left(t_{k-m_{\mathbf{y}}}\right),\mathbf{u}\left(t_k\right),\dots ,\mathbf{u}\left(t_{k-m_{\mathbf{u}}}\right)\right)=$${\left[f_1(·),\dots ,f_N(·)\right]}^{\top }\in {\mathbb{R}}^N$ is the functions vector. Taking the NARX model (36) as an example, we set that $d_y=1$, $d_u=2$, $m_y=2$, $m_u=2$. This yields $\mathrm{f}(·)\in {\mathbb{R}}^{28}$ and, thus, $\mathrm{w}\in {\mathbb{R}}^{28}$. Since $\mathrm{w}\in {\mathbb{R}}^4$, only 4 of the 28 linked weights $w_i$ are non-zero. In our study, we use k = 1000 samples for learning with white Gaussian noise. The last 60 in generated data sequence is selected for testing and the predicting result is compared with the true value. The estimated parameter w agrees with the true value as shown in Figure 3. The predicting performance of Algorithm 1 is shown in the Figure 4. From the Figure 4, the predicted and exact trajectories match well with different ${\xi }_i\left(t\right)=0.1,0.3$. When Algorithm 1 is executed 8 times, the average of the RMSE of output are 0.021 and 0.074, which are tolerable in the application.

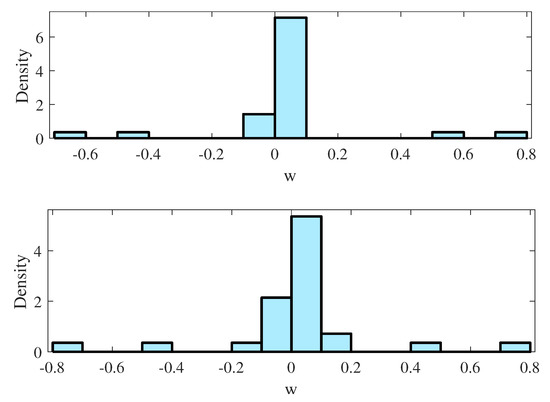
Figure 3. The distribution of w: the above is true w, the below is the estimated w model.

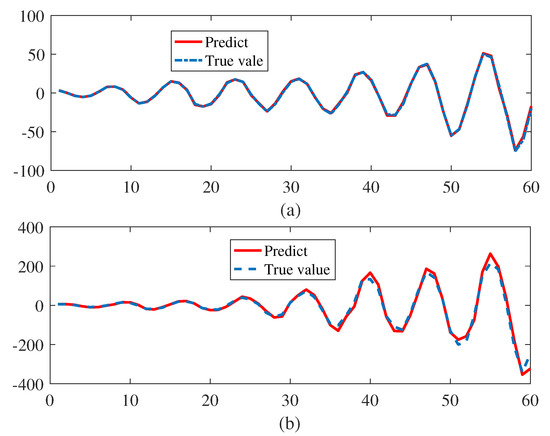
Figure 4. Output of the state model for 60 testing data in example 2: (a) $\xi =0.1$ and (b) $\xi =0.3$.

5.3. Example 3: Kernel State-Space Models (KSSM) for Autoregressive Modeling

Kernel state-space models (KSSM) is autoregressive model, which satisfy the $\tau$-order difference equation. As seen below, the model may be described as a first-order multivariate process.

$${\overline{\mathbf{x}}}_{t+1}=F_t\left({\overline{\mathbf{x}}}_t\right)+V_t$$

(38)

where ${\overline{\mathbf{x}}}_t={\left[{\mathbf{x}}_t,\dots ,{\mathbf{x}}_{t-\tau +1}\right]}^T$, $F_t\left({\overline{\mathbf{x}}}_t\right)={[f_t\left({\mathbf{x}}_t,\dots ,{\mathbf{x}}_{t-\tau +1}\right),{\mathbf{x}}_t,\cdots ,{\mathbf{x}}_{t-\tau +2}]}^T$, and $V_t=$${[{\xi }_t,0,\dots ,0]}^T$.

The hidden state of an SSM can then be viewed as the process ${\overline{\mathbf{x}}}_t$, producing an SSM formulation of a complex autoregressive model with noisy $V_t$. By using non-linear autoregressive modeling with a fixed number of delayed samples, the model can be utilized to predict time series. In addition, if the state-transition function $f_t$ is defined using kernels (39), we derive the suggested KSSM suited for autoregressive time series.

$$\begin{array}{cc}\hfill \left[\begin{array}{c}{\mathbf{x}}_{t+1}\\ {\mathbf{x}}_t\\ ⋮\\ {\mathbf{x}}_{t-\tau +2}\end{array}\right]& =\left[\begin{array}{c}\sum _{i=1}^N{w}_i{k}_i\left(x_i\left(t_k\right)\right)\\ {\mathbf{x}}_t\\ ⋮\\ {\mathbf{x}}_{t-\tau +2}\end{array}\right]+\left[\begin{array}{c}{\xi }_t\\ 0\\ ⋮\\ 0\end{array}\right]\hfill \\ \hfill Y_t& =h\left({\overline{\mathbf{x}}}_t\right)+V_t,\hfill \end{array}$$

(39)

where $Y_t$ is the observed process, $h\left({\overline{\mathbf{x}}}_t\right)$ is the observation function, $V_t$ is observation noise, and $w=[w_1,\cdots w_N]$ is the weight. Periodic time series is widely used in physics, engineering and biology. We take Fourier kernel function in the KSSM. Consider 5 candidate kernel functions for $k_i(·)$: $sin{x}_i$, $cos{x}_i$, $x_i$, $sin2x_i$ and $cos2x_i.$

Algorithm 1 is applied in the identification of parameter w in (39). The RMSE of w is 0.16, which is a satisfactory result. The estimation data in the experiment has 500 sample points, and Figure 5 shows the simulated outputs of the two processes evaluated on the validation set. In Figure 5, we compare the true and estimated value w using the probability distribution and dispersoid distribution. It can see that the sparse effect of the algorithm proposed in this paper is obvious.

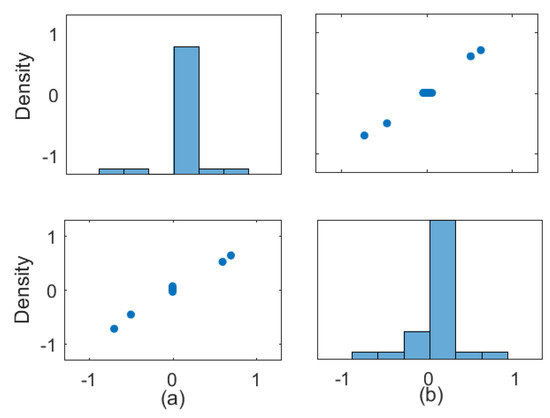
Figure 5. Compare of distribution of w with sparsity: (a) sparse value and (b) true value.

6. Conclusions

The parameter estimation of non-linear discrete-time state-space systems with noisy state data are the subject of this work. For parameter estimation and prediction, a novel sparse Bayesian convex optimisation method (NSSI-SBSA) is presented, which considers approximation method, parameter prior, and posterior. The fundamental problem with identification is divided into two parts: the first step, the improved Stein approach is used to create a new optimisation objective function. The second step is to create a reweighted $L_1$-regularized least squares solver, with the regularization value chosen from the optimization point. The new objective function is more information-rich and can easily extract more critical information from the raw data than the previous study. From the three examples, the NSSI-SBSA algorithm usually captures more information about the reliance of the data indicators than the methods discussed in the introduction part.