Modified Whiteside’s Line-Based Transepicondylar Axis for Imageless Total Knee Arthroplasty
Abstract
:1. Introduction
2. Methodology
2.1. Defining the Procedure for a Coordinate System
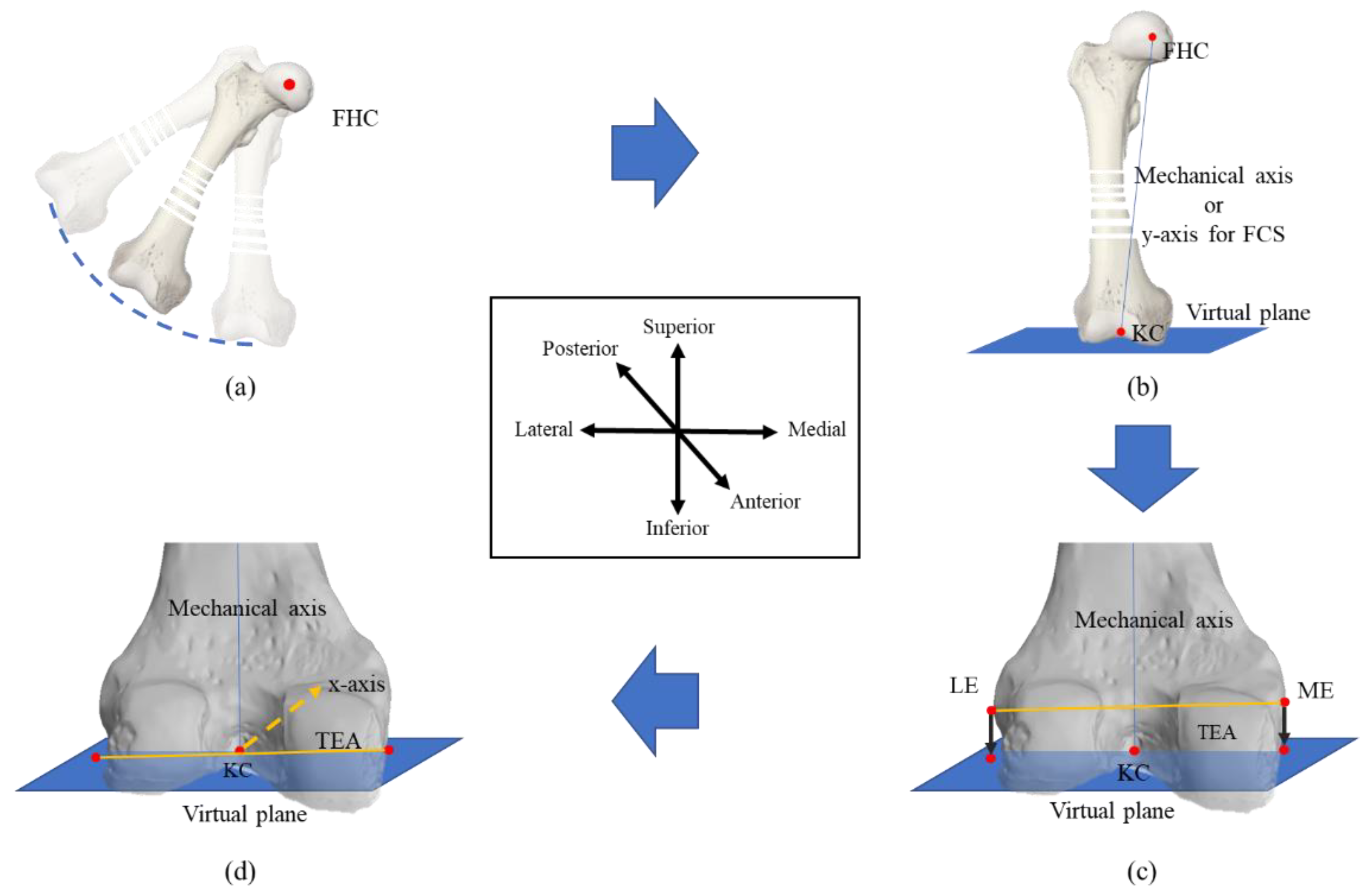
2.1.1. Femoral Coordinate System
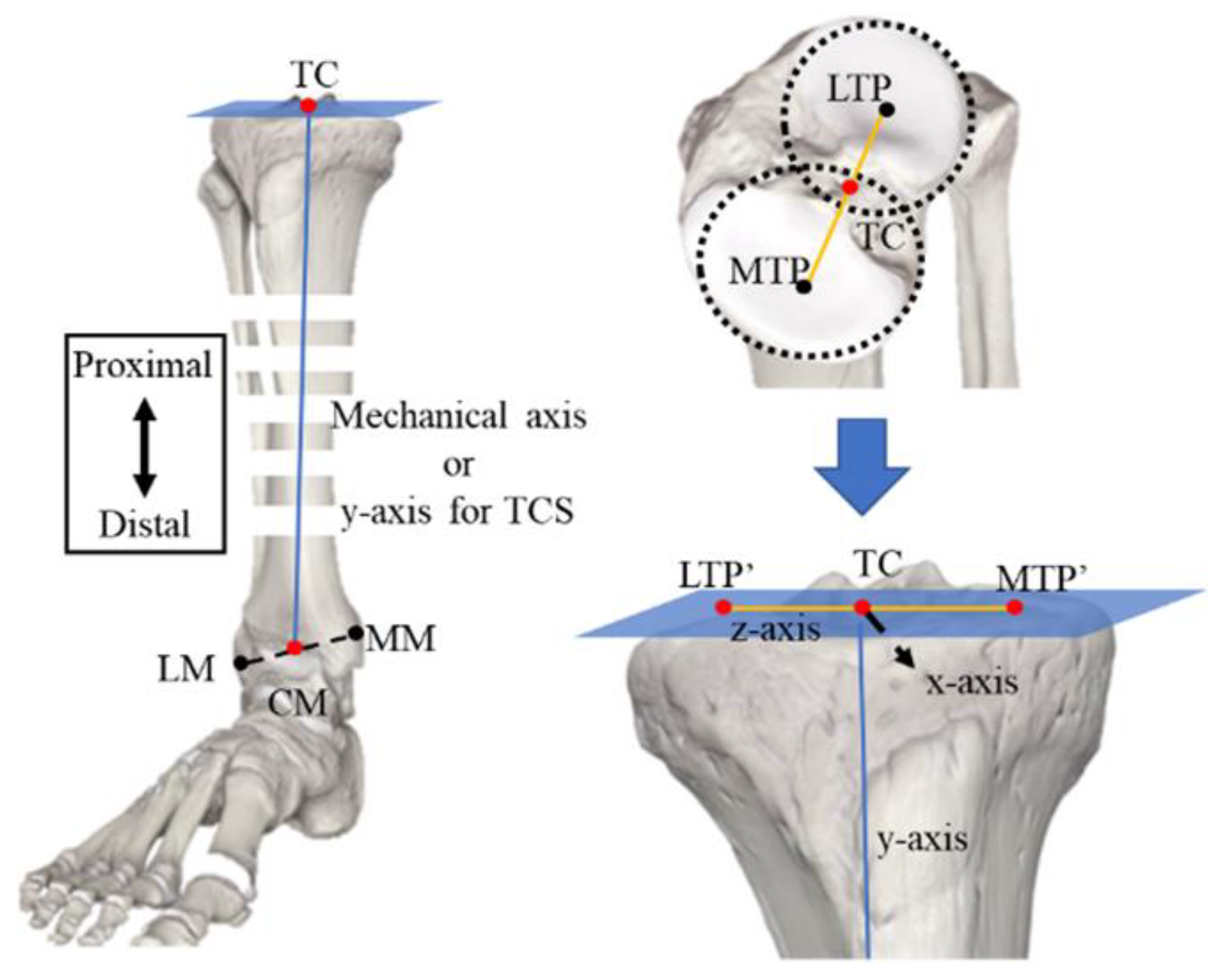
2.1.2. Tibial Coordinate System
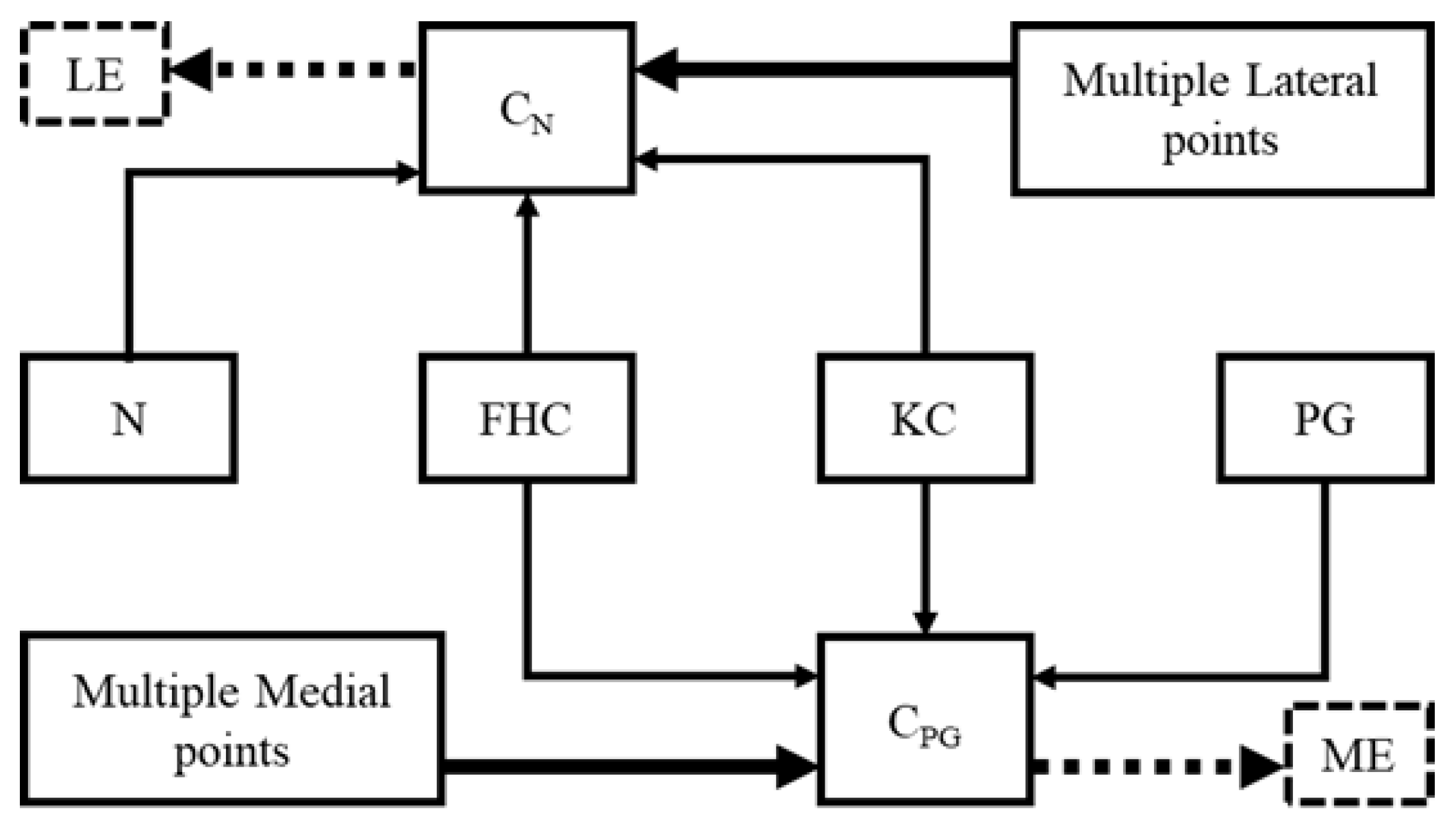
2.2. Modified Whiteside’s Line
| Algorithm 1: Modified Whiteside’s line for FCS |
| Input: KC, FHC // Chosen be probe sensor MPoints, LPoints // A cloud of points on the lateral and medial sides Output: xaxis, yaxis, zaxis // FCS yaxis := (FHC – KC) // A plane normal to the y-axis and passing through KC VP := ∏ (yaxis, KC) CN := ∏ (N, KC, FHC) CPG := ∏ (PG, KC, FHC) // Function 1: Selection of prominent point from MPoints ME := Function 1 (CPG, MPoints) LE := Function 1 (CN, LPoints) // Function 2: Projection of prominent point on the virtual plane MEProjected := Function 2 (ME, VP) LEProjected := Function 2 (LE, VP) zaxis := (MEProjected – LEProjected) xaxis := yaxis x zaxis chosen point := Function 1 (plane equation, cloud points) for i := 1 to # cloud points ith cloud point := (x, y, z) ith cloud point, 4th column := |ax+by+cz+d|/sqrt(a2 + b2 + c2) endfor j := find indices of max(ith cloud point, 4th column) chosen point := jth cloud point endFunction 1 Projected point := Function 2 (point, plane) point := (xo, yo, zo) x := xo + at; y := yo + bt; z := zo + ct; substitute (x, y, z) in plane and solve for “t” Projected point := substitute “t” in (x, y, z) endFunction2 |
3. Experimental Setup
3.1. CAD Model
3.2. Sensing System
4. Results and Discussion
4.1. Validation of the Sensing System with CAD Results
4.2. Repeatability Challenge in Conventional Techniques
4.3. Modified Whiteside’s Line—CAD Results
4.4. Modified Whiteside’s Line—Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
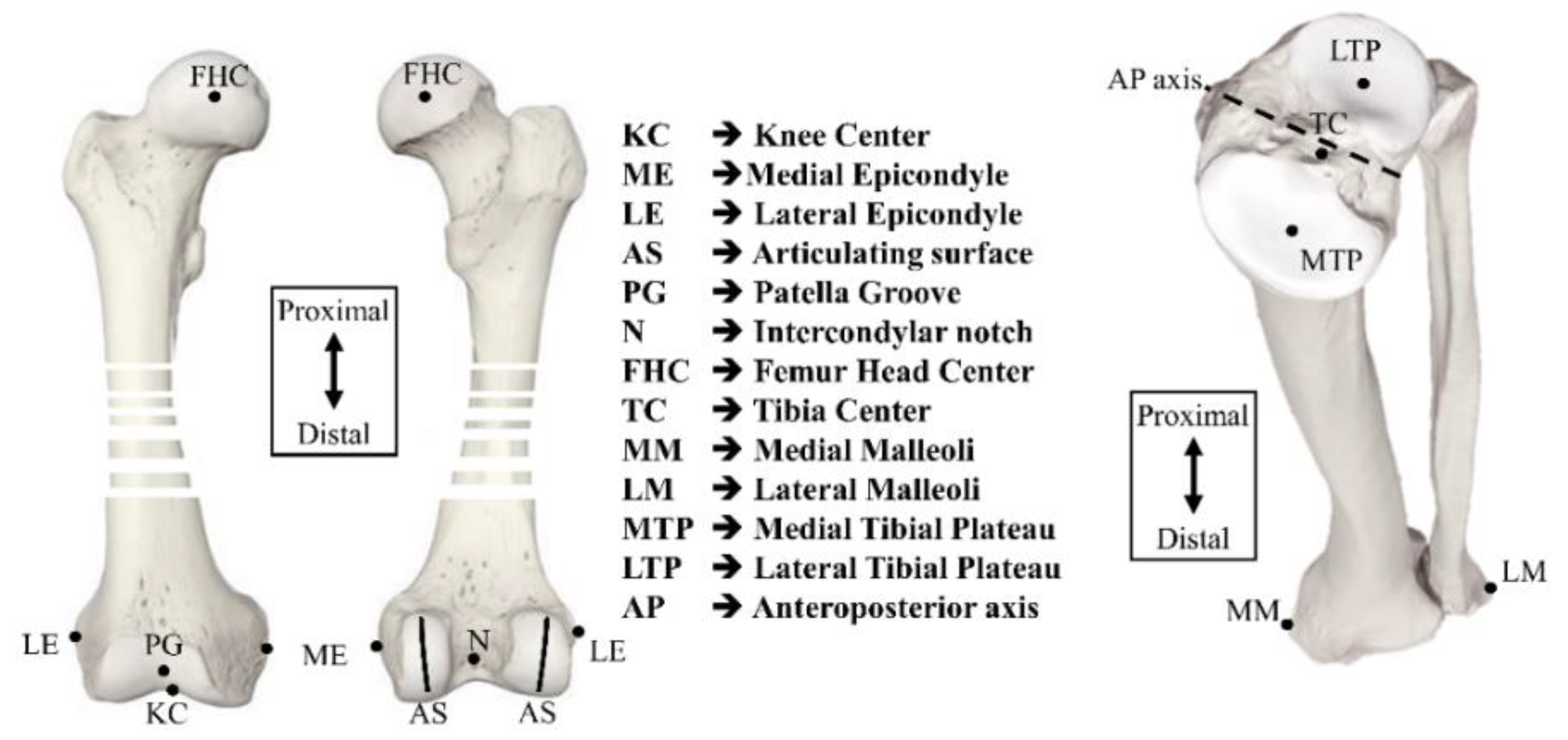
Nomenclature
| Transformation matrix from frame A to B | |
| Distance between origins of frame B w.r.t frame A | |
| Rotation matrix defining the orientation of frame B w.r.t frame A | |
| AP axis | Anteroposterior axis |
| aTEA | anatomical Transepicondylar axis |
| CAD−GCS CAD | global coordinate system |
| CAD−FCS CAD | femoral coordinate system |
| C−CS | Common coordinate system: a common coordinate system between sensor and CAD system for validation of sensing system |
| CM | Center of malleoli |
| FCS | Femoral coordinate system |
| FHC | Femur head center |
| GCS | Global coordinate system |
| HTM | Homogeneous transformation matrix |
| KC | Knee center |
| LE | Lateral epicondylar |
| LM | Lateral malleoli |
| LTP | Lateral tibial plateau |
| CN | Central plane defined by KC, FHC, and N |
| CPG | Central plane defined by KC, FHC, and PG |
| Test-FCSs | Femoral coordinate systems defined using conventional methods to check their repeatability |
| Standard-FCS | Femoral coordinate system marked by anatomical points printed on the bone |
| ME | Medial epicondylar |
| MM | Medial malleoli |
| MTP | Medial tibial plateau |
| N | Intercondylar notch |
| PG | Patella groove |
| PCA | Posterior condylar axis |
| S−GCS | Sensor−global coordinate system |
| S−FCS | Sensor−femoral coordinate system |
| sTEA | surgical Transepicondylar axis |
| TC | Tibia center |
| TCS | Tibial coordinate system |
| TEA | Transepicondylar axis |
| TKA | Total knee arthroplasty |
References
- Richmond, J.C. Surgery for Osteoarthritis of the Knee. Rheum. Dis. Clin. N. Am. 2008, 34, 815–825. [Google Scholar] [CrossRef] [PubMed]
- Carr, A.J.; Robertsson, O.; Graves, S.; Price, A.J.; Arden, N.K.; Judge, A.; Beard, D.J. Knee Replacement. Lancet 2012, 379, 1331–1340. [Google Scholar] [CrossRef]
- Overhoff, H.M.; Lazovic, D.; Liebing, M.; Macher, C. Total Knee Arthroplasty: Coordinate System Definition and Planning Based on 3-D Ultrasound Image Volumes. Int. Congr. Ser. 2001, 1230, 292–299. [Google Scholar] [CrossRef]
- Foley, K.A.; Muir, J.M. Improving Accuracy in Total Knee Arthroplasty: A Cadaveric Comparison of a New Surgical Navigation Tool, Intellijoint KNEE, with Computed Tomography Imaging; Intellijoint Surgical, Inc.: Waterloo, ON, USA, 2019. [Google Scholar]
- Chauhan, S.K.; Scott, R.G.; Breidahl, W.; Beaver, R.J. Computer-Assisted Knee Arthroplasty versus a Conventional Jig-Based Technique. J. Bone Jt. Surgery. Br. Vol. 2004, 86-B, 372–377. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Doro, L.C.; Hughes, R.E.; Miller, J.D.; Schultz, K.F.; Hallstrom, B.; Urquhart, A.G. The Reproducibility of a Kinematically-Derived Axis of the Knee versus Digitized Anatomical Landmarks Using a Knee Navigation System. Open Biomed. Eng. J. 2008, 2, 52–56. [Google Scholar] [CrossRef] [Green Version]
- Stiehl, J.B. Computer Navigation in Primary Total Knee Arthroplasty. J. Knee Surg. 2007, 20, 158–164. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- van der Linden–van der Zwaag, H.M.J.; Valstar, E.R.; van der Molen, A.J.; Nelissen, R.G.H.H. Transepicondylar Axis Accuracy in Computer Assisted Knee Surgery: A Comparison of the CT-Based Measured Axis versus the CAS-Determined Axis. Comput. Aided Surg. 2008, 13, 200–206. [Google Scholar] [CrossRef] [PubMed]
- Iwaki, H.; Pinskerova, V.; Freeman, M.A.R. Tibiofemoral Movement 1: The Shapes and Relative Movements of the Femur and Tibia in the Unloaded Cadaver Knee. J. Bone Jt. Surgery. Br. Vol. 2000, 82-B, 1189–1195. [Google Scholar] [CrossRef]
- Renault, J.-B.; Aüllo-Rasser, G.; Donnez, M.; Parratte, S.; Chabrand, P. Articular-Surface-Based Automatic Anatomical Coordinate Systems for the Knee Bones. J. Biomech. 2018, 80, 171–178. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yoshioka, Y.; Siu, D.; Cooke, T.D. The Anatomy and Functional Axes of the Femur. J. Bone Jt. Surg. Am. 1987, 69, 873–880. [Google Scholar] [CrossRef]
- Johal, P.; Williams, A.; Wragg, P.; Hunt, D.; Gedroyc, W. Tibio-Femoral Movement in the Living Knee. A Study of Weight Bearing and Non-Weight Bearing Knee Kinematics Using ‘Interventional’ MRI. J. Biomech. 2005, 38, 269–276. [Google Scholar] [CrossRef] [PubMed]
- Nam, J.-H.; Koh, Y.-G.; Kang, K.; Park, J.-H.; Kang, K.-T. The Posterior Cortical Axis as an Alternative Reference for Femoral Component Placement in Total Knee Arthroplasty. J. Orthop. Surg. Res. 2020, 15, 603. [Google Scholar] [CrossRef] [PubMed]
- Jabalameli, M.; Rahbar, M.; Bagheri, A.; Hadi, H.; Moradi, A.; Radi, M.; Mokhtari, T. Evaluation of Distal Femoral Rotational Alignment According to Transepicondylar Axis and Whiteside’s Line: A Study in Iranian Population. Shafa Orthop. J. 2013, 4, 122–127. [Google Scholar]
- Middleton, F.R.; Palmer, S.H. How Accurate Is Whiteside’s Line as a Reference Axis in Total Knee Arthroplasty? Knee 2007, 14, 204–207. [Google Scholar] [CrossRef]
- Whiteside, L.A.; Arima, J. The Anteroposterior Axis for Femoral Rotational Alignment in Valgus Total Knee Arthroplasty. Clin. Orthop. Relat. Res. 1995, 321, 168–172. [Google Scholar] [CrossRef]
- Kobayashi, H.; Akamatsu, Y.; Kumagai, K.; Kusayama, Y.; Ishigatsubo, R.; Muramatsu, S.; Saito, T. The Surgical Epicondylar Axis Is a Consistent Reference of the Distal Femur in the Coronal and Axial Planes. Knee Surg. Sports Traumatol. Arthrosc. 2014, 22, 2947–2953. [Google Scholar] [CrossRef]
- Valkering, K.P.; Tuinebreijer, W.E.; Sunnassee, Y.; van Geenen, R.C.I. Multiple Reference Axes Should Be Used to Improve Tibial Component Rotational Alignment: A Meta-Analysis. J. ISAKOS 2018, 3, 337–344. [Google Scholar] [CrossRef]
- Tanavalee, A.; Yuktanandana, P.; Ngarmukos, C. Surgical Epicondylar Axis vs Anatomical Epicondylar Axis for Rotational Alignment of the Femoral Component in Total Knee Arthroplasty. J. Med. Assoc. Thail. = Chotmaihet Thangphaet 2001, 84 (Suppl. 1), S401-8. [Google Scholar]
- Yoshino, N.; Takai, S.; Ohtsuki, Y.; Hirasawa, Y. Computed Tomography Measurement of the Surgical and Clinical Transepicondylar Axis of the Distal Femur in Osteoarthritic Knees. J. Arthroplast. 2001, 16, 493–497. [Google Scholar] [CrossRef] [PubMed]
- Victor, J.; Van Doninck, D.; Labey, L.; Van Glabbeek, F.; Parizel, P.; Bellemans, J. A Common Reference Frame for Describing Rotation of the Distal Femur: A Ct-Based Kinematic Study Using Cadavers. J. Bone Jt. Surg. Br. 2009, 91, 683–690. [Google Scholar] [CrossRef] [Green Version]
- Kinzel, V.; Ledger, M.; Shakespeare, D. Can the Epicondylar Axis Be Defined Accurately in Total Knee Arthroplasty? Knee 2005, 12, 293–296. [Google Scholar] [CrossRef] [PubMed]
- Pitocchi, J.; Wesseling, M.; van Lenthe, G.H.; Pérez, M.A. Finite Element Analysis of Custom Shoulder Implants Provides Accurate Prediction of Initial Stability. Mathematics 2020, 8, 1113. [Google Scholar] [CrossRef]
- Witoolkollachit, P.; Seubchompoo, O. The Comparison of Femoral Component Rotational Alignment with Transepicondylar Axis in Mobile Bearing TKA, CT-Scan Study. J. Med. Assoc. Thail. = Chotmaihet Thangphaet 2008, 91, 1051–1058. [Google Scholar]
- Stiehl, J.B.; Abbott, B.D. Morphology of the Transepicondylar Axis and Its Application in Primary and Revision Total Knee Arthroplasty. J. Arthroplast. 1995, 10, 785–789. [Google Scholar] [CrossRef]
- Schnurr, C.; Nessler, J.; König, D.P. Is Referencing the Posterior Condyles Sufficient to Achieve a Rectangular Flexion Gap in Total Knee Arthroplasty? Int. Orthop. (SICOT) 2008, 33, 1561. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fehring, T.K.; Odum, S.; Griffin, W.L.; Mason, J.B.; Nadaud, M. Early Failures in Total Knee Arthroplasty. Clin. Orthop. Relat. Res. 2001, 392, 315–318. [Google Scholar] [CrossRef] [PubMed]
- Geary, M.B.; Macknet, D.M.; Ransone, M.P.; Odum, S.D.; Springer, B.D. Why Do Revision Total Knee Arthroplasties Fail? A Single-Center Review of 1632 Revision Total Knees Comparing Historic and Modern Cohorts. J Arthroplast. 2020, 35, 2938–2943. [Google Scholar] [CrossRef] [PubMed]
- Dalury, D.F.; Pomeroy, D.L.; Gorab, R.S.; Adams, M.J. Why Are Total Knee Arthroplasties Being Revised? J. Arthroplast. 2013, 28, 120–121. [Google Scholar] [CrossRef] [PubMed]
- Stoeckl, B.; Nogler, M.; Krismer, M.; Beimel, C.; Moctezuma de la Barrera, J.-L.; Kessler, O. Reliability of the Transepicondylar Axis as an Anatomical Landmark in Total Knee Arthroplasty. J. Arthroplast. 2006, 21, 878–882. [Google Scholar] [CrossRef] [PubMed]
- Jerosch, J.; Peuker, E.; Philipps, B.; Filler, T. Interindividual Reproducibility in Perioperative Rotational Alignment of Femoral Components in Knee Prosthetic Surgery Using the Transepicondylar Axis. Knee Surg. Sports Traumatol. Arthrosc. 2002, 10, 194–197. [Google Scholar] [CrossRef] [PubMed]
- Davis, E.T.; Pagkalos, J.; Gallie, P.A.M.; Macgroarty, K.; Waddell, J.P.; Schemitsch, E.H. Defining the Errors in the Registration Process During Imageless Computer Navigation in Total Knee Arthroplasty: A Cadaveric Study. J. Arthroplast. 2014, 29, 698–701. [Google Scholar] [CrossRef] [PubMed]
- Yau, W.P.; Leung, A.; Chiu, K.Y.; Tang, W.M.; Ng, T.P. Intraobserver Errors in Obtaining Visually Selected Anatomic Landmarks during Registration Process in Nonimage-Based Navigation-Assisted Total Knee Arthroplasty: A Cadaveric Experiment. J. Arthroplast. 2005, 20, 591–601. [Google Scholar] [CrossRef] [PubMed]
- Yau, W.P.; Leung, A.; Liu, K.G.; Yan, C.H.; Wong, L.L.S.; Chiu, K.Y. Interobserver and Intra-Observer Errors in Obtaining Visually Selected Anatomical Landmarks during Registration Process in Non-Image-Based Navigation-Assisted Total Knee Arthroplasty. J. Arthroplast. 2007, 22, 1150–1161. [Google Scholar] [CrossRef] [PubMed]
- Davis, E.T.; Pagkalos, J.; Gallie, P.A.M.; Macgroarty, K.; Waddell, J.P.; Schemitsch, E.H. A Comparison of Registration Errors with Imageless Computer Navigation during MIS Total Knee Arthroplasty versus Standard Incision Total Knee Arthroplasty: A Cadaveric Study. Comput. Aided Surg. 2015, 20, 7–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pagkalos, J.; Davis, E.; Gallie, P.; Macgroarty, K.; Waddell, J.; Schemitsch, E. The Effect of the Registration Process Error on Component Alignment during Imageless Computer Navigation for Knee Arthroplasty: A Cadaveric Study. Orthop. Proc. 2013, 95-B, 68. [Google Scholar] [CrossRef]
- Liu, W.; Ding, H.; Zhu, Z.; Wang, G.; Zhou, Y. An Image-Free Surgical Navigation System for Total Knee Arthroplasty. In Proceedings of the 2011 4th International Conference on Biomedical Engineering and Informatics (BMEI), Shanghai, China, 15–17 October 2011; Volume 3, pp. 1353–1357. [Google Scholar]
- Perrin, N.; Stindel, E.; Roux, C. BoneMorphing versus Freehand Localization of Anatomical Landmarks: Consequences for the Reproducibility of Implant Positioning in Total Knee Arthroplasty. Comput. Aided Surg. 2005, 10, 301–309. [Google Scholar] [CrossRef] [PubMed]
- Bae, D.K.; Song, S.J. Computer Assisted Navigation in Knee Arthroplasty. Clin. Orthop. Surg. 2011, 3, 259–267. [Google Scholar] [CrossRef] [PubMed]
- Stindel, E.; Briard, J.-L.; Lavallée, S.; Dubrana, F.; Plaweski, S.; Merloz, P.; Lefèvre, C.; Troccaz, J. Bone Morphing: 3D Reconstruction Without Pre- or Intraoperative Imaging—Concept and Applications. In Navigation and Robotics in Total Joint and Spine Surgery; Stiehl, J.B., Konermann, W.H., Haaker, R.G., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 39–45. ISBN 978-3-642-59290-4. [Google Scholar]
- Anatomy Standard Landing Page. Available online: https://www.anatomystandard.com/ (accessed on 8 August 2022).
- Femur Bone | 3D CAD Model Library | GrabCAD. Available online: https://grabcad.com/library/femur-bone-3 (accessed on 8 August 2022).
- YD, S. Fast Geometric Fit Algorithm for Sphere Using Exact Solution. arXiv 2015, arXiv:1506.02776 [cs]. [Google Scholar]
- Diduch, D.R.; Iorio, R.; Long, W.J.; Scott, W.N. Insall & Scott Surgery of the Knee; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Schlatterer, B.; Linares, J.-M.; Chabrand, P.; Sprauel, J.-M.; Argenson, J.-N. Influence of the Optical System and Anatomic Points on Computer-Assisted Total Knee Arthroplasty. Orthop. Traumatol. Surg. Res. 2014, 100, 395–402. [Google Scholar] [CrossRef]
- Walker, P.S.; Heller, Y.; Yildirim, G.; Immerman, I. Reference Axes for Comparing the Motion of Knee Replacements with the Anatomic Knee. Knee 2011, 18, 312–316. [Google Scholar] [CrossRef]
- Lee, Y.S.; Park, S.J.; Shin, V.I.; Lee, J.H.; Kim, Y.H.; Song, E.K. Achievement of Targeted Posterior Slope in the Medial Opening Wedge High Tibial Osteotomy: A Mathematical Approach. Ann. Biomed. Eng. 2010, 38, 583–593. [Google Scholar] [CrossRef]
- Yau, W.P.; Chiu, K.Y.; Tang, W.M. How Precise Is the Determination of Rotational Alignment of the Femoral Prosthesis in Total Knee Arthroplasty: An In Vivo Study. J. Arthroplast. 2007, 22, 1042–1048. [Google Scholar] [CrossRef] [PubMed]
- Bundrick, C.M.; Sherry, D.L. Distance From a Point to a Line and a Point to a Plane Via Synthetic Methods. Sch. Sci. Math. 1978, 78, 304–306. [Google Scholar] [CrossRef]
- Craig, J.J. Introduction to Robotics: Mechanics and Control; Pearson Educación: London, UK, 2005; ISBN 978-970-26-0772-4. [Google Scholar]
- Sohail, M.; Butt, S.U.; Baqai, A.A. An Analytical Approach for Positioning Error and Mode Shape Analysis of n—Legged Parallel Manipulator. IJCIM 2018, 31, 677–691. [Google Scholar] [CrossRef]
- Hancock, C.W.; Winston, M.J.; Bach, J.M.; Davidson, B.S.; Eckhoff, D.G. Cylindrical Axis, Not Epicondyles, Approximates Perpendicular to Knee Axes. Clin. Orthop. Relat. Res. 2013, 471, 2278–2283. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lozano, R.; Campanelli, V.; Howell, S.; Hull, M. Kinematic Alignment More Closely Restores the Groove Location and the Sulcus Angle of the Native Trochlea than Mechanical Alignment: Implications for Prosthetic Design. Knee Surg. Sports Traumatol. Arthrosc. 2019, 27, 1504–1513. [Google Scholar] [CrossRef]

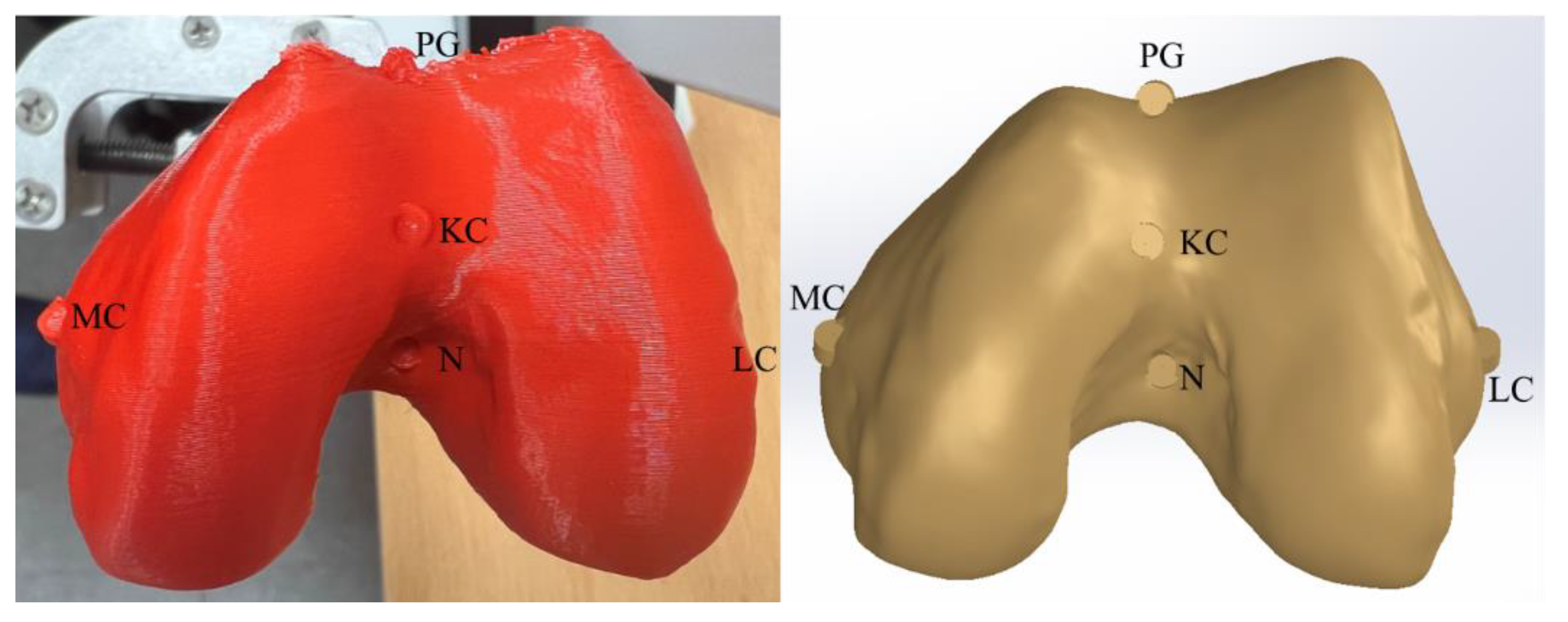
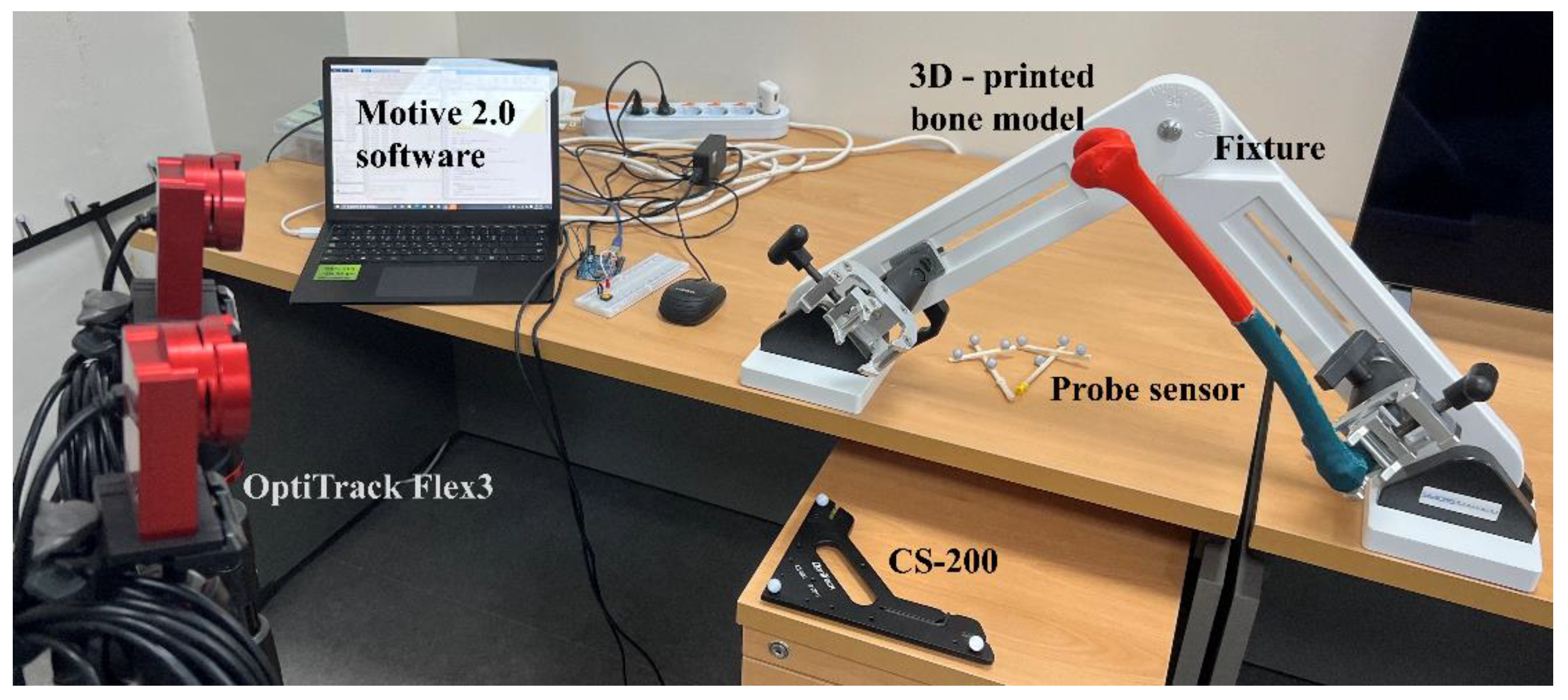

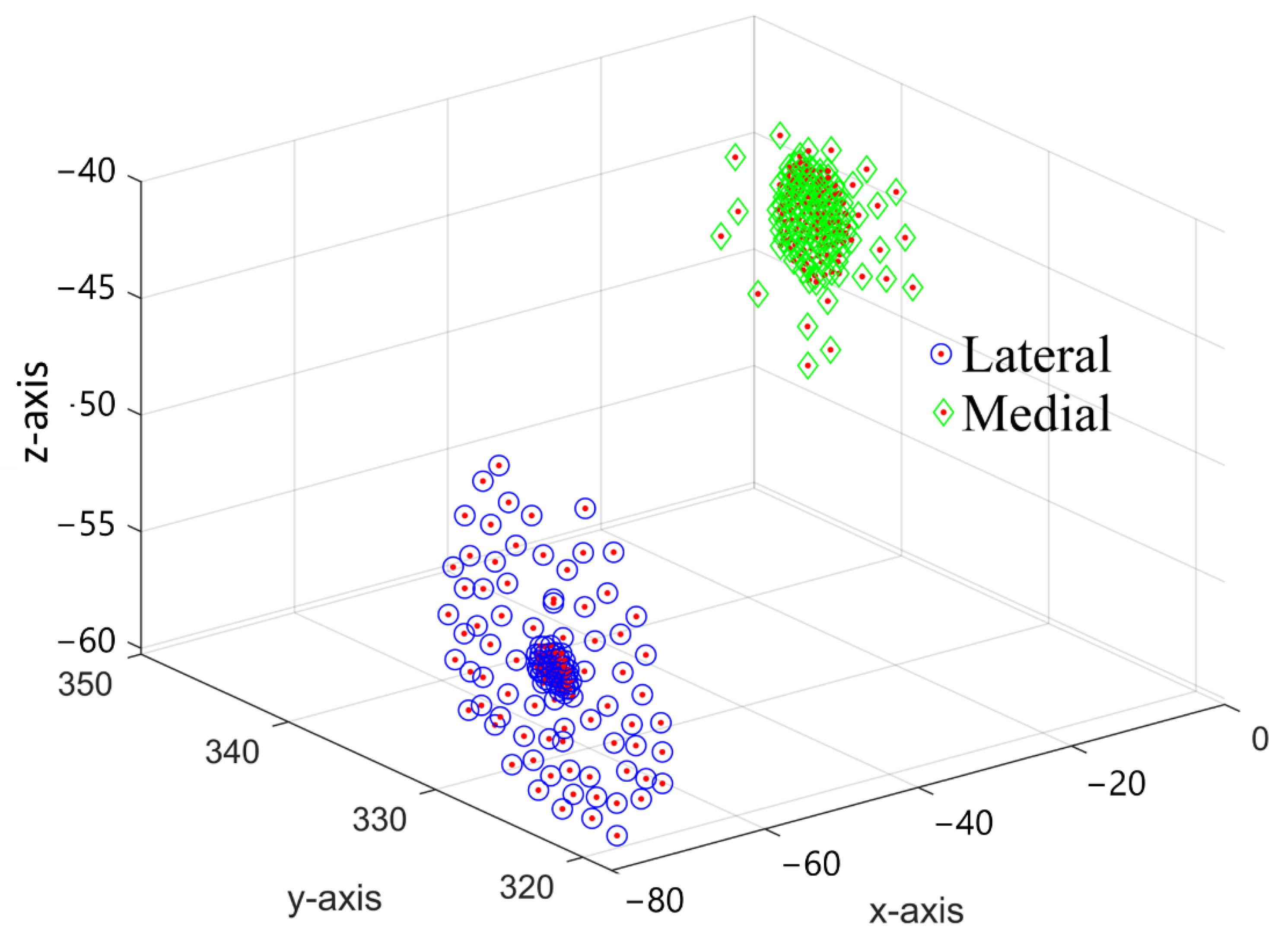

| Anatomical Point | CAD−GCS | CAD−GCS → CAD−FCS |
|---|---|---|
| KC | [−44.64, 345.84, −40.47] | [~0, ~0, ~0] |
| FHC | [49.95, −28.66, 1.51] | [0, 388.54, 0] |
| ME | [−9.53, 341.24, −45.05] | [−10.27, 12.49, 31.83] |
| LE | [−74.88, 324.47, −54.09] | [−10.27, 11.76, −36.23] |
| PG | [−44.82, 331.51, −24.65] | [14.60, 15.48, −1.77] |
| N | [−42.30, 332.39, −52.65] | [−13.32, 12.22, −2.81] |
| Anatomical Point | S−GCS | S−GCS → S−FCS |
|---|---|---|
| KC | [519.53, 271.44, 41.12] | [~0, ~0, ~0] |
| FHC | [428.93, 63.77, −226.45] | [0, 350.61, 0] |
| ME | [500.89, 246.93, 51.80] | [−10.27, 11.19, 28.83] |
| LE | [547.84, 269.21, 17.85] | [−10.26, 11.75, −33.23] |
| PG | [522.99, 251.59, 35.60] | [14.37, 15.07, −1.63] |
| N | [506.83, 272.67, 28.73] | [−12.87, 12.00, −2.50] |
| Method | Direction | Orientation Error (deg) | |
|---|---|---|---|
| Whiteside’s line | Anterior | Lateral | 6.73 |
| Medial | 5.77 | ||
| Posterior | Lateral | 3.36 | |
| Medial | 5.50 | ||
| aTEA | Lateral | Anterior | 2.33 |
| Posterior | 2.49 | ||
| Medial | Anterior | 2.37 | |
| Posterior | 2.47 | ||
| Modified Whiteside’s line | Anterior | Lateral | 0.72 |
| Medial | 1.33 | ||
| Modified Whiteside’s Line | Orientation Error (deg) | |
|---|---|---|
| PG → ME LE → Printed | PG-P1 | 0.9268 |
| PG-P2 | 0.6428 | |
| PG-P3 | 0.3441 | |
| PG-P4 | 0.4069 | |
| PG-P5 | 1.9197 | |
| N → LE ME → Printed | N-P1 | 0.4586 |
| N-P2 | 0.7948 | |
| N-P3 | 0.9684 | |
| N-P4 | 0.7948 | |
| N-P5 | 0.7663 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sohail, M.; Park, J.; Kim, J.Y.; Kim, H.S.; Lee, J. Modified Whiteside’s Line-Based Transepicondylar Axis for Imageless Total Knee Arthroplasty. Mathematics 2022, 10, 3670. https://doi.org/10.3390/math10193670
Sohail M, Park J, Kim JY, Kim HS, Lee J. Modified Whiteside’s Line-Based Transepicondylar Axis for Imageless Total Knee Arthroplasty. Mathematics. 2022; 10(19):3670. https://doi.org/10.3390/math10193670
Chicago/Turabian StyleSohail, Muhammad, Jaehyun Park, Jun Young Kim, Heung Soo Kim, and Jaehun Lee. 2022. "Modified Whiteside’s Line-Based Transepicondylar Axis for Imageless Total Knee Arthroplasty" Mathematics 10, no. 19: 3670. https://doi.org/10.3390/math10193670
APA StyleSohail, M., Park, J., Kim, J. Y., Kim, H. S., & Lee, J. (2022). Modified Whiteside’s Line-Based Transepicondylar Axis for Imageless Total Knee Arthroplasty. Mathematics, 10(19), 3670. https://doi.org/10.3390/math10193670







