Approximation of the Solution of Delay Fractional Differential Equation Using AA-Iterative Scheme

Abstract

The aim of this paper is to propose a new faster iterative scheme (called $AA$-iteration) to approximate the fixed point of $(b,\eta )$-enriched contraction mapping in the framework of Banach spaces. It is also proved that our iteration is stable and converges faster than many iterations existing in the literature. For validity of our proposed scheme, we presented some numerical examples. Further, we proved some strong and weak convergence results for b-enriched nonexpansive mapping in the uniformly convex Banach space. Finally, we approximate the solution of delay fractional differential equations using $AA$-iterative scheme.

1. Introduction and Preliminaries

The proof of the Banach contraction principle (BCP) [1] is based on convergence of the most simplest iterative process named as the sequence of successive approximations or Picard iterative process. This principle solves a fixed point problem for contraction mapping defined on a complete metric space and has become an important tool to prove the existence and approximation of solutions of nonlinear functional equations such as differential equations, integral equations and partial differential equations. In certain cases, the existence of solution of fixed point problem is guaranteed, but finding the exact solution is not possible. In such a situation, an approximation of the solution of the given problem is much desired, which gave rise to development of the different iterative processes [2,3,4,5,6,7].

Many authors have proposed and applied different fixed point iterative schemes for approximation of the solution of linear and nonlinear equations and inclusion. It is always preferred to develop an iterative scheme, which is better than others in the sense that the solution is approximated in a fewer number of steps. In this paper, we shall develop an iterative process and compare it with some well-known iterative processes existing in the literature. Throughout this paper, the set $\{0,1,2,\cdots \}$ is denoted by ${\mathbb{Z}}^{+}$. Let U be a normed space, $\Omega$ a nonempty closed convex, ${\Omega }^{{}^{\prime }}$ a nonempty bounded closed convex subsets of U and T a self mapping on $\Omega$. The set $\{p^{*}\in \Omega :p^{*}=T{p}^{*}\}$ of all fixed points of T is denoted by $F\left(T\right).$

In 1991, Sahu [8] proved the following:

Lemma 1

([8]). Suppose that U is a uniformly convex Banach space and $0<a\le k_n\le b<1$ for all $n\in \mathbb{N}$. Let $\left\{p_n\right\}$ and $\left\{q_n\right\}$ be two sequences in U such that

$$\begin{array}{ccc}\hfill \underset{n\to \infty }{lim\; sup}\parallel p_n\parallel & \le & l,\underset{n\to \infty }{lim\; sup}\parallel q_n\parallel \le land\hfill \\ \hfill \underset{n\to \infty }{lim\; sup}\parallel (1-k_n)p_n+k_n{q}_n\parallel & =& l\hfill \end{array}$$

hold for some $l\ge 0.$ Then ${lim}_{n\to \infty }\parallel p_n-q_n\parallel =0$.

Recall that a mapping T is called Lipschitzian if there exists a constant $L>0$ such that

$$\parallel Tp-Tq\parallel \le L\parallel p-q\parallel$$

holds for all $p,q\in \Omega .$ If we take $L\in (0,1)$ in the above inequality, then T is called a contraction. The mapping T is called nonexpansive if we set $L=1$ in the above inequality.

Berinde [9] introduced the concept of enriched nonexpansive mapping on a normed space as follows:

A self mapping T on $\Omega$ is said to be an enriched nonexpansive if for all $p,q\in \Omega$, there exists $b\in [0,\infty )$ such that

$$\left|\right|b(p-q)+Tp-Tq\left|\right|\le (b+1)\left|\right|p-q\left|\right|.$$

(1)

To highlight the parameter b in $\left(1\right),$ T is termed as b-enriched nonexpansive mapping.

A mapping $T:\Omega \to \Omega$ is said to be an enriched contraction [10] if for all $p,q\in \Omega ,$ there exists $b\in [0,\infty )$ and $\eta \in (0,b+1)$ such that

$$\left|\right|b(p-q)+Tp-Tq\left|\right|\le \eta \left|\right|p-q\left|\right|.$$

(2)

Again to highlight the parameter b in $\left(2\right),$ T is called a $(b,\eta )$-enriched contraction. It was shown that $(b,\eta )$-enriched contraction mapping on $\Omega$ has a unique fixed point, which can be approximated by means of the Krasnoselskii’s iterative scheme [11].

Definition 1

([12]). A mapping $T:\Omega \to U$ is said to be demiclosed at $q^{*}$, if whenever a sequence $p_n\rightharpoonup p^{*}$ in Ω and $T{p}_n\to q^{*}$ in U, it follows that $T{p}^{*}=q^{*}.$

Lemma 2

([13]). Let Ω be nonempty closed convex subset of a uniformly convex Banach space U and T a nonexpansive mapping on Ω. Then $I-T$ is demiclosed at zero.

Remark 1

([14]). Let T be a self mapping on Ω. For any $\lambda \in [0,1]$, the averaged mapping $T_{\lambda }$ on Ω given by

$$T_{\lambda }p=(1-\lambda )p+\lambda Tp$$

has the property that $F\left(T\right)=F\left(T_{\lambda }\right)$. Clearly, $T_0=I$ and $T_1=T$ are the trivial cases.

There are several iterative processes which are used to approximate fixed point of a certain nonlinear operator. One of the most important factors to decide the preference of one iterative process over the other is the rate of convergence. In order to compare convergence rates between two iteration processes, we use the following useful definition of Berinde [15].

Definition 2.

Suppose that sequences $\left\{{\alpha }_n\right\}$ and $\left\{{\beta }_n\right\}$ converge to the same point $l^{*}$ with the following error estimates

$$\begin{array}{cc}\hfill ∥{\alpha }_n-l^{*}∥& \le p_n,\hfill \\ \hfill ∥{\beta }_n-l^{*}∥& \le q_n.\hfill \end{array}$$

If ${lim}_{n\to \infty }\frac{p_n}{q_n}=0$, then $\left\{{\alpha }_n\right\}$ converges faster than $\left\{{\beta }_n\right\}$.

Let us recall that for the given $p_0^{\left(0\right)}$ in $\Omega ,$ the sequence $\{p_n^{\left(0\right)}:n\in {\mathbb{Z}}^{+}\}$ defined by

$$p_{n+1}^{\left(0\right)}=T{p}_n^{\left(0\right)},n\in {\mathbb{Z}}^{+}$$

(3)

is known as the sequence of successive approximations or Picard iteration [16]. The well-known Banach contraction principle states that $\left\{p_n^{\left(0\right)}\right\}$ converges to a unique fixed point of T for any choice of a starting point $p_0^{\left(0\right)}$ in $\Omega$ provided that T is a contraction mapping. However, the Picard iteration does not need to converge to fixed point of nonexpansive mapping. For instance, the self mapping $Tx=1-x$ on $[0,1]$ does not converge to its fixed point $\frac{1}{2},$ for any choice of $x\in [0,1]$ other than $\frac{1}{2}.$ On the other hand, averaged operator for any $\lambda \in (0,1)$ converges to fixed point of T for any choice of x and hence in certain cases, it is useful to consider an averaged operator in an iterative scheme than a mapping T itself.

Let us choose an initial guess $p_0^{\left(1\right)}$ in $\Omega .$ The sequence $\{p_n^{\left(1\right)}:n\in {\mathbb{Z}}^{+}\}$ defined by

$$p_{n+1}^{\left(1\right)}=(1-k_n)p_n^{\left(1\right)}+k_{n}T{p}_n^{\left(1\right)},n\in {\mathbb{Z}}^{+}$$

(4)

is called Mann iteration sequence [17], where the sequence $\left\{k_n\right\}$ of parameters in $(0,1)$ satisfies certain conditions.

The sequence $\{p_n^{\left(2\right)}:n\in {\mathbb{Z}}^{+}\}$ defined by

$$\left\{\begin{array}{c}\begin{array}{cc}{p}_0^{\left(2\right)}\hfill & \in \Omega \hfill \\ p_{n+1}^{\left(2\right)}\hfill & =(1-k_n)p_n^{\left(2\right)}+k_{n}T{q}_n^{\left(2\right)}\hfill \\ q_n^{\left(2\right)}\hfill & =(1-o_n)p_n^{\left(2\right)}+o_{n}T{p}_n^{\left(2\right)},n\in {\mathbb{Z}}^{+}\hfill \end{array}\hfill \end{array}\right.$$

(5)

is known as Ishikawa iteration scheme [18], where $\left\{o_n\right\}$ and $\left\{k_n\right\}$ are some appropriate sequences in $(0,1)$.

Noor [19] proposed a three step iteration scheme to construct a sequence $\{p_n^{\left(3\right)}:n\in {\mathbb{Z}}^{+}\}$ as follows:

$$\left\{\begin{array}{cc}\begin{array}{c}{p}_0^{\left(3\right)}\in \hfill \\ p_{n+1}^{\left(3\right)}=\hfill \end{array}\hfill & \begin{array}{c}\Omega \hfill \\ (1-k_n)p_n^{\left(3\right)}+k_{n}T{q}_n^{\left(3\right)}\hfill \end{array}\hfill \\ q_n^{\left(3\right)}=\hfill & (1-o_n)p_n^{\left(3\right)}+o_{n}T{r}_n^{\left(3\right)}\hfill \\ r_n^{\left(3\right)}=\hfill & (1-w_n)p_n^{\left(3\right)}+w_{n}T{p}_n^{\left(3\right)}\forall n\in {\mathbb{Z}}^{+}\hfill \end{array}\right.$$

(6)

where $\left\{w_n\right\},\left\{o_n\right\}$, $\left\{k_n\right\}$ in $(0,1)$ satisfy certain conditions.

In 2007, Agarwal et al. [20] defined a sequence $\{p_n^{\left(4\right)}:n\in {\mathbb{Z}}^{+}\}$ known as S-iteration scheme given by

$$\left\{\begin{array}{cc}\begin{array}{c}{p}_0^{\left(4\right)}\in \hfill \\ p_{n+1}^{\left(4\right)}=\hfill \end{array}\hfill & \begin{array}{c}\Omega \hfill \\ (1-k_n)T{p}_n^{\left(4\right)}+k_{n}T{q}_n^{\left(4\right)}\hfill \end{array}\hfill \\ q_n^{\left(4\right)}=\hfill & (1-o_n)p_n^{\left(4\right)}+o_{n}T{p}_n^{\left(4\right)},n\in {\mathbb{Z}}^{+}\hfill \end{array}\right.$$

(7)

where $\left\{o_n\right\}$, $\left\{k_n\right\}$ are appropriate sequences in $(0,1)$.

It was proved that the rate of convergence of iteration scheme (7) is same as the Picard iteration scheme but faster than Mann iteration scheme for the class of contraction mappings [20].

An iterative scheme $\{p_n^{\left(5\right)}:n\in {\mathbb{Z}}^{+}\}$ introduced in [21] has a faster rate of convergence than $S-$ iteration for approximating the fixed points of contraction mappings. This scheme is given as:

$$\left\{\begin{array}{cc}{p}_0^{\left(5\right)}\in \hfill & \Omega \hfill \\ p_{n+1}^{\left(5\right)}=\hfill & (1-k_n)T{q}_n^{\left(5\right)}+k_{n}T{r}_n^{\left(5\right)}\hfill \\ q_n^{\left(5\right)}=\hfill & (1-o_n)T{p}_n^{\left(5\right)}+o_{n}T{r}_n^{\left(5\right)}\hfill \\ r_n^{\left(5\right)}=\hfill & (1-w_n)p_n^{\left(5\right)}+w_{n}T{p}_n^{\left(5\right)},\forall n\in {\mathbb{Z}}^{+}\hfill \end{array}\right.$$

(8)

where $\left\{w_n\right\},\left\{o_n\right\}$ and $\left\{k_n\right\}$ in $(0,1)$ satisfy certain appropriate conditions.

An iterative sequence $\{p_n^{\left(6\right)}:n\in {\mathbb{Z}}^{+}\}$

$$\left\{\begin{array}{cc}{p}_0^{\left(6\right)}\in \hfill & \Omega \hfill \\ p_{n+1}^{\left(6\right)}=\hfill & (1-k_n)T{r}_n^{\left(6\right)}+k_{n}T{q}_n^{\left(6\right)}\hfill \\ q_n^{\left(6\right)}=\hfill & (1-o_n)r_n^{\left(6\right)}+o_{n}T{r}_n^{\left(6\right)}\hfill \\ r_n^{\left(6\right)}=\hfill & (1-w_n)p_n^{\left(6\right)}+w_{n}T{p}_n^{\left(6\right)},\forall n\in {\mathbb{Z}}^{+}\hfill \end{array}\right.$$

(9)

proposed by Thakur et al. [6] has a better rate of convergence than iterative sequence in [21], where the sequences $\left\{w_n\right\},\left\{o_n\right\}$ and $\left\{k_n\right\}$ are given sequences in $(0,1)$.

In 2018, Ullah et al. [22] introduced M-iteration sequence $\{p_n^{\left(7\right)}:n\in {\mathbb{Z}}^{+}\}$ as follows

$$\left\{\begin{array}{cc}{p}_0^{\left(7\right)}\in \hfill & \Omega \hfill \\ p_{n+1}^{\left(7\right)}=\hfill & T{q}_n^{\left(7\right)}\hfill \\ q_n^{\left(7\right)}=\hfill & T{r}_n^{\left(7\right)}\hfill \\ r_n^{\left(7\right)}=\hfill & (1-w_n)p_n^{\left(7\right)}+w_{n}T{p}_n^{\left(7\right)},\forall n\in {\mathbb{Z}}^{+}\hfill \end{array}\right.$$

(10)

for approximating the fixed points of Suzuki’s generalized nonexpansive mappings, where $\left\{w_n\right\}\subset (0,1)$.

Ali et al. [2] modified an M-iteration sequence by introducing F-iteration sequence $\{p_n^{\left(8\right)}:n\in {\mathbb{Z}}^{+}\}$ given by

$$\left\{\begin{array}{cc}{p}_0^{\left(8\right)}\in \hfill & \Omega \hfill \\ p_{n+1}^{\left(8\right)}=\hfill & T{q}_n^{\left(8\right)}\hfill \\ q_n^{\left(8\right)}=\hfill & T{r}_n^{\left(8\right)}\hfill \\ r_n^{\left(8\right)}=\hfill & T((1-w_n)p_n^{\left(8\right)}+w_{n}T{p}_n^{\left(8\right)}),\forall n\in {\mathbb{Z}}^{+}\hfill \end{array}\right.$$

(11)

where $\left\{w_n\right\}\subset (0,1)$. They showed that F-iteration sequence has a better rate of convergence than M-iteration and all other iterative schemes presented in [2].

For practical purposes, we deal with an approximate sequence $\left\{a_n\right\};$ we obtain it because of numerical approximation of operator and round off errors, instead of a theoretical sequence $\left\{p_n\right\}$ obtained through an iterative process $p_{n+1}=f(T,p_n)$ for some given function f.

The approximate sequence $\left\{a_n\right\}$ converges to fixed point of T if and only if the given fixed point iterative scheme is stable. The notion of the stability for a fixed point iterative scheme was introduced by Ostrowski [23].

Definition 3.

Let $\left\{a_n\right\}$ be an approximate sequence of $\left\{p_n\right\}$ in a subset Ω of a Banach space U. Then a given iterative process $p_{n+1}=f(T_{\lambda },p_n)$ for some function f, converging to a fixed point $p^{*}$ of self mapping T on Ω, is said to be T-stable or stable with respect to T provided that ${lim}_{n\to \infty }{e}_n=0$ if and only if ${lim}_{n\to \infty }{a}_n=p^{*}$, where $\left\{e_n\right\}$ is given by

$$e_n=\parallel a_{n+1}-f(T,a_n)\parallel ,\forall n\in {\mathbb{Z}}^{+}.$$

Following results are needed in the sequel.

Lemma 3

([15]). Let $\left\{u_n\right\}$ and $\left\{e_n\right\}$ be sequences of positive real numbers satisfying the following inequality:

$$u_{n+1}\le (1-{\upsilon }_n)u_n+e_n$$

where ${\upsilon }_n\in (0,1)$ for all $n\in {\mathbb{Z}}^{+}$ with ${\mathsf{\Sigma }}_{n=0}^{\infty }{\upsilon }_n=\infty$. If ${lim}_{n\to \infty }\frac{e_n}{{\upsilon }_n}=0,$ then ${lim}_{n\to \infty }{u}_n=0$.

Question: Continuing in this direction, we pose the following question:

Is it possible to construct an iterative scheme which is faster than iterative schemes (3)–(11).

To answer the above question in affirmative, we introduce an $AA$-iterative scheme $\{p_n:n\in {\mathbb{Z}}^{+}\}$ for an averaged mapping to approximate the fixed points of enriched contraction mappings as follows:

$$\left\{\begin{array}{cc}{p}_0\in \hfill & \Omega \hfill \\ p_{n+1}=\hfill & T_{\lambda }{q}_n\hfill \\ q_n=\hfill & T_{\lambda }((1-k_n)T_{\lambda }{s}_n+k_n{T}_{\lambda }{r}_n)\hfill \\ r_n=\hfill & T_{\lambda }((1-o_n)s_n+o_n{T}_{\lambda }{s}_n)\hfill \\ s_n=\hfill & (1-w_n)p_n+w_n{T}_{\lambda }{p}_n,\forall n\in {\mathbb{Z}}^{+}\hfill \end{array}\right.$$

(12)

where $\left\{w_n\right\},\left\{o_n\right\}$ and $\left\{k_n\right\}$ are sequences of parameters in $(0,1)$.

The aim of this paper is to show that an $AA$-iterative scheme has a faster rate of convergence than $\left(3\right)$–$\left(11\right)$. Strong and week convergence results are also established for a b-enriched nonexpansive mapping. Numerical examples are presented to compare the rate of convergence with Ishikawa, Noor, Agarwal et al., Abbas et al. and Thakur et al., M-iteration and F-iteration for classes of contraction and $(b,\eta )$-enriched contraction mappings. As an application, we approximate the solution of delay fractional differential equations by using our proposed scheme.

2. Convergence and Stability Results

In this section, we establish convergence and stability of AA-iterative scheme $\left(12\right)$ constructed with $(b,\eta )$-enriched contractions mapping in arbitrary Banach space.

Theorem 1.

Let Ω be a nonempty closed and convex subset of a Banach space U and $T:\Omega \to \Omega$ a $(b,\eta )$-enriched contraction mapping with $F\left(T\right)\ne \varnothing$. Then, the sequence $\left\{p_n\right\}$ defined by $\left(12\right)$ converges to a fixed point of $T.$

Proof. 

Take $b=\frac{1}{\lambda }-1$, it follows that $\lambda \in (0,1)$. Then $\left(2\right)$ becomes

$$\parallel (\frac{1}{\lambda }-1)(p-q)+Tp-Tq\parallel \le \eta \parallel p-q\parallel ,$$

which can be written in an equivalent form as follows:

$$\parallel T_{\lambda }p-T_{\lambda }q\parallel \le \epsilon \parallel p-q\parallel ,$$

(13)

where $\epsilon =\lambda \eta$. As $\eta \in (0,b+1)$, $\epsilon \in (0,1)$. Thus an averaged operator $T_{\lambda }$ is a contraction with contractive constant $\epsilon$. Let $p^{*}\in F\left(T\right).$ Then, we have

$$\begin{array}{cc}\hfill \parallel s_n-p^{*}\parallel & =\parallel (1-w_n)p_n+w_n{T}_{\lambda }{p}_n-p^{*}\parallel \hfill \\ \hfill & \le (1-w_n)\parallel p_n-p^{*}\parallel +w_n\epsilon \parallel p_n-p^{*}\parallel \hfill \\ \hfill & =(1-(1-\epsilon )w_n)\parallel p_n-p^{*}\parallel .\hfill \end{array}$$

Further,

$$\begin{array}{cc}\hfill \parallel r_n-p^{*}\parallel & =\parallel T_{\lambda }((1-o_n)s_n+o_n{T}_{\lambda }{s}_n)-p^{*}\parallel \hfill \\ \hfill & \le \epsilon [(1-o_n)\parallel s_n-p^{*}\parallel +o_n\epsilon \parallel s_n-p^{*}\parallel \hfill \\ \hfill & =\epsilon [1-o_n+o_n\epsilon ]\parallel s_n-p^{*}\parallel \hfill \\ \hfill & \le \epsilon [1-(1-\epsilon )o_n)][1-(1-\epsilon )w_n)]\parallel p_n-p^{*}\parallel .\hfill \end{array}$$

Moreover,

$$\begin{array}{cc}\hfill \parallel q_n-p^{*}\parallel & =\parallel T_{\lambda }((1-k_n)T_{\lambda }{s}_n+k_n{T}_{\lambda }{r}_n)-p^{*}\parallel \hfill \\ \hfill & \le \epsilon \parallel (1-k_n)T_{\lambda }{s}_n+k_n{T}_{\lambda }{r}_n-p^{*}\parallel \hfill \\ \hfill & \le \epsilon [(1-k_n)\epsilon \parallel s_n-p^{*}\parallel +k_n\epsilon \parallel r_n-p^{*}\parallel ]\hfill \\ \hfill & \le {\epsilon }^2[(1-k_n)\parallel s_n-p^{*}\parallel +k_n\parallel r_n-p^{*}\parallel ].\hfill \end{array}$$

(14)

Note that

$$\begin{array}{cc}\hfill (1-k_n)\parallel s_n-p^{*}\parallel & \le (1-k_n)(1-(1-\epsilon )w_n)\parallel p_n-p^{*}\parallel \hfill \\ \hfill & =[(1-(k_n+w_n)+(w_n-k_n{w}_n)\epsilon ]\parallel p_n-p^{*}\parallel ,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill k_n\parallel r_n-p^{*}\parallel & \le k_n[\epsilon [1-(1-\epsilon )o_n)][1-(1-\epsilon )w_n)]\parallel p_n-p^{*}\parallel ]\hfill \\ \hfill & =\epsilon [k_n-k_n{o}_n-k_n{w}_n+\epsilon (k_n{o}_n+k_n{w}_n)+k_n{o}_n{w}_n\hfill \\ \hfill & -2\epsilon k_n{o}_n{w}_n+{\epsilon }^2{k}_n{o}_n{w}_n]\parallel p_n-p^{*}\parallel .\hfill \end{array}$$

Now by $\left(14\right)$, we have

$$\begin{array}{cc}\hfill \parallel q_n-p^{*}\parallel & \le {\epsilon }^2(1-k_n-w_n+k_n{w}_n+\epsilon [k_n+w_n-2k_n{w}_n-k_n{o}_n+k_n{o}_n{w}_n]\hfill \\ \hfill & +{\epsilon }^2[k_n{o}_n+k_n{w}_n-2k_n{o}_n{w}_n]+{\epsilon }^3\left[k_n{o}_n{w}_n\right])\parallel p_n-p^{*}\parallel \hfill \\ \hfill & \le {\epsilon }^2(1-k_n-w_n+k_n{w}_n+\epsilon [k_n+w_n-2k_n{w}_n-k_n{o}_n+k_n{o}_n{w}_n]\hfill \\ \hfill & +\epsilon [k_n{o}_n+k_n{w}_n-2k_n{o}_n{w}_n]+\epsilon \left[k_n{o}_n{w}_n\right])\parallel p_n-p^{*}\parallel \hfill \\ \hfill & ={\epsilon }^2[1-k_n-w_n+k_n{w}_n+\epsilon k_n+\epsilon w_n-\epsilon k_n{w}_n]\parallel p_n-p^{*}\parallel \hfill \\ \hfill & ={\epsilon }^2[1-(1-\epsilon )(k_n+w_n-k_n{w}_n)]\parallel p_n-p^{*}\parallel .\hfill \end{array}$$

Thus,

$$\begin{array}{cc}\hfill \parallel p_{n+1}-p^{*}\parallel & =\parallel T_{\lambda }{q}_n-p^{*}\parallel \hfill \\ \hfill & \le \epsilon \parallel q_n-p^{*}\parallel \hfill \\ \hfill & \le \epsilon \left[{\epsilon }^2[1-(1-\epsilon )(k_n+w_n-k_n{w}_n)]\right]\parallel p_n-p^{*}\parallel \hfill \\ \hfill & \le {\epsilon }^3[1-(1-\epsilon )(k_n+w_n-k_n{w}_n)]\parallel p_n-p^{*}\parallel .\hfill \end{array}$$

(15)

Inductively, we can obtain that

$$\parallel p_{n+1}-p^{*}\parallel \le {\epsilon }^{3n}[1-(1-\epsilon )(k_n+w_n-k_n{w}_n)]\parallel p_0-p^{*}\parallel .$$

(16)

As $0<{\epsilon }^{3n}\left(1-(1-\epsilon )(k_n+w_n-k_n{w}_n)\right)<1$, $\left\{p_n\right\}$ converges to $p^{*}$. □

Theorem 2.

Let Ω be a closed convex subset of a uniformly convex Banach space U and T a $(b,\eta )$-enriched contraction with $F\left(T\right)\ne \varnothing$. Suppose that the sequences $\left\{p_n^{\left(1\right)}\right\}$, $\left\{p_n^{\left(2\right)}\right\}$, $\left\{p_n^{\left(3\right)}\right\}$, $\left\{p_n^{\left(4\right)}\right\}$, $\left\{p_n^{\left(5\right)}\right\}$, $\left\{p_n^{\left(6\right)}\right\}$, $\left\{p_n^{\left(7\right)}\right\}$, $\left\{p_n^{\left(8\right)}\right\}$, $\left\{p_n\right\}$ given by iterative schemes $\left(4\right)$, $\left(5\right)$, $\left(6\right)$, $\left(7\right)$, $\left(8\right)$, $\left(9\right)$, $\left(10\right)$, $\left(11\right)$, $\left(12\right)$, respectively, converge to $p^{*}\in F\left(T\right)$. Then, $\left\{p_n\right\}$ converges at a rate faster than the other schemes.

Proof. 

Let $p^{*}\in F\left(T\right).$ As proved in Theorem 3 of [21], we have

$$\begin{array}{cc}\hfill \parallel p_{n+1}^{\left(4\right)}-p^{*}\parallel & \le {\epsilon }^n{\left(1-(1-\epsilon )k_n{o}_n{w}_n\right)}^n\parallel p_1^{\left(4\right)}-p^{*}\parallel \forall n\in \mathbb{N}.\hfill \\ \hfill \parallel p_{n+1}^{\left(4\right)}-p^{*}\parallel & \le {\epsilon }^n{\left(1-(1-\epsilon )k_n{o}_n{w}_n\right)}^n\parallel p_1^{\left(4\right)}-p^{*}\parallel =a_n\left(\mathrm{say}\right).\hfill \end{array}$$

(17)

Now, by $\left(16\right)$ in above theorem, we have

$$\parallel p_{n+1}-p^{*}\parallel ={\epsilon }^{3n}{\left(1-(1-\epsilon )(k_n+w_n-k_n{w}_n)\right)}^n\parallel p_1-p^{*}\parallel =b_n\left(\mathrm{say}\right).$$

Then,

$$\begin{array}{cc}\hfill \frac{b_n}{a_n}& =\frac{{\epsilon }^{3n}{\left(1-(1-\epsilon )(k_n+w_n-k_n{w}_n)\right)}^n\parallel p_1-p^{*}\parallel }{{\epsilon }^n{\left(1-(1-\epsilon )k_n{o}_n{w}_n\right)}^n\parallel p_1^{\left(4\right)}-p^{*}\parallel }\hfill \\ \hfill & ={\epsilon }^{2n}{\left(\frac{1-(1-\epsilon )(k_n+w_n-k_n{w}_n)}{1-(1-\epsilon )k_n{o}_n{w}_n}\right)}^n\frac{\parallel p_1-p^{*}\parallel }{\parallel p_1^{\left(4\right)}-p^{*}\parallel }.\hfill \end{array}$$

(18)

So, we have $\frac{b_n}{a_n}\to 0$ as $n\to \infty$. Definition (2) implies that $\left\{p_n\right\}$ converges faster than $\left\{p_n^{\left(4\right)}\right\}$ to the fixed point $p^{*}.$ Now, the inequality proved in Theorem 3.1 of Thakur et al. [6]

$$\parallel p_{n+1}^{\left(5\right)}-p^{*}\parallel \le {\epsilon }^n{(1-(1-\epsilon )w_n)}^n\parallel p_1^{\left(5\right)}-p^{*}\parallel .$$

Let

$$\parallel p_{n+1}^{\left(5\right)}-p^{*}\parallel ={\epsilon }^n{(1-(1-\epsilon )w_n)}^n\parallel p_1^{\left(5\right)}-p^{*}\parallel =c_n.$$

So,

$$\begin{array}{cc}\frac{b_n}{c_n}\hfill & =\frac{{\epsilon }^{3n}{\left(1-(1-\epsilon )(k_n+w_n-k_n{w}_n)\right)}^n\parallel p_1-p^{*}\parallel }{{\epsilon }^n{(1-(1-\epsilon )w_n)}^n\parallel p_1^{\left(5\right)}-p^{*}\parallel }\hfill \\ \hfill & ={\epsilon }^{2n}{\left(\frac{1-(1-\epsilon )(k_n+w_n-k_n{w}_n)}{1-(1-\epsilon )w_n}\right)}^n\frac{\parallel p_1-p^{*}\parallel }{\parallel p_1^{\left(5\right)}-p^{*}\parallel }.\hfill \end{array}$$

(19)

So, we have $\frac{b_n}{c_n}\to 0$ as $n\to \infty$. It implies that $\left\{p_n\right\}$ converges faster than $\left\{p_n^{\left(5\right)}\right\}$ to the fixed point $p^{*}.$

Similarly, we can show that the sequence $\left\{p_n\right\}$ has better rate of convergence than all other sequences define above. □

Theorem 3.

Let Ω be a nonempty closed and convex subset of a Banach space U and $T:\Omega \to \Omega$ a $(b,\eta )$-enriched contraction mapping. Then, the iterative scheme defined in $\left(12\right)$ is $T_{\lambda }$-stable for $\lambda =\frac{1}{b+1}$.

Proof. 

Let $\left\{a_n\right\}$ be an approximate sequence of $\left\{p_n\right\}$ in $\Omega$. The sequence defined by iteration $\left(12\right)$ is:

$p_{n+1}=f(T_{\lambda },p_n)$ and $e_n=\parallel a_{n+1}-f(T_{\lambda },a_n)\parallel$, $n\in \mathbb{N}.$

We need to show that ${lim}_{n\to \infty }{e}_n=0$ if and only if ${lim}_{n\to \infty }{a}_n=p^{*}.$

If ${lim}_{n\to \infty }{e}_n=0$, it follows from $\left(12\right)$ that

$$\begin{array}{cc}\hfill \parallel a_{n+1}-p^{*}\parallel & \le \parallel a_{n+1}-f(T_{\lambda },a_n)\parallel +\parallel f(T_{\lambda },a_n)-p^{*}\parallel \hfill \\ \hfill & =e_n+\parallel p_{n+1}-p^{*}\parallel .\hfill \end{array}$$

(20)

By Theorem 1, we have

$$\parallel a_{n+1}-p^{*}\parallel \le e_n+{\epsilon }^3[1-(1-\epsilon )(k_n+w_n-k_n{w}_n)]\parallel a_n-p^{*}\parallel .$$

Let

$${\alpha }_n=\parallel a_n-p^{*}\parallel \mathrm{and}{\beta }_n=(1-\epsilon )(k_n+w_n-k_n{w}_n).$$

Then,

$${\alpha }_n\le {\epsilon }^3(1-{\beta }_n){\alpha }_n+e_n.$$

Since, ${lim}_{n\to \infty }{e}_n=0$, $\frac{e_n}{{\beta }_n}\to 0$ as $n\to \infty .$

Now, by Lemma 3, we have ${lim}_{n\to \infty }{\alpha }_n=0$ and hence ${lim}_{n\to \infty }{a}_n=p^{*}.$

Conversely, if ${lim}_{n\to \infty }{a}_n=p^{*},$ then we have

$$\begin{array}{cc}\hfill e_n=& \parallel a_{n+1}-f(T_{\lambda },a_n)\parallel \hfill \\ \hfill \le & \parallel a_{n+1}-p^{*}\parallel +\parallel f(T_{\lambda },a_n)-p^{*}\parallel \hfill \\ \hfill \le & \parallel a_{n+1}-p^{*}\parallel +{\epsilon }^3[1-(1-\epsilon )(k_n+w_n-k_n{w}_n)]\parallel a_n-p^{*}\parallel .\hfill \end{array}$$

(21)

This implies that ${lim}_{n\to \infty }{e}_n=0.$ Hence, the iterative scheme $\left(12\right)$ is $T_{\lambda }$-stable. □

We now present an example to support our assertion that our iterative process $\left(12\right)$ converges faster than all other iterative schemes considered herein for the class of $(b,\eta )$-enriched contraction mappings.

Example 1.

Let $U=\mathbb{R}$ and $\Omega =[0,10].$ Let $T:\Omega \to \Omega$ be a mapping given by $T\left(p\right)=10-p$ for all $p\in \Omega .$ Choose $k_n=\frac{10}{11},o_n=\frac{10}{13}$ and $w_n=\frac{5}{6}$, with the initial value of $p_1=8.$

Note that T is $(\frac{3}{5},\frac{5}{8})$-enriched contraction with fixed point 5. So $T_{\frac{5}{8}}\left(p\right)=\frac{25-p}{4}$.

Our iteration $\left(12\right)$, F-iteration $\left(11\right),$ M-iteration $\left(10\right),$ Thakur et al. $\left(9\right),$ Abbas and Nazir $\left(8\right),$ Agarwal et al. $\left(7\right)$ and Noor $\left(6\right)$ iterative processes are given in

Table 1. Convergence comparison of iterative schemes for $(b,\eta )$-enriched contraction mapping.

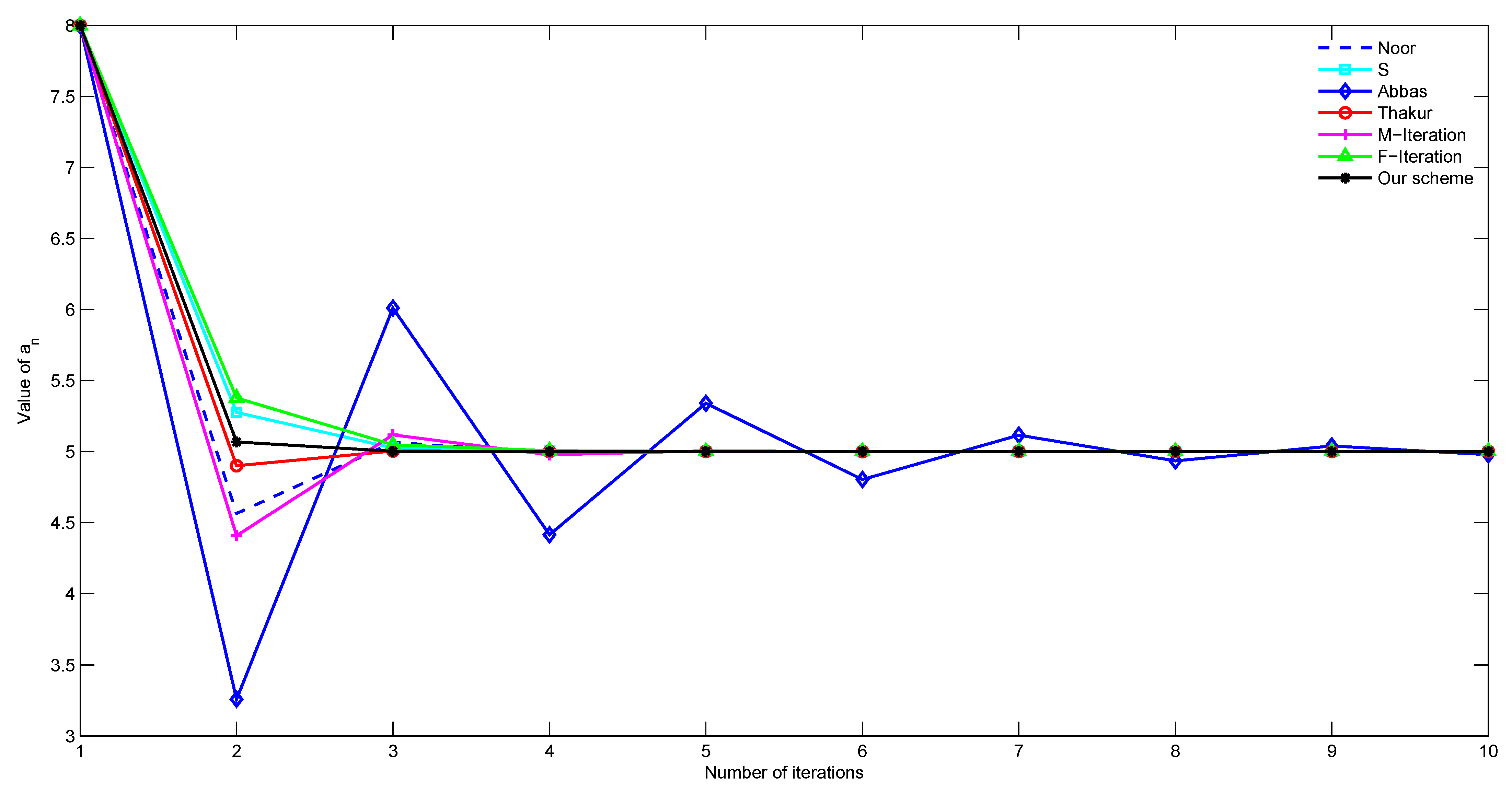
Steps	Our Scheme	F-Iteration	M-Iteration	Thakur	Abbas	Agarwal (S)	Noor
1	8.0000000000	8.0000000000	8.0000000000	8.0000000000	8.0000000000	8.0000000000	8.0000000000
2	5.0676378241	5.3769675444	4.4076224301	4.8998176879	3.2590564957	5.2755013581	4.5632864505
3	5.0015249584	5.0473681765	5.1169703950	5.0033454985	6.0102947616	5.0253003327	5.0635729080
4	5.0000343816	5.0059520883	4.9769031205	4.9998882800	4.4137112990	5.0023234253	4.9907456165
5	5.0000007751	5.0007479147	5.0045606911	5.0000037307	5.3402318351	5.0002133689	5.0013471715
6	5.0000000174	5.0000939798	4.9990994496	4.9999998754	4.8025585322	5.0000195944	4.9998038906
7	5.0000000003	5.0000118091	5.0001778219	5.0000000041	5.1145781469	5.0000017994	5.0000285478
8	5.0000000000	5.0000014838	4.9999648874	4.9999999998	4.9335086397	5.0000001652	4.9999958442
9	5.0000000000	5.0000001864	5.0000069333	5.0000000000	5.0385859005	5.0000000151	5.0000006049
10	5.0000000000	5.0000000234	4.9999986309	4.9999999999	4.9776080423	5.0000000013	4.9999999119
11	5.0000000000	5.0000000029	5.0000002703	5.0000000000	5.0129943777	5.0000000001	5.0000000128
12	5.0000000000	5.0000000003	4.9999999466	5.0000000000	4.9924591741	5.0000000000	4.9999999981
13	5.0000000000	5.0000000000	5.0000000105	5.0000000000	5.0043760505	5.0000000000	5.0000000002
14	5.0000000000	5.0000000000	4.9999999979	5.0000000000	4.9974605143	5.0000000000	4.9999999999
15	5.0000000000	5.0000000000	5.0000000004	5.0000000000	5.0014737003	5.0000000000	5.0000000000

.

Note that all sequences converge to $p^{*}=5$. The comparison shows that our iteration scheme $\left(12\right)$ converges faster than all the other schemes.

Here we present another numerical example to support our claim.

Example 2.

Let $U=\mathbb{R}$, and $\Omega =[1,50].$ Let $T:\Omega \to \Omega$ be defined as

$$T\left(p\right)=\sqrt{p^2-6p+48}$$

for all $p\in \Omega .$ Choose $k_n=\frac{3}{4},o_n=\frac{1}{2}$ and $w_n=\frac{1}{4}$, with the initial value of $p_1=32.$

Our iteration scheme $\left(12\right)$ along with other iterative schemes for $\lambda =1$ are given in

Table 2. Convergence comparison of iterative schemes for contraction mapping.

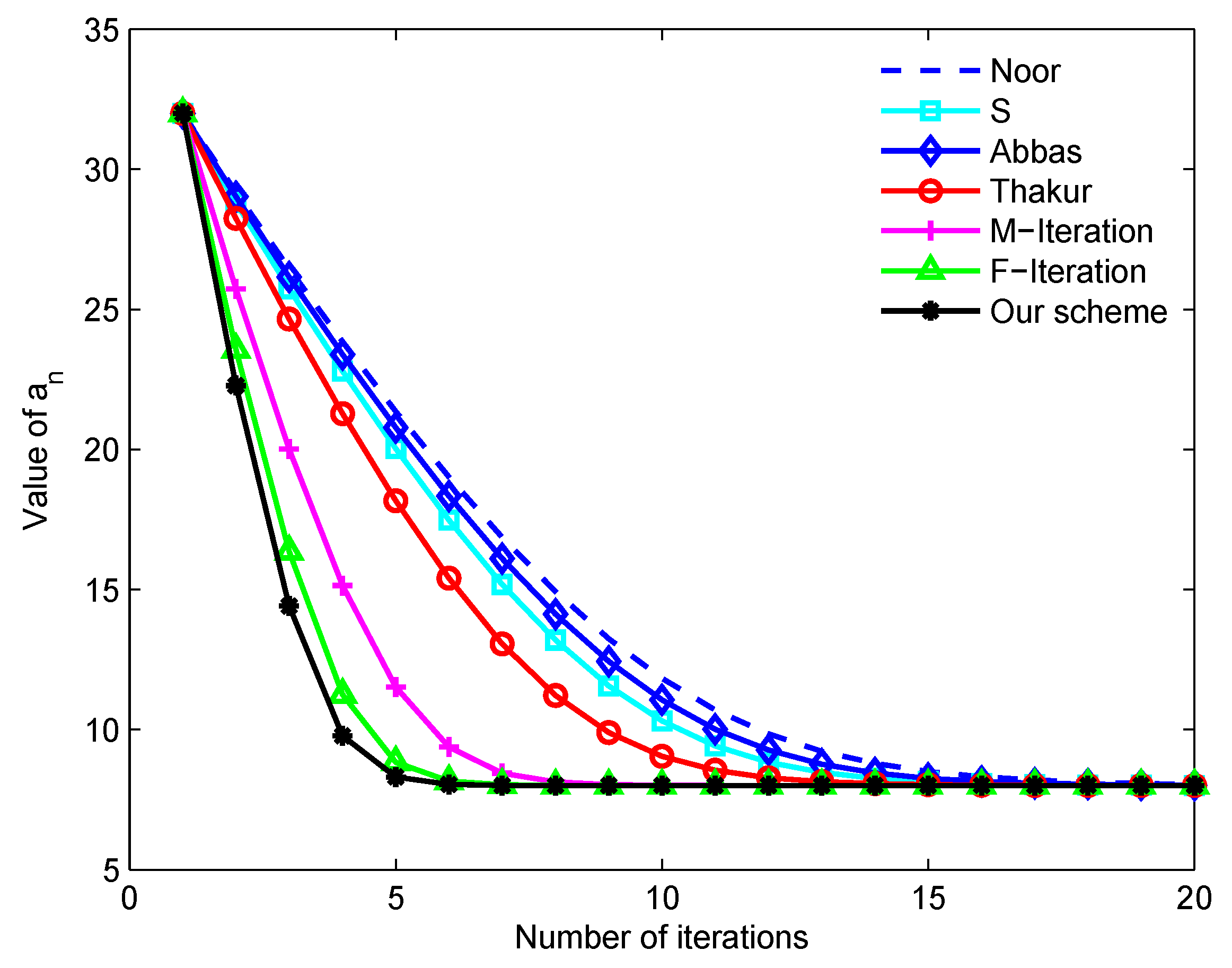
Steps	Our Scheme	F-Iteration	M-Iteration	Thakur	Abbas	Agarwal (S)	Noor	Ishikawa
1	32.000000	32.000000	32.000000	32.000000	32.000000	32.000000	32.000000	32.000000
2	22.278205	23.567093	25.724609	28.244764	28.597925	28.809511	29.184632	29.393312
3	14.413304	16.360701	20.010430	24.655942	25.328526	25.733352	26.459743	26.862041
4	9.773593	11.249118	15.144634	21.277941	22.223234	22.796602	23.842420	24.419226
5	8.306540	8.830832	11.514396	18.169031	19.322437	20.031078	21.353609	22.080669
6	8.044444	8.101773	9.373660	15.402469	16.676705	17.476424	19.018608	19.865335
7	8.006238	8.028979	8.445143	13.061008	14.345486	15.179932	16.867035	17.795540
8	8.000871	8.005104	8.131183	11.216802	12.389581	13.192971	14.931542	15.896548
9	8.000122	8.000896	8.037368	9.894756	10.853750	11.561186	13.244292	14.195061
10	8.000017	8.000157	8.010535	9.042566	9.742503	10.307701	11.830495	12.715924
11	8.000002	8.000027	8.002961	8.545043	9.006551	9.416511	10.700014	11.476899
12	8.000000	8.000004	8.000832	8.275745	8.557262	8.830642	9.840935	10.482609
13	8.000000	8.000001	8.000234	8.136916	8.299859	8.470871	9.219950	9.720547
14	8.000000	8.000000	8.000065	8.067312	8.158591	8.260996	8.790497	9.162136
15	8.000000	8.000000	8.000018	8.032926	8.083060	8.142693	8.503861	8.768990
16	8.000000	8.000000	8.000005	8.016066	8.043271	8.077396	8.317512	8.501076
17	8.000000	8.000000	8.000001	8.007829	8.022479	8.041793	8.198569	8.322954
18	8.000000	8.000000	8.000000	8.003813	8.011660	8.022512	8.123571	8.206601
19	8.000000	8.000000	8.000000	8.001857	8.006044	8.012111	8.076659	8.131513
20	8.000000	8.000000	8.000000	8.000904	8.003131	8.006510	8.047462	8.083445
21	8.000000	8.000000	8.000000	8.000440	8.001622	8.003498	8.029349	8.052835
22	8.000000	8.000000	8.000000	8.000214	8.000840	8.001879	8.018135	8.033409
23	8.000000	8.000000	8.000000	8.000104	8.000435	8.001010	8.011200	8.021107
24	8.000000	8.000000	8.000000	8.000051	8.000225	8.000542	8.006915	8.013328
25	8.000000	8.000000	8.000000	8.000025	8.000117	8.000291	8.004269	8.008413
26	8.000000	8.000000	8.000000	8.000012	8.000060	8.000156	8.002635	8.005309
27	8.000000	8.000000	8.000000	8.000006	8.000031	8.000084	8.001626	8.003350
28	8.000000	8.000000	8.000000	8.000003	8.000016	8.000045	8.001004	8.002114
29	8.000000	8.000000	8.000000	8.000001	8.000008	8.000024	8.000619	8.001334
30	8.000000	8.000000	8.000000	8.000000	8.000004	8.000013	8.000382	8.000841
31	8.000000	8.000000	8.000000	8.000000	8.000002	8.000007	8.000236	8.000531
32	8.000000	8.000000	8.000000	8.000000	8.000001	8.000003	8.000146	8.000335
33	8.000000	8.000000	8.000000	8.000000	8.000000	8.000002	8.000090	8.000211
34	8.000000	8.000000	8.000000	8.000000	8.000000	8.000001	8.000055	8.000133
35	8.000000	8.000000	8.000000	8.000000	8.000000	8.000000	8.000034	8.000084
36	8.000000	8.000000	8.000000	8.000000	8.000000	8.000000	8.000021	8.000053
37	8.000000	8.000000	8.000000	8.000000	8.000000	8.000000	8.000013	8.000033
38	8.000000	8.000000	8.000000	8.000000	8.000000	8.000000	8.000008	8.000021
39	8.000000	8.000000	8.000000	8.000000	8.000000	8.000000	8.000004	8.000013
40	8.000000	8.000000	8.000000	8.000000	8.000000	8.000000	8.000003	8.000008
41	8.000000	8.000000	8.000000	8.000000	8.000000	8.000000	8.000001	8.000005
42	8.000000	8.000000	8.000000	8.000000	8.000000	8.000000	8.000000	8.000003
43	8.000000	8.000000	8.000000	8.000000	8.000000	8.000000	8.000000	8.000002
44	8.000000	8.000000	8.000000	8.000000	8.000000	8.000000	8.000000	8.000001
45	8.000000	8.000000	8.000000	8.000000	8.000000	8.000000	8.000000	8.000000

.

All sequences converge to $p^{*}=8.$ The comparison shows that our iteration scheme $\left(12\right)$ has a better rate of convergence than other schemes.

In Table 1 we have the following observations regarding the convergence of fixed point of $(b,\eta )$-enriched contraction mapping mapping by taking initial point $x_1=8$. Observe that our iterative scheme converges to the fixed point $p^{*}=5$ in eight iterations while other described iterative schemes took more than 10 iterations for convergence.

In Table 2 we have the following observations regarding the convergence of fixed point of contraction mapping mapping by taking initial point $x_1=32$. Observe that our iterative scheme converges to the fixed point $p^{*}=8$ in 12 iterations, $F-$ Iteration in 14 iterations, M-iteration in 17 iterations and other iterative schemes took more than 30 iterations for convergence.

In Figure 1 and Figure 2, we test the convergence of different iteration processes for $(b,\eta )$-enriched contraction and contraction, respectively. Observe that in both cases our iterative scheme is more stable and converges faster to their fixed points than other iterative scheme.

3. Convergence Results for b-Enriched Nonexpansive Mappings

This section deals with some convergence results of an iterative process $\left(12\right).$

Theorem 4.

Let ${\Omega }^{{}^{\prime }}$ be a nonempty closed bounded convex subset of a uniformly convex Banach space U and $T:{\Omega }^{{}^{\prime }}\to {\Omega }^{{}^{\prime }}$ a b-enriched nonexpansive mapping. Then $F\left(T\right)\ne \varnothing$.

Proof. 

Since T is a b-enriched nonexpansive mapping, take $b=\frac{1}{\lambda }-1$.It follows that $\lambda \in (0,1)$. Then by $\left(1\right)$ we have

$$\parallel (\frac{1}{\lambda }-1)(p-q)+Tp-Tq\parallel \le (b+1)\parallel p-q\parallel ,$$

which can be written in equivalent form as

$$\parallel T_{\lambda }p-T_{\lambda }q\parallel \le \parallel p-q\parallel .$$

(22)

That is the averaged operator $T_{\lambda }$ is nonexpansive. By means of the Browder’s fixed point theorem, it follows that $T_{\lambda }$ has at least one fixed point. By remark 1 $,$ $F\left(T_{\lambda }\right)=F\left(T\right)\ne \varnothing$. □

Lemma 4.

Let ${\Omega }^{{}^{\prime }}$ be a nonempty bounded closed convex subset of a uniformly convex Banach space U and $T:{\Omega }^{{}^{\prime }}\to {\Omega }^{{}^{\prime }}$ a b-enriched nonexpansive mapping. If $\left\{p_n\right\}$ is a sequence defined in $\left(12\right)$ and $F\left(T\right)\ne \varnothing ,$ then ${lim}_{n\to \infty }\parallel p_n-p^{*}\parallel$ exists for all $p^{*}\in F\left(T\right).$

Proof. 

By Theorem 4, an averaged operator $T_{\lambda }$ is nonexpansive. Let $p^{*}\in F\left(T_{\lambda }\right).$ Then,

$$\begin{array}{cc}\hfill \parallel s_n-p^{*}\parallel & =\parallel (1-w_n)p_n+w_n{T}_{\lambda }{p}_n-p^{*}\parallel \hfill \\ \hfill & \le (1-w_n)\parallel p_n-p^{*}\parallel +w_n\parallel T_{\lambda }{p}_n-p^{*}\parallel \hfill \\ \hfill & \le (1-w_n)\parallel p_n-p^{*}\parallel +w_n\parallel p_n-p^{*}\parallel \hfill \\ \hfill & \le \parallel p_n-p^{*}\parallel .\hfill \end{array}$$

(23)

Thus,

$$\begin{array}{cc}\hfill \parallel r_n-p^{*}\parallel & =\parallel T_{\lambda }((1-o_n)s_n+o_n{T}_{\lambda }{s}_n)-p^{*}\parallel \hfill \\ \hfill & \le \parallel (1-o_n)s_n+o_n{T}_{\lambda }{s}_n-p^{*}\parallel \hfill \\ \hfill & \le (1-o_n)\parallel s_n-p^{*}\parallel +o_n\parallel T_{\lambda }{s}_n-p^{*}\parallel \hfill \\ \hfill & \le (1-o_n)\parallel s_n-p^{*}\parallel +o_n\parallel s_n-p^{*}\parallel \hfill \\ \hfill & \le \parallel s_n-p^{*}\parallel \hfill \\ \hfill & \le \parallel p_n-p^{*}\parallel ,\hfill \end{array}$$

(24)

and

$$\begin{array}{cc}\hfill \parallel q_n-p^{*}\parallel & =\parallel T_{\lambda }((1-k_n)T_{\lambda }{s}_n+k_n{T}_{\lambda }{r}_n)-p^{*}\parallel \hfill \\ \hfill & \le \parallel (1-k_n)T_{\lambda }{s}_n+k_n{T}_{\lambda }{r}_n-p^{*}\parallel \hfill \\ \hfill & \le (1-k_n)\parallel T_{\lambda }{s}_n-p^{*}\parallel +k_n\parallel T_{\lambda }{r}_n-p^{*}\parallel \hfill \\ \hfill & \le (1-k_n)\parallel s_n-p^{*}\parallel +k_n\parallel r_n-p^{*}\parallel \hfill \\ \hfill & \le (1-k_n)\parallel s_n-p^{*}\parallel +k_n\parallel s_n-p^{*}\parallel \hfill \\ \hfill & \le \parallel s_n-p^{*}\parallel \hfill \\ \hfill & \le \parallel p_n-p^{*}\parallel .\hfill \end{array}$$

(25)

Now,

$$\begin{array}{cc}\hfill \parallel p_{n+1}-p^{*}\parallel & =\parallel T_{\lambda }{q}_n-p^{*}\parallel \hfill \\ \hfill & \le \parallel q_n-p^{*}\parallel \hfill \\ \hfill & \le \parallel p_n-p^{*}\parallel .\hfill \end{array}$$

(26)

So, $\{\parallel p_n-p^{*}\parallel \}$ is a bounded monotone decreasing sequence. Therefore, ${lim}_{n\to \infty }\parallel p_n-p^{*}\parallel$ exists for all $p^{*}\in F\left(T_{\lambda }\right)=F\left(T\right).$ □

Lemma 5.

Let T, ${\Omega }^{{}^{\prime }}$ and U be as given in Lemma 4 and $\left\{p_n\right\}$ a sequence defined by $\left(12\right)$ and $F\left(T\right)\ne \varnothing .$ Then ${lim}_{n\to \infty }\parallel p_n-T_{\lambda }{p}_n\parallel =0$, where $\lambda =\frac{1}{b+1}.$

Proof. 

Let $p^{*}\in F\left(T\right).$ Then, by Lemma 4, ${lim}_{n\to \infty }\parallel p_n-p^{*}\parallel$ exists. Suppose that

$$\underset{n\to \infty }{lim}\parallel p_n-p^{*}\parallel =l.$$

(27)

By taking limit supremum as $n\to \infty$ on both sides of $\left(23\right)$–$\left(25\right)$, we have

$$\begin{array}{cc}\hfill & \underset{n\to \infty }{lim\; sup}\parallel s_n-p^{*}\parallel \le l,\underset{n\to \infty }{lim\; sup}\parallel r_n-p^{*}\parallel \le l,\mathrm{and}\hfill \\ \hfill & \underset{n\to \infty }{lim\; sup}\parallel q_n-p^{*}\parallel \le l.\hfill \end{array}$$

(28)

Since, $T_{\lambda }$ is nonexpansive mapping, we have

$$\begin{array}{ccc}\hfill \parallel T_{\lambda }{p}_n-p^{*}\parallel & \le & \parallel p_n-p^{*}\parallel ,\hfill \\ \hfill \parallel T_{\lambda }{r}_n-p^{*}\parallel & \le & \parallel r_n-p^{*}\parallel ,\mathrm{and}\hfill \\ \hfill \parallel T_{\lambda }{q}_n-p^{*}\parallel & \le & \parallel q_n-p^{*}\parallel .\hfill \end{array}$$

By taking limit supremum on both sides, we obtain

$$\begin{array}{cc}\hfill \underset{n\to \infty }{lim\; sup}\parallel T_{\lambda }{p}_n-p^{*}\parallel & \le l\hfill \\ \hfill \underset{n\to \infty }{lim\; sup}\parallel T_{\lambda }{s}_n-p^{*}\parallel & \le l\hfill \\ \hfill \underset{n\to \infty }{lim\; sup}\parallel T_{\lambda }{r}_n-p^{*}\parallel & \le l\hfill \\ \hfill \underset{n\to \infty }{lim\; sup}\parallel T_{\lambda }{q}_n-p^{*}\parallel & \le l.\hfill \end{array}$$

(29)

Since,

$$\begin{array}{cc}\hfill l& =\underset{n\to \infty }{lim\; inf}\parallel p_{n+1}-p^{*}\parallel \hfill \\ \hfill & =\underset{n\to \infty }{lim\; inf}\parallel T{q}_n-p^{*}\parallel \hfill \\ \hfill & \le \underset{n\to \infty }{lim\; inf}\parallel q_n-p^{*}\parallel .\hfill \end{array}$$

(30)

So, from $\left(28\right)$ and $\left(30\right)$, we have

$$\underset{n\to \infty }{lim}\parallel q_n-p^{*}\parallel =l$$

and

$$\begin{array}{cc}\hfill l& =\underset{n\to \infty }{lim}\parallel q_n-p^{*}\parallel \hfill \\ \hfill & =\underset{n\to \infty }{lim}\parallel q_n-p^{*}\parallel .\hfill \end{array}$$

So,

$$\begin{array}{cc}\hfill \parallel q_n-p^{*}\parallel & =\parallel T_{\lambda }((1-k_n)T_{\lambda }{s}_n+k_n{T}_{\lambda }{r}_n)-p^{*}\parallel \hfill \\ \hfill & \le \parallel (1-k_n)T_{\lambda }{s}_n+k_n{T}_{\lambda }{r}_n-p^{*}\parallel \hfill \\ \hfill & \le (1-k_n)\parallel s_n-p^{*}\parallel +k_n\parallel r_n-p^{*}\parallel \hfill \\ \hfill & \le \parallel s_n-p^{*}\parallel .\hfill \end{array}$$

(31)

Taking lim inf as $n\to \infty$ on both sides of the above, we obtain

$$l\le \underset{n\to \infty }{lim\; inf}\parallel s_n-p^{*}\parallel .$$

This implies that

$$\begin{array}{cc}\hfill l& =\underset{n\to \infty }{lim}\parallel s_n-p^{*}\parallel \hfill \\ \hfill & =\underset{n\to \infty }{lim}\parallel (1-w_n)p_n+w_n{T}_{\lambda }{p}_n-p^{*}\parallel \hfill \\ \hfill & =\underset{n\to \infty }{lim}\parallel (1-w_n)(p_n-p^{*})+w_n(T_{\lambda }{p}_n-p^{*})\parallel .\hfill \end{array}$$

(32)

from $\left(27\right)$, $\left(29\right)$ and $\left(32\right)$ and by Lemma 1, we have

$$\underset{n\to \infty }{lim}\parallel p_n-T_{\lambda }{p}_n\parallel =0.$$

□

Theorem 5.

Let ${\Omega }^{{}^{\prime }}$ be a nonempty closed bounded convex subset of a real uniformly convex Banach space U which satisfies the Opial’s condition [24], and $T:{\Omega }^{{}^{\prime }}\to {\Omega }^{{}^{\prime }}$ a b-enriched nonexpansive mapping with $F\left(T\right)\ne \varnothing .$ If $\left\{p_n\right\}$ is a sequence defined by $\left(12\right)$, then $\left\{p_n\right\}$ converges weakly to a fixed point of T.

Proof. 

Let $p^{*}\in F\left(T\right)$. Then ${lim}_{n\to \infty }\parallel p_n-p^{*}\parallel$ exists. We prove that $\left\{p_n\right\}$ has a unique subsequential limit in $F\left(T\right).$ Let a and b be two weak limits of the subsequences $\left\{p_{n_i}\right\}$ and $\left\{p_{n_j}\right\}$ of $\left\{p_n\right\},$ respectively. As, ${lim}_{n\to \infty }\parallel p_n-T_{\lambda }{p}_{n_k}\parallel =0$ and $I-T_{\lambda }$ is demiclosed with respect to zero, where $\lambda =\frac{1}{b+1}$, by Lemma 2 we obtain that $T_{\lambda }a=a$. Similarly, we can show that $b\in F\left(T_{\lambda }\right).$ From Lemma 4, ${lim}_{n\to \infty }\parallel p_n-b\parallel$ exists. Next, we prove the uniqueness. If $a\ne b$, then by the Opial’s condition, we have

$$\begin{array}{cc}\hfill \underset{n\to \infty }{lim}\parallel p_n-a\parallel & \le \underset{n_i\to \infty }{lim}\parallel p_{n_i}-a\parallel \hfill \\ \hfill & <\underset{n_i\to \infty }{lim}\parallel p_{n_i}-b\parallel \hfill \\ \hfill & =\underset{n\to \infty }{lim}\parallel p_n-b\parallel \hfill \\ \hfill & =\underset{n_j\to \infty }{lim}\parallel p_{n_j}-b\parallel \hfill \\ \hfill & <\underset{n_j\to \infty }{lim}\parallel p_{n_j}-a\parallel \hfill \\ \hfill & =\underset{n\to \infty }{lim}\parallel p_n-a\parallel ,\hfill \end{array}$$

(33)

a contradiction, so $a=b$ and hence $\left\{p_n\right\}$ converges weakly to a fixed point of $T_{\lambda }=F\left(T\right)$. □

Theorem 6.

Let ${\Omega }^{{}^{\prime }}$ be a nonempty closed bounded convex subset of a uniformly convex Banach space U and $T:{\Omega }^{{}^{\prime }}\to {\Omega }^{{}^{\prime }}$ a b-enriched nonexpansive mapping. If $\left\{p_n\right\}$ is a sequence defined by $\left(12\right)$ and $F\left(T\right)\ne \varnothing ,$ then $\left\{p_n\right\}$ converges to a point in $F\left(T\right)$ if and only if ${lim\; inf}_{n\to \infty }d(p_n,F\left(T\right))=0$ or ${lim\; sup}_{n\to \infty }d(p_n,F\left(T\right))=0$, where $d(p_n,F\left(T\right))=inf\{\parallel p_n-p^{*}\parallel :p^{*}\in F\left(T\right)\}.$

Proof. 

Necessity is obvious.

Conversely, Since $p^{*}\in F\left(T_{\lambda }\right)$, so $d(p_n,F\left(T\right))=d(p_n,F\left(T_{\lambda }\right))$.

Suppose that ${lim\; inf}_{n\to \infty }d(p_n,F\left(T_{\lambda }\right))=0.$ As proved in Lemma 5, ${lim}_{n\to \infty }\parallel p_n-p^{*}\parallel$ exists for all $p^{*}\in F\left(T_{\lambda }\right),$ by the given assumption we have ${lim\; inf}_{n\to \infty }d(p_n,F\left(T_{\lambda }\right))=0,$ therefore ${lim}_{n\to \infty }d(p_n,F\left(T_{\lambda }\right))=0.$ We now show that $\left\{p_n\right\}$ is a Cauchy sequence in ${\Omega }^{{}^{\prime }}.$ As ${lim}_{n\to \infty }d(p_n,F\left(T_{\lambda }\right))=0,$ for given $ϵ>0$ there is $m_0\in \mathbb{N}$ such that for all $n\ge m_0,$ we have

$$d(p_n,F\left(T_{\lambda }\right))<\frac{ϵ}{2},$$

which implies that

$$inf\{\parallel p_n-p^{*}\parallel :p^{*}\in F\left(T_{\lambda }\right)\}<\frac{ϵ}{2}.$$

In particular, $inf\{\parallel p_{m_0}-p^{*}\parallel :p^{*}\in F\left(T_{\lambda }\right)\}<\frac{ϵ}{2}$. Hence there exists $p^{*}\in F\left(T_{\lambda }\right)$ such that

$$\parallel p_{m_0}-p^{*}\parallel <\frac{ϵ}{2}.$$

Now, for $m,n\ge m_0$

$$\begin{array}{cc}\hfill \parallel p_{m+n}-p_n\parallel & \le \parallel p_{m+n}-p^{*}\parallel +\parallel p_n-p^{*}\parallel \hfill \\ \hfill & \le \parallel p_{m_0}-p^{*}\parallel +\parallel p_{m_0}-p^{*}\parallel \hfill \\ \hfill & \le 2\parallel p_{m_0}-p^{*}\parallel \hfill \\ \hfill & \le ϵ.\hfill \end{array}$$

(34)

This shows that $\left\{p_n\right\}$ is a Cauchy sequence in ${\Omega }^{{}^{\prime }}$. As ${\Omega }^{{}^{\prime }}$ is closed and bounded subset of the Banach space U, there exists a point $q^{*}\in {\Omega }^{{}^{\prime }}$ such that ${lim}_{n\to \infty }{p}_n=q^{*}.$ Now, ${lim}_{n\to \infty }d(p_n,F\left(T_{\lambda }\right))=0$ gives that

$$d(p_n,F\left(T_{\lambda }\right))=0\Rightarrow q^{*}\in F\left(T_{\lambda }\right)=F\left(T\right).$$

□

Sentor and Dotson [25] introduced the notion of mapping satisfying Condition (I) which is given as follows:

Definition 4.

A mapping $T:{\Omega }^{{}^{\prime }}\to {\Omega }^{{}^{\prime }}$ is said to satisfy Condition (I), if there is a nondecreasing function $h:[0,\infty )\to [0,\infty )$ with $h\left(0\right)=0$ and $h\left(r\right)>0,\forall$$r>0$ such that

$$d(p,Tp)\ge h\left(d\right(p,F\left(T\right)\left)\right),$$

for all $p\in {\Omega }^{{}^{\prime }},$ where $d(p,F\left(T\right))=inf\{d(p,p^{*}):p^{*}\in F\left(T\right)\}$.

We now prove a strong convergence result by using the Condition (I).

Theorem 7.

Let ${\Omega }^{{}^{\prime }}$ be a nonempty closed bounded convex subset of a uniformly convex Banach space U and $T:{\Omega }^{{}^{\prime }}\to {\Omega }^{{}^{\prime }}$ a b-enriched nonexpansive mapping. Let $\left\{p_n\right\}$ be a sequence defined by $\left(12\right)$ and $F\left(T\right)\ne \varnothing$. If $T_{\lambda }$ satisfies Condition (I) for the value of $\lambda =\frac{1}{b+1}$, then $\left\{p_n\right\}$ converges strongly to a fixed point of T.

Proof. 

We proved in Lemma 5 that

$$\underset{n\to \infty }{lim}\parallel p_n-T_{\lambda }{p}_n\parallel =0.$$

From condition (I), we get

$$\underset{n\to \infty }{lim}h\left(d(p_n,F\left(T_{\lambda }\right))\right)\le \underset{n\to \infty }{lim}\parallel p_n-T_{\lambda }{p}_n\parallel =0.$$

That is, ${lim}_{n\to \infty }h\left(d(p_n,F\left(T_{\lambda }\right))\right)=0$. Since, $h:[0,\infty )\to [0,\infty )$ is a nondecreasing function with $h\left(0\right)=0$ and $h\left(r\right)>0,\forall r\in (0,\infty )$, we have ${lim}_{n\to \infty }d(p_n,F\left(T_{\lambda }\right))=0$. By Theorem 6, the sequence $\left\{p_n\right\}$ converges strongly to a point in $F\left(T_{\lambda }\right)=F\left(T\right)$. □

4. Application: Solution of Delay Fractional Differential Equations

In 1967, Caputo proposed a new form of fractional differentiation called Caputo’s fractional derivatives, which is defined as:

$${}^C{D}_t^{\alpha }f\left(t\right)=\frac{1}{\Gamma (\alpha -n)}{\int }_a^t{f}^{\left(n\right)}(\tau ){(t-\tau )}^{n-\alpha -1}d\tau ,(n-1<\alpha <n).$$

Under natural conditions on the function $f\left(t\right)$, for $\alpha \to n$ the Caputo derivative becomes a conventional n-th derivative of the function $f\left(t\right).$ The main advantage of Caputo’s approach is that the initial conditions for fractional differential equations with Caputo derivatives take on the same form as for integer-order differential equations, i.e., contain the limit value of integer-order derivatives of unknown functions at the lower terminal $t=a.$

In 2017, Cong and Tuan [26] obtained the existence and uniqueness of global solution of delay fractional differential equations by using properties of Mittag–Leffler functions and BCP. Many authors have solved the delay differential equations of fractional order using different approaches. For more details, we refer to [27,28,29,30,31].

Here, we estimate the solution of a delay fractional differential equation [26] by using an iterative scheme $\left(12\right)$ with $\alpha \in (0,1).$ Let $h>0$ be any constant and $\rho \in C([j-h,j]:{\mathbb{R}}^n)$ be a continuous mapping.

Consider the following delay Caputo fractional differential equation

$${}^c{D}^{\alpha }p\left(t\right)=f(t,p\left(t\right),p(t-h)),t\in [j,M]$$

(35)

with initial condition

$$p\left(t\right)=\rho \left(t\right),t\in [j-\tau ,j],$$

(36)

where $p\in {\mathbb{R}}^n,$$f:[j,M]\times {\mathbb{R}}^n\times {\mathbb{R}}^n\to {\mathbb{R}}^n$ is continuous, $\tau >0$ and $M>0.$ Suppose that the following conditions are fulfilled.

$\left(c_1\right)$

f satisfies the Lipschitz condition with respect to 2nd and 3rd variables: That is, there exists a positive constant $L_f$ (depending on f) such that

$$\parallel f(t,p,q)-f(t,\widehat{p},\widehat{q})\parallel \le L_f(\parallel p-\widehat{p}\parallel +\parallel q-\widehat{q}\parallel )$$

for all $t\in {\mathbb{R}}^{+}$ and $p,\widehat{p},q,\widehat{q}\in {\mathbb{R}}^n.$

$\left(c_2\right)$

There exists a positive constant ${\beta }_L$ depending upon L such that ${\beta }_L>2L$, that is, $\frac{2L}{{\beta }_L}<1.$

A function $p^{*}\in C([j-h,M]:{\mathbb{R}}^n)\cap C^1([j,M]:{\mathbb{R}}^n)$ is called solution of the initial value problem if it satisfies $\left(35\right)$ and $\left(36\right)$.

It is known that [32] finding the solution of $\left(35\right)$ and $\left(36\right)$ is equivalent to finding the solution of the following integral equation

$$p\left(t\right)=\rho \left(t\right)+\frac{1}{\Gamma (\alpha )}{\int }_j^t{(t-\tau )}^{(\alpha -1)}f(\tau ,p(\tau ),p(\tau -h))d\tau \forall t\in [j,M],$$

with $p\left(t\right)=\rho \left(t\right)$, $\forall t\in [j-h,M].$ Define a norm ${\parallel .\parallel }_{{\beta }_L}$ on $C([j-h,j]:{\mathbb{R}}^n)$ by

$${\parallel \rho \parallel }_{{\beta }_L}=\frac{sup\parallel \rho \left(t\right)\parallel }{E_{\alpha }\left({\beta }_L{t}^{\alpha }\right)},\mathrm{for}\mathrm{any}\rho \in C([j-h,j]:{\mathbb{R}}^n)$$

where $E_{\alpha }:\mathbb{R}\to \mathbb{R}$ is a Mittag–Leffler function defined as:

$$E_{\alpha }\left(t\right)={\mathsf{\Sigma }}_{n=0}^{\infty }\frac{t^n}{\Gamma (\alpha n+1)},\forall t\in \mathbb{R}.$$

Note that $C([j-h,j]:{\mathbb{R}}^n,\parallel .{\parallel }_{{\beta }_L})$ is a Banach space.

Wang et al. [27] proved the existence and uniqueness of solution of delay differential Equations $\left(35\right)$ and $\left(36\right)$ provided that the condition $\left(c_1\right)$ holds. In the following theorem, we obtain an approximation of the solution using an iterative scheme $\left(12\right)$ for $\lambda =1.$

Theorem 8.

Let ρ and f be functions as given above. If the conditions ($c_1$) and $\left(c_2\right)$ are satisfied, then the problem $\left(35\right)$ and $\left(36\right)$ has a unique solution $p^{*}\in C([j-h,M]:{\mathbb{R}}^n)\cap C^1([j,M]:{\mathbb{R}}^n)$ and the sequence $\left\{p_n\right\}$ defined by $\left(12\right)$ converges to $p^{*}$.

Proof. 

The existence of unique solution $p^{*}$ is followed from [26]. Let $\left\{p_n\right\}$ be a sequence of defined by $\left(12\right)$. Define an operator $T$ on $C([j-h,M]:{\mathbb{R}}^n)\cap C^1([j,M]:{\mathbb{R}}^n)$ by:

$$Tp\left(t\right)=\left\{\begin{array}{cc}\rho \left(j\right)+\frac{1}{\Gamma (\alpha )}{\int }_j^t{(t-\tau )}^{(\alpha -1)}f\left(\tau ,p(\tau ),p(\tau -h)\right)d\tau ,\hfill & t\in [j,M],\hfill \\ \rho \left(t\right)\hfill & t\in [j-\tau ,j].\hfill \end{array}\right.$$

We now prove that $p_n\to p^{*}$ as $n\to \infty$.

For $t\in [j-\tau ,j],$ it is easy to see that $p_n\to p^{*}$ as $n\to \infty$.

Now, if $t\in [j,M]$, then using the proposed iterative process and conditions $\left(c_1\right)$ and $\left(c_2\right),$ we obtain

$$\begin{array}{cc}\hfill \parallel s_n-p^{*}\parallel & =\parallel (1-w_n)p_n+w_n{T}_1{p}_n-p^{*}\parallel \hfill \\ \hfill & \le (1-w_n)\parallel p_n-p^{*}\parallel +w_n\parallel T_1{p}_n-p^{*}\parallel .\hfill \end{array}$$

(37)

Taking supremum over $[j-h,M]$ on both sides of the above inequality, we have

$$\begin{array}{cc}\hfill \underset{t\in [j-h,M]}{sup}\parallel s_n-p^{*}\parallel =& (1-w_n)\underset{t\in [j-h,M]}{sup}\parallel p_n-p^{*}\parallel +w_n\underset{t\in [j-h,M]}{sup}\parallel T_1{p}_n-T_1{p}^{*}\parallel \hfill \\ \hfill =& (1-w_n)\underset{t\in [j-h,M]}{sup}\parallel p_n-p^{*}\parallel +w_n\underset{t\in [j-h,M]}{sup}\parallel \rho \left(j\right)+\hfill \\ \hfill & \frac{1}{\Gamma (\alpha )}{\int }_j^t{(t-\tau )}^{(\alpha -1)}f(\tau ,p_n(\tau ),p_n(\tau -h))d\tau -\rho \left(j\right)-\hfill \\ \hfill & \frac{1}{\Gamma (\alpha )}{\int }_j^t{(t-\tau )}^{(\alpha -1)}f(\tau ,p^{*}(\tau ),p^{*}(\tau -h))d\tau \parallel \hfill \\ \hfill =& (1-w_n)\underset{t\in [j-h,M]}{sup}\parallel p_n-p^{*}\parallel +w_n\underset{t\in [j-h,M]}{sup}\parallel \hfill \\ \hfill & \frac{1}{\Gamma (\alpha )}{\int }_j^t{(t-\tau )}^{(\alpha -1)}f(\tau ,p_n(\tau ),p_n(\tau -h))d\tau -\hfill \\ \hfill & \frac{1}{\Gamma (\alpha )}{\int }_j^t{(t-\tau )}^{(\alpha -1)}f(\tau ,p^{*}(\tau ),p^{*}(\tau -h))d\tau \parallel \hfill \\ \hfill \le & (1-w_n)\underset{t\in [j-h,M]}{sup}\parallel p_n-p^{*}\parallel +w_n\underset{t\in [j-h,M]}{sup}\frac{1}{\Gamma (\alpha )}{\int }_j^t{(t-\tau )}^{(\alpha -1)}\hfill \\ \hfill & L_f(\parallel p_n(\tau )-p^{*}(\tau )\parallel +\parallel p_n(\tau -h))-p^{*}(\tau -h)\parallel )d\tau \hfill \\ \hfill \le & (1-w_n)\underset{t\in [j-h,M]}{sup}\parallel p_n-p^{*}\parallel +w_n\frac{L_f}{\Gamma (\alpha )}{\int }_j^t{(t-\tau )}^{(\alpha -1)}d\tau \hfill \\ \hfill & \left(\underset{t\in [j-h,M]}{sup}(\parallel p_n(\tau )-p^{*}(\tau )\parallel +\underset{t\in [j-h,M]}{sup}\parallel p_n(\tau -h))-p^{*}(\tau -h)\parallel \right).\hfill \end{array}$$

(38)

Dividing by $E_{\alpha }\left({\beta }_L{t}^{\alpha }\right)$ on both sides of the above equality, we obtain

$$\begin{array}{cc}\hfill \frac{{sup}_{t\in [j-h,M]}\parallel s_n-p^{*}\parallel }{E_{\alpha }\left({\beta }_L{t}^{\alpha }\right)}=& \frac{(1-w_n){sup}_{t\in [j-h,M]}\parallel p_n-p^{*}\parallel }{E_{\alpha }\left({\beta }_L{t}^{\alpha }\right)}+w_n\frac{L_f}{\Gamma (\alpha )}{\int }_j^t{(t-\tau )}^{(\alpha -1)}d\tau \hfill \\ \hfill & (\frac{{sup}_{t\in [j-h,M]}\parallel p_n(\tau )-p^{*}(\tau )\parallel }{E_{\alpha }\left({\beta }_L{t}^{\alpha }\right)}\hfill \\ & +\frac{{sup}_{t\in [j-h,M]}\parallel p_n(\tau -h))-p^{*}(\tau -h)\parallel }{E_{\alpha }\left({\beta }_L{t}^{\alpha }\right)})\hfill \\ \hfill \parallel s_n-p^{*}{\parallel }_{{\beta }_L}=& (1-w_n){\parallel p_n-p^{*}\parallel }_{{\beta }_L}+\frac{w_n}{\Gamma (\alpha )}{\int }_j^t{(t-\tau )}^{(\alpha -1)}d\tau \hfill \\ \hfill & L_f(\parallel p_n(\tau )-p^{*}{(\tau )\parallel }_{{\beta }_L}+\parallel p_n(\tau -h)-p^{*}(\tau -h){\parallel }_{{\beta }_L})\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill =& (1-w_n)\parallel p_n-p^{*}{\parallel }_{{\beta }_L}+w_n\left(2L_f\right){\parallel p_n-p^{*}\parallel }_{{\beta }_L}\frac{1}{\Gamma (\alpha )}{\int }_j^t{(t-\tau )}^{(\alpha -1)}d\tau \hfill \\ \hfill & \mathrm{multiply}\mathrm{and}\mathrm{divide}\mathrm{the}\mathrm{right}\mathrm{end}\mathrm{term}\mathrm{by}{E}_{\alpha }\left({\beta }_L{t}^{\alpha }\right),\mathrm{then}\mathrm{we}\mathrm{have}\hfill \\ \hfill =& (1-w_n)\parallel p_n-p^{*}{\parallel }_{{\beta }_L}+\frac{w_n\left(2L_f\right)}{E_{\alpha }\left({\beta }_L{t}^{\alpha }\right)}{\parallel p_n-p^{*}\parallel }_{{\beta }_L}\frac{1}{\Gamma (\alpha )}\hfill \\ \hfill & {\int }_j^t{(t-\tau )}^{(\alpha -1)}{E}_{\alpha }\left({\beta }_L{t}^{\alpha }\right)d\tau \hfill \\ \hfill =& (1-w_n)\parallel p_n-p^{*}{\parallel }_{{\beta }_L}+\frac{w_n\left(2L_f\right)}{E_{\alpha }\left({\beta }_L{t}^{\alpha }\right)}{\parallel p_n-p^{*}\parallel }_{{\beta }_L}.{}^c{I}^{\alpha }\left({}^c{D}^{\alpha }\left(\frac{E_{\alpha }\left({\beta }_L{t}^{\alpha }\right)}{{\beta }_L}\right)\right)\hfill \\ \hfill =& (1-w_n)\parallel p_n-p^{*}{\parallel }_{{\beta }_L}+\frac{w_n\left(2L_f\right)}{E_{\alpha }\left({\beta }_L{t}^{\alpha }\right)}.\frac{E_{\alpha }\left({\beta }_L{t}^{\alpha }\right)}{{\beta }_L}{\parallel p_n-p^{*}\parallel }_{{\beta }_L}\hfill \\ \hfill =& (1-w_n)\parallel p_n-p^{*}{\parallel }_{{\beta }_L}+\frac{w_n\left(2L_f\right)}{{\beta }_L}{\parallel p_n-p^{*}\parallel }_{{\beta }_L}.\hfill \end{array}$$

(40)

As $\frac{2L_f}{{\beta }_L}<1$, we obtain

$$\parallel s_n-p^{*}{\parallel }_{{\beta }_L}\le {\parallel p_n-p^{*}\parallel }_{{\beta }_L}.$$

(41)

Let $u_n=(1-o_n)s_n+o_n{T}_{\lambda }{s}_n$. Then by following similar arguments to those given above, we have

$$\parallel u_n-p^{*}{\parallel }_{{\beta }_L}\le \parallel s_n-p^{*}{\parallel }_{{\beta }_L}\le {\parallel p_n-p^{*}\parallel }_{{\beta }_L}.$$

(42)

Thus,

$$\begin{array}{cc}\hfill \parallel r_n-p^{*}\parallel =& \parallel T{u}_n-T{p}^{*}\parallel \hfill \\ \hfill =& \parallel \rho \left(j\right)+\frac{1}{\Gamma (\alpha )}{\int }_j^t{(t-\tau )}^{(\alpha -1)}f(\tau ,u_n(\tau ),u_n(\tau -h))d\tau -\rho \left(j\right)-\hfill \\ \hfill & \frac{1}{\Gamma (\alpha )}{\int }_j^t{(t-\tau )}^{(\alpha -1)}f(\tau ,p^{*}(\tau ),p^{*}(\tau -h))d\tau \parallel \hfill \\ \hfill \le & \frac{1}{\Gamma (\alpha )}{\int }_j^t{(t-\tau )}^{(\alpha -1)}{L}_f\left(\parallel u(\tau )-p^{*}(\tau )\parallel +\parallel u(\tau -h)-p^{*}(\tau -h)\parallel \right)d\tau .\hfill \end{array}$$

(43)

Taking supremum over $[j-h,M]$ and dividing by $E_{\alpha }\left({\beta }_L{t}^{\alpha }\right)$ on both sides of the above inequality, we obtain

$$\begin{array}{cc}\hfill \underset{t\in [j-h,M]}{sup}\frac{\parallel r_n-p^{*}\parallel }{E_{\alpha }\left({\beta }_L{t}^{\alpha }\right)}=& \frac{1}{\Gamma (\alpha )}{\int }_j^t{(t-\tau )}^{(\alpha -1)}{L}_f[\underset{t\in [j-h,M]}{sup}\frac{\parallel U(\tau )-p^{*}(\tau )\parallel }{E_{\alpha }\left({\beta }_L{t}^{\alpha }\right)}\hfill \\ & +\underset{t\in [j-h,M]}{sup}\frac{\parallel U(t-h)-p^{*}(t-h)\parallel }{E_{\alpha }\left({\beta }_L{t}^{\alpha }\right)}]dt\hfill \\ \hfill \parallel r_n-p^{*}{\parallel }_{{\beta }_L}\le & \frac{2L_f}{E_{\alpha }\left({\beta }_L{t}^{\alpha }\right)}{\parallel u_n-p^{*}\parallel }_{{\beta }_L}\frac{1}{\Gamma (\alpha )}{\int }_j^t{(t-\tau )}^{(\Gamma -1)}{E}_{\alpha }\left({\beta }_L{t}^{\alpha }\right)d\tau \hfill \\ \hfill =& \frac{2L_f}{E_{\alpha }\left({\beta }_L{t}^{\alpha }\right)}{\parallel u_n-p^{*}\parallel }_{{\beta }_L}.{}^c{I}^{\alpha }\left({}^c{D}^{\alpha }\left(\frac{E_{\alpha }\left({\beta }_L{t}^{\alpha }\right)}{{\beta }_L}\right)\right)\hfill \\ \hfill =& \frac{2L_f}{E_{\alpha }\left({\beta }_L{t}^{\alpha }\right)}.\frac{E_{\alpha }\left({\beta }_L{t}^{\alpha }\right)}{{\beta }_L}{\parallel u_n-p^{*}\parallel }_{{\beta }_L}\hfill \\ \hfill =& \frac{2L_f}{{\beta }_L}{\parallel u_n-p^{*}\parallel }_{{\beta }_L}.\hfill \end{array}$$

(44)

Again by $\frac{2L_f}{{\beta }_L}<1$, we obtain

$$\parallel r_n-p^{*}{\parallel }_{{\beta }_L}\le {\parallel u_n-p^{*}\parallel }_{{\beta }_L}.$$

(45)

So,

$$\parallel r_n-p^{*}{\parallel }_{{\beta }_L}\le {\parallel p_n-p^{*}\parallel }_{{\beta }_L}.$$

(46)

Similarly,

$$\begin{array}{cc}\hfill \parallel q_n-p^{*}{\parallel }_{{\beta }_L}\le & \parallel p_n-p^{*}{\parallel }_{{\beta }_L}.\hfill \end{array}$$

(47)

$$\begin{array}{cc}\hfill \parallel p_{n+1}-p^{*}{\parallel }_{{\beta }_L}\le & \parallel p_n-p^{*}{\parallel }_{{\beta }_L}.\hfill \end{array}$$

(48)

If we set, $\parallel p_n-p^{*}{\parallel }_{{\beta }_L}={\nu }_n$, then we have

$${\nu }_{n+1}\le {\nu }_n\forall n\in \mathbb{N}.$$

(49)

Thus $\left\{{\nu }_n\right\}$ is a monotone decreasing sequence of positive real numbers. Further, it is bounded sequence, we obtain

$$\underset{n\to \infty }{lim}{\nu }_n=inf\left\{{\nu }_n\right\}=0.$$

So,

$$\underset{n\to \infty }{lim}{\parallel p_n-p^{*}\parallel }_{{\beta }_L}=0.$$

□

5. Conclusions

In this paper we approximate the fixed point of $(b,\eta )$-enriched contraction mapping by using a new iterative scheme (define by Abbas and Asghar) in the frame work of Banach spaces. It is also proved that the proposed iterative scheme is stable and converges faster than Picard, Mann, Ishikawa, Noor, Agarwal, Abbas, Thakur, M-iteration and F-iteration. We presented some numerical examples to support our claim. Further, we proved some strong and weak convergence results for b-enriched nonexpansive mapping in uniformly convex Banach space. In the end, using our proposed iterative scheme we approximated the solution of delay fractional differential equations.