A Versatile and Efficient Novel Approach for Mendelian Randomization Analysis with Application to Assess the Causal Effect of Fetal Hemoglobin on Anemia in Sickle Cell Anemia
Abstract
1. Introduction
2. Method
2.1. Model
2.1.1. MREPS for Samples from the Extreme Tails of Outcome Distribution
2.1.2. MREPS for Samples from the Extreme Tails of Risk Factor Distribution
2.1.3. MREPS for Random Samples
2.2. Estimation and Hypothesis Testing
2.2.1. Samples Drawn from the Extreme Tails of Outcome
2.2.2. Samples Drawn from the Extreme Tails of Risk Factor
2.2.3. Random Samples
3. Simulations
- (a)
- Equal-sized combined effects of 9 and 25 independent SNPs: two separate cases were considered by using different numbers, 9 and 25, of SNPs. The genotype data of each SNP was independently generated under HWE as mentioned above. Then, the equal sized combined effect was considered by using , where and is the summation of the 9 independent SNP genotype values for the ith individual. Similarly, for the 25 SNPs, , where and is the summation of the 25 independent SNP genotype values for the ith individual. This case represents the utilization of the summary of multiple SNPs with equal-sized association with the risk factor as an IV.
- (b)
- Different-sized combined effects of 9 and 25 SNPs: with this setting, turned out to be for . Each independently generated SNP under HWE was multiplied by randomly generated from for 9 SNPs and from for 25 SNPs separately. Then, the summation of these products considered as under 9 and 25 SNPs separately for each i. This scenario represents the utilization of the summary of multiple SNPs with different-sized association with the risk factor as an IV.
- (c)
- A few large and many small effects of 9 and 25 SNPs: two SNPs generated under H-WE were multiplied by 0.46 and the rest SNPs multiplied by 0.092 separately for 9 and 25 SNPs. Next, for each i, the summations of these products separately considered as for 9 and 25 SNPs. This represents the utilization of the summary of multiple SNPs with very few large associations and a large number of week associations with the risk factor as an IV.
- (d)
- A combination of valid and invalid SNPs as an IV, 9 and 25 SNPs: Among 9 SNPs g-enerated under HWE, 4 SNPs were multiplied by 0.37 while multiplying the rest by 0, and the summation of the resulting values was considered as for the ith individual. Similarly, among 25 SNPs, 12 SNPs were multiplied by 0.14 while multiplying the rest by 0, and the resulting summation was considered as for the ith individual. This case represents the utilization of the summary of few valid and many invalid SNPs as an IV.
3.1. Comparison: Bias, Rejection Proportion, Standard Error, and Coverage Percentage
3.2. Comparison: The Optimum Cost-Effective Subsample Size
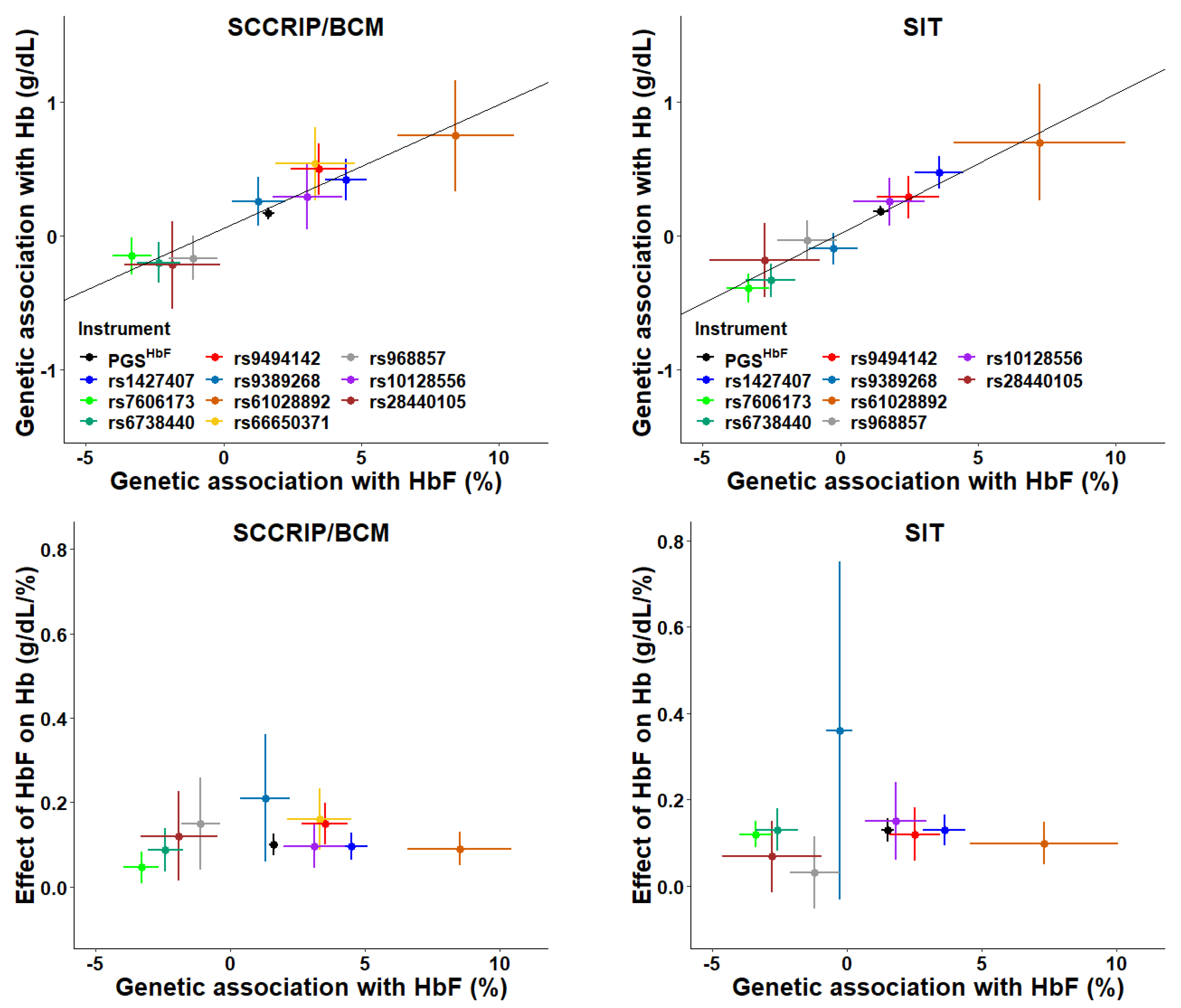
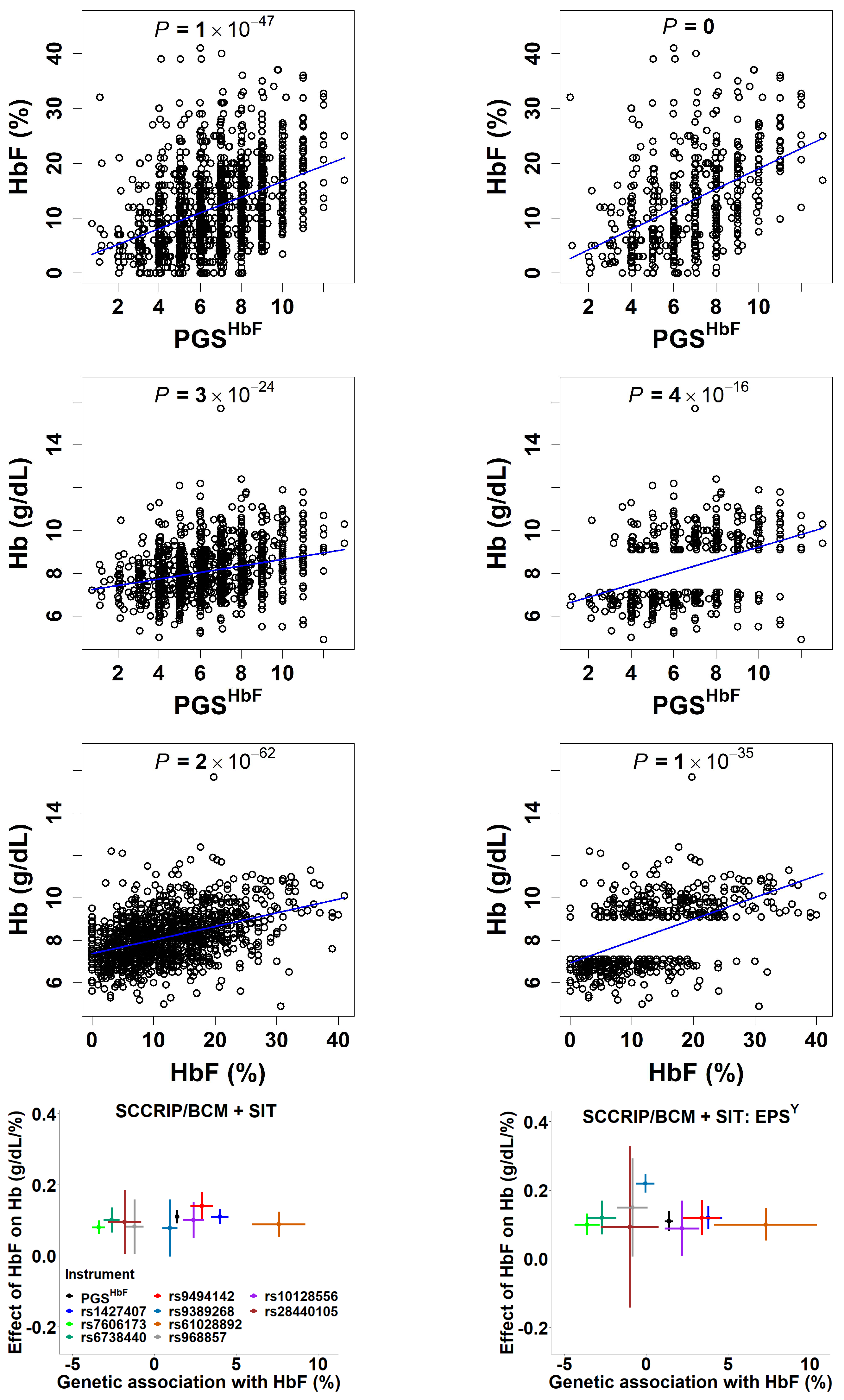
4. Unravelling the Effect of HbF on Anemia in Sickle Cell Anemia
5. Discussion
Supplementary Materials
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Code Availability
Acknowledgments
Conflicts of Interest
Abbreviations
| MR | Mendalian randomization |
| 2SLS | Two-stage least-squares |
| GWAS | Genome-wide association study |
| EPS | Extreme phenotype sequencing |
| MREPS | MR analysis under extreme or random phenotype sampling |
| IV | Instrumental variables |
| NGS | Next generation sequencing |
| WBC | White blood cell count |
| CI | Confidence intervals |
| HbF | Total fetal hemoglobin |
| Hb | Hemoglobin |
| SCA | Sickle cell anemia |
| SCCRIP | Sickle cell clinical research intervention program |
| BCM | Baylor college of medicine |
| SIT | Silent Cerebral Infarct Transfusion |
| LIML | Limited information maximum likelihood |
| MLE | Maximum likelihood estimator |
| SE | Standard errors |
| EPS design constructed upon the risk factor | |
| EPS design constructed upon the outcome | |
| HWE | Hardy–Weinberg equilibrium |
| SNP | Single nucleotide polymorphisms |
| HbS | Sickle hemoglobin |
| FDR | False discovery rate |
| CP | Coverage percentage |
| Polygenic Score of HbF |
References
- Davey Smith, G.; Ebrahim, S. ‘Mendelian randomization’: Can genetic epidemiology contribute to understanding environmental determinants of disease?*. Int. J. Epidemiol. 2003, 32, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Davey Smith, G.; Hemani, G. Mendelian randomization: Genetic anchors for causal inference in epidemiological studies. Hum. Mol. Genet. 2014, 23, R89–R98. [Google Scholar] [CrossRef]
- Lawlor, D.A.; Harbord, R.M.; Sterne, J.A.C.; Timpson, N.; Davey Smith, G. Mendelian randomization: Using genes as instruments for making causal inferences in epidemiology. Stat. Med. 2008, 27, 1133–1163. [Google Scholar] [CrossRef]
- Lamina, C. Digging into the extremes: A useful approach for the analysis of rare variants with continuous traits? BMC Proc. 2011, 5, S105. [Google Scholar] [CrossRef] [PubMed]
- Dorr, C.; Wu, B.; Remmel, R.; Muthusamy, A.; Schladt, D.; Abrahante, J.E.; Guan, W.; Mannon, R.; Matas, A.; Oetting, W.; et al. Identification of genetic variants associated with tacrolimus metabolism in kidney transplant recipients by extreme phenotype sampling and next generation sequencing. Pharm. J. 2019, 19, 375–389. [Google Scholar] [CrossRef] [PubMed]
- Kleinstein, S.E.; Rein, M.; Abdelmalek, M.F.; Guy, C.D.; Goldstein, D.B.; Diehl, A.M.; Moylan, C.A. Whole-Exome Sequencing Study of Extreme Phenotypes of NAFLD. Hepatol. Commun. 2018, 2, 1021–1029. [Google Scholar] [CrossRef] [PubMed]
- Peloso, G.; Rader, D.; Gabriel, S.; Kathiresan, S.; Daly, M.J.; Neale, B.M. Phenotypic extremes in rare variant study designs. Eur. J. Hum. Genet. 2016, 24, 924–930. [Google Scholar] [CrossRef] [PubMed]
- Amanat, S.; Requena, T.; Lopez-Escamez, J.A. A Systematic Review of Extreme Phenotype Strategies to Search for Rare Variants in Genetic Studies of Complex Disorders. Genes 2020, 11, 987. [Google Scholar] [CrossRef] [PubMed]
- Amanat, S.; Gallego-Martinez, A.; Sollini, J.; Perez-Carpena, P.; Espinosa-Sánchez, J.; Aran, I.; Soto-Varela, A.; Batuecas-caletrio, A.; Canlon, B.; May, P.; et al. Burden of Rare Variants in Synaptic Genes in Patients with Severe Tinnitus: An Exome Based Extreme Phenotype Study. EBioMedicine 2020, 66, 103309. [Google Scholar] [CrossRef]
- Perez-Gracia, J.L.; Pita, G.; Segura, V.; Pajares, M.J.; Fusco, J.P.; Andueza, M.P.; Sanchez-Bayona, R.; Guruceaga, E.; Mora, M.I.; Gurpide, A.; et al. Whole exome sequencing of germline DNA of individuals presenting extreme phenotypes of high and low risk to develop tobacco-induced lung adenocarcinoma (LUAD) according to KRAS status. J. Clin. Oncol. 2019, 37, 1540. [Google Scholar] [CrossRef]
- Emond, M.J.; Louie, T.; Emerson, J.; Zhao, W.; Mathias, R.A.; Knowles, M.R.; Wright, F.A.; Rieder, M.J.; Tabor, H.K.; Nickerson, D.A.; et al. Exome sequencing of extreme phenotypes identifies DCTN4 as a modifier of chronic Pseudomonas aeruginosa infection in cystic fibrosis. Nat. Genet. 2012, 44, 886–889. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Levran, O.; Kim, J.; Zhang, T.; Chen, X.; Suo, C. Extreme sampling design in genetic association mapping of quantitative trait loci using balanced and unbalanced case-control samples. Sci. Rep. 2019, 9, l15504. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Fang, J.; Shen, H.; Wang, Y.P.; Deng, H.W. EPS-LASSO: Test for high-dimensional regression under extreme phenotype sampling of continuous traits. Bioinformatics 2018, 34, 1996–2003. [Google Scholar] [CrossRef] [PubMed]
- Kang, G.; Bi, W.; Zhao, Y.; Zhang, J.F.; Yang, J.J.; Xu, H.; Loh, M.L.; Hunger, S.P.; Relling, M.V.P.S.; Cheng, C. A new system identification approach to identify genetic variants in sequencing studies for a binary phenotype. Hum. Hered. 2014, 78, 104–116. [Google Scholar] [CrossRef] [PubMed]
- Liyanage, J.S.S.; Estepp, J.H.; Srivastava, K.; Li, Y.; Mori, M.; Kang, G. GMEPS: A fast and efficient likelihood approach for genome-wide mediation analysis under extreme phenotype sequencing. Stat. Appl. Genet. Mol. Biol. 2022, 21. [Google Scholar] [CrossRef]
- Bi, W.; Li, Y.; Smeltzer, M.P.; Gao, G.; Zhao, S.; Kang, G. STEPS: An efficient prospective likelihood approach to genetic association analyses of secondary traits in extreme phenotype sequencing. Biostatistics 2020, 21, 33–49. [Google Scholar] [CrossRef]
- Angrist, J.D.; Imbens, G.W. Two-Stage Least Squares Estimation of Average Causal Effects in Models with Variable Treatment Intensity. J. Am. Stat. Assoc. 1995, 90, 431–442. [Google Scholar] [CrossRef]
- Anderson, T. Origins of the limited information maximum likelihood and two-stage least squares estimators. J. Econom. 2005, 127, 1–16. [Google Scholar] [CrossRef]
- Hayashi, F. Econometrics; Princeton University Press: Princeton, NJ, USA, 2000. [Google Scholar]
- Anderson, T.W.; Kunitomo, N.; Sawa, T. Evaluation of the Distribution Function of the Limited Information Maximum Likelihood Estimator. Econometrica 1982, 50, 1009–1027. [Google Scholar] [CrossRef][Green Version]
- Hankins, J.; Estepp, J.; Hodges, J.; Villavicencio, M.; Robison, L.; Weiss, M.; Kang, G.; Schreiber, J.; Porter, J.; Kaste, S.; et al. Sickle Cell Clinical Research and Intervention Program (SCCRIP): A lifespan cohort study for sickle cell disease progression from the pediatric stage into adulthood. Pediatr. Blood Cancer 2018, 65, e27228. [Google Scholar] [CrossRef]
- Rampersaud, E.; Kang, G.; Palmer, L.E.; Rashkin, S.R.; Wang, S.; Bi, W.; Alberts, N.M.; Anghelescu, D.; Barton, M.; Birch, K.; et al. A polygenic score for acute vaso-occlusive pain in pediatric sickle cell disease. Blood Adv. 2021, 5, 2839–2851. [Google Scholar] [CrossRef] [PubMed]
- Chaturvedi, S.; Bhatnagar, P.; Bean, C.; Steinberg, M.; Milton, J.; Casella, J.; Barron-Casella, E.; Arking, D.; DeBaun, M. Genome-wide association study to identify variants associated with acute severe vaso-occlusive pain in sickle cell anemia. Blood 2017, 130, 686–688. [Google Scholar] [CrossRef] [PubMed]
- Baiocchi, M.; Cheng, J.; Small, D.S. Instrumental variable methods for causal inference. Stat. Med. 2014, 33, 2297–2340. [Google Scholar] [CrossRef] [PubMed]
- Fox, J.; Nie, Z.; Byrnes, J. sem: Structural Equation Models. R Package Version 3.1-15. 2022. Available online: https://CRAN.R-project.org/package=sem.
- Ghalanos, A.; Theussl, S. Rsolnp: General Non-linear Optimization Using Augmented Lagrange Multiplier Method. R package version 1.16. 2015. Available online: https://CRAN.R-project.org/package=Rsolnp.
- Ye, Y. Interior Algorithms for Linear, Quadratic, and Linearly Constrained Non-Linear Programming. Ph.D. Thesis, Department of ESS, Stanford University, Stanford, CA, USA, 1987. [Google Scholar]
- Burgess, S.; Thompson, S. Use of allele scores as instrumental variables for Mendelian randomization. Int. J. Epidemiol. 2013, 42, 1134–1144. [Google Scholar] [CrossRef] [PubMed]
- Ware, R.; de Montalembert, M.; Tshilolo, L.; Abboud, M. Sickle cell disease. Lancet 2017, 390, 311–323. [Google Scholar] [CrossRef]
- Gill, F.; Sleeper, L.; Weiner, S.; Brown, A.; Bellevue, R.; Grover, R.; Pegelow, C.; Vichinsky, E. Clinical events in the first decade in a cohort of infants with sickle cell disease. Cooperative Study of Sickle Cell Disease. Blood 1995, 86, 776–783. [Google Scholar] [CrossRef]
- Statius van Eps, L.; Pinedo-Veels, C.; de Vries, G.; de Koning, J. Nature of concentrating defect in sickle-cell nephropathy. Microradioangiographic studies. Lancet 1970, 1, 450–452. [Google Scholar] [CrossRef]
- Lester, L.; Sodt, P.; Hutcheon, N.; Arcilla, R. Cardiac abnormalities in children with sickle cell anemia. Chest 1990, 98, 1169–1174. [Google Scholar] [CrossRef]
- Ohene-Frempong, K.; Weiner, S.; Sleeper, L.; Miller, S.; Embury, S.; Moohr, J.; Wethers, D.; Pegelow, C.; Gill, F. Cerebrovascular accidents in sickle cell disease: Rates and risk factors. Blood 1998, 91, 288–294. [Google Scholar]
- McCarville, M.B.; Luo, Z.; Huang, X.; Rees, R.C.; Rogers, Z.R.; Miller, S.T.; Thompson, B.; Kalpatthi, R.; Wang, W.C.; BABY HUG Investigators. Abdominal ultrasound with scintigraphic and clinical correlates in infants with sickle cell anemia: Baseline data from the BABY HUG trial. AJR Am. J. Roentgenol. 2011, 196, 1399–1404. [Google Scholar] [CrossRef][Green Version]
- Rogers, Z.R.; Wang, W.C.; Luo, Z.; Iyer, R.V.; Shalaby-Rana, E.; Dertinger, S.D.; Shulkin, B.L.; Miller, J.H.; Files, B.; Lane, P.A.; et al. Biomarkers of splenic function in infants with sickle cell anemia: Baseline data from the BABY HUG Trial. Blood 2011, 117, 2614–2617. [Google Scholar] [CrossRef] [PubMed]
- Ware, R.E.; Rees, R.C.; Sarnaik, S.A.; Iyer, R.V.; Alvarez, O.A.; Casella, J.F.; Shulkin, B.L.; Shalaby-Rana, E.; Strife, C.F.; Miller, J.H.; et al. Renal function in infants with sickle cell anemia: Baseline data from the BABY HUG trial. J. Pediatr. 2010, 156, 66–70. [Google Scholar] [CrossRef] [PubMed]
- Pavlakis, S.; Rees, R.; Huang, X.; Brown, R.; Casella, J.; Iyer, R.; Kalpatthi, R.; Luden, J.; Miller, S.; Rogers, Z.; et al. Transcranial doppler ultrasonography (TCD) in infants with sickle cell anemia: Baseline data from the BABY HUG trial. Pediatr. Blood Cancer 2010, 54, 256–259. [Google Scholar] [CrossRef] [PubMed]
- Miller, S.; Wang, W.; Iyer, R.; Rana, S.; Lane, P.; Ware, R.; Li, D.; Rees, R.; BABY-HUG Investigators. Urine concentrating ability in infants with sickle cell disease: Baseline data from the phase III trial of hydroxyurea (BABY HUG). Pediatr. Blood Cancer 2010, 54, 265–268. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Pavlakis, S.; Helton, K.; McKinstry, R.; Casella, J.; Adams, R.; Rees, R.; BABY HUG Investigators. MRI abnormalities of the brain in one-year-old children with sickle cell anemia. Pediatr. Blood Cancer 2008, 51, 643–646. [Google Scholar] [CrossRef]
- Platt, O.; Brambilla, D.; Rosse, W.; Milner, P.; Castro, O.; Steinberg, M.; Klug, P. Mortality in sickle cell disease. Life expectancy and risk factors for early death. N. Engl. J. Med. 1994, 330, 1639–1644. [Google Scholar] [CrossRef]
- Danjou, F.; Zoledziewska, M.; Sidore, C.; Steri, M.; Busonero, F.; Maschio, A.; Mulas, A.; Perseu, L.; Barella, S.; Porcu, E.; et al. Genome-wide association analyses based on whole-genome sequencing in Sardinia provide insights into regulation of hemoglobin levels. Nat. Genet. 2015, 47, 1264–1271. [Google Scholar] [CrossRef]
- Stadhouders, R.; Aktuna, S.; Thongjuea, S.; Aghajanirefah, A.; Pourfarzad, F.; van Jcken, W.; Lenhard, B.; Rooks, H.; Best, S.; Menzel, S.; et al. HBS1L-MYB intergenic variants modulate fetal hemoglobin via long-range MYB enhancers. J. Clin. Investig. 2014, 124, 1699–1710. [Google Scholar] [CrossRef] [PubMed]
- Stadhouders, R.; Thongjuea, S.; Andrieu-Soler, C.; Palstra, R.; Bryne, J.; Van Den Heuvel, A.; Stevens, M.; de Boer, E.; Kockx, C.; van der Sloot, A.; et al. Dynamic long-range chromatin interactions control Myb proto-oncogene transcription during erythroid development. EMBO J. 2012, 31, 986–999. [Google Scholar] [CrossRef]
- Suzuki, M.; Yamazaki, H.; Mukai, H.; Motohashi, H.; Shi, L.; Tanabe, O.; Engel, J.; Yamamoto, M. Disruption of the Hbs1l-Myb locus causes hereditary persistence of fetal hemoglobin in a mouse model. Mol. Cell. Biol. 2013, 33, 1687–1695. [Google Scholar] [CrossRef] [PubMed]
- Yawn, B.P.; Buchanan, G.; Afenyi-Annan, A.; Ballas, S.; Hassell, K.; James, A.; Jordan, L.; Lanzkron, S.; Lottenberg, R.; Savage, W.; et al. Management of sickle cell disease: Summary of the 2014 evidence-based report by expert panel members. JAMA 2014, 312, 1033–1048. [Google Scholar] [CrossRef]
- Estepp, J.; Smeltzer, M.; Kang, G.; Li, C.; Wang, W.; Abrams, C.; Aygun, B.; Ware, R.; Nottage, K.; Hankins, J. A clinically meaningful fetal hemoglobin threshold for children with sickle cell anemia during hydroxyurea therapy. Am. J. Hematol. 2017, 92, 1333–1339. [Google Scholar] [CrossRef] [PubMed]
- Lebensburger, J.; Pestina, T.; Ware, R.; Boyd, K.; Persons, D. Hydroxyurea therapy requires HbF induction for clinical benefit in a sickle cell mouse model. Haematologica 2010, 95, 1599–1603. [Google Scholar] [CrossRef] [PubMed]
- Meier, E.; Byrnes, C.; Weissman, M.; Noel, P.; Luban, N.; Miller, J. Expression patterns of fetal hemoglobin in sickle cell erythrocytes are both patient- and treatment-specific during childhood. Pediatr. Blood Cancer 2011, 56, 103–109. [Google Scholar] [CrossRef]
- Das, S.; Forer, L.; Schönherr, S.; Sidore, C.; Locke, A.; Kwong, A.; Vrieze, S.; Chew, E.; Levy, S.; McGue, M.; et al. Next-generation genotype imputation service and methods. Nat. Genet. 2016, 48, 1284–1287. [Google Scholar] [CrossRef]
- Gardner, K.; Fulford, T.; Silver, N.; Rooks, H.; Angelis, N.; Allman, M.; Nkya, S.; Makani, J.; Howard, J.; Kesse-Adu, R.; et al. g(HbF): A genetic model of fetal hemoglobin in sickle cell disease. Blood Adv. 2018, 2, 235–239. [Google Scholar] [CrossRef] [PubMed]
- Bowden, J.; Davey, S.G.; Burgess, S. Mendelian randomization with invalid instruments: Effect estimation and bias detection through egger regression. Int. J. Epidemiol. 2015, 44, 512–525. [Google Scholar] [CrossRef]
- Sargan, J.D. The Estimation of Economic Relationships using Instrumental Variables. Econometrica 1958, 26, 393–415. [Google Scholar] [CrossRef]
- Burgess, S.; Thompson, S.G. Mendelian Randomization: Methods for Causal Inference Using Genetic Variants; Chapman and Hall/CRC: Boca Raton, FL, USA, 2021. [Google Scholar]
- Bhanushali, A.A.; Patra, P.; Nair, D.; Verma, H.; Das, B. Genetic variant in the BCL11A (rs1427407), but not HBS1-MYB (rs6934903) loci associate with fetal hemoglobin levels in Indian sickle cell disease patients. Blood Cells Mol. Dis. 2015, 54, 4–8. [Google Scholar] [CrossRef]
- Benjamini, Y.; Hochberg, Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. R. Stat. Soc. 1995, 57, 289–300. [Google Scholar] [CrossRef]
- Steinberg, M.; Sebastiani, P. Genetic modifiers of sickle cell disease. Am. J. Hematol. 2012, 87, 795–803. [Google Scholar] [CrossRef] [PubMed]


| Mean | Mean SE | Bias % | Rejection Proportion | CP | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Number of SNPs | MREPS | 2SLS | MREPS | 2SLS | MREPS | 2SLS | MREPS | 2SLS | MREPS | 2SLS | ||||||
| (a) Equal-sized IV—risk factor associations | ||||||||||||||||
| 9 | 0 | −0.004 | −0.02 | 0.07 | 0.3 | - | - | 0.06 | 0.05 | 94.6 | 95.1 | |||||
| 0.2 | 0.21 | 0.54 | 0.08 | 0.17 | −3.19 | −169.66 | 0.77 | 0.86 | 93.5 | 42.1 | ||||||
| 0.4 | 0.41 | 0.82 | 0.09 | 0.1 | −2.02 | −105.3 | 0.99 | 1.0 | 94.5 | 5.9 | ||||||
| 25 | 0 | −0.01 | −0.02 | 0.11 | 1.13 | - | - | 0.05 | 0.05 | 95.3 | 94.7 | |||||
| 0.2 | 0.19 | 0.51 | 0.12 | 0.28 | 4.84 | −155.91 | 0.48 | 0.64 | 95 | 62.7 | ||||||
| 0.4 | 0.41 | 0.82 | 0.13 | 0.16 | −2.6 | −104.03 | 0.89 | 0.97 | 94.6 | 25.7 | ||||||
| (b) Different-sized IV—risk factor associations | ||||||||||||||||
| 9 | 0 | −0.005 | −0.04 | 0.07 | 0.28 | - | - | 0.04 | 0.03 | 96.2 | 96.8 | |||||
| 0.2 | 0.2 | 0.53 | 0.07 | 0.16 | −1.02 | −166.89 | 0.79 | 0.88 | 94.3 | 39.1 | ||||||
| 0.4 | 0.4 | 0.82 | 0.08 | 0.1 | −0.99 | −104.72 | 1.0 | 1.0 | 94.2 | 4.2 | ||||||
| 25 | 0 | −0.01 | −0.11 | 0.12 | 0.58 | - | - | 0.04 | 0.04 | 95.7 | 95.7 | |||||
| 0.2 | 0.18 | 0.51 | 0.12 | 0.28 | 8.28 | −153.52 | 0.46 | 0.61 | 95.4 | 61.4 | ||||||
| 0.4 | 0.41 | 0.81 | 0.13 | 0.17 | −1.96 | −102.81 | 0.86 | 0.96 | 94.8 | 27.8 | ||||||
| (c) A combination of few large and many small IV - risk factor associations | ||||||||||||||||
| 9 | 0 | −0.0006 | −0.01 | 0.05 | 0.21 | - | - | 0.06 | 0.05 | 94.1 | 95.1 | |||||
| 0.2 | 0.2 | 0.54 | 0.06 | 0.12 | −1.45 | −170.85 | 0.94 | 0.97 | 93.2 | 20.1 | ||||||
| 0.4 | 0.41 | 0.82 | 0.06 | 0.07 | −1.34 | −105.3 | 1.0 | 1.0 | 93 | 0.5 | ||||||
| 25 | 0 | −0.0002 | −0.01 | 0.05 | 0.18 | - | - | 0.05 | 0.06 | 94.7 | 94.5 | |||||
| 0.2 | 0.2 | 0.54 | 0.05 | 0.1 | −1.15 | −171.2 | 0.97 | 0.99 | 93.3 | 12.4 | ||||||
| 0.4 | 0.4 | 0.82 | 0.06 | 0.06 | −1.1 | −104.93 | 1.0 | 1.0 | 93.1 | 0.1 | ||||||
| (d) A combination of valid and invalid IV - risk factor associations | ||||||||||||||||
| 9 | 0 | −0.002 | −0.02 | 0.05 | 0.19 | - | - | 0.06 | 0.05 | 93.9 | 95.2 | |||||
| 0.2 | 0.2 | 0.54 | 0.05 | 0.11 | −1.42 | −170.38 | 0.95 | 0.97 | 91.5 | 18.7 | ||||||
| 0.4 | 0.4 | 0.82 | 0.06 | 0.07 | −1.04 | −104.89 | 1.0 | 1.0 | 93 | 0.2 | ||||||
| 25 | 0 | −0.005 | −0.03 | 0.08 | 0.31 | - | - | 0.05 | 0.05 | 94.9 | 95.5 | |||||
| 0.2 | 0.21 | 0.54 | 0.08 | 0.17 | −4.16 | −170.31 | 0.75 | 0.84 | 93.4 | 43.8 | ||||||
| 0.4 | 0.41 | 0.82 | 0.09 | 0.11 | −2.91 | −106.12 | 0.99 | 1.0 | 93.9 | 6.7 | ||||||
| SE () | p-Value () | SE () | p-Value () | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cohort/Design | IV | MREPS | 2SLS | MREPS | 2SLS | MREPS | 2SLS | MREPS | 2SLS | MREPS | 2SLS | MREPS | 2SLS |
| SCCRIP/BCM | PGSHbF | 0.1 | 0.1 | 0.013 | 0.013 | 1.6 | - | 0.083 | - | 0 | - | ||
| 0.096 | 0.095 | 0.016 | 0.016 | 4.5 | - | 0.3 | - | 0 | - | ||||
| SIT | PGSHbF | 0.15 | 0.15 | 0.014 | 0.023 | 0 | 1.3 | - | 0.14 | - | 0 | - | |
| 0.15 | 0.15 | 0.024 | 0.027 | 3.3 | - | 0.52 | - | - | |||||
| Combined | PGSHbF | 0.11 | 0.11 | 0.01 | 0.01 | 0 | 0 | 1.4 | - | 0.076 | - | 0 | - |
| 0.11 | 0.11 | 0.011 | 0.012 | 0 | 0 | 4 | - | 0.27 | - | 0 | - | ||
| EPSY | PGSHbF | 0.11 | 0.11 | 0.015 | 0.016 | 1.4 | - | 0.13 | - | 0 | - | ||
| 0.12 | 0.12 | 0.017 | 0.019 | 3.8 | - | 0.44 | - | 0 | - | ||||
| EPSX | PGSHbF | 0.098 | 0.11 | 0.013 | 0.018 | 1.7 | - | 0.18 | - | 0 | - | ||
| 0.095 | 0.11 | 0.013 | 0.019 | 5.4 | - | 0.67 | - | - | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liyanage, J.S.S.; Estepp, J.H.; Srivastava, K.; Rashkin, S.R.; Sheehan, V.A.; Hankins, J.S.; Takemoto, C.M.; Li, Y.; Cui, Y.; Mori, M.; et al. A Versatile and Efficient Novel Approach for Mendelian Randomization Analysis with Application to Assess the Causal Effect of Fetal Hemoglobin on Anemia in Sickle Cell Anemia. Mathematics 2022, 10, 3743. https://doi.org/10.3390/math10203743
Liyanage JSS, Estepp JH, Srivastava K, Rashkin SR, Sheehan VA, Hankins JS, Takemoto CM, Li Y, Cui Y, Mori M, et al. A Versatile and Efficient Novel Approach for Mendelian Randomization Analysis with Application to Assess the Causal Effect of Fetal Hemoglobin on Anemia in Sickle Cell Anemia. Mathematics. 2022; 10(20):3743. https://doi.org/10.3390/math10203743
Chicago/Turabian StyleLiyanage, Janaka S. S., Jeremie H. Estepp, Kumar Srivastava, Sara R. Rashkin, Vivien A. Sheehan, Jane S. Hankins, Clifford M. Takemoto, Yun Li, Yuehua Cui, Motomi Mori, and et al. 2022. "A Versatile and Efficient Novel Approach for Mendelian Randomization Analysis with Application to Assess the Causal Effect of Fetal Hemoglobin on Anemia in Sickle Cell Anemia" Mathematics 10, no. 20: 3743. https://doi.org/10.3390/math10203743
APA StyleLiyanage, J. S. S., Estepp, J. H., Srivastava, K., Rashkin, S. R., Sheehan, V. A., Hankins, J. S., Takemoto, C. M., Li, Y., Cui, Y., Mori, M., Burgess, S., DeBaun, M. R., & Kang, G. (2022). A Versatile and Efficient Novel Approach for Mendelian Randomization Analysis with Application to Assess the Causal Effect of Fetal Hemoglobin on Anemia in Sickle Cell Anemia. Mathematics, 10(20), 3743. https://doi.org/10.3390/math10203743








