Sensitivity Analysis of Krasovskii Passivity-Based Controllers †
Abstract
:1. Introduction
1.1. Literature Review
1.2. Contributions and Paper Structure
- (i)
- The ad hoc analysis proposed in [19], based on a trial and error methodology, is replaced with a more rigorous treatment using the sensitivity analysis of the resulting closed-loop system. To measure the sensitivity, we consider the length of the curve described by the dominant eigenvalue of the Jacobian of the closed-loop system.
- (ii)
- The length of the path of the aforementioned dominant eigenvalues can be used as a performance index which can be minimized in terms of K-PBC’s parameters, resulting in a non-convex optimization problem. In the current paper, there are two possibilities presented to formulate the optimization problem: one by minimizing only the sensitivity of the inner closed-loop system, and the latter by minimizing this sensitivity function with an extra constraint of having the inner dynamics at least twice as fast as the dominant dynamics imposed by the outer dynamical path planning.
- (iii)
- The two said optimization problems formulated in this journal paper are non-convex by nature. As such, a global optimization technique is required in order to find the sub-optimal value of the controller’s parameters. For the purpose of this paper, we developed a slightly modified version of the Artificial Bee Colony (ABC) algorithm [20], the main modification being in terms of stopping criteria and abandonment counters management, all modifications increasing the speed of the algorithm and avoiding the search in the unfeasible zone. Being a metaheurisitc approach for a non-convex optimization problem, only a sub-optimal value of these parameters can be guaranteed, but the exploration ability of the ABC algorithm leads to good results.
- (iv)
- Finally, in order to prove the efficiency of the proposed method, we present an end-to-end design approach for a nonideal DC-DC single-ended primary-inductor converter (SEPIC), starting from the method of constructing the passivity output, along with designing the outer dynamical path planning for the linearized system around a desired equilibrium point, and also the solution to the optimization problem regarding the sub-optimal choice of the K-PBC’s parameters. All results presented are obtained using the MATLAB-based toolbox initially described in [21] and extended in [13] for the nonlinear model.
1.3. Notations
2. Mathematical Background
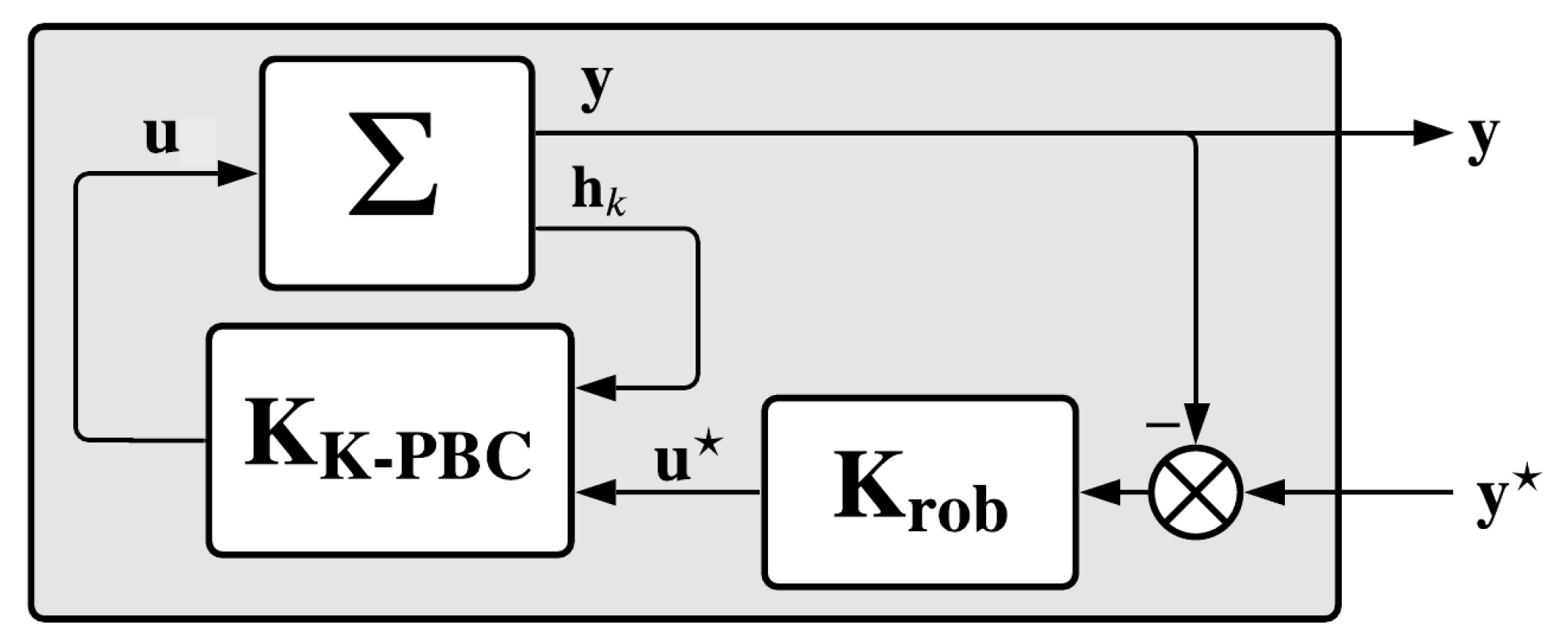
2.1. Krasovskii Passivity
2.2. Dynamic Path-Planning
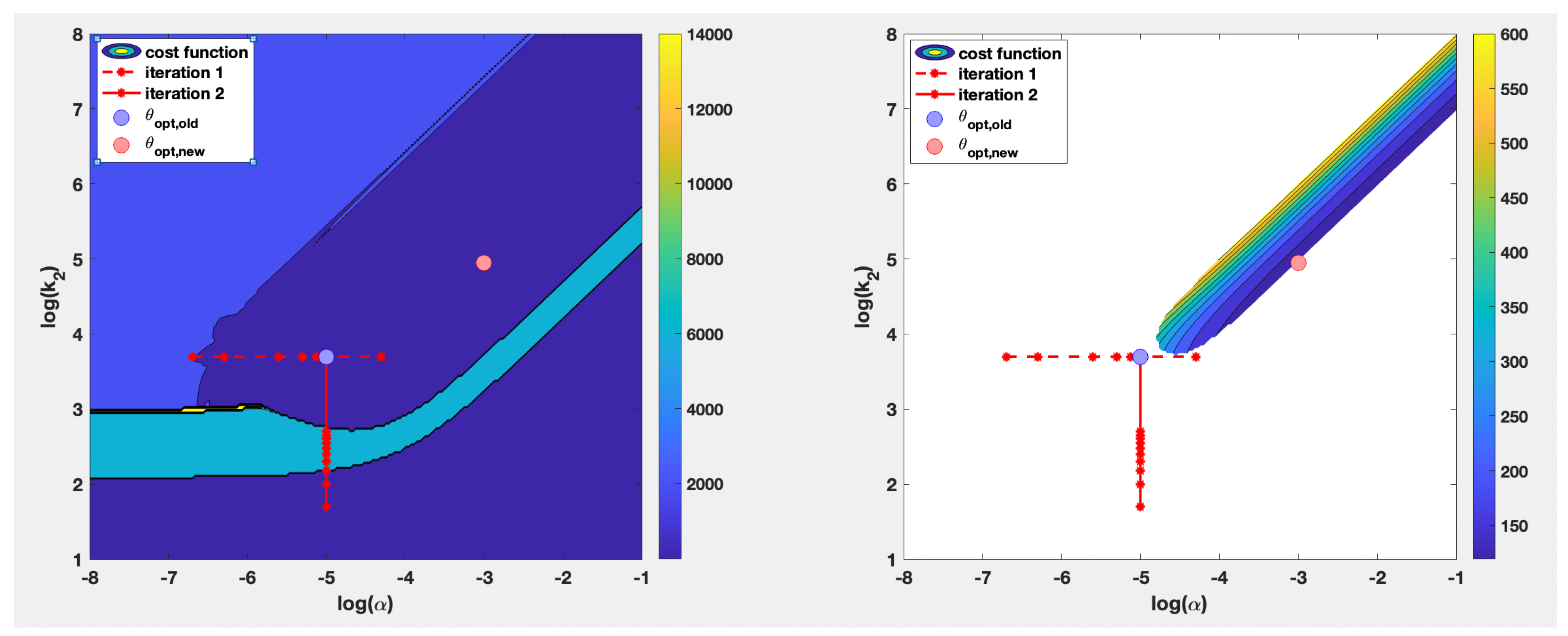
3. Sensitivity Analysis
3.1. Problem Formulation
3.2. Metaheuristic Solution
4. Numerical Results
- The inductors and with the associated parasitic resistances and ;
- The capacitors , and with the associated parasitic resistances , and ;
- For the ON state of each switching element: the parasitic resistance and voltage drop ;
- The variable resistor R considered the output load;
- The external voltage source E.
- For sensitivity weighting: the bandwidth (rad/s), with a peak amplitude , and a maximum allow steady-state error ;
- For complementary sensitivity: the bandwidth (rad/s), with a peak amplitude , a roll-off (dB/dec), and a maximum amplitude at high frequencies ;
- For control effort: the main goal was to have a command with amplitude less than 1.
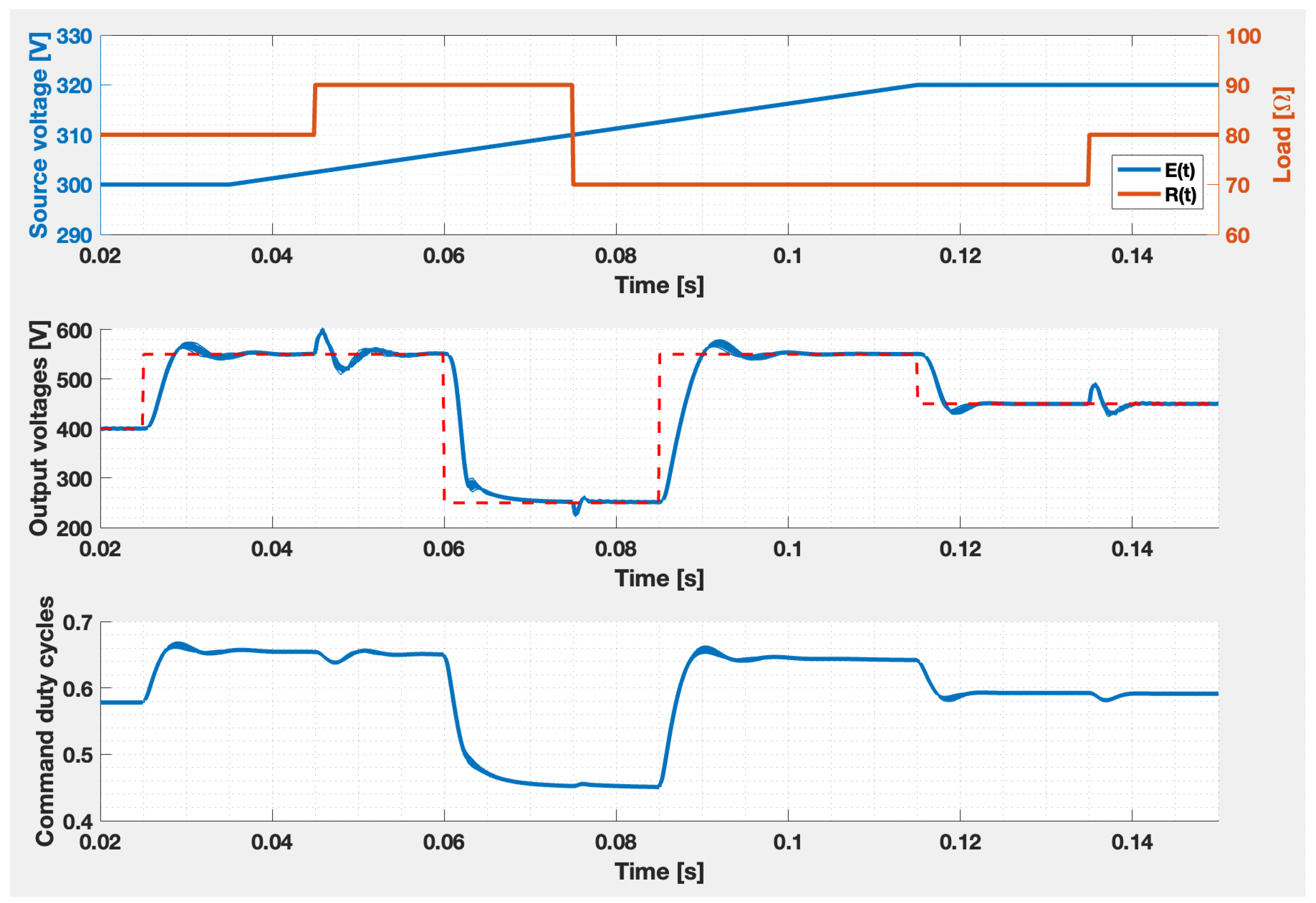
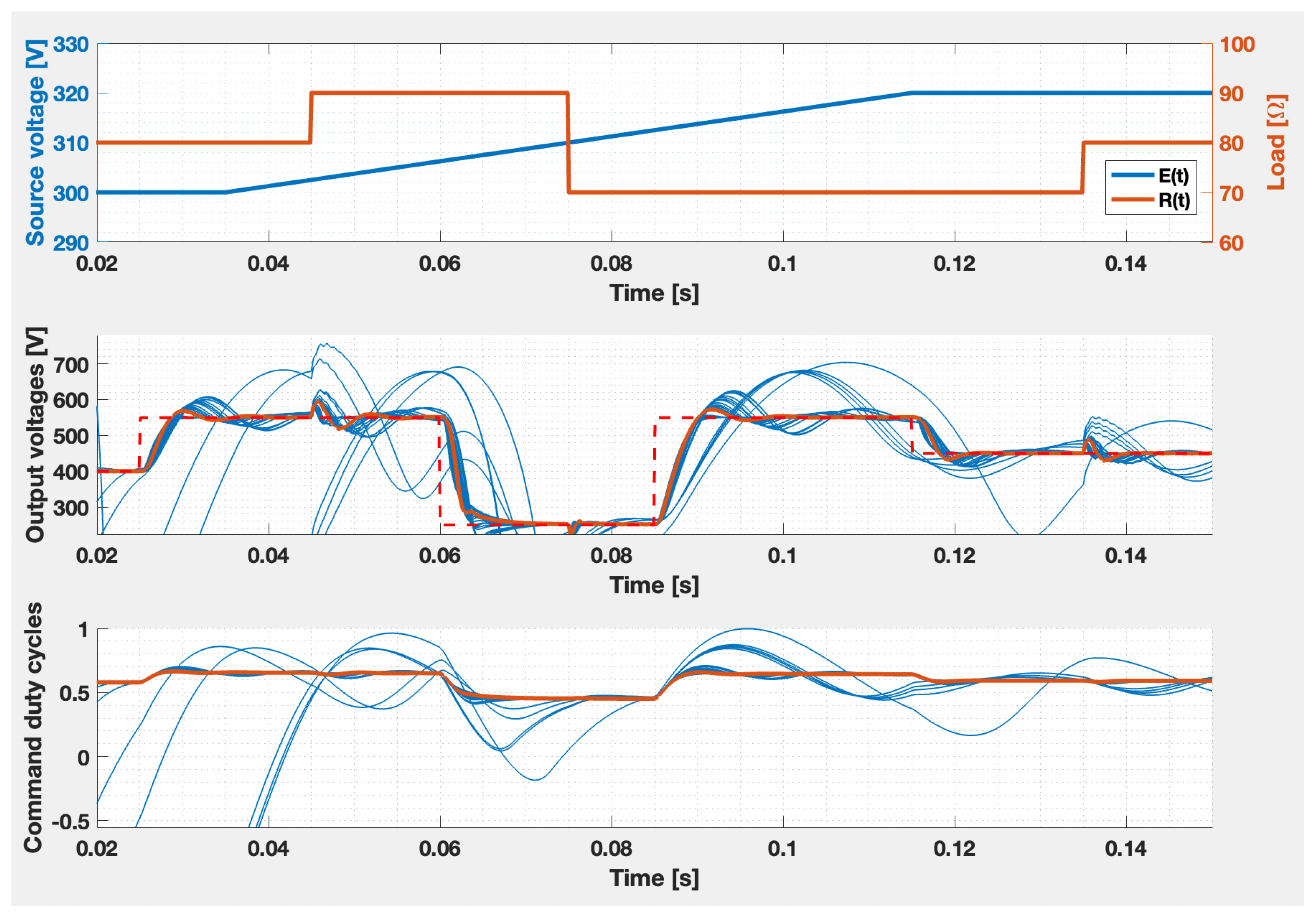
- The external voltage has an initial value of 300 (V), while at (s) a ramp evolution is present until (s) when the value of 320 (V) is reached;
- the output load has an initial value of , while at (s) its value is and at (s), the final value being again ;
- the reference signal has an initial value of 400 (V), and is successively changed to 550 (V) at (s), to 250 (V) at (s), to 550 (V) at (s), and to 450 (V) at (s).
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ABC | Artificial Bee Colony |
| DC | Direct Current |
| K-PBC | Krasovskii Passivity-Based Controller |
| LFT | Linear Fractional Transform |
| LLFT | Lower Linear Fractional Transform |
| LMI | Linear Matrix Inequality |
| LTI | Linear and Time-Invariant |
| NP | Non-Deterministic Polynomial Time |
| PBC | Passivity-Based Controller |
| PI | Proportional–Integrative |
| RCF | Robust Control Framework |
| SISO | Single-Input Single-Output |
| SEPIC | Single-Ended Primary-Inductor Converter |
| S-PBC | Shifted Passivity-Based Controller |
| ULFT | Upper Linear Fractional Transform |
References
- Willems, J.C. Dissipative dynamical systems part II: Linear systems with quadratic supply rates. Arch. Ration. Mech. Anal. 1972, 45, 352–393. [Google Scholar] [CrossRef]
- Khalil, H. Nonlinear Systems; Prentice Hall: Prentice, NJ, USA, 1996. [Google Scholar]
- van der Schaft, A.J. L2-Gain and Passivity Techniques in Nonlinear Control, 3rd ed.; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Bao, J.; Lee, P.L. Process Control—The Passive Systems Approach, 1st ed.; Springer: London, UK, 2007. [Google Scholar]
- Pavlov, A.; Marconi, L. Incremental passivity and output regulation. In Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006. [Google Scholar]
- Pang, H.; Zhao, J. Incremental passivity and output regulation for switched nonlinear systems. Int. J. Control 2017, 90, 2072–2084. [Google Scholar] [CrossRef]
- van der Schaft, A.J. On differential passivity. IFAC Proc. Vol. 2013, 46, 21–25. [Google Scholar] [CrossRef] [Green Version]
- Forni, F.; Sepulchre, R.; van der Schaft, A.J. On differential passivity of physical systems. In Proceedings of the 52nd IEEE Conference on Decision and Control, Firenze, Italy, 10–13 December 2013; pp. 6580–6585. [Google Scholar]
- Li, N.; Scherpen, J.; van der Schaft, A.; Sun, Z. A passivity approach in port-Hamiltonian form for formation control and velocity tracking. In Proceedings of the 2022 European Control Conference (ECC), London, UK, 12–15 July 2022. [Google Scholar]
- Simpson-Porco, J.W. Equilibrium-Independent Dissipativity With Quadratic Supply Rates. IEEE Trans. Autom. Control 2019, 64, 1440–1455. [Google Scholar] [CrossRef] [Green Version]
- Kosaraju, K.C.; Kawano, Y.; Scherpen, J.M.A. Krasovskii’s Passivity. In Proceedings of the 11th IFAC Symposium on Nonlinear Control Systems NOLCOS, Vienna, Austria, 4–6 September 2019; Volume 52, pp. 466–471. [Google Scholar]
- Kawano, Y.; Kosaraju, K.C.; Scherpen, J.M.A. Krasovskii and Shifted Passivity-Based Control. IEEE Trans. Autom. Control 2021, 66, 4926–4932. [Google Scholar] [CrossRef]
- Mihaly, V.; Şuşcă, M.; Dobra, P. Krasovskii Passivity and μ-Synthesis Controller Design for Quasi-Linear Affine Systems. Energies 2021, 14, 5571. [Google Scholar] [CrossRef]
- Mihaly, V.; Şuşcă, M.; Morar, D.; Dobra, P. Polytopic Robust Passivity Cascade Controller Design for Nonlinear Systems. In Proceedings of the 22nd European Control Conference, London, UK, 13–15 July 2022. [Google Scholar]
- Silani, A.; Cucuzzella, M.; Scherpen, J.M.A.; Yazdanpanah, M.J. Robust output regulation for voltage control in DC networks with time-varying loads. Automatica 2022, 135, 109997. [Google Scholar] [CrossRef]
- Geromel, J.C.; Colaneri, P.; Bolzern, P. Passivity of switched linear systems: Analysis and control design. Syst. Control Lett. 2012, 61, 549–554. [Google Scholar] [CrossRef]
- Hughes, T.H. A theory of passive linear systems with no assumptions. Automatica 2017, 86, 87–97. [Google Scholar] [CrossRef] [Green Version]
- Hughes, T.H. On reciprocal systems and controllability. Automatica 2019, 101, 396–408. [Google Scholar] [CrossRef]
- Mihaly, V.; Şuşcă, M.; Morar, D.; Dobra, P. Closed-Loop System Sensitivity Analysis for Passivity-Based Controller Parameters. In Proceedings of the IEEE International Conference on Automation, Quality and Testing, Robotics, Cluj-Napoca, Romania, 19–21 May 2022. [Google Scholar]
- Pham, D.T.; Ghanbarzadeh, A.; Koc, E.; Otri, S.; Rahim, S.; Zaidi, M. The Bees Algorithm; Technical Note; Manufacturing Engineering Centre, Cardiff University: Cardiff, UK, 2005. [Google Scholar]
- Şuşcă, M.; Mihaly, V.; Stănese, M.; Morar, D.; Dobra, P. Unified CACSD Toolbox for Hybrid Simulation and Robust Controller Synthesis with Applications in DC-to-DC Power Converter Control. Mathematics 2021, 9, 731. [Google Scholar] [CrossRef]
- Packard, A.; Doyle, J.; Balas, G. Linear Multivariable Robust Control with a μ Perspective. J. Dyn. Syst. Meas. Control 1993, 115, 426–438. [Google Scholar] [CrossRef]
- Balas, G.; Chiang, R.; Packard, A.; Safonov, M. Robust Control Toolbox—User’s Guide; The MathWorks: Natick, MA, USA, 2020. [Google Scholar]



| Parameter | Nominal Value | Tolerance | Parameter | Nominal Value | Tolerance |
|---|---|---|---|---|---|
| (mH) | 1.71 (mH) | ||||
| 130 (m) | 110 (m] | ||||
| () | 80 (m) | ||||
| (F) | (F) | ||||
| 270 (m) | 350 (m) | ||||
| (F) | 270 (m) | ||||
| (V) | (V) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mihaly, V.; Şuşcă, M.; Morar, D.; Dobra, P. Sensitivity Analysis of Krasovskii Passivity-Based Controllers. Mathematics 2022, 10, 3750. https://doi.org/10.3390/math10203750
Mihaly V, Şuşcă M, Morar D, Dobra P. Sensitivity Analysis of Krasovskii Passivity-Based Controllers. Mathematics. 2022; 10(20):3750. https://doi.org/10.3390/math10203750
Chicago/Turabian StyleMihaly, Vlad, Mircea Şuşcă, Dora Morar, and Petru Dobra. 2022. "Sensitivity Analysis of Krasovskii Passivity-Based Controllers" Mathematics 10, no. 20: 3750. https://doi.org/10.3390/math10203750








