Figure 1.
Standard model fit diagnostics for the upper tail of the DPMW-PPR model fitted to the simulated data with . (The top left corner is the return level plot, the top right corner is the quantile plot, the bottom left corner is the probability plot, and the bottom right corner is the density plot).
Figure 1.
Standard model fit diagnostics for the upper tail of the DPMW-PPR model fitted to the simulated data with . (The top left corner is the return level plot, the top right corner is the quantile plot, the bottom left corner is the probability plot, and the bottom right corner is the density plot).
Figure 2.
Standard model fit diagnostics for the DPMW-PPR model fitted to the simulated data with . (The top left corner is the return level plot, the top right corner is the quantile plot, the bottom left corner is the probability plot, and the bottom right corner is the density plot).
Figure 2.
Standard model fit diagnostics for the DPMW-PPR model fitted to the simulated data with . (The top left corner is the return level plot, the top right corner is the quantile plot, the bottom left corner is the probability plot, and the bottom right corner is the density plot).
Figure 3.
Standard model fit diagnostics for the upper tail of DPMW-PPR model fitted to the simulated data with . (The top left corner is the return level plot, the top right corner is the quantile plot, the bottom left corner is the probability plot, and the bottom right corner is the density plot).
Figure 3.
Standard model fit diagnostics for the upper tail of DPMW-PPR model fitted to the simulated data with . (The top left corner is the return level plot, the top right corner is the quantile plot, the bottom left corner is the probability plot, and the bottom right corner is the density plot).
Figure 4.
Standard model fit diagnostics for the DPMW-PPR model fitted to the simulated data with . (The top left corner is the return level plot, the top right corner is the quantile plot, the bottom left corner is the probability plot, and the bottom right corner is the density plot).
Figure 4.
Standard model fit diagnostics for the DPMW-PPR model fitted to the simulated data with . (The top left corner is the return level plot, the top right corner is the quantile plot, the bottom left corner is the probability plot, and the bottom right corner is the density plot).
Figure 5.
Standard model fit diagnostics for the upper tail of the DPMW-PPR model fitted to the simulated data with . (The top left corner is the return level plot, the top right corner is the quantile plot, the bottom left corner is the probability plot, and the bottom right corner is the density plot).
Figure 5.
Standard model fit diagnostics for the upper tail of the DPMW-PPR model fitted to the simulated data with . (The top left corner is the return level plot, the top right corner is the quantile plot, the bottom left corner is the probability plot, and the bottom right corner is the density plot).
Figure 6.
Standard model fit diagnostics for the DPMW-PPR model fitted to the simulated data with . (The top left corner is the return level plot, the top right corner is the quantile plot, the bottom left corner is the probability plot, and the bottom right corner is the density plot).
Figure 6.
Standard model fit diagnostics for the DPMW-PPR model fitted to the simulated data with . (The top left corner is the return level plot, the top right corner is the quantile plot, the bottom left corner is the probability plot, and the bottom right corner is the density plot).
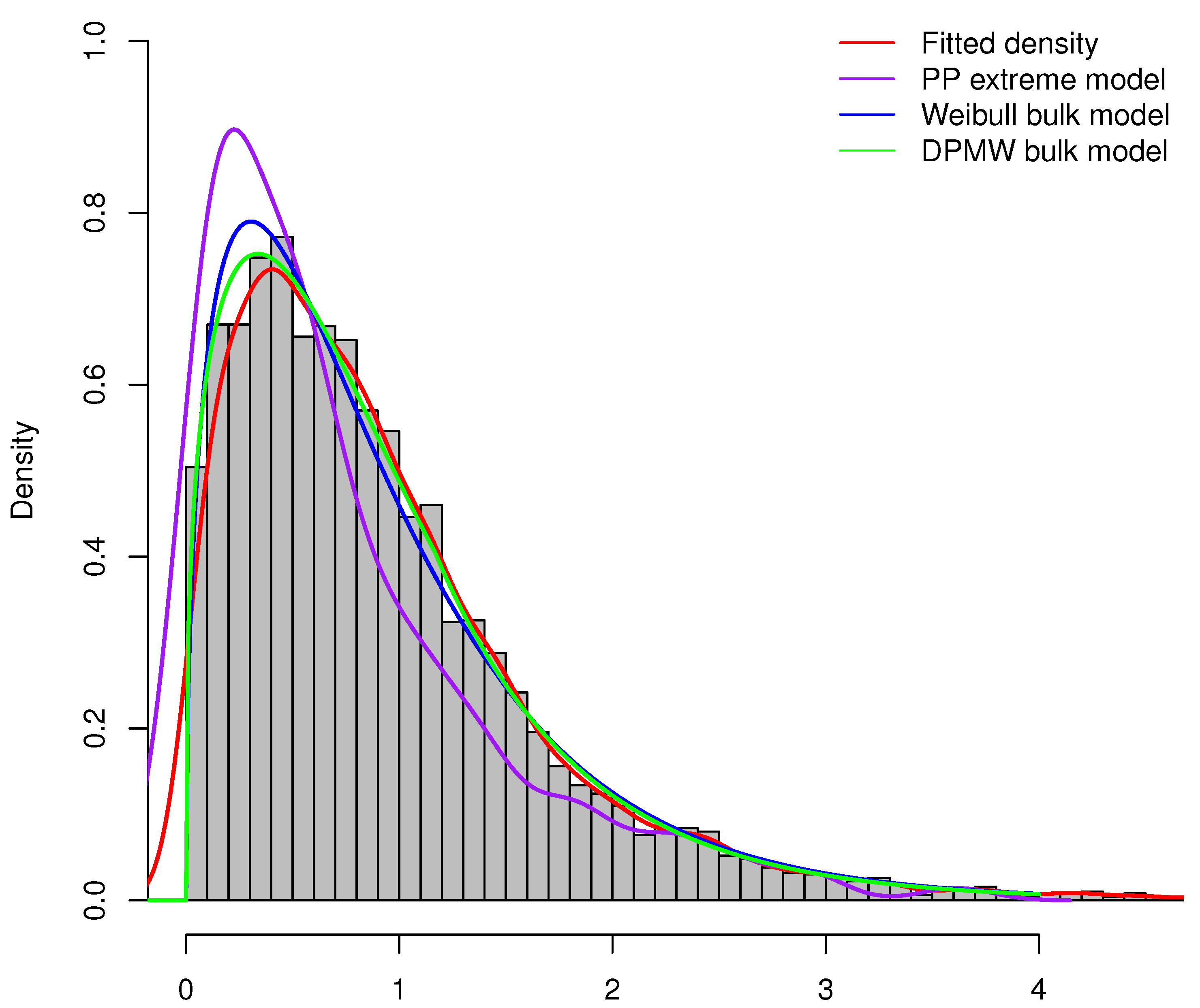
Figure 7.
The posterior density plot for three models (the DPMW-PPR model, the PP extreme value model and the WMPP extreme model) with . The red line shows the true density function, the green line, the blue line and the purple line are the posterior density function of the DPMW-PPR model, the WMPP extreme model and the PP extreme value model, respectively.
Figure 7.
The posterior density plot for three models (the DPMW-PPR model, the PP extreme value model and the WMPP extreme model) with . The red line shows the true density function, the green line, the blue line and the purple line are the posterior density function of the DPMW-PPR model, the WMPP extreme model and the PP extreme value model, respectively.
Figure 8.
The posterior density plot for three models (the DPMW-PPR model, the PP extreme value model and the WMPP extreme model) with . The red line shows the true density function, the green line, the blue line and the purple line are the posterior density function of the DPMW-PPR model, the WMPP extreme model and the PP extreme value model, respectively.
Figure 8.
The posterior density plot for three models (the DPMW-PPR model, the PP extreme value model and the WMPP extreme model) with . The red line shows the true density function, the green line, the blue line and the purple line are the posterior density function of the DPMW-PPR model, the WMPP extreme model and the PP extreme value model, respectively.
Figure 9.
The posterior density plot for three models (the DPMW-PPR model, the PP extreme value model and the WMPP extreme model) with . The red line shows the true density function, the green line, the blue line and the purple line are the posterior density function of the DPMW-PPR model, the WMPP extreme model and the PP extreme value model, respectively.
Figure 9.
The posterior density plot for three models (the DPMW-PPR model, the PP extreme value model and the WMPP extreme model) with . The red line shows the true density function, the green line, the blue line and the purple line are the posterior density function of the DPMW-PPR model, the WMPP extreme model and the PP extreme value model, respectively.
Figure 10.
Time series of the Iowa river monthly flow.
Figure 10.
Time series of the Iowa river monthly flow.
Figure 11.
Decomposition of additive time series for Iowa river monthly flow.
Figure 11.
Decomposition of additive time series for Iowa river monthly flow.
Figure 12.
Parameter u varying over time for the data of Iowa river flow. The green line is the estimate of the parameter u. The shaded area is the confidence interval of the estimates.
Figure 12.
Parameter u varying over time for the data of Iowa river flow. The green line is the estimate of the parameter u. The shaded area is the confidence interval of the estimates.
Figure 13.
Return levels expected every 10, 50 and 100 years. Green: expected return every 10 years; red: expected return every 50 years; blue: expected return every 100 years.
Figure 13.
Return levels expected every 10, 50 and 100 years. Green: expected return every 10 years; red: expected return every 50 years; blue: expected return every 100 years.
Figure 14.
Standard model fit diagnostics for the DPMW-PPR model fitted to the Iowa River monthly flow. (The top left corner is the return level plot, the top right corner is the quantile plot, the bottom left corner is the probability plot, and the bottom right corner is the density plot).
Figure 14.
Standard model fit diagnostics for the DPMW-PPR model fitted to the Iowa River monthly flow. (The top left corner is the return level plot, the top right corner is the quantile plot, the bottom left corner is the probability plot, and the bottom right corner is the density plot).
Figure 15.
The posterior density plot for three models (the DPMW-PPR model, the PP extreme value model and the WMPP extreme model) fitted to the Iowa River monthly flow data. The red line shows the true density function, the green line, the blue line and the purple line are the posterior density function of the DPMW-PPR model, the WMPP extreme model and the PP extreme value model, respectively.
Figure 15.
The posterior density plot for three models (the DPMW-PPR model, the PP extreme value model and the WMPP extreme model) fitted to the Iowa River monthly flow data. The red line shows the true density function, the green line, the blue line and the purple line are the posterior density function of the DPMW-PPR model, the WMPP extreme model and the PP extreme value model, respectively.
Figure 16.
Time series of the Patuxent river daily flow.
Figure 16.
Time series of the Patuxent river daily flow.
Figure 17.
Decomposition of additive time series for Patuxent river daily flow.
Figure 17.
Decomposition of additive time series for Patuxent river daily flow.
Figure 18.
Parameter u varying over time for the data of Patuxent river flow. The green line is the estimate of the parameter u. The shaded area is the confidence interval of the estimates.
Figure 18.
Parameter u varying over time for the data of Patuxent river flow. The green line is the estimate of the parameter u. The shaded area is the confidence interval of the estimates.
Figure 19.
Return levels expected every 10, 50 and 100 years for Patuxent river daily flow. Green: expected return every 10 years; red: expected return every 50 years; blue: expected return every 100 years.
Figure 19.
Return levels expected every 10, 50 and 100 years for Patuxent river daily flow. Green: expected return every 10 years; red: expected return every 50 years; blue: expected return every 100 years.
Figure 20.
Standard model fit diagnostics for the DPMW-PPR model fitted to the Patuxent river daily flow. (The top left corner is the return level plot, the top right corner is the quantile plot, the bottom left corner is the probability plot, and the bottom right corner is the density plot).
Figure 20.
Standard model fit diagnostics for the DPMW-PPR model fitted to the Patuxent river daily flow. (The top left corner is the return level plot, the top right corner is the quantile plot, the bottom left corner is the probability plot, and the bottom right corner is the density plot).
Figure 21.
The posterior density plot for three models (the DPMW-PPR model, the PP extreme value model and the WMPP extreme model) fitted to the Patuxent river daily flow. The red line shows the true density function, the green line, the blue line and the purple line are the posterior density function of the DPMW-PPR model, the WMPP extreme model and the PP extreme value model, respectively.
Figure 21.
The posterior density plot for three models (the DPMW-PPR model, the PP extreme value model and the WMPP extreme model) fitted to the Patuxent river daily flow. The red line shows the true density function, the green line, the blue line and the purple line are the posterior density function of the DPMW-PPR model, the WMPP extreme model and the PP extreme value model, respectively.
Table 1.
Estimates for the regression coefficients of simulations with sample .
Table 1.
Estimates for the regression coefficients of simulations with sample .
| | | | |
| Posterior mean | 5.8712 | −0.0288 | 0.7027 |
| Credibility interval | (5.2592, 6.4832) | (−0.0548, −0.0028) | (0.4917, 0.9138) |
| Interval length | 1.224 | 0.0520 | 0.4221 |
| | | | |
| Posterior mean | −0.2861 | 0.0225 | 0.2601 |
| Credibility interval | (−0.3758, −0.1964) | (−0.0337, 0.0786) | (0.1402, 0.3809) |
| Interval length | 0.1794 | 0.1124 | 0.2407 |
| | | | |
| Posterior mean | 0.5870 | −0.0186 | 0.0401 |
| Credibility interval | (0.0345, 1.1396) | (−0.0292, −0.0081) | (−0.100, 0.1804) |
| Interval length | 1.1051 | 0.0211 | 0.2802 |
Table 2.
Estimates for the regression coefficients of simulations with sample .
Table 2.
Estimates for the regression coefficients of simulations with sample .
| | | | |
| Posterior mean | 5.4863 | −0.0585 | 0.5424 |
| Credibility interval | (5.0157, 5.9568) | (−0.1572, 0.0402) | (0.4517, 0.6331) |
| Interval length | 0.9411 | 0.1974 | 0.1814 |
| | | | |
| Posterior mean | −0.2404 | 0.0209 | 0.2639 |
| Credibility interval | (−0.3058, −0.1751) | (−0.0328, 0.0476) | (0.2025, 0.3254) |
| Interval length | 0.1308 | 0.1074 | 0.1229 |
| | | | |
| Posterior mean | 0.4708 | −0.0142 | 0.0230 |
| Credibility interval | (0.2685, 0.6731) | (−0.0218, −0.0066) | (−0.0186, 0.0646) |
| Interval length | 0.4046 | 0.0152 | 0.0831 |
Table 3.
Estimates for the regression coefficients of simulations with sample .
Table 3.
Estimates for the regression coefficients of simulations with sample .
| | | | |
| Posterior mean | 5.4952 | −0.0485 | 0.5036 |
| Credibility interval | (5.2433, 5.7471) | (−0.0698, −0.0271) | (0.4822, 0.5249) |
| Interval length | 0.5038 | 0.0426 | 0.0428 |
| | | | |
| Posterior mean | −0.2518 | 0.0132 | 0.2753 |
| Credibility interval | (−0.2602, −0.2434) | (−0.0255, 0.0520) | (0.2636, 0.2871) |
| Interval length | 0.0168 | 0.0774 | 0.0234 |
| | | | |
| Posterior mean | 0.4162 | −0.0173 | 0.0248 |
| Credibility interval | (0.3156, 0.5168) | (−0.0214, −0.0132) | (−0.0093, 0.0589) |
| Interval length | 0.2012 | 0.0082 | 0.0682 |
Table 4.
Estimates and credibility interval for the regression coefficients of the Iowa river monthly flow.
Table 4.
Estimates and credibility interval for the regression coefficients of the Iowa river monthly flow.
| | | | |
| Posterior mean | 496.8886 | 209.1493 | −188.5929 |
| Credibility interval | (442.9628, 550.8143) | (132.8868, 285.4118) | (−264.8554, −112.3304) |
| | | | |
| Posterior mean | 581.5001 | 214.7011 | −199.2846 |
| Credibility interval | (538.5956, 624.4043) | (171.4820, 257.9182) | (−256.3556, −142.2444) |
| | | | |
| Posterior mean | 5.1310 | 0.1875 | −0.5595 |
| Credibility interval | (5.0304, 5.2316) | (0.0637, 0.3113) | (−0.7006, −0.4184) |
| | | | |
| Posterior mean | −0.1859 | −0.1653 | −0.1273 |
| Credibility interval | (−0.2448, −0.1270) | (−0.2409, −0.0897) | (−0.2091, −0.0455) |
Table 5.
Estimates and credibility interval for the regression coefficients of the Patuxent river daily flow.
Table 5.
Estimates and credibility interval for the regression coefficients of the Patuxent river daily flow.
| | | | |
| Posterior mean | 20.0316 | −4.5074 | 3.2883 |
| Credibility interval | (19.6799, 20.3834) | (−5.0068, −4.0080) | (2.7932, 3.7834) |
| | | | |
| Posterior mean | 167.3000 | 11.1576 | 9.2531 |
| Credibility interval | (115.4776, 219.1224) | (4.8359, 17.4793) | (2.7590, 15.7472) |
| | | | |
| Posterior mean | 4.5040 | 0.1822 | −0.0208 |
| Credibility interval | (3.9989, 5.0091) | (0.0411, 0.3233) | (−0.0445, −0.0029) |
| | | | |
| Posterior mean | 0.5538 | 0.0642 | −0.0452 |
| Credibility interval | (0.3828, 0.7248) | (−0.0982, 0.2266) | (−0.1933, 0.1029) |