A Data-Driven Parameter Prediction Method for HSS-Type Methods

Abstract

Some matrix-splitting iterative methods for solving systems of linear equations contain parameters that need to be specified in advance, and the choice of these parameters directly affects the efficiency of the corresponding iterative methods. This paper uses a Bayesian inference-based Gaussian process regression (GPR) method to predict the relatively optimal parameters of some HSS-type iteration methods and provide extensive numerical experiments to compare the prediction performance of the GPR method with other existing methods. Numerical results show that using GPR to predict the parameters of the matrix-splitting iterative methods has the advantage of smaller computational effort, predicting more optimal parameters and universality compared to the currently available methods for finding the parameters of the HSS-type iteration methods.

1. Introduction

Solving linear equations is one of the most fundamental topics in matrix computation, and with the development of science and technology, many important problems in the natural sciences and engineering can often be reduced to the following linear equation:

$$Ax=b,$$

(1)

where $x,b\in {\mathbb{C}}^n$, $A\in {\mathbb{C}}^{n\times n}$ is a large sparse non-Hermitian and positive definite matrix.

There are many powerful matrix-splitting iterative methods for solving systems of linear equations, such as the successive over-relaxation (SOR) method [1], the symmetric SOR (SSOR) method [2], the accelerated over-relaxation (AOR) method [3] and the symmetric AOR (SAOR) method [4]. Many researchers have applied them to different problems and made some improvements [5,6,7,8]. Considering the specificity of the problem and solving Equation (1) more efficiently, many new matrix-splitting iterative methods have been proposed. Bai et al. offered the Hermitian and skew-Hermitian splitting (HSS) method and the inexact HSS method [9]. To improve the efficiency of the HSS method, Bai et al. proposed the preconditioned HSS (PHSS) [10]. Due to the promising performance of the HSS method, some HSS-type iteration methods were presented. These methods can be mainly divided into the following two forms. The first one is accelerated HSS-type methods. Such as the generalized HSS method [11], the lopsided HSS (LHSS) method [12], the generalized PHSS method [13], the asymmetric HSS method [14] and the new HSS (NHSS) method [15]. In addition, Yang et al. offered the minimum residual HSS method [16] by applying the minimum residual technique to the HSS method and Li et al. [17] proposed the single-step HSS (SHSS) method. Based on the shift-splitting method and the SHSS method, Li et al. established the SHSS-SS method [18].

Apart from the accelerated HSS-type methods, some other HSS-type methods focused on the applications to different kinds of problems. Such as the saddle-point problems [19,20,21,22,23,24], solving the matrix equation [25,26,27,28,29,30,31,32], and solving the complex symmetric linear systems [33,34,35] and the nonlinear systems [36,37].

These iteration methods contain splitting parameters that need to be specified in advance. At present, there are three main methods of selecting the splitting parameters. The first is obtaining relatively optimal parameters by traversing or experimenting within some intervals [26,38,39]. The advantage of this traversal method is that it can obtain relatively accurate optimal parameters, but it requires large amount of calculation and consumes a lot of extra time, especially when the dimension of the coefficient matrix is large. The second is estimating optimal parameters through theoretical analysis [40,41]. Some researchers find optimal parameters by minimizing the spectral radius of the iterative matrix. However, solving this optimization problem is very difficult in theoretical analysis and practical computation. Bai et al. [42] proposed an accurate formula for computing the optimal parameters of the HSS method by directly minimizing the spectral radius of the iterative matrix, but the coefficient matrix is a two-by-two matrix or a two-by-two block matrix with specific forms. Some researchers find quasi-optimal parameters by minimizing the upper bound of the spectral radius of the iterative matrix of some iteration methods [9,12,17,18]. By a reasonable and simple optimization principle, Chen [43] proposed an accurate estimate to the optimal parameter of the HSS iteration method. Huang [44] and Yang [45] estimated the optimal parameters of the HSS method by solving a cubic polynomial equation and a quartic polynomial equation, respectively. Huang [46] proposed variable-parameter HSS methods and the parameter in it updated at each step of the iteration. The above theoretical methods contain the following limitations. First, the method is only available case by case, which means it is less universal. Second, the method needs to compute the maximum or the minimum eigenvalues of the matrix, but this is time-consuming work. Jiang et al. [47] proposed the third estimation method, the Bayesian inference-based Gaussian process regression (GPR) method, to predict the optimal parameters in some alternating direction iterative methods. This method uses a training set to learn a mapping between the dimension of linear systems and relatively optimal splitting parameters.

The choice of splitting parameters can greatly affect the efficiency of the HSS-type iteration methods [47,48], which makes the parameter selection of great importance. For computing the splitting parameters of the HSS-type iteration methods, to overcome the limitations of the traversal method and the theoretical methods, we use the GPR method to predict the splitting parameters of some HSS-type iteration methods. The main contributions of this work are:

• We apply the GPR method for the prediction of optimal splitting parameters of some HSS-type methods, which is a new application.
• We provide extensive numerical experiments to compare the prediction performance of the GPR method with the traversal method and the theoretical methods.

The results of numerical experiments show that: comparing to the traversal method, the GPR method can predict almost the same parameters as the traversal method does but with less computational effort; comparing to the theoretical method, the GPR method can predict better optimal parameters than the theoretical method and is more universal (unlike the theoretical method available case by case, the GPR method is suitable for all the HSS-type iteration methods tested). Moreover, the theoretical methods need to compute the maximum or the minimum eigenvalues (or singular values) of the matrix but this is a time-consuming work when the dimension of the matrix is large and the GPR method overcomes this limitation.

The rest of the paper is organized as follows. In Section 2, we present Gaussian process regression method based on Bayesian inference. In Section 3, we present the iteration scheme of some HSS-type iteration methods, the corresponding convergence conditions and the theoretical methods for estimating the relatively optimal splitting parameters. In Section 4, we illustrate the efficiency of the GPR method by numerical experiments. Finally, in Section 5, we include some concluding remarks and prospects.

Throughout the paper, the sets of $n\times n$ complex and real matrices are denoted by ${\mathbb{C}}^{n\times n}$ and ${\mathbb{R}}^{n\times n}$, respectively. If $X\in {\mathbb{C}}^{n\times n}$, let $X^T$,$X^{-1}$,$X^{*}$,${∥X∥}_2$,${∥X∥}_F$ denote the transpose, inverse, conjugate transpose, the Euclidean norm and Frobenius norm of X, respectively. The notations $\lambda \left(X\right)=({\lambda }_1\left(X\right),{\lambda }_2\left(X\right),\cdots ,{\lambda }_n\left(X\right))$, $\sigma \left(X\right)=({\sigma }_1\left(X\right),{\sigma }_2\left(X\right),\cdots ,{\sigma }_n\left(X\right))$, $\rho \left(X\right)$ denote the eigenvalue set, singular value set and spectral radius of X, respectively. The symbol ⊗ denotes the Kronecker product. I represents the identity matrix.

2. Gaussian Process Regression Method

In this section, we present a Gaussian process regression method based on Bayesian inference. Gaussian process regression is an application of non-parametric Bayesian estimation to regression problems and has a wide range of applications in the field of machine learning.

2.1. Bayesian Inference

Bayesian inference is a method that infers the population distribution or the characteristic number of the population according to the sample information and the prior information. Prior information is some information about statistical problems before sampling. Taking inferrance of the distribution of an unknown quantity $\theta$ as an example, Bayesian inference believes that $\theta$ can be regarded as a random variable before obtaining the sample information, so it can be described by a probability distribution and this distribution is a prior distribution. After obtaining the samples, the population distribution, samples and the prior distribution are combined by Bayesian formula to obtain a new distribution about the unknown quantity $\theta$, which is a posterior distribution. We can find that the process of Bayesian inference is essentially the process of updating prior information through sample information.

The Bayesian inference-based Gaussian process regression method is Bayesian inference with Gaussian process as a prior distribution. The definition of Gaussian process is given below.

Definition 1.

Gaussian process (GP) is a collection of random variables $\{X_t,t\in T\}$ and for any finite subset $\{t_1,t_2,\dots ,t_k\}$ of T, $(X_{t_1},X_{t_2},\dots ,X_{t_k})$ follows the joint Gaussian distribution.

In our question, we expect to obtain a mapping $f(·)$ from the dimension of linear systems to relatively optimal splitting parameters, so that for each given dimension $n_{*}$, the mapping can output the corresponding relatively optimal splitting parameter ${\alpha }_{*}=f\left(n_{*}\right)$. To this end, this paper uses the GPR to fit this mapping $f\left(n\right)$.

2.2. Model Building

Following the steps of Bayesian inference, firstly, we give prior information. For each given $n\in N^{+}$, the corresponding optimal splitting parameter $\alpha$ is a random variable, and we denote $\alpha$ as $f\left(n\right)$ to reflect the correspondence between $\alpha$ and n. Considering that, in general, the observed $\alpha$ would be polluted by addition noise, the observed $\alpha$ may not be exactly equal to $f\left(n\right)$. It is

$$\alpha =f\left(n\right)+\eta ,$$

(2)

where $\eta$ is the addition noise and we assume that $\eta$ follows a Gaussian distribution with zero mean and variance ${\sigma }^2$, i.e., $\eta \sim N(0,{\sigma }^2)$. The desirable range of $\sigma$ is ${10}^{-2}\le \sigma \le {10}^{-6}$. In this work, we take $\sigma ={10}^{-4}$. We also assume that $f\left(n\right)$ are independent of each other. Obviously, our task is to obtain $f(·)$.

Considering random process $\{f\left(n\right),n\in N^{+}\}$ and assuming this process is a GP, we have

$$f\left(n\right)\sim GP\left(\mu \right(n),k(n,n\left)\right),$$

where $\mu (·)$ and $(·,·)$ denote mean function and covariance function of the GP $f\left(n\right)$, respectively. Once $\mu (·)$ and $k(·,·)$ have been determined, the GP is also determined. The selection of $\mu (·)$ and $k(·,·)$ is shown in Section 2.3.

Next, we obtain sample information. Assume that we have a training set $D=\left\{\left(n_i,{\alpha }_i\right)\mid i=1,2,\cdots ,d\right\}:=\{\mathbf{n},\alpha \}$ where $(n_i,{\alpha }_i)$ is an input–output pair. $n_i$ is the dimension of the coefficient matrix and ${\alpha }_i$ is the optimal splitting parameter in a matrix-splitting iterative method. Obviously, the training set is the sample information. According to the prior information, $\{f\left(n_i\right),i=1,2,\cdots ,d\}$ follows the joint Gaussian distribution, i.e.,

$$f\left(\mathbf{n}\right):=\left(\begin{array}{c}f\left(n_1\right)\\ ⋮\\ f\left(n_d\right)\end{array}\right)\sim N\left(\left(\begin{array}{c}\mu \left(n_1\right)\\ ⋮\\ \mu \left(n_d\right)\end{array}\right),\left(\begin{array}{ccc}k\left(n_1,n_1\right)& \cdots & k\left(n_1,n_d\right)\\ ⋮& \ddots & ⋮\\ k\left(n_d,n_1\right)& \cdots & k\left(n_1,n_d\right)\end{array}\right)\right).$$

Or equally,

$$f\left(\mathbf{n}\right)\sim N\left(\mu \right(\mathbf{n}),k(\mathbf{n},\mathbf{n}\left)\right),$$

where $\mathbf{n}={(n_1,n_2,\dots ,n_d)}^T$. From Equation (2), the distribution of the corresponding observed $\alpha$ is

$$\alpha \sim N\left(\mu \left(\mathbf{n}\right),k(\mathbf{n},\mathbf{n})+{\sigma }^2{I}_d\right)$$

(3)

where $I_d$ is a d-order identity matrix.

Finally, we can update the prior information by using the sample information. That is to say, to predict new dimensional vector ${\mathbf{n}}_{*}={(n_1,n_2,\dots ,n_m)}^T$, we can obtain the distribution of the optimal splitting parameters corresponding to ${\mathbf{n}}_{*}$, i.e., the conditional distribution ${\mathbf{f}}_{*}|\mathbf{n},\alpha ,{\mathbf{n}}_{*}$, where ${\mathbf{f}}_{*}={(f\left(n_1\right),f\left(n_2\right),\dots ,f\left(n_m\right))}^T$. According to the prior information, the sample $\alpha$ and predicted value of ${\mathbf{n}}_{*}$ follow the joint Gaussian distribution. From Equation (3), we have

$$\left(\begin{array}{c}\alpha \hfill \\ {\mathbf{f}}_{*}\hfill \end{array}\right)\sim N\left(\left(\begin{array}{c}\mu \left(\mathbf{n}\right)\hfill \\ \mu \left({\mathbf{n}}_{*}\right)\hfill \end{array}\right),\left(\begin{array}{cc}k(\mathbf{n},\mathbf{n})+{\sigma }^2{I}_d& k\left(\mathbf{n},{\mathbf{n}}_{*}\right)\\ k\left({\mathbf{n}}_{*},\mathbf{n}\right)& k\left({\mathbf{n}}_{*},{\mathbf{n}}_{*}\right)\end{array}\right)\right).$$

(4)

To obtain the conditional distribution ${\mathbf{f}}_{*}|\mathbf{n},\alpha ,{\mathbf{n}}_{*}$ from Equation (4), we have the following theorem [49].

Theorem 1.

Let $\mathbf{x}$ and $\mathbf{y}$ be jointly Gaussian random vectors, i.e.,

$$\left(\begin{array}{c}\mathbf{x}\hfill \\ \mathbf{y}\hfill \end{array}\right)\sim N\left(\left(\begin{array}{c}{\mu }_x\hfill \\ {\mu }_y\hfill \end{array}\right),\left(\begin{array}{cc}A& C\\ C^T& B\end{array}\right)\right),$$

then the marginal distribution of $\mathbf{x}$ and the conditional distribution of $\mathbf{x}$ given by $\mathbf{y}$ are

$$\begin{array}{cc}\hfill & \mathbf{x}\sim N\left({\mu }_x,A\right),\hfill \\ \hfill & \mathbf{x}\mid \mathbf{y}\sim N\left({\mu }_x+C{B}^{-1}\left(\mathbf{y}-{\mu }_y\right),A-C{B}^{-1}{C}^T\right).\hfill \end{array}$$

From Theorem 1, we have

$${\mathbf{f}}_{*}\mid \mathbf{n},\alpha ,{\mathbf{n}}_{*}\sim N\left({\mu }_{*},{\sigma }_{*}^2\right),$$

where

$$\begin{array}{cc}\hfill & {\mu }_{*}=k\left({\mathbf{n}}_{*},\mathbf{n}\right){\left[k(\mathbf{n},\mathbf{n})+{\sigma }^2{I}_d\right]}^{-1}(\alpha -\mu \left(\mathbf{n}\right))+\mu \left({\mathbf{n}}_{*}\right),\hfill \\ & {\sigma }_{*}^2=k\left({\mathbf{n}}_{*},{\mathbf{n}}_{*}\right)-k\left({\mathbf{n}}_{*},\mathbf{n}\right){\left[k(\mathbf{n},\mathbf{n})+{\sigma }^2{I}_d\right]}^{-1}k\left(\mathbf{n},{\mathbf{n}}_{*}\right).\hfill \end{array}$$

For the predicted value ${\mathbf{n}}_{*}$, one can use the mean value of the above Gaussian distribution as its estimated value, i.e., ${\mathbf{f}}_{*}={\mu }_{*}$. Now, we have successfully obtained the function $f(·)$, and denoted the independent variable of $f(·)$ by ${\mathbf{n}}_{*}$; then, $f\left({\mathbf{n}}_{*}\right):={\mu }_{*}\left({\mathbf{n}}_{*}\right)$.

2.3. Model Selection

In this section, we determine $\mu (·)$ and $k(·,·)$. In this work, we let $\mu (·)=0$, other ways can refer to [49]. For covariance function, the exponential kernel function is

$$k(x,y)={\sigma }_f^{2}exp\left(\frac{-\parallel x-y\parallel }{2{\iota }^2}\right),$$

where $\theta =\{\iota ,{\sigma }_f\}$ is the hyperparameter. In this work, maximum likelihood estimation is used to select the values of the hyperparameter $\theta$. Specifically, when we have a training set $D=\left\{\left(n_i,{\alpha }_i\right)\mid i=1,2,\cdots ,d\right\}:=\{\mathbf{n},\mathit{\alpha }\}$, the likelihood function L of $\theta$ can be derived as

$$\begin{array}{cc}\hfill L:=logp(\mathit{\alpha }\mid \mathbf{n},\theta )=& -\frac{1}{2}{\mathit{\alpha }}^T{\left[k_{\theta }(\mathbf{n},\mathbf{n})+{\sigma }^2{I}_d\right]}^{-1}\mathit{\alpha }\hfill \\ \hfill & -\frac{1}{2}logdet\left(k_{\theta }(\mathbf{n},\mathbf{n})+{\sigma }^2{I}_d\right).\hfill \end{array}$$

The optimal hyperparameter $\theta$ is ${\theta }^{*}=arg\underset{\theta }{max}L$.

In practice, to avoid a large amount of calculation, we generally produced the training set from a set of small-scale systems.

3. Matrix-Splitting Iterative Methods

In this section, we recall some matrix-splitting iteration methods, including the HSS method, the NHSS method, the LHSS method, the SHSS method, the SHSS-SS method, the MHSS method and the MSNS method. We mainly focus on their iterative schemes, convergence and theoretical methods involving estimating optimal splitting parameters.

3.1. Matrix-Splitting Methods for Non-Hermitian Positive Definite Linear Systems

Consider the linear Equation (1).

$$Ax=b,$$

(5)

where $x,b\in {\mathbb{C}}^n$, $A\in {\mathbb{C}}^{n\times n}$ is non-singular. Let $M,N\in {\mathbb{C}}^{n\times n}$ be splitting matrices such that

$$A=M+N.$$

For the HSS method, the NHSS method, the LHSS method, the SHSS method and the SHSS-SS method, they all split A into Hermitian and skew-Hermitian parts. i.e.,

$$M=\frac{A+A^{*}}{2},N=\frac{A-A^{*}}{2}.$$

(6)

3.1.1. HSS Iteration Method

The scheme of HSS iteration [9] is as follows.

Definition 2.

Given an initial guess $x^0$, for $k=0,1,2,\cdots ,$ until $x^{\left(k\right)}$ converges, compute

$$\begin{array}{cc}\hfill & (\alpha I+M)x^{(k+\frac{1}{2})}=(\alpha I-N)x^{\left(k\right)}+b,\hfill \\ \hfill & (\alpha I+N)x^{(k+1)}=(\alpha I-M)x^{(k+\frac{1}{2})}+b,\hfill \end{array}$$

where α is a given positive constant.

For the convergence property of the HSS iteration, we have the following theorem [9]:

Theorem 2.

Let A in Equation (5) be a positive definite matrix, the matrixes $M,N$ be defined in the same way as Equation (6) and let α be a positive constant. Then, the iteration matrix $M\left(\alpha \right)$ of the HSS iteration is given by

$$M\left(\alpha \right)={(\alpha I+N)}^{-1}(\alpha I-M){(\alpha I+M)}^{-1}(\alpha I-N),$$

and its spectral radius $\rho \left(M\right(\alpha \left)\right)$ is bounded by

$$\sigma \left(\alpha \right)\equiv \underset{\lambda \in \lambda \left(M\right)}{max}\left|\frac{\alpha -{\lambda }_i}{\alpha +{\lambda }_i}\right|,$$

(7)

where $\lambda \left(M\right)$ is the spectral set of the matrix M. Therefore, it holds that

$$\rho \left(M\right(\alpha \left)\right)\le \sigma \left(\alpha \right)<1,$$

i.e., the HSS iteration converges to the unique solution of the Equation (5).

Equation (7) provides a theoretical method to estimate the optimal splitting parameter, that is, by minimizing the upper bound $\sigma \left(\alpha \right)$ of the spectral radius of the iteration matrix $M\left(\alpha \right)$ of the HSS iteration to obtain the quasi-optimal splitting parameter ${\alpha }^{*}$, and it is shown by the following theorem [9].

Theorem 3.

The conditions are the same as Theorem 2: let ${\lambda }_{min}$ and ${\lambda }_{max}$ be the minimum and the maximum eigenvalues of the matrix M, respectively. Then

$${\alpha }^{*}\equiv arg\underset{\alpha }{min}\left\{\underset{{\gamma }_{min}\le \lambda \le {\gamma }_{max}}{max}\left|\frac{\alpha -\lambda }{\alpha +\lambda }\right|\right\}=\sqrt{{\lambda }_{min}{\lambda }_{max}}.$$

The HSS iteration needs to solve two linear systems with coefficient matrices $\alpha I+H$ and $\alpha I+S$, which is costly and impractical. An approach to overcome this disadvantage is to solve two subproblems iteratively and this result is the inexact HSS (IHSS) iteration method.

Definition 3.

Given an initial guess $x^0$, for $k=0,1,2,\cdots ,$ until $x^{\left(k\right)}$ converges,

1. 

Approximately solve $(\alpha I+M){\overline{z}}^{\left(k\right)}={\overline{r}}^{\left(k\right)}({\overline{r}}^{\left(k\right)}=b-A{\overline{x}}^{\left(k\right)})$ by employing an inner iteration (e.g., the CG method), such that the residual ${\overline{p}}^{\left(k\right)}={\overline{r}}^{\left(k\right)}-(\alpha I+M){\overline{z}}^{\left(k\right)}$ satisfies

$$∥{\overline{p}}^{\left(k\right)}∥\le {\epsilon }_k∥{\overline{r}}^{\left(k\right)}∥,$$

and then compute ${\overline{x}}^{(k+\frac{1}{2})}={\overline{x}}^{\left(k\right)}+{\overline{z}}^{\left(k\right)}$;

2. 

Approximately solve $(\alpha I+N){\overline{z}}^{(k+\frac{1}{2})}={\overline{r}}^{(k+\frac{1}{2})}({\overline{r}}^{(k+\frac{1}{2})}=b-A{\overline{x}}^{(k+\frac{1}{2})}$) by employing an inner iteration (e.g., some Krylov subspace method), such that the residual ${\overline{q}}^{(k+\frac{1}{2})}={\overline{r}}^{(k+\frac{1}{2})}-(\alpha I+N){\overline{z}}^{(k+\frac{1}{2})}$ satisfies

$$∥{\overline{q}}^{(k+\frac{1}{2})}∥\le {\eta }_k∥{\overline{r}}^{(k+\frac{1}{2})}∥,$$

and then compute ${\overline{x}}^{(k+1)}={\overline{x}}^{(k+\frac{1}{2})}+{\overline{z}}^{(k+\frac{1}{2})}$, here α is a given positive constant.

The convergence property and the choice of the tolerance ${\epsilon }_k$ and ${\eta }_k$ can refer to [9].

3.1.2. NHSS Iteration Method

The scheme of NHSS [15] iteration is as follows.

Definition 4.

Given an initial guess $x^0$, for $k=0,1,2,\cdots ,$ until $x^{\left(k\right)}$ converges, compute

$$\begin{array}{cc}\hfill & M{x}^{(k+\frac{1}{2})}=-N{x}^{\left(k\right)}+b,\hfill \\ \hfill & (\alpha I+M)x^{(k+1)}=(\alpha I-N)x^{(k+\frac{1}{2})}+b,\hfill \end{array}$$

where α is a given positive constant.

For the convergence property of the NHSS iteration, we have the following theorem [15]:

Theorem 4.

Let A in Equation (5) be a positive definite and normal matrix; the matrixes $M,N$ be defined in the same way as Equation (6) and let α be a positive constant. Then, the iteration matrix $M\left(\alpha \right)$ of the NHSS iteration is

$$M\left(\alpha \right)={(\alpha I+M)}^{-1}(\alpha I-N)M^{-1}(-N).$$

The spectral radius $\rho \left(M\right(\alpha \left)\right)$ is bounded by

$$\sigma \left(\alpha \right)\equiv \frac{{\sigma }_{max}\sqrt{{\alpha }^2+{\sigma }_{max}^2}}{{\lambda }_{min}\left(\alpha +{\lambda }_{min}\right)},$$

(8)

where ${\sigma }_{max}$ is the maximum singular value of the matrix N and ${\lambda }_{min}$ is the minimum eigenvalue of the matrix M. Moreover, if ${\sigma }_{max}\le {\lambda }_{min}$, then

$$M\left(\alpha \right)\le \sigma \left(\alpha \right)<1,$$

i.e., the NHSS iteration converges to the unique solution of Equation (5).

Equation (8) provides a theoretical method to estimate the optimal splitting parameter, that is, by minimizing the upper bound $\sigma \left(\alpha \right)$ of the spectral radius of the iteration matrix $M\left(\alpha \right)$ of the NHSS iteration to obtain the quasi-optimal splitting parameter ${\alpha }^{*}$, and it is given by Theorem 5 [15].

Theorem 5.

The conditions are the same as Theorem 4; then, the quasi-optimal splitting parameter of the NHSS iteration is

$${\alpha }^{*}=\frac{{\sigma }_{max}^2}{{\lambda }_{min}}.$$

3.1.3. LHSS Iteration Method

The scheme of LHSS iteration [12] is as follows.

Definition 5.

Given an initial guess $x^0$, for $k=0,1,2,\cdots ,$ until $x^{\left(k\right)}$ converges, compute

$$\begin{array}{cc}\hfill & M{x}^{(k+\frac{1}{2})}=-N{x}^{\left(k\right)}+b,\hfill \\ \hfill & (\alpha I+N)x^{(k+1)}=(\alpha I-M)x^{(k+\frac{1}{2})}+b,\hfill \end{array}$$

where α is a given positive constant.

For the convergence property of the LHSS iteration, we have the following theorem [12]:

Theorem 6.

Let A in Equation (5) be non-singular and α be a positive constant. Then, the LHSS iteration converges to the unique solution of Equation (5). Moreover, the spectral radius of the iterative matrix of the LHSS iteration satisfies

$$\begin{array}{c}\rho \left(M\left(\alpha \right)\right)<\frac{{\sigma }_{max}}{\sqrt{{\alpha }^2+{\sigma }_{max}^2}}\underset{{\lambda }_i\in \lambda \left(M\right)}{max}\left|\frac{\alpha -{\lambda }_i}{{\lambda }_i}\right|,\hfill \end{array}$$

(9)

where

$$M\left(\alpha \right)={(\alpha I+N)}^{-1}{(\alpha I-M)}^{-1}(-N).$$

By minimizing the upper bound of the spectral radius of the iteration matrix of the LHSS iteration in Equation (9), we can obtain the quasi-optimal splitting parameter ${\alpha }^{*}$ using Theorem 7 [12].

Theorem 7.

The conditions are the same as Theorem 6: let ${\lambda }_{min}$ and ${\lambda }_{max}$ be the minimum and the maximum eigenvalues of the matrix M, respectively. Let ${\sigma }_{max}$ be the maximum singular value of the matrix N. Then

$${\alpha }^{*}=\frac{2{\lambda }_{max}{\lambda }_{min}}{{\lambda }_{max}+{\lambda }_{min}}.$$

To improve the efficiency of the LHSS iteration method, we have the following ILHSS iteration method.

Definition 6.

Given an initial guess $x^0$, for $k=0,1,2,\cdots ,$ until $x^{\left(k\right)}$ converges,

1. 

Approximately solve $M{\overline{z}}^{\left(k\right)}={\overline{r}}^{\left(k\right)}({\overline{r}}^{\left(k\right)}=b-A{\overline{x}}^{\left(k\right)})$ by employing an inner iteration (e.g., the CG method), such that the residual ${\overline{p}}^{\left(k\right)}={\overline{r}}^{\left(k\right)}-M{\overline{z}}^{\left(k\right)}$ satisfies

$$∥{\overline{p}}^{\left(k\right)}∥\le {\epsilon }_k∥{\overline{r}}^{\left(k\right)}∥,$$

and then compute ${\overline{x}}^{(k+\frac{1}{2})}={\overline{x}}^{\left(k\right)}+{\overline{z}}^{\left(k\right)}$;

2. 

Approximately solve $(\alpha I+N){\overline{z}}^{(k+\frac{1}{2})}={\overline{r}}^{(k+\frac{1}{2})}({\overline{r}}^{(k+\frac{1}{2})}=b-A{\overline{x}}^{(k+\frac{1}{2})}$) by employing an inner iteration (e.g., a Krylov subspace method), such that the residual ${\overline{q}}^{(k+\frac{1}{2})}={\overline{r}}^{(k+\frac{1}{2})}-(\alpha I+N){\overline{z}}^{(k+\frac{1}{2})}$ satisfies

$$∥{\overline{q}}^{(k+\frac{1}{2})}∥\le {\eta }_k∥{\overline{r}}^{(k+\frac{1}{2})}∥,$$

and then compute ${\overline{x}}^{(k+1)}={\overline{x}}^{(k+\frac{1}{2})}+{\overline{z}}^{(k+\frac{1}{2})}$, where α is a given positive constant.

The convergence property and the choice of the tolerance ${\epsilon }_k$ and ${\eta }_k$ can refer to [12].

3.1.4. SHSS Iteration Method

The scheme of SHSS iteration [17] is as follows.

Definition 7.

Given an initial guess $x^0$, for $k=0,1,2,\cdots ,$ until $x^{\left(k\right)}$ converges, compute

$$\begin{array}{cc}\hfill & (\alpha I+M)x^{(k+1)}=(\alpha I-N)x^{\left(k\right)}+b.\hfill \end{array}$$

where α is a given positive constant.

For the convergence property of the SHSS iteration, we have the following theorem [17]:

Theorem 8.

Let A in Equation (5) be positive definite. Let ${\lambda }_{min}$ and ${\lambda }_{max}$ be the minimum and the maximum eigenvalues of the matrix M, respectively. Let ${\sigma }_{max}$ be the maximum singular value of the matrix N. The spectral radius of the iteration matrix of the SHSS iteration method is bounded by

$$\sigma \left(\alpha \right)=\frac{\sqrt{{\alpha }^2+{\sigma }_{max}^2}}{\alpha +{\lambda }_{min}}.$$

Moreover,

(i) 

If ${\lambda }_{min}\ge {\sigma }_{max}$, then $\sigma \left(\alpha \right)<1$ for any $\alpha >0$, which means that the SHSS iteration method is unconditional convergent;

(ii) 

If ${\lambda }_{min}<{\sigma }_{max}$, then $\sigma \left(\alpha \right)<1$ (which means the SHSS iteration method is convergent) if and only if

$$\alpha >max\left\{0,\frac{{\sigma }_{max}^2-{\lambda }_{min}^2}{2{\lambda }_{min}}\right\}.$$

The quasi-optimal splitting parameter ${\alpha }^{*}$ of the SHSS-SS iteration method is shown by Theorem 9 [17].

Theorem 9.

The conditions are the same as Theorem 8, then

$${\alpha }^{*}=\frac{{\sigma }_{max}^2}{{\lambda }_{min}}.$$

3.1.5. SHSS-SS Iteration Method

The scheme of SHSS-SS iteration [18] is as follows.

Definition 8.

Given an initial guess $x^0$, for $k=0,1,2,\cdots ,$ until $x^{\left(k\right)}$ converges, compute

$$\begin{array}{cc}\hfill & (\alpha I+M)x^{(k+\frac{1}{2})}=(\alpha I-N)x^{\left(k\right)}+b,\hfill \\ \hfill & (\alpha I+A)x^{(k+1)}=(\alpha I-A)x^{(k+\frac{1}{2})}+2b,\hfill \end{array}$$

where α is a given positive constant.

For the convergence property of the SHSS-SS iteration, we have the following theorem [18]:

Theorem 10.

Let A in Equation (5) be non-Hermitian and positive definite. Let ${\lambda }_{min}$ and ${\lambda }_{max}$ be the minimum and the maximum eigenvalues of the matrix M, respectively. Let ${\sigma }_{max}$ be the maximum singular value of the matrix N. If α satisfies

$$\alpha >max\left\{0,\frac{{\sigma }_{max}^2-{\lambda }_{min}^2}{2{\lambda }_{min}}\right\},$$

then the SHSS-SS iteration converges to the unique solution of Equation (5).

The quasi-optimal splitting parameter ${\alpha }^{*}$ of the SHSS-SS iteration method is as follows [18].

Theorem 11.

The conditions are the same as Theorem 10, then

$${\alpha }^{*}=\frac{{\sigma }_{max}^2}{{\lambda }_{min}}.$$

3.2. Matrix-Splitting Methods for Complex Symmetric Linear Systems

Considering the linear equation of the form

$$Ax\equiv (W+iT)x=b,$$

(10)

where $W,T\in {\mathbb{R}}^{n\times n}$ are symmetric positive definite matrix and symmetric positive semi-definite matrix, respectively, $b\in {\mathbb{R}}^n$ and $i=\sqrt{-1}$. Here, we let $T\ne 0$, so A in Equation (10) is non-Hermitian.

3.2.1. HSS Iteration Method and MHSS Iteration Method

As the matrix W is positive definite, so the matrix A in Equation (10) is non-Hermitian positive definite. We can straightforwardly use the HSS method to solve Equation (10). The scheme of HSS iteration is as follows.

Definition 9.

Given an initial guess $x^0$, for $k=0,1,2,\cdots ,$ until $x^{\left(k\right)}$ converges, compute

$$\begin{array}{c}(\alpha I+W)x^{(k+\frac{1}{2})}=(\alpha I-iT)x^{\left(k\right)}+b,\hfill \\ (\alpha I+iT)x^{(k+1)}=(\alpha I-W)x^{(k+\frac{1}{2})}+b,\hfill \end{array}$$

(11)

where α is a given positive constant.

However, solving the linear sub-system with its coefficient matrix being the shifted skew-Hermitian $\alpha I+iT$ is very difficult in some cases. To avoid this, Bai et al. [33] proposed the modified HSS (MHSS) method. The scheme of MHSS iteration is as follows.

Definition 10.

Given an initial guess $x^0$, for $k=0,1,2,\cdots ,$ until $x^{\left(k\right)}$ converges, compute

$$\begin{array}{cc}\hfill & (\alpha I+W)x^{(k+\frac{1}{2})}=(\alpha I-iT)x^{\left(k\right)}+b,\hfill \\ \hfill & (\alpha I+T)x^{(k+1)}=(\alpha I+iW)x^{(k+\frac{1}{2})}-ib,\hfill \end{array}$$

where α is a given positive constant.

For the convergence property of the MHSS iteration, we have the following theorem [33]:

Theorem 12.

The conditions are the same as for Equation (11) and let α be a positive constant. Then, the iteration matrix $M\left(\alpha \right)$ of the MHSS iteration is

$$M\left(\alpha \right)={(\alpha I+T)}^{-1}(\alpha I+iW){(\alpha I+W)}^{-1}(\alpha I-iT),$$

and its spectral radius $\rho \left(M\right(\alpha \left)\right)$ is bounded by

$$\sigma \left(\alpha \right)\equiv \underset{{\lambda }_j\in \lambda \left(M\right)}{max}\frac{\sqrt{{\alpha }^2+{\lambda }_j^2}}{\alpha +{\lambda }_j},$$

where $\lambda \left(M\right)$ is the spectral set of the matrix M. Therefore, we have

$$M\left(\alpha \right)\le \sigma \left(\alpha \right)<1,$$

i.e., the MHSS iteration converges to the unique solution of Equation (11).

The quasi-optimal splitting parameter ${\alpha }^{*}$ of the MHSS method is as follows [33].

Theorem 13.

The conditions are the same as Theorem 12, let ${\lambda }_{min}$ and ${\lambda }_{max}$ be the minimum and the maximum eigenvalues of the matrix W, respectively. Then

$${\alpha }^{*}=\sqrt{{\lambda }_{min}{\lambda }_{max}}.$$

Similar to the HSS iteration method and LHSS iteration method, the MHSS iteration method has its inexact version as well [33].

3.2.2. MSNS Iteration Method

The scheme of MSNS iteration [50] is as follows.

Definition 11.

Given an initial guess $x^0$, for $k=0,1,2,\cdots ,$ until $x^{\left(k\right)}$ converges, compute

$$\begin{array}{cc}\hfill & (\alpha I+T)x^{(k+\frac{1}{2})}=(i\alpha W+T^2)x^{\left(k\right)}+iTb,\hfill \\ \hfill & (i\alpha WI-T^2)x^{(k+1)}=(\alpha I-T)x^{(k+\frac{1}{2})}+iTb,\hfill \end{array}$$

where α is a given positive constant.

For the convergence property of the MSNS iteration, we have the following theorem [50]:

Theorem 14.

Let W be a real symmetric indefinite matrix, T be a real symmetric definite positive matrix and α be a positive constant. Then, the spectral radius $\rho \left(M\right(\alpha \left)\right)$ of the iteration matrix $M\left(\alpha \right)$ of the MSNS iteration is bounded by

$$\sigma \left(\alpha \right)\equiv \underset{{\mu }_j\in \mu \left(T\right)}{max}\left|\frac{\alpha -{\mu }_j}{\alpha +{\mu }_j}\right|,$$

where $\mu \left(T\right)$ is the spectral set of the matrix T. Moreover, it holds that

$$\rho \left(M\right(\alpha \left)\right)\le \sigma \left(\alpha \right)<1,$$

i.e., the MSNS iteration converges to the unique solution of Equation (11).

The quasi-optimal splitting parameter ${\alpha }^{*}$ of the MSNS method is as follows [50].

Theorem 15.

The conditions are the same as Theorem 14, let ${\mu }_{min}$ and ${\mu }_{max}$ be the minimum and the maximum eigenvalues of the matrix T, respectively. Then

$${\alpha }^{*}=\sqrt{{\mu }_{min}{\mu }_{max}}.$$

4. Numerical Results

In this section, we present extensive numerical examples to show the power of the GPR method compared with the traversal method and theoretical method. We take a three-dimensional convection-diffusion equation and $\mathrm{Pad}\acute{\mathrm{e}}$ approximation in the time integration of a parabolic partial differential equations as examples.

In the following numerical experiments, all tests are started with a zero vector. All iterative methods are terminated if the relative residual error satisfies ${∥r^{\left(k\right)}∥}_2/{∥r^{\left(0\right)}∥}_2\le {10}^{-6}$, where $r^{\left(k\right)}=b-A{x}^{\left(k\right)}$ is the k-step residual. “IT” and “CPU” denote the required iterations and the CPU time (in seconds), respectively. “Traversal time” denotes the required CPU time (in seconds) to obtain the optimal splitting parameters by the traversal method. “Training time” denotes the required CPU time (in seconds) to produce the training set and train the GPR model. We use

$$\frac{|\mathrm{Traversal}\mathrm{time}-\mathrm{Training}\mathrm{time}|}{\mathrm{Traversal}\mathrm{time}}$$

to make a comparison of the calculation amount of the traversal method and the GPR method. Obviously, the larger this quantity is, the longer the traversal time of the traversal method will take compared to the training time of the GPR method.

For the traversal method, the optimal splitting parameter minimizes the iterations of the corresponding iteration method when solving linear systems and it is obtained by traversing interval $(0,3]$ with a step size of $0.01$.

For the GPR method, the training set is produced by using the traversal method for a set of small-scale systems and their dimensions are shown later.

For the IHSS method and the ILHSS method, we use the CG method to solve the linear systems with the coefficient matrix $\alpha I+M$ and the GMRES method to solve linear systems with the coefficient matrix $\alpha I+N$. The inner CG and GMRES iterates are terminated if the current residuals of the inner iterations satisfy

$$\frac{{∥p^{\left(j\right)}∥}_2}{{∥r^{\left(k\right)}∥}_2}\le max\left\{0.1\times {0.8}^k,1\times {10}^{-7}\right\}\mathrm{and}\frac{{∥q^{\left(j\right)}∥}_2}{{∥r^{\left(k\right)}∥}_2}\le max\left\{0.1\times {0.8}^k,1\times {10}^{-6}\right\},$$

where $p^{\left(j\right)}$ and $q^{\left(j\right)}$ are, respectively, the residuals of the jth inner CG and GMRES, $r^{\left(k\right)}$ is the residual of the kth outer iteration.

All computations are carried out using MATLAB 2018b on a personal computer with a 1.8 GHz CPU Intel Core i5 and 8G memory.

Example 1.

Consider the following three-dimensional convection-diffusion equation

$$-\left(u_{xx}+u_{yy}+u_{zz}\right)+q\left(u_x+u_y+u_z\right)=f(x,y,z),$$

(12)

on the unit cube $\Omega :=[0,1]\times [0,1]\times [0,1]$, with constant coefficient q and subject to Dirichlet-type boundary conditions. When the seven-point finite difference discretization and the equidistant step-size $h=\frac{1}{n+1}$ (n is the degree of freedom along each dimension) is used on all the three directions applied to Equation (12), we obtain the linear system with the coefficient matrix

$$A=T_x\otimes I\otimes I+I\otimes T_y\otimes I+I\otimes I\otimes T_z,$$

(13)

where $T_x$,$T_y$ and $T_z$ are tridiagonal matrices. If the first order derivatives are approximated by the centered difference scheme, we have

$$\begin{array}{c}{T}_x=tridiag\left(t_2,t_1,t_3\right),T_y=tridiag\left(t_2,0,t_3\right),\hfill \\ T_z=tridiag\left(t_2,0,t_3\right),\hfill \end{array}$$

with $t_1=6$, $t_2=-1-r$, $t_3=-1+r$ and $r=\frac{qh}{2}$(mesh Reynolds number).

According to [9,51,52], for the centred difference scheme, the extreme eigenvalues and singular values of matrices M and N in Equation (6) are

$$\begin{array}{cc}\hfill & \underset{1⩽i⩽n^3}{min}{\lambda }_i\left(M\right)=6(1-cos\pi h),\underset{1⩽i⩽n^3}{max}{\lambda }_i\left(M\right)=6(1+cos\pi h),\hfill \\ \hfill & \underset{1⩽i⩽n^3}{max}{\sigma }_i\left(N\right)=6rcos\pi h.\hfill \end{array}$$

Therefore, the theoretical method of the HSS method, the LHSS method, the NHSS method, the SHSS method and the SHSS-SS method to obtain the optimal splitting parameters can be easily calculated.

Let $q=1$ in Equation (12). The discretization of Equation (12) leads to a system of linear equations $Ax=b$, where $A\in {\mathbb{R}}^{n^3\times n^3}$ is defined by Equation (13), and set the exact solution $x_e={(1,1,\dots ,1)}^T\in {\mathbb{R}}^{n^3}$, then, $b=A{x}_e$.

In this experiment, we apply the GPR method to compare with the traversal method and the theoretical method, respectively. Concretely, first, we use the HSS method, IHSS method, LHSS method and ILHSS method to solve the 3D convection-diffusion equation, and the splitting parameters are selected using the traversal method and the GPR method, respectively. Numerical experiments results show that the GPR can predict almost the same parameters as the traversal method does, but with less calculation. Finally, we use the HSS method, the NHSS method, the LHSS method, the SHSS method and the SHSS-SS method to solve the 3D convection-diffusion equation, and the splitting parameters are selected using the theoretical method and the GPR method, respectively. Numerical results show that the GPR method can compute better optimal parameters than the theoretical method, which means that the GPR method can be applied to a wide range of matrix-splitting iterative methods and is highly universal.

The GPR method vs. the traversal method. We first use the HSS method, the IHSS method, the LHSS method and the ILHSS method to solve the 3D convection-diffusion equation and the splitting parameters are selected using the traversal method and the GPR method, respectively.

Table 1. Results of the HSS method for solving 3D convection-diffusion equation with traversal method and GPR method.

${\mathit{n}}^3$	HSS (Traversal Method)			HSS (GPR)				$\frac{|\mathbf{Traversal}\mathbf{time}-\mathbf{Training}\mathbf{time}|}{\mathbf{Traversal}\mathbf{time}}$	Traversal Time
	${\mathit{\alpha }}_{\mathbf{trav}}$	IT	CPU	${\mathit{\alpha }}_{\mathbf{gpr}}$	IT	CPU	Training Set
$8^3$ (512)	1.7500	32	0.2500	1.7533	32	0.2813	$[2^3,4^3]$	93.73%	0.12 h
${12}^3$ (1728)	1.2600	46	0.6719	1.2920	46	0.6706	$[1^3,6^3]$	97.02%	0.59 h
${16}^3$ (4096)	1.0000	59	2.5625	1.0673	60	3.3125	$[1^3,4^3]$	99.45%	1.53 h
${20}^3$ (8000)	0.8400	72	7.7969	0.8424	72	6.0152	$[2^3,7^3,{10}^3]$	88.53%	2.42 h
${24}^3$ (13,824)	0.7200	85	25.2031	0.7090	86	25.6250	$[1^3,6^3,{10}^3]$	91.83%	5.69 h
${28}^3$ (21,952)	0.6200	99	54.4063	0.6527	100	55.1875	$[1^3,7^3,{10}^3]$	93.43%	>6 h
${32}^3$ (32,768)	0.5600	111	115.7344	0.5457	112	117.2031	$[1^3,7^3,{10}^3]$	95.99%	>6 h
${36}^3$ (46,656)	0.5000	124	193.6406	0.5007	124	193.3594	$[1^3,5^3,7^3,{13}^3]$	97.79%	>6 h

,

Table 2. Results of the IHSS method for solving 3D convection-diffusion equation with traversal method and GPR method.

${\mathit{n}}^3$	IHSS (Traversal Method)			IHSS (GPR)				$\frac{|\mathbf{Traversal}\mathbf{time}-\mathbf{Training}\mathbf{time}|}{\mathbf{Traversal}\mathbf{time}}$	Traversal Time
	${\mathit{\alpha }}_{\mathbf{trav}}$	IT	CPU	${\mathit{\alpha }}_{\mathbf{gpr}}$	IT	CPU	Training Set
${32}^3$ (32,768)	0.6200	125	47.7969	0.6389	125	47.7656	$[2^3,6^3,{10}^3]$	98.03%	3.25 h
${48}^3$ (110,592)	0.4500	187	257.7188	0.4647	187	256.1250	$[2^3,7^3,{10}^3]$	99.37%	>6 h
${64}^3$ (262,144)	0.3600	246	680.7031	0.3502	249	693.2031	$[1^3,4^3,5^3,{10}^3,{12}^3]$	99.89%	>6 h

,

Table 3. Results of the LHSS method for solving 3D convection-diffusion equation with traversal method and GPR method.

${\mathit{n}}^3$	LHSS (Traversal Method)			LHSS (GPR)				$\frac{|\mathbf{Traversal}\mathbf{time}-\mathbf{Training}\mathbf{time}|}{\mathbf{Traversal}\mathbf{time}}$	Traversal Time
	${\mathit{\alpha }}_{\mathbf{trav}}$	IT	CPU	${\mathit{\alpha }}_{\mathbf{gpr}}$	IT	CPU	Training Set
$8^3$ (512)	1.5300	5	0.0938	1.7323	5	0.0469	$[2^3,3^3,4^3]$	92.09%	0.07 h
${12}^3$ (1728)	1.1200	5	0.1781	1.3161	5	0.1250	$[2^3,3^3,4^3]$	98.90%	0.47 h
${16}^3$ (4096)	0.8700	5	0.3406	0.9999	5	0.3750	$[2^3,3^3,4^3]$	99.50%	1.04 h
${20}^3$ (8000)	0.7100	5	0.8125	0.7597	5	0.8106	$[2^3,3^3,4^3]$	99.65%	1.46 h
${24}^3$ (13,824)	0.6000	5	1.2969	0.6497	5	1.6719	$[1^3,6^3,{10}^3]$	91.44%	2.50 h
${28}^3$ (21,952)	0.5100	5	3.9531	0.5340	5	2.9219	$[1^3,6^3,{10}^3]$	92.20%	2.74 h
${32}^3$ (32,768)	0.4500	5	10.6094	0.4949	5	5.2813	$[1^3,7^3,{10}^3]$	93.27%	3.20 h
${36}^3$ (46,656)	0.4000	5	10.2188	0.4158	5	8.3281	$[1^3,7^3,{10}^3]$	94.82%	4.15 h

and

Table 4. Results of the ILHSS method for solving 3D convection-diffusion equation with traversal method and GPR method.

${\mathit{n}}^3$	ILHSS (Traversal Method)			ILHSS (GPR)				$\frac{|\mathbf{Traversal}\mathbf{time}-\mathbf{Training}\mathbf{time}|}{\mathbf{Traversal}\mathbf{time}}$	Traversal Time
	${\mathit{\alpha }}_{\mathbf{trav}}$	IT	CPU	${\mathit{\alpha }}_{\mathbf{gpr}}$	IT	CPU	Training Set
${32}^3$ (32,768)	1.4100	7	2.3281	1.4789	7	2.3031	$[4^3,8^3]$	98.02%	0.37 h
${48}^3$ (110,592)	1.4300	7	10.2969	1.4394	7	7.4219	$[4^3,8^3]$	99.35%	1.11 h
${64}^3$ (262,144)	1.4100	7	37.7031	1.4155	7	36.8281	$[4^3,7^3,{12}^3]$	99.49%	3.04 h

and Figure 1 show the numerical results.

From Table 1, Table 2, Table 3 and Table 4 and Figure 1, we know that the GPR method can predict almost the same parameters as the traversal method does. It uses a training set from a set of small-scale systems and its training time is much less than the traversal time of the traversal method. Thus, the GPR method requires less calculation than the traversal method.

From Figure 2, we can have a visual representation of what the mapping $f\left(n\right)$ we want to fit looks like.

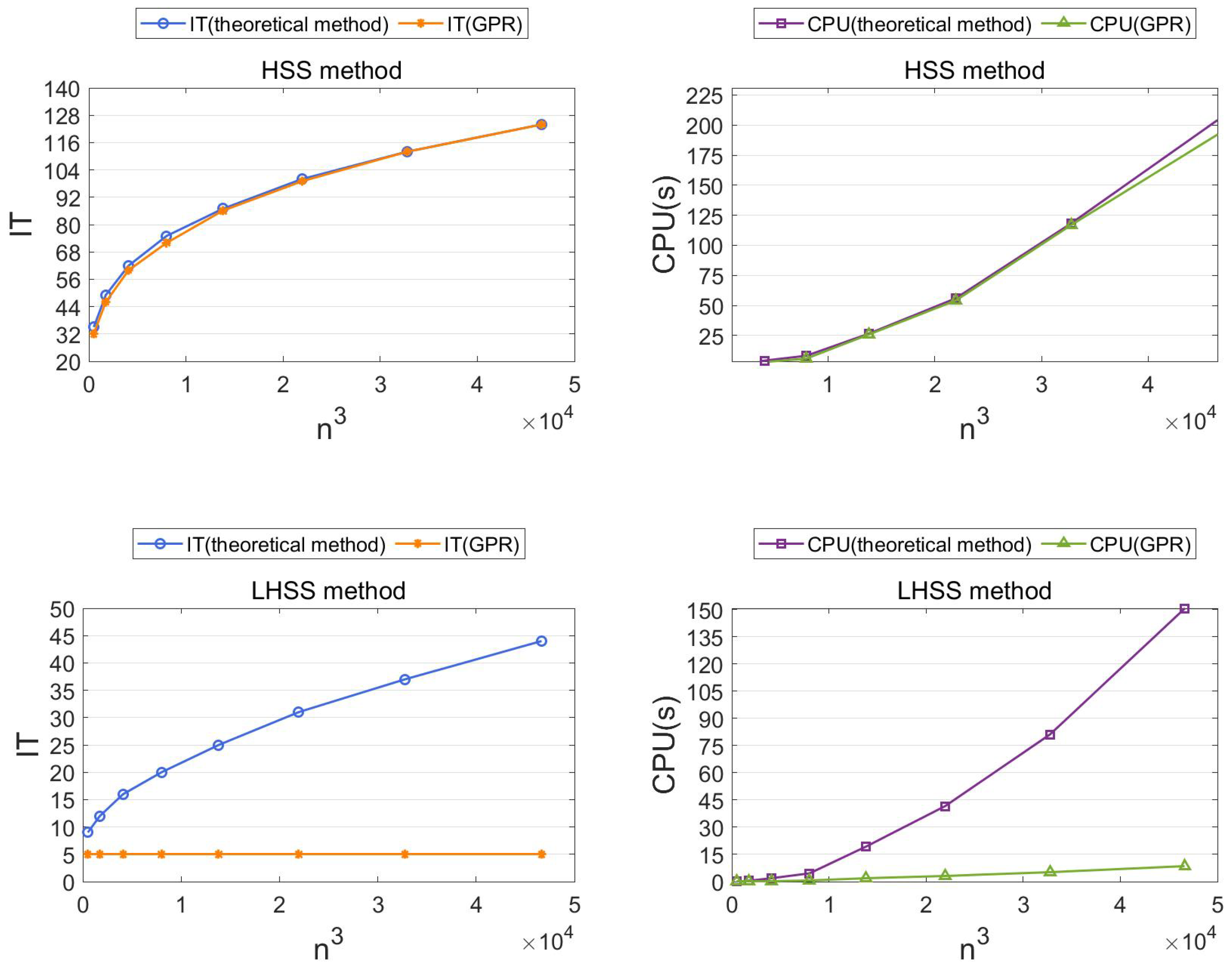
The GPR method vs. the theoretical method. We use the HSS method, the NHSS, the LHSS method, the SHSS method and the SHSS-SS method to solve the 3D convection-diffusion equation, and the splitting parameters are selected using the theoretical method (given in Theorems 3, 5, 7, 9 and 11) and the GPR method, respectively.

Table 5. Results of the HSS method for solving 3D convection-diffusion equation with theoretical method and GPR method.

${\mathit{n}}^3$	HSS (Theoretical Method)			HSS (GPR)
	${\mathit{\alpha }}_{\mathbf{theo}}$	IT	CPU	${\mathit{\alpha }}_{\mathbf{gpr}}$	IT	CPU	Training Set
$8^3$ (512)	2.0521	35	0.6406	1.7533	32	0.2813	$[2^3,4^3]$
${12}^3$ (1728)	1.4359	49	1.3594	1.2920	46	0.6706	$[1^3,6^3]$
${16}^3$ (4096)	1.1025	62	4.1406	1.0673	60	3.3125	$[1^3,4^3]$
${20}^3$ (8000)	0.8943	75	8.2031	0.8424	72	6.0152	$[2^3,7^3,{10}^3]$
${24}^3$ (13,824)	0.7520	87	26.4844	0.7090	86	25.6250	$[1^3,6^3,{10}^3]$
${28}^3$ (21,952)	0.6487	100	55.8438	0.6312	99	54.1875	$[3^3,4^3,{16}^3]$
${32}^3$ (32,768)	0.5703	112	118.2188	0.5457	112	117.2031	$[1^3,7^3,{10}^3]$
${36}^3$ (46,656)	0.5088	124	205.2500	0.5007	124	193.3594	$[1^3,5^3,7^3,{13}^3]$

,

Table 6. Results of the LHSS method for solving 3D convection-diffusion equation with theoretical method and GPR method.

${\mathit{n}}^3$	LHSS (Theoretical Method)			LHSS (GPR)
	${\mathit{\alpha }}_{\mathbf{theo}}$	IT	CPU	${\mathit{\alpha }}_{\mathbf{gpr}}$	IT	CPU	Training Set
$8^3$ (512)	0.7091	9	0.0469	1.7323	5	0.0469	$[2^3,3^3,4^3]$
${12}^3$ (1728)	0.3436	12	0.4688	1.3161	5	0.1250	$[2^3,3^3,4^3]$
${16}^3$ (4096)	0.2026	16	1.8750	0.9999	5	0.3750	$[2^3,3^3,4^3]$
${20}^3$ (8000)	0.1333	20	4.5625	0.7597	5	0.8106	$[2^3,3^3,4^3]$
${24}^3$ (13,824)	0.0943	25	19.3438	0.6497	5	1.6719	$[1^3,6^3,{10}^3]$
${28}^3$ (21,952)	0.0701	31	41.5938	0.5340	5	2.9219	$[1^3,6^3,{10}^3]$
${32}^3$ (32,768)	0.0542	37	81.1719	0.4949	5	5.2813	$[1^3,7^3,{10}^3]$
${36}^3$ (46,656)	0.0432	44	150.7188	0.4158	5	8.3281	$[1^3,7^3,{10}^3]$

,

Table 7. Results of the NHSS method for solving 3D convection-diffusion equation with theoretical method and GPR method.

${\mathit{n}}^3$	NHSS (Theoretical Method)			NHSS (GPR)
	${\mathit{\alpha }}_{\mathbf{theo}}$	IT	CPU	${\mathit{\alpha }}_{\mathbf{gpr}}$	IT	CPU	Training Set
$8^3$ (512)	0.2711	4	0.0469	0.0100	4	0.0494	$[2^3,3^3,4^3]$
${12}^3$ (1728)	0.2880	5	0.1869	0.0100	3	0.1406	$[2^3,3^3,4^3]$
${16}^3$ (4096)	0.2945	5	0.4063	0.0100	3	0.1563	$[2^3,3^3,4^3]$
${20}^3$ (8000)	0.2978	5	0.8750	0.0100	3	0.6281	$[2^3,3^3,4^3]$
${24}^3$ (13,824)	0.2996	5	2.0156	0.0100	3	1.4063	$[1^3,6^3,{10}^3]$
${28}^3$ (21,952)	0.3007	5	5.2656	0.0100	3	4.1156	$[1^3,6^3,{10}^3]$
${32}^3$ (32,768)	0.3014	5	7.6250	0.0100	3	5.4375	$[1^3,7^3,{10}^3]$
${36}^3$ (46,656)	0.3020	5	14.1406	0.0100	3	9.6406	$[1^3,7^3,{10}^3]$

,

Table 8. Results of the SHSS method for solving 3D convection-diffusion equation with theoretical method and GPR method.

${\mathit{n}}^3$	SHSS (Theoretical Method)			SHSS (GPR)
	${\mathit{\alpha }}_{\mathbf{theo}}$	IT	CPU	${\mathit{\alpha }}_{\mathbf{gpr}}$	IT	CPU	Training Set
$8^3$ (512)	0.2711	15	0.0781	0.0100	7	0.0281	$[2^3,3^3,4^3]$
${12}^3$ (1728)	0.2880	25	0.3438	0.0100	6	0.0781	$[2^3,3^3,4^3]$
${16}^3$ (4096)	0.2945	39	1.4063	0.0100	6	0.1563	$[2^3,3^3,4^3]$
${20}^3$ (8000)	0.2978	55	4.7500	0.0100	6	0.5625	$[2^3,3^3,4^3]$
${24}^3$ (13,824)	0.2996	75	13.6250	0.0100	7	3.4219	$[1^3,6^3,{10}^3]$
${28}^3$ (21,952)	0.3007	97	38.9375	0.0100	7	11.7813	$[1^3,6^3,{10}^3]$
${32}^3$ (32,768)	0.3014	122	100.5469	0.0100	8	15.1094	$[1^3,7^3,{10}^3]$
${36}^3$ (46,656)	0.3020	150	220.4844	0.0100	9	17.1563	$[1^3,7^3,{10}^3]$

and

Table 9. Results of the SHSS-SS method for solving 3D convection-diffusion equation with theoretical method and GPR method.

${\mathit{n}}^3$	SHSS-SS (Theoretical Method)			SHSS-SS (GPR)
	${\mathit{\alpha }}_{\mathbf{theo}}$	IT	CPU	${\mathit{\alpha }}_{\mathbf{gpr}}$	IT	CPU	Training Set
$8^3$ (512)	0.2711	7	0.0469	0.0100	7	0.0438	$[2^3,3^3,4^3]$
${12}^3$ (1728)	0.2880	7	0.4063	0.0100	6	0.3281	$[2^3,3^3,4^3]$
${16}^3$ (4096)	0.2945	12	1.5625	0.0100	6	0.6563	$[2^3,3^3,4^3]$
${20}^3$ (8000)	0.2978	17	6.0625	0.0100	6	3.3906	$[2^3,3^3,4^3]$
${24}^3$ (13,824)	0.2996	24	16.7969	0.0100	6	9.2656	$[1^3,6^3,{10}^3]$
${28}^3$ (21,952)	0.3007	31	52.7188	0.0100	6	25.9063	$[1^3,6^3,{10}^3]$
${32}^3$ (32,768)	0.3014	40	139.7031	0.0100	6	46.2344	$[1^3,7^3,{10}^3]$
${36}^3$ (46,656)	0.3020	49	309.8125	0.0100	6	60.8906	$[1^3,7^3,{10}^3]$

and Figure 3 and Figure 4 show the numerical results.

From Table 5, Table 6, Table 7, Table 8 and Table 9 and Figure 3 and Figure 4, we know that the GPR method can predict better optimal parameters than the theoretical method. Unlike the theoretical method available case-by-case, the GPR method is suitable for the five iterative methods, which means that the GPR method is highly universal.

Example 2.

Consider the following complex symmetric linear systems.

$$\left[\left(K+\frac{3-\sqrt{3}}{\tau }I\right)+\mathrm{i}\left(K+\frac{3+\sqrt{3}}{\tau }I\right)\right]x=b,$$

(14)

where K is the five-point centered difference matrix approximating the negative Laplacian operator with homogeneous Dirichlet boundary conditions, on a uniform mesh in the unit square $[0,1]\times [0,1]$ with mesh-size $h=\frac{1}{m+1}$. $K\in {\mathbb{R}}^{m^2\times m^2}$ and $K=I\otimes V_m+V_m\otimes I$, with $V_m=h^{-2}tridiag(-1,2,-1)\in {\mathbb{R}}^{m\times m}$. In addition, the right-hand side vector b with its jth entry $b_j$ is given by

$$b_j=\frac{(1-\mathrm{i})j}{\tau {(j+1)}^2},j=1,2,\dots ,n.$$

Let $\tau =h$ and normalize coefficient matrix and right-hand side by multiplying both by $h^2$. Refer to [53] for more details.

In this experiment, we apply the GPR method to compare with the traversal method and the theoretical method, respectively. Concretely, first, we use the HSS method and the MHSS method to solve Equation (14), and the splitting parameters are selected using the traversal method and the GPR method, respectively. Then, we use the HSS method, the MHSS method and the MSNS method to solve Equation (14), and the splitting parameters are selected using the theoretical method and the GPR method, respectively. Since the extreme eigenvalues of matrix M and extreme singular value of matrix N cannot be explicitly obtained, we use MATLAB built-in function “eigs(MaxIterations’,500,’Tolerance’,1e-5)” and “svds(MaxIterations’,500,’Tolerance’,1e-5)” to calculate them.

The GPR method vs. the traversal method. We first use the HSS method and the MHSS method to solve Equation (14) and the splitting parameters are selected using the traversal method and the GPR method, respectively.

Table 10. Results of the HSS method for solving Equation (14) with traversal method and GPR method.

${\mathit{m}}^2$	HSS (Traversal Method)			HSS (GPR)				$\frac{|\mathbf{Traversal}\mathbf{time}-\mathbf{Training}\mathbf{time}|}{\mathbf{Traversal}\mathbf{time}}$	Traversal Time
	${\mathit{\alpha }}_{\mathbf{trav}}$	IT	CPU	${\mathit{\alpha }}_{\mathbf{gpr}}$	IT	CPU	Training Set
${32}^2$ (1024)	0.5800	63	0.6563	0.5935	64	0.6250	$[2^2,4^2,{10}^2]$	96.53%	0.07 h
${64}^2$ (4096)	0.3900	94	4.9844	0.3831	95	4.8594	$[2^2,4^2,6^2,{10}^2]$	99.36%	0.46 h
${96}^2$ (9216)	0.3100	117	18.0156	0.3093	118	19.0469	$[5^2,7^2,{12}^2]$	99.76%	1.67 h
${128}^2$ (16,384)	0.2700	136	40.7969	0.2783	135	35.6094	$[5^2,8^2,{12}^2]$	99.90%	3.78 h
${160}^2$ (25,600)	0.2500	151	71.4688	0.2514	152	72.1094	$[6^2,{10}^2,{14}^2]$	99.91%	>6 h
${192}^2$ (36,864)	0.2200	166	121.9531	0.2226	165	114.6875	$[6^2,8^2,{14}^2]$	99.95%	>6 h
${224}^2$ (50,176)	0.2100	178	181.4063	0.2089	178	181.0406	$[6^2,{10}^2,{11}^2]$	99.98%	>6 h
${256}^2$ (65,536)	0.2000	191	271.4375	0.1912	191	271.2344	$[8^2,{11}^2,{13}^2]$	99.99%	>6 h

and

Table 11. Results of the MHSS method for solving Equation (14) with traversal method and GPR method.

${\mathit{m}}^2$	MHSS (Traversal Method)			MHSS (GPR)				$\frac{|\mathbf{Traversal}\mathbf{time}-\mathbf{Training}\mathbf{time}|}{\mathbf{Traversal}\mathbf{time}}$	Traversal Time
	${\mathit{\alpha }}_{\mathbf{trav}}$	IT	CPU	${\mathit{\alpha }}_{\mathbf{gpr}}$	IT	CPU	Training Set
${32}^2$ (1024)	0.7800	53	0.1094	0.7979	53	0.1006	$[3^2,6^2,{14}^2]$	83.20%	0.01 h
${64}^2$ (4096)	0.5500	72	0.7344	0.5440	73	0.7813	$[3^2,{10}^2,{14}^2]$	96.64%	0.08 h
${96}^2$ (9216)	0.4600	86	6.4063	0.4825	87	6.7813	$[3^2,9^2,{12}^2,{14}^2]$	99.45%	0.63 h
${128}^2$ (16,384)	0.4000	98	11.7500	0.4068	98	11.6719	$[4^2,6^2,{10}^2,{13}^2]$	99.71%	1.14 h
${160}^2$ (25,600)	0.3600	108	20.7500	0.3593	108	20.6063	$[4^2,7^2,{10}^2,{13}^2]$	99.81%	1.91 h
${192}^2$ (36,864)	0.3300	117	35.6094	0.3227	118	36.4844	$[{10}^2,{20}^2,{40}^2]$	99.39%	3.46 h
${224}^2$ (50,176)	0.3100	125	57.0938	0.3114	125	57.0781	$[{10}^2,{20}^2,{30}^2,{60}^2]$	98.88%	5.25 h
${256}^2$ (65,536)	0.2900	133	81.6563	0.2990	133	81.2500	$[{10}^2,{30}^2,{40}^2,{60}^2]$	99.57%	>6 h

and Figure 5 show the numerical results.

From Table 10 and Table 11 and Figure 5, we know that the GPR method can predict almost the same parameters as the traversal method does. It uses a training set obtained by using the traversal method for small-scale systems and its training time is much less than the traversal time of the traversal method. Thus, the GPR method requires less calculation than the traversal method.

The GPR method vs. the theoretical method. We use the HSS method, the MHSS method and the MSNS method to solve Equation (14), and the splitting parameters are selected using the theoretical method (given in Theorem 3, 13 and 14) and the GPR method, respectively.

Table 12. Results of the HSS method for solving Equation (14) with theoretical method and GPR method.

${\mathit{m}}^2$	HSS (Theoretical Method)			HSS (GPR)
	${\mathit{\alpha }}_{\mathbf{theo}}$	IT	CPU	${\mathit{\alpha }}_{\mathbf{gpr}}$	IT	CPU	Training Set
${32}^2$ (1024)	0.6734	71	0.7031	0.5935	64	0.6250	$[2^2,4^2,{10}^2]$
${64}^2$ (4096)	0.4402	102	5.2180	0.3831	95	4.8594	$[2^2,4^2,6^2,{10}^2]$
${96}^2$ (9216)	0.3486	124	30.0469	0.3093	118	19.0469	$[5^2,7^2,{12}^2]$
${128}^2$ (16,384)	0.2970	141	40.9531	0.2783	135	35.6094	$[5^2,8^2,{12}^2]$
${160}^2$ (25,600)	0.2630	156	74.3750	0.2514	152	72.1094	$[6^2,{10}^2,{14}^2]$
${192}^2$ (36,864)	0.2384	170	122.8906	0.2226	165	114.6875	$[6^2,8^2,{14}^2]$
${224}^2$ (50,176)	0.2196	182	190.9844	0.2089	178	181.6406	$[6^2,{10}^2,{11}^2]$
${256}^2$ (65,536)	0.2047	193	273.9531	0.1912	191	271.2344	$[8^2,{11}^2,{13}^2]$

,

Table 13. Results of the MHSS method for solving Equation (14) with theoretical method and GPR method.

${\mathit{m}}^2$	MHSS (Theoretical Method)			MHSS (GPR)
	${\mathit{\alpha }}_{\mathbf{theo}}$	IT	CPU	${\mathit{\alpha }}_{\mathbf{gpr}}$	IT	CPU	Training Set
${32}^2$ (1024)	0.6734	59	0.1719	0.7979	53	0.1006	$[3^2,6^2,{14}^2]$
${64}^2$ (4096)	0.4402	88	0.9219	0.5440	73	0.7813	$[3^2,{10}^2,{14}^2]$
${96}^2$ (9216)	0.3486	109	8.0469	0.4825	87	6.7813	$[3^2,9^2,{12}^2,{14}^2]$
${128}^2$ (16,384)	0.2970	127	15.4844	0.4068	98	11.6719	$[4^2,6^2,{10}^2,{13}^2]$
${160}^2$ (25,600)	0.2630	142	26.5938	0.3593	108	20.6063	$[4^2,7^2,{10}^2,{13}^2]$
${192}^2$ (36,864)	0.2384	156	50.4531	0.3227	118	36.4844	$[{10}^2,{20}^2,{40}^2]$
${224}^2$ (50,176)	0.2196	169	75.5000	0.3114	125	57.0781	$[{10}^2,{20}^2,{30}^2,{60}^2]$
${256}^2$ (65,536)	0.2047	181	109.7188	0.2990	133	81.2500	$[{10}^2,{30}^2,{40}^2,{60}^2]$

and

Table 14. Results of the MSNS method for solving Equation (14) with theoretical method and GPR method.

${\mathit{m}}^2$	MSNS (Theoretical Method)			MSNS (GPR)
	${\mathit{\alpha }}_{\mathbf{theo}}$	IT	CPU	${\mathit{\alpha }}_{\mathbf{gpr}}$	IT	CPU	Training Set
${32}^2$ (1024)	1.1456	42	1.2344	1.0317	38	0.7969	$[4^2,{11}^2]$
${64}^2$ (4096)	0.7906	57	7.4375	0.7376	54	6.6563	$[3^2,4^2,9^2]$
${96}^2$ (9216)	0.6399	68	26.9531	0.5745	64	25.4531	$[6^2,{13}^2,{20}^2]$
${128}^2$ (16,384)	0.5516	77	53.6250	0.4934	74	50.1094	$[7^2,{10}^2,{24}^2]$
${160}^2$ (25,600)	0.4920	85	100.4688	0.4365	83	85.4219	$[6^2,{10}^2,{15}^2,{20}^2]$
${192}^2$ (36,864)	0.4483	92	189.4063	0.4217	89	182.1719	$[7^2,{10}^2,{15}^2,{27}^2]$
${224}^2$ (50,176)	0.4145	99	254.5938	0.3855	96	238.6875	$[7^2,{10}^2,{15}^2,{24}^2]$
${256}^2$ (65,536)	0.3873	104	335.6563	0.3628	102	328.0313	$[7^2,{10}^2,{15}^2,{21}^2]$

and Figure 6 show the numerical results.

From Table 12, Table 13 and Table 14 and Figure 6, we know that the GPR method can predict better optimal parameters than the theoretical method. Unlike the theoretical method only available case-by-case, the GPR method is suitable for the three iterative methods, which means that the GPR method is highly universal.

5. Conclusions

In this paper, we use the Bayesian inference-based Gaussian process regression (GPR) method to predict the relatively optimal parameters of some matrix-splitting iteration methods and provide extensive numerical experiments to compare the prediction performance of the GPR method with other methods. The GPR method learns a mapping between the dimension of linear systems and relatively optimal splitting parameters using a small training data set. Numerical results show that the GPR method requires less calculation than the traversal method. It is more universal and can predict more optimal parameters than the theoretical methods.

There is still lots of work to study the proposed methods. For example, the first one is to apply the GPR method to some iteration methods with multi-parameters or some non HSS-type iteration methods. The second one is to measure the predictive performance of the GPR method when the true optimal parameters to predict are unknown. The third one is to choose other mean functions and covariance functions to improve the predictive performance of the GPR method.