Teaching Algorithms to Develop the Algorithmic Thinking of Informatics Students
Abstract
:1. Introduction
2. Algorithms and Their Learning
3. The Role of the Knight’s Tour Problem and Its Didactic Potential
| Algorithm 1: Algorithm to determine the possibility of making the next move |
| procedure try move; begin initializing stroke selection; repeat select another candidate from a list of other moves; if acceptable then begin record move; if the chessboard is not full then begin try next move; if unsuccessful then delete previous record end end until (move was successful) ∨ (there are no other candidates) end. |
4. Method
4.1. Description of the Method
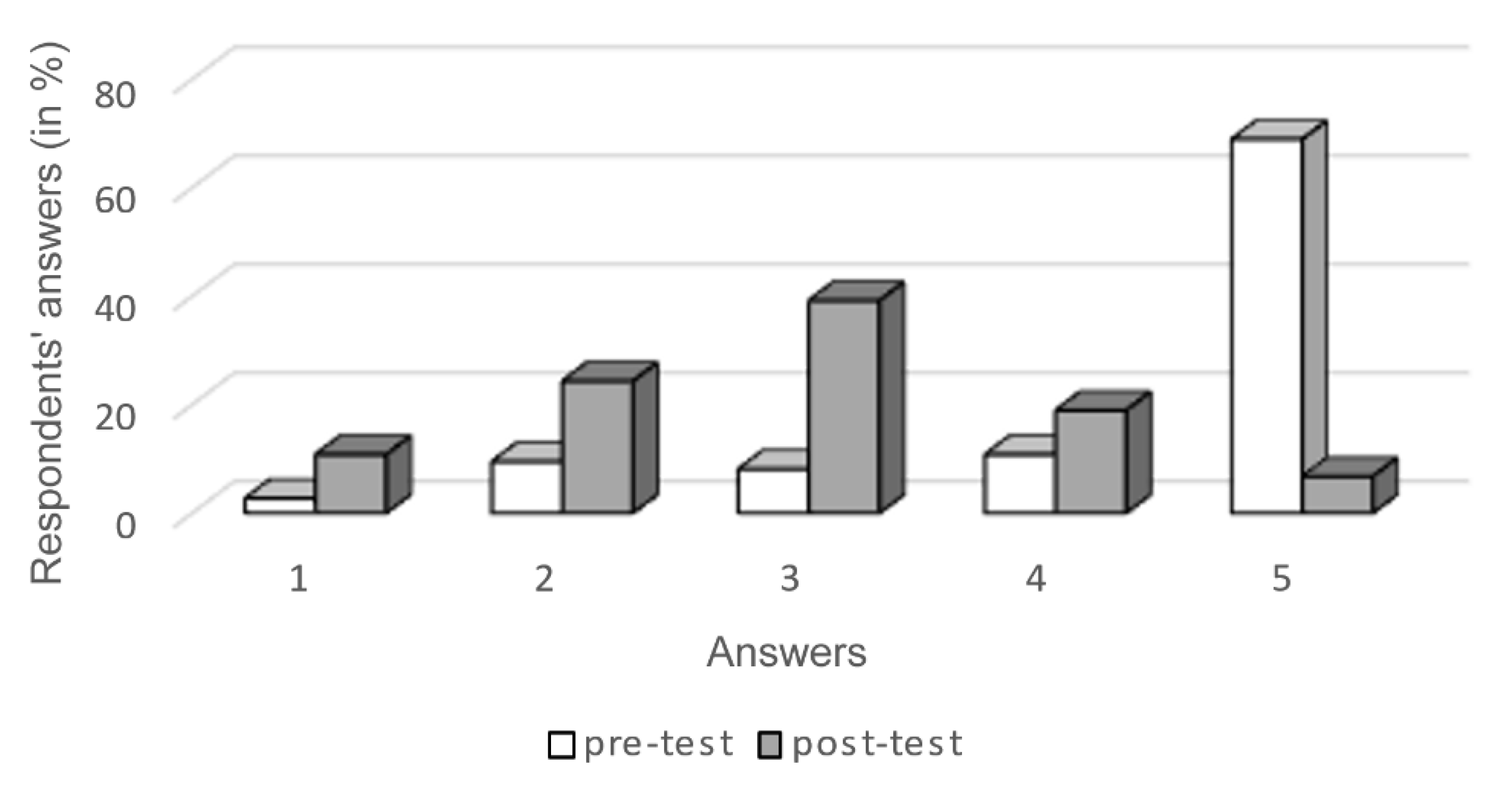
4.2. Data Analysis and Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Türker, P.M.; Pala, F.K. The effect of algorithm education on students’ computer programming self-efficacy perceptions and computational thinking skills. Int. J. Comput. Sci. Educ. Sch. 2020, 3, 19–32. [Google Scholar]
- Ching, Y.H.; Hsu, Y.C.; Baldwin, S. Developing computational thinking with educational technologies for young learners. Tech. Trends 2018, 62, 563–573. [Google Scholar] [CrossRef] [Green Version]
- International Society for Technology in Education-ISTE. Computational Thinking for All. Available online: https://www.iste.org/explore/articleDetail?articleid=152 (accessed on 23 August 2021).
- Chondrogiannis, E.; Symeonaki, E.; Papachristos, D.; Loukatos, D.; Arvanitis, K.G. Computational Thinking and STEM in Agriculture Vocational Training: A Case Study in a Greek Vocational Education Institution. Eur. J. Investig. Health Psychol. Educ. 2021, 11, 230–250. [Google Scholar] [CrossRef] [PubMed]
- Knuth, D.E. Algorithmic thinking and mathematical thinking. Am. Math. Mon. 1985, 92, 170–181. [Google Scholar] [CrossRef]
- Leron, U.; Dubinsky, E. An abstract algebra story. Am. Math. Mon. 1995, 102, 227–242. [Google Scholar] [CrossRef]
- Misfeldt, M.; Ejsing-Duun, S. Learning mathematics through programming: An instrumental approach to potentials and pitfalls. In CERME 9-Ninth Congress of the European Society for Research in Mathematics Education; The European Society for Research in Mathematics Education (ERME): Prague, Czech Republic, 2015; pp. 2524–2530. [Google Scholar]
- Denning, P.J. The profession of IT Beyond computational thinking. Commun. ACM 2009, 52, 28–30. [Google Scholar]
- Wing, J.M. Computational thinking. Commun. ACM 2006, 49, 33–35. [Google Scholar] [CrossRef]
- Rowe, E.; Almeda, M.V.; Asbell-Clarke, J.; Scruggs, R.; Baker, R.; Bardar, E.; Gasca, S. Assessing implicit computational thinking in Zoombinis puzzle gameplay. Comput. Hum. Behav. 2021, 120, 106707. [Google Scholar] [CrossRef]
- Jona, K.; Wilensky, U.; Trouille, L.; Horn, M.S.; Orton, K.; Weintrop, D.; Beheshti, E. Embedding computational thinking in science, technology, engineering, and math (CT-STEM). In Future Directions in Computer Science Education Summit Meeting; Stanford University: Orlando, FL, USA, 2014. [Google Scholar]
- Orton, K.; Weintrop, D.; Beheshti, E.; Horn, M.; Jona, K.; Wilensky, U. Bringing Computational Thinking into High School Mathematics and Science Classrooms; International Society of the Learning Sciences: Singapore, 2016. [Google Scholar]
- Repenning, A.; Webb, D.C.; Koh, K.H.; Nickerson, H.; Miller, S.B.; Brand, C.; Repenning, N. Scalable game design: A strategy to bring systemic computer science education to schools through game design and simulation creation. ACM Trans. Comput. Educ. (TOCE) 2015, 15, 1–31. [Google Scholar] [CrossRef]
- Tatar, D.; Harrison, S.; Stewart, M.; Frisina, C.; Musaeus, P. Proto-computational thinking: The uncomfortable underpinnings. In Emerging Research, Practice, and Policy on Computational Thinking; Springer: Cham, Switzerland, 2017; pp. 63–81. [Google Scholar]
- Futschek, G. Algorithmic thinking: The key for understanding computer science. In International Conference on Informatics in Secondary Schools-Evolution and Perspectives; Springer: Berlin/Heidelberg, Germany, 2006; pp. 159–168. [Google Scholar]
- Broley, L.; Caron, F.; Saint-Aubin, Y. Levels of programming in mathematical research and university mathematics education. Int. J. Res. Undergrad. Math. Educ. 2018, 4, 38–55. [Google Scholar] [CrossRef]
- Çamoğlu, K. Algorithm, 6th ed.; Kodlab: İstanbul, Turkey, 2018. [Google Scholar]
- Kiss, G.; Arki, Z. The influence of game-based programming education on the algorithmic thinking. Procedia-Soc. Behav. Sci. 2017, 237, 613–617. [Google Scholar] [CrossRef]
- Knuth, D.E. Computer science and its relation to mathematics. Am. Math. Mon. 1974, 81, 323–343. [Google Scholar] [CrossRef]
- Anderson, J.R. Acquisition of cognitive skill. Psychol. Rev. 1982, 89, 369–406. [Google Scholar] [CrossRef]
- Star, J.R. Reconceptualizing procedural knowledge. J. Res. Math. Educ. 2005, 36, 404–411. [Google Scholar]
- Lithner, J. Principles for designing mathematical tasks that enhance imitative and creative reasoning. ZDM 2017, 49, 937–949. [Google Scholar] [CrossRef] [Green Version]
- Lukhele, R.B.; Murray, H.; Olivier, A. Learners’ understanding of the addition of fractions. In Proceedings of the Fifth Annual Congress of the Association for Mathematics Education of South Africa; Port Elizabeth Technikon: Port Elizabeth, South Africa, 1999; Volume 1, pp. 87–97. [Google Scholar]
- Leung, F.K.S. Mathematics education in East Asia and the West: Does culture matter? In Mathematics Education in Different Cultural Traditions: A Comparative Study of East Asia and the West; Leung, F.K.S., Graf, K.-D., Lopez-Real, F.J., Eds.; Springer: New York, NY, USA, 2006; pp. 21–46. [Google Scholar]
- Bergqvist, T.; Lithner, J. Mathematical reasoning in teachers’ presentations. J. Math. Behav. 2012, 31, 252–269. [Google Scholar] [CrossRef]
- Shield, M.; Dole, S. Assessing the potential of mathematics textbooks to promote deep learning. Educ. Stud. Math. 2013, 82, 183–199. [Google Scholar] [CrossRef]
- Boesen, J.; Helenius, O.; Bergqvist, E.; Bergqvist, T.; Lithner, J.; Palm, T.; Palmberg, B. Developing mathematical competence: From the intended to the enacted curriculum. J. Math. Behav. 2014, 33, 72–87. [Google Scholar] [CrossRef]
- Freudenthal, H. Didactical Phenomenology of Mathematical Structures; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1986; Volume 1. [Google Scholar]
- Hiebert, J.; Carpenter, T. Learning and teaching with understanding. In Handbook of Research on Mathematics Teaching and Learning; Grouws, D., Ed.; Simon Schuster Macmillan: New York, NY, USA, 1992; pp. 65–97. [Google Scholar]
- Moreno, R. Decreasing cognitive load for novice students: Effects of explanatory versus corrective feedback in discovery-based multimedia. Instr. Sci. 2004, 32, 99–113. [Google Scholar] [CrossRef]
- Oakes, J.; Lipton, M.; Anderson, L.; Stillman, J. Teaching to Change the World; Routledge: New York, NY, USA, 2018. [Google Scholar] [CrossRef]
- Brousseau, G. Theory of Didactical Situations in Mathematics: Didactique des Mathématiques, 1970–1990; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006; Volume 19. [Google Scholar]
- Fan, L.; Bokhove, C. Rethinking the role of algorithms in school mathematics: A conceptual model with focus on cognitive development. ZDM 2014, 46, 481–492. [Google Scholar] [CrossRef]
- Jonsson, B.; Norqvist, M.; Liljekvist, Y.; Lithner, J. Learning mathematics through algorithmic and creative reasoning. J. Math. Behav. 2014, 36, 20–32. [Google Scholar] [CrossRef] [Green Version]
- Wirebring, L.K.; Lithner, J.; Jonsson, B.; Liljekvist, Y.; Norqvist, M.; Nyberg, L. Learning mathematics without a suggested solution method: Durable effects on performance and brain activity. Trends Neurosci. Educ. 2015, 4, 6–14. [Google Scholar] [CrossRef]
- Naseer, M.; Zhang, W.; Zhu, W. Prediction of coding intricacy in a software engineering team through machine learning to ensure cooperative learning and sustainable education. Sustainability 2020, 12, 8986. [Google Scholar] [CrossRef]
- Rittle-Johnson, B.; Star, J.R.; Durkin, K. Developing procedural flexibility: Are novices prepared to learn from comparing procedures? Br. J. Educ. Psychol. 2012, 82, 436–455. [Google Scholar] [CrossRef]
- Kilpatrick, J.; Swafford, J.; Findell, B. Adding it Up: Helping Children Learn Mathematics; National Research Council, Ed.; National Academy Press: Washington, DC, USA, 2001; Volume 2101. [Google Scholar]
- Wegener, I. Branching Programs and Binary Decision Diagrams: Theory and Applications; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2000; ISBN 0-898-71458-3. [Google Scholar]
- Kondrak, G.; Van Beek, P. A theoretical evaluation of selected backtracking algorithms. Artif. Intell. 1997, 89, 365–387. [Google Scholar] [CrossRef] [Green Version]
- Van Beek, P. Backtracking search algorithms. In Foundations of Artificial Intelligence; Elsevier: Amsterdam, The Netherlands, 2006; Volume 2, pp. 85–134. [Google Scholar]
- Wirth, N. Algorithms and Data Structures, 2nd ed.; Alfa: Bratislava, Slovakia, 1989; p. 488. ISBN 80-05-00153-3. (In Slovak) [Google Scholar]
- Dewey, J. How We Think; D. C Heath Co Publishers: Chicago, IL, USA, 1910. [Google Scholar]
- Stuart, A. A test for homogeneity of the marginal distributions in a two-way classification. Biometrika 1955, 42, 412–416. [Google Scholar] [CrossRef]
- Maxwell, A.E. Comparing the classification of subjects by two independent judges. Br. J. Psychiatry 1970, 116, 651–655. [Google Scholar] [CrossRef]
- Abbasi, N.; Dokoohaki, S.; Jamali, H. The Application of Stuart-Maxwell Test in Determining the Identically Distributed Correct Choice. Appl. Math. Sci. 2009, 3, 447–450. [Google Scholar]
- Agresti, A. Categorical Data Analysis, 3rd ed.; John Wiley & Sons Inc: Hoboken, NJ, USA, 2013; p. 752. ISBN 0470463635. [Google Scholar]
- McNemar, Q. Note on the sampling error of the difference between correlated proportions or percentages. Psychometrika 1947, 12, 153–157. [Google Scholar] [CrossRef]
- Denning, P.J.; Tedre, M. Computational Thinking; Mit Press: Cambridge, MA, USA, 2019; ISBN 9780262536561. [Google Scholar]
- Araya, R.; Isoda, M.; González, O. A Framework for Computational Thinking in Preparation for Transitioning to a Super Smart Society. J. Southeast Asian Educ. 2020, 1, 1–16. [Google Scholar]
- Lisarelli, G.; Baccaglini-Frank, A.; Di Martino, P. From how to why: A quest for the common mathematical meanings behind two different division algorithms. J. Math. Behav. 2021, 63, 100897. [Google Scholar] [CrossRef]
- Fuson, K.C.; Kalchman, M.; Bransford, J.D. Mathematical understanding: An introduction. In How Students Learn: History, Mathematics, and Science in the Classroom; National Research Council: Washington, DC, USA, 2005; pp. 217–256. [Google Scholar]
- Hiebert, J. What research says about the NCTM standards. In A Research Companion to Principles and Standards for School Mathematics; National Council of Teachers of Mathematics: Reston, VA, USA, 2003; pp. 5–23. [Google Scholar]
- Lithner, J. Students’ mathematical reasoning in university textbook exercises. Educ. Stud. Math. 2003, 52, 29–55. [Google Scholar] [CrossRef]
- Escalera Chávez, M.E.; Moreno García, E.; Rojas Kramer, C.A. Confirmatory Model to Measure Attitude towards Mathematics in Higher Education Students: Study Case in SLP Mexico. Int. Electron. J. Math. Educ. 2019, 14, 163–168. [Google Scholar]
- Laudano, F.; Tortoriello, F.S.; Vincenzi, G. An experience of teaching algorithms using inquiry-based learning. Int. J. Math. Educ. Sci. Technol. 2020, 51, 344–353. [Google Scholar] [CrossRef]
- Olteanu, C. Reflection-for-action and the choice or design of examples in the teaching of mathematics. Math. Educ. Res. J. 2017, 29, 349–367. [Google Scholar] [CrossRef]
- Căprioară, D. Problem solving-purpose and means of learning mathematics in school. Procedia-Soc. Behav. Sci. 2015, 191, 1859–1864. [Google Scholar] [CrossRef] [Green Version]
- Amar, G.I.; Suranto, S. The Use of Creative Problem Solving Based Genetic Mutation Module in Higher Education. Int. J. High. Educ. 2021, 10, 33–45. [Google Scholar] [CrossRef]
- García, T.; Boom, J.; Kroesbergen, E.H.; Núñez, J.C.; Rodríguez, C. Planning, execution, and revision in mathematics problem solving: Does the order of the phases matter? Stud. Educ. Eval. 2019, 61, 83–93. [Google Scholar] [CrossRef]
- Elia, I.; van den Heuvel-Panhuizen, M.; Kolovou, A. Exploring strategy use and strategy flexibility in non-routine problem solving by primary school high achievers in mathematics. ZDM 2009, 41, 605–618. [Google Scholar] [CrossRef]
- Abdullah, A.H.; Rahman, S.N.S.A.; Hamzah, M.H. Metacognitive skills of Malaysian students in non-routine mathematical problem solving. Bolema: Bol. De Educ. Matemática 2017, 31, 310–322. [Google Scholar] [CrossRef] [Green Version]
- Baroody, A.J. The development of adaptive expertise and flexibility: The integration of conceptual and procedural knowledge. In The Development of Arithmetic Concepts and Skills: Constructing Adaptive Expertise; Baroody, A.J., Dowker, A., Eds.; Erlbaum: Mahwah, NJ, USA, 2003; pp. 1–34. [Google Scholar]
- Rittle-Johnson, B.; Schneider, M. Developing conceptual and procedural knowledge of mathematics. In Oxford Handbook of Numerical Cognition; Oxford University Press: Oxford, UK, 2015; pp. 1118–1134. [Google Scholar] [CrossRef]
- Fuson, K.C. A Forum for Researchers: Issues in Place-Value and Multidigit Addition and Subtraction Learning and Teaching for Research on Mathematics Teaching. J. Res. Math. Educ. 1990, 21, 273–280. [Google Scholar] [CrossRef]
- Benton, L.; Saunders, P.; Kalas, I.; Hoyles, C.; Noss, R. Designing for learning mathematics through programming: A case study of pupils engaging with place value. Int. J. Child-Comput. Interact. 2018, 16, 68–76. [Google Scholar] [CrossRef]
- Phonapichat, P.; Wongwanich, S.; Sujiva, S. An analysis of elementary school students’ difficulties in mathematical problem solving. Procedia-Soc. Behav. Sci. 2014, 116, 3169–3174. [Google Scholar] [CrossRef]



| … … … | ||||
| ... | n |
| … … … | ||||
| ... | 1 |
| Cognitive Level | Question | |
|---|---|---|
| 1 | 1. question | 44.363 * |
| 5. question | 2.787 | |
| 9. question | 44.224 * | |
| 2 | 2. question | 20.941 * |
| 6. question | 4.156 | |
| 10. question | 35.844 * | |
| 3 | 3. question | 24.178 * |
| 7. question | 2.313 | |
| 11. question | 37.926 * |
| Item 4 | Post-Test (in%) | Sum | ||||
|---|---|---|---|---|---|---|
| Pre-Test (in%) | 1 | 2 | 3 | 4 | 5 | |
| 1 | 4 | 0 | 0 | 0 | 0 | 4 |
| 2 | 0 | 1 | 4 | 3 | 1 | 9 |
| 3 | 1 | 0 | 1 | 1 | 4 | 8 |
| 4 | 1 | 4 | 3 | 3 | 5 | 16 |
| 5 | 1 | 5 | 5 | 11 | 39 | 62 |
| sum | 8 | 11 | 14 | 18 | 50 | 100 |
| Item 8 | Post-Test (in%) | Sum | ||||
|---|---|---|---|---|---|---|
| Pre-Test (in%) | 1 | 2 | 3 | 4 | 5 | |
| 1 | 50 | 16 | 8 | 1 | 1 | 77 |
| 2 | 5 | 5 | 5 | 0 | 0 | 16 |
| 3 | 1 | 3 | 0 | 0 | 0 | 4 |
| 4 | 1 | 0 | 0 | 0 | 0 | 1 |
| 5 | 1 | 0 | 0 | 0 | 0 | 1 |
| sum | 59 | 24 | 14 | 1 | 1 | 100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonda, D.; Ďuriš, V.; Tirpáková, A.; Pavlovičová, G. Teaching Algorithms to Develop the Algorithmic Thinking of Informatics Students. Mathematics 2022, 10, 3857. https://doi.org/10.3390/math10203857
Gonda D, Ďuriš V, Tirpáková A, Pavlovičová G. Teaching Algorithms to Develop the Algorithmic Thinking of Informatics Students. Mathematics. 2022; 10(20):3857. https://doi.org/10.3390/math10203857
Chicago/Turabian StyleGonda, Dalibor, Viliam Ďuriš, Anna Tirpáková, and Gabriela Pavlovičová. 2022. "Teaching Algorithms to Develop the Algorithmic Thinking of Informatics Students" Mathematics 10, no. 20: 3857. https://doi.org/10.3390/math10203857
APA StyleGonda, D., Ďuriš, V., Tirpáková, A., & Pavlovičová, G. (2022). Teaching Algorithms to Develop the Algorithmic Thinking of Informatics Students. Mathematics, 10(20), 3857. https://doi.org/10.3390/math10203857








