A Method for Reducing Transcendental Dispersion Relations to Nonlinear Ordinary Differential Equations in a Wide Class of Wave Propagation Problems
Abstract
:1. Introduction
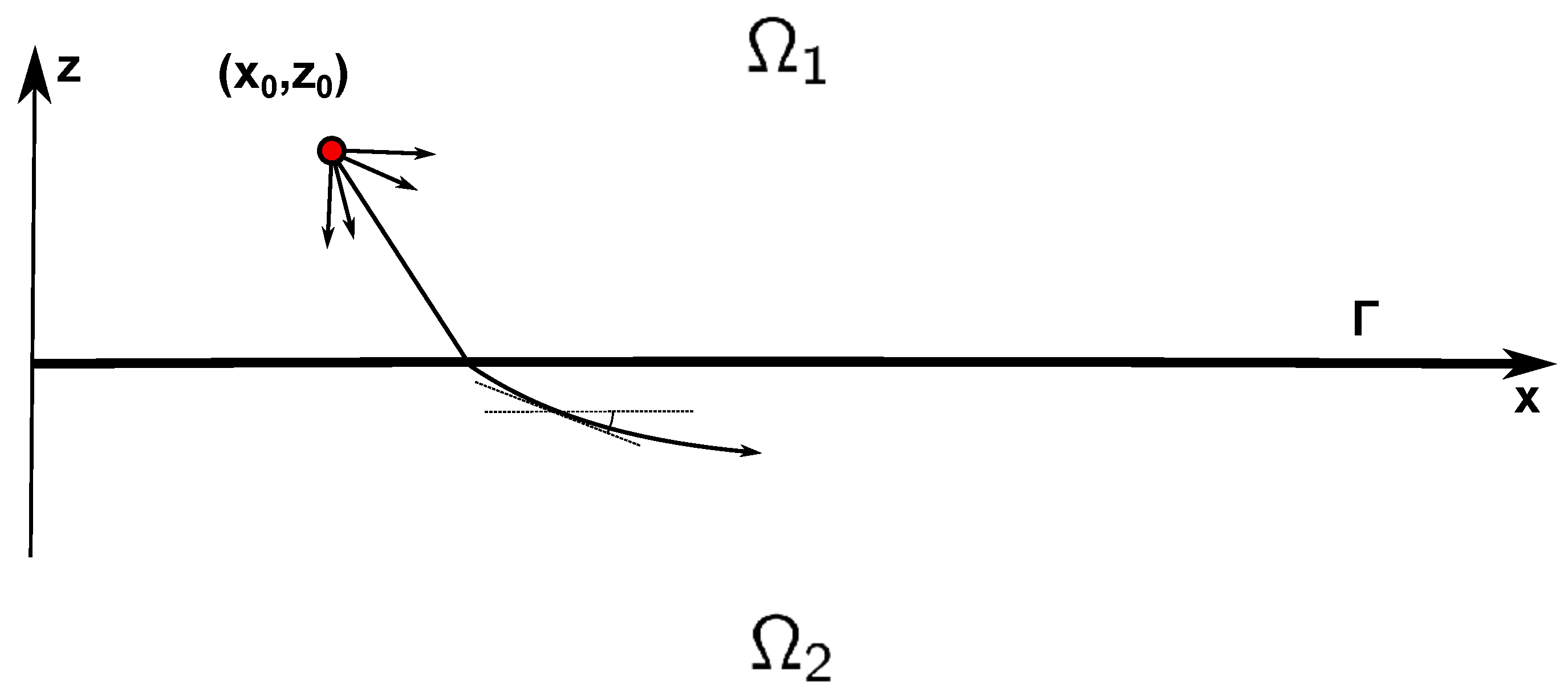
2. Problem Statement
2.1. Waveguide with Infinite Cross-Section
Dispersion Equation
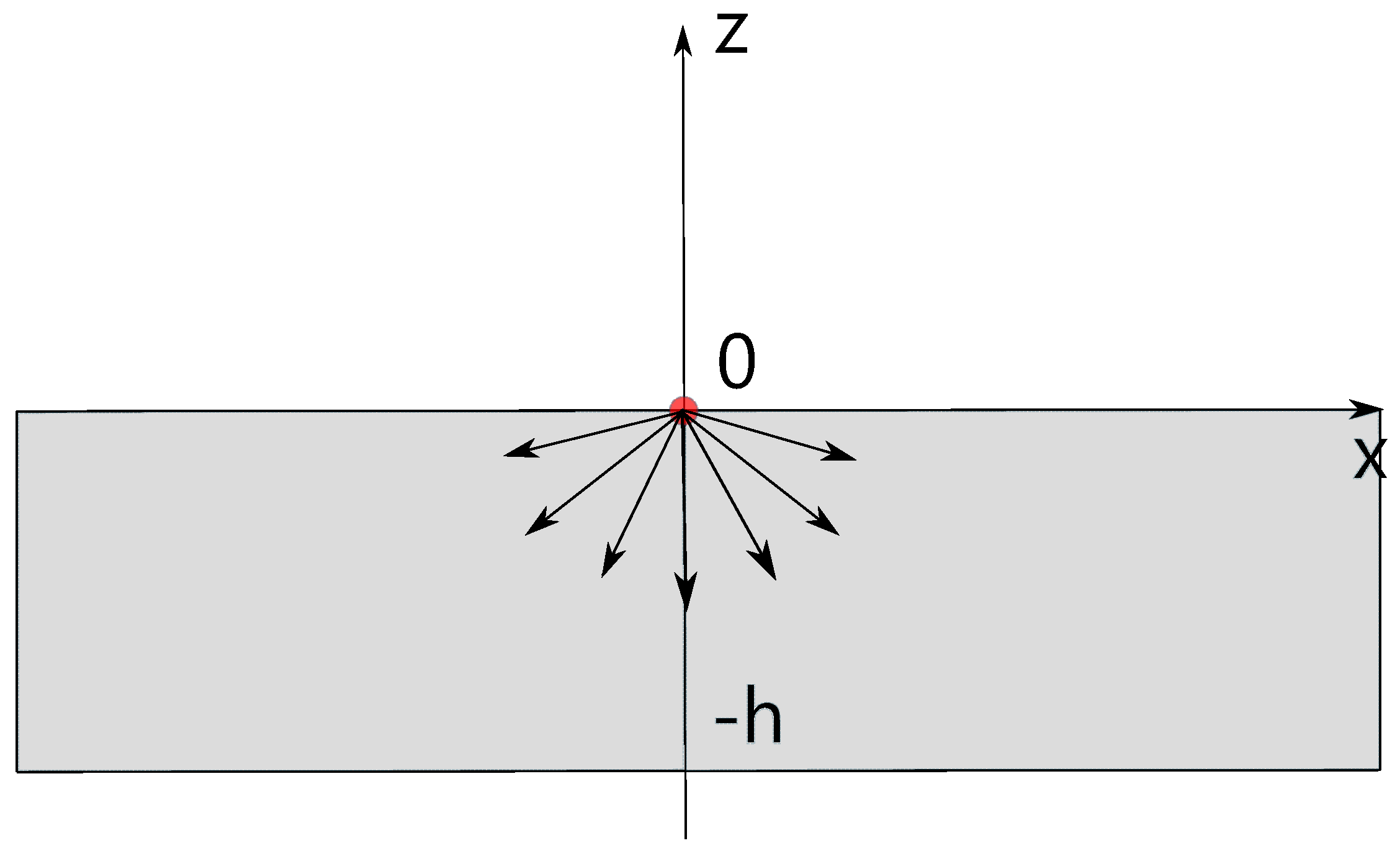
2.2. Airy Waveguide with the Compact Cross-Section
2.2.1. Dispersion Equation
2.2.2. Reduction of Equation (20)
3. Multi-Layered Waveguide
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics: Non-Relativistic Theory; Elsevier: Amsterdam, The Netherlands, 2013; Volume 3. [Google Scholar]
- Jensen, F.B.; Kuperman, W.A.; Porter, M.B.; Schmidt, H. Computational Ocean Acoustics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Petrov, P.; Prants, S.; Petrova, T. Analytical Lie-algebraic solution of a 3D sound propagation problem in the ocean. Phys. Lett. A 2017, 381, 1921–1925. [Google Scholar] [CrossRef]
- Virieux, J.; Farra, V.; Madariaga, R. Ray tracing for earthquake location in laterally heterogeneous media. J. Geophys. Res. Solid Earth 1988, 93, 6585–6599. [Google Scholar] [CrossRef]
- Vallée, O.; Soares, M. Airy Functions and Applications to Physics; World Scientific Publishing Company: Singapore, 2010. [Google Scholar]
- Levy, M. Parabolic Equation Methods for Electromagnetic Wave Propagation; IET: London, UK, 2000. [Google Scholar]
- Warner, G.A.; Dosso, S.E.; Dettmer, J.; Hannay, D.E. Bayesian environmental inversion of airgun modal dispersion using a single hydrophone in the Chukchi Sea. J. Acoust. Soc. Am. 2015, 137, 3009–3023. [Google Scholar] [CrossRef] [PubMed]
- Bonnel, J.; Thode, A.; Wright, D.; Chapman, R. Nonlinear time-warping made simple: A step-by-step tutorial on underwater acoustic modal separation with a single hydrophone. J. Acoust. Soc. Am. 2020, 147, 1897–1926. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Buldyrev, V.S. An investigation of the Green’s function in a problem of diffraction by a transparent circular cylinder. I. Zhurnal Vychislitel’noi Mat. I Mat. Fiz. 1964, 4, 275–286. [Google Scholar] [CrossRef]
- Buldyrev, V. Interference of short waves in the problem of diffraction by an inhomogeneous cylinder of arbitrary cross section. Izv. Vyssh. Uchebn. Zaved. Radiofiz. 1967, 10, 699–711. [Google Scholar]
- Babič, V.M.; Buldyrev, V.S. Asymptotic Methods in Short-Wavelength Diffraction Theory; Alpha Science International Limited: Oxford, UK, 2009. [Google Scholar]
- Brekhovskikh, L. Waves in Layered Media; Academic Press: Cambridge, MA, USA, 1960. [Google Scholar]
- Zavorokhin, G.; Matskovskiy, A. A Nonstationary Problem of Diffraction of Acoustic Waves from a Point Source by an Interface of Two Half-Planes with Positive Effective Curvature. J. Math. Sci. 2021, 252, 612–618. [Google Scholar] [CrossRef]
- Fock, V.A. Electromagnetic Diffraction and Propagation Problems; Pergamon Press: Oxford, UK, 1965. [Google Scholar]
- Shanin, A.; Knyazeva, K.; Korolkov, A. Riemann surface of dispersion diagram of a multilayer acoustical waveguide. Wave Motion 2018, 83, 148–172. [Google Scholar] [CrossRef]
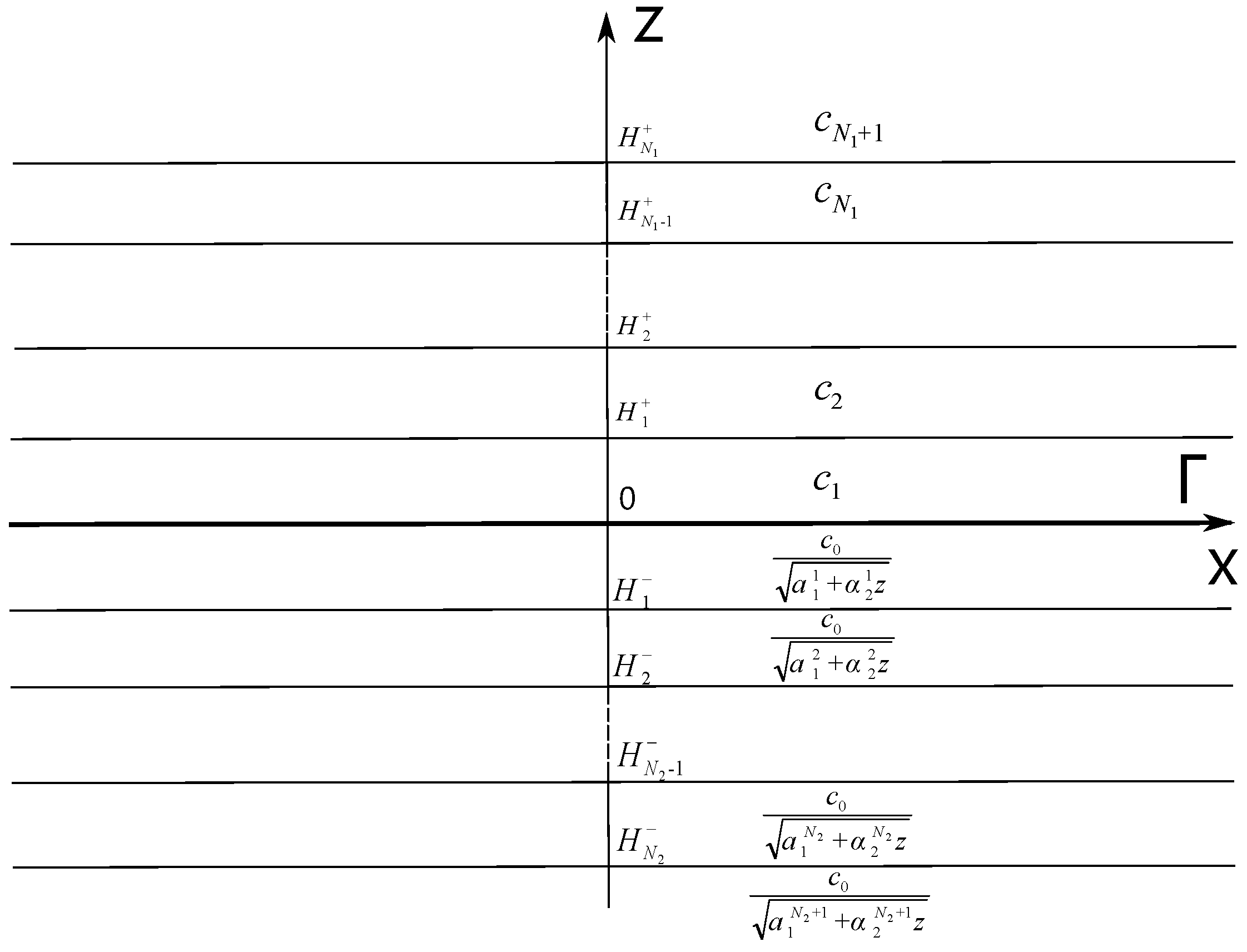
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matskovskiy, A.; Zavorokhin, G.; Petrov, P. A Method for Reducing Transcendental Dispersion Relations to Nonlinear Ordinary Differential Equations in a Wide Class of Wave Propagation Problems. Mathematics 2022, 10, 3866. https://doi.org/10.3390/math10203866
Matskovskiy A, Zavorokhin G, Petrov P. A Method for Reducing Transcendental Dispersion Relations to Nonlinear Ordinary Differential Equations in a Wide Class of Wave Propagation Problems. Mathematics. 2022; 10(20):3866. https://doi.org/10.3390/math10203866
Chicago/Turabian StyleMatskovskiy, Andrey, German Zavorokhin, and Pavel Petrov. 2022. "A Method for Reducing Transcendental Dispersion Relations to Nonlinear Ordinary Differential Equations in a Wide Class of Wave Propagation Problems" Mathematics 10, no. 20: 3866. https://doi.org/10.3390/math10203866







