Analytical Derivations of New Specifications for Stochastic Frontiers with Applications

Abstract

In this paper, we propose the analytical derivations of new specifications for the stochastic frontier (SF) approach. In order to avoid some limitations of the traditional SF method, we introduce dependence between the two error components through copula functions and the asymmetry of the random error assigning a generalized logistic distribution. We report the density functions of the overall error term, some important summary measures and the derivation of the efficiency scores for both cost and production frontiers. Finally, we propose two empirical applications in order to test our methodological approach: the first one refers to the estimation of production frontiers for the Italian airport system; the second one investigates the cost efficiency of the Italian banking sector.

1. Introduction

The original formulation of the SF model is based on the pioneering works of [1,2,3] (see [4,5,6] for a recent and comprehensive overview). In this context, the two error components of an SF are assumed to be independent. First, u is a positive random variable interpreted as a measure of a firm’s inefficiency, and it reflects the difference between the observation and the best frontier for each decision-making unit in the sample. Second, v is a symmetric random variable capturing random shocks, measurement errors and other statistical noise.

As it is well known from the previous literature, the traditional SF approach suffers from three hypotheses.

(i) The first one refers to the selection of the distribution of random variables u and v. The most popular proposal includes the normal–half normal model [1], the normal–exponential model [2], normal–truncated normal model [3], normal–gamma model [7] and others [8].

(ii) The hypothesis of independence between u and v, in some contexts, could be very strong. The importance of including dependence in the economic context is explained because it contributes to capturing the effects of shocks that could affect both error components.

(iii) In different applications of standards, some authors have highlighted a difference between the expected and estimated sign of asymmetry of the composite error. Precisely, the third central moment of $ϵ$, for a standard SF model, is

$$\begin{array}{c}\hfill E\left\{{\left[ϵ-E\left(ϵ\right)\right]}^3\right\}=-E\left\{{\left[u-E\left(u\right)\right]}^3\right\}.\end{array}$$

(1)

Given expression (1), a positive skewness for the inefficiency term u means an expected negative skewness for the composite error $ϵ$. Nevertheless, in many applications, the asymmetry of $ϵ$ is positive. This is the well-known “wrong skewness” anomaly in SF models [9]. To overcome this problem, several authors have proposed the use of distribution functions with negative asymmetry for u. (For example, Ref. [10] uses the binomial probability function, Ref. [11] suggests the Weibull distribution and [12,13] consider a double truncated normal distribution) Recently, in order to obtain the desired direction of residual skewness, a finite sample adjustment to existing estimators was proposed [14,15], and in [16], the authors propose a new approach to the problem by generalizing the distribution used for the inefficiency variable. Finally, by showing that their assumptions do not produce a wrong skewness problem, Ref. [17] proposes a specification with independence between the error components u and v, the Laplace distribution for v and the exponential (truncated Laplace) distribution for the inefficiency. The authors show that with the presence of the Laplace distribution, in the absence of inefficiency, the MLE reduces to the Least Absolute Deviations (LAD) estimator. In the context of the stochastic frontier of production functions, Ref. [18] highlighted that the expected sign of the composite error depends both on the sign of the asymmetry of u and v and on the dependence between u and v and, therefore, ultimately the wrong skewness anomaly is a model specification problem.

Our main contributions are to fill some gaps in the literature. First, we propose a generalization of SF by removing the hypotheses of independence between the two error components. Second, we employ a more flexible distribution than the Normal function for the random noise v, which is also able to capture asymmetry. (This is a topical issue since the literature that models the asymmetry of v is burgeoning [16,19,20]) Third, we report the analytical derivation of density for both cost and production frontiers. Fourth, two empirical applications are provided to show the robustness of the model. Especially when referring to the last contribution, our findings highlight that the best specifications are those capturing the dependence between u and v and the asymmetry of v.

From a statistical point of view, by introducing the dependence, we intend to generalize the traditional SF approach. Indeed our model can capture the dependence between u and v when data reveal its presence. However, our specification permits the collapse of the traditional SF model with independence, where the dependence is not an issue in a specific empirical context. Further, from an economic point of view, there are no reasons to assume the independence of these error components in a productive industry [18,21,22,23]. Ref. [18] provides several reasons for the existence of factors leading to the dependence between the two error components. For example, in the agriculture sector, the absence of dependence is difficult to observe because, in this industry, current managerial decisions are influenced by past natural shocks. As highlighted in [18], a disturbance in one season will affect both future decisions (thus the inefficiency component) and the random error component. This could explain the presence of dependence between u and v. Other justifications for the dependence are due to misspecification errors or to unexpected events, which affect both managerial decisions (efficiency) and the random component error, generating potential dependence between u and v.

In the next sections, we extend the proposal of [18] to the case of the stochastic cost frontier, the proposed models help to overcome the aforementioned limits of the traditional SF. The paper is organized as follows. Section 2 introduces our research question and shows our methodological contributions for both production and cost frontiers. In Section 3, we report two empirical applications in order to test our methodological improvements. In Section 4, we conclude.

2. Stochastic Frontiers: What Is New

In this section, we propose a model that can be easily used for both cost and production functions. To this end, in our specifications, the J-indicator is equal to 1 for cost frontier models, while $J=-1$ in the case of production frontiers. The generic model for a sample of N firms is described as follows:

$$\begin{array}{cc}\hfill \overline{y}& =\overline{x}\beta +Ju+v\hfill \end{array}$$

(2)

where $\overline{y}$ is a vector of the dimension $(N\times 1)$ of a firm’s outputs in a production frontier or a vector of firm’s costs in a cost frontier. (Here and throughout the rest of the paper, overlined variables denote the logarithmic transformation of the original variables. For example, $\overline{y}=log\left(y\right)$); $\overline{x}$ is a matrix of dimension of $(N\times K)$ of inputs for a production frontier or is a matrix of outputs and inputs prices in a cost function; $\beta$ is a $(K\times 1)$ vector of unknowns elasticities; v is a $(N\times 1)$ vector of random errors; u is a $(N\times 1)$ vector of random variables describing the inefficiencies associated with each firm (for a detailed discussion, see [4]). In order to take into account the difficulties reported above, following [18], we propose a more flexible specification of the model by considering a general joint density $f_{u,v}(·,·,\Theta )$ for a couple of random variables $(u,v)$, where $\Theta$ is the vector that includes the marginal and dependence parameters, obtained using the property of the copula function. In particular, for any copula $C\left(F\right(u),G(v\left)\right)$, the joint pdf can be expressed as $f_{u,v}(u,v)=f\left(u\right)g\left(v\right)c\left(F\left(u\right),G\left(v\right)\right)$ where $c\left(F\left(u\right),G\left(v\right)\right)=\frac{{\partial }^{2}C(F\left(u\right),G\left(v\right))}{\partial F\left(u\right)\partial G\left(v\right)}$.

The probability density function (pdf) of the composite error $ϵ:=Ju+v$ is obtained by the convolution of two dependent random variables as follows

$$f_{ϵ}\left(ϵ\right)={\int }_{{\Re }^{+}}{f}_{u,v}(u,ϵ-Ju)du.$$

In a nutshell, the likelihood function of our model can be expressed as follows

$$L=\prod _{i=1}^N{f}_{ϵ}({\overline{y}}_i-{\overline{x}}_i\beta ;\Theta )$$

(3)

where ${\overline{x}}_i$ is the $i^{th}$ row of matrix $\overline{x}$ and ${\overline{y}}_i-{\overline{x}}_i\beta ={ϵ}_i$. In (3), $f_{ϵ}(·;\Theta )$ is the pdf of a convolution obtained marginalizing the joint pdf $f(u,v;\Theta )$; the latter is obtained once the copula function, $C_{\theta }(F_u(·),G_v(·);\Theta )$, has been chosen and the marginal distribution functions, $F_u(·)$ and $G_v(·)$, specified. Finally, we derive the calculation of Technical Efficiency ($T{E}_{\Theta }$):

$$T{E}_{\Theta }=E\left[e^{-u}\right|ϵ={ϵ}^{*}]=\frac{1}{f_{ϵ}(.;\Theta )}{\int }_{{\Re }^{+}}{e}^{-u}{f}_{u,v}(u,ϵ-Ju;\Theta )du.$$

(4)

Taking into consideration the general framework described above, after simple but tedious algebra, the third central moment of the composite error turns out to be

$$\begin{array}{ccc}\hfill E\left\{{\left[ϵ-E\left(ϵ\right)\right]}^3\right\}& =& JE\left\{{\left[u-E\left(u\right)\right]}^3\right\}+E\left\{{\left[v-E\left(v\right)\right]}^3\right\}\hfill \\ & +& 3cov\left(u^2,v\right)+3Jcov\left(u,v^2\right)-6\left[E\left(u\right)+JE\left(v\right)\right]cov(u,v)\hfill \end{array}$$

(5)

The proof of this statement is available upon request. We highlight that Equation (5) generalizes the results reported in [18] as it is valid for both cost and production stochastic frontiers.

Unlike Equation (1), from Equation (5) it is clear that the expected sign of the asymmetry of the composite error, $ϵ$, is influenced by both the sign of the asymmetry of u and v and by the dependence between u and v. As described in [18], Equation (5) shows that the wrong skewness problem is a consequence of all assumptions underlying the specification of standard SF.

In the next section, we consider a very flexible specification of the SF model, introducing skewness in the random error v and dependence between the two error components u and v.

2.1. A Special Case: Modeling Dependence with the Copula Function

Nowadays, the copula function is a well-established methodological tool in the Statistical and Econometric literature, and the main reference books are those of [24,25,26,27], just to name a few.

In a nutshell, the usefulness of the copula function lies in the fact that it allows the construction of bivariate (multivariate) distribution functions with specified marginal distribution functions not necessarily belonging to the same family. Furthermore, a copula has been found to be a very effective tool for studying the dependence between random variables involved. The first use of copula functions in the stochastic frontier literature appears to be [23], to take into account the possible dependence between accidental error, v, and inefficiency, u. Since then, several other authors have used the copula function in the context of SF; for recent surveys, see [28,29].

Our specifications include the following components. Similarly to [18], we choose the generalized logistic (GL) distribution for the random error v, with pdf given by

$$g=g(v;{\alpha }_v,{\delta }_v)=\frac{{\alpha }_v}{{\delta }_v}\frac{e^{-\frac{v+{\delta }_v\left[\Psi \left({\alpha }_v\right)-\Psi \left(1\right)\right]}{{\delta }_v}}}{{\left(1+e^{-\frac{v+{\delta }_v\left[\Psi \left({\alpha }_v\right)-\Psi \left(1\right)\right]}{{\delta }_v}}\right)}^{{\alpha }_v+1}}$$

and distribution function (df)

$$G=G(v;{\alpha }_v,{\delta }_v)={\left(1+e^{-\frac{v+{\delta }_v\left[\Psi \left({\alpha }_v\right)-\Psi \left(1\right)\right]}{{\delta }_v}}\right)}^{-{\alpha }_v}$$

with ${\alpha }_v$, ${\delta }_v$>0, and $v\in \Re$. We remember that this distribution is centered on zero, i.e., $E\left(V\right)=0$ regardless of the values assumed by ${\alpha }_v$ and ${\delta }_v$, and the parameter ${\alpha }_v$ of the GL distribution is an indicator of the direction of the skewness; in particular, the distribution is symmetric for ${\alpha }_v=1$, asymmetrically negative for ${\alpha }_v\in (0,1)$ and asymmetrically positive for ${\alpha }_v>1$; the exponential distribution for the inefficiency error u, with pdf

$$f=f(u;{\delta }_u)=\frac{1}{{\delta }_u}{e}^{-\frac{u}{{\delta }_u}}$$

and df is given by

$$F=F(u;{\delta }_u)=\left(1-e^{-\frac{u}{{\delta }_u}}\right)$$

with ${\delta }_u>0$. This pdf is appropriate for describing the inefficiency component because it has positive support, $u>0$; finally, the FGM copula function for the dependence structure between u and v, with a copula function given by

$$C(F,G)=FG\left(1+\theta (1-F)(1-G)\right)$$

and density copula

$$c(F,G)=1+\theta (1-2F)(1-2G)$$

with $\theta \in [-1,1]$, dependence parameter; in particular, for $\theta =0$, we have independence, for $\theta <0$ or $\theta >0$, we have negative or positive dependence, respectively.

We observe that from our specification, it is possible to obtain the one proposed by [23] setting ${\alpha }_v=1$.

In the case of a production frontier (for $J=-1$), Ref. [18] provides the pdf of the composite error by proving the following theorem,

Theorem 1.

Assuming that $u\sim Exp({\delta }_u)$, $v\sim GL({\delta }_v,{\alpha }_v)$ and the dependence between u and v is modeled by $FGM$ copula. Let $k_1\left(ϵ\right)$ be defined as $k_1\left(ϵ\right)=exp\{-\frac{ϵ+{\delta }_v\left[\Psi \left({\alpha }_v\right)-\Psi \left(1\right)\right]}{{\delta }_v}\}$.

The density function of the composite error for a production frontier is

$$\begin{array}{cc}\hfill f_{ϵ}(ϵ;\Theta )=& w_{1,P}\left(ϵ\right){}_2{F}_1\left({\alpha }_v+1,\frac{{\delta }_v}{{\delta }_u}+1;\frac{{\delta }_v}{{\delta }_u}+2;-k_1\left(ϵ\right)\right)+\hfill \\ \hfill & w_{2,P}\left(ϵ\right){}_2{F}_1\left({\alpha }_v+1,2\frac{{\delta }_v}{{\delta }_u}+1;2\frac{{\delta }_v}{{\delta }_u}+2;-k_1\left(ϵ\right)\right)+\hfill \\ \hfill & w_{3,P}\left(ϵ\right){}_2{F}_1\left(2{\alpha }_v+1,\frac{{\delta }_v}{{\delta }_u}+1;\frac{{\delta }_v}{{\delta }_u}+2;-k_1\left(ϵ\right)\right)+\hfill \\ \hfill & w_{4,P}\left(ϵ\right){}_2{F}_1\left(2{\alpha }_v+1,2\frac{{\delta }_v}{{\delta }_u}+1;2\frac{{\delta }_v}{{\delta }_u}+2;-k_1\left(ϵ\right)\right)\hfill \end{array}$$

(6)

where the Hypergeometric Functions are denoted by ${}_2{F}_1(.,.;.;.)$. Denoted with $\Gamma (a+1)=a!$, the Gamma mathematical function, Pochhammer’s symbol is simply a way of indicating the following ratio

$${\left(x\right)}_n={\displaystyle \frac{\Gamma (x+n)}{\Gamma \left(x\right)}}={\displaystyle \frac{(x+n-1)(x+n-2)...(x+1)x(x-1)!}{(x-1)!}}=(x+n-1)(x+n-2)...(x+1)x$$

The hypergeometric function ${}_2{F}_1(a,b;c;s)$ is defined by the series

$$\sum _{i=0}^{\infty }\frac{{\left(a\right)}_i{\left(b\right)}_i}{{\left(c\right)}_i}\frac{s^i}{i!}$$

for $\left|s\right|<1$ (see, for example, [30]). The series has the following integral representation due to Euler, if $b>0$ and $c>0$, then

$${}_2{F}_1(a,b;c;s)=\frac{\Gamma \left(c\right)}{\Gamma (c-b)\Gamma \left(b\right)}{\int }_0^1{t}^{b-1}{(1-t)}^{c-b-1}{(1-st)}^{-a}dt$$

and the functions $w_{j,P}(.)$, for $j=1,2,3,4$ are, respectively, defined as:

$$\begin{array}{cc}\hfill & w_{1,P}\left(ϵ\right)=(1-\theta )\frac{{\alpha }_v{k}_1\left(ϵ\right)}{{\delta }_v+{\delta }_u}{w}_{2,P}\left(ϵ\right)=2\theta \frac{{\alpha }_v{k}_1\left(ϵ\right)}{2{\delta }_v+{\delta }_u}\hfill \\ \hfill & w_{3,P}\left(ϵ\right)=2\theta \frac{{\alpha }_v{k}_1\left(ϵ\right)}{{\delta }_v+{\delta }_u}{w}_{4,P}\left(ϵ\right)=-4\theta \frac{{\alpha }_v{k}_1\left(ϵ\right)}{2{\delta }_v+{\delta }_u}\hfill \end{array}$$

Proof. 

For proof of Theorem 1, see [18].  □

For the purposes of the present work, we prove the following proposition valid in the case of a stochastic frontier cost function.

Theorem 2.

Assuming that $u\sim Exp\left({\delta }_u\right)$, $v\sim GL({\delta }_v,{\alpha }_v)$ and the dependence between u and v is modeled by $FGM$ copula. Let $k_1\left(ϵ\right)$ be defined as $k_1\left(ϵ\right)=exp\{-\frac{ϵ+{\delta }_v\left[\Psi \left({\alpha }_v\right)-\Psi \left(1\right)\right]}{{\delta }_v}\}$. The density function of the composite error for a cost frontier, $ϵ=u+v$, is

$$\begin{array}{cc}\hfill f_{ϵ}(ϵ;\Theta )& =w_{1,C}\left(ϵ\right){}_2{F}_1\left({\alpha }_v+1,{\alpha }_v+\frac{{\delta }_v}{{\delta }_u};{\alpha }_v+\frac{{\delta }_v}{{\delta }_u}+1;-k_1{\left(ϵ\right)}^{-1}\right)+\hfill \\ \hfill & w_{2,C}\left(ϵ\right){}_2{F}_1\left(2{\alpha }_v+1,2{\alpha }_v+\frac{{\delta }_v}{{\delta }_u};2{\alpha }_v+\frac{{\delta }_v}{{\delta }_u}+1;-k_1{\left(ϵ\right)}^{-1}\right)+\hfill \\ \hfill & w_{3,C}\left(ϵ\right){}_2{F}_1\left({\alpha }_v+1,{\alpha }_v+2\frac{{\delta }_v}{{\delta }_u};{\alpha }_v+2\frac{{\delta }_v}{{\delta }_u}+1;-k_1{\left(ϵ\right)}^{-1}\right)+\hfill \\ \hfill & w_{4,C}\left(ϵ\right){}_2{F}_1\left(2{\alpha }_v+1,2{\alpha }_v+2\frac{{\delta }_v}{{\delta }_u};2{\alpha }_v+2\frac{{\delta }_v}{{\delta }_u}+1;-k_1{\left(ϵ\right)}^{-1}\right)\hfill \end{array}$$

(7)

where the functions $w_{j,C}(.)$, for $j=1,2,3,4$ are, respectively, defined as:

$$\begin{array}{cc}\hfill & w_{1,C}\left(ϵ\right)=(1-\theta )\frac{{\alpha }_v{k}_1{\left(ϵ\right)}^{-{\alpha }_v}}{{\delta }_u\left({\alpha }_v+\frac{{\delta }_v}{{\delta }_u}\right)}{w}_{2,C}\left(ϵ\right)=2\theta \frac{{\alpha }_v{k}_1{\left(ϵ\right)}^{-2{\alpha }_v}}{{\delta }_u\left(2{\alpha }_v+\frac{{\delta }_v}{{\delta }_u}\right)}\hfill \\ \hfill & w_{3,C}\left(ϵ\right)=2\theta \frac{{\alpha }_v{k}_1{\left(ϵ\right)}^{-{\alpha }_v}}{{\delta }_u\left({\alpha }_v+2\frac{{\delta }_v}{{\delta }_u}\right)}{w}_{4,C}\left(ϵ\right)=-4\theta \frac{{\alpha }_v{k}_1{\left(ϵ\right)}^{-2{\alpha }_v}}{{\delta }_u\left(2{\alpha }_v+2\frac{{\delta }_v}{{\delta }_u}\right)}\hfill \end{array}$$

Proof. 

For the proof of the Theorem 2, see Appendix A.  □

In addition, using the result of Appendix A, the expected value, the variance and the third central moment of the composite error are given by:

$$E\left[ϵ\right]={\delta }_u,$$

(8)

$$V\left[ϵ\right]={\delta }_u^2+{\delta }_v^2[{\Psi }^{\prime }\left({\alpha }_v\right)+{\Psi }^{\prime }\left(1\right)]+{\displaystyle \frac{\theta {\delta }_u{\delta }_v}{2}}[\Psi \left(2{\alpha }_v\right)-\Psi \left({\alpha }_v\right)]$$

(9)

and

$$\begin{array}{cc}\hfill E{[ϵ-E\left(ϵ\right)]}^3=& -2{\delta }_u^3+{\delta }_v^3[{\Psi }^{″}\left({\alpha }_v\right)-{\Psi }^{″}\left(1\right)]+\frac{3}{4}\theta {\delta }_u^2{\delta }_v[\Psi \left(2{\alpha }_v\right)-\Psi \left({\alpha }_v\right)]\hfill \\ \hfill & -\frac{3}{4}\theta {\delta }_u{\delta }_v^2\left\{2\left[{\Psi }^{\prime }\left({\alpha }_v\right)+{\Psi }^{\prime }\left(1\right)\right]-{\left[\Psi \left(2{\alpha }_v\right)-\Psi \left({\alpha }_v\right)\right]}^2\right.\hfill \\ \hfill & -{\Psi }^{\prime }\left(2{\alpha }_v\right)-{\Psi }^{\prime }\left(1\right)\hfill \end{array}$$

(10)

where $\Psi (·)$, ${\Psi }^{\prime }(·)$ and ${\Psi }^{″}(·)$ are, respectively, the Digamma, Trigamma and Tetragamma functions.

To appreciate the flexibility of our model, we point out that according on the values of some parameters, we can specify the following four possible models:

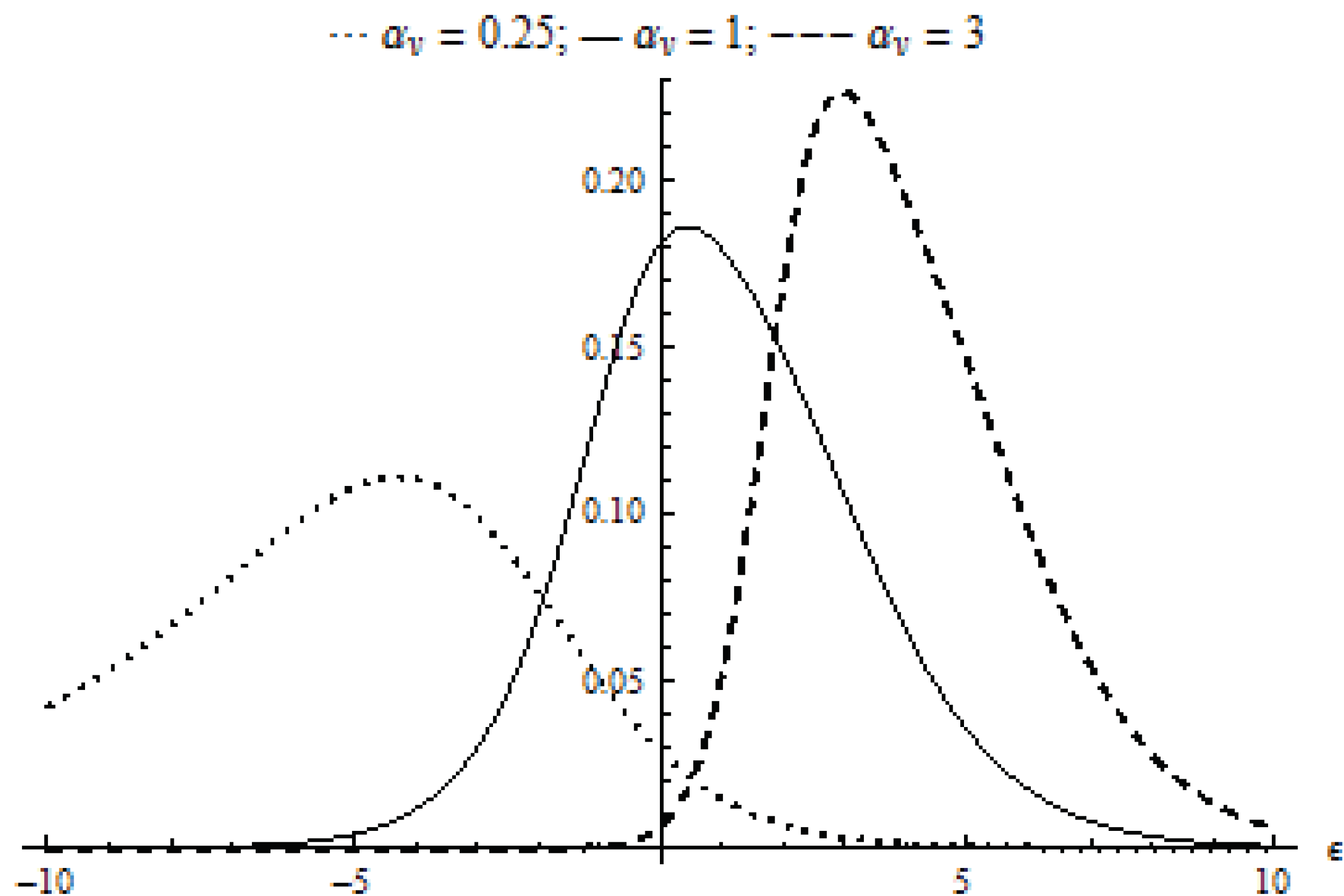
• for $\theta =0$ and ${\alpha }_v=1$, we get the model of independence (between inefficiency error, u, and random error, v) and symmetry of v, denoted by $(I,S)$;
• for $\theta =0$ and ${\alpha }_v\ne 1$, we have the model of independence and asymmetry, denoted by $(I,A)$;
• for $\theta \ne 0$ and ${\alpha }_v=1$, we obtain the model of dependence and symmetry, denoted by $(D,S)$;
• for $\theta \ne 0$ and ${\alpha }_v\ne 1$, we have the model of dependence and asymmetry, denoted by $(D,A)$

2.2. Calculation of Efficiency Scores

Given Theorem 1 and its Proof in [18], we derive the formula to calculate the Technical Efficiency scores $T{E}_{\Theta }$ related to production frontiers.

We can write

$$\begin{array}{cc}\hfill T{E}_{\Theta }=& E\left[e^{-u}\right|ϵ={ϵ}^{*}]=\frac{1}{f_{ϵ}(.;\Theta )}{\int }_{{\Re }^{+}}{e}^{-u}{f}_{u,v}(u,ϵ+u;\Theta )du\hfill \end{array}$$

(11)

where $f(u,ϵ+u)$ is derived in [18].

We emphasize the appropriate use of the results reported in Appendix A, after algebra, we obtain:

$$T{E}_{\Theta }=E\left[e^{-u}\right|ϵ]=\frac{{\overline{\omega }}_1\left(ϵ\right){\overline{H}}_1\left(ϵ\right)+\theta [{\overline{\omega }}_1\left(ϵ\right){\overline{H}}_1\left(ϵ\right)-2{\overline{\omega }}_2\left(ϵ\right){\overline{H}}_2\left(ϵ\right)-2{\overline{\omega }}_3\left(ϵ\right){\overline{H}}_3\left(ϵ\right)+4{\overline{\omega }}_4\left(ϵ\right){\overline{H}}_4\left(ϵ\right)]}{{\omega }_1\left(ϵ\right)H_1\left(ϵ\right)-\theta [{\omega }_1\left(ϵ\right)H_1\left(ϵ\right)-2{\omega }_2\left(ϵ\right)H_2\left(ϵ\right)-2{\omega }_3\left(ϵ\right)H_3\left(ϵ\right)+4{\omega }_4\left(ϵ\right)H_4\left(ϵ\right)]}$$

(12)

where the H-$functions$ represent hypergeometric functions. In particular, we have:

$$\begin{array}{cc}\hfill {\overline{H}}_1& ={}_2{F}_1\left({\alpha }_v+1,\frac{{\delta }_v}{{\delta }_u}+{\delta }_v+1;\frac{{\delta }_v}{{\delta }_u}+{\delta }_v+2;-k_1\left(ϵ\right)\right)\hfill \\ \hfill H_1& ={}_2{F}_1\left({\alpha }_v+1,\frac{{\delta }_v}{{\delta }_u}+1;\frac{{\delta }_v}{{\delta }_u}+2;-k_1\left(ϵ\right)\right)\hfill \\ \hfill {\overline{H}}_2& =\frac{1}{\left[{\delta }_v\left(\frac{1}{{\delta }_u}+1\right)\right]}{}_2{F}_1\left({\alpha }_v+1,{\delta }_v\left(\frac{1}{{\delta }_u}+1\right)+1;{\delta }_v\left(\frac{1}{{\delta }_u}+1\right)+2;-k_1\left(ϵ\right)\right)\hfill \\ \hfill & -\frac{1}{\left[{\delta }_v\left(\frac{2}{{\delta }_u}+1\right)\right]}{}_2{F}_1\left({\alpha }_v+1,{\delta }_v\left(\frac{2}{{\delta }_u}+1\right)+1;{\delta }_v\left(\frac{2}{{\delta }_u}+1\right)+2;-k_1\left(ϵ\right)\right)\hfill \\ \hfill H_2& ={}_2{F}_1\left({\alpha }_v+1,2\frac{{\delta }_v}{{\delta }_u}+1;2\frac{{\delta }_v}{{\delta }_u}+2;-k_1\left(ϵ\right)\right)\hfill \\ \hfill {\overline{H}}_3& ={}_2{F}_1\left(2{\alpha }_v+1,\frac{{\delta }_v}{{\delta }_u}+{\delta }_v+1;\frac{{\delta }_v}{{\delta }_u}+{\delta }_v+2;-k_1\left(ϵ\right)\right)\hfill \\ \hfill H_3& ={}_2{F}_1\left(2{\alpha }_v+1,\frac{{\delta }_v}{{\delta }_u}+1;\frac{{\delta }_v}{{\delta }_u}+2;-k_1\left(ϵ\right)\right)\hfill \\ \hfill {\overline{H}}_4& =\frac{1}{\left[{\delta }_v\left(\frac{1}{{\delta }_u}+1\right)\right]}{}_2{F}_1\left(2{\alpha }_v+1,{\delta }_v\left(\frac{1}{{\delta }_u}+1\right)+1;{\delta }_v\left(\frac{1}{{\delta }_u}+1\right)+2;-k_1\left(ϵ\right)\right)\hfill \\ \hfill & -\frac{1}{\left[{\delta }_v\left(\frac{2}{{\delta }_u}+1\right)\right]}{}_2{F}_1\left(2{\alpha }_v+1,{\delta }_v\left(\frac{2}{{\delta }_u}+1\right)+1;{\delta }_v\left(\frac{2}{{\delta }_u}+1\right)+2;-k_1\left(ϵ\right)\right)\hfill \\ \hfill H_4& ={}_2{F}_1\left(2{\alpha }_v+1,2\frac{{\delta }_v}{{\delta }_u}+1;2\frac{{\delta }_v}{{\delta }_u}+2;-k_1\left(ϵ\right)\right)\hfill \end{array}$$

and where the $\omega$-$functions$ are, respectively, defined as:

$$\begin{array}{cc}\hfill & {\overline{\omega }}_1\left(ϵ\right)={\overline{\omega }}_3\left(ϵ\right)=\frac{{\alpha }_v{k}_1\left(ϵ\right)}{{\delta }_u\left[{\delta }_v\left(\frac{1}{{\delta }_u}+1\right)\right]}{\overline{\omega }}_2\left(ϵ\right)={\overline{\omega }}_4\left(ϵ\right)=\frac{{\alpha }_v{k}_1\left(ϵ\right)}{{\delta }_u}\hfill \\ \hfill & {\omega }_1\left(ϵ\right)={\omega }_3\left(ϵ\right)=\frac{{\alpha }_v{k}_1\left(ϵ\right)}{{\delta }_v+{\delta }_v}{\omega }_2\left(ϵ\right)={\omega }_4\left(ϵ\right)=\frac{{\alpha }_v{k}_1\left(ϵ\right)}{2{\delta }_v+{\delta }_v}\hfill \end{array}$$

Finally, the cost efficiency scores $C{E}_{\Theta }$ are obtained through

$$C{E}_{\Theta }=E\left[e^{-u}\right|ϵ={ϵ}^{*}]=\frac{1}{f_{ϵ}(.;\Theta )}{\int }_{{\Re }^{+}}{e}^{-u}{f}_{u,v}(u,ϵ-u;\Theta )du$$

(13)

Given Theorem 2, we derive the formula to calculate the Cost Efficiency scores $C{E}_{\Theta }$ for our model.

Bearing in mind that $ϵ=u+v$ in a cost SF, then we can write

$$\begin{array}{cc}\hfill C{E}_{\Theta }=& E\left[e^{-u}\right|ϵ={ϵ}^{*}]=\frac{1}{f_{ϵ}(.;\Theta )}{\int }_{{\Re }^{+}}{e}^{-u}{f}_{u,v}(u,ϵ-u;\Theta )du=\frac{1}{f_{ϵ}(.;\Theta )}Int\hfill \end{array}$$

(14)

where

$$\begin{array}{cc}\hfill Int=& {\int }_{{\Re }^{+}}{e}^{-u}\{(1+\theta )f\left(u\right)g(ϵ-u)-2\theta f\left(u\right)g(ϵ-u)G(ϵ-u)\hfill \\ \hfill -& 2\theta f\left(u\right)g(ϵ-u)F\left(u\right)+4\theta f\left(u\right)g(ϵ-u)F\left(u\right)G(ϵ-u)(u,ϵ-u;\Theta )\}du\hfill \\ \hfill =& (1+\theta ){\int }_{{\Re }^{+}}{e}^{-u}f\left(u\right)g(ϵ-u)du-2\theta {\int }_{{\Re }^{+}}{e}^{-u}f\left(u\right)g(ϵ-u)G(ϵ-u)du\hfill \\ \hfill -& 2\theta {\int }_{{\Re }^{+}}{e}^{-u}f\left(u\right)g(ϵ-u)F\left(u\right)du+4\theta {\int }_{{\Re }^{+}}{e}^{-u}f\left(u\right)g(ϵ-u)F\left(u\right)G(ϵ-u)(u,ϵ-u;\Theta )du\hfill \end{array}$$

(15)

We underline that, with appropriate manipulation, the above integrals can be obtained using the results reported in Appendix A.

After algebra and putting $k_1\left(ϵ\right)=exp\{-\frac{ϵ+{\delta }_v\left[\Psi \left({\alpha }_v\right)-\Psi \left(1\right)\right]}{{\delta }_v}\}$, we obtain:

$$C{E}_{\Theta }=E\left[e^{-u}\right|ϵ]=\frac{{\overline{\omega }}_1{\overline{H}}_1\left(ϵ\right)-\theta [{\overline{\omega }}_1\left(ϵ\right){\overline{H}}_1\left(ϵ\right)-2{\overline{\omega }}_2\left(ϵ\right){\overline{H}}_2\left(ϵ\right)-2{\overline{\omega }}_3\left(ϵ\right){\overline{H}}_3\left(ϵ\right)+4{\overline{\omega }}_4\left(ϵ\right){\overline{H}}_4\left(ϵ\right)]}{{\omega }_1{H}_1\left(ϵ\right)-\theta [{\omega }_1\left(ϵ\right)H_1\left(ϵ\right)-2{\omega }_2\left(ϵ\right)H_2\left(ϵ\right)-2{\omega }_3\left(ϵ\right)H_3\left(ϵ\right)+4{\omega }_4\left(ϵ\right)H_4\left(ϵ\right)]}$$

(16)

where the H-$functions$ represent hypergeometric functions. In particular, we have:

$$\begin{array}{cc}\hfill & {\overline{H}}_1={}_2{F}_1\left({\alpha }_v+1,{\alpha }_v+{\delta }_v\left(\frac{1}{{\delta }_u}+1\right);{\alpha }_v+{\delta }_v\left(\frac{1}{{\delta }_u}+1\right)+1;-k_1{\left(ϵ\right)}^{-1}\right)\hfill \\ \hfill & H_1={}_2{F}_1\left({\alpha }_v+1,{\alpha }_v+\frac{{\delta }_v}{{\delta }_u};{\alpha }_v+\frac{{\delta }_v}{{\delta }_u}+1;-k_1{\left(ϵ\right)}^{-1}\right)\hfill \\ \hfill & {\overline{H}}_2={}_2{F}_1\left(2{\alpha }_v+1,2{\alpha }_v+{\delta }_v\left(\frac{1}{{\delta }_u}+1\right);2{\alpha }_v+{\delta }_v\left(\frac{1}{{\delta }_u}+1\right)+1;-k_1{\left(ϵ\right)}^{-1}\right)\hfill \\ \hfill & H_2={}_2{F}_1\left(2{\alpha }_v+1,2{\alpha }_v+\frac{{\delta }_v}{{\delta }_u};2{\alpha }_v+\frac{{\delta }_v}{{\delta }_u}+1;-k_1{\left(ϵ\right)}^{-1}\right)\hfill \\ \hfill & {\overline{H}}_3={}_2{F}_1\left({\alpha }_v+1,{\alpha }_v+{\delta }_v\left(\frac{2}{{\delta }_u}+1\right);{\alpha }_v+{\delta }_v\left(\frac{2}{{\delta }_u}+1\right)+1;-k_1{\left(ϵ\right)}^{-1}\right)\hfill \\ \hfill & H_3={}_2{F}_1\left({\alpha }_v+1,{\alpha }_v+2\frac{{\delta }_v}{{\delta }_u};{\alpha }_v+2\frac{{\delta }_v}{{\delta }_u}+1;-k_1{\left(ϵ\right)}^{-1}\right)\hfill \\ \hfill & {\overline{H}}_4={}_2{F}_1\left(2{\alpha }_v+1,2{\alpha }_v+{\delta }_v\left(\frac{2}{{\delta }_u}+1\right);2{\alpha }_v+{\delta }_v\left(\frac{2}{{\delta }_u}+1\right)+1;-k_1{\left(ϵ\right)}^{-1}\right)\hfill \\ \hfill & H_4={}_2{F}_1\left(2{\alpha }_v+1,2{\alpha }_v+2\frac{{\delta }_v}{{\delta }_u};2{\alpha }_v+2\frac{{\delta }_v}{{\delta }_u}+1;-k_1{\left(ϵ\right)}^{-1}\right)\hfill \end{array}$$

(17)

and where the functions ${\omega }_1(.)$, ${\omega }_2(.)$, ${\omega }_3(.)$ and ${\omega }_4(.)$ are, respectively, defined as:

$$\begin{array}{cc}\hfill & {\overline{\omega }}_1\left(ϵ\right)=\frac{{\alpha }_v{k}_1{\left(ϵ\right)}^{-{\alpha }_v}}{{\delta }_u\left[{\alpha }_v+{\delta }_v\left(\frac{1}{{\delta }_u}+1\right)\right]}{\overline{\omega }}_2\left(ϵ\right)=\frac{{\alpha }_v{k}_1{\left(ϵ\right)}^{-2{\alpha }_v}}{{\delta }_u\left[2{\alpha }_v+{\delta }_v\left(\frac{1}{{\delta }_u}+1\right)\right]}\hfill \\ \hfill & {\omega }_1\left(ϵ\right)=\frac{{\alpha }_v{k}_1{\left(ϵ\right)}^{-{\alpha }_v}}{{\delta }_u\left({\alpha }_v+\frac{{\delta }_v}{{\delta }_u}\right)}{\omega }_2\left(ϵ\right)=\frac{{\alpha }_v{k}_1{\left(ϵ\right)}^{-2{\alpha }_v}}{{\delta }_u\left(2{\alpha }_v+\frac{{\delta }_v}{{\delta }_u}\right)}\hfill \\ \hfill & {\overline{\omega }}_3\left(ϵ\right)=\frac{{\alpha }_v{k}_1{\left(ϵ\right)}^{-{\alpha }_v}}{{\delta }_u\left[{\alpha }_v+{\delta }_v\left(\frac{2}{{\delta }_u}+1\right)\right]}{\overline{\omega }}_4\left(ϵ\right)=\frac{{\alpha }_v{k}_1{\left(ϵ\right)}^{-2{\alpha }_v}}{{\delta }_u\left[2{\alpha }_v+{\delta }_v\left(\frac{2}{{\delta }_u}+1\right)\right]}\hfill \\ \hfill & {\omega }_3\left(ϵ\right)=\frac{{\alpha }_v{k}_1{\left(ϵ\right)}^{-{\alpha }_v}}{{\delta }_u\left[{\alpha }_v+2\frac{{\delta }_v}{{\delta }_u}\right)]}{\omega }_4\left(ϵ\right)=\frac{{\alpha }_v{k}_1{\left(ϵ\right)}^{-2{\alpha }_v}}{{\delta }_u\left(2{\alpha }_v+2\frac{{\delta }_v}{{\delta }_u}\right)}\hfill \end{array}$$

(18)

2.3. Some Important Results

In this section, following [18], we consider the impact of asymmetry and dependence on the variance of $ϵ$ in each of the four models described above.

First, we observe that for ${\alpha }_v=1$, given that ${\psi }^{\prime }\left(1\right)=\frac{{\pi }^2}{6}$ and $\psi \left(2\right)-\psi \left(1\right)=1$, and by Equation (9), the variance of composite error for the model with dependence and symmetry is given by

$$\begin{array}{c}\hfill V_{ϵ}^{(D,S)}={\delta }_u^2+\frac{{\pi }^2}{3}{\delta }_v^2+{\displaystyle \frac{\theta {\delta }_u{\delta }_v}{2}}\end{array}$$

(19)

Moreover, we highlight that the variance in composite error in the cases of (a) independence and asymmetry and (b) independence and symmetry are given, respectively, by $V_{ϵ}^{(I,A)}={\delta }_u^2+{\delta }_v^2\left[{\psi }^{\prime }\left({\alpha }_v\right)+{\psi }^{\prime }\left(1\right)\right]$ and $V{ϵ}^{(I,S)}={\delta }_u^2+\frac{{\pi }^2}{3}{\delta }_v^2$. Obviously, the variance in the composite error in the case of dependence and asymmetry is $V{ϵ}^{(D,A)}=V\left(ϵ\right)$, as reported in Equation (9). Next, we show the effects of ${\alpha }_v$ on the distribution function of $ϵ$. In the case of maximum positive dependence ($\theta =1$) between u and v, from Figure 1, it is evident that the influence on the tails of the ${\alpha }_v$ is greater in the case of negative asymmetry. With reference to the wrong skewness anomaly, this result is consistent with that found in [18].

3. Empirical Applications of New SF Methodology

We show the strong potentiality of the methodological tools derived in the previous sections by applying the new SF specifications to two economic phenomena. In detail, we use data from Italian airports for estimating production frontiers and data on Italian banks in order to estimate cost efficiency.

3.1. Production Frontiers and Airport Efficiency

The Italian system consists of 47 airports open to commercial aviation. Given the data availability, our models for Italian airports are estimated using annual data on 43 airports for the period 2008–2016, consisting of 17 airports located in the northern part of Italy, 9 in the center and 17 in the southern part, including islands. In 2016, traffic exceeded 10 million passengers per year in three airports, Rome Fiumicino and Milan Malpensa are the most important intercontinental hubs, and Bergamo Orio al Serio. Seven airports can be classified as medium-sized airports (where traffic exceeds 5 million passengers per year but is lower than 10 million), providing further long-haul and domestic routes, such as Milan Linate, Napoli or Rome Ciampino airports. The remaining airports can be classified as small regional airports (where traffic is lower than 5 million passengers), providing a limited number of international and domestic connections.

One important variable for understanding the dimension of airport systems is the Work Load Unit (WLU), which corresponds to one passenger or to one quintal of goods or mail. As already proposed by [31], WLU can be seen as an aggregate output index for airport systems. Traffic and technical airside information have been collected from ENAC (National Civil Aviation Association) and the balance sheets of airport management companies. This information has been integrated with data provided by ICCSAI—International Center for Competitive Studies in the Aviation Industry [32]. Specifically, input variables (i.e., x variables) used in this paper include proxies of capital—number of check-in counters (CHECK, $x_1$), terminal area (TERM, $x_2$) in squared meters and runway length (RUN, $x_3$) in meters—while the amount of WLU is a measure of the output, i.e., y variable (WLU). (Due to lack of data, we abstract from labor input. Moreover, we have not been able to collect the hourly number of landing and taking-off movements due to a lack of data. This variable takes into account both the runway length and the airport’s aviation technology level—e.g., some aviation infrastructure such as ground control radars and runway lighting systems [33]. We then use runway length, given an airport’s aviation technology level, as a proxy of runway capacity following [34,35]) All these continuous variables are taken as logarithms. In detail, the economic model for the production function we estimate is as follows:

$$log\left(y_{it}\right)={\beta }_0+\sum _{j=1}^3{\beta }_{j}log\left(x_{itj}\right)+\frac{1}{2}\sum _{l=1}^3\sum _{m=1}^3{\beta }_{lm}log\left(x_{lit}\right)log\left(x_{mit}\right)+v-u,$$

(20)

where $\beta$s are the parameters to be estimated.

The estimates are shown in

Table 1. Estimated production frontiers on data of Italian airports.

	Classic SF	IS Model	IA Model	DS Model	DA Model
Constant	1.549 ***	1.073 ***	1.148 ***	1.136 ***	1.271 ***
$ln\left(x_1\right)$	1.176 ***	−0.006	−0.023	−0.107	0.100
$ln\left(x_2\right)$	−0.045	0.729 ***	0.661 ***	0.723 ***	0.564 ***
$ln\left(x_3\right)$	1.429 ***	1.074 ***	1.186 ***	1.143 ***	1.308 ***
$ln{\left(x_1\right)}^2$	1.766 *	1.721 **	0.990	2.044 **	0.846
$ln{\left(x_2\right)}^2$	1.159 ***	−0.197	0.078	0.798 **	0.936 ***
$ln{\left(x_3\right)}^2$	0.172	−0.312	0.030	0.388	0.168
$ln\left(x_1\right)ln\left(x_2\right)$	−4.670 ***	0.204	0.195	−2.310 **	−2.737 ***
$ln\left(x_1\right)ln\left(x_3\right)$	2.507 ***	−0.602	−0.111	1.656 **	3.000 ***
$ln\left(x_2\right)ln\left(x_3\right)$	−1.329 **	−0.163	−0.862 *	−1.808 ***	−1.963 ***
${\sigma }^2$	2.947 ***
$\gamma$	0.984 ***
${\delta }_u$		0.661 ***	0.736 ***	0.733 ***	0.756 ***
${\alpha }_v$			3.503 ***		2.825 ***
${\delta }_v$		0.268 ***	0.284 ***	0.288 ***	0.315 ***
${\theta }_{FGM}$				0.929 ***	0.673 *
Mean efficiency	0.4255	0.6211	0.6022	0.5858	0.5865
Log-Lik	−512.1404	−461.96	−446.31	−454.45	−435.42
Obs	379	379	379	379	379
k	12	12	13	13	14
AIC	1048.28	947.93	918.62	934.90	898.84

Significance levels: 0 ‘***’ 0.05 ‘**’ 0.1 ‘*’. Our elaborations on data are from ENAC and ICSSAI.

, and they were realized using the software R-project. (In order to avoid problems arising from different units of measurement, we standardize all the continuous variables included in the frontiers.)

In the first block of the table, there are the estimated coefficients of the deterministic component of the production frontiers. The significance of the coefficients varies across models. It remains quite robust in our best specifications, which are the DS and DA models.

In this regard, in order to make comparisons among models, we employ the Akaike Information Criterion (AIC). Ref. [36] employs the measure ${\Delta }_i=AI{C}_i-AI{C}_{min}$ and considers that models having ${\Delta }_i\le 2$ are supported by substantial evidence, those for which $4\le {\Delta }_i\le 7$ have less support and those for which ${\Delta }_i>10$ have no support. By using the AIC statistic, we find that our full DA model is preferable with respect to the others, especially with respect to the classic SF estimation. It is worth noticing that the gamma parameter for the classic SFA is equal to $\frac{{{\sigma }_u}^2}{\sigma {}^2}$, which is the ratio between the variance of the inefficiency component and the variance of the composite error. The estimated value of gamma is 0.984, which confirms the importance of the inefficiency component in explaining the deviations in economic units from the efficient frontier.

In the best specification (DA model), first-order coefficients of the Translog frontier are all statistically significant, with the exception of the number of check-ins (CHECK). The same happens for the second-order coefficients. Further, all interaction effects are statistically significant as a confirmation of the multi-output features of airport activity. As for the estimated parameters of the error components, we find evidence of strong and significant dependence between the random error and the inefficiency component. In fact, the association measure of the FGM copula (${\theta }_{FGM}$) is always greater than 0.673, and also, in the DS model, we estimate a strong dependence between u and v (0.929), providing support to the existence of dependence in our sample.

Finally, the asymmetry parameter of the random error v, ${\alpha }_v$, is fairly greater than 1 in both specifications IA and DA, meaning a positive skewness of v.

It is worth noticing that when we implement our four specifications, there are noticeable differences in the estimated average efficiency scores.

3.2. The Cost Efficiency of the Banking System

The data used were extracted from the Italian Banking Association Banking Data (ABI), which provides the balance sheets of Italian banks. Data are for 2011. The variables we include in the model are selected according to the intermediation approach [37,38]. In order to show the new SF specifications for cost efficiency, we estimate Cobb–Douglas cost frontiers using the total costs as the dependent variable of our models. In detail, we follow the approach of [39,40].

Indeed, our dependent variable, $Cost(y,w)$, is the total cost of each bank. It is the sum of administrative expenses, interest expense, operating expenses, commission expenses and depreciation of fixed assets.

As for the specification of the deterministic component of the cost frontier for banks, we consider loans to customers ($y_1$) as the main banking output. Moreover, as requested by the intermediation approach, we introduce another output, which is the non-interest income or commission income ($y_2$). (The choice of this output lies in consideration of the range of non-traditional «collateral» services for which banks obtain positive gains [39,40]). The third output used in our model is the amount of securities ($y_3$), which is the sum of loans to other banks, equities and bonds. From the side of inputs, we employ labor, capital and deposits. In detail, labor is measured as the number of employees of individual banks, and the cost of labor is calculated as the ratio of personnel expenses to the number of employees ($w_l$). As in [39,40], the cost of capital ($w_k$) is measured as the ratio of expenses that are not considered in the other input variables in the frontier model and the banking product. Specifically, the numerator includes administrative expenses (excluding personnel expenses), operating expenses, the interest expense net of interest on amounts due to customers, depreciation of fixed assets and commission expenses. (The administrative expenses include cost items, such as those relating to electricity, rent and maintenance of various types) Finally, the third input is given by the deposits from customers. Thus, the cost of deposits is given by the ratio of interest paid to customers and the total amount of deposits ($w_d$).

As suggested by the theoretical framework, we consider the homogeneity of the cost functions with respect to the input prices. Therefore, we estimate the following model:

$$\begin{array}{c}\hfill log\left(\frac{Cost}{w_d}\right)={\beta }_0+\sum _{j=1}^3{\beta }_{j}log\left(y_j\right)+\sum _{n=l}^k{\gamma }_{n}log\left(\frac{w_n}{w_d}\right)+u+v,\end{array}$$

(21)

The estimates, shown in

Table 2. Estimated cost frontiers for Italian banks in 2011.

	Classic SF	IS Model	IA Model	DS Model	DA Model
Constant	−0.816 ***	−1.044 ***	−1.512 ***	−0.811 ***	−0.937 ***
$log\left(loans\right)$	0.315 ***	0.421 ***	0.427 ***	0.437 ***	0.438 ***
$log\left(commincome\right)$	0.488 ***	0.424 ***	0.421 ***	0.404 ***	0.410 ***
$log\left(securities\right)$	0.098 ***	0.085 ***	0.086 ***	0.093 ***	0.091 ***
$log\left(\frac{w_l}{w_d}\right)$	0.720 ***	0.672 ***	0.721 ***	0.625 ***	0.633 ***
$log\left(\frac{w_k}{w_d}\right)$	0.258 ***	0.317 ***	0.275 ***	0.360 ***	0.359 ***
${\sigma }^2$	0.158 ***
$\gamma$	0.832 ***
${\delta }_u$		0.193 ***	0.204 ***	0.206 ***	0.223 ***
${\alpha }_v$			0.295 ***		0.224 **
${\delta }_v$		0.070 ***	0.031 ***	0.074 ***	0.027 **
${\theta }_{FGM}$				−0.474	−0.637
Mean efficiency	0.7811	0.8477	0.7295	0.8388	0.6854
Log-Lik	−52.88	59.64	77.94	66.42	91.40
Obs	621	621	621	621	621
k	8	8	9	9	10
AIC	121.76	−103.29	−137.89	−114.84	−162.79

Significance levels: 0 ‘***’ 0.05 ‘**’. Our elaborations on data from ABI.

, were realized using the software R-project. The estimated elasticities of the Cobb–Douglas frontier are all significant in all specifications. In detail, they signal decreasing returns to scale of the cost frontiers. This finding is robust across models. As regards the classic SF, the estimated gamma parameter is equal to 0.832, which also, in this case, confirms the importance of the inefficiency component in explaining the deviations from the efficient frontier.

By also using the AIC criterion for the Italian banks, the DA model results in the best specification, even if we reject the hypothesis of dependence. In fact, in both DS and DA models, we estimate a negative but not significant ${\theta }_{FGM}$ parameter. As regards the shape parameter ${\alpha }_v$, in both models IA and DA, the estimated value is less than 1, indicating a negative asymmetry of the random error v.

4. Conclusions

In this paper, we analytically derive a generalization of the stochastic frontier approach. In particular, we introduce (i) the dependence between the two error components through copula functions and (ii) the asymmetry of the random error assigning a generalized logistic distribution. With respect to [18], the main methodological contribution of the work is related to the analytical derivations of the density function of the composite error for cost frontier and also the writing of the mathematical expressions for both cost and production efficiency scores. In the two empirical applications, we demonstrate that the new specifications significantly improve the standard SF estimations. In detail, we find that, from a statistical point of view, the best specification is the model that is able to capture both the asymmetry of the random error and the dependence between the inefficiency and the accidental term. From our findings, different strands of research could be deepened in the future. In particular, it is worth noticing that both the temporal and spatial dimensions could be introduced in this framework, with the aim of further extending the generalization proposed in this paper.