Finite-Time Stability of a Second-Order Bang–Bang Sliding Control Type
Abstract
:1. Introduction
1.1. Motivation
1.2. Contribution
1.3. Manuscript Organization
1.4. Notation and Definitions
2. Problem Statement
3. Strictly Lyapunov Function for Stability Analysis
- P1
- Function V is strictly positive definite for all
- P2
- The time derivative of function V can be upper-bounded as follows:
- P3
- Function V is absolutely continuous, strictly positive definite, and differentiable for all . Given its obviousness, this property is not discussed here.
4. Numerical Simulations
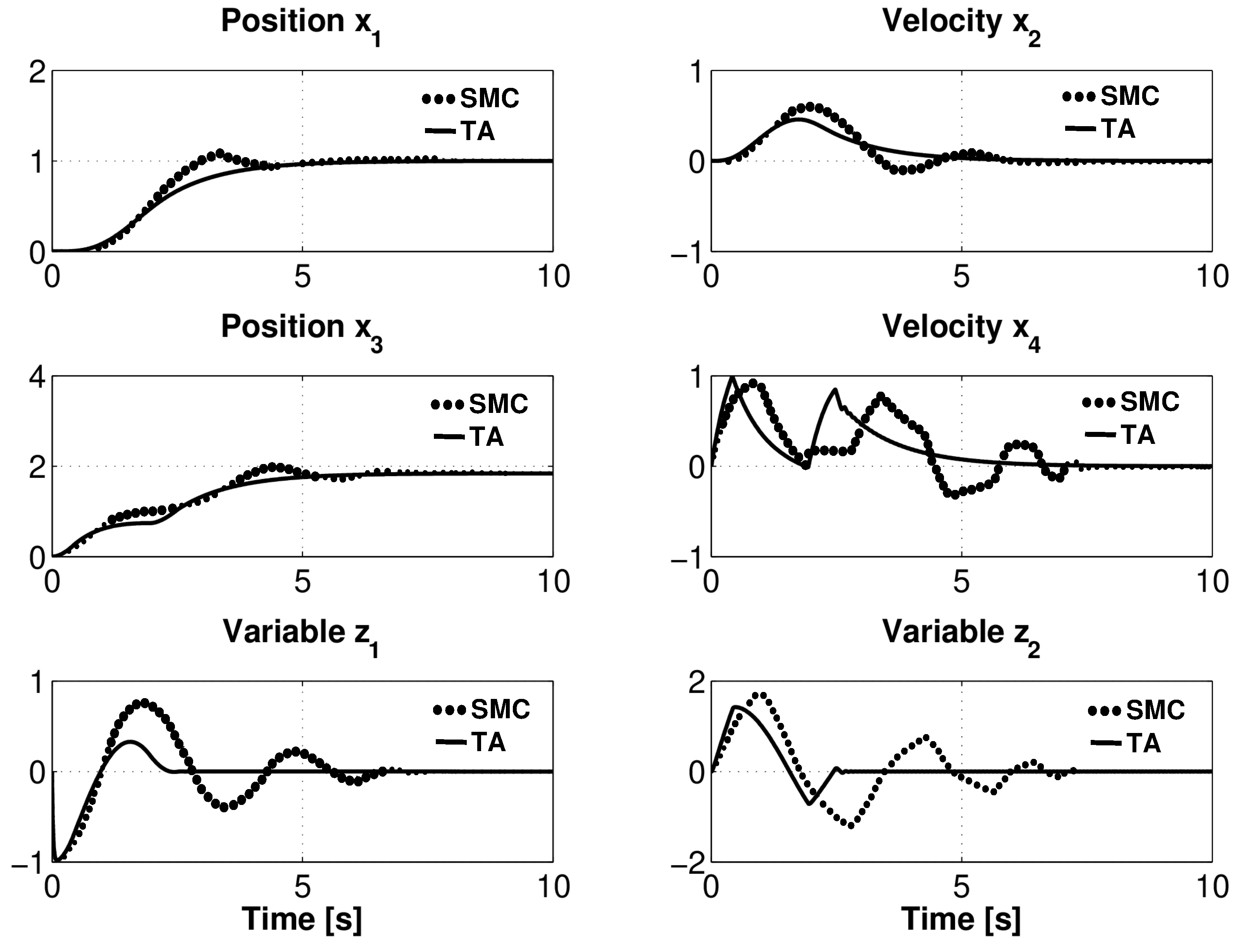
4.1. Flexible Manipulator
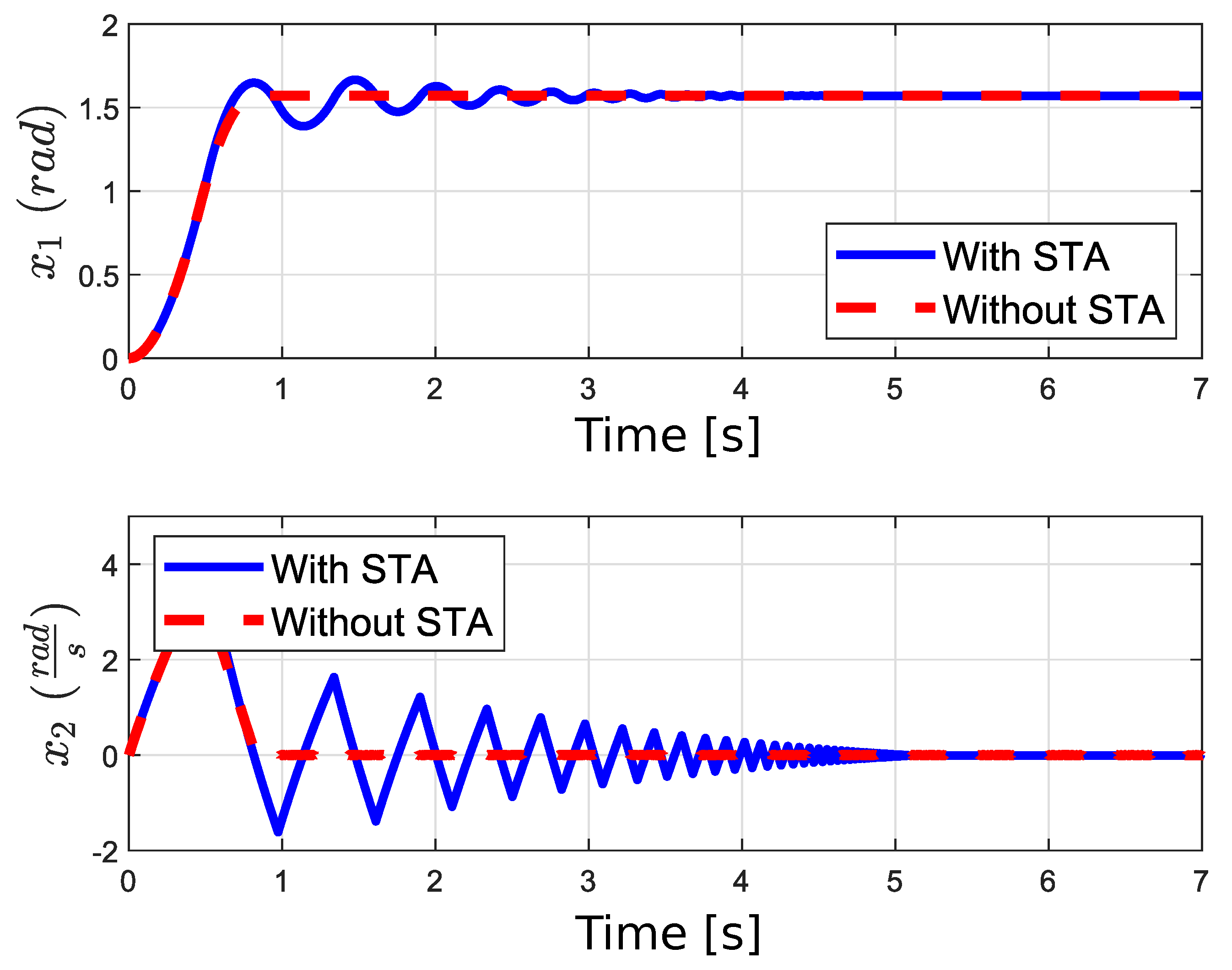
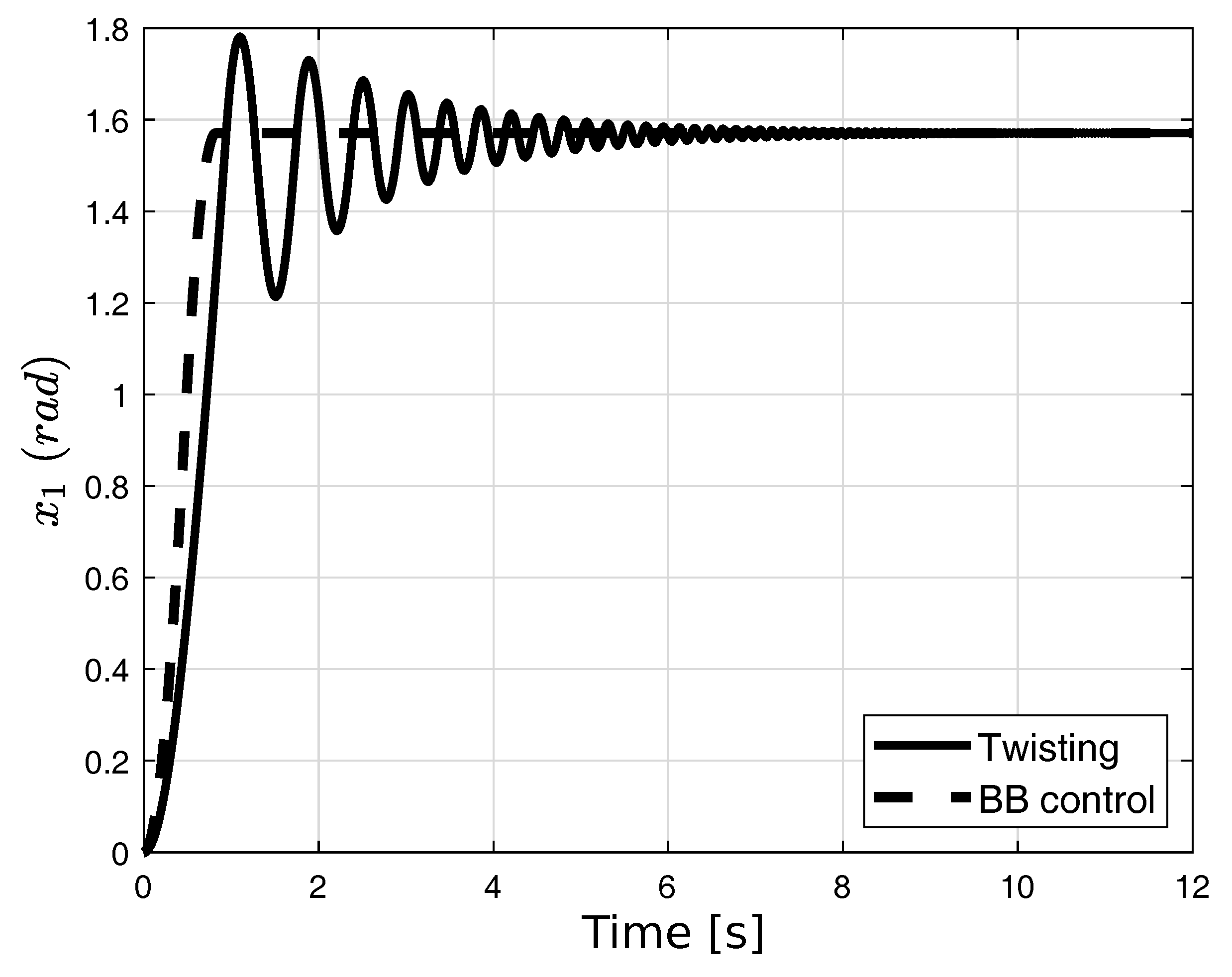
4.2. Simple Pendulum
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Proof of Homogeneity
Appendix A.2. V Is Strictly Positive and Proper
Appendix A.3. Proof of the Inequality (uid16)
References
- Utkin, V.I. Sliding Modes in Control and Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Sira-Ramirez, H. On the dynamical sliding mode control of nonlinear systems. Int. J. Control 1993, 57, 1039–1061. [Google Scholar] [CrossRef]
- Edwards, C.; Spurgeon, S. Sliding Mode Control: Theory and Applications; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Shtessel, Y.; Edwards, C.; Fridman, L.; Levant, A. Sliding Mode Control and Observation; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Filippov, A.F.; Arscott, F.M. Differential Equations with Discontinuous Righthand Sides: Control Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1988; Volume 18. [Google Scholar]
- Orlov, Y.V. Discontinuous Systems: Lyapunov Analysis and Robust Synthesis under Uncertainty Conditions; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Levant, A. Robust exact differentiation via sliding mode technique. Automatica 1998, 34, 379–384. [Google Scholar] [CrossRef]
- Davila, J.; Fridman, L.; Levant, A. Second-order sliding-mode observer for mechanical systems. IEEE Trans. Autom. Control 2005, 50, 1785–1789. [Google Scholar] [CrossRef]
- Levant, A. Homogeneity approach to high-order sliding mode design. Automatica 2005, 41, 823–830. [Google Scholar] [CrossRef]
- Moreno, J.A.; Osorio, M. A Lyapunov approach to second-order sliding mode controllers and observers. In Proceedings of the 2008 47th IEEE Conference on Decision and Control, Cancún, Mexico, 9–11 December 2008; pp. 2856–2861. [Google Scholar]
- Cruz-Zavala, E.; Sanchez, T.; Nuño, E.; Moreno, J.A. Lyapunov-based finite-time control of robot manipulators. Int. J. Robust Nonlinear Control 2021, 31, 3090–3114. [Google Scholar] [CrossRef]
- Polyakov, A.; Poznyak, A. Lyapunov function design for finite-time convergence analysis: “Twisting” controller for second-order sliding mode realization. Automatica 2009, 45, 444–448. [Google Scholar] [CrossRef]
- Polyakov, A.; Poznyak, A.S. Method of Lyapunov Functions for Systems with Higher-Order Sliding Modes; Springer: Berlin/Heidelberg, Germany, 2011; Volume 72, pp. 944–963. [Google Scholar]
- Cruz-Zavala, E.; Moreno, J.A. Levant’s arbitrary-order exact differentiator: A Lyapunov approach. IEEE Trans. Autom. Control 2018, 64, 3034–3039. [Google Scholar] [CrossRef]
- Rueda-Escobedo, J.G.; Moreno, J.A. Strong Lyapunov functions for two classical problems in adaptive control. Automatica 2021, 124, 109250. [Google Scholar] [CrossRef]
- Mercado-Uribe, A.; Moreno, J.A.; Polyakov, A.; Efimov, D. Integral control design using the implicit lyapunov function approach. In Proceedings of the 2019 IEEE 58th Conference on Decision and Control (CDC), Nice, France, 11–13 December 2019; pp. 3316–3321. [Google Scholar]
- Castillo, I.; Steinberger, M.; Fridman, L.; Moreno, J.A.; Horn, M.A. Lyapunov based Saturated Super-Twisting Algorithm. In Emerging Trends in Sliding Mode Control; Springer: Berlin/Heidelberg, Germany, 2021; pp. 47–68. [Google Scholar]
- Polyakov, A.; Efimov, D.; Perruquetti, W. Finite-time and fixed-time stabilization: Implicit Lyapunov function approach. Automatica 2015, 51, 332–340. [Google Scholar] [CrossRef] [Green Version]
- Polyakov, A.; Efimov, D.; Perruquetti, W. Finite-time stabilization using implicit lyapunov function technique. In Proceedings of the IFAC Nolcos 2013, Toulouse, France, 4–6 September 2013. [Google Scholar]
- Polyakov, A.; Efimov, D.; Perruquetti, W.; Richard, J.P. Implicit lyapunov-krasovski functionals for time delay systems. In Proceedings of the Conference on Decision and Control, Los Angeles, CA, USA, 15–17 December 2014. [Google Scholar]
- Wang, X.; Yau, S.; Huang, J. A study of tracking-differentiator. In Proceedings of the 39th IEEE Conference on Decision and Control, Sydney, Australia, 12–15 December 2000; Volume 5, pp. 4783–4784. [Google Scholar]
- Sun, D. Comments on active disturbance rejection control. IEEE Trans. Ind. Electron. 2007, 6, 3428–3429. [Google Scholar]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Bernuau, E.; Efimov, D.; Perruquetti, W.; Polyakov, A. On homogeneity and its application in sliding mode control. J. Frankl. Inst. 2014, 351, 1866–1901. [Google Scholar] [CrossRef] [Green Version]
- Bhat, S.P.; Bernstein, D.S. Finite-time stability of continuous autonomous systems. SIAM J. Control Optim. 2000, 38, 751–766. [Google Scholar] [CrossRef]
- Sage, A.P.; White, C.C. Optimum Systems Control; Prentice-Hall Englewood Cliffs: Hoboken, NJ, USA, 1977; Volume 2. [Google Scholar]
- Emaru, T.; Tsuchiya, T. Research on estimating smoothed value and differential value by using sliding mode system. IEEE Trans. Robot. Autom. 2003, 19, 391–402. [Google Scholar] [CrossRef]
- Orlov, Y.; Aoustin, Y.; Chevallereau, C. Finite time stabilization of a perturbed double integrator—Part I: Continuous sliding mode-based output feedback synthesis. IEEE Trans. Autom. Control 2011, 56, 614–618. [Google Scholar] [CrossRef]
- Bacciotti, A.; Rosier, L. Liapunov Functions and Stability in Control Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Poznyak, A.S. Advanced Mathematical Tools for Automatic Control Engineers: Stochastic Techniques; Elsevier Science: Amsterdam, The Netherlands, 2009; Volume 2. [Google Scholar]
- Estrada, A.; Loria, A.; Santiesteban, R.; Fridman, L. Cascaded-based stabilization of time-varying systems using second-order sliding modes. IMA J. Math. Control Inf. 2013, 30, 115–128. [Google Scholar] [CrossRef] [Green Version]
- Riachy, S.; Orlov, Y.; Floquet, T.; Santiesteban, R.; Richard, J.P. Second-order sliding mode control of underactuated mechanical systems I: Local stabilization with application to an inverted pendulum. Int. J. Robust Nonlinear Control 2008, 18, 529–543. [Google Scholar] [CrossRef]



| Perturbation | |
|---|---|
| 2.087 | |
| 1.939 | |
| 1.851 | |
| 1.996 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aguilar-Ibanez, C.; Salgado Ramos, I.J.; Suarez-Castanon, M.S.; Rubio, J.d.J.; Meda-Campana, J.A. Finite-Time Stability of a Second-Order Bang–Bang Sliding Control Type. Mathematics 2022, 10, 3937. https://doi.org/10.3390/math10213937
Aguilar-Ibanez C, Salgado Ramos IJ, Suarez-Castanon MS, Rubio JdJ, Meda-Campana JA. Finite-Time Stability of a Second-Order Bang–Bang Sliding Control Type. Mathematics. 2022; 10(21):3937. https://doi.org/10.3390/math10213937
Chicago/Turabian StyleAguilar-Ibanez, Carlos, Ivan J. Salgado Ramos, Miguel S. Suarez-Castanon, Jose de Jesus Rubio, and Jesus A. Meda-Campana. 2022. "Finite-Time Stability of a Second-Order Bang–Bang Sliding Control Type" Mathematics 10, no. 21: 3937. https://doi.org/10.3390/math10213937
APA StyleAguilar-Ibanez, C., Salgado Ramos, I. J., Suarez-Castanon, M. S., Rubio, J. d. J., & Meda-Campana, J. A. (2022). Finite-Time Stability of a Second-Order Bang–Bang Sliding Control Type. Mathematics, 10(21), 3937. https://doi.org/10.3390/math10213937








