Convergence Criteria of a Three-Step Scheme under the Generalized Lipschitz Condition in Banach Spaces
Abstract
:1. Introduction
2. Special and Generalized Lipschitz Conditions
- (i)
- If satisfies the radius-Lipschitz condition with κ-averagein which , , and κ and are positive integrable, then
- (ii)
- If satisfies the center-Lipschitz condition with -averagein which is ND, then we obtain
3. Ball Convergence
4. Uniqueness Ball
5. Convergence under the Weak -Average
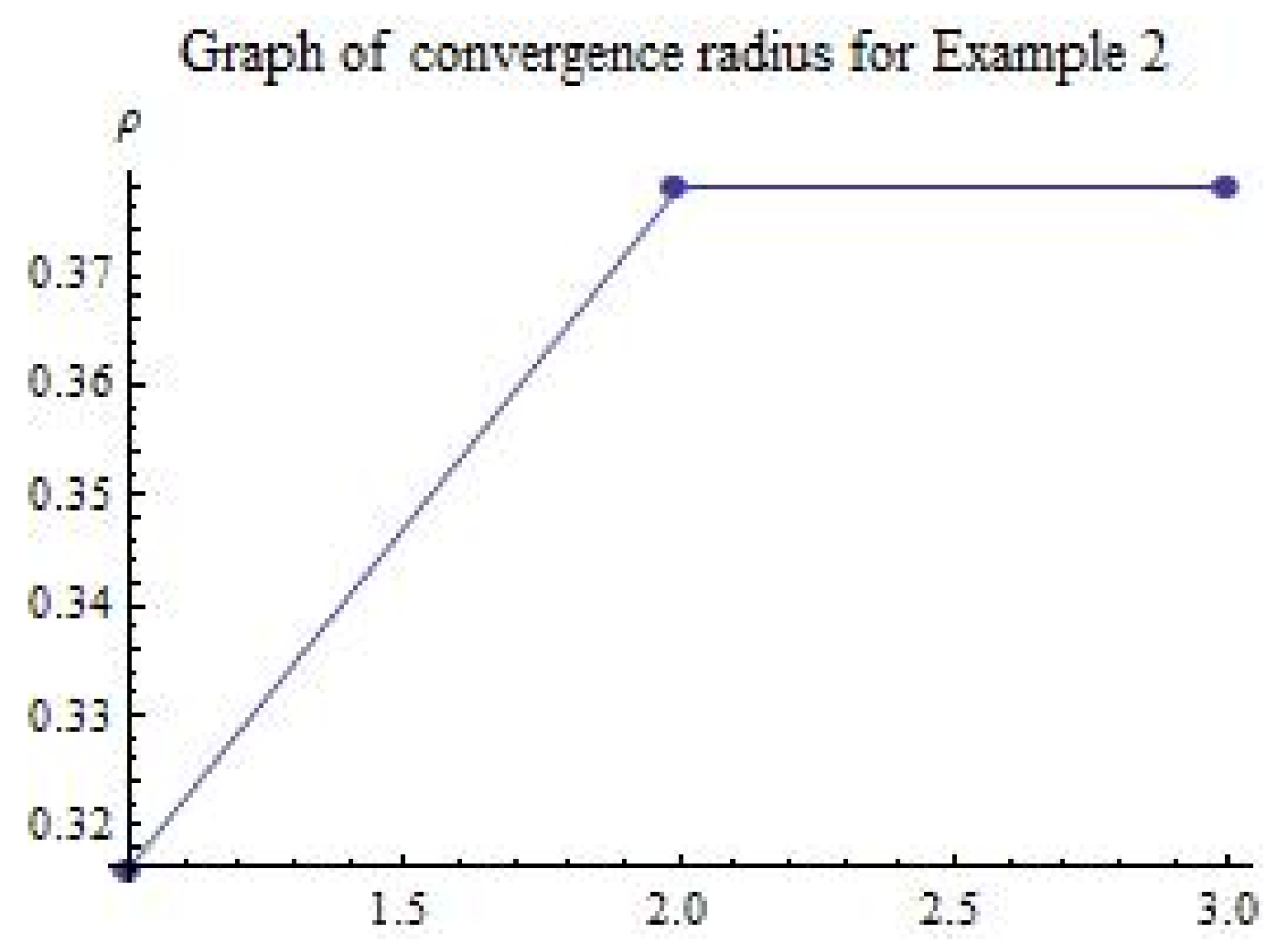
6. Numerical Examples
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ortega, J.M.; Rheinboldt, W.C. Iterative Solution of Nonlinear Equations in Several Variables; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2000. [Google Scholar]
- Kantorovich, L.V.; Akilov, G.P. Functional Analysis; Pergamon Press: Oxford, UK, 1982. [Google Scholar]
- Argyros, I.K. The Theory and Applications of Iteration Methods, 2nd ed.; Engineering Series CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar]
- Argyros, I.K.; Magreñán, Á.A. Iterative Methods and Their Dynamics with Applications: A Contemporary Study; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Ezquerro, J.A.; Gutiérrez, J.M.; Hernández, M.A.; Romero, N.; Rubio, M.J. The Newton Method: From Newton to Kantorovich. Gac. R. Soc. Mat. Esp. 2010, 13, 53–76. (In Spanish) [Google Scholar]
- Ezquerro, J.A.; Hernandez, M.A. Newton’s Scheme: An Updated Approach of Kantorovich’s Theory; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Proinov, P.D. General local convergence theory for a class of iterative processes and its applications to Newton’s method. J. Complex. 2009, 25, 38–62. [Google Scholar] [CrossRef] [Green Version]
- Rall, L.B. Computational Solution of Nonlinear Operator Equations; Robert, E., Ed.; Krieger Publishing Company: New York, NY, USA, 1979. [Google Scholar]
- Ren, H.; Argyros, I.K. On the complexity of extending the convergence ball of Wang’s method for finding a zero of a derivative. J. Complex. 2021, 64, 101526. [Google Scholar] [CrossRef]
- Saxena, A.; Argyros, I.K.; Jaiswal, J.P.; Argyros, C.; Pardasani, K.R. On the Local convergence of two-step Newton type Method in Banach Spaces under generalized Lipschitz Conditions. Mathematics 2021, 9, 669. [Google Scholar] [CrossRef]
- Verma, R.U. New Trends in Fractional Programming; Nova Science Publishers: New York, NY, USA, 2019. [Google Scholar]
- Wang, X. Convergence of Newton’s method and uniqueness of the solution of equations in Banach space. IMA J. Numer. Anal. 2000, 20, 123–134. [Google Scholar] [CrossRef] [Green Version]
- Homeier, H.H.H. On Newton-type methods with cubic convergence. J. Comput. Appl. Math. 2005, 176, 425–432. [Google Scholar] [CrossRef] [Green Version]
- Kou, J.; Li, Y.; Wang, X. A modification of Newton method with third-order convergence. Appl. Math. Comput. 2006, 181, 1106–1111. [Google Scholar] [CrossRef]
- Nazeer, W.; Tanveer, M.; Kang, S.M.; Naseem, A. A new Householder’s method free from second derivatives for solving nonlinear equations and polynomiography. J. Nonlinear Sci. Appl. 2016, 9, 998–1007. [Google Scholar] [CrossRef] [Green Version]
- Traub, J.F. Iterative Methods for the Solution of Equations; Chelsea Publishing Company: New York, NY, USA, 1977. [Google Scholar]
- Zhanlav, T.; Chuluunbaatar, O.; Ankhbayar, G. On Newton-type methods with fourth and fifth-order convergence. Discret. Contin. Model. Appl. Comput. Sci. 2010, 2, 30–35. [Google Scholar]
- Sulaiman, I.M.; Mamat, M.; Owoyemi, A.E.; Ghazali, P.L.; Rivaie, M.; Malik, M. The convergence properties of some descent conjugate gradient algorithms for optimization models. J. Math. Comput. Sci. 2021, 22, 204–215. [Google Scholar] [CrossRef]
- Chen, J.; Li, W. Convergence behaviour of inexact Newton methods under weak Lipschitz condition. J. Comput. Appl. Math. 2006, 191, 143–164. [Google Scholar] [CrossRef] [Green Version]
- Kanwar, V.; Kukreja, V.K.; Singh, S. On some third-order iterative methods for solving nonlinear equations. Appl. Math. Comput. 2005, 171, 272–280. [Google Scholar]
- Magreñán, Á.A.; Argyros, I. A Contemporary Study of Iterative Methods; Elsevier: Amsterdam, The Netherlands; Academic Press: New York, NY, USA, 2018. [Google Scholar]
- Sharma, D.; Parhi, S.K. On the local convergence of modified Weerakoon’s method in Banach spaces. J. Anal. 2020, 28, 867–877. [Google Scholar] [CrossRef]
- George, S.; Argyros, I.K.A.; Jidesh, P. On the local convergence of Newton-like methods with fourth and fifth–order of convergence under hypotheses only on the first Frechet derivative. Novi Sad J. Math. 2017, 47, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.H.; Li, C. Convergence of Newton’s method and uniqueness of the solution of equations in Banach spaces II. Acta Math. Sin. 2003, 19, 405–412. [Google Scholar] [CrossRef]
- Shakhno, S. On a two-step iterative process under generalized Lipschitz conditions for first-order divided differences. J. Math. Sci. 2010, 168, 576–584. [Google Scholar] [CrossRef]
- Cǎtinaş, E. The inexact, inexact perturbed, and quasi-Newton methods are equivalent models. Math. Comput. 2005, 74, 291–301. [Google Scholar] [CrossRef]
- Magreñán, Á.A.; Gutiérrez, J.M. Real dynamics for damped Newton’s method applied to cubic polynomials. J. Comput. Appl. Math. 2015, 275, 527–538. [Google Scholar] [CrossRef]
- Potra, F.A.; Pták, V. Non-Discrete Induction and Iterative Processes; Research Notes in Mathematics; Pitman (Advanced Publishing Program): Boston, MA, USA, 1984. [Google Scholar]
- Singh, S.; Martínez, E.; Maroju, P.; Behl, R. A study of the local convergence of a fifth order iterative method. Indian J. Pure Appl. Math. 2020, 51, 439–455. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saxena, A.; Jaiswal, J.P.; Pardasani, K.R.; Argyros, I.K. Convergence Criteria of a Three-Step Scheme under the Generalized Lipschitz Condition in Banach Spaces. Mathematics 2022, 10, 3946. https://doi.org/10.3390/math10213946
Saxena A, Jaiswal JP, Pardasani KR, Argyros IK. Convergence Criteria of a Three-Step Scheme under the Generalized Lipschitz Condition in Banach Spaces. Mathematics. 2022; 10(21):3946. https://doi.org/10.3390/math10213946
Chicago/Turabian StyleSaxena, Akanksha, Jai Prakash Jaiswal, Kamal Raj Pardasani, and Ioannis K. Argyros. 2022. "Convergence Criteria of a Three-Step Scheme under the Generalized Lipschitz Condition in Banach Spaces" Mathematics 10, no. 21: 3946. https://doi.org/10.3390/math10213946
APA StyleSaxena, A., Jaiswal, J. P., Pardasani, K. R., & Argyros, I. K. (2022). Convergence Criteria of a Three-Step Scheme under the Generalized Lipschitz Condition in Banach Spaces. Mathematics, 10(21), 3946. https://doi.org/10.3390/math10213946





