Speed Fluctuation Suppression Strategy of Servo System with Flexible Load Based on Pole Assignment Fuzzy Adaptive PID
Abstract
:1. Introduction
2. Modeling of a Servo System with Flexible Load
- The shear deformation and axial deformation are ignored, and only the deformation caused by transverse vibration is considered;
- The transverse deformation is small deformation;
- The beam is much longer than its cross-section size.
3. System Control Policy and Parameter Tuning
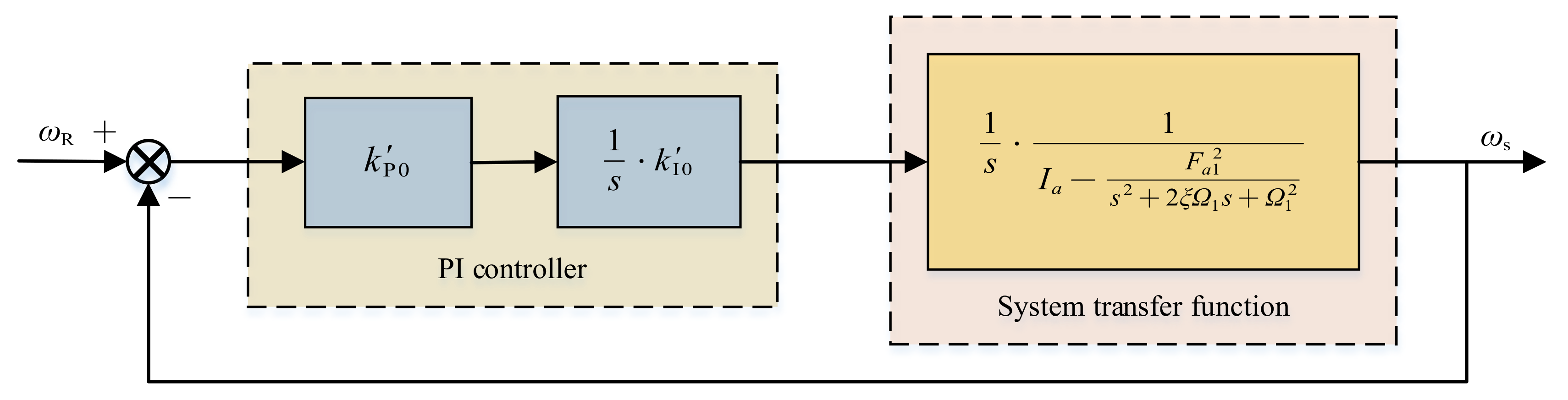
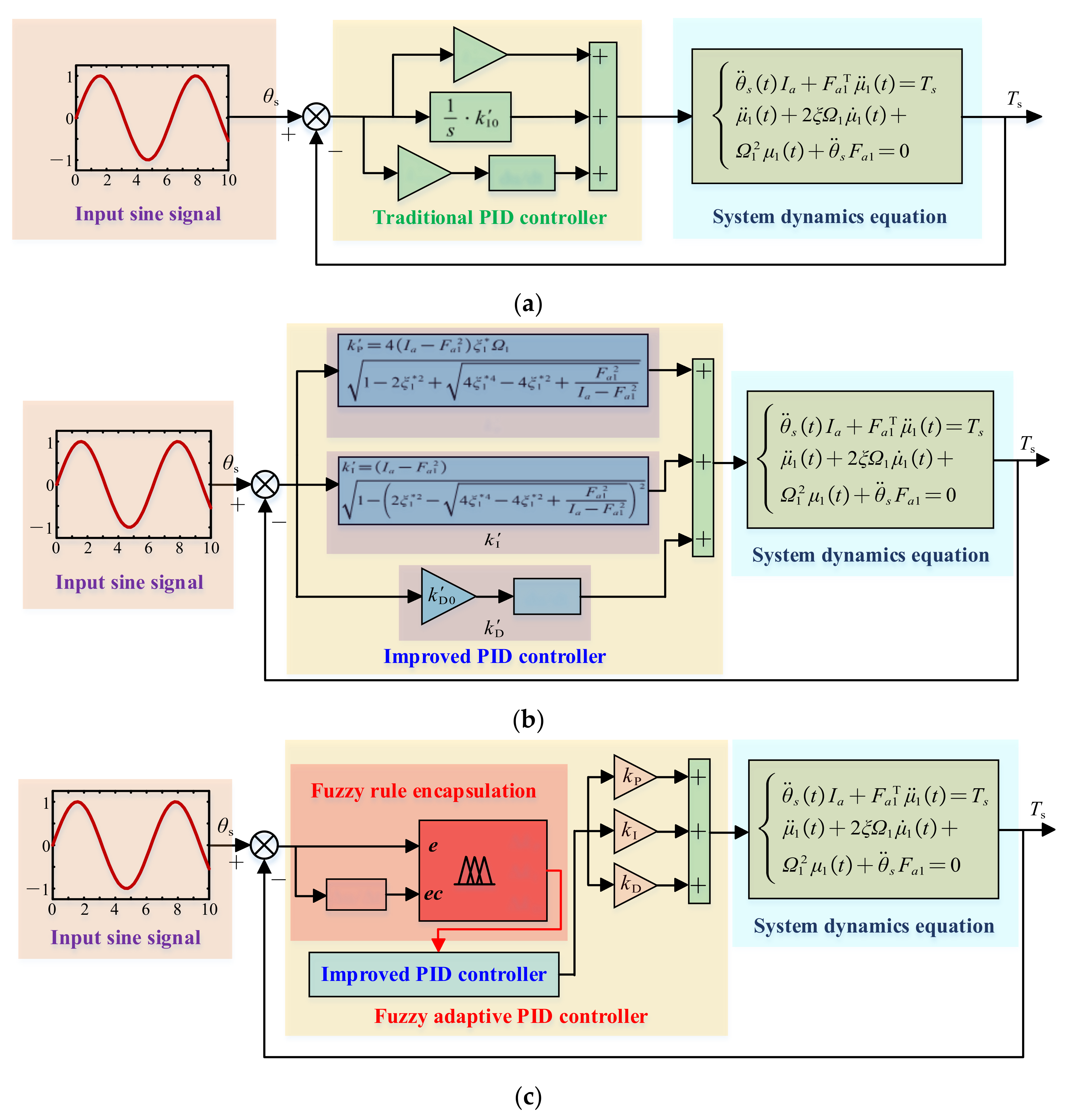
3.1. Design of Servo System Controller Considering Speed Loop
3.2. The Same Real-Part Pole Assignment Method Is Used to Set PI Parameters
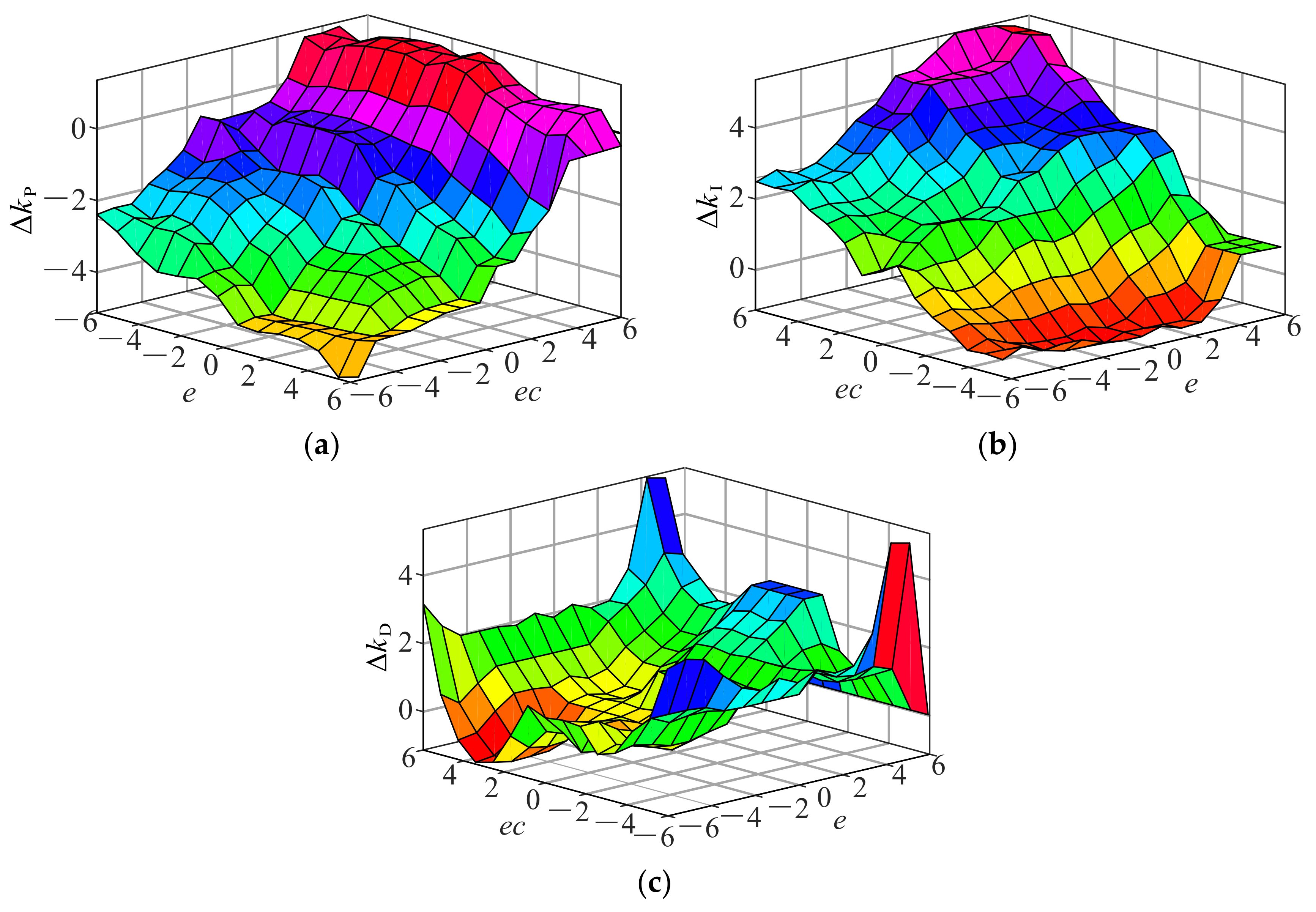
3.3. Fuzzy Adaptive Control Strategy Combined with Pole Assignment
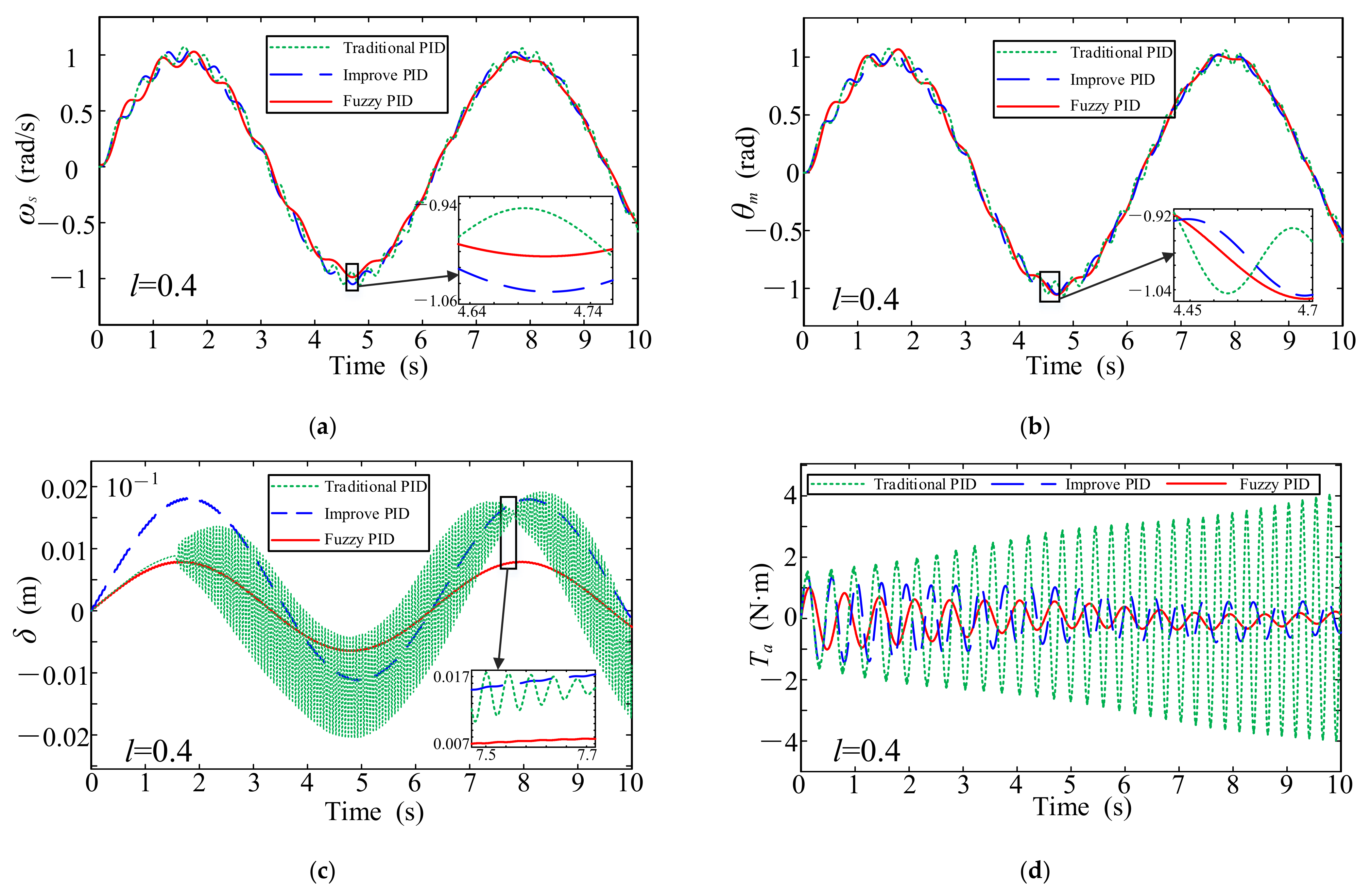
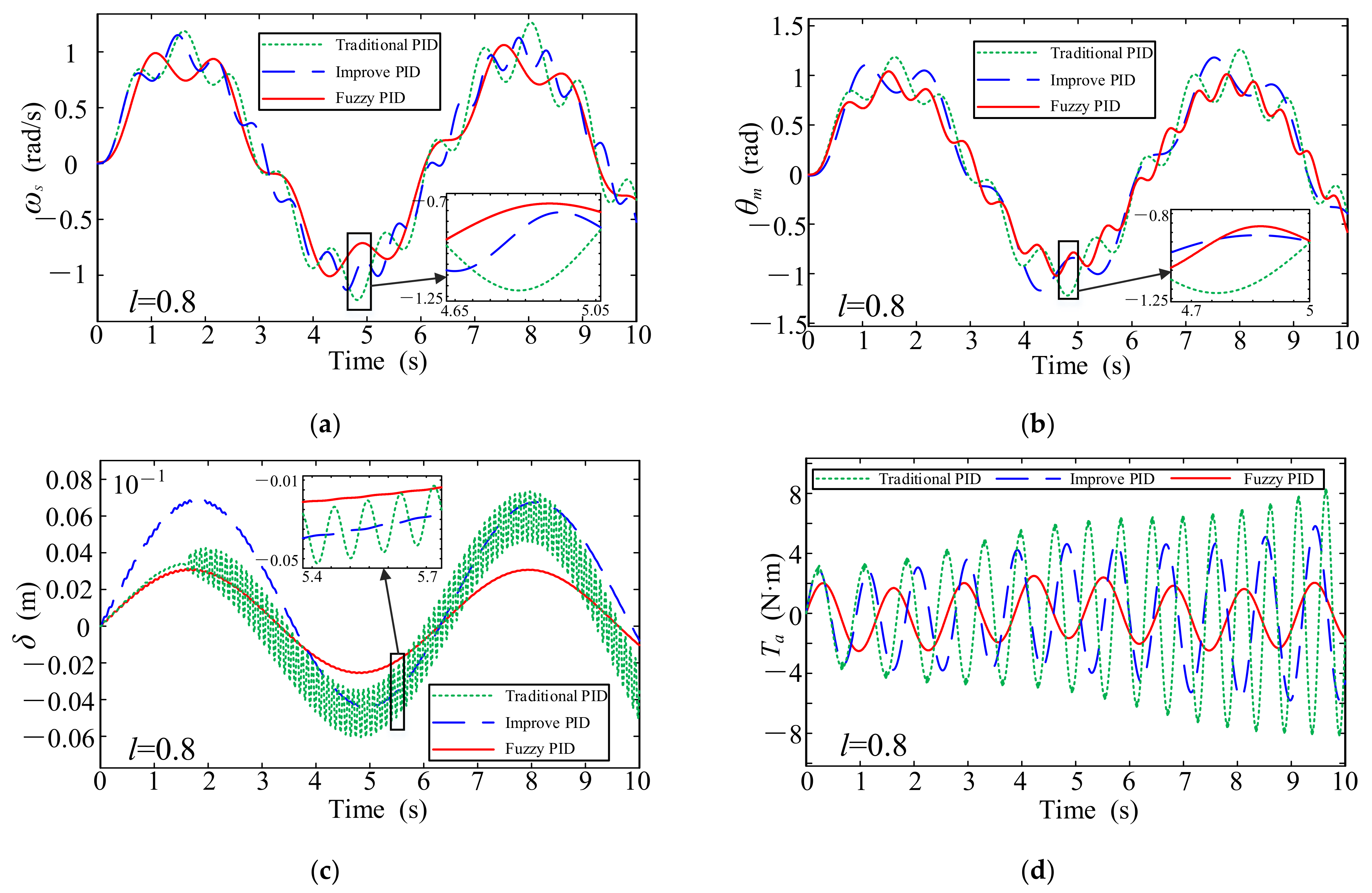
4. Numerical Simulation Analysis of the System
5. Conclusions
- (1)
- The dynamic modeling of the servo-driven flexible-load system established in this paper takes into account that the flexibility in the load will cause significant fluctuations in the system speed output, which will cause a large deviation in the system angle and displacement output. The unified dynamic model of the system is established.
- (2)
- The proposed fuzzy adaptive tuning PID control strategy combined with pole assignment is based on the traditional PID parameters. Firstly, the same real-part pole assignment method is used to adjust PI parameters, and then the fuzzy adaptive control strategy is applied to adjust the adjusted PID parameters to adjust the input variables of the system in real time. The simulation results show that the control strategy is stable and reliable when used to suppress system vibration.
- (3)
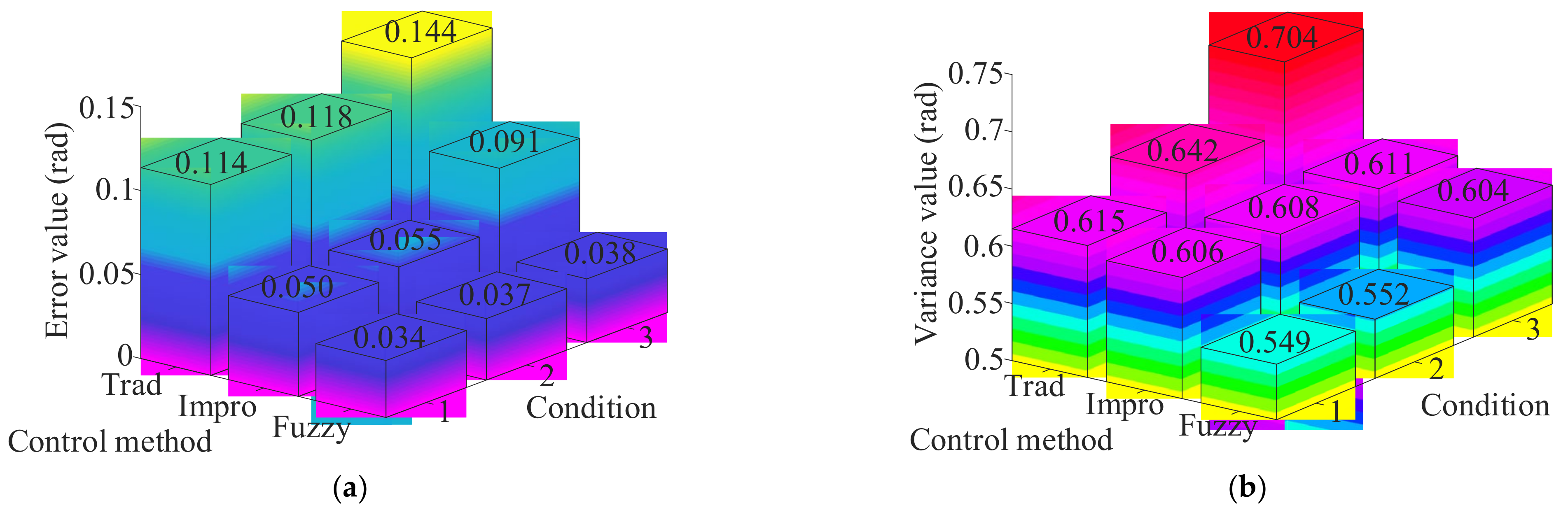
- By comparing the system output angle error and flexible load terminal deformation under three different working conditions, it can be seen that the system angle error and flexible load deformation increase with the increase of flexible load length. The control strategy proposed in this paper can reduce the system output angle error and the deformation of the flexible load by 10% on average. From the angle of error analysis, it is proved that the control strategy proposed in this paper can effectively reduce the speed fluctuation of the servo-driven flexible-load system and improve the working accuracy of the system.
Author Contributions
Funding
Conflicts of Interest
References
- Wu, J.J.; Zhang, Z.K. An Improved Procedure for Manufacture of 3D Tubes with Springback Concerned in Flexible Bending Process. Chin. J. Aeronaut. 2021, 34, 267–276. [Google Scholar] [CrossRef]
- He, W.; Meng, T.T.; He, X.Y.; Sun, C.Y. Iterative Learning Control for a Flapping Wing Micro Aerial Vehicle Under Distributed Disturbances. IEEE Trans. Cybern. 2019, 49, 1524–1535. [Google Scholar] [CrossRef] [PubMed]
- McGarry, L.; Butterfield, J.; Murphy, A. Assessment of ISO Standardisation to Identify an Industrial Robot’s Base Frame. Robot. Comput. Integr. Manuf. 2022, 74, 102275. [Google Scholar] [CrossRef]
- Stefano, M.D.; Balachandran, R.; Secchi, C. A Passivity-Based Approach for Simulating Satellite Dynamics with Robots: Discrete-Time Integration and Time-Delay Compensation. IEEE Trans. Rob. 2020, 36, 189–203. [Google Scholar] [CrossRef] [Green Version]
- Efafi, M.; Hosseini, S.A.A.; Tourajizadeh, H. Robust Control and Vibration Reduction of a 3D Nonlinear Flexible Robotic Arm. Iran. J. Sci. Technol. Trans. Mech. Eng. 2022, 144, 1–7. [Google Scholar] [CrossRef]
- Geng, R.H.; Bian, Y.S.; Zhang, L.; Guo, Y.Z. A Saturation-Based Method for Primary Resonance Control of Flexible Manipulator. Machines 2022, 10, 284. [Google Scholar] [CrossRef]
- Li, Y.Y.; Ge, S.S.; Wei, Q.P.; Gan, T.; Tao, X.L. An Online Trajectory Planning Method of a Flexible-Link Manipulator Aiming at Vibration Suppression. IEEE Access 2020, 8, 130616–130632. [Google Scholar] [CrossRef]
- Oh, S.; Kong, K. High-Precision Robust Force Control of a Series Elastic Actuator. IEEE/ASME Trans. Mechatron. 2017, 22, 71–80. [Google Scholar] [CrossRef]
- Lightcap, C.A.; Banks, S.A. An Extended Kalman Filter for Real-Time Estimation and Control of a Rigid-Link Flexible-Joint Manipulator. IEEE Trans. Control Syst. Technol. 2010, 18, 91–103. [Google Scholar] [CrossRef]
- Krysko, A.V.; Awrejcewicz, J.; Kutepov, I.E.; Krysko, V.A. Stability of Curvilinear Euler-Bernoulli Beams in Temperature Fields. Int. J. Non-Linear Mech. 2017, 94, 207–215. [Google Scholar] [CrossRef]
- He, X.Y.; Song, Y.H.; Han, Z.J.; Zhang, S.; Jing, P.; Qi, S.W. Adaptive Inverse Backlash Boundary Vibration Control Design for an Euler–Bernoulli Beam System. J. Frankl. Inst. 2020, 357, 3434–3450. [Google Scholar] [CrossRef]
- Parviz, H.; Fakoor, M. Free Vibration of a Composite Plate with Spatially Varying Gaussian Properties Under Uncertain Thermal Field Using Assumed Mode Method. Phys. A Stat. Mech. Its Appl. 2020, 559, 125085. [Google Scholar] [CrossRef]
- Hao, T.; Wang, H.S.; Xu, F.; Wang, J.C.; Miao, Y.Z. Uncalibrated Visual Servoing for a Planar Two Link Rigid-Flexible Manipulator Without Joint-Space-Velocity Measurement. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 1935–1947. [Google Scholar] [CrossRef]
- Sun, C.Y.; Gao, H.J.; He, W.; Yu, Y. Fuzzy Neural Network Control of a Flexible Robotic Manipulator Using Assumed Mode Method. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 5214–5227. [Google Scholar] [CrossRef]
- Ji, H.R.; Li, D.X. A Novel Nonlinear Finite Element Method for Structural Dynamic Modeling of Spacecraft Under Large Deformation. Thin-Walled Struct. 2021, 165, 107926. [Google Scholar] [CrossRef]
- Grazioso, S.; Di Gironimo, G.; Iglesias, D.; Siciliano, B. Screw-Based Dynamics of a Serial/Parallel Flexible Manipulator for DEMO Blanket Remote Handling. Fusion Eng. Des. 2019, 139, 39–46. [Google Scholar] [CrossRef]
- Shao, M.Q.; Huang, Y.M.; Silberschmidt, V.V. Alvaro Cunha. Intelligent Manipulator with Flexible Link and Joint: Modeling and Vibration Control. Shock Vib. 2020, 2020, 4671358. [Google Scholar] [CrossRef] [Green Version]
- Matsuno, F.; Asano, T.; Sakawa, Y. Modeling and Quasi-Static Hybrid Position Force Control of Constrained Planar 2-Link Flexible Manipulators. IEEE Trans. Robot. Autom. 1994, 10, 287–297. [Google Scholar] [CrossRef]
- Lu, E.; Li, W.; Yang, X.F.; Wang, Y.Q.; Liu, Y.F. Optimal Placement and Active Vibration Control for Piezoelectric Smart Flexible Manipulators Using Modal H-2 Norm. J. Intell. Mater. Syst. Struct. 2018, 29, 2333–2343. [Google Scholar] [CrossRef]
- Wang, J.F.; Cao, F.F.; Liu, J.K. Nonlinear Partial Differential Equation Modeling and Adaptive Fault-Tolerant Vibration Control of Flexible Rotatable Manipulator in Three-Dimensional Space. Int. J. Adapt. Control Signal Process. 2021, 35, 2138–2154. [Google Scholar] [CrossRef]
- Tang, L.W.; Gouttefarde, M.; Sun, H.N.; Yin, L.R.; Zhou, C.J. Dynamic Modelling and Vibration Suppression of a Single-Link Flexible Manipulator with Two Cables. Mech. Mach. Theory 2021, 162, 104347. [Google Scholar] [CrossRef]
- Chu, M.; Zhang, Y.H.; Chen, G.; Sun, H.X. Effects of Joint Controller on Analytical Modal Analysis of Rotational Flexible Manipulator. Chin. J. Mech. Eng. 2015, 28, 460–469. [Google Scholar] [CrossRef]
- Shang, D.Y.; Li, X.P.; Yin, M.; Li, F.J. Control Method of Flexible Manipulator Servo System Based on a Combination of RBF Neural Network and Pole Placement Strategy. Mathematics 2021, 9, 896. [Google Scholar] [CrossRef]
- Shang, D.Y.; Li, X.P.; Yin, M.; Li, F.J. Speed Control Method for Dual-Flexible Manipulator with a Telescopic Arm Considering Bearing Friction Based on Adaptive PI Controller with DOB. Alex. Eng. J. 2022, 61, 4741–4756. [Google Scholar] [CrossRef]
- Kim, S.M.; Kim, H.; Boo, K.; Brennan, M.J. Demonstration of Non-Collocated Vibration Control of a Flexible Manipulator Using Electrical Dynamic Absorbers. Smart Mater. Struct. 2013, 22, 127001. [Google Scholar] [CrossRef]
- Wu, Q.C.; Wang, X.S.; Chen, B.; Wu, H.T.; Shao, Z.Y. Development and Hybrid Force/Position Control of a Compliant Rescue Manipulator. Mechatronics 2017, 46, 143–153. [Google Scholar] [CrossRef]
- Dindorf, R.; Wos, P. A Case Study of a Hydraulic Servo Drive Flexibly Connected to a Boom Manipulator Excited by the Cyclic Impact Force Generated by a Hydraulic Rock Breaker. IEEE Access 2022, 10, 7734–7752. [Google Scholar] [CrossRef]
- Ding, Y.S.; Xiao, X.; Huang, X.R.; Sun, J.X. System Identification and a Model-Based Control Strategy of Motor Driven System with High Order Flexible Manipulator. Ind. Robot 2019, 46, 672–681. [Google Scholar] [CrossRef]
- Li, X.P.; Shang, D.Y.; Li, H.Y.; Li, F.J. Resonant Suppression Method Based on PI control for Serial Manipulator Servo Drive System. Sci. Prog. 2020, 103, 36850420950130. [Google Scholar] [CrossRef]
- Gao, H.J.; He, W.; Song, Y.H.; Zhang, S.; Sun, C.Y. Modeling and Neural Network Control of a Flexible Beam with Unknown Spatiotemporally Varying Disturbance Using Assumed Mode Method. Neurocomputing 2018, 314, 458–467. [Google Scholar] [CrossRef]
- Wang, H.P.; Zhou, X.Y.; Tian, Y. Robust Adaptive Fault-Tolerant Control Using RBF-Based Neural Network for a Rigid-Flexible Robotic System with Unknown Control Direction. Int. J. Robust Nonlinear Control 2022, 32, 1272–1302. [Google Scholar] [CrossRef]
- Ma, H.; Zhou, Q.; Li, H.Y.; Lu, R.Q. Adaptive Prescribed Performance Control of A Flexible-Joint Robotic Manipulator With Dynamic Uncertainties. IEEE Trans. Cybern. 2021, 3091531, 1–11. [Google Scholar] [CrossRef]



| The Characteristic Root | |||
| The Values | 1.875 | 4.694 | 7.855 |
| ec/e | PB | PM | PS | ZO | NS | NM | NB |
|---|---|---|---|---|---|---|---|
| PB | NB | NB | NM | NM | NM | ZO | ZO |
| PM | PB | ZO | PM | PM | ZO | ZO | NS |
| PS | PB | PM | PM | PM | PS | PS | NS |
| ZO | NM | NM | NS | ZO | PS | PS | PM |
| NS | NS | NS | ZO | PS | PS | PM | PM |
| NM | NS | ZO | PS | PS | PM | PB | PB |
| NB | ZO | ZO | PS | PM | PM | PB | PB |
| ec/e | PB | PM | PS | ZO | NS | NM | NB |
|---|---|---|---|---|---|---|---|
| PB | PB | PB | PM | PS | PS | ZO | ZO |
| PM | PB | PB | PM | PM | PS | ZO | ZO |
| PS | PB | PM | PS | PS | ZO | NS | NM |
| ZO | PM | PS | NS | PS | PS | ZO | ZO |
| NS | PM | PS | PS | ZO | PS | ZO | ZO |
| NM | ZO | ZO | NS | NS | NM | NB | NB |
| NB | ZO | NS | NS | NM | NM | NB | NB |
| ec/e | PB | PM | PS | ZO | NS | NM | NB |
|---|---|---|---|---|---|---|---|
| PB | PB | PS | PS | PS | PM | PB | PB |
| PM | PB | PB | PS | PS | PM | PM | PB |
| PS | ZO | ZO | NS | NS | ZO | ZO | ZO |
| ZO | ZO | NS | NS | ZO | NS | NS | ZO |
| NS | ZO | NS | NS | NS | NM | NM | ZO |
| NM | ZO | NS | NS | NM | NB | NS | PS |
| NB | PS | NM | NB | NB | NB | NS | PS |
| Determinants | Condition 1 | Condition 2 | Condition 3 |
|---|---|---|---|
| Flexible load length l/m | 0.4 | 0.6 | 0.8 |
| Flexural stiffness of a flexible load EI/Nm2 | 400 | 400 | 400 |
| Line density of flexible load ρA/kg/m2 | 5 | 3.333 | 2.5 |
| Modal coupling coefficient Fai/kg1/2m | 0.455 | 0.6826 | 0.9101 |
| Inertia of a flexible load Jl/kgm2 | 0.1067 | 0.24 | 0.427 |
| Modal frequencies of flexible loads ωi/rad/s | 196.5294 | 106.9771 | 69.4836 |
| Characteristic roots of the mode function β1 | 1.875 | 1.875 | 1.875 |
| Moment of inertia of motor Jm/kgm2 | 0.36 | 0.72 | 1.28 |
| Torsional stiffness ks/Nm/rad | 405 | 405 | 405 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Wang, Y.; Wang, M. Speed Fluctuation Suppression Strategy of Servo System with Flexible Load Based on Pole Assignment Fuzzy Adaptive PID. Mathematics 2022, 10, 3962. https://doi.org/10.3390/math10213962
Liu X, Wang Y, Wang M. Speed Fluctuation Suppression Strategy of Servo System with Flexible Load Based on Pole Assignment Fuzzy Adaptive PID. Mathematics. 2022; 10(21):3962. https://doi.org/10.3390/math10213962
Chicago/Turabian StyleLiu, Xiangchen, Yihan Wang, and Minghai Wang. 2022. "Speed Fluctuation Suppression Strategy of Servo System with Flexible Load Based on Pole Assignment Fuzzy Adaptive PID" Mathematics 10, no. 21: 3962. https://doi.org/10.3390/math10213962






