A General-Purpose Multi-Dimensional Convex Landscape Generator
Abstract
:1. Introduction
1.1. Continuous Optimization Problems in Evolutionary Computation
1.2. Convexity and General Convex Functions
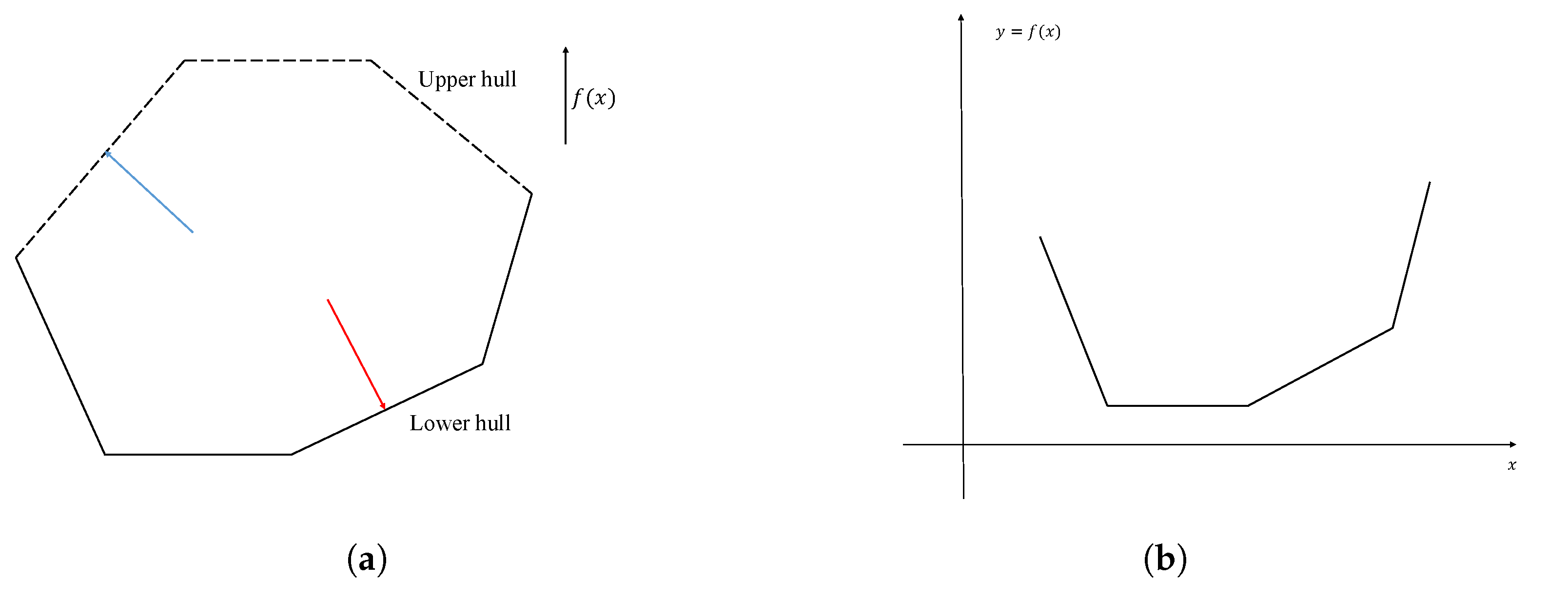
1.3. Convex Hull
2. Methodology: Multi-Dimensional Convex Landscape Generator
2.1. Convex Function Landscape Construction (Offline Process)
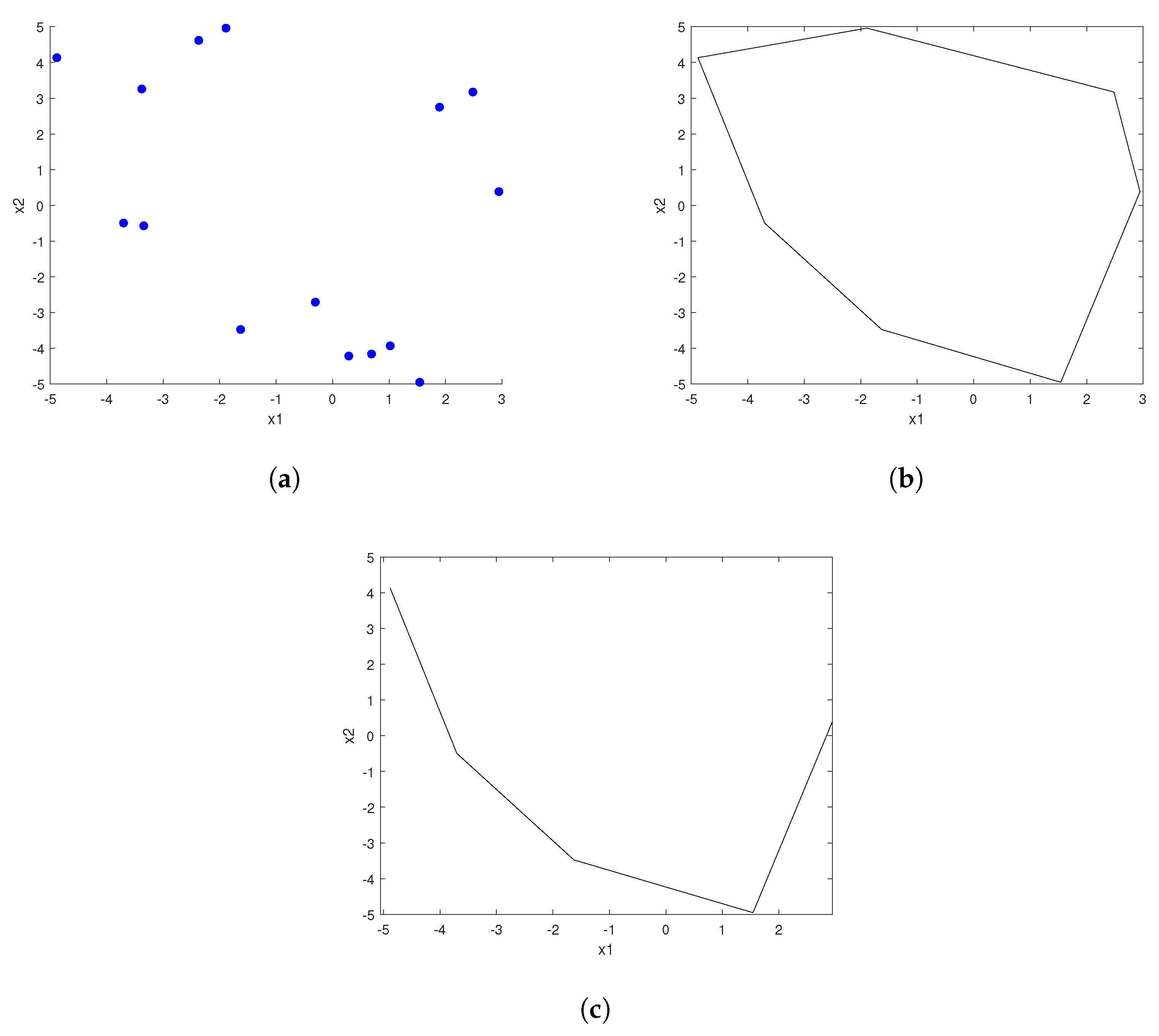
2.1.1. Generate Some Random Points and Use “Quick Hull” Algorithm to Construct a Convex Hull
2.1.2. Remove the Upper Hull
2.1.3. Computational Complexity
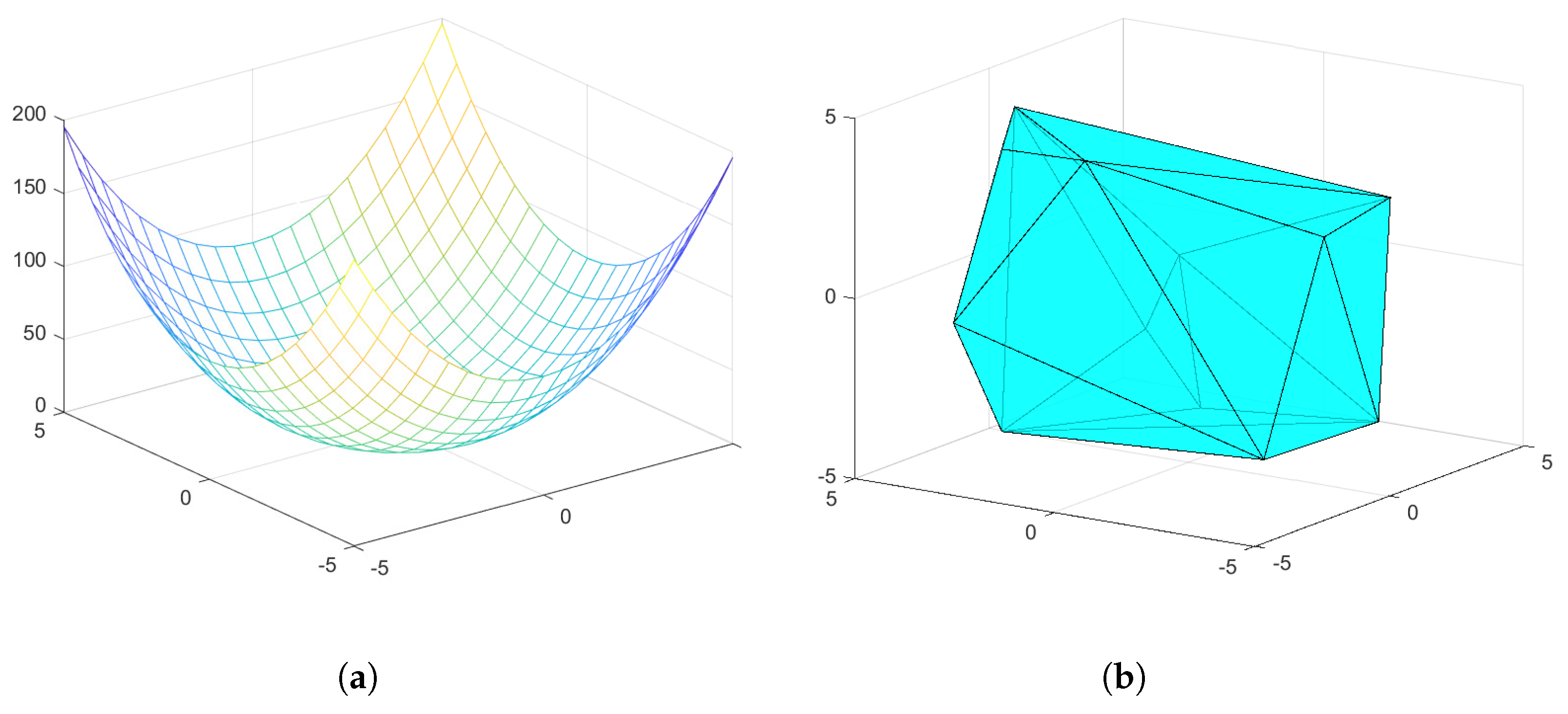
2.1.4. Examples of the Landscape Construction
2.2. Fitness Evaluation (Online Process)
3. Experiments
3.1. Relationship between the Number of Vertices N and the Number of Polygons M
3.2. Verifying the Convexity in High Dimensions by the Nonconvexity Measure of the Landscape
3.3. Using the BFGS Algorithm to Solve the Convex Function
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Taylan, P.; Weber, G.W.; Beck, A. New approaches to regression by generalized additive models and continuous optimization for modern applications in finance, science and technology. Optimization 2007, 56, 675–698. [Google Scholar] [CrossRef]
- Boyd, S.; Boyd, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Hansen, N.; Auger, A.; Ros, R.; Mersmann, O.; Tušar, T.; Brockhoff, D. COCO: A platform for comparing continuous optimizers in a black-box setting. Optim. Methods Softw. 2021, 36, 114–144. [Google Scholar] [CrossRef]
- Liang, J.; Qu, B.; Suganthan, P.; Hernández-Díaz, A.G. Problem Definitions and Evaluation Criteria for the CEC 2013 Special Session on Real-Parameter Optimization; Technical Report; Computational Intelligence Laboratory, Zhengzhou University, China and Nanyang Technological University: Singapore, 2013. [Google Scholar]
- Suganthan, P.; Hansen, N.; Liang, J.; Deb, K.; Chen, Y.P.; Auger, A.; Tiwari, S. Problem Definitions and Evaluation Criteria for the CEC 2005 Special Session on Real-Parameter Optimization; Technical Report; Nanyang Technological University: Singapore, 2005. [Google Scholar]
- Gallagher, M.; Yuan, B. A general-purpose tunable landscape generator. IEEE Trans. Evol. Comput. 2006, 10, 590–603. [Google Scholar] [CrossRef] [Green Version]
- Rönkkönen, J.; Li, X.; Kyrki, V.; Lampinen, J. A framework for generating tunable test functions for multimodal optimization. Soft Comput. 2011, 15, 1689–1706. [Google Scholar] [CrossRef]
- Das, S.; Suganthan, P. Problem Definitions and Evaluation Criteria for CEC 2011 Competition on Testing Evolutionary Algorithms on Real World Optimization Problems; Technical Report; Jadavpur University: Kolkata, India, 2011. [Google Scholar]
- Karaboga, D.; Akay, B. A comparative study of artificial bee colony algorithm. Appl. Math. Comput. 2009, 214, 108–132. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Das, S.; Suganthan, P.N. Differential evolution: A survey of the state-of-the-art. IEEE Trans. Evol. Comput. 2010, 15, 4–31. [Google Scholar] [CrossRef]
- Salawudeen, A.T.; Mu’azu, M.B.; Yusuf, A.; Adedokun, A.E. A Novel Smell Agent Optimization (SAO): An extensive CEC study and engineering application. Knowl.-Based Syst. 2021, 232, 107486. [Google Scholar] [CrossRef]
- Panwar, D.; Saini, G.; Agarwal, P. Human Eye Vision Algorithm (HEVA): A Novel Approach for the Optimization of Combinatorial Problems. In Artificial Intelligence in Healthcare; Springer: Berlin/Heidelberg, Germany, 2022; pp. 61–71. [Google Scholar]
- Hansen, N. The CMA evolution strategy: A comparing review. In Towards a New Evolutionary Computation; Springer: Berlin/Heidelberg, Germany, 2006; pp. 75–102. [Google Scholar]
- Fletcher, R. Practical Methods of Optimization; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Finck, S.; Hansen, N.; Ros, R.; Auger, A. Real-Parameter Black-Box Optimization Benchmarking 2009: Presentation of the Noiseless Functions; Technical Report; Citeseer: Princeton, NJ, USA, 2010. [Google Scholar]
- Kerschke, P.; Trautmann, H. Automated algorithm selection on continuous black-box problems by combining exploratory landscape analysis and machine learning. Evol. Comput. 2019, 27, 99–127. [Google Scholar] [CrossRef] [Green Version]
- Mersmann, O.; Bischl, B.; Trautmann, H.; Preuss, M.; Weihs, C.; Rudolph, G. Exploratory landscape analysis. In Proceedings of the 13th Annual Conference on GENETIC and Evolutionary Computation, Dublin, Ireland, 12–16 July 2011; pp. 829–836. [Google Scholar]
- Malan, K.M.; Engelbrecht, A.P. A survey of techniques for characterising fitness landscapes and some possible ways forward. Inf. Sci. 2013, 241, 148–163. [Google Scholar] [CrossRef] [Green Version]
- Malan, K.M.; Engelbrecht, A.P. Fitness landscape analysis for metaheuristic performance prediction. In Recent Advances in the Theory and Application of Fitness Landscapes; Springer: Berlin/Heidelberg, Germany, 2014; pp. 103–132. [Google Scholar]
- Muñoz, M.A.; Smith-Miles, K.A. Performance analysis of continuous black-box optimization algorithms via footprints in instance space. Evol. Comput. 2017, 25, 529–554. [Google Scholar] [CrossRef]
- Muñoz, M.A.; Smith-Miles, K. Generating new space-filling test instances for continuous black-box optimization. Evol. Comput. 2020, 28, 379–404. [Google Scholar] [CrossRef] [PubMed]
- Lou, Y.; Yuen, S.Y. On constructing alternative benchmark suite for evolutionary algorithms. Swarm Evol. Comput. 2019, 44, 287–292. [Google Scholar] [CrossRef]
- Biswas, S.; Das, S.; Suganthan, P.N.; Coello, C.A.C. Evolutionary multiobjective optimization in dynamic environments: A set of novel benchmark functions. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 6–11 July 2014; pp. 3192–3199. [Google Scholar]
- Gee, S.B.; Tan, K.C.; Abbass, H.A. A benchmark test suite for dynamic evolutionary multiobjective optimization. IEEE Trans. Cybern. 2016, 47, 461–472. [Google Scholar] [CrossRef] [PubMed]
- Jiang, S.; Kaiser, M.; Yang, S.; Kollias, S.; Krasnogor, N. A scalable test suite for continuous dynamic multiobjective optimization. IEEE Trans. Cybern. 2019, 50, 2814–2826. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Nguyen, T.T.; Zeng, S.; Yang, M.; Wu, M. An open framework for constructing continuous optimization problems. IEEE Trans. Cybern. 2018, 49, 2316–2330. [Google Scholar] [CrossRef] [PubMed]
- Kudela, J.; Matousek, R. New Benchmark Functions for Single-Objective Optimization Based on a Zigzag Pattern. IEEE Access 2022, 10, 8262–8278. [Google Scholar] [CrossRef]
- Yazdani, D.; Omidvar, M.N.; Cheng, R.; Branke, J.; Nguyen, T.T.; Yao, X. Benchmarking continuous dynamic optimization: Survey and generalized test suite. IEEE Trans. Cybern. 2020, 52, 3380–3393. [Google Scholar] [CrossRef]
- Yazdani, D.; Cheng, R.; Yazdani, D.; Branke, J.; Jin, Y.; Yao, X. A survey of evolutionary continuous dynamic optimization over two decades—Part B. IEEE Trans. Evol. Comput. 2021, 25, 630–650. [Google Scholar] [CrossRef]
- Dullerud, G.E.; Paganini, F. A Course in Robust Control Theory: A Convex Approach; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 36. [Google Scholar]
- Hardy, G.H.; Littlewood, J.E.; Pólya, G. Inequalities; Cambridge University Press: Cambridge, UK, 1952. [Google Scholar]
- Kim, C.E.; Rosenfeld, A. Digital straight lines and convexity of digital regions. IEEE Trans. Pattern Anal. Mach. Intell. 1982, 149–153. [Google Scholar] [CrossRef]
- Kim, C.E.; Rosenfeld, A. Convex digital solids. IEEE Trans. Pattern Anal. Mach. Intell. 1982, PAMI-4, 612–618. [Google Scholar] [CrossRef]
- Chassery, J.M.; Garbay, C. An iterative segmentation method based on a contextual color and shape criterion. IEEE Trans. Pattern Anal. Mach. Intell. 1984, PAMI-6, 794–800. [Google Scholar] [CrossRef] [PubMed]
- Lin, M.C.; Manocha, D.; Cohen, J.; Gottschalk, S. Collision Detection: Algorithms and applications. In Algorithms for robotic Motion and Manipulation; Citeseer: Princeton, NJ, USA, 1997; pp. 129–142. [Google Scholar]
- O’Rourke, J. Computational Geometry in C; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Jarvis, R.A. On the identification of the convex hull of a finite set of points in the plane. Inf. Process. Lett. 1973, 2, 18–21. [Google Scholar] [CrossRef]
- Barber, C.B.; Dobkin, D.P.; Huhdanpaa, H. The quickhull algorithm for convex hulls. ACM Trans. Math. Softw. (TOMS) 1996, 22, 469–483. [Google Scholar] [CrossRef] [Green Version]
- Tamura, K.; Gallagher, M. Quantitative measure of nonconvexity for black-box continuous functions. Inf. Sci. 2019, 476, 64–82. [Google Scholar] [CrossRef]
- Gray, A.; Abbena, E.; Salamon, S. Modern Differential Geometry of Curves and Surfaces with Mathematica®; Chapman and Hall/CRC: Boca Raton, FL, USA, 2017. [Google Scholar]
- Mark, d.B.; Otfried, C.; Marc, v.K.; Mark, O. Computational Geometry Algorithms and Applications; Spinger: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Gellert, W.; Hellwich, M.; Kästner, H.; Küstner, H. The VNR Concise Encyclopedia of Mathematics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Lay, D.C. Linear Algebra and Its Applications; Pearson Education India: Delhi, India, 2003. [Google Scholar]







| Dimension | Problem of BBOB | NCR Value | N | NCR Value |
|---|---|---|---|---|
| f1 | 0 | 10 | 0 | |
| d = 2 | f7 | 0.0912 | 12 | 0 |
| f21 | 0.4804 | 15 | 0 | |
| f1 | 0 | 10 | 0 | |
| d = 5 | f6 | 0.0448 | 12 | 0 |
| f16 | 0.4616 | 15 | 0 | |
| f1 | 0 | 12 | 0 | |
| d = 10 | f7 | 0.0096 | 14 | 0 |
| f15 | 0.0016 | 15 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Yuen, S.Y.; Chung, K.W.; Sung, C.W. A General-Purpose Multi-Dimensional Convex Landscape Generator. Mathematics 2022, 10, 3974. https://doi.org/10.3390/math10213974
Liu W, Yuen SY, Chung KW, Sung CW. A General-Purpose Multi-Dimensional Convex Landscape Generator. Mathematics. 2022; 10(21):3974. https://doi.org/10.3390/math10213974
Chicago/Turabian StyleLiu, Wenwen, Shiu Yin Yuen, Kwok Wai Chung, and Chi Wan Sung. 2022. "A General-Purpose Multi-Dimensional Convex Landscape Generator" Mathematics 10, no. 21: 3974. https://doi.org/10.3390/math10213974





