Closed-Form Solutions to a Forced Damped Rotational Pendulum Oscillator
Abstract
:1. Introduction
2. Analytical Solutions to the Rotational Pendulum-Type Oscillators
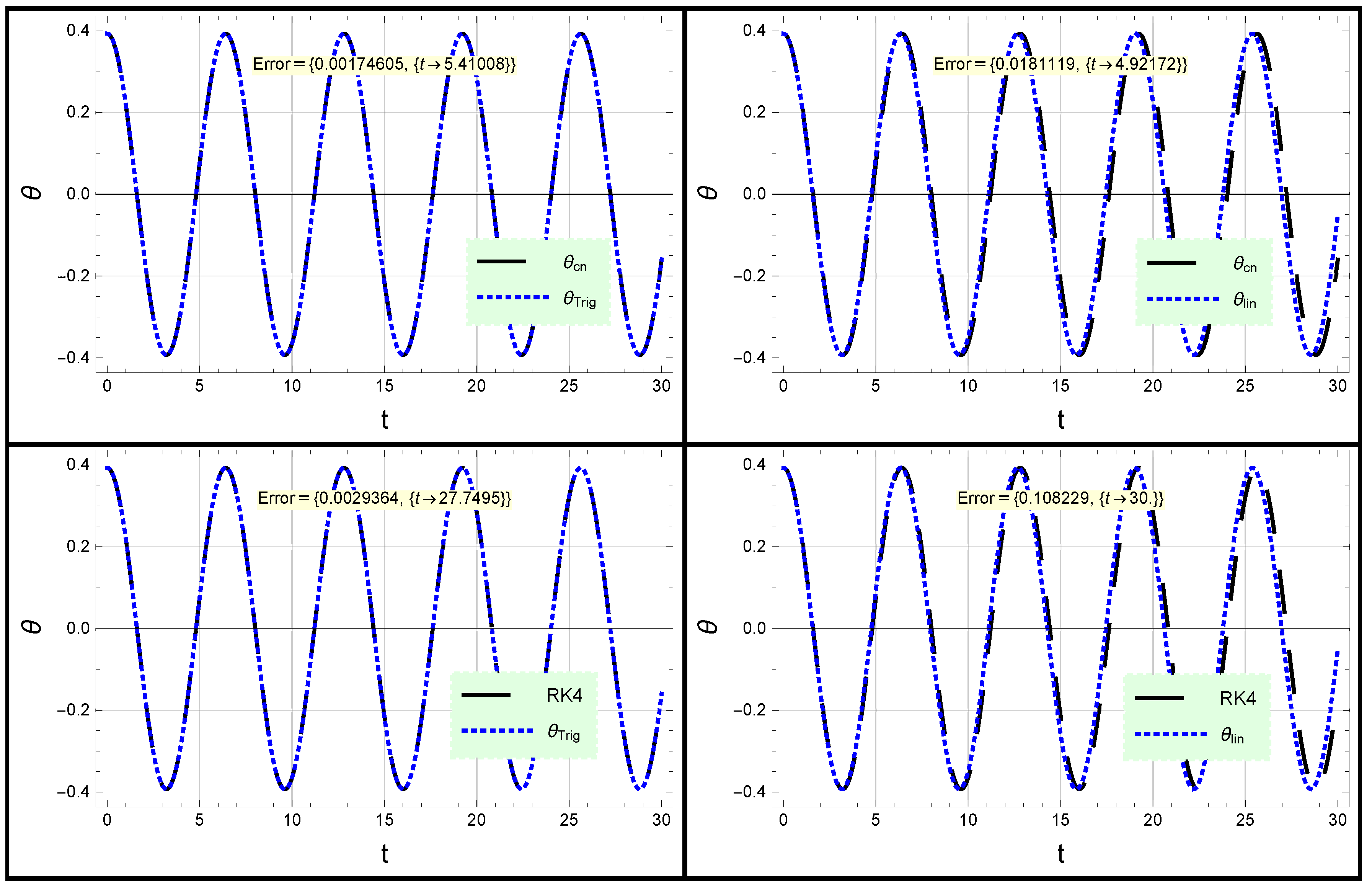
2.1. Conserved Rotational Pendulum Oscillator
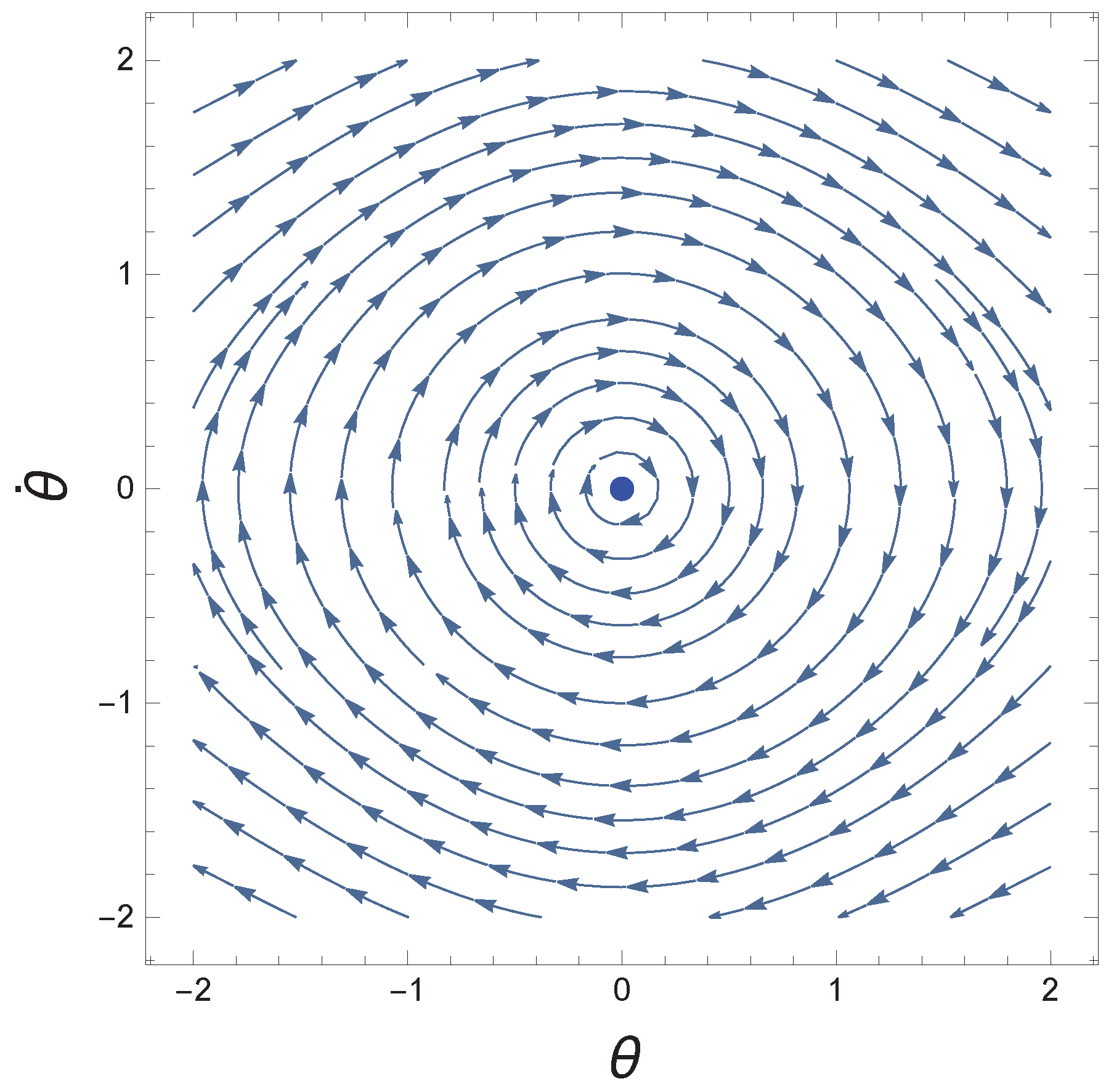
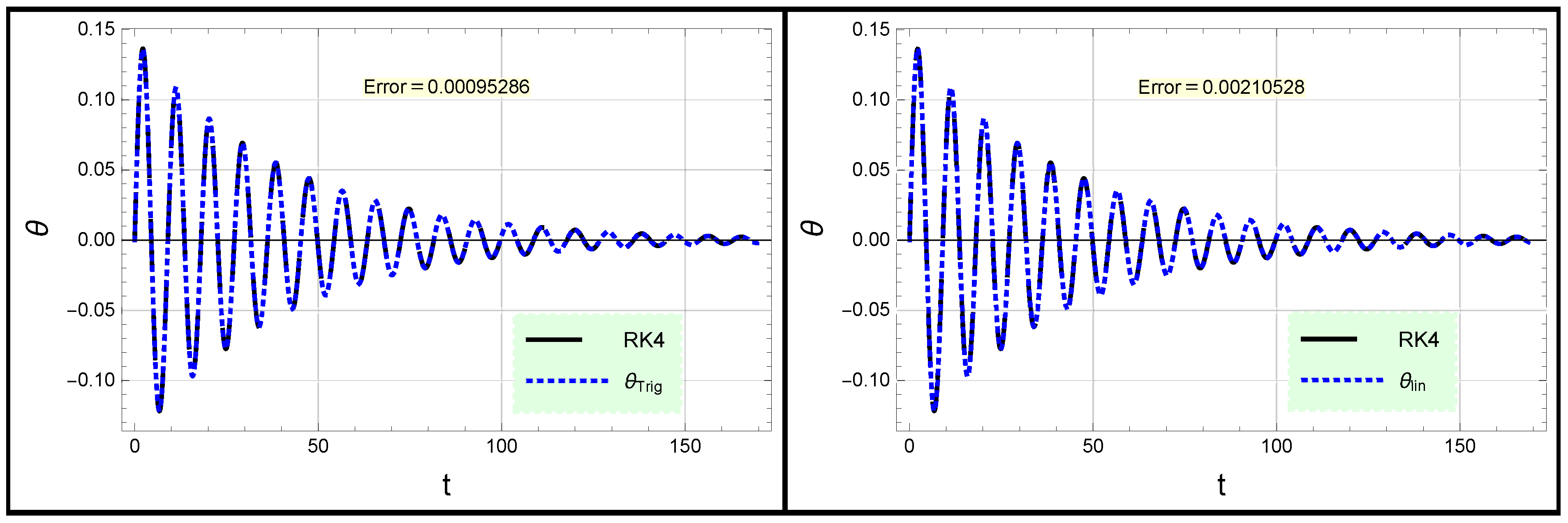
2.2. Unforced Damped Rotational Pendulum Oscillator
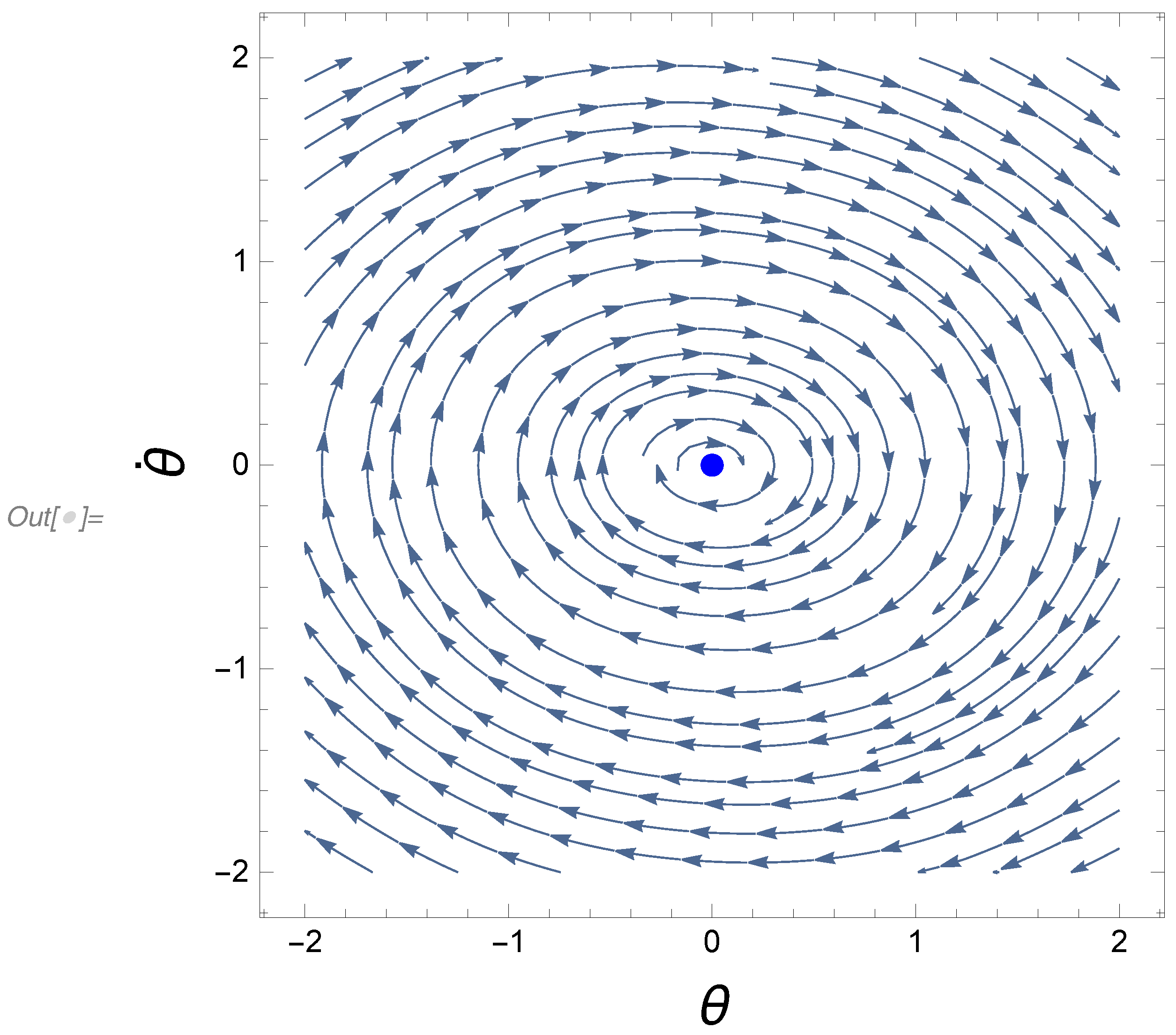
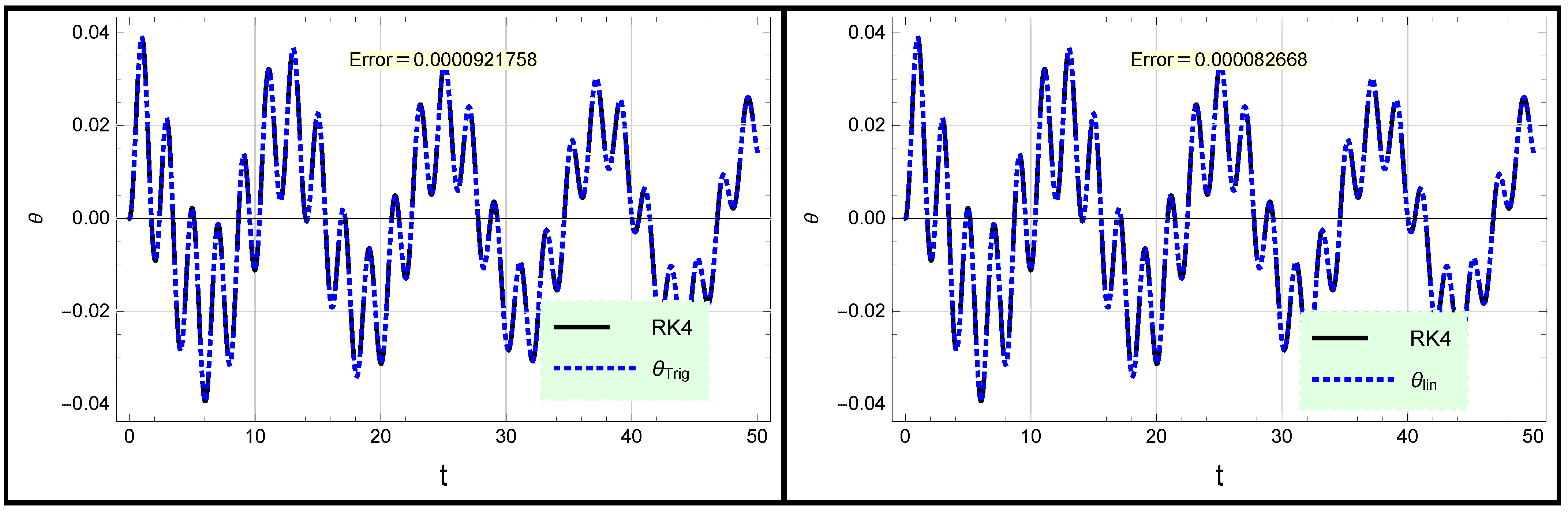
3. Forced Damped Rotational Pendulum Oscillator
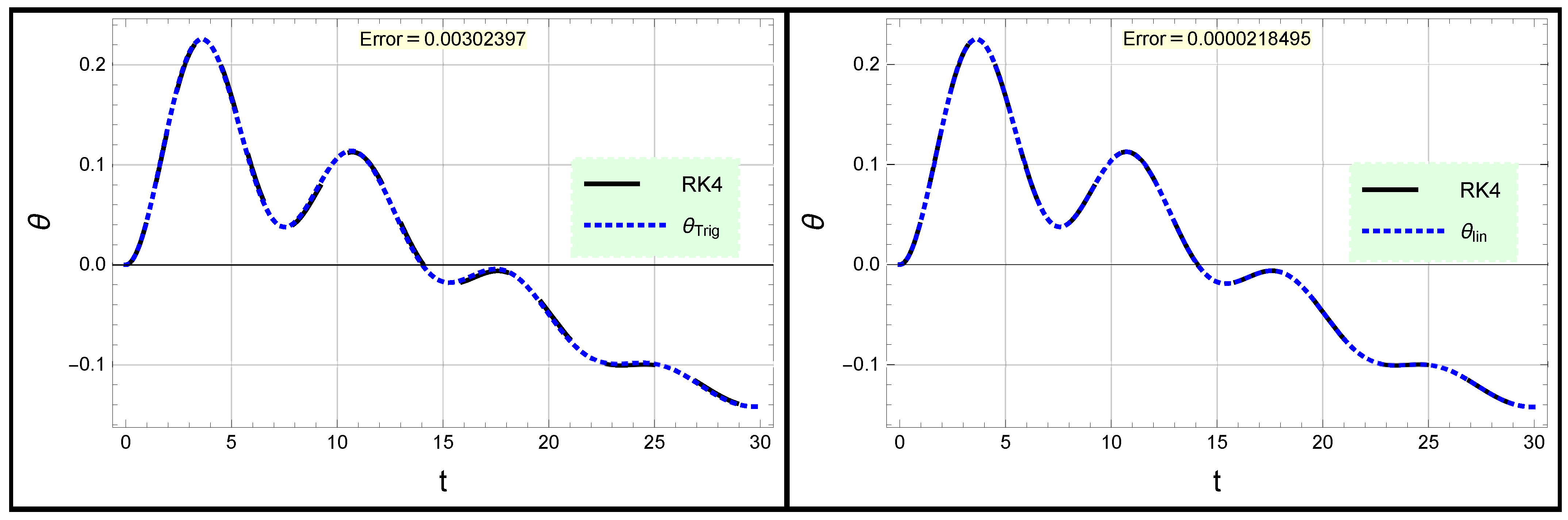
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Wazwaz, A.-M. Partial Differential Equations and Solitary Waves Theory; Higher Education Press: Beijing, China, 2009. [Google Scholar]
- El-Tantawy, S.A.; Salas, A.H.; Alharthi, M.R. On the Analytical and Numerical Solutions of the Linear Damped NLSE for Modeling Dissipative Freak Waves and Breathers in Nonlinear and Dispersive Mediums: An Application to a Pair-Ion Plasma. Front. Phys. 2021, 9, 580224. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; El-Awady, E.I. Cylindrical and spherical Akhmediev breather and freak waves in ultracold neutral plasmas. Phys. Plasmas 2018, 25, 012121. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Aboelenen, T. Simulation study of planar and nonplanar super rogue waves in an electronegative plasma: Local discontinuous Galerkin method. Phys. Plasmas 2017, 24, 052118. [Google Scholar] [CrossRef]
- Aljahdaly, N.H.; El-Tantawy, S.A. Simulation study on nonlinear structures in nonlinear dispersive media. Chaos 2020, 30, 053117. [Google Scholar] [CrossRef] [PubMed]
- El-Dib, Y.O. The simplest approach to solving the cubic nonlinear jerk oscillator with the non-perturbative method. Math. Methods Appl. Sci. 2022, 45, 5165. [Google Scholar] [CrossRef]
- Alyousef, H.A.; Alharthi, M.R.; Salas, A.H.; El-Tantawy, S.A. Optimal analytical and numerical approximations to the (un)forced (un)damped parametric pendulum oscillator. Commun. Theor. Phys. 2022, 74, 105002. [Google Scholar] [CrossRef]
- He, J.H.; El-Dib, Y.O. The reducing rank method to solve third-order Duffing equation with the homotopy perturbation. Numer. Method Partial. Differ. Equ. 2021, 37, 1800–1808. [Google Scholar] [CrossRef]
- Bezziou, M.; Dahmani, Z.; Jebril, I.; Belhamiti, M.M. Solvability for a Differential System of Duffing Type Via Caputo-Hadamard Approach. Appl. Math. Inf. Sci. 2022, 16, 341–352. [Google Scholar]
- Bezziou, M.; Jebril, I.; Dahmani, Z. A new nonlinear duffing system with sequential fractional derivatives. Chaos Solitons Fractals 2021, 151, 111247. [Google Scholar] [CrossRef]
- He, J.-H.; Amer, T.S.; Elnaggar, S.; Galal, A.A. Periodic Property and Instability of a Rotating Pendulum System. Axioms 2021, 10, 191. [Google Scholar] [CrossRef]
- Hieu, D.V.; Hai, N.Q.; Hung, D.T. The equivalent linearization method with a weighted averaging for solving undamped nonlinear oscillators. J. Appl. Math. 2018, 2018, 7487851. [Google Scholar] [CrossRef]
- Big-Alabo, A.; Ossia, C.V. Periodic oscillation and bifurcation analysis of pendulum with spinning support using a modified continuous piecewise linearization method. Int. J. Appl. Comput. Math. 2019, 5, 114. [Google Scholar] [CrossRef]
- Liao, S.J.; Chwang, A.T. Application of homotopy analysis method in nonlinear oscillations. J. Appl. Mech. Trans. ASME 1988, 65, 914–922. [Google Scholar] [CrossRef]
- González-Gaxiola, O.; Rach, R.; de Chávez, J.R. Solution for a rotational pendulum system by the Rach–Adomian–Meyers decomposition method. Nonlinear Eng. 2022, 11, 156–167. [Google Scholar] [CrossRef]
- Lai, S.K.; Lim, C.W.; Lin, Z.; Zhang, W. Analytical analysis for large amplitude oscillation of a rotational pendulum system. Appl. Math Comput. 2011, 217, 6115–6124. [Google Scholar] [CrossRef]
- Khan, N.A.; Khan, N.A.; Riaz, F. Dynamic analysis of rotating pendulum by Hamiltonian approach. Chin. J. Math. 2013, 2013, 237370. [Google Scholar] [CrossRef] [Green Version]
- Alhejaili, W.; Salas, A.H.; El-Tantawy, S.A. Novel Approximations to the (Un) forced Pendulum–Cart System: Ansatz and KBM Methods. Mathematics 2022, 10, 2908. [Google Scholar] [CrossRef]
- Salas, A.H.; Albalawi, W.; El-Tantawy, S.A.; El-Sherif, L.S. Some Novel Approaches for Analyzing the Unforced and Forced Duffing–Van der Pol Oscillators. J. Math. 2022, 2022, 2174192. [Google Scholar] [CrossRef]
- Alhejaili, W.; Salas, A.H.; El-Tantawy, S.A. Approximate solution to a generalized Van der Pol equation arising in plasma oscillations. AIP Adv. 2022, 12, 105104. [Google Scholar] [CrossRef]
- He, J.-H. Some asymptotic methods for strongly nonlinear equations. Int. J. Mod. Phys. B 2006, 20, 1141–1199. [Google Scholar] [CrossRef] [Green Version]
- Alsuwaiyan, A.S.; Shaw, S.W. Performance and dynamics stability of general-path centrifugal pendulum vibration absorbers. J. Sound Vib. 2002, 252, 791–815. [Google Scholar] [CrossRef]
- Fischer, O. Wind-excited vibrations-solution by passive dynamic vibration absorbers of different types. J. Wind Eng. Ind. Aerodyn. 2007, 95, 1028–1039. [Google Scholar] [CrossRef]
- Wu, S.T. Active pendulum vibration absorbers with a spinning support. J. Sound Vib. 2009, 323, 1–16. [Google Scholar] [CrossRef]
- Hu, H.; Tang, J.-H. Solution of a Duffing-harmonic oscillator by the method of harmonic balance. J Sound Vib. 2006, 249, 637–639. [Google Scholar] [CrossRef]
- Nayfeh, A.H. Problems in Perturbation; Wiley: New York, NY, USA, 1985. [Google Scholar]
- Mohyud-Din, S.T.; Noor, M.A.; Noor, K.I. Parameter-expansion techniques for strongly nonlinear oscillators. Int. J. Nonlinear Sci. Numer. 2009, 10, 581–583. [Google Scholar]
- Big-Alabo, A.; Onyinyechukwu, O.C. Dynamic analysis of crank mechanism with complex trigonometric nonlinearity: A comparative study of approximate analytical methods. SN Appl. Sci. 2019, 1, 652. [Google Scholar] [CrossRef] [Green Version]
- Khan, Y.; Mirzabeigy, A. Improved accuracy of He’s energy balance method for analysis of conservative nonlinear oscillator. Neural. Comput. Appl. 2014, 25, 889–895. [Google Scholar] [CrossRef]
- Al-Jawary, M.A.; Ibraheem, G.H. Two meshless methods for solving nonlinear ordinary differential equations in engineering mand applied sciences. Nonlinear Eng. 2020, 9, 244–255. [Google Scholar]
- Elías-Zu niga, A. Solution of the damped cubic-quintic Duffing oscillator by using Jacobi elliptic functions. Appl. Math. Comput. 2014, 246, 474–481. [Google Scholar]
- Singh, H.; Srivastava, H.M.; Kumar, D. A reliable algorithm for the approximate solution of the nonlinear Lane-Emden type equations arising in astrophysics. Numer. Methods Partial. Differ. Equ. 2018, 34, 1524–1555. [Google Scholar]
- He, J.-H. Hamiltonian approach to nonlinear oscillators. Phys. Lett. A 2010, 374, 2312–2314. [Google Scholar] [CrossRef]
- Ganji, D.D.; Sadighi, A. Application of He’s homotopy-perturbation method to nonlinear coupled systems of reaction-diffusion equations. Int. J. Nonlinear Sci. Numer. Simul. 2006, 7, 411–418. [Google Scholar] [CrossRef]
- Gorji, M.; Ganji, D.D.; Soleimani, S. New application of He’s homotopy perturbation method. Int. J. Nonlinear Sci. Numer. Simul. 2007, 8, 319–328. [Google Scholar] [CrossRef]
- Zeng, D.Q. Nonlinear oscillator with discontinuity by the maxmin approach. Chaos Soliton Fractals 2009, 42, 2885–2889. [Google Scholar] [CrossRef]
- Wazwaz, A.-M. Solving the non-isothermal reaction-diffusion model equations in a spherical catalyst by the variational iteration method. Chem. Phys. Lett. 2017, 679, 132–136. [Google Scholar] [CrossRef]
- Wazwaz, A.-M. The variational iteration method: A powerful scheme for handling linear and nonlinear diffusion equations. Comput. Math. Appl. 2007, 54, 933–939. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salas, A.H.; Abu Hammad, M.; Alotaibi, B.M.; El-Sherif, L.S.; El-Tantawy, S.A. Closed-Form Solutions to a Forced Damped Rotational Pendulum Oscillator. Mathematics 2022, 10, 4000. https://doi.org/10.3390/math10214000
Salas AH, Abu Hammad M, Alotaibi BM, El-Sherif LS, El-Tantawy SA. Closed-Form Solutions to a Forced Damped Rotational Pendulum Oscillator. Mathematics. 2022; 10(21):4000. https://doi.org/10.3390/math10214000
Chicago/Turabian StyleSalas, Alvaro H., Ma’mon Abu Hammad, Badriah M. Alotaibi, Lamiaa S. El-Sherif, and Samir A. El-Tantawy. 2022. "Closed-Form Solutions to a Forced Damped Rotational Pendulum Oscillator" Mathematics 10, no. 21: 4000. https://doi.org/10.3390/math10214000