The Bayesian Posterior and Marginal Densities of the Hierarchical Gamma–Gamma, Gamma–Inverse Gamma, Inverse Gamma–Gamma, and Inverse Gamma–Inverse Gamma Models with Conjugate Priors
Abstract
1. Introduction
2. Main Results
2.1. Preliminaries
2.2. Common Typical Problems for the Eight Hierarchical Models That Do Not Have Conjugate Priors
2.3. The Bayesian Posterior and Marginal Densities of the Eight Hierarchical Models That Have Conjugate Priors
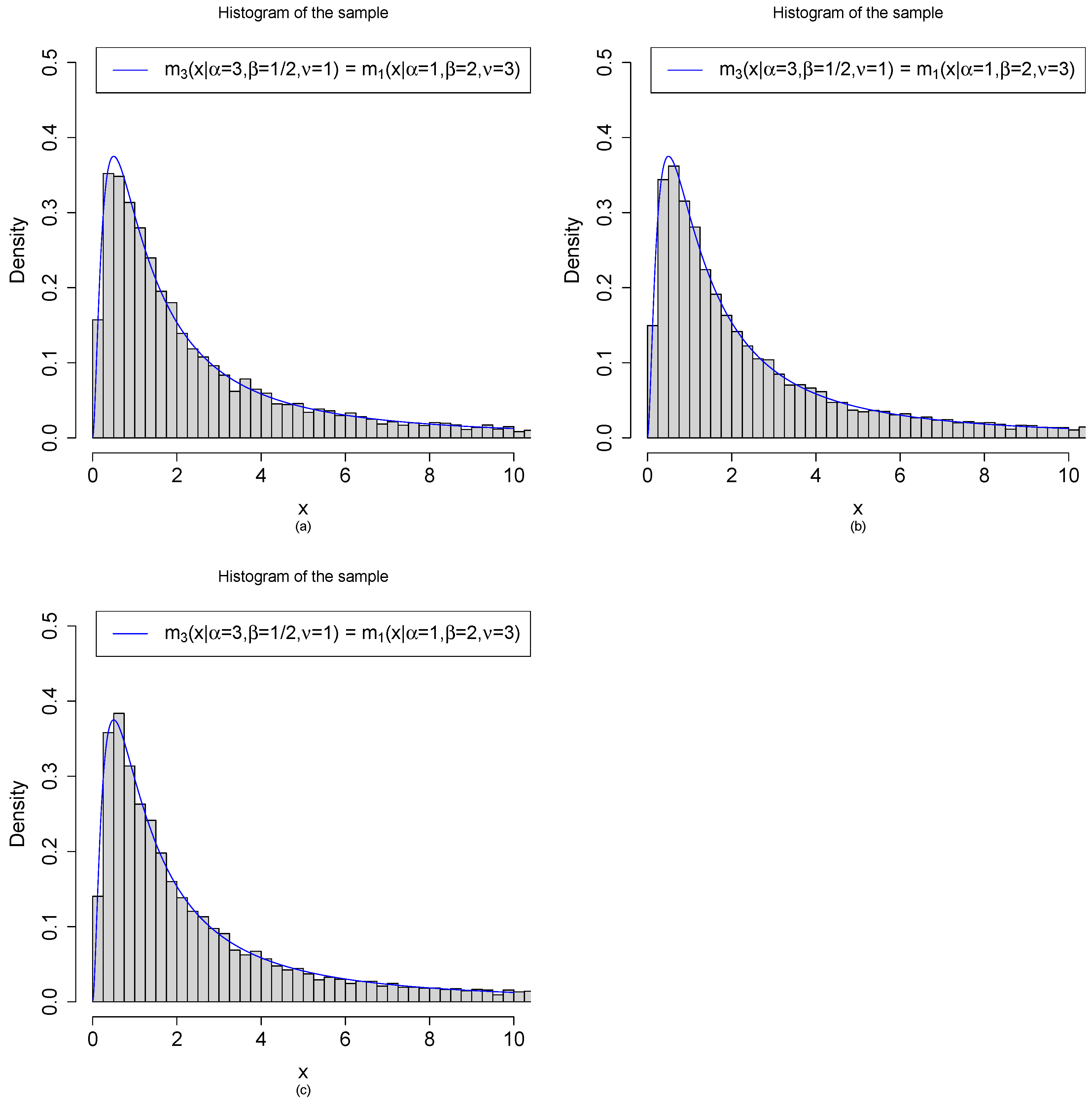
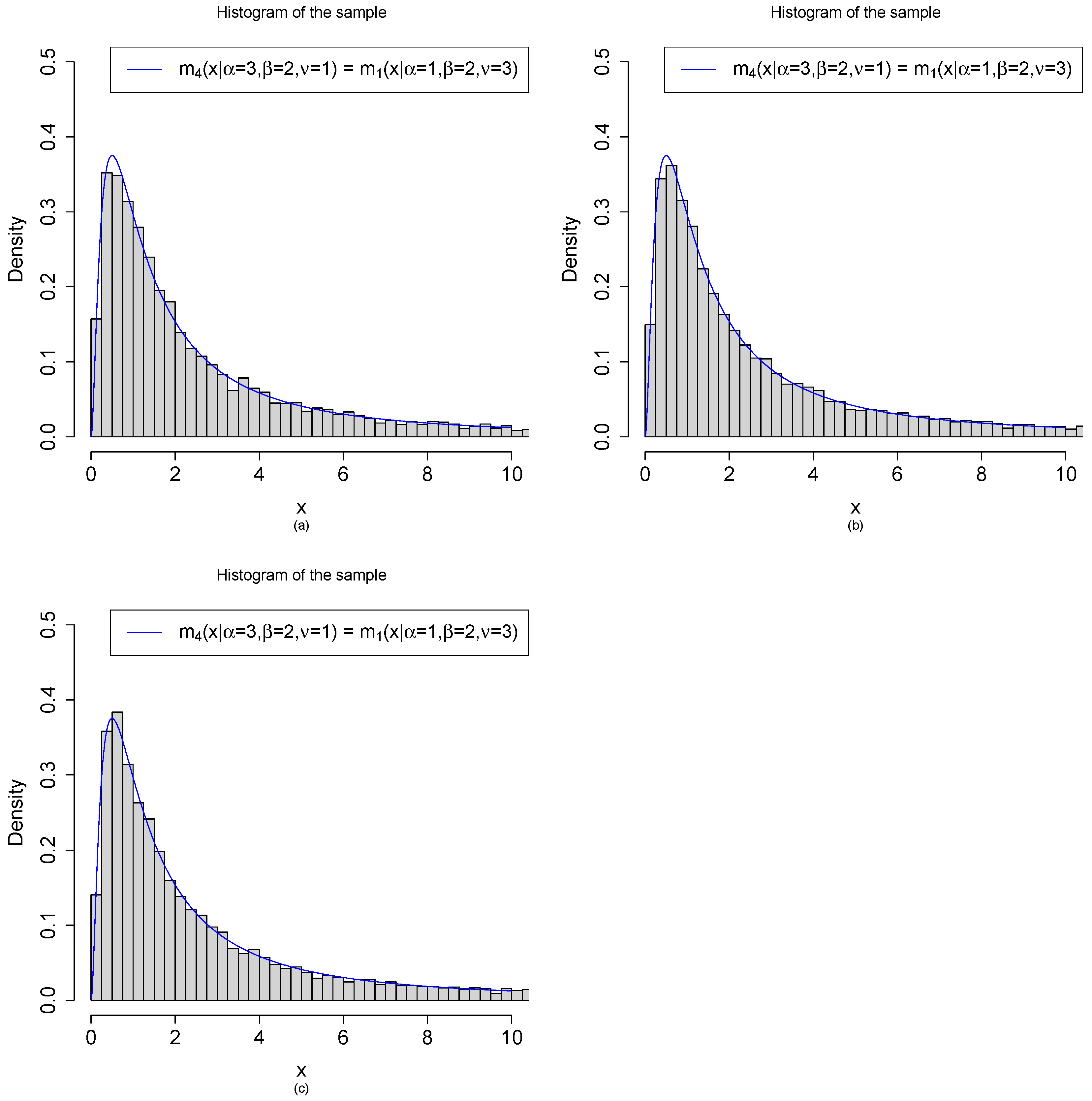
2.4. Relations among the Marginal Densities
2.5. Relations among the Random Variables of the Marginal Densities and the Beta Densities
2.6. Random Variable Generations for the Gamma and Inverse Gamma Distributions
3. Simulations
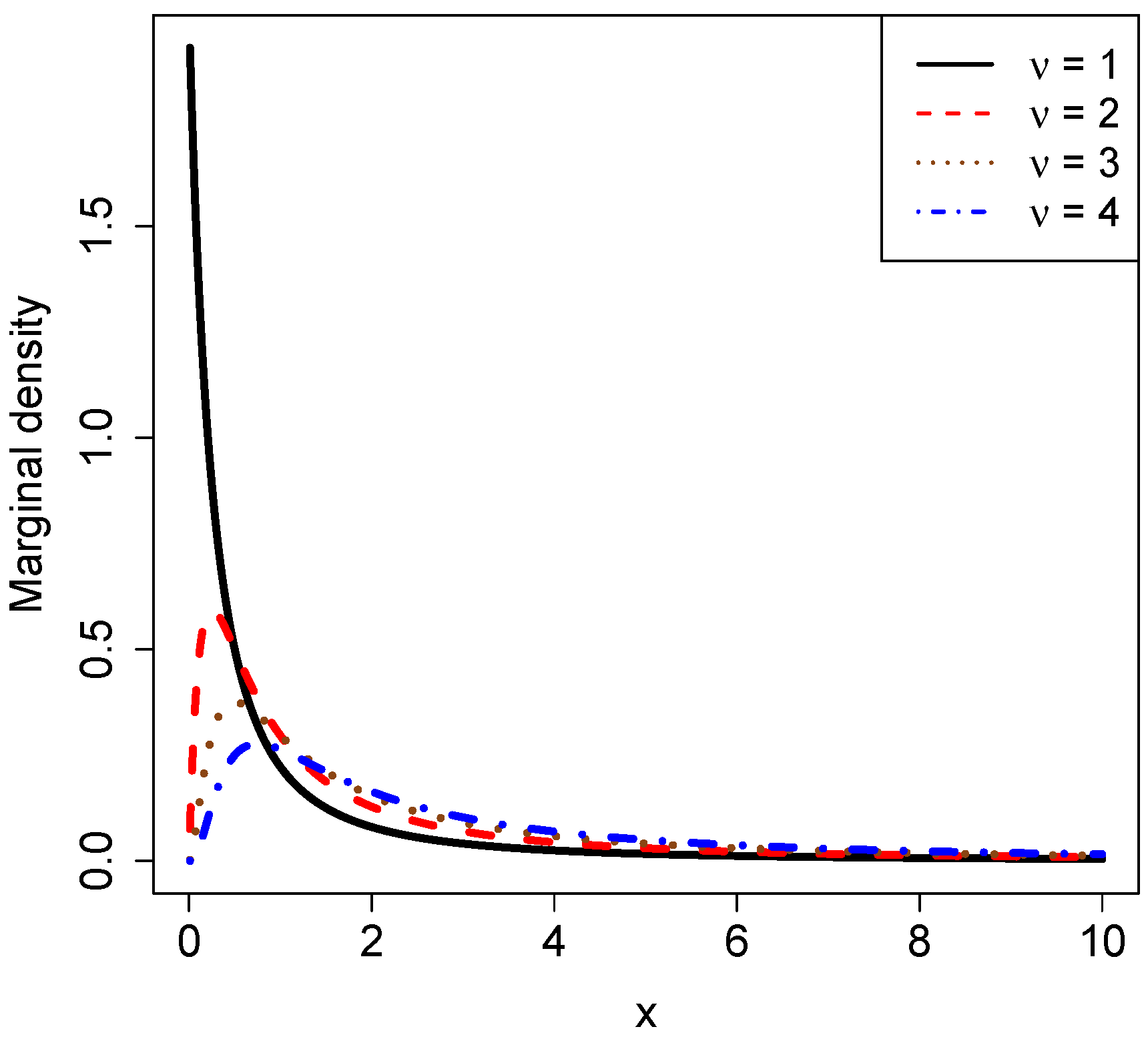
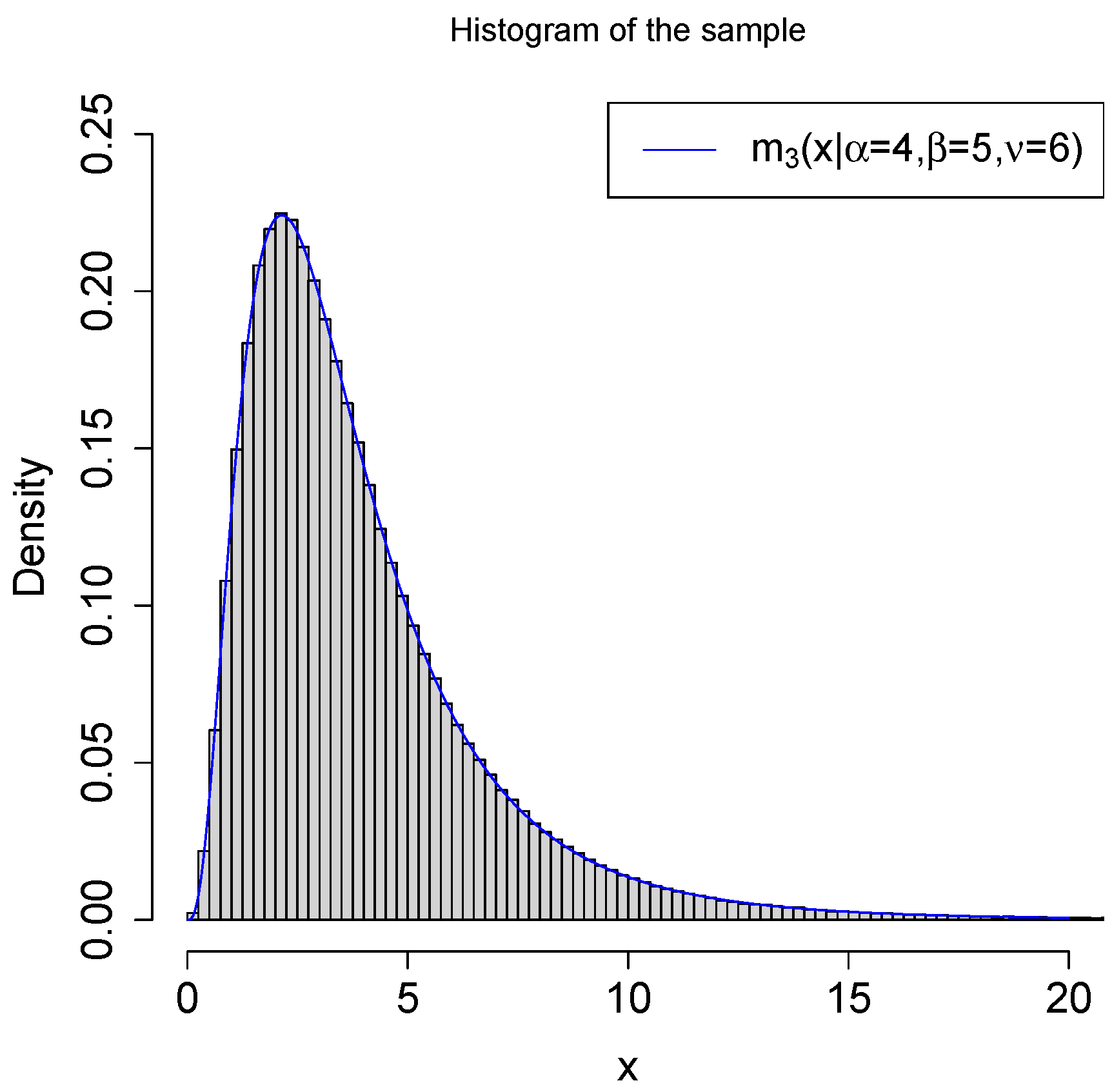
3.1. Marginal Densities for Various Hyperparameters
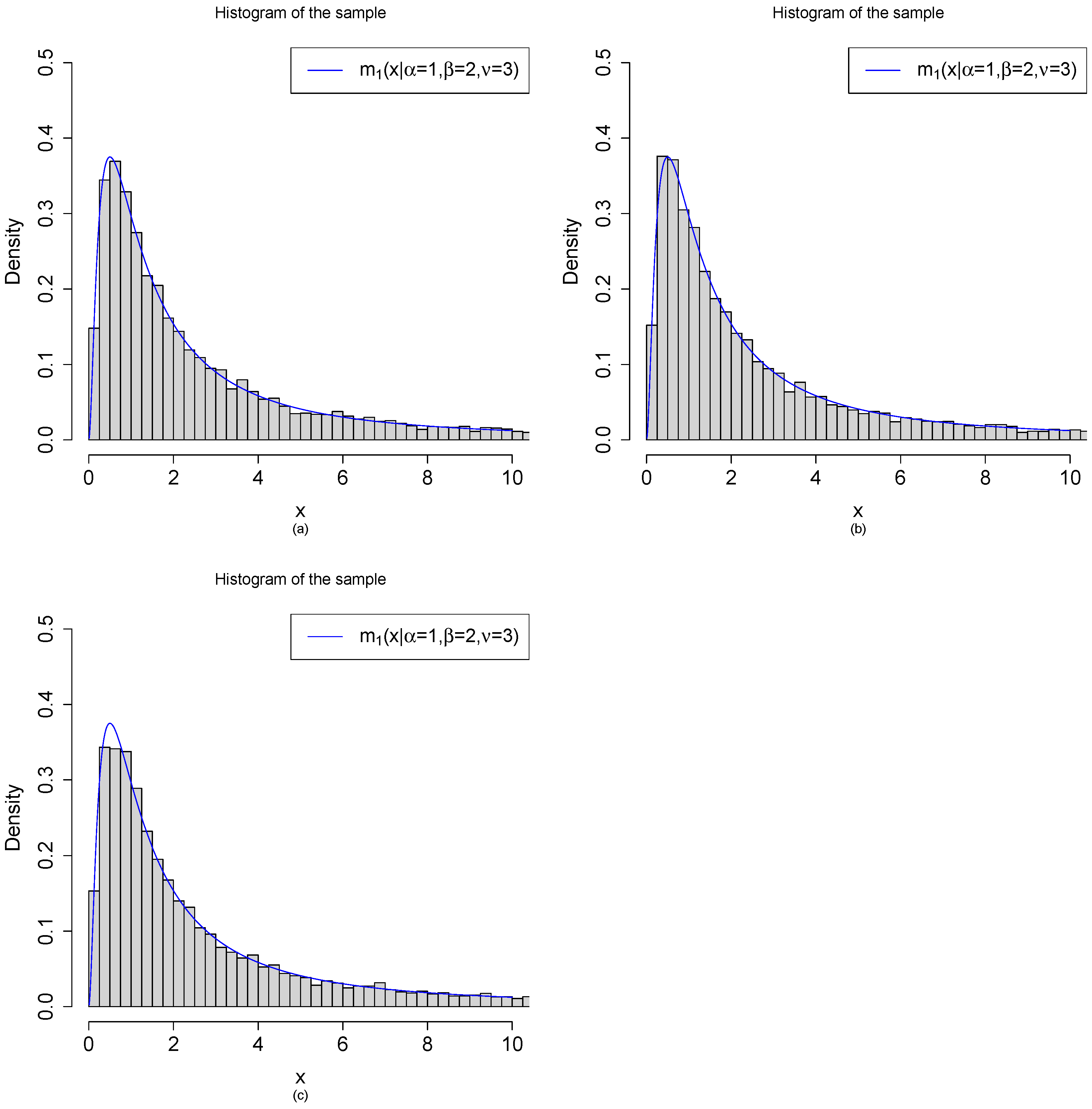
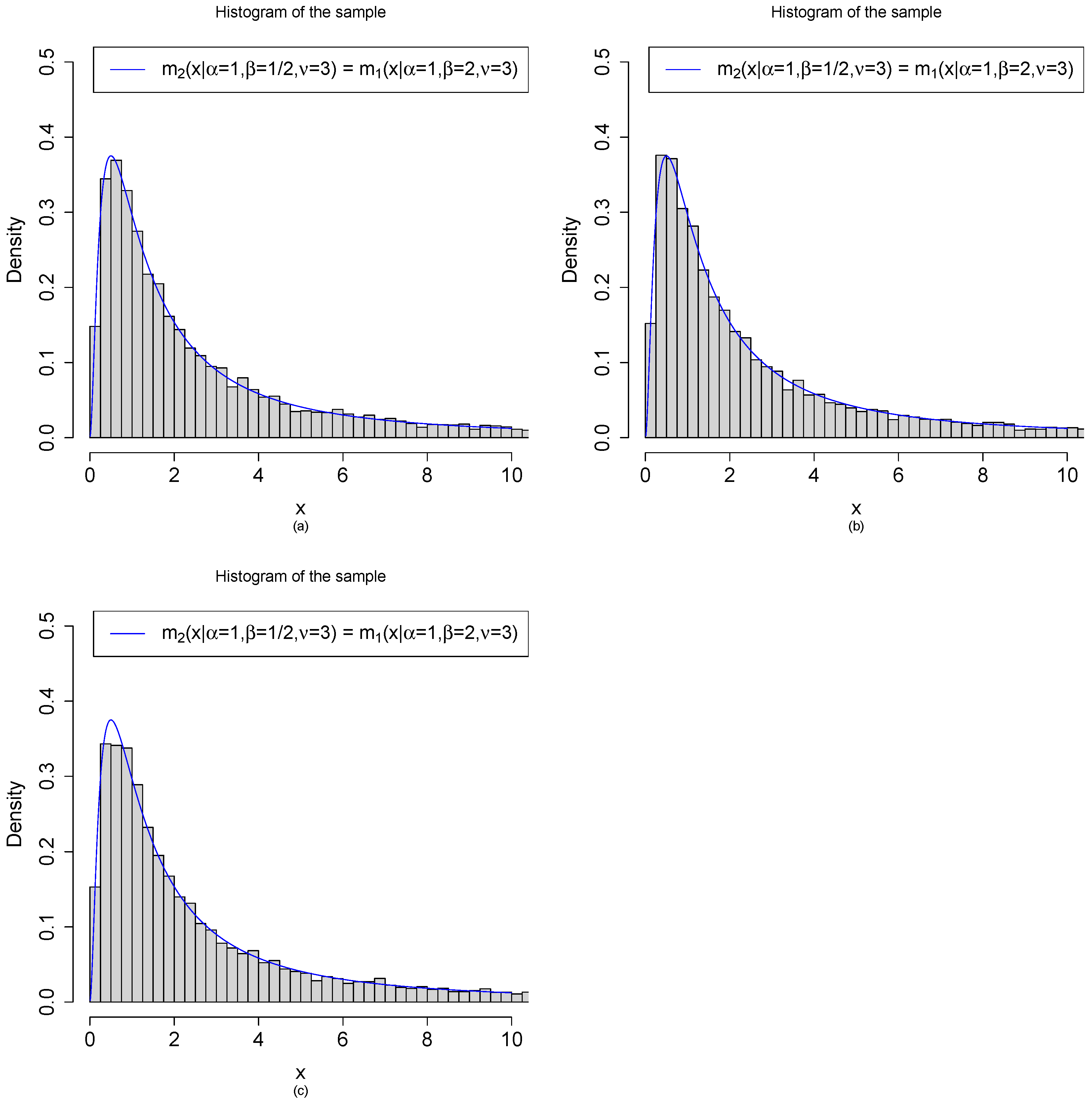
3.2. Random Variable Generations from the Marginal Density by Three Methods
- (a)
- Method 1: are generated from the model. First, we draw iid from . After that, we draw independently from .
- (b)
- Method 2: are generated from the model. First, we draw iid from . After that, we draw independently from .
- (c)
- Method 3: are generated from the transformations of beta random variables. First, we draw iid from . After that, are obtained by the transformations .
- (a)
- Method 1: are generated from the model. First, we draw iid from . After that, we draw independently from .
- (b)
- Method 2: are generated from the model. First, we draw iid from . After that, we draw independently from .
- (c)
- Method 3: are generated from the transformations of beta random variables. First, we draw iid from . After that, are obtained by the transformations .
- (a)
- Method 1: are generated from the model. First, we draw iid from . After that, we draw independently from .
- (b)
- Method 2: are generated from the model. First, we draw iid from . After that, we draw independently from .
- (c)
- Method 3: are generated from the transformations of beta random variables. First, we draw iid from . After that, are obtained by the transformations .
- (a)
- Method 1: are generated from the model. First, we draw iid from . After that, we draw independently from .
- (b)
- Method 2: are generated from the model. First, we draw iid from . After that, we draw independently from .
- (c)
- Method 3: are generated from the transformations of beta random variables. First, we draw iid from . After that, are obtained by the transformations .
3.3. Transformations of the Moment Estimators of the Hyperparameters of One of the Eight Hierarchical Models That Have Conjugate Priors
3.4. The Marginal Densities of the Eight Hierarchical Models That Do Not Have Conjugate Priors
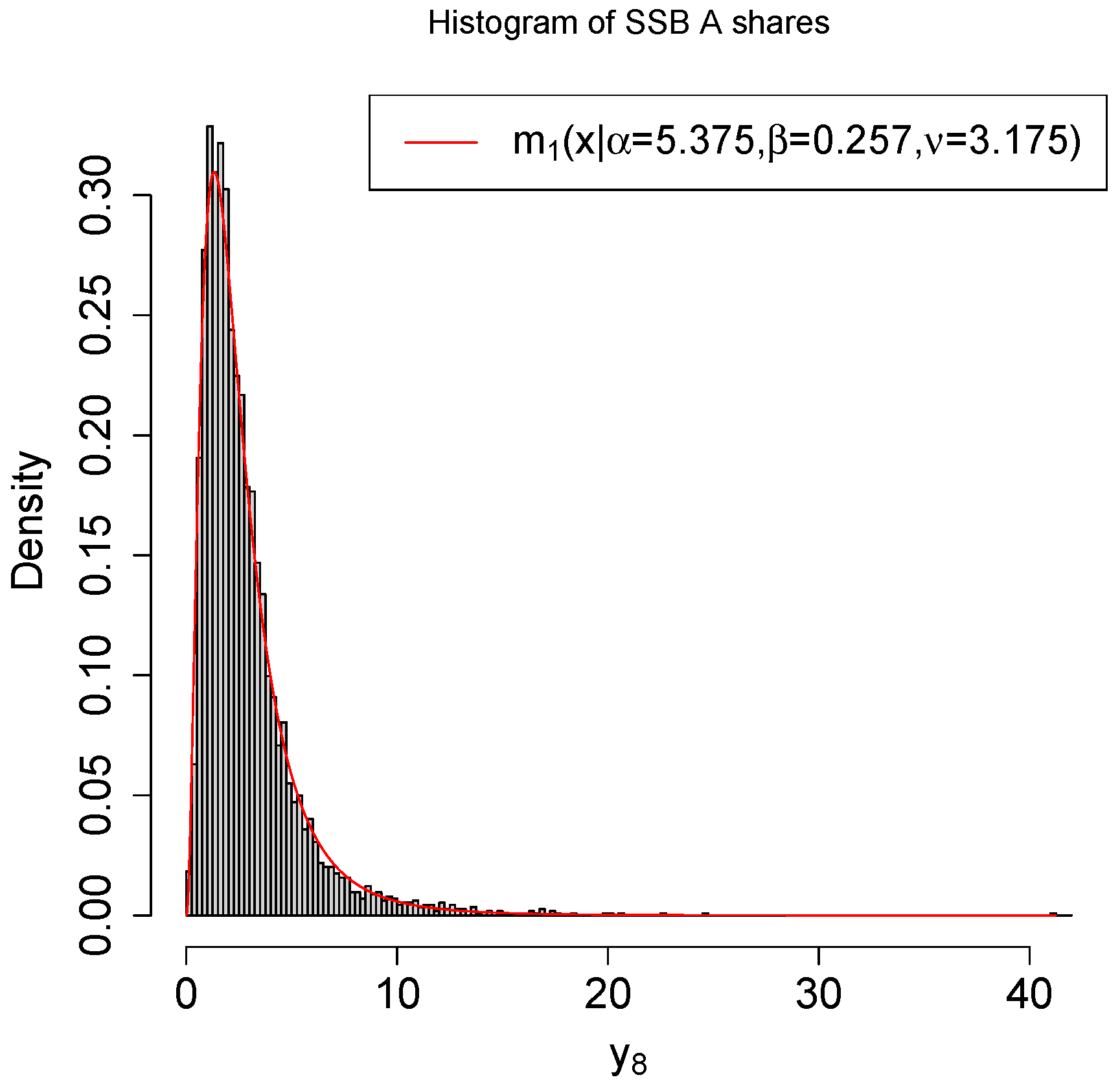
4. A Real Data Example
5. Conclusions and Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Casella, G.; Berger, R.L. Statistical Inference, 2nd ed.; Pacific Grove: Duxbury, MA, USA, 2002. [Google Scholar]
- Shumway, R.; Gurland, J. Fitting the poisson binomial distribution. Biometrics 1960, 16, 522–533. [Google Scholar] [CrossRef]
- Chen, L.H.Y. Convergence of poisson binomial to poisson distributions. Ann. Probab. 1974, 2, 178–180. [Google Scholar] [CrossRef]
- Ehm, W. Binomial approximation to the poisson binomial distribution. Stat. Probab. Lett. 1991, 11, 7–16. [Google Scholar] [CrossRef]
- Daskalakis, C.; Diakonikolas, I.; Servedio, R.A. Learning Poisson Binomial Distributions. Algorithmica 2015, 72, 316–357. [Google Scholar] [CrossRef]
- Duembgen, L.; Wellner, J.A. The density ratio of Poisson binomial versus Poisson distributions. Stat. Probab. Lett. 2020, 165, 1–7. [Google Scholar] [CrossRef]
- Geoffroy, P.; Weerakkody, G. A Poisson-Gamma model for two-stage cluster sampling data. J. Stat. Comput. Simul. 2001, 68, 161–172. [Google Scholar] [CrossRef]
- Vijayaraghavan, R.; Rajagopal, K.; Loganathan, A. A procedure for selection of a gamma-Poisson single sampling plan by attributes. J. Appl. Stat. 2008, 35, 149–160. [Google Scholar] [CrossRef]
- Wang, J.P. Estimating species richness by a Poisson-compound gamma model. Biometrika 2010, 97, 727–740. [Google Scholar] [CrossRef] [PubMed]
- Jakimauskas, G.; Sakalauskas, L. Note on the singularity of the Poisson-gamma model. Stat. Probab. Lett. 2016, 114, 86–92. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Wang, Z.Y.; Duan, Z.M.; Mi, W. The empirical Bayes estimators of the parameter of the Poisson distribution with a conjugate gamma prior under Stein’s loss function. J. Stat. Comput. Simul. 2019, 89, 3061–3074. [Google Scholar] [CrossRef]
- Schmidt, M.; Schwabe, R. Optimal designs for Poisson count data with Gamma block effects. J. Stat. Plan. Inference 2020, 204, 128–140. [Google Scholar] [CrossRef]
- Cabras, S. A Bayesian-deep learning model for estimating COVID-19 evolution in Spain. Mathematics 2021, 9, 2921. [Google Scholar] [CrossRef]
- Wu, S.J. Poisson-Gamma mixture processes and applications to premium calculation. Commun. Stat.-Theory Methods 2022, 51, 5913–5936. [Google Scholar] [CrossRef]
- Singh, S.K.; Singh, U.; Sharma, V.K. Expected total test time and Bayesian estimation for generalized Lindley distribution under progressively Type-II censored sample where removals follow the beta-binomial probability law. Appl. Math. Comput. 2013, 222, 402–419. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Zhou, M.Q.; Xie, Y.H.; Song, W.H. The Bayes rule of the parameter in (0,1) under the power-log loss function with an application to the beta-binomial model. J. Stat. Comput. Simul. 2017, 87, 2724–2737. [Google Scholar] [CrossRef]
- Luo, R.; Paul, S. Estimation for zero-inflated beta-binomial regression model with missing response data. Stat. Med. 2018, 37, 3789–3813. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Xie, Y.H.; Song, W.H.; Zhou, M.Q. Three strings of inequalities among six Bayes estimators. Commun. Stat.-Theory Methods 2018, 47, 1953–1961. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Xie, Y.H.; Song, W.H.; Zhou, M.Q. The Bayes rule of the parameter in (0,1) under Zhang’s loss function with an application to the beta-binomial model. Commun. Stat.-Theory Methods 2020, 49, 1904–1920. [Google Scholar] [CrossRef]
- Gerstenkorn, T. A compound of the generalized negative binomial distribution with the generalized beta distribution. Cent. Eur. J. Math. 2004, 2, 527–537. [Google Scholar] [CrossRef]
- Broderick, T.; Mackey, L.; Paisley, J.; Jordan, M.I. Combinatorial clustering and the beta negative binomial process. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 290–306. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, C.C.F.; Cristino, C.T.; Lima, P.F. Unimodal behaviour of the negative binomial beta distribution. Sigmae 2015, 4, 1–5. [Google Scholar]
- Heaukulani, C.; Roy, D.M. The combinatorial structure of beta negative binomial processes. Bernoulli 2016, 22, 2301–2324. [Google Scholar] [CrossRef]
- Zhou, M.Q.; Zhang, Y.Y.; Sun, Y.; Sun, J.; Rong, T.Z.; Li, M.M. The empirical Bayes estimators of the probability parameter of the beta-negative binomial model under Zhang’s loss function. Chin. J. Appl. Probab. Stat. 2021, 37, 478–494. [Google Scholar]
- Jiang, C.J.; Cockerham, C.C. Use of the multinomial dirichlet model for analysis of subdivided genetic populations. Genetics 1987, 115, 363–366. [Google Scholar] [CrossRef] [PubMed]
- Lenk, P.J. Hierarchical bayes forecasts of multinomial dirichlet data applied to coupon redemptions. J. Forecast. 1992, 11, 603–619. [Google Scholar] [CrossRef]
- Duncan, K.A.; Wilson, J.L. A Multinomial-Dirichlet Model for Analysis of Competing Hypotheses. Risk Anal. 2008, 28, 1699–1709. [Google Scholar] [CrossRef] [PubMed]
- Samb, R.; Khadraoui, K.; Belleau, P.; Deschenes, A.; Lakhal-Chaieb, L.; Droit, A. Using informative Multinomial-Dirichlet prior in a t-mixture with reversible jump estimation of nucleosome positions for genome-wide profiling. Stat. Appl. Genet. Mol. Biol. 2015, 14, 517–532. [Google Scholar] [CrossRef] [PubMed]
- Grover, G.; Deo, V. Application of Parametric Survival Model and Multinomial-Dirichlet Bayesian Model within a Multi-state Setup for Cost-Effectiveness Analysis of Two Alternative Chemotherapies for Patients with Chronic Lymphocytic Leukaemia. Stat. Appl. 2020, 18, 35–53. [Google Scholar]
- Mao, S.S.; Tang, Y.C. Bayesian Statistics, 2nd ed.; China Statistics Press: Beijing, China, 2012. [Google Scholar]
- Zhang, Y.Y.; Ting, N. Bayesian sample size determination for a phase III clinical trial with diluted treatment effect. J. Biopharm. Stat. 2018, 28, 1119–1142. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.Y.; Ting, N. Sample size considerations for a phase III clinical trial with diluted treatment effect. Stat. Biopharm. Res. 2020, 12, 311–321. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Rong, T.Z.; Li, M.M. The estimated and theoretical assurances and the probabilities of launching a phase iii trial. Chin. J. Appl. Probab. Stat. 2022, 38, 53–70. [Google Scholar]
- Zhang, Y.Y.; Ting, N. Can the concept be proven? Stat. Biosci. 2021, 13, 160–177. [Google Scholar] [CrossRef]
- Robert, C.P. The Bayesian Choice: From Decision-Theoretic Motivations to Computational Implementation, 2nd ed.; Springer: New York, NY, USA, 2007. [Google Scholar]
- Zhang, Y.Y. The Bayes rule of the variance parameter of the hierarchical normal and inverse gamma model under Stein’s loss. Commun. Stat.-Theory Methods 2017, 46, 7125–7133. [Google Scholar] [CrossRef]
- Chen, M.H. Bayesian Statistics Lecture; Statistics Graduate Summer School, School of Mathematics and Statistics, Northeast Normal University: Changchun, China, 2014. [Google Scholar]
- Xie, Y.H.; Song, W.H.; Zhou, M.Q.; Zhang, Y.Y. The Bayes posterior estimator of the variance parameter of the normal distribution with a normal-inverse-gamma prior under Stein’s loss. Chin. J. Appl. Probab. Stat. 2018, 34, 551–564. [Google Scholar]
- Zhang, Y.Y.; Rong, T.Z.; Li, M.M. The empirical Bayes estimators of the mean and variance parameters of the normal distribution with a conjugate normal-inverse-gamma prior by the moment method and the MLE method. Commun. Stat.-Theory Methods 2019, 48, 2286–2304. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, Y.Y.; Sun, Y. The empirical Bayes estimators of the rate parameter of the inverse gamma distribution with a conjugate inverse gamma prior under Stein’s loss function. J. Stat. Comput. Simul. 2021, 91, 1504–1523. [Google Scholar] [CrossRef]
- Lee, M.; Gross, A. Lifetime distributions under unknown environment. J. Stat. Plan. Inference 1991, 29, 137–143. [Google Scholar]
- Pham, T.; Almhana, J. The generalized gamma distribution: Its hazard rate and strength model. IEEE Trans. Reliab. 1995, 44, 392–397. [Google Scholar] [CrossRef]
- Agarwal, S.K.; Kalla, S.L. A generalized gamma distribution and its application in reliability. Commun. Stat.-Theory Methods 1996, 25, 201–210. [Google Scholar] [CrossRef]
- Agarwal, S.K.; Al-Saleh, J.A. Generalized gamma type distribution and its hazard rate function. Commun. Stat.-Theory Methods 2001, 30, 309–318. [Google Scholar] [CrossRef]
- Kobayashi, K. On generalized gamma functions occurring in diffraction theory. J. Phys. Soc. Jpn. 1991, 60, 1501–1512. [Google Scholar] [CrossRef]
- Al-Saleh, J.A.; Agarwal, S.K. Finite mixture of certain distributions. Commun. Stat.-Theory Methods 2002, 31, 2123–2137. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- Berger, J.O. Statistical Decision Theory and Bayesian Analysis, 2nd ed.; Springer: New York, NY, USA, 1985. [Google Scholar]
- Maritz, J.S.; Lwin, T. Empirical Bayes Methods, 2nd ed.; Chapman & Hall: London, UK, 1989. [Google Scholar]
- Carlin, B.P.; Louis, A. Bayes and Empirical Bayes Methods for Data Analysis, 2nd ed.; Chapman & Hall: London, UK, 2000. [Google Scholar]




| Prior | ||||
|---|---|---|---|---|
| Likelihood | ||||
| Moment Estimators of the Hyperparameters | Transformations from the Model | |||||
|---|---|---|---|---|---|---|
| Model 1 () | ||||||
| Model 2 () | ||||||
| Model 3 () | ||||||
| Model 4 () | ||||||
| Model 5 () | ||||||
| Model 6 () | ||||||
| Model 7 () | ||||||
| Model 8 () | ||||||
| Fit Marginal Densities | D-Value | p-Value |
|---|---|---|
| <2.2 | ||
| <2.2 | ||
| <2.2 | ||
| <2.2 | ||
| 4.7 | ||
| 4.7 | ||
| 4. | ||
| 4.7 | ||
| Sample Size | Mean | Variance | Standard Deviation | Skewness | Kurtosis |
|---|---|---|---|---|---|
| 4575 |
| Transformations | Moment Estimators | KS Test | |||
|---|---|---|---|---|---|
| D-Value | p-Value | ||||
| <2.2 | |||||
| <2.2 | |||||
| NA | NA | ||||
| NA | NA | ||||
| NA | NA | ||||
| NA | NA | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Zhang, Y.-Y. The Bayesian Posterior and Marginal Densities of the Hierarchical Gamma–Gamma, Gamma–Inverse Gamma, Inverse Gamma–Gamma, and Inverse Gamma–Inverse Gamma Models with Conjugate Priors. Mathematics 2022, 10, 4005. https://doi.org/10.3390/math10214005
Zhang L, Zhang Y-Y. The Bayesian Posterior and Marginal Densities of the Hierarchical Gamma–Gamma, Gamma–Inverse Gamma, Inverse Gamma–Gamma, and Inverse Gamma–Inverse Gamma Models with Conjugate Priors. Mathematics. 2022; 10(21):4005. https://doi.org/10.3390/math10214005
Chicago/Turabian StyleZhang, Li, and Ying-Ying Zhang. 2022. "The Bayesian Posterior and Marginal Densities of the Hierarchical Gamma–Gamma, Gamma–Inverse Gamma, Inverse Gamma–Gamma, and Inverse Gamma–Inverse Gamma Models with Conjugate Priors" Mathematics 10, no. 21: 4005. https://doi.org/10.3390/math10214005
APA StyleZhang, L., & Zhang, Y.-Y. (2022). The Bayesian Posterior and Marginal Densities of the Hierarchical Gamma–Gamma, Gamma–Inverse Gamma, Inverse Gamma–Gamma, and Inverse Gamma–Inverse Gamma Models with Conjugate Priors. Mathematics, 10(21), 4005. https://doi.org/10.3390/math10214005






