An SDP Dual Relaxation for the Robust Shortest-Path Problem with Ellipsoidal Uncertainty: Pierra’s Decomposition Method and a New Primal Frank–Wolfe-Type Heuristics for Duality Gap Evaluation
Abstract
:1. Introduction
2. The Robust Shortest-Path Problem
2.1. Problem Statement
2.2. Exact Method for Solving the Robust Problem
2.3. A Heuristic Approach Based on Frank–Wolfe
| Algorithm 1 DFW: a Frank–Wolfe based algorithm to solve (7) |
|
3. A Lower Bound by SDP Relaxation
3.1. Bidualization of a Quadratic Problem
3.2. Applying This Bidualization to Compute a Lower Bound for the Robust Shortest-Path Problem
3.2.1. Bidualization of the Addressed Problem
- the vector of size is defined block-wise as , so that if ,
- for any , is such that if , and 0 if else, so that , and for ,
- is an matrix such that and 0 elsewhere, so that and ,
- for any , is a matrix, such that if and , and 0 if else. So that , , and for ,
- is an matrix such that and the other entries are zeros, so that ,
- is an matrix such that and the other entries are zeros, so that .
- (1)
- For any , write , where is defined by
- (2)
- For any , write , where is defined by
3.2.2. The Biduality Gap
3.3. Solving the SDP Problem
3.3.1. Pierra’s Decomposition through Formalization in a Product Space
| Algorithm 2 Pierra’s algorithm to solve (23) |
|
3.3.2. Adaptation of Pierra’s Algorithm to Solve the Considered SDP Problem
| Algorithm 3 Pierra’s algorithm to solve the SDP problem (19) |
|
4. Experimental Results
4.1. Experimental Setup
4.2. Numerical Evaluation of the Heuristic Approach DFW
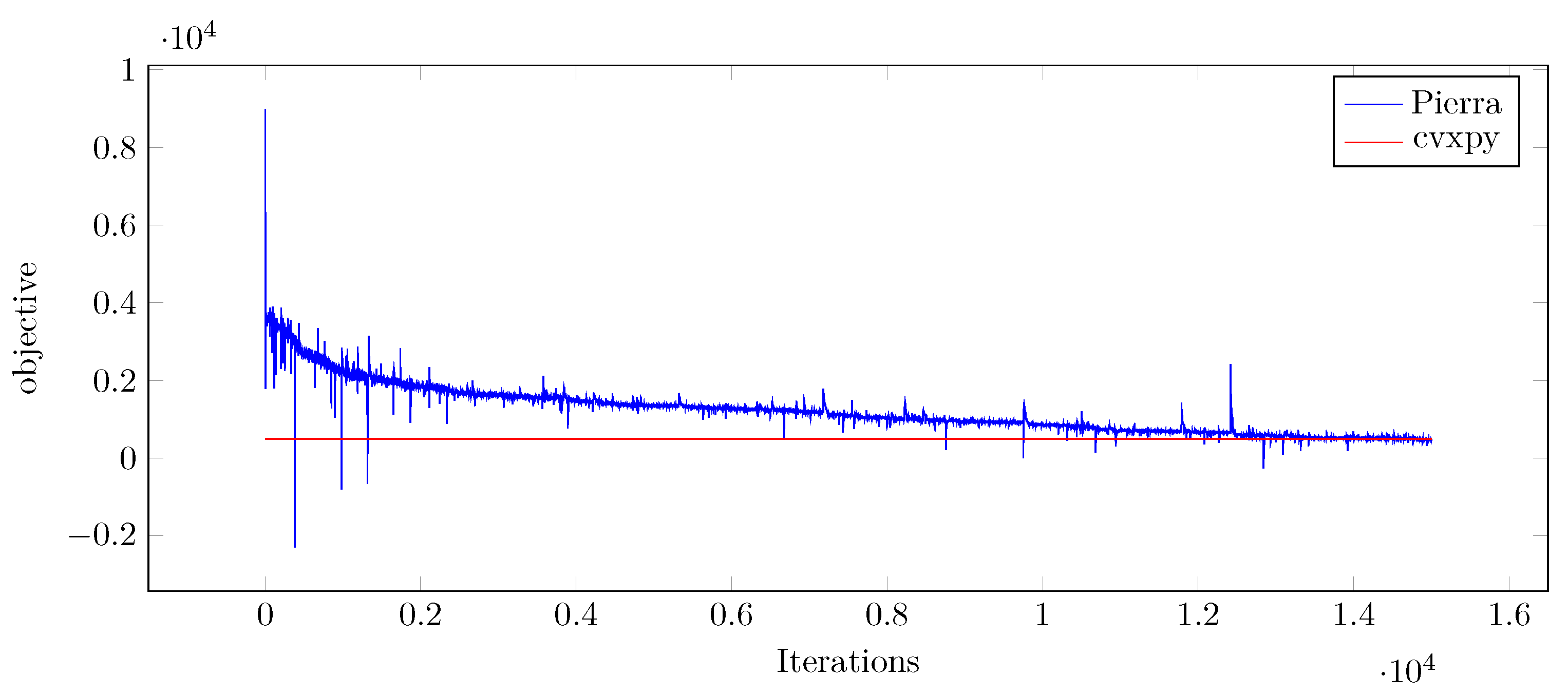
4.3. Numerical Results of Pierra’s Algorithm
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Sparse Computations
- 1:
- 1:
- 2:
- 3:
- 4:
- 5:
- 1:
- 1:
- 2:
- 3:
- 1:
- 1:
- 2:
- 3:
- 4:
- 5:
- 1:
- 1:
- 2:
- for i between 1 and m.
- 3:
- 4:
- 1:
- 1:
- 2:
- 3:
- 4:
- 1:
- 1:
- 2:
- 3:
- 4:
References
- Kouvelis, P.; Yu, G. Robust Discrete Optimization and Its Applications; Springer Science & Business Media: New York, NY, USA, 2013; Volume 14. [Google Scholar]
- Li, Z.; Ding, R.; Floudas, C.A. A comparative theoretical and computational study on robust counterpart optimization: I. Robust linear optimization and robust mixed integer linear optimization. Ind. Eng. Chem. Res. 2011, 50, 10567–10603. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ben-Tal, A.; Goryashko, A.; Guslitzer, E.; Nemirovski, A. Adjustable robust solutions of uncertain linear programs. Math. Program. 2004, 99, 351–376. [Google Scholar] [CrossRef]
- Hanasusanto, G.A.; Kuhn, D.; Wiesemann, W. K-adaptability in two-stage distributionally robust binary programming. Oper. Res. Lett. 2016, 44, 6–11. [Google Scholar] [CrossRef] [Green Version]
- Rahimian, H.; Mehrotra, S. Distributionally robust optimization: A review. arXiv 2019, arXiv:1908.05659. [Google Scholar]
- Baron, O.; Berman, O.; Fazel-Zarandi, M.M.; Roshanaei, V. Almost Robust Discrete Optimization. Eur. J. Oper. Res. 2019, 276, 451–465. [Google Scholar] [CrossRef]
- Buhmann, J.M.; Gronskiy, A.Y.; Mihalák, M.; Pröger, T.; Šrámek, R.; Widmayer, P. Robust optimization in the presence of uncertainty: A generic approach. J. Comput. Syst. Sci. 2018, 94, 135–166. [Google Scholar] [CrossRef]
- Hazan, E. Introduction to online convex optimization. Found. Trends® Optim. 2016, 2, 157–325. [Google Scholar] [CrossRef] [Green Version]
- Liu, B. Some research problems in uncertainty theory. J. Uncertain Syst. 2009, 3, 3–10. [Google Scholar]
- Gao, Y. Shortest path problem with uncertain arc lengths. Comput. Math. Appl. 2011, 62, 2591–2600. [Google Scholar] [CrossRef] [Green Version]
- Markowitz, H. Portfolio selection. J. Financ. 1952, 7, 77–91. [Google Scholar]
- Poss, M. Robust combinatorial optimization with knapsack uncertainty. Discret. Optim. 2018, 27, 88–102. [Google Scholar] [CrossRef] [Green Version]
- Nikolova, E. Approximation algorithms for reliable stochastic combinatorial optimization. In Approximation, Randomization, and Combinatorial Optimization. Algorithms and Techniques; Springer: Berlin/Heidelberg, Germany, 2010; pp. 338–351. [Google Scholar]
- Baumann, F.; Buchheim, C.; Ilyina, A. A Lagrangean decomposition approach for robust combinatorial optimization. In Technical Report; Optimization Online; 2014; Available online: http://www.optimization-online.org/DB_FILE/2014/07/4471.pdf (accessed on 22 October 2019).
- Atamtürk, A.; Narayanan, V. Polymatroids and mean-risk minimization in discrete optimization. Oper. Res. Lett. 2008, 36, 618–622. [Google Scholar] [CrossRef] [Green Version]
- Buchheim, C.; Kurtz, J. Robust combinatorial optimization under convex and discrete cost uncertainty. EURO J. Comput. Optim. 2018, 6, 211–238. [Google Scholar] [CrossRef]
- Al Dahik, C.; Al Masry, Z.; Chrétien, S.; Nicod, J.M.; Rabehasaina, L. A Frank-Wolfe Based Algorithm for Robust Discrete Optimization under Uncertainty. In Proceedings of the 2020 Prognostics and Health Management Conference (PHM-Besançon), Besançon, France, 4–7 May 2020; IEEE: New York, NY, USA, 2020; pp. 247–252. [Google Scholar]
- Boyd, S.; Boyd, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Anjos, M.F.; Lasserre, J.B. Handbook on Semidefinite, Conic and Polynomial Optimization; Springer Science & Business Media: New York, NY, USA, 2011; Volume 166. [Google Scholar]
- Scobey, P.; Kabe, D. Vector quadratic programming problems and inequality constrained least squares estimation. J. Indust. Math. Soc. 1978, 28, 37–49. [Google Scholar]
- Fletcher, R. A nonlinear programming problem in statistics (educational testing). SIAM J. Sci. Stat. Comput. 1981, 2, 257–267. [Google Scholar] [CrossRef]
- Boyd, S.; El Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; Siam: Philadelphia, PA, USA, 1994; Volume 15. [Google Scholar]
- Goemans, M.X.; Williamson, D.P. Improved approximation algorithms for maximum cut and satisfiability problems using semidefinite programming. J. ACM (JACM) 1995, 42, 1115–1145. [Google Scholar] [CrossRef]
- Karger, D.; Motwani, R.; Sudan, M. Approximate graph coloring by semidefinite programming. J. ACM (JACM) 1998, 45, 246–265. [Google Scholar] [CrossRef]
- Goemans, M.X.; Williamson, D.P. New 34-approximation algorithms for the maximum satisfiability problem. SIAM J. Discret. Math. 1994, 7, 656–666. [Google Scholar] [CrossRef]
- Lemaréchal, C.; Oustry, F. Semidefinite relaxations and Lagrangian duality with application to combinatorial optimization. Ph.D. Thesis, National Institute for Research in Digital Science and Technology (INRIA), Grenoble-Rhone-Alpes, France, 1999. [Google Scholar]
- Goemans, M.X. Semidefinite programming in combinatorial optimization. Math. Program. 1997, 79, 143–161. [Google Scholar] [CrossRef]
- Wolkowicz, H. Semidefinite and Lagrangian relaxations for hard combinatorial problems. In Proceedings of the IFIP Conference on System Modeling and Optimization, Cambridge, UK, 12–16 July 1999; Springer: Berlin/Heidelberg, Germany, 1999; pp. 269–309. [Google Scholar]
- Nesterov, Y.; Nemirovski, A. Interior-Point Polynomial Algorithms in Convex Programming; Studies in Applied and Numerical Mathematics Series; Book Code AM13; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1994; pp. ix + 396. [Google Scholar]
- Boyd, S.; Parikh, N.; Chu, E. Distributed Optimization and Statistical Learning Via the Alternating Direction Method of Multipliers; Now Publishers Inc.: Delft, The Netherlands, 2011. [Google Scholar]
- Pierra, G. Decomposition through Formalization in a Product Space. Math. Program. 1984, 28, 96–115. [Google Scholar] [CrossRef]
- Schrijver, A. A course in combinatorial optimization. CWI Kruislaan 2003, 413, 1098. [Google Scholar]
- Chew, V. Confidence, prediction, and tolerance regions for the multivariate normal distribution. J. Am. Stat. Assoc. 1966, 61, 605–617. [Google Scholar] [CrossRef]
- Ilyina, A. Combinatorial Optimization under Ellipsoidal Uncertainty. Ph.D. Thesis, Technische Universität Dortmund, Dortmund Germany, 2017. [Google Scholar]
- IBM Academic Portal. Available online: https://www.ibm.com/academic (accessed on 22 October 2019).
- Frank, M.; Wolfe, P. An algorithm for quadratic programming. Nav. Res. Logist. Q. 1956, 3, 95–110. [Google Scholar] [CrossRef]
- Lee, J. A First Course in Combinatorial Optimization; Cambridge University Press: Cambridge, UK, 2004; Volume 36. [Google Scholar]
- Diamond, S.; Boyd, S. CVXPY: A Python-embedded modeling language for convex optimization. J. Mach. Learn. Res. 2016, 17, 2909–2913. [Google Scholar]
- Karloff, H. How Good is the Goemans–Williamson MAX CUT Algorithm? SIAM J. Comput. 1999, 29, 336–350. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Benson, S.J.; Ye, Y.; Zhang, X. Solving large-scale sparse semidefinite programs for combinatorial optimization. SIAM J. Optim. 2000, 10, 443–461. [Google Scholar] [CrossRef] [Green Version]
| Mean Relative Gap | Standard Deviation Relative Gap | Mean Performance Ratio | |||||
|---|---|---|---|---|---|---|---|
| Optim Gap | Bidual | Naive | Bidual | Naive | Bidual | Naive | |
| 3 | 0 | 0.212 | 0.401 | 0.050 | 0.052 | 0.7879 | 0.599 |
| 4 | 0 | 0.174 | 0.486 | 0.037 | 0.130 | 0.826 | 0.514 |
| 5 | 0 | 0.182 | 0.371 | 0.022 | 0.216 | 0.818 | 0.629 |
| 6 | 0 | 0.157 | 0.289 | 0.024 | 0.150 | 0.842 | 0.711 |
| 7 | 0 | 0.196 | 0.560 | 0.091 | 0.185 | 0.804 | 0.440 |
| 8 | 0 | 0.136 | 0.573 | 0.036 | 0.114 | 0.864 | 0.427 |
| 9 | 0 | 0.120 | 0.501 | 0.031 | 0.120 | 0.880 | 0.499 |
| 10 | 0 | 0.124 | 0.748 | 0.056 | 0.217 | 0.876 | 0.252 |
| Time (s) | Storage Needed (mB) | ||||
|---|---|---|---|---|---|
| L | CVXPY | Pierra | CVXPY | Pierra | Optimality Percentage of Pierra (% CVXPY) |
| 3 | 11 | 3.7 | 1.29792 | 0.13632 | 96.4% |
| 4 | 49.6761 | 97.2 | 9.2 | 0.50496 | 77% |
| 5 | 145.93 | 631 | 40.45 | 1.358848 | 86% |
| 6 | 394.2456 | 1005.4 | 132.88 | 3.008448 | 92.2% |
| 7 | 935.8 | 2275 | 358.82 | 5.841792 | 92.4% |
| 8 | 2274.85 | 7826 | 841.73 | 10.32448 | 96% |
| 9 | 4724.6 | 22338 | 1776.192 | 16.99968 | 97% |
| 10 | 9244.87 | 63585 | 3451.17 | 26.488128 | 99.93% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dahik, C.A.; Al Masry, Z.; Chrétien, S.; Nicod, J.-M.; Rabehasaina, L. An SDP Dual Relaxation for the Robust Shortest-Path Problem with Ellipsoidal Uncertainty: Pierra’s Decomposition Method and a New Primal Frank–Wolfe-Type Heuristics for Duality Gap Evaluation. Mathematics 2022, 10, 4009. https://doi.org/10.3390/math10214009
Dahik CA, Al Masry Z, Chrétien S, Nicod J-M, Rabehasaina L. An SDP Dual Relaxation for the Robust Shortest-Path Problem with Ellipsoidal Uncertainty: Pierra’s Decomposition Method and a New Primal Frank–Wolfe-Type Heuristics for Duality Gap Evaluation. Mathematics. 2022; 10(21):4009. https://doi.org/10.3390/math10214009
Chicago/Turabian StyleDahik, Chifaa Al, Zeina Al Masry, Stéphane Chrétien, Jean-Marc Nicod, and Landy Rabehasaina. 2022. "An SDP Dual Relaxation for the Robust Shortest-Path Problem with Ellipsoidal Uncertainty: Pierra’s Decomposition Method and a New Primal Frank–Wolfe-Type Heuristics for Duality Gap Evaluation" Mathematics 10, no. 21: 4009. https://doi.org/10.3390/math10214009






