Stochastic Modeling of Within-Host Dynamics of Plasmodium Falciparum
Abstract
1. Introduction
2. Materials and Methods
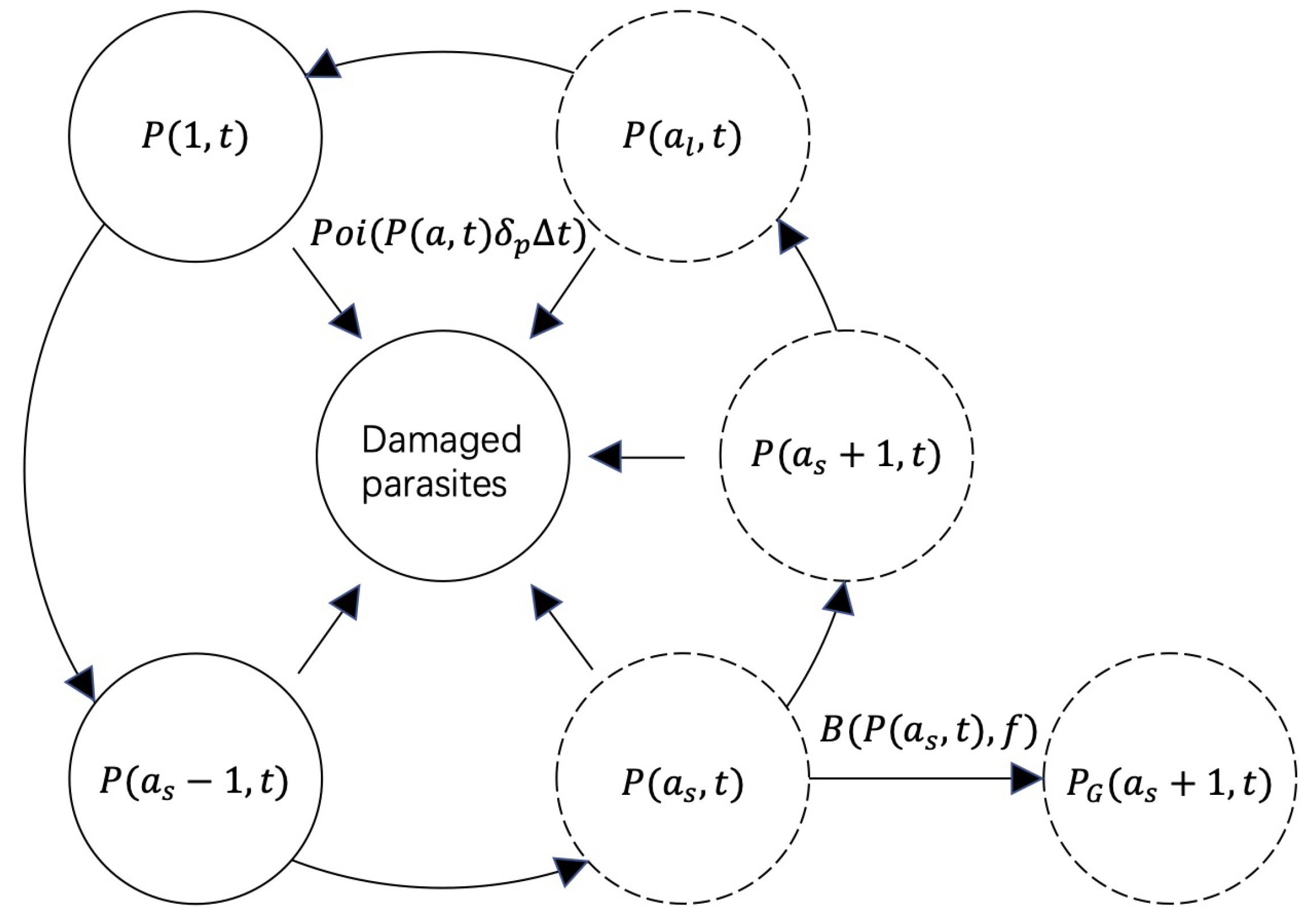
2.1. The Stochastic Model of Within-Host Malaria Dynamics
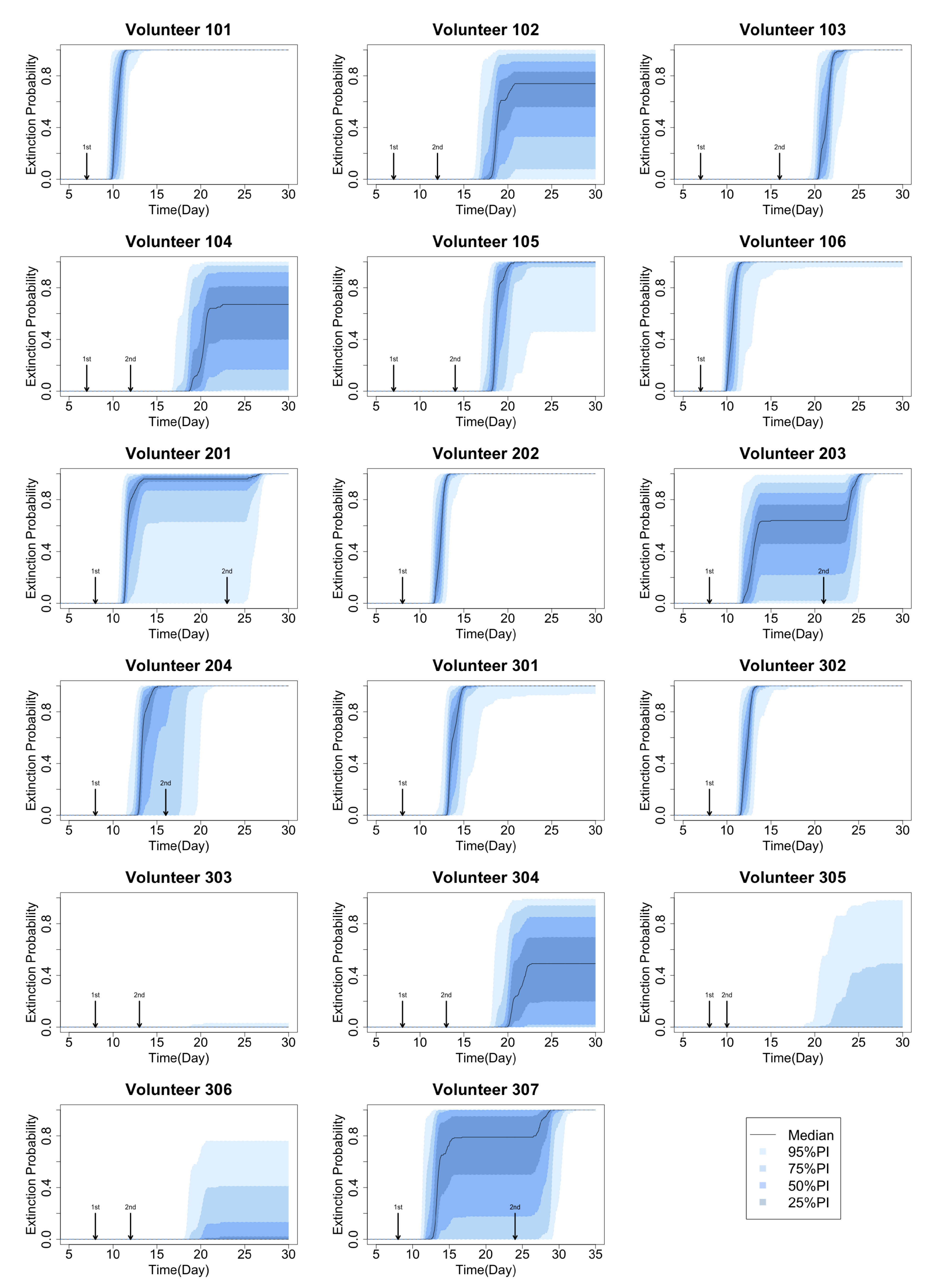
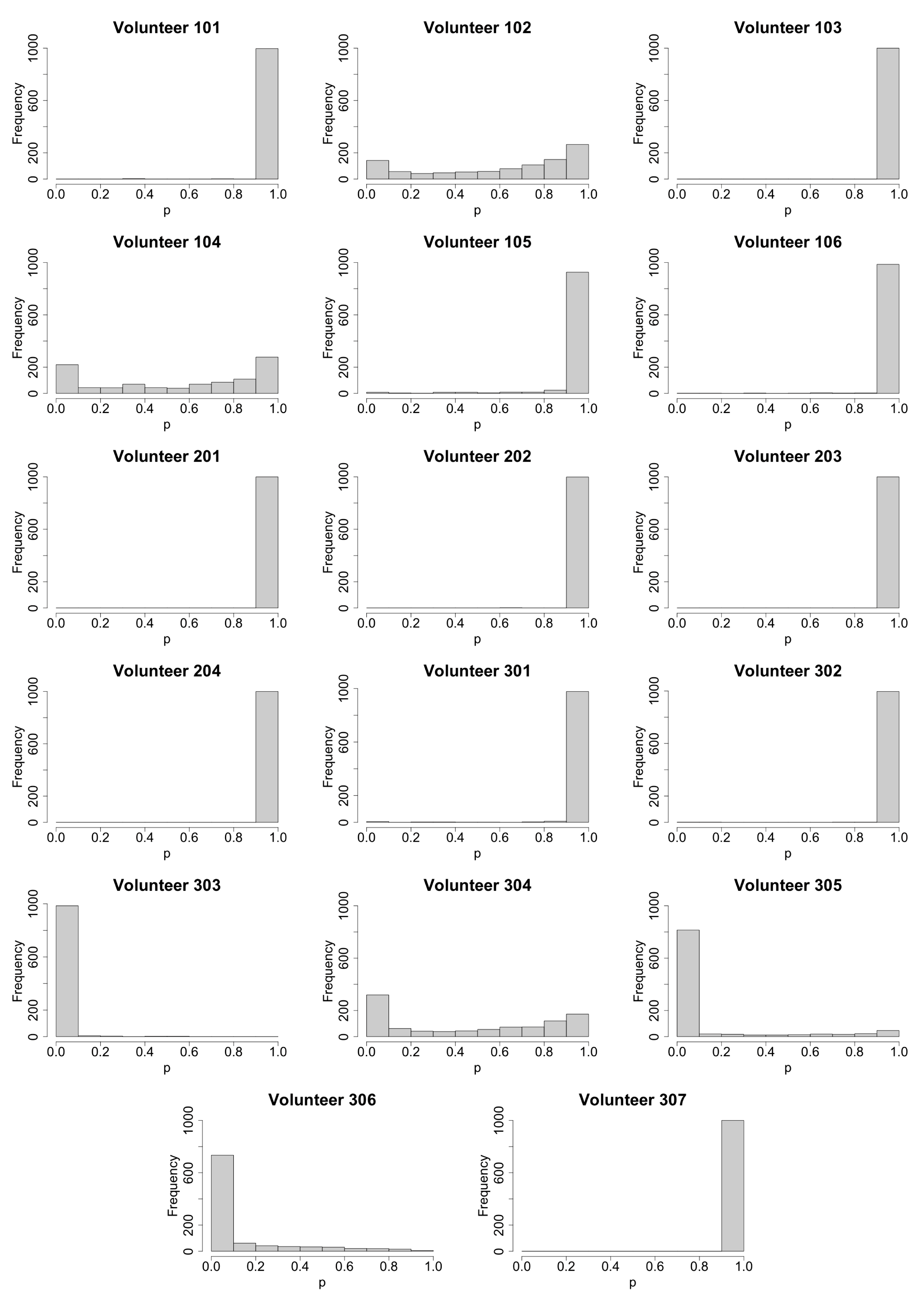
2.2. Method for Calculating Extinction Probability
2.3. Method for Calculating the Correlations between Model Parameters and Extinction Probability
3. Results
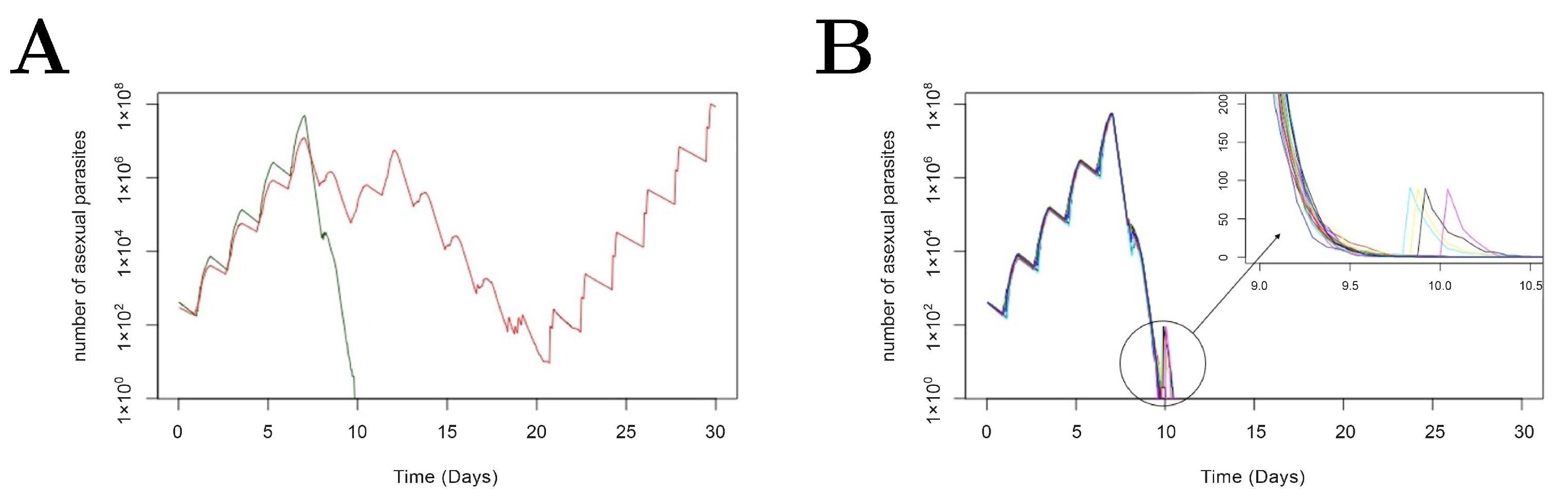
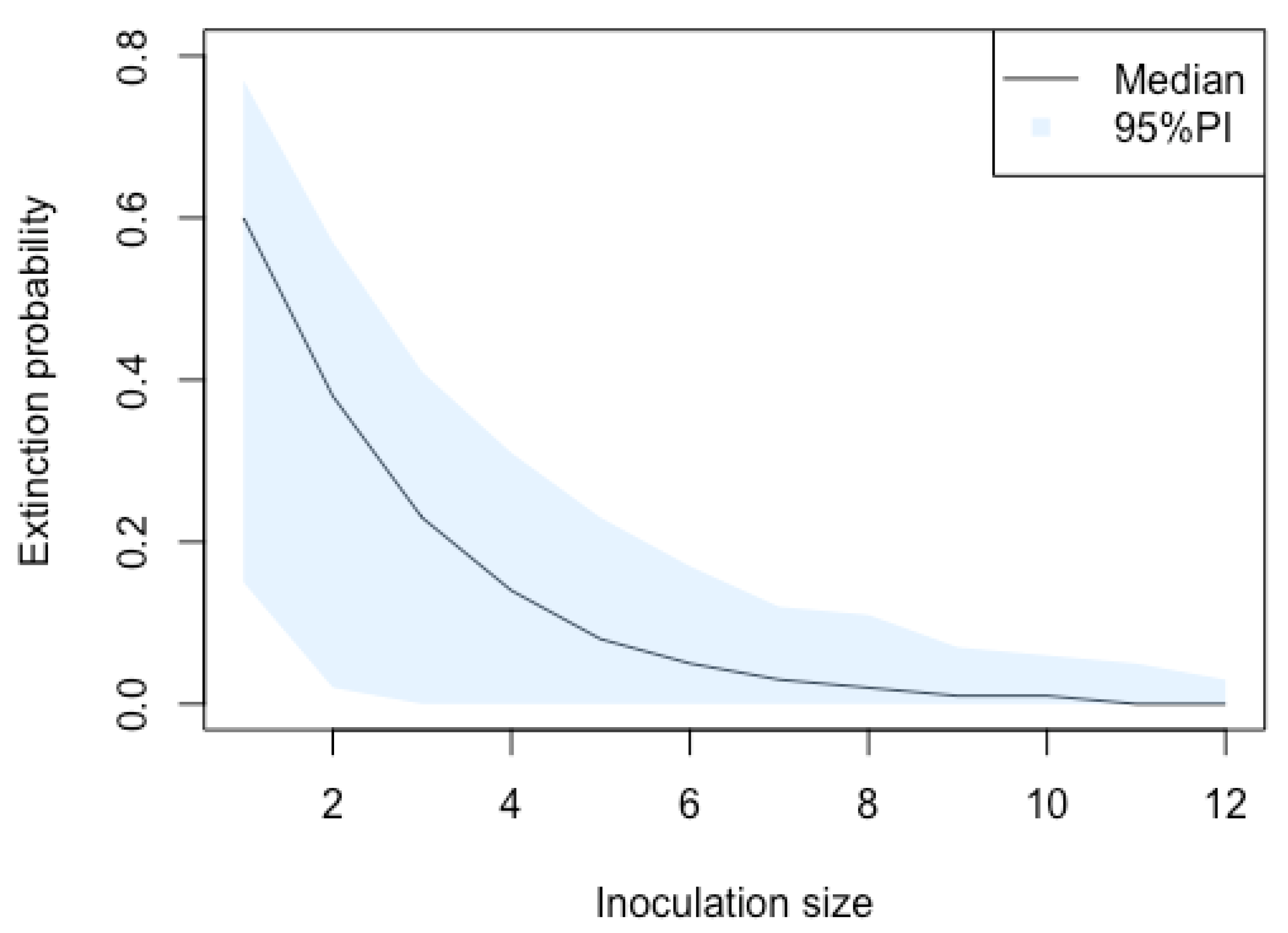
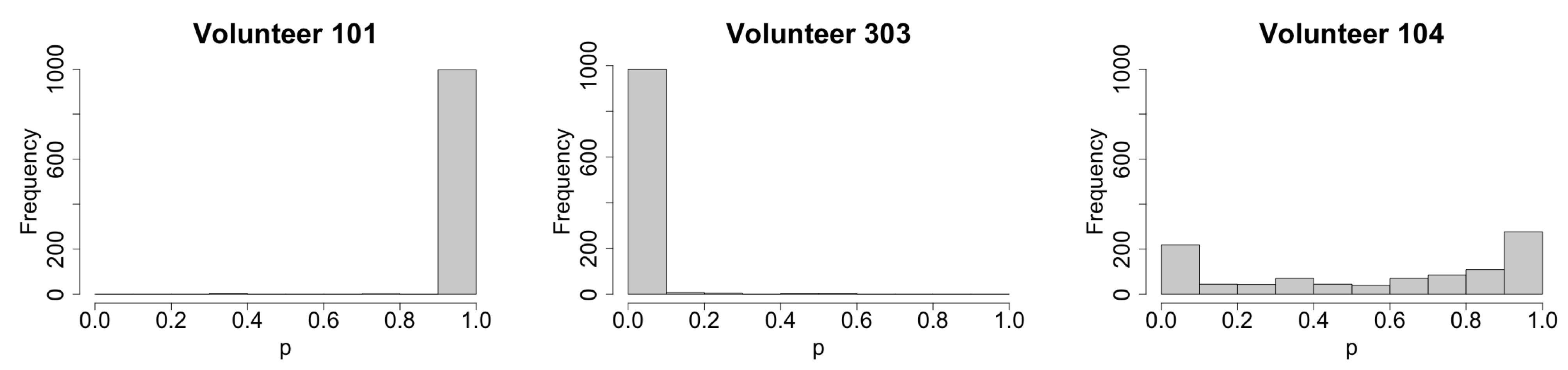
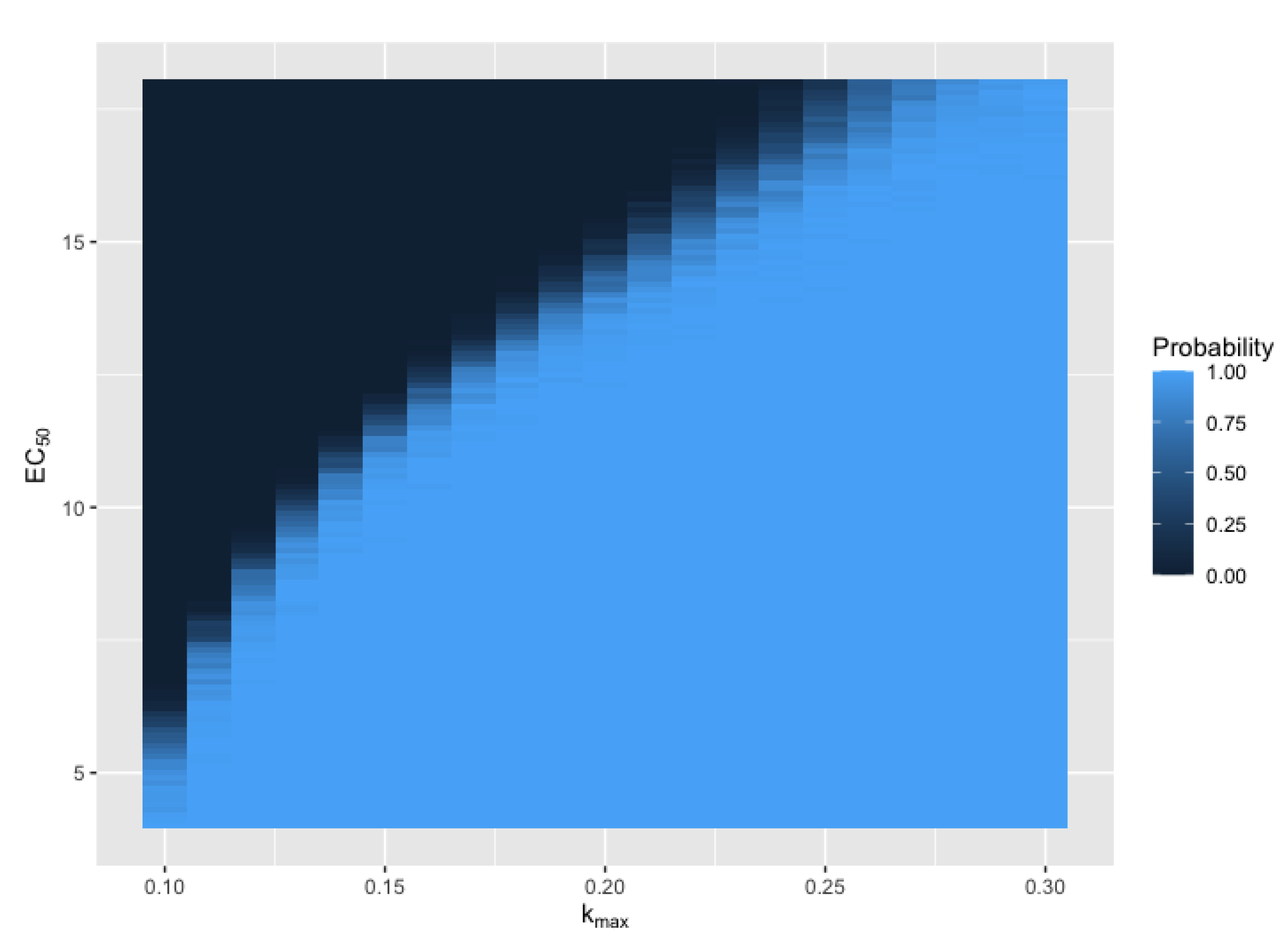
3.1. Stochastic Effect and Extinction Probability
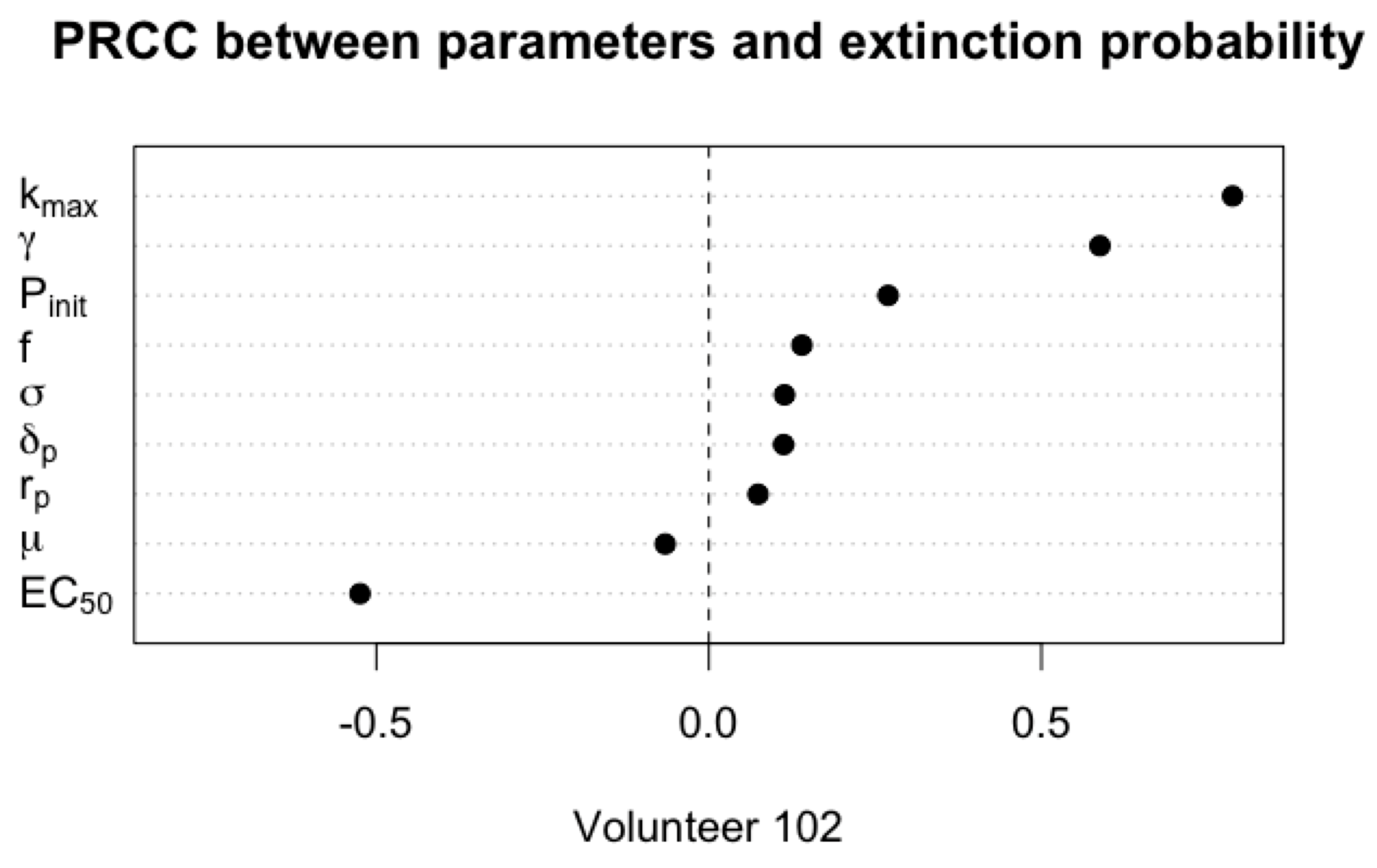
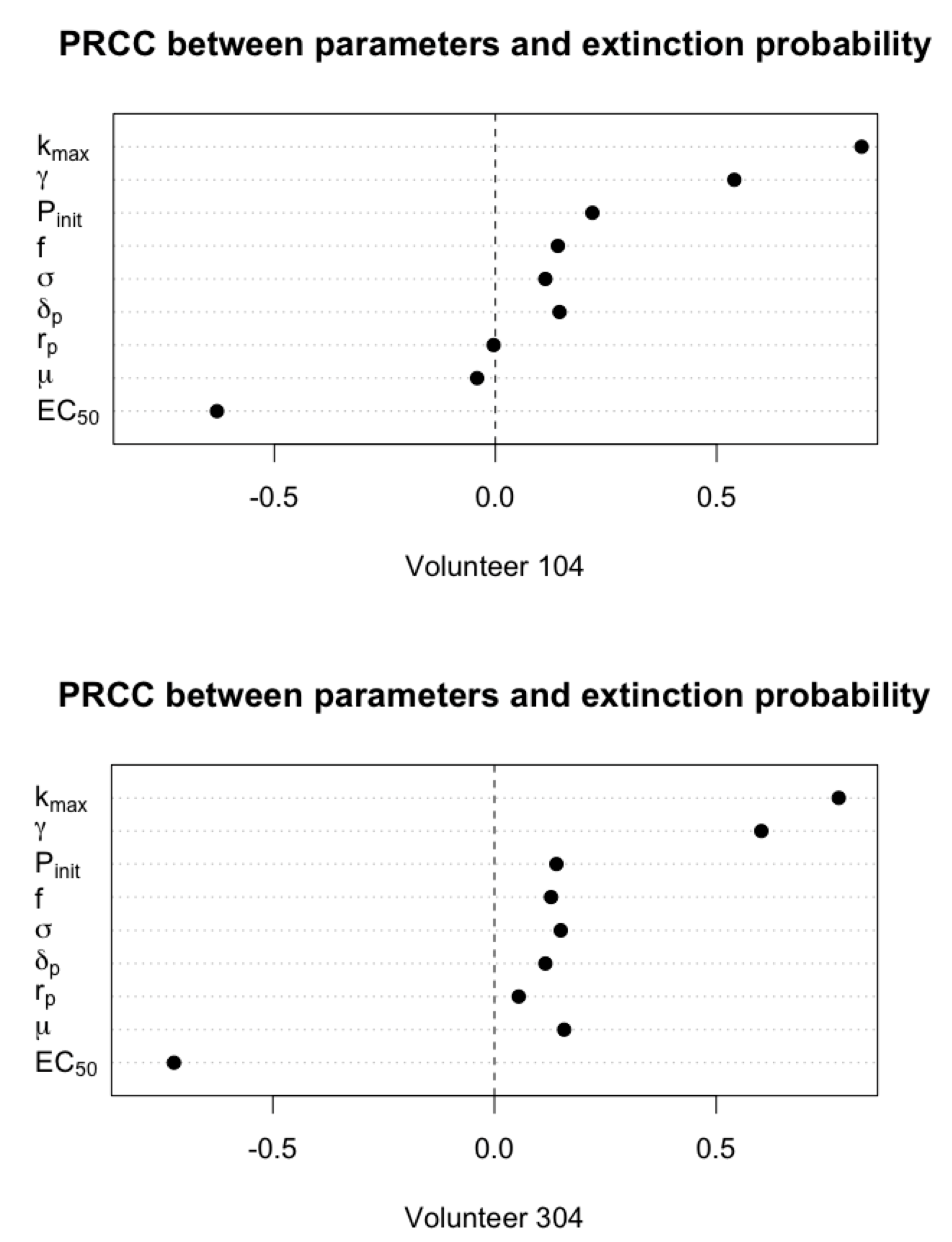
3.2. Primary Parameters Affecting Extinction Probability
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| P. | Plasmodium |
| RBC | Red blood cell |
| pRBC | parasitized red blood cell |
| VIS | Volunteer infection study |
| PRCC | Partial rank correlation coefficient |
Appendix A
References
- Caraballo, H.; King, K. Emergency department management of mosquito-borne illness: Malaria, dengue, and West Nile virus. Emerg. Med. Pract. 2014, 16, 1–23. [Google Scholar] [PubMed]
- Lin, J.T.; Juliano, J.J.; Wongsrichanalai, C. Drug-Resistant Malaria: The Era of ACT. Curr. Infect. Dis. Rep. 2010, 12, 165–173. [Google Scholar] [CrossRef]
- Alonso, P.L.; Brown, G.V.; Arévalo-Herrera, M.; Binka, F.N.; Chitnis, C.E.; Collins, F.; Doumbo, O.K.; Greenwood, B.; Hall, B.F.; Levine, M.M.; et al. A Research Agenda to Underpin Malaria Eradication. PLoS Med. 2011, 8, e1000406. [Google Scholar] [CrossRef] [PubMed]
- Simpson, J.A.; Zaloumis, S.G.; DeLivera, A.M.; Price, R.N.; McCaw, J.M. Making the Most of Clinical Data: Reviewing the Role of Pharmacokinetic-Pharmacodynamic Models of Anti-malarial Drugs. AAPS J. 2014, 16, 962–974. [Google Scholar] [CrossRef] [PubMed]
- Hoshen, M.B.; Heinrich, R.; Stein, W.D.; Ginsburg, H. Mathematical modelling of the within-host dynamics of Plasmodium falciparum. Parasitology 2000, 121, 227–235. [Google Scholar] [CrossRef] [PubMed]
- Smith, T.A.; Dietz, K.; Vounatsou, P.; Muller, I.; English, M.; Marsh, K. Bayesian age-stage modelling of Plasmodium falciparum sequestered parasite loads in severe malaria patients. Parasitology 2004, 129, 289–299. [Google Scholar] [CrossRef] [PubMed]
- Saralamba, S.; Pan-ngum, W.; Maude, R.J.; Lee, S.J.; Tarning, J.; Lindegårdh, N.; Chotivanich, K.; Nosten, F.H.; Day, N.P.J.; Socheat, D.; et al. Intrahost modeling of artemisinin resistance in Plasmodium falciparum. Proc. Natl. Acad. Sci. USA 2010, 108, 397–402. [Google Scholar] [CrossRef] [PubMed]
- Zaloumis, S.G.; Humberstone, A.J.; Charman, S.A.; Price, R.N.; Moehrle, J.J.; Gamo-Benito, J.; McCaw, J.M.; Jamsen, K.M.; Smith, K.; Simpson, J.A. Assessing the utility of an anti-malarial pharmacokinetic-pharmacodynamic model for aiding drug clinical development. Malar. J. 2012, 11, 303. [Google Scholar] [CrossRef] [PubMed]
- Cao, P.; Collins, K.A.; Zaloumis, S.; Wattanakul, T.; Mccaw, J.M. Modeling the dynamics of Plasmodium falciparum gametocytes in humans during malaria infection. eLife 2019, 8, e49058. [Google Scholar] [CrossRef] [PubMed]
- Ockenhouse, C.; Regules, J.A.; Tosh, D.M.; Cowden, J.J.; Kathcart, A.K.; Cummings, J.F.; Paolino, K.M.; Moon, J.E.; Komisar, J.L.; Kamau, E.; et al. Ad35.CS.01 - RTS,S/AS01 Heterologous Prime Boost Vaccine Efficacy against Sporozoite Challenge in Healthy Malaria-Naïve Adults. PLoS ONE 2015, 10, e0131571. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Pérez, G.P.; Legarda, A.; Muñoz, J.; Sim, B.K.L.; Ballester, M.R.; Dobaño, C.; Moncunill, G.; Campo, J.J.; Cisteró, P.; Jiménez, A.; et al. Controlled human malaria infection by intramuscular and direct venous inoculation of cryopreserved Plasmodium falciparum sporozoites in malaria-naïve volunteers: Effect of injection volume and dose on infectivity rates. Malar. J. 2015, 14, 1–13. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Collins, K.A.; Wang, C.Y.T.; Adams, M.; Mitchell, H.; Rampton, M.; Elliott, S.; Reuling, I.J.; Bousema, T.; Sauerwein, R.W.; Chalon, S.; et al. A controlled human malaria infection model enabling evaluation of transmission-blocking interventions. J. Clin. Investig. 2018, 128, 1551–1562. [Google Scholar] [CrossRef] [PubMed]
- Chughlay, M.F.; Gaaloul, M.E.; Donini, C.; Campo, B.; Berghmans, P.J.; Lucardie, A.; Marx, M.W.; Cherkaoui-Rbati, M.H.; Langdon, G.; Angulo-Barturen, I.; et al. Chemoprotective Antimalarial Activity of P218 against Plasmodium falciparum: A Randomized, Placebo-Controlled Volunteer Infection Study. Am. J. Trop. Med. Hyg. 2021, 104, 1348–1358. [Google Scholar] [CrossRef]
- Gillespie, D.T. Approximate accelerated stochastic simulation of chemically reacting systems. J. Chem. Phys. 2001, 115, 1716–1733. [Google Scholar] [CrossRef]
- Marino, S.; Hogue, I.B.; Ray, C.J.; Kirschner, D.E. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol. 2008, 254, 178–196. [Google Scholar] [CrossRef] [PubMed]
- Cao, P.; Klonis, N.; Zaloumis, S.G.; Dogovski, C.; Xie, S.C.; Saralamba, S.; White, L.J.; Fowkes, F.J.I.; Tilley, L.; Simpson, J.A.; et al. A Dynamic Stress Model Explains the Delayed Drug Effect in Artemisinin Treatment of Plasmodium falciparum. Antimicrob. Agents Chemother. 2017, 61, e00618-17. [Google Scholar] [CrossRef] [PubMed]
- Alahakoon, P.; McCaw, J.M.; Taylor, P.G. Estimation of the probability of epidemic fade-out from multiple outbreak data. Epidemics 2022, 38, 100539. [Google Scholar] [CrossRef]
- Bradley, J.; Stone, W.; Da, D.F.; Morlais, I.; Dicko, A.; Cohuet, A.; Guelbéogo, W.M.; Mahamar, A.; Nsango, S.E.; Soumare, H.M.; et al. Predicting the likelihood and intensity of mosquito infection from sex specific Plasmodium falciparum gametocyte density. eLife 2018, 7, e34463. [Google Scholar] [CrossRef] [PubMed]
- Mulder, B.; Tchuinkam, T.; Dechering, K.J.; Verhave, J.P.; Carnevale, P.; Meuwissen, J.H.; Robert, V. Malaria transmission-blocking activity in experimental infections of Anopheles gambiae from naturally infected Plasmodium falciparum gametocyte carriers. Trans. R. Soc. Trop. Med. Hyg. 1994, 88, 121–125. [Google Scholar] [CrossRef][Green Version]

| Parameter | Description | Unit |
|---|---|---|
| Inoculation size | unitless | |
| Mean of the initial age distribution | h | |
| SD of the initial age distribution | h | |
| Replication number | unitless | |
| Maximum rate of parasite killing by drug | h | |
| Half-maximum effective concentration of drug | ng/mL | |
| Hill coefficient for drug | unitless | |
| f | Fraction of parasites entering sexual development | unitless |
| Death rate of asexual and sexual parasites | h | |
| Sequestration age of asexual parasites (fixed to be 25) | h | |
| Length of life cycle of asexual parasites (fixed to be 42) | h |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; McCaw, J.M.; Cao, P. Stochastic Modeling of Within-Host Dynamics of Plasmodium Falciparum. Mathematics 2022, 10, 4057. https://doi.org/10.3390/math10214057
Sun X, McCaw JM, Cao P. Stochastic Modeling of Within-Host Dynamics of Plasmodium Falciparum. Mathematics. 2022; 10(21):4057. https://doi.org/10.3390/math10214057
Chicago/Turabian StyleSun, Xiao, James M. McCaw, and Pengxing Cao. 2022. "Stochastic Modeling of Within-Host Dynamics of Plasmodium Falciparum" Mathematics 10, no. 21: 4057. https://doi.org/10.3390/math10214057
APA StyleSun, X., McCaw, J. M., & Cao, P. (2022). Stochastic Modeling of Within-Host Dynamics of Plasmodium Falciparum. Mathematics, 10(21), 4057. https://doi.org/10.3390/math10214057






