Mixed Variational-like Inclusion Involving Yosida Approximation Operator in Banach Spaces
Abstract
:1. Introduction
2. Formulation and Preliminaries
- (i)
- P is called -Lipschitz continuous with Lipschitz constant if
- (ii)
- g is called -Lipschitz continuous, if ∃ a constant satisfying
- (iii)
- g is called k-strongly accretive if for some such that
- (iv)
- η is called Lipschitz continuous with constant if
- (v)
- η is called δ-strongly monotone, if ∃ a constant satisfying
3. An Iterative Algorithm and Convergence Result
| Algorithm 1: Iterative Algorithm. |
For any and from (7), let
|
Following the above approach inductively, we get, for any and , compute and by iterative process such that
|
4. Numerical Example
- (i)
- the function g is Lipschitz continuous with constant . i.e.,
- (ii)
- Let be defined asThen, the η-subdifferential of ψ, which is, .Now, for , we compute the η-proximal operator and YAO:andClearly, is -Lipschitz continuous, where and is -Lipschitz continuous, where .
- (iii)
- is strongly accretive with constant . Astherefore,
- (iv)
- Let be the functions and be the multivalued functions given byAccordingly,
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Baiocchi, C.; Capelo, A. Variational and Quasivariational Inequalities, Applications to Free Boundary Problems; Wiley: New York, NY, USA, 1984. [Google Scholar]
- Giannessi, F.; Maugeri, A. Variational Inequalities and Network Equilibrium Problems; Plenum Press: New York, NY, USA, 1995. [Google Scholar]
- Glowinski, R.; Lions, J.; Tremolieres, R. Numercial Analysis of Variational Inequalities; North-Holland: Amsterdam, The Netherlands, 1981. [Google Scholar]
- Harker, P.T.; Pang, J.S. Finite-dimensional variational inequality and nonlinear complementarity problems. Math. Program. 1990, 48, 161–220. [Google Scholar] [CrossRef]
- Kinderlehrer, D.; Stampacchia, G. An Introduction to Variational Inequalities and Their Applications; Academic Press: New York, NY, USA, 1980. [Google Scholar]
- Hassouni, A.; Moudafi, A. A perturbed algorithm for variational inclusions. J. Math. Anal. Appl. 1994, 185, 706–712. [Google Scholar] [CrossRef] [Green Version]
- Adly, S. Perturbed algorithms and sensitivity analysis for a general class of variational inclusions. J. Math. Anal. Appl. 1996, 201, 609–630. [Google Scholar] [CrossRef] [Green Version]
- Huang, N.J. Generalized nonlinear variational inclusions with noncompact valued mappings. Appl. Math. Lett. 1996, 9, 25–29. [Google Scholar] [CrossRef] [Green Version]
- Kazmi, K.R. Mann and Ishikawa perturbed iterative algorithms for generalized quasivariational inclusions. J. Math. Anal. Appl. 1997, 209, 572–584. [Google Scholar] [CrossRef] [Green Version]
- Ding, X.P. Perturbed proximal point algorithms for generalized quasivariational inclusions. J. Math. Anal. Appl. 1997, 210, 88–101. [Google Scholar] [CrossRef] [Green Version]
- Lescarret, C. Cas d‘addition des applications monotones maximales dans un espace de Hilbert. C. R. I‘Acadimic Sci. 1965, 261, 1160–1163. [Google Scholar]
- Browder, F.E. On the unification of the calculus of variations and the theory of monotone nonlinear operators in Banach spaces. Proc. Natl. Acad. Sci. USA 1966, 56, 419–425. [Google Scholar] [CrossRef] [Green Version]
- Konnov, I.V.; Volotskaya, E.O. Mixed variational inequalities and economic equilibrium problems. J. Appl. Math. 2002, 2, 289–314. [Google Scholar] [CrossRef] [Green Version]
- Zarantonello, E.H. Solving Functional Equations by Contractive Averaging; Tech. Report 160; Mathematics Research Center, United States Army, University of Wisconsin: Madison, WI, USA, 1960. [Google Scholar]
- Minty, G.J. Monotone (nonlinear) operators in Hilbert space. Duke Math. J. 1962, 29, 341–346. [Google Scholar] [CrossRef]
- Ram, T.; Iqbal, M. Generalized monotone mappings with an application to variational inclusions. Commun. Math. Appl. 2022, 13, 477–491. [Google Scholar] [CrossRef]
- Ahmad, R.; Ishtyak, M.; Rahaman, M.; Ahmad, I. Graph convergence and generalized Yosida approximation operator with an application. Math Sci. 2017, 11, 155–163. [Google Scholar] [CrossRef] [Green Version]
- Cao, H.W. Yosida approximation equations technique for system of generalized set-valued variational inclusions. J. Inequal. Appl. 2013, 2013, 455. [Google Scholar] [CrossRef] [Green Version]
- Lan, H.Y. Generalized Yosida approximations based on relatively A-maximal m-relaxed monotonicity frameworks. Abstr. Appl. Anal. 2013, 157190. [Google Scholar]
- Qin, X.; Cho, S.Y.; Wang, L. A regularization method for treating zero points of the sum of two monotone operators. Fixed Point Theory Appl. 2014, 2014, 75. [Google Scholar] [CrossRef] [Green Version]
- Ceng, L.C.; Wen, C.F.; Yao, Y. Iteration approaches to hierarchical variational inequalities for infinite nonexpansive mappings and finding zero points of m-accretive operators. J. Nonlinear Var. Anal. 2017, 1, 213–235. [Google Scholar]
- Qin, X.; Petrusel, A.; Yao, J.C. CQ iterative algorithms for fixed points of nonexpansive mappings and split feasibility problems in Hilbert spaces. J. Nonlinar Convex Anal. 2018, 19, 251–264. [Google Scholar]
- Rajpoot, A.K.; Ahmad, R.; Ishtyak, M.; Wen, C.-F. Mixed variational inequality problem involving generalized Yosida approximation operator in q-uniformly smooth banach space. J. Math. 2022, 2022, 5668372. [Google Scholar] [CrossRef]
- Akram, M.; Chen, J.W.; Dilshad, M. Generalized Yosida approximation operator with an application to a system of Yosida inclusions. J. Nonlinear Funct. Anal. 2018, 2018, 17. [Google Scholar]
- Penot, J.-P.; Ratsimahalo, R. On the Yosida approximaton of operators. Proc. R. Soc. Edinb. Math. 2001, 131, 945–966. [Google Scholar] [CrossRef]
- Yu, Y. Convergence analysis of a Halpern type algorithm for accretive operators. Nonlinear Anal. 2012, 75, 5027–5031. [Google Scholar] [CrossRef]
- Zeng, L.C.; Guu, S.M.; Yao, J.C. Characterization of H-monotone operators with applications to variational inclusions. Comput. Math. Appl. 2005, 50, 329–337. [Google Scholar] [CrossRef] [Green Version]
- Ding, X.P.; Lou, C.L. Perturbed proximal point algorithms for general quasi-variational-like inclusions. J. Comput. Appl. Math. 2000, 113, 153–165. [Google Scholar] [CrossRef] [Green Version]
- Verma, R.U. On generalized variational inequalities involving relaxed Lipschitz and relaxed monotone operators. J. Math. Anal. Appl. 1997, 213, 387–392. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.-H.; Ansari, Q.H.; Yao, J.-C. A perturbed algorithm for strongly nonlinear variational-like inclusions. Bull. Aust. Math. Soc. 2000, 62, 417–426. [Google Scholar] [CrossRef]
- Ahmad, R.; Siddiqi, A.H.; Khan, Z. Proximal point algorithm for generalized multivalued nonlinear quasi-variational-like inclusions in Banach spaces. Appl. Math. Comput. 2005, 163, 295–308. [Google Scholar] [CrossRef]
- Ahmad, R.; Siddiqi, A.H. Mixed variational-like inclusions and Jη-proximal operator equations in Banach spaces. J. Math. Anal. Appl. 2007, 327, 515–524. [Google Scholar] [CrossRef] [Green Version]
- Nadler, S.B., Jr. Multi-valued contraction mappings. Pac. J. Math. 1969, 30, 475–488. [Google Scholar] [CrossRef] [Green Version]

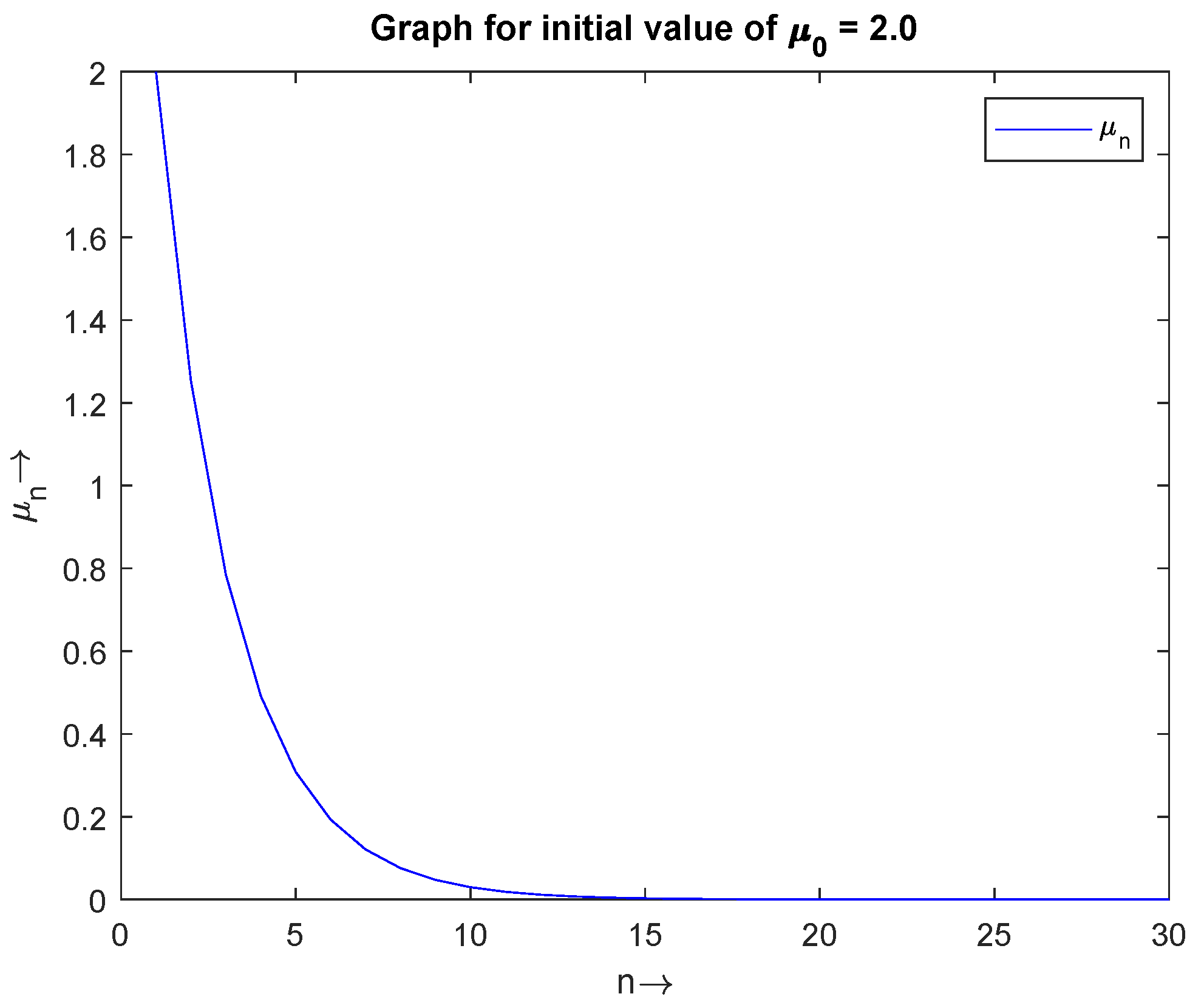

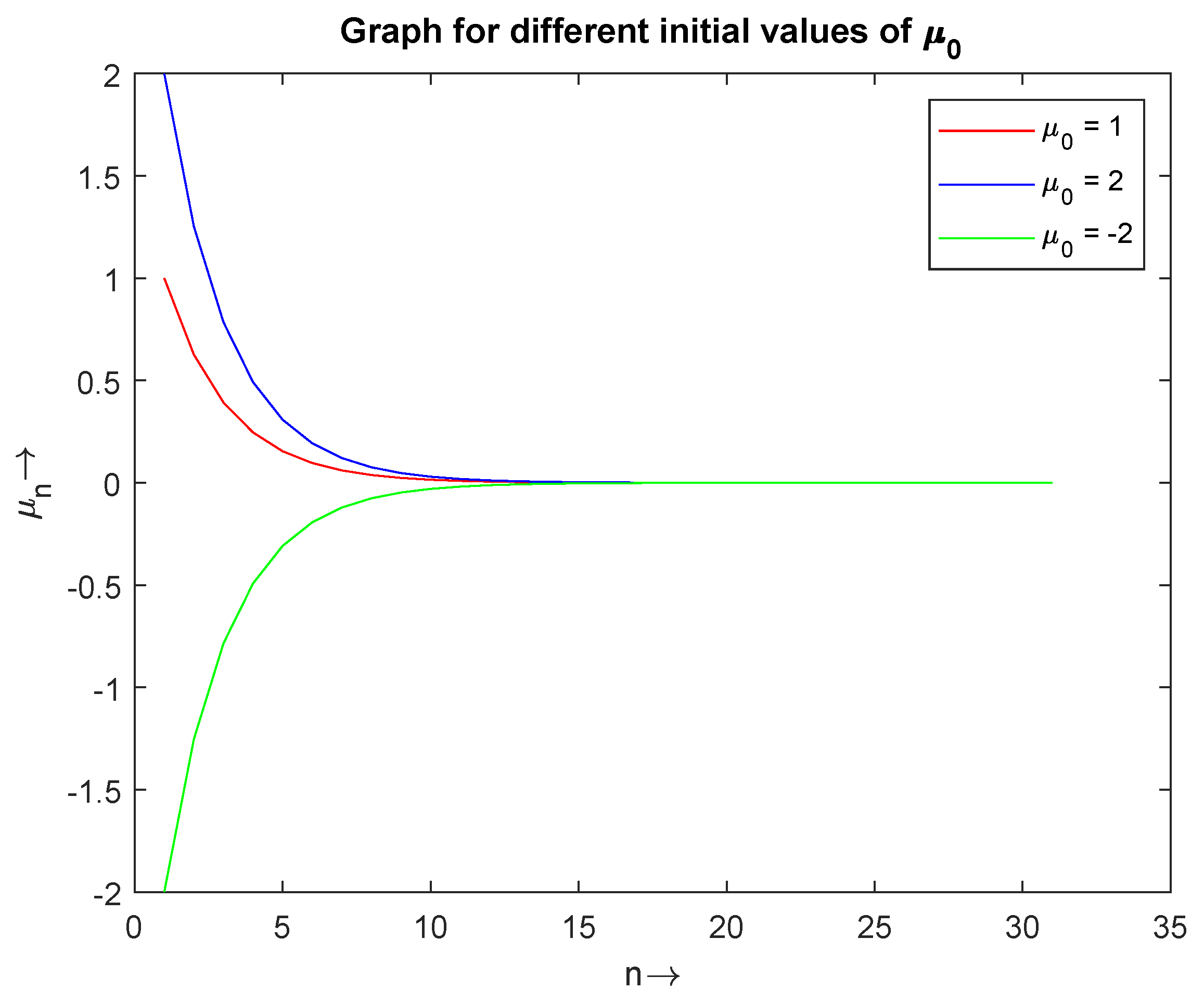
| No. of | No. of | No. of | |||
|---|---|---|---|---|---|
| Iterations | Iterations | Iterations | |||
| 1 | 1.0000 | 1 | 2.0000 | 1 | −2.0000 |
| 2 | 0.6265 | 2 | 1.2530 | 2 | −1.2530 |
| 3 | 0.3925 | 3 | 0.7850 | 3 | −0.7850 |
| 4 | 0.2459 | 4 | 0.4918 | 4 | −0.4918 |
| 5 | 0.1540 | 5 | 0.3081 | 5 | −0.3081 |
| 6 | 0.0965 | 6 | 0.1930 | 6 | −0.1930 |
| 7 | 0.0605 | 7 | 0.1209 | 7 | −0.1209 |
| 8 | 0.0379 | 8 | 0.0757 | 8 | −0.0757 |
| 9 | 0.0237 | 9 | 0.0474 | 9 | −0.0474 |
| 10 | 0.0149 | 10 | 0.0296 | 10 | −0.0296 |
| 14 | 0.0023 | 14 | 0.0045 | 14 | −0.0045 |
| 18 | 0.0004 | 18 | 0.0007 | 18 | −0.0007 |
| 22 | 0.0001 | 22 | 0.0001 | 22 | −0.0001 |
| 26 | 0.0000 | 26 | 0.0000 | 26 | 0.0000 |
| 30 | 0.0000 | 30 | 0.0000 | 30 | 0.0000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, F.A.; Iqbal, M.; Ram, T.; Mohammed, H.I.A. Mixed Variational-like Inclusion Involving Yosida Approximation Operator in Banach Spaces. Mathematics 2022, 10, 4067. https://doi.org/10.3390/math10214067
Khan FA, Iqbal M, Ram T, Mohammed HIA. Mixed Variational-like Inclusion Involving Yosida Approximation Operator in Banach Spaces. Mathematics. 2022; 10(21):4067. https://doi.org/10.3390/math10214067
Chicago/Turabian StyleKhan, Faizan Ahmad, Mohd Iqbal, Tirth Ram, and Hamid I. A. Mohammed. 2022. "Mixed Variational-like Inclusion Involving Yosida Approximation Operator in Banach Spaces" Mathematics 10, no. 21: 4067. https://doi.org/10.3390/math10214067
APA StyleKhan, F. A., Iqbal, M., Ram, T., & Mohammed, H. I. A. (2022). Mixed Variational-like Inclusion Involving Yosida Approximation Operator in Banach Spaces. Mathematics, 10(21), 4067. https://doi.org/10.3390/math10214067






