A Practical Approach to Identify the Phases Sequence in Five Phase Machines with Combined Star–Pentagon Configuration

Abstract

Due to the significant advantages of a high torque density, better fault tolerance and high efficiency, the combined star–pentagon winding has recently gained researchers’ interest. In this paper, a simple method to identify the sequence of phases of a five-phase machine with combined star–pentagon winding was proposed. This was accomplished using resistance measurements between adjacent and non-adjacent phases. The analysis was conducted to clarify the phase sequence identification method. A case study of a 5.5 kW five-phase synchronous reluctance motor with combined star–pentagon winding was considered to simply apply the proposed method using an LCR meter for resistance measurements. The parasitic and wire resistances are dominant in the studied case, and this did not influence the accuracy of this method.

1. Introduction

The current advances in the field of multiphase machines helped them to be one of the topics of significant interest to researchers in the field of variable speed drive systems [1,2,3,4,5]. Multiphase machines are preferred in some applications due to their noteworthy advantages compared to three-phase machines [6,7]. Five-phase machines have been favored compared to other multiphase machines, e.g., six and seven-phase machines [8,9]. This is largely because of the reduced size of the power converter. In the literature, it was found that the five-phase Induction machine can maintain about 70% of the rated torque with one-phase opened, while the asymmetrical six-phase machine works at only 66% of the rated torque [10,11]. There has been much interest in improving the performance of the five-phase machines. One of the key strategies that were used to improve the torque density of the five-phase machines is increasing the fundamental winding factor and the magnitude of the fundamental component of the magnetomotive force (MMF). This was achieved using innovative winding configurations [12,13,14,15]. Several research activities were conducted to improve the performance of five-phase machines using different types of winding configurations [16,17,18,19]. A combined star–pentagon configuration is one of the possibilities to obtain improved performance in five-phase machines. It was demonstrated that using a dual five-phase winding configuration connected in a combined star–pentagon reduces the losses of the induced eddy currents in the permanent magnets and in the rotor core while maintaining the five-phase terminals as in the traditional five-phase connections. The combined star–pentagon winding provides the required phase shift between the two windings (18°) to cancel all harmonics below the MMF component that generates the torque [20,21,22,23,24]. In [20], it was found that the output power of the five-phase induction machine with the combined star–pentagon winding with one phase opened was increased by about 16% compared to the star-connected winding. A dynamic and a steady state model for the combined star–pentagon winding were studied in [21,22]. In [23], a 20-slot/18-pole permanent magnet (PM) machine was introduced with a combined star–pentagon configuration. The torque density was increased by about 1.2% under healthy operating conditions compared to the star-connected winding. In [25], the average torque of a five-phase synchronous reluctance motor (synchronous reluctance motor) was increased by about 17% with combined star–pentagon winding compared to the three-phase star-connected winding.

The focus of this paper was electrical machines that are rewound with the combined star–pentagon winding. The first step after rewinding the machine is to identify the sequence of phases so that it can be correctly connected to the power converter. The conventional and common method [26,27,28] is to couple the tested machine to a prime mover and connect a capacitor bank in parallel with the tested machine to help the voltage build up. In this method, the tested machine works as a generator. A multi-channel oscilloscope is required to display the induced voltages of the tested machine, and hence the sequence of phases is identified. It was noticed that the capacitor bank could be removed in the case of a PM rotor or using a separate supply to magnetize the steel of the machine, as in [27,28]. The authors of [29] presented an approach for automatically detecting and correcting erroneous phase sequence connections. For the work in [29], current controllers in the simultaneously revolving and stationary reference frames were studied. The investigation was carried out for three-phase balanced and sinusoidal grid voltage operating conditions. Smart meters have completely covered the low-voltage distribution network in recent years. Data-driven single-phase meter phase identification is a possibility because of the abundance of smart meter measurement data. Numerous research successes have been achieved in this area, mostly using two methodologies based on correlation analysis and clustering. References [30,31] used timing voltage correlation analysis for phase identification of single-phase meters in distribution networks as part of the correlation analysis-based technique. Despite the simplicity of this technique, the recognition accuracy might still be increased. A technique of phase identification based on gray correlation was presented in [32], and it is most suited to the case of limited datasets. In terms of clustering-based approaches, references [33,34,35] all clustered voltage or power curves for phase detection based on K-means or modified K-means algorithms, which were implemented. A phase identification approach based on t-SNE dimensionality reduction with Birch clustering was presented in reference [36]. In terms of accuracy, the clustering-based strategy surpasses the correlation analysis-based approach, but the unsupervised clustering method requires correct phase information of at least three meters to supply labels for the clustering results. As was discussed, these methods [26,27,28,29,30,31,32,33,34,35,36] were used for phase sequence identification; however, the sequence of phases was identified using several components and/or different strategies. These components may not be readily available. For example, the availability of a prime mover, capacitor bank and multi-channel oscilloscope, and in some cases, these components might not be available, especially in industrial locations.

The rewound combined star–pentagon introduced in [5] is a new winding that resulted in higher average torque and lower torque ripple compared to the star-connected winding. Moreover, this winding is important as it gives the old machine a second life with better performance. However, after refurbishing the old machine, the first step is identifying the sequence of phases so that the machine can be correctly connected to the inverter. This sequence could be identified using the conventional method, which is to run the machine as a generator and observe the waveforms of the induced voltages using a scope; then, the user can identify the sequence. However, some of the equipment needed for this method might not be available, e.g., a capacitor bank, etc. Therefore, the focus of this paper was to propose a simple method to identify the sequence of phases in a five-phase machine with combined star–pentagon winding. This method is cost and time efficient. This is performed using resistance measurements between adjacent and non-adjacent phases with the means of an LCR meter [37,38]. A case study of a 5.5 kW five-phase synchronous reluctance motor with combined star–pentagon winding was studied to clarify the steps to identify the sequence of phases. The proposed practical technique has not been previously introduced or published. Furthermore, the simplicity of this technique might be viewed as an advantage for the combined star–pentagon winding arrangements.

2. Proposed Method to Identify the Phase Sequence

This section introduces the steps of implementation of a combined star–pentagon winding and the required steps to identify the sequence of phases. In a five-phase machine of the stator of S-slots and 2P-poles, the number of slots per pole per phase (q) can be calculated from (1). In order to implement the combined star–pentagon winding, these slots per pole per phase (q) were divided into two groups, i.e., red and green colored inFigure 1. It is recommended to divide them into two equal parts as much as possible to obtain a maximum winding factor and an improved torque density [5]. The coils of each group are connected in series. The first group in each phase was star-connected, and the second group was pentagon-connected; then, the whole system was connected, as shown in Figure 2, to obtain the combined star–pentagon configuration. In (2), $q_s$ and $q_p$ represent the number of stator-slots occupied by coils that are star and pentagon-connected, respectively.

$$q=\frac{S}{2P\times 5}$$

(1)

$$q=q_s+q_p$$

(2)

The relation between the current in the star-connected winding and in the pentagon-connected winding can be given as follows:

$$I_s=I_p\times 2\sin \frac{\pi }{5}=1.1756\times I_p$$

(3)

where $I_s$ and $I_p$ represent the current in the star and in the pentagon winding, respectively.

In order to obtain the same MMF from the two windings, the relation between the number of turns in the two windings was calculated as in (4) [20]. Hence, the copper volume and the copper losses were the same as in the conventional star-connected five-phase machine.

$$N_{cp}=N_{cs}\times 1.1756$$

(4)

where $N_{cs}$ and $N_{cp}$ represent the number of turs in the star and in the pentagon winding, respectively.

The phase shift between the two windings is 18°, as shown in Figure 3. Figure 4 shows that the combined star–pentagon synchronous reluctance motor (5ph-SP) outperforms the star-connected three-phase synchronous reluctance motor (3ph-S) and also the star-connected five-phase synchronous reluctance motor (5ph-S). The results of Figure 4 were obtained using 2D Ansys Maxwell transient simulations. The average torque and the torque ripples were recorded at different line currents and also at different current angles. It was proved that the combined star–pentagon synchronous reluctance motor achieves 13.35% higher torque compared to the three-phase one and 6.37% higher torque compared to the star-connected five-phase synchronous reluctance motor.

The method of identification of the sequence of phases is based on measuring the equivalent resistance between different terminals of the machine. In order to identify the sequence of phases in a combined star–pentagon winding, the equivalent circuit was analyzed in two cases, i.e., between two adjacent terminals and between two nonadjacent terminals. This is shown in Figure 5.

The per-phase resistance of the star-connected winding is given by (5), and the per-phase resistance in the pentagon winding is given by (6). Based on the relation between the current in the star winding and the current in the pentagon winding, the relation between the conductor’s cross-sectional area can be described as in (7).

$$R_s=\frac{\rho L_{mt}\times N_{cs}}{a_{cs}\times a}$$

(5)

$$R_p=\frac{\rho L_{mt}\times N_{cp}}{a_{cp}\times a}=1.382R_s$$

(6)

$$a_{cp}=\frac{a_{cs}}{1.1756}$$

(7)

where a is the number of parallel circuits, $\rho$ is the copper resistivity and $L_{mt}$ is the mean length of coil turn. $a_{cs}$ and $a_{cp}$ are the conductor cross-sectional area for the star and pentagon winding, respectively.

Figure 5a analyzes the equivalent resistance between two adjacent phases. The obtained equivalent resistance, in this case, can be described as in (8). The equivalent resistance between two nonadjacent phases is shown in Figure 5b and can be given by (9). Hence, the measured resistance in the case of the non-adjacent phases is higher than the measured resistance between the adjacent phases.

$$R_{adj}=2R_s+\frac{4R_p\times R_p}{5R_p}=2R_s+0.8R_p$$

(8)

$$R_{Nadj}=2R_s+\frac{2R_p\times 3R_p}{5R_p}=2R_s+1.2R_p$$

(9)

In order to identify the sequence of five phases, six readings must be recorded. This can be simply described in the following steps:

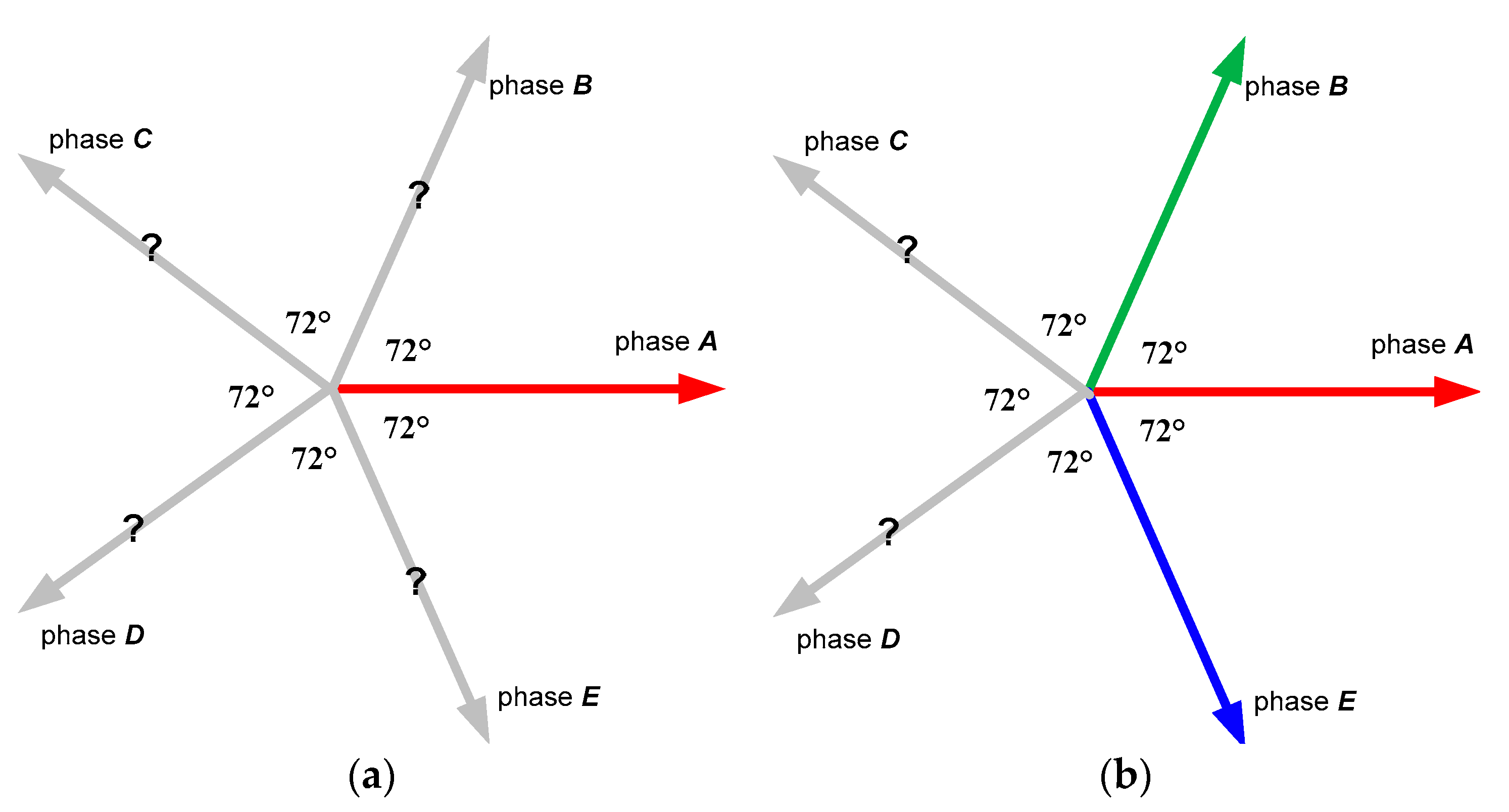
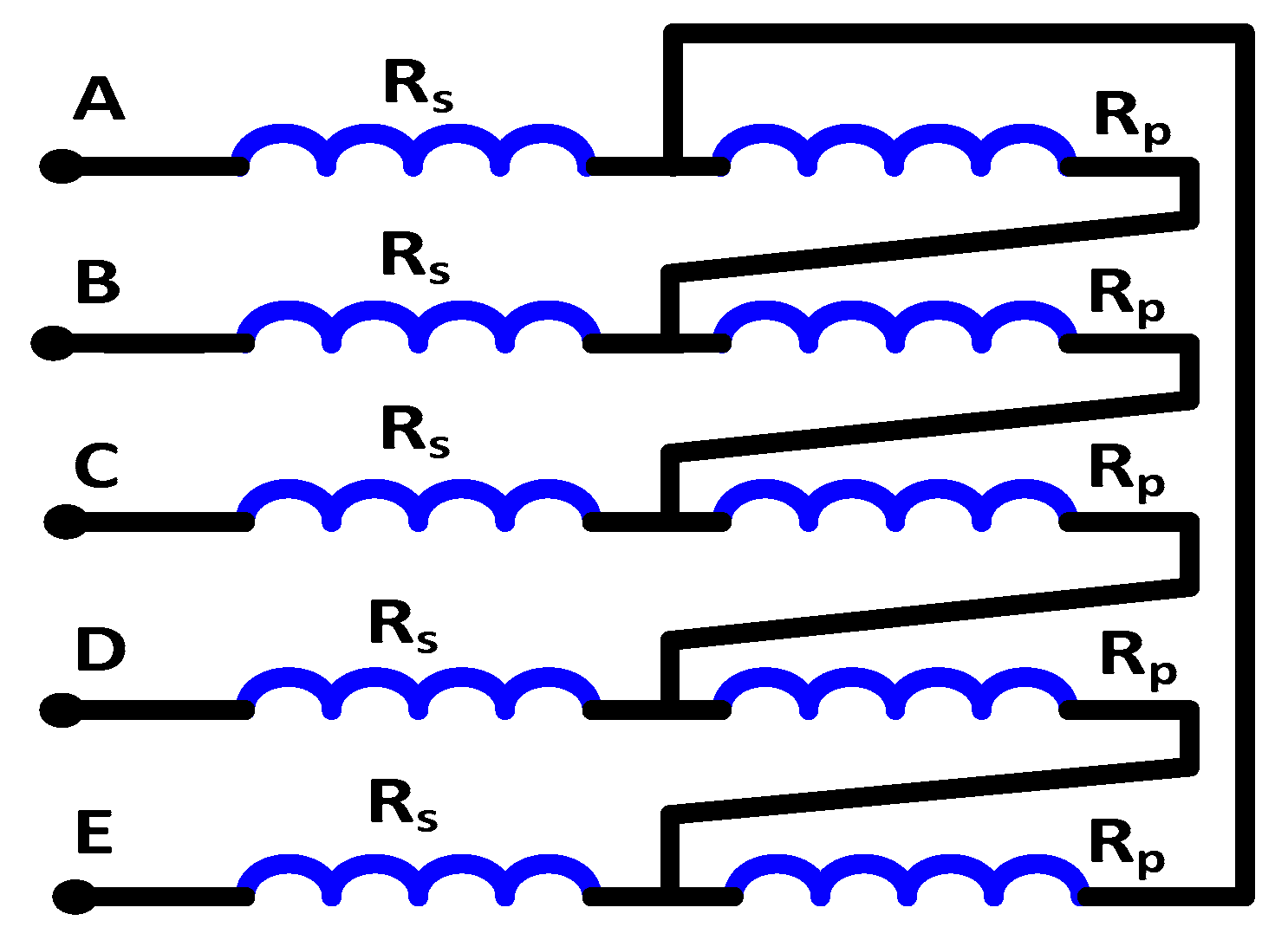
• The first terminal of the machine (consider it phase A) is connected to the positive terminal of the ohmmeter, and the negative terminal is connected to the other four terminals. The four readings of the ohmmeter will have two equal high values and two equal low values. The terminals that give the lower reading are the adjacent terminals (phases B and E) to the machine’s first terminal. Hence, the sequence of the three terminals of the five-phase machine (phases A, B and E) is known after performing the first step;
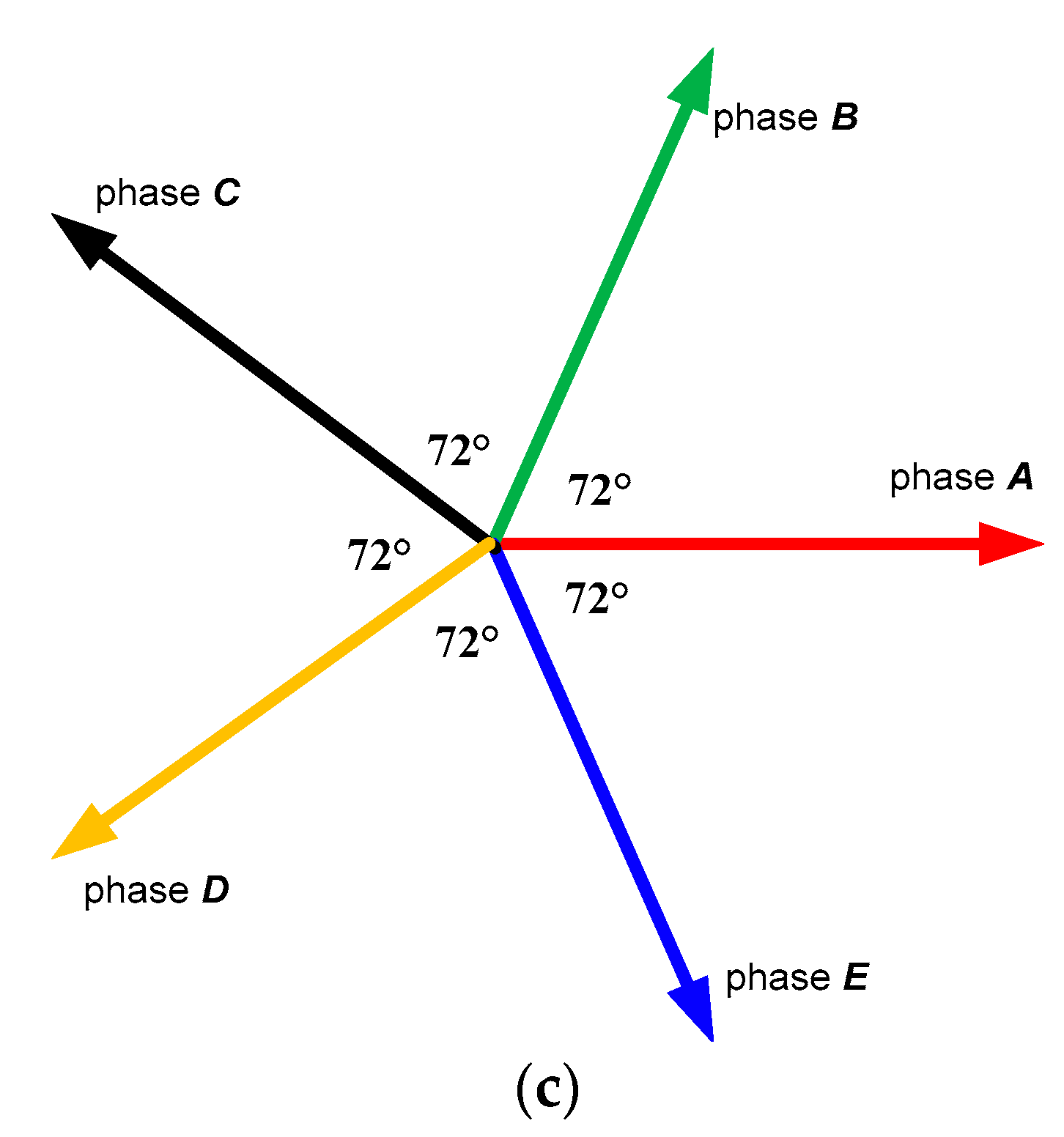
• In the second step, one of the adjacent terminals (select phase B) of the machine’s first terminal (phase A) is connected to the positive terminal of the ohmmeter, and the other terminal of the ohmmeter is connected to the other two terminals of the machine (nonadjacent terminals to the machine first terminal) (phases C and D). The terminal that gives the lower reading is the adjacent terminal (phase C) to the connected one (phase B) to the ohmmeter positive terminal. Hence, the sequence of phases is identified.

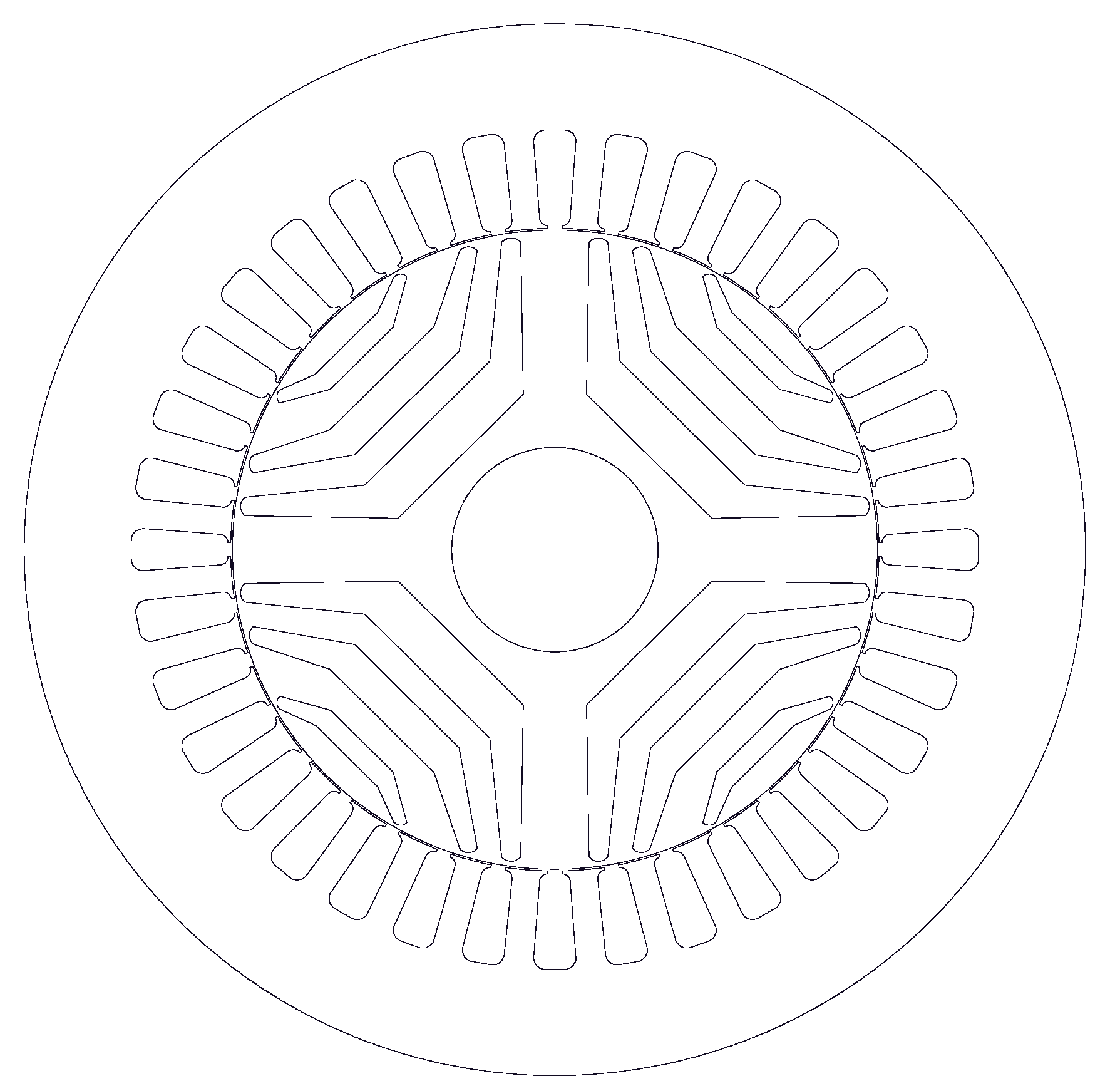
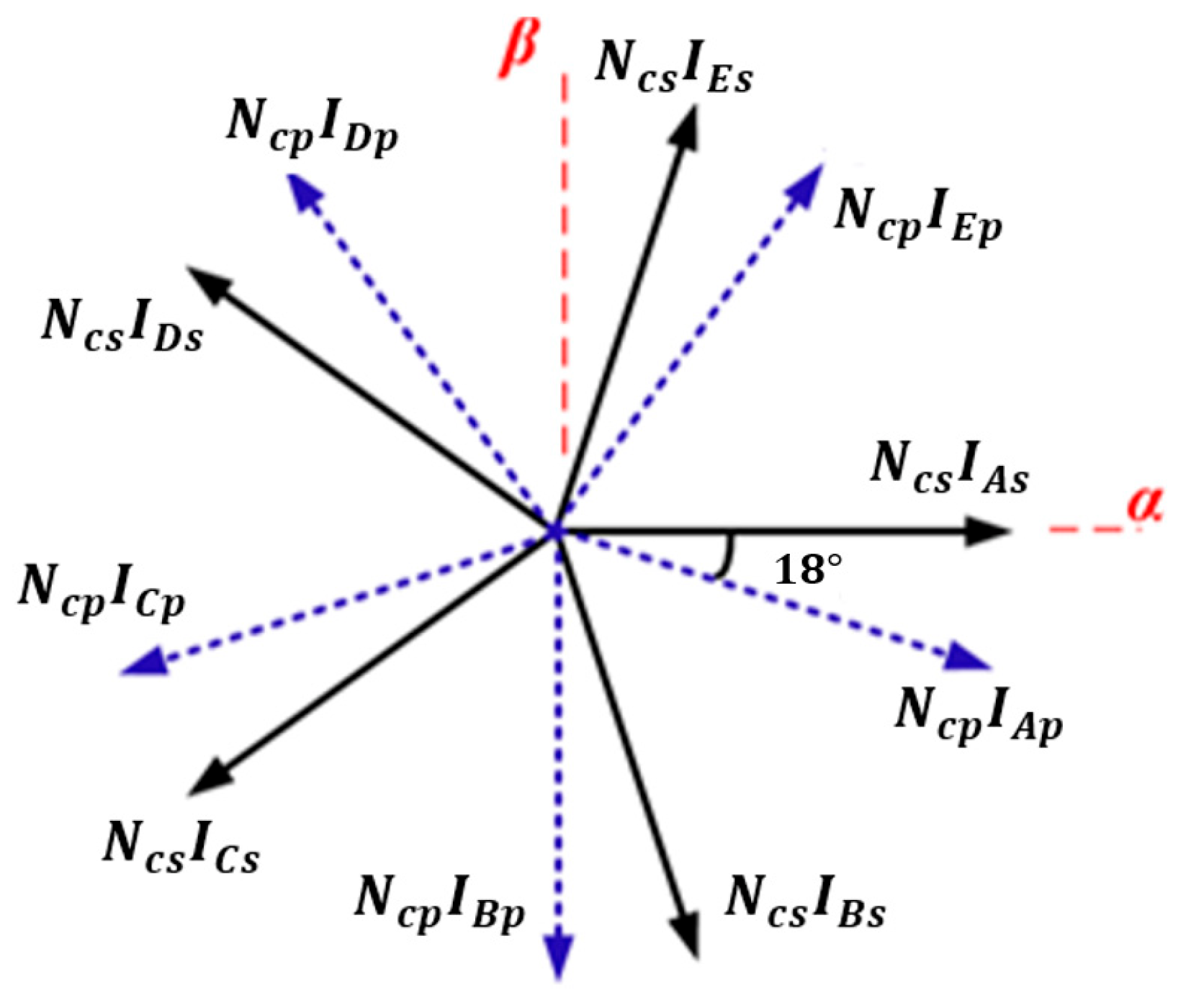
3. Case Study

In this section, a case study of a 5.5 kW five-phase synchronous reluctance motor with a combined star–pentagon winding, shown in Figure 6, was implemented to validate the introduced method to identify the phase sequence. This machine has low resistance values (around 0.2 ohm per phase) to check the validity and accuracy of the proposed method in terms of the determination of the phase sequence. The specification of the synchronous reluctance motor is summarized in Table 1 and Figure 7. As shown in Figure 6, there are five terminals for the five-phase synchronous reluctance motor with the combined star–pentagon configuration. The five terminals’ colors are red (r), black (k), green (g), yellow (y) and blue (b). An LCR meter was used to measure the winding resistance. As this is simply shown in Figure 8, the previously described steps to identify the sequence of phases were applied as follows:

• The red terminal can be considered as phase A as indicated in Figure 9a and Figure 10a. The question mark (?) in Figure 9a,b means that the sequence order of this terminal is not identified yet;
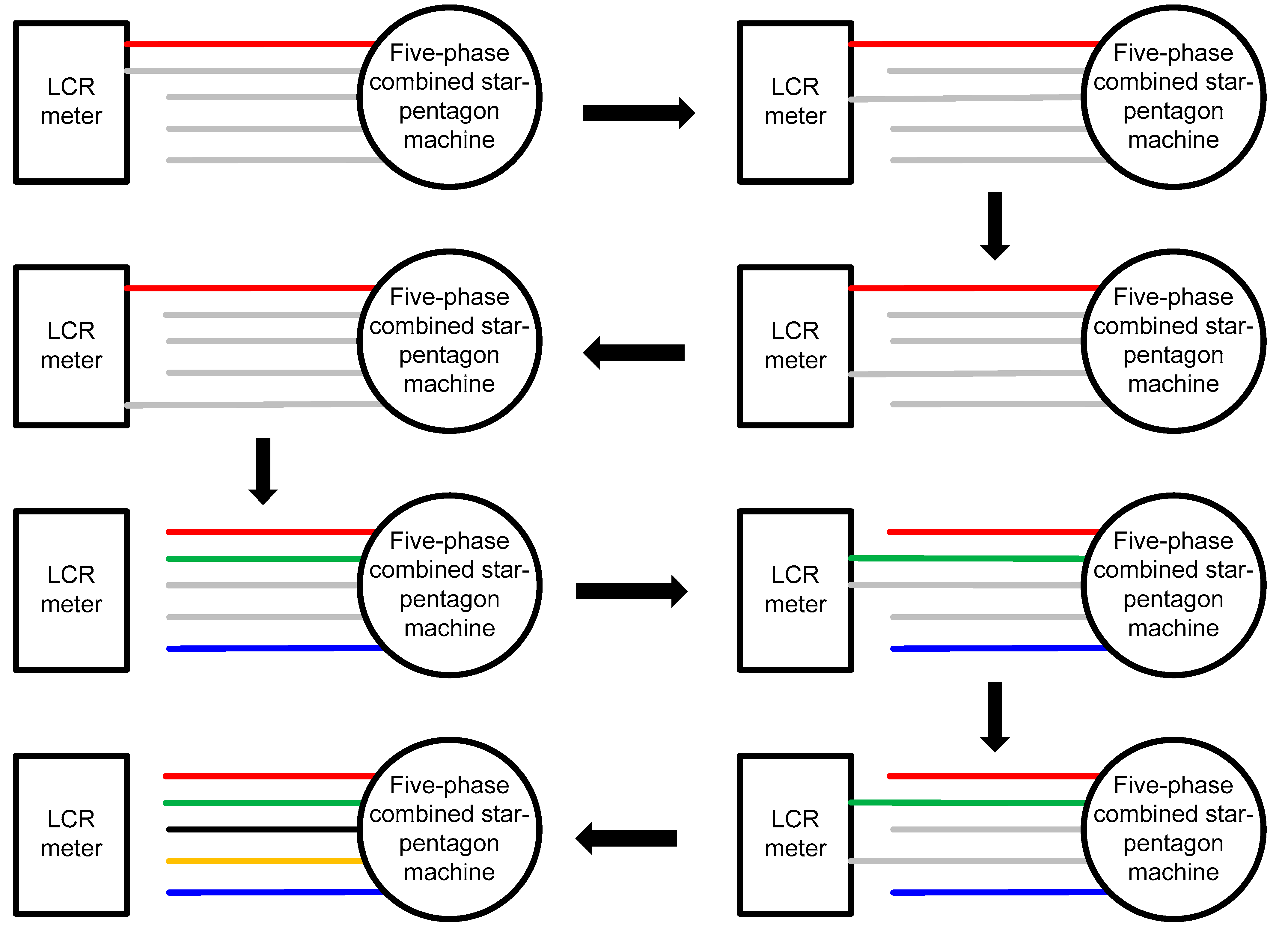
• This terminal (red terminal or terminal that is considered as phase A) is connected to the positive terminal of the LCR meter, and the other terminal of the LCR meter is consecutively connected to the other four terminals of the machine (terminals k, g, y and b), as shown in Figure 10. The red terminal has two adjacent terminals and two nonadjacent terminals. Hence there are two higher values of resistance, and two lower values of resistance measured relative to the red terminal;
• The green and the blue terminals give lower resistance relative to the red terminal compared to the yellow and black terminals, as shown in Table 2 and Figure 10e;
• The green and blue terminals are the adjacent terminals to the red terminal. The green terminal can be considered as phase B, and the blue terminal can be considered as phase E as described in Figure 9b and Figure 10;
• However, it is not obvious which one of the yellow and the black terminals is phase C or D. In order to specify which one is phase C or D, the green terminal (phase B) is connected to the positive terminal of the LCR meter, and the other terminal of the LCR meter is connected once to the black terminal and once to the yellow terminal as shown in Figure 10. The terminal that gives the lower reading is the adjacent terminal to the green terminal (phase B);
• As shown in Table 2, the black terminal gives a lower resistance relative to the green terminal (phase B). Hence, it is the adjacent terminal (phase C), and the yellow terminal is phase D, as indicated in Figure 9c and Figure 10;
• Table 3, Figure 9c and Figure 10 show the obtained sequence of phases.

Figure 6. Photograph of a five-synchronous reluctance motor with LCR meter, (a) measurement resistance between two adjacent phases and (b) nonadjacent phases.

Figure 6. Photograph of a five-synchronous reluctance motor with LCR meter, (a) measurement resistance between two adjacent phases and (b) nonadjacent phases.

Figure 7. Cross-section of the five-phase SynRM.

Figure 7. Cross-section of the five-phase SynRM.

Figure 8. Flow chart of phases sequence identification.

Figure 8. Flow chart of phases sequence identification.

Figure 9. Steps of phases sequence identification represented in star of slot phasors, (a) phasors of phases before applying the first test, (b) the result of the first step and (c) the final result of the two setps. The question mark (?) means that the sequence order of this terminal is not identified yet.

Figure 9. Steps of phases sequence identification represented in star of slot phasors, (a) phasors of phases before applying the first test, (b) the result of the first step and (c) the final result of the two setps. The question mark (?) means that the sequence order of this terminal is not identified yet.

Figure 10. Detailed steps of phases sequence identification.

Figure 10. Detailed steps of phases sequence identification.

Table 1. The five-phase SynRM geometrical parameters.

Parameter	Value	Parameter	Value
Stator bore diameter (D1O)	110 mm	Air gap length (Lg)	0.3 mm
Stator inner diameter (D)	180 mm	Number of slots (S)	36
Rotor outer diameter (Dro)	109.4 mm	Pole pairs (P)	2
Rotor inner diameter (Dri)	35 mm	Rated frequency (F)	100 Hz
Axial length (L)	140 mm	Rated power (Pr)	5.5 kW
Number of turns of star coil per phase	24	Number of turns of pentagon coil per phase	29
Stator/Rotor steel	M270-50A/M330-50A	Rated current (Is)	12.3 A
Rotor flux barriers per pole (Nfb)	3	Number of phases (m)	5
$\mathrm{Phase}\mathrm{resistance}(R_{ph}$)	0.25	$\mathrm{Star}\mathrm{coil}\mathrm{resistance}(R_s$)	0.125

Table 1. The five-phase SynRM geometrical parameters.

Parameter	Value	Parameter	Value
Stator bore diameter (D1O)	110 mm	Air gap length (Lg)	0.3 mm
Stator inner diameter (D)	180 mm	Number of slots (S)	36
Rotor outer diameter (Dro)	109.4 mm	Pole pairs (P)	2
Rotor inner diameter (Dri)	35 mm	Rated frequency (F)	100 Hz
Axial length (L)	140 mm	Rated power (Pr)	5.5 kW
Number of turns of star coil per phase	24	Number of turns of pentagon coil per phase	29
Stator/Rotor steel	M270-50A/M330-50A	Rated current (Is)	12.3 A
Rotor flux barriers per pole (Nfb)	3	Number of phases (m)	5
$\mathrm{Phase}\mathrm{resistance}(R_{ph}$)	0.25	$\mathrm{Star}\mathrm{coil}\mathrm{resistance}(R_s$)	0.125

Table 2. The obtained measured resistances.

Parameter	Value	Parameter	Value
Rrg	0.365 Ω	Rry	0.588 Ω
Rrb	0.394 Ω	Rgk	0.352 Ω
Rrk	0.552 Ω	Rgy	0.566 Ω

Table 2. The obtained measured resistances.

Parameter	Value	Parameter	Value
Rrg	0.365 Ω	Rry	0.588 Ω
Rrb	0.394 Ω	Rgk	0.352 Ω
Rrk	0.552 Ω	Rgy	0.566 Ω

Table 3. The obtained sequence of phases.

Terminal	Phase	Terminal	Phase
Red terminal	A	Yellow terminal	D
Green terminal	B	Blue terminal	E
Black terminal	C

Table 3. The obtained sequence of phases.

Terminal	Phase	Terminal	Phase
Red terminal	A	Yellow terminal	D
Green terminal	B	Blue terminal	E
Black terminal	C

4. Comparative Analysis of the Proposed and Conventional Methods

This section analyses and compares the proposed method to identify the sequence of phases in five-phase combined star–pentagon machines with the conventional methods. As shown in Figure 11 and

Table 4. Comparison between the proposed and the conventional method of identification of phase sequence.

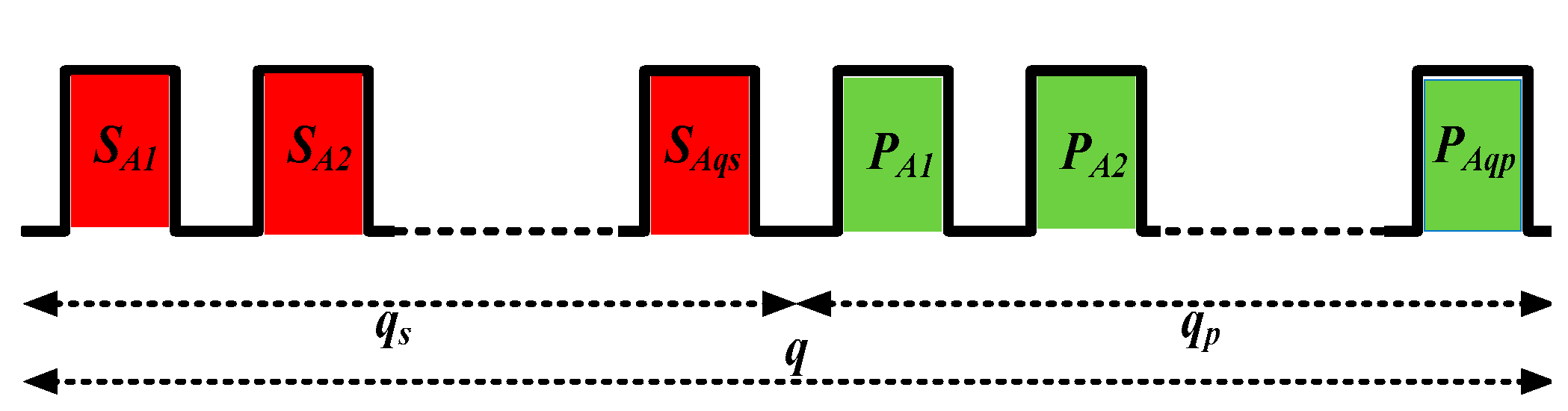
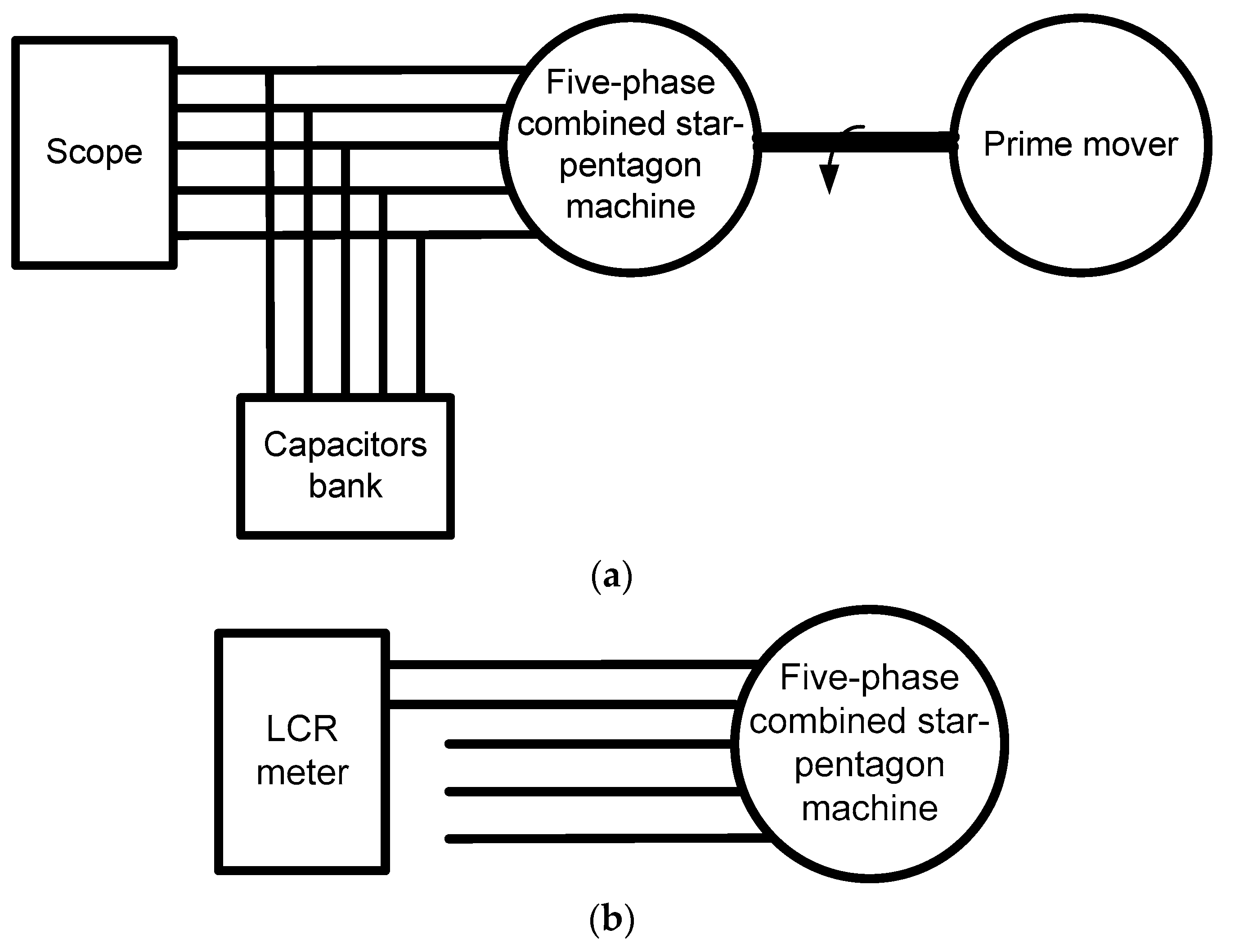
	Conventional Method	Proposed Method
Prime mover	Yes	No
Scope	Yes	No
Capacitor bank	Yes	No
LCR meter	No	Yes
Cost	High	Low
Time	much	Few
Type	Dynamic test	Static test

, there are many components required in the conventional method, such as a prime mover, capacitor bank and scope by which the researcher can observe the waveforms of the generated voltage of the examined machine (five-phase combined star–pentagon machine). Note that the examined machine works as a generator in this method, so the conventional method is considered a dynamic test approach. However, the proposed approach in this paper only uses the LCR meter for measuring the resistance between different terminals. Therefore, this method is considered more economical than conventional methods. In addition, there is no dynamic operation during the application of this method. Hence it is considered a static test. Moreover, the proposed method is cheaper than the conventional methods.

During the practical validation of this method, the errors in measurements and the parasitic inputs, which indeed existed, did not affect the correctness of the obtained sequence, and the performance of the motor with the identified phase sequence was tested under both speed and torque control mode with great agreements with its simulated performance. For the shortcuts, which did not exist in our case, if there is a shortcut, the obtained measurements will be totally different from what was expected, and the user will realize that there is a problem with the machine. Hence, this method can be considered as a checker for the status of the machine as well.

5. Conclusions

This paper proposed a simple, cost- and time-efficient method to identify the sequence of phases in a five-phase machine with a combined star–pentagon configuration. This method depends on measuring the resistance between the adjacent and the non-adjacent phases. The phases are identified using only six measurements. The effectiveness of the proposed method was proved in determining the sequence of the phases even at low resistance values. The parasitic and wire resistances are dominant in the studied case, and this does not influence the accuracy of the proposed method.