Gamification for Maths and Physics in University Degrees through a Transportation Challenge

Abstract

Our society is immersed in the Fourth Industrial Revolution due to the fast evolution of the new technologies that are modifying the labor market. In the near future, technologies related to Industry 4.0 will produce totally new goods and services. Therefore, the educational systems should adapt their programs to the future needs of an uncertain labor market. In particular, mathematics will play a key role in future jobs and there is a strong need to connect its teaching methodologies to the new technological scene. This work uses the STEAM approach (science, technology, engineering, arts and mathematics) along with active methodologies and educational robotics with the aim of developing a new strategy for the application of mathematics and physics in an engineering degree. In particular, a transportation challenge is posed to tackle the teaching–learning process of the Bézier curves and their applications in physics. A pilot project is developed using a LEGO EV3 robot and an active methodology, where students become the center of the learning process. The experimental results of the pilot study indicate an increase in the motivation due to the use of robots and the realistic context of the challenge.

1. Introduction

Today’s society is immersed in the Fourth Industrial Revolution due to the appearance of new technologies such as artificial intelligence, the internet of things, nanotechnology, among others. The term “Fourth Industrial Revolution” arose in 2015, coined by Klaus Schwab, who was an executive chairman of the World Economic Forum, as indicated in [1]. It is important to remark that, although the majority of the society considers that we are currently in the “Fourth Industrial Revolution”, some authors such as Rifkin [2] considered the first two Industrial Revolutions as a unique one and named the 3rd, according to [1,3], as the second one. This fourth (or third) Industrial Revolution is affecting all industries and sectors and even society. Technologies from Industry 4.0 can produce completely new goods and services. The use of different types of sensors and wearable devices as well as techniques from analysis and robotics, among others, will allow improvements in goods and society in general.

The Fourth Industrial Revolution is also modifying the labor market to such an extent that access will be difficult for workers not able to adapt to the new reality. Many jobs will be replaced by machines and “65% of students currently entering the educational system will perform jobs that do not exist today”, as pointed out in [4]. This will require young people to acquire new skills not present in current educational models, since many of the existing plans are designed to meet the needs of the last century. The European Economic and Social Committee urges that “national education and training systems adapt their programs as quickly as possible, so that educational programs can better correspond to the needs of the labor market” according to the European Economic and Social Committee in [5].

The new educational models should focus on aspects related to the acquisition of scientific and technological skills, the development of creativity and innovation as well as the use of new methodologies, in order to offer students the necessary tools to adapt to new environments.

Mathematics is going to play an important role in the jobs of the future. For this reason, it is currently one of the most demanded degrees in many companies. However, its teaching–learning process, both in form and content, needs an in-depth review. Skills such as computational thinking, critical thinking, creativity, technological literacy, collaborative problems like in [6], etc., should be acquired through math subjects. The COVID pandemic has highlighted some challenges, being one of them the collaboration with scholars from other disciplines (interdisciplinarity), as indicated in [7]. In this context, the STEAM movement (science, technology, engineering, arts and mathematics) acquires great relevance (see the works in [8,9]).

Educational robotics fulfills the aforementioned objectives, promoting many of the competences that the students must acquire in order to face an uncertain employment situation. Robotics also allows active learning not only in mathematics, as in [10], but also in other types of subjects, such as Programming (see [11]). From an early age, it is possible to promote computational thinking through robotics (see [12]). There are many related works that prove technology to be a very useful tool for active learning since it facilitates the development of the aforementioned skills. In [13], the effective learning of mathematics is achieved through a robotic platform, which is the tool that stimulate students to develop meaningful learning. This requires the development of an appropriate strategy as well as a proper teacher training.

At university level, the knowledge acquired in mathematics subjects has direct consequences in the rest of the subjects and especially in Physics, where mathematics plays the role of “the language of Physics”, as indicated in [14]. Thus, it is possible to predict the students’ success or failure in physics subjects through their M=math skills, as studied in [15,16,17]. The results of these investigations show that insufficient skills in mathematics (analytical, algebraic manipulation, geometry, calculus, tables, interpretation of graphs, etc.), specially those related to the resolution of physics problems, are the cause of poor students’ performance in physics majors. In this sense, Mathematics is related to a large number of different courses, especially physics [14] and, specifically, students’ success in the physics course depend on their mathematics skills, as pointed out in [15,16,17]. Similarly, these subjects condition the results in engineering subjects since, as demonstrated in [18], there is a direct relationship between the number of years taken by students to pass the basic subjects of mathematics and physics and the number of years taken in completing the degree.

In this work, a STEAM project is presented at university that allows students to learn a part of mathematics necessary in the practice of the Designer profession: the Bézier curves and their applications. This is carried out through a project developed in the form of a transportation challenge that uses a LEGO EV3 robot to explain kinematic concepts and formulate these type of curves with an active methodology. The main objective is to generate positive emotions that motivate students to learn mathematics and that translate into positive attitudes towards this discipline. The results of the experimental design indicate an increased motivation in learning mathematical and physical concepts related to the use of robots and the realistic context of the challenge. The paper is structured as follows. Section 2 introduces the state of the art of STEAM/STEAM approaches for learning, active methodologies and the use of robotics in education. Section 3 presents the authors’ related previous work. Section 4 describes the research purpose of the paper. Section 5 details the methodology of the work, where the challenge and the different developed applications are described. Section 6 details the results and discussion of the project. Finally, conclusions are drawn in Section 7.

2. Background

2.1. STEM and STEAM Learning

The term STEM refers to the realization of projects and initiatives for the promotion and development of scientific-technological skills and competencies in the students involving the participation of the STEM disciplines (see [19]). From an educational perspective, the goal is the intentional integration of the four disciplines in order to solve real-world problems according to Sanders in [19]. In this overall, interdisciplinary and integrative approach, Science provides the scientific method, Technology and Engineering teach the techniques and tools neeeded to build objects and solve technological problems and, finally, mathematics provides a mode of expression and representation that allows the interpretation of the environment and the application of problem solving strategies that promote the logical and critical thinking.

The implementation of the STEM learning approach has generated a profound debate on how to integrate the four disciplines. As a result, two different approaches have been established: the traditionalist approach, in which the four disciplines are developed independently, and the integrative approach, in which the four disciplines are developed jointly, see [20]. Among them, the integrative approach has been the most accepted, where the four disciplines are considered together in a single teaching–learning practice following Sanders in [19]. Still, some researchers believe that an equitable interaction is more appropriate like in [21], while others place some disciplines above the others [22]. In [19], it was remarked that, even though the four disciplines were developed jointly, there was no real connection between them. In this sense, [23] found out that educational institutions used very different methodologies to establish and connect the four disciplines. To solve this problem, [20] proposed the inclusion of a new discipline, Art, in the STEM context. As a consequence, the learning approach was coined STEAM. In STEAM learning, art promotes interdisciplinarity, eases the communication and understanding of reality, and provides creativity in strategies and solutions [24]. In [20], a very broad concept of art is proposed, including the so-called fine arts and other fields such as language and social sciences. The combination of apparently opposed disciplines, scientific and artistic, provides “the necessary variety and diversity for innovative product design” [25]. These disciplines are complementary in the sense that “Science provides a methodological tool in art and art provides a creative model to the development of Science” [26]. The European Parliament [27] considers the inclusion of art essential as it facilitates the acquisition of key competences. In particular, art in STEAM is maily concerned with creativity and creativity, which includes divergent thinking [28] that leads to multiple solutions to a single problem.

2.2. Affective Domain

The affective domain can be described as a set of feelings, moods and states of mind that differ from pure cognition. Three specific components stand out among them: attitudes, beliefs and emotions [29,30]. These are described in the following paragraphs:

• A belief can be described as a knowledge or feeling of certainty acquired and determined by past situations, significant in the person’s mental context, and that generates specific reactions without full awareness [31].
• An emotion is an automatic affective response that arises from an important event for the individual, that results from complex learning, social influence and the subject’s own interpretation [32].
• With respect to attitude, there is not a unique definition in the literature. Nevertheless, most authors define attitude as a prediposition towards something in particular, such as mathematics [32]. The attitude of students towards mathematics has a long tradition in mathematics education and a theoretical discussion about it can be found in [33].

According to [29,30], these factors interact cyclically in the way of perceiving mathematics. This implies that positive emotions generate positive attitudes that, in turn, modify beliefs in mathematics.

Attitudes are considered one of the key variables that explain performance in mathematics [34,35,36,37,38]. In a previous authors’ work [35] an estimate is presented that indicates that attitudes constitute 30% of the explanatory factors of performance, and a conclusion is drawn indicating that students with more positive attitudes towards mathematics develop a better mathematical performance. For that reason, new methodologies should be aimed at engaging students in their learning process, enhancing their attitude towards mathematics.

2.3. Active Methodologies

There are many ways to teach and learn, but the truth is that some are more efficient than others. All of them allow students to learn contents and pass exams. Nevertheless, a reflection has to be made on whether the student has internalized the competences associated with the content taught in that subject and whether he/she is capable of using this knowledge in other subjects. The new generations of students, the famous Z generation and those to come, learn differently and need new multimedia formats. In the field of leisure and culture, they rely on platforms such as Netflix or HBO; they do not look for information in books but rather listen to YouTubers and Influencers to catch up on current trends in fashion, politics, culture, etc. This is the profile of the current student, which is also linked to a rather uncertain professional future. Therefore, the educational system based on master classes whose origin dates back to the first universities of the XI century has become obsolete. Probably, the faculty has the gift of public speaking and can offer quality lectures, but the student body needs another type of interaction. This leads to the use of the so-called active methodologies.

The future of jobs is uncertain. Much evidence already indicates that the $85\%$ of the jobs that will exist in 2030 have not yet been created [39]. Many jobs will be destroyed but, at the same time, many others will appear in which technology and data management will define a new scenario, different from the present one. Robots are going to replace many works done by humans but those robots will have to be programmed. For that reason, today’s students must be prepared for a changing society. They must be autonomous and endowed with capacities that were not relevant before. The development of skills where the students are capable of meeting challenges and solving situations must be promoted, accompanying them with a humanistic component.

The achievement of these objectives entails the evolution and maturation of the educational system, which encourages, both in pre-university and university classrooms, activities where the students are able to learn through problems, projects, challenges, games, etc. All these methodologies stimulate the students to have a different attitude towards learning and to live a completely different experience.

According to Crisol-Moya et al. [40], students and lecturers in Higher Education are moving to a new learning model called learning-centered. If lecturers use active methodologies, it is necessary to introduce new roles in their teaching classes. In active methodologies, the student is the main subject and center of the learning process. There are many works that reveal the effectiveness of an active learning model [41] that enhances motivation, the need to discover, and the autonomy of learning. It also transforms the passive attitude, from receiver of knowledge and instructions, to an active attitude, in which search, inquiry, creativity and innovation are present throughout the process. The main goal is for the student to acquire meaningful learning and a change is sought in the learning acquisition experience. This type of learning allows to train critical, creative and prepared people to face the unknown challenges of the future.

The work of Fernández et al. [42] on these active methodologies, with more than one thousand of students, analyze the consequences of applying active methodologies taking into account three factors: the attendance, the coordination of activities and how the students learn all learning outcomes in each course. The study is really interesting because the academic results are much better comparing with traditional teaching methods. It is also important to distinguish that students need to change their roles and they need to play an active role in this process.

On the other hand, universities need to change how lecturers work, via what Crisol in [43] call a cultural change. In this process it is necessary to remove the lecturer from the center and collocate on the center of the learning process the persons who are going to learn: the students. For that reason, Crisol introduces in [43] the concept of methodological renewal. This renewal is based on active methodologies and the change of roles: lecturers and also students.

In this model, the lecturer plays the role of a learning supervisor, accompanying the students through their professional and personal development process. The lecturer abandons the role of instructor, empowering students with the need to discover, the motivation to learn and the awareness of the need to learn from every new situation, challenge or stage.

There are different active methodologies. Among them, the flipped classroom is one of the most widely used. This methodology compels the students to build their own knowledge at their own pace, as it is known that each student internalizes the knowledge at a different rate. It is applied in [44] to the mathematics subject, where different data are analyzed and the effectiveness of this type of methodology is shown.

Another active methodology is the challenge-based learning (CBL). This methodology implies the posing of a global question or challenge at the beginning of the learning activity, with the aim of focusing the students’ learning on a feasible and close challenge, which engages them in the search of effective and posible solutions. The whole learning process involves research, documentation, ideation and communication, as well as the development of personal and social skills such as teamwork, negotiation, consensus and leadership, as fundamental elements of emotional intelligence. The challenge-based learning is approached in an innovative and creative way, which makes it possible to detect other problems or challenges to be solved. Therefore, it implies a broader vision when compared to project-based learning. Both methodologies, PBL and CBL, use the cooperative learning as basic methodology and their implementation implies a new organizational structure of the classroom, a different way of managing assessment systems and times, as well as a change in the teacher’s role and training.

Recently, gamification is being used as a sophisticated tool to improve the teaching–learning process, as it leads to the enhancement of the quality of the teaching process in general [45]. The so-called Game-Based Learning [46] is a promising tool to motivate and engage the students in their learning process. In fact, the introduction of games in the curriculum has proven to increase the motivation and interest of students and, therefore, can be an effective tool for students to learn, as shown in [47].

2.4. Educational Robotics

In recent years, low-cost robots such as Adept, E-Puck, Moway, LEGO Mindstorms, etc., have appeared. These robots do not offer the same accuracy as industrial robots but enough when the goal is to take advantage of their virtues at an educational level. Robotics and computational thinking are topics to be investigated [48]. Among all these low-cost robotic platforms, LEGO Mindstorms stands out. The starter kit provides the software and hardware necessary to create a wide variety of prototypes. There are many types of LEGO Mindstorms applications in assisted teaching for undergraduate and graduate students in the literature related to the teaching of computer programming. The work in [49] investigated how the achievements of engineering students were affected by robotics when learning the logic of different programming algorithms, using LEGO Mindstorms EV3 in an introductory computer programming course. The statistical results demonstrated that the use of a LEGO robot improved student achievement. LEGO Mindstorms has been used to teach the most common programming languages such as C, Java, ADA, Python, Labview, and Matlab/Simulink. In some cases, the goal was just to teach code. In other cases, the programming language was assumed to be familiar and used in class to reinforce their knowledge [50]. There are also applications related to the teaching of control techniques [51], robotics [52], and other technological subjects.

Educational robotics promote computational thinking, as indicated in Section 1. However, when robots are used in the students’ learning process, three important factors must be taken into account for the development of a successful active methodology [53]. The first one is the need for a proper hardware and software platform. The second one is how to adapt the pedagogic concepts in the developed platform. Finally the last challenge is the training of teachers and students. Teachers need to update their courses to introduce robotics and studens must learn how to interact with the robots to play an active role in their learning process.

2.5. EXPLORIA Project: A New Way of Conceiving the University

The EXPLORIA project arose from the need to enhance university learning methodologies and adapt them to the new trends and needs of the professional market.

In this sense, CEU University is developing different pilot projects in degrees such as Advertising, Political Sciences and Engineering in Industrial Design and Product Development with the aim of rethinking the learning processes of university students in the current context such. Among the pilot degrees, the Degree in Industrial Design and Product Development integrates majors belonging to the STEAM classification. The first-year subjects included the STEAM classification are specified in

Table 1. 1st year STEAM subjects from the Degree in Industrial Design and Product Development.

1st Semester	STEAM	2nd Semester	STEAM
Physics	S,T,M	Physics Extension	S,T,M
Mathematics	M	Mathematics Extension	M
History of art	A	Anthropology	S
Basic Design	A,S,T	Advanced Design	A,S,T
Shape representation	A	Descriptive geometry	A,S,T

.

The goal of the EXPLORIA project is the development of an integral competence map of the learning process. In this map, the majors lose their individuality, in the sense of agglutinating isolated and disconnected content from other disciplines, and become part of an integrated teaching–learning process where the competencies and learning outcomes of the subjects are considered as a whole, for the development of a global and comprehensive learning.

The pilot project uses integrated learning as well as temporal sequences focused on different learning objectives related to Bloom’s taxonomy: understand, apply, experiment and develop [54]. In this way, active methodologies allow the student to approach all the levels of learning: learning by doing. Students develop critical and creative thinking through analysis, both formal and empirical, develop innovation and creativity, as well as the capacity for global and multidisciplinary analysis, imperative in the current context. Students also develop the necessary connections to address the resolution of various challenges and problems that require the integration of knowledge from various disciplines. Students are then prepared to respond to complex problems, in changing, unstable and complex situations.

The 1st year of the Degree in Industrial Design and Product Development is structured in five concepts that will articulate the itinerary of this course, making them coincide with the basic fundamentals of design: shape, volume, colour, space and structure, as shown in

Table 2. 1st year of the Degree in Industrial Design and Product Development.

MODULE I	MODULE II
Act I: Shape	Act IV: Space
Act II: Volume	Act V: Structure
Act III: Colour	Act VI: Project

.

In general, an act usually lasts 4 weeks and in the fifth week a milestone or challenge is introduced that students must solve integrating all the learning obtained during the previous 4 weeks, building a true STEAM project. During the four weeks that the event lasts, the different subjects linked to different STEAM disciplines generate joint activities, at least two, where students discover the connections between them: Mathematics+Arts, Mathematics+Physics, Physics+Arts+Basic Design, etc. These activities prepare them for the challenge they will face in the fifth week. In the EXPLORIA project, one of the objectives for students and lecturers is to create a learning community, where students discover knowledge with the support of their mentors. This implies a closeness between teacher and student that allows a better assessment of the progress of the learning process and the acquisition of skills in the classroom.

3. Previous Works

3.1. EXPLORIA Project

Our previous works [55,56] show the results obtained using this methodology. In [56], the integration of the different subjects in a STEAM learning demonstrated an improvement of the students’ interest in mathematics, as well as their understanding of why it is necessary to learn it.

As an additional section within this project, the improvement of the learning of physics concepts following the same work scheme based on challenges was proposed. This approach was used in [55] to teach physical concepts within a mechanical engineering subject based on different practical exercises. The results showed that the use of physics concepts outside their usual context, and integrated with other topics of the subject, represents a significant improvement in student learning.

3.2. LEGO Robots

Regarding LEGO robots employed in educational robotics at university, most platforms use the pre-EV3 version, the NXT. In addition, existing EV3-based systems are not capable of interacting with LEGO EV3 robots in real time. In [57], a new educational platform is presented, in which the use of Matlab and Simulink is proposed to achieve a real-time interaction between a LEGO EV3 robot and the environment. For that purpose, Matlab and Simulink run in parallel on the computer, exchanging the relevant information in real time in order to interact with robots. This new platform was tested with different autonomous navigation algorithms to verify its usefulness.

4. Research Objectives

The main objective of this work can be summarized as the introduction of technology in the learning process of mathematics through physics, fostering an active attitude of students in learning new mathematical concepts by means of the creation of synergies between different courses.

The use of technology in courses such as mathematics or physics is essential to prepare students for the uncertain future jobs that will appear in a few years. They need to develop skills in different areas to acquire the best possible preparation. It is well known that when students participate in the learning process, they understand and apply this knowledge much better than with a passive attitude, just listening to content. Probably with a classical teaching model, students are trained to prepare and pass an exam. However, the most important issue is to prepare students for the applications of these contents, developing new skills. It is of vital importance to understand and apply all the skills acquired by students through their studies. Moreover, many courses are often organised in isolation and, for that reason, students do not connect the contents of all the courses they take in a semester or in a year. The philosphy under EXPLORIA is to develop the enough synergies between courses to show students the connection between courses and the importance of studying and understanding every subject. In the end, students should have a connected mind map including all contents and skills.

To develop the aim of this paper a pilot STEAM project has been presented and analyzed. This STEAM project has been designed for the students to learn some mathematical concepts (parametric curves) necessary in the practice of the Designer profession, in an integrated and applied manner. This project is part of the sequence of STEAM projects proposed by the EXPLORIA methodology as a learning model and is framed in the second semester of the first year. The STEAM projects developed in EXPLORIA can be carried out individually or in groups. The project presented in this study is designed as an individual project and is aimed at changing the affective domain towards mathematics through physics, increasing the students’ motivation to learn its contents. To this aim, robotics is used to express the need to know and understand the abstract contents taught in mathematical disciplines for the solution of real problems. This particular project is focused on the representation and operation with vectors, as well as the handling of parametric curves, such as Bézier curves, necessary for the understanding of computer-aided design. This content is taught in the subjects Mathematics Extensionand Physics Extension (Table 1).

In the present work, mathematics is channeled through physics with the aim of achieving a challenge: the transportation challenge. The challenge is to transport an object on a mobile robot, a LEGO EV3, from an start position to a goal position without falling, using a Bézier curve acting as the robot’s trajectory. The students must select an object and calculate, through the moment of the force, the maximum acceleration for the object not to fall. Afterwards, students must design a Bézier curve using an applet developed in Geogebra, moving the control points to meet the design constraint. Finally, the generated trajectory is tested on the LEGO EV3 through an application programmed in Matlab.

Table 3. STEAM concepts in the transportation challenge.

STEAM Area	Project Matter
Science	Physical part, Moment of a Force, Kinematics
Technology and Engineering	Robotics, transportation and navigation problem
Technology and Engineering	Dot and cross product, Bézier curves and Frenet’s Frame
Art	Bézier curves to design shapes moving control points

shows a summary of the activities developed in the transportation challenge and their link with the STEAM areas. Let us highlight the link with art. The art is related to the Bézier curves, but not by the calculation of control points through optimization algorithms, but by the use of control points to modify the curvatures in a similar way as a sculptor would. Bézier curves and Bézier surfaces are commonly used in Design programs, where objects are modeled by moving control points. The goal of this activity is to instruct them in the understanding and use of the Bézier curves, necessary for the design and product development.

This project is developed in the Act IV: Space, during the 4 weeks that the act lasts. It connects the STEAM areas of Science (physics) and Maths (M) using Bézier curves. In parallel, other activities that connect Bézier curves with Design and take place, preparing students to connect all STEAM areas during week 5 through the challenge.

5. Materials and Methods

5.1. Research Design and Data Analysis

An experimental design using a multiple-question survey was carried out and assessed with a Likert scale. Qualitative analysis was performed using specific questionnaires that pass Cronbach’s test, following the experts in education, such as, for example [58,59].

The Cronbach’s alpha test is used to analyze if the multiple-question survey created for the research project is suitable for its purpose [59]. This statistic is commonly employed in Science Education. The objective of the test is to estimate the reliability of the questionnaire to assess the students’ perception of mathematics in relation to the solution of real-life problems. The resulting $\alpha$ coefficient of reliability ranges from 0 to 1. Depending on the value of $\alpha$, the internal consistency of the test can be classified as: excellent, good, acceptable, questionable, poor or unacceptable. In this type of test, reliability is achieved when p > 0.7. If $0.8\le \alpha <0.9$, the internal consistency is classified as good. Higher values imply excellent reliability.

5.2. Participants

The participants in this work were the students from the Degree in Industrial Design and Product Development of the 2020/2021 academic year. The number of students in the sample group was 24. Most of them were local students (from Spain) except for three who came from abroad (El Salvador, Colombia and Honduras). The age of the participants ranged between 18 and 20 years old (similarly distributed), except for one of them who was 24 years old.

6. The Transportation Challenge

6.1. Context of the Transportation Challenge

At the end of the 18th century, the introduction of the steam engine entailed the First Industrial Revolution. A century later, the irruption of electricity and oil as the main sources of energy led to the Second Industrial Revolution. Around 1970, changes in information and communication technologies began and led to the Third Industrial Revolution, also called the Intelligence Revolution. This third revolution only dates back to 2006, when it was outlined by the American sociologist and economist Jeremy Rifkin [2], and endorsed by the European Parliament. Today’s society is immersed in the Fourth Industrial Revolution, due to the appearance of new technologies such as artificial intelligence, the internet of things, nanotechnology, mobile robotics, the autonomous car, among others. The definition of “Fourth Industrial Revolution” was coined in 2015 by Klaus Schwab, executive chairman of the World Economic Forum [1].

The first known Automated Guided Vehicle was introduced by Barret Electronics of Northbrook, Illinois, USA in 1953 [60]. However, its massive appearance in industry began only two decades ago, driven by the advances made in the Third Industrial Revolution, but especially in the Fourth Industrial Revolution. Today, it is common to see this type of vehicles in the industry transporting heavy loads and interacting with operators and other human-guided vehicles (see Figure 1).

There are two types of vehicles, the Automated Guided Vehicle (AGV) and the Autonomous Mobile Robot (AMR). The main difference between them lies in their on-board artificial intelligence. An AGV has minimal on-board intelligence on board and can only obey simple programming instructions. They are usually guided by lines or magnetic sensors placed on the ground. On the contrary, the AMR navigates through maps constructed by means of a learning process that begins with a scan of the environment using sensors or a previously drawn map that represents the facility environment. These maps are updated as the robot navigates and are used to design the trajectories for the robot to follow. In this sense, the autonomous vehicle could be placed at the same level of intelligence. Brands such as Google, Tesla, and other well-known manufacturers are making rapid progress in bringing the autonomous vehicle to the market.

All these intelligent and autonomous vehicles have a handicap to solve, which is a hot research topic today: the generation of optimal trajectories. The objective of an optimal trajectory is not only to avoid collision with obstacles, but to transport a passenger or a load, in the smoothest and most economical way, from an origin to a destination. One of the mostly used alternatives in the literature to generate proper trajectories is the use of Bézier curves [61,62]. Among other properties, Bézier curves are smooth by definition and can approximate any other curve, such as the clothoid, also commonly used as a trajectory for vehicles and robots, as in [63].

6.2. The Transportation Challenge Description

The challenge consists in the transportation of an object on a LEGO EV3 robot, from a start position to a goal position without falling, using a Bézier curve as the trajectory of the robot. The students select an object and calculate, through the moment of the force, the limiting acceleration for the object not to fall. Afterwards, students must design a Bézier curve using an applet developed in Geogebra, by moving the control points to meet the design constraint. Finally, the resulting trajectory is tested on the LEGO EV3 through an application programmed in Matlab.

The challenge is developed in seven sessions, with the following content:

• Session 1. The project starts with a motivational session related to the problem to be solved from the viewpoint of mobile robotics. The concepts of AGVs and AMRs, autonomous robots employed in the transportation of materials in industry and society, are introduced.
• Session 2. A mathematics session is taught to work the physical meaning and the procedures related to the vector product and the dot product.
• Session 3. A Physics session is carried out where the moment of a force:

  $$M=D\times F$$
  (where × means the cross product) is explained and a practical exercise is solved regarding its calculation on a bottle of water.
• Session 4. A mathematics session is taught where the Bézier curves and the Frenet’s Frame are explained.
• Session 5. A physics session is performed where kinematic concepts are explained: the accelerations suffered by a moving object when following a curved path, the centripetal and centrifugal components of the acceleration and the calculation of the limit centripetal acceleration given an object to be transported. Mathematical concepts are also tackled and, in particular, the capacity of parametric curves to approximate any desired curve, circle or Clothoid. The latter is thoroughly explained given its mathematical properties and, thus, its application to road design and to the generation of mobile robot trajectories according to Montés et al. [63]. Students select an object and calculate the limit centripetal acceleration.
• Session 6. A mathematics session is done where the developed Geogebra applet is explained. The students use it to design the path to be followed by the robot moving the control points of the Bézier curve and simulating it to verify its compliance with the centripetal acceleration restriction calculated in the previous session.
• Session 7. A final experimentation session is carried out, where the trajectories designed by the students are tested on the Matlab application to control de LEGO EV3 robot. The students verify if the designed trajectory manages to transport the object to the destination without falling. If not, the students redesign the trajectory until the selected object is successfully transported to the destination.

6.3. Software Development for the Transportation Challenge

6.3.1. GeoGebra Applet for Bézier Curve Design

GeoGebra is a mathematical software oriented to the simulation and representation of graphs related to all areas of mathematics. It allows the creation of static and dynamic materials to assist students in understanding concepts visually and interactively. The use of this software is a research topic and many contributions can be found in the literature at different educational levels, including university as we can see in the following articles [64,65,66]. In this work, a differential geometry applet has been developed for the joint activity of physics and mathematics subjects in “the transportation challenge”. The target is for students to associate Frenet’s Frame to the trajectory of a mobile robot describing a Bézier curve of order 6, to visualize the physical concepts of acceleration and velocity, as well as their decomposition (centripetal and centrifugal acceleration). After selecting the object to be transported and calculating the limit centripetal acceleration that the object can withstand in order not to fall, the students design the Bézier curve, moving the control points, and simulate the path that will be traveled in a maximum time. The applet provides the control points of the resulting Bézier curve that will later be incorporated into the Matlab program that controls the LEGO robot. An example developed with this subprogram is displayed in Figure 2, where the value of the accelerations at point P is shown, as well as the vector representation of the velocity and acceleration. When the student presses the "Play" button, point P travels from the starting point to the end point of the curve, showing the values and vectors at each position. The applet can be found at [67].

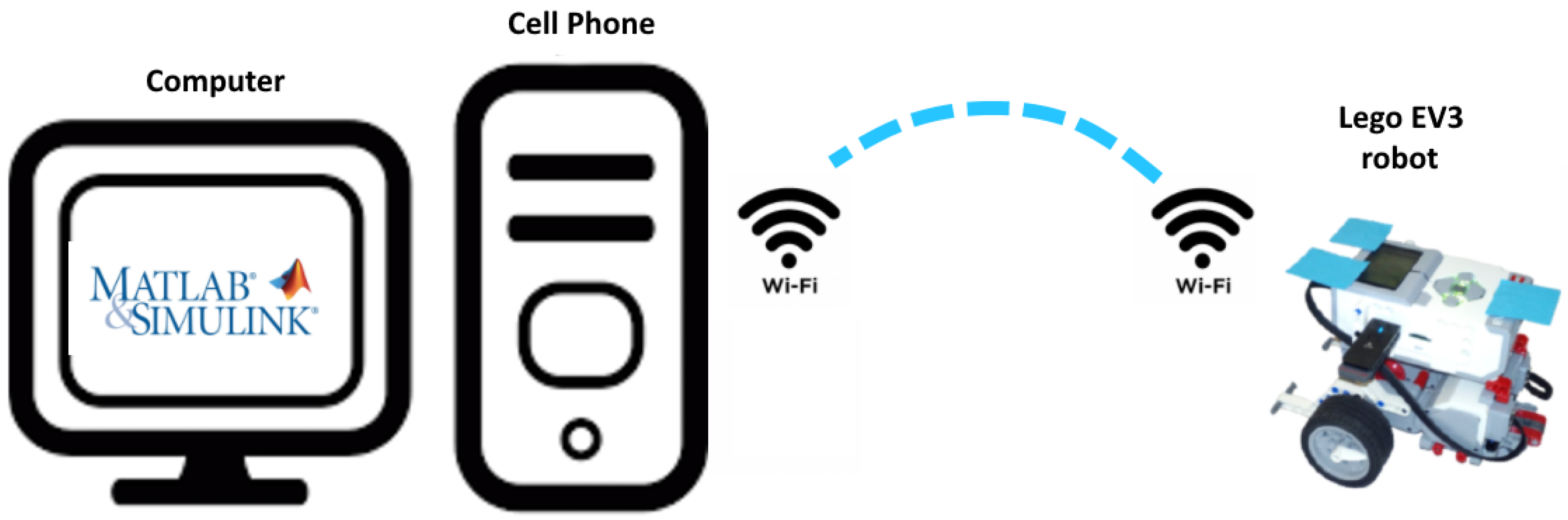
6.3.2. Matlab Application for LEGO EV3 Robot Navigation

A LEGO EV3 unidirectional robot has been built using LEGO blocks with the MINDSTORMS kit, equipped with two traction wheels, a caster wheel and a Wi-Fi connection with a USB dongle to communicate with the computer. The traction wheels motors are equipped with encoders that provide the angular motor positions. A local 2.4 GHz Wi-Fi network is required in order to communicate with the robot. This network can be generated from a cell phone or an specific router. Once the network is created, both the computer and the robot must connect to it in order to establish communication. The complete setup is shown in Figure 3.

The robot control application has been developed in MATLAB^®, a scientific software from MathWorks^®. This software provides a free package to communicate and control LEGO devices from MATLAB^®, called “MATLAB Support Package for LEGO MINDSTORMS EV3 Hardware”. It allows the measurement of the sensors included in the device (color, gyro, ultrasonic, encoders, infrared touch and ultra-sonic sensors) as well as the control of actuators. When working with Matlab, the code is executed on the computer that communicates with the robot via a Wi-Fi connection in order to command the motors. This package allows the implementation of different off-board educational applications, due to the possibility of building almost anything with LEGO blocks.

An application has been designed in Matlab for the control of the LEGO EV3 robot. The interface is shown in Figure 4. In order to make the robot follow a Bézier curve, the student has to establish communication first. For that purpose, the IP address of the Wi-Fi router (cell phone) has to be introduced as well as the Lego Hardware ID, which identifies the specific LEGO brick controller. Once the connection is established, the control points of a 6-order Bézier curve must be introduced for the program to calculate the path to be followed by the robot. This path is initially depicted on the right side window in blue. A button “Follow Bézier” starts the robot motion and, as it proceeds, the path in the window turns red. The robot dimensions are included in the inverse kinematics calculation in the path following algorithm programmed in Matlab as well as a proportional control for the motors.

6.4. Experimental Design

In order to test the results of the innovative methodology described above, an experimental design was carried out through a descriptive analysis, based on a qualitative perspective, following education experts [68].

The participants were the students of the 1st year of the Engineering in Industrial Design and Product Development degree (course 2020–2021), composed of 30 students (9 women and 21 men). The sessions were planned as described in Section 6.2 and used in the sessions of the mathematics and physics subjects of this degree. The students attended individual sessions, being all developed by the same teachers.

Data collection was conducted through an ad hoc questionnaire with 12 items, detailed in

Table 4. Questionnaire answered by 1st year students.

ID	Question
1	Do you know what mathematical models are used for in robotics?
2	Do you know what the vectors in the Geogebra application represent?
3	Do you know what a Bézier curve/Clothoid curve is?
4	Do you understand the influence of the control points on the Bézier curve?
5	Do you know why forces appear in the robot and in the objects it carries?
6	Do you understand the influence of the control points on the forces
	suffered by the robot and the objects it carries?
7	Do you understand the influence of the control points on the position and orientation
	of the robot at the beginning and at the end of the path?
8	Do you understand the influence of the intrinsic parameter on the Bézier curve/path?
9	Did the interaction with the Geogebra applet help you understand the topic??
10	Did the interaction with the robot help you understand the topic?
11	Would you be able to use what you have learned in one of your projects?
12	How easy is it to generate a robot path from a Bézier curve?
13	What do you think about the transport challenge exercise using Geogebra and robotics?

. The answers followed a Likert scale with a range of five points: from 1 = totally disagree to 5 = totally agree.

7. Results

Pictures of the experimental session can be seen in Figure 5. The answers to the questions in Table 4 are collected in

Table 5. Answers to the questionnaire.

Question	Strongly Disagree	Disagree	Undecided	Agree	Strongly Agree	Mean
1	0	4	14	4	2	3.16
2	0	4	10	6	4	3.41
3	0	4	8	10	2	3.41
4	0	4	10	10	0	3.25
5	0	0	12	8	4	3.66
6	1	2	8	10	3	3.5
7	0	4	8	10	2	3.41
8	1	10	8	4	1	2.75
9	0	0	4	16	4	4
10	0	0	4	16	4	4
11	0	2	12	8	2	3.41
12	0	2	4	16	2	3.75

.

As mentioned before, the Cronbach’s alpha test of the multiple-question survey shown in Table 4 was performed to assess its internal reliability, obtaining a $\alpha$ value of 0.8852. This value indicates that the reliabilty of the survey was good, as $0.8\le \alpha <0.9$.

The perception of the use of the Geogebra applet and the Matlab application to control the LEGO EV3 mobile robot to apply mathematics through physics has been positive from the viewpoint of students.

Interesting results can be obtained analyzing the answers in Table 5 in terms of percentages. Focusing on question 1, 25% of the students claim to know the mathematical models used in robotics while 58% of the students are not clear whether they know them or not. Regarding question 2, 41% of students affirm they understand the meaning of the vectors appearing in the Geogebra application while another 41% are undecided about it. Question 3 indicates that 50% of the students clearly know what Bezier and Clothoid curves are while 41% are cannot identify the features of this type of curves. Question 4 reflects the student’s understanding about the effect of the Bézier curve control points on its shape. 41% of the students show knowledge about the influence while another 41% are undecided in the answer. Identical percetages appear in question 5, where students assess their understanding of the cause and effect of forces on systems. Question 6 indicates the students’ knowledge about the influence of the control points on the forces that appear on the robot. In this case, 58% of the students understand the underlying principle, while 33% are undecided. Question 7 is related to the continuity and the derivative at the initial and final points of the Bézier curve and its relation to the orientation of the robot. In this occasion, 50% of the students understand the physical meaning of these mathematical concepts while the 33% of the students express doubts about them. Question 8 assesses the knowledge of the operation of the intrinsic parameter of the Bezier curve. In this regard, 45% of the students ignore its operation while only 20% of the students explicitly indicate that they know the operation of this parameter. Questions 9 and 10 are related to the ability of the Geogebra application and the robot to help the students understand the contents. In both cases, 83% of the students affirm that the use of these tools has facilitated their learning. Question 11 tries to find out if they feel capable enough to use the lessons learned in any of their projects, which results in a 41% of the students answering affirmatively and 50% doubting whether they would be able to use them. Question 12 asks the students if they consider it difficult to generate a trajectory of a robot with the mobility restrictions proposed in this challenge. In this case, 75% of the students consider easy to generate trajectories for a robot. Question 13 is intended for students to express their opinion. Some of the answers are:

• “I found it very interesting because we applied some data obtained by us to a robot so that we could verify if it could happen.”
• “It helped to generate a practical case to apply the theory learned in class. Therefore, the learning was more dynamic, which is a positive point.”
• “It is very well related and helps to understand how, from functions and curves, one can go into real life and make an object fulfill a specific function.”
• “The topic of being able to relate maths to robotics in that way seemed interesting to me. A very cool experiment.”

8. Discussion and Limitations of the Pilot Study

The EXPLORIA project carried out in the Engineering in Industrial Design and Product Development degree has had significant impact on the students’ learning process. As demonstrated in our previous works [56], the students have changed their misconceptions about mathematics and have begun to understand the necessity of learning maths for solving real-life problems.

The EXPLORIA project is organized as a logical sequence of STEAM projects, each of them focused on a specific challenge related to the degree. In this project the challenge of transportation is posed, which integrates two well-known and contrasted methodologies in the literature to improve student learning: the use of Geogebra and educational robotics.

The major limitation for the use of STEAM projects in compulsory education in Spain is the absence of this methodological paradigm within the national curricula. For this reason, it is not usual to find this type of project integrated into the normal functioning of the classroom, since they are usually developed as extracurricular activities.

One of the first STEAM projects developed accounting for the national curricula in primary education was developed in our previous works [69,70], and, following the same methodology, it has been developed at university level in the EXPLORIA project [56] as well as in the project presented in this work, since the project is conceived to replace the conventional regulated teaching.

An important drawback found in the implementation of this methodology is that the teachers’ schedule depends on the learning sequence and it cannot be completely set a priori since the sequence of contents necessary to complete the challenge is perfectly known but unalterable (1—vectors, 2—vector product, 3—moment of a force, etc.). Therefore, the teachers’ schedule must be in accordance with this order. In addition, the hour distribution is not balanced among weeks, as common in traditional degrees. This implies difficulties in the organization of the teaching activities. However, this limitation could be overcome with an in-depth study of the hours devoted to every content and the implication of several teachers with similar training, capable of teaching similar contents.

Another important disadvantage is the number of students involved in this pilot STEAM project. However, the use of the Cronbach’s alpha statistic test justifies the reliability of the questionnaire answered by the students of the pilot project after completing the transportation challenge. The resulting $\alpha$ value of the questionnaire is inside of the interval where the the reliability of the survey is considered as good. Although the number of students is not large, the Cronbach test validates the reliability of the results obtained in this project.

The answers to questions 10 and 11 related to the usefulness of the interaction with the robot and Geogebra to understand the topic have been very positive, as most of the students confirm its utility. In general, the students have demonstrated a high level of understanding of the Mathematical concepts. However, question 8 indicates that these developments have not been sufficient for students to understand the influence of the intrinsic parameter of the Bézier curve on the shape of the curve. As mentioned in the introduction, one of the objectives of the EXPLORIA project is to create a lecturer/student learning community where the lecturer is perceived as a mentor who helps the student discover knowledge. This proximity allows the lecturer to assess, through individual questions made to the student, what is the level of skills acquisition. In the case of this project, the perception of the lecturers and the responses of the students are aligned.

Furthermore, many of the students are hesitant to have acquired the desired knowledge despite of the fact that all of them were able to overcome the challenge of transporting the object from point A to point B and only 10% failed on their first attempt. This implies that they are not sure of their knowledge. The fact that the challenge has been raised individually may have caused indecisive students not to consolidate their knowledge. This problem will be addressed in future improvements of this project through the completion of some additional practical exercises, so that they feel confident of what they have learned and through the combination of group and individual exercises.

To conclude, it is important to point out that there are no studies in the literature, to the authors’ knowledge, of implementations of STEAM projects in university degrees that imply a complete modification of structure and methodology. If we compare the results obtained in the presented project and the results obtained in our previous works [55,56], we can verify that the results are similar in terms of satisfaction and knowledge acquired with the EXPLORIA methodology.

9. Conclusions

This paper presents the challenge of transportation as a pilot STEAM project to learn mathematics related to the branch of design engineering through robotics and physics. The integration of disciplines, together with the use of active methodologies, mobile robotics and the GeoGebra application generates a motivating and encouraging effect on the students and, therefore, a greater understanding of the subject, as corroborated by the questionnaire carried out with the students.

The project is framed in the EXPLORIA project that, as shown in previous works, allows students to change their initial perception of mathematics through the concatenation of STEAM projects linking different subjects.

STEAM learning is an ideal channel to teach mathematics at university level adapted to the degree in which it is being taught. It generates a better understanding of the contents and a positive change of impression towards Mathematics.

The present pilot project implements the integration of two well-known tools to improve teaching, Geogebra and robotics, which allow to merge the learning of mathematics and physics. The results show the generation of a very positive impact on students and lecturers, with the development of a strong connection between them that helps students discover knowledge and enhances their attitude towards mathematics. However, the configuration used in this work does not generate deep enough learning for students to feel confident about their acquired knowledge. This result may be due to little practice related to the design and application of parametric curves and robotics. As future work and improvement of the transportation challenge, more exercises in the design and application of parametric curves and robotics may be posed. For example, a second exercise could be proposed that includes a restriction on the acceleration of the robot and the avoidance of a static obstacle. It would also be important that the first or second exercise could be carried out in a group to strengthen the learning process and the consolidation of knowledge. Finally, a larger group of students should be used in order to consolidate the results of the presented methodology.