Earthquake Catastrophe Bond Pricing Using Extreme Value Theory: A Mini-Review Approach
Abstract
:1. Introduction
- (a)
- Discussing the implementation of EVT in an ECBPM;
- (b)
- Analyzing the methods or models used in developing the ECBPM;
- (c)
- Discussing the literature gaps of the selected articles;
- (d)
- Performing bibliometric analysis based on co-words.
2. Introductory Literature on the Study Topic
3. Materials and Methods
3.1. Materials
3.2. Methods
- (a)
- Reviewing the ECBPM mathematical model to ascertain the models and methods used in its development by answering the questions compiled in the planning stage;
- (b)
- Comparing the results of the developed models;
- (c)
- Determining the literature gap from the earthquake catastrophe bond pricing model using EVT. The aim was to identify a gap that would be helpful in developing future study models and methods.
- (d)
- Using the VOSviewer application to conduct bibliometric co-word analysis, which is defined as scientific mapping of the relationships between studies [40].
4. Results
4.1. Planning
- QR1: What is the purpose of the study?
- QR2: What method or model is used in the study?
- QR3: What type of trigger is used?
- QR4: What types of perils are used in the simulation?
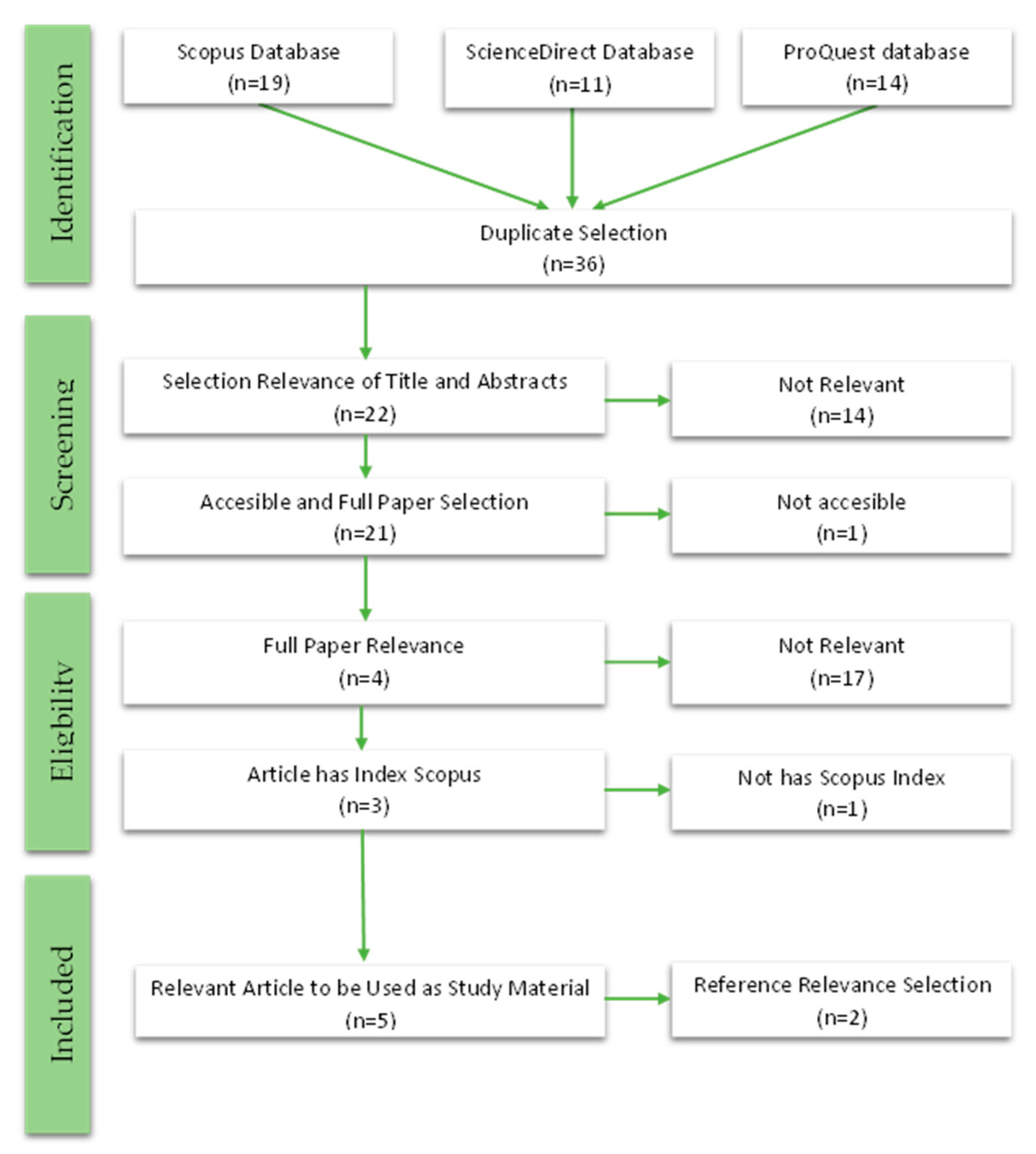
4.2. Searching Strategy
4.3. Analysis Data
4.3.1. Overviews of Previous Models
4.3.2. Comparison of Previous Models
4.3.3. Literature Gap
- (a)
- (b)
- The earthquake severity depends on its location, magnitude, and depth, which are not discussed in the five selected articles.
- (c)
- Earthquake magnitude distribution modeled using GEV can eliminate extreme data for a period [29].
- (d)
- (e)
- (f)
- (g)
- (h)
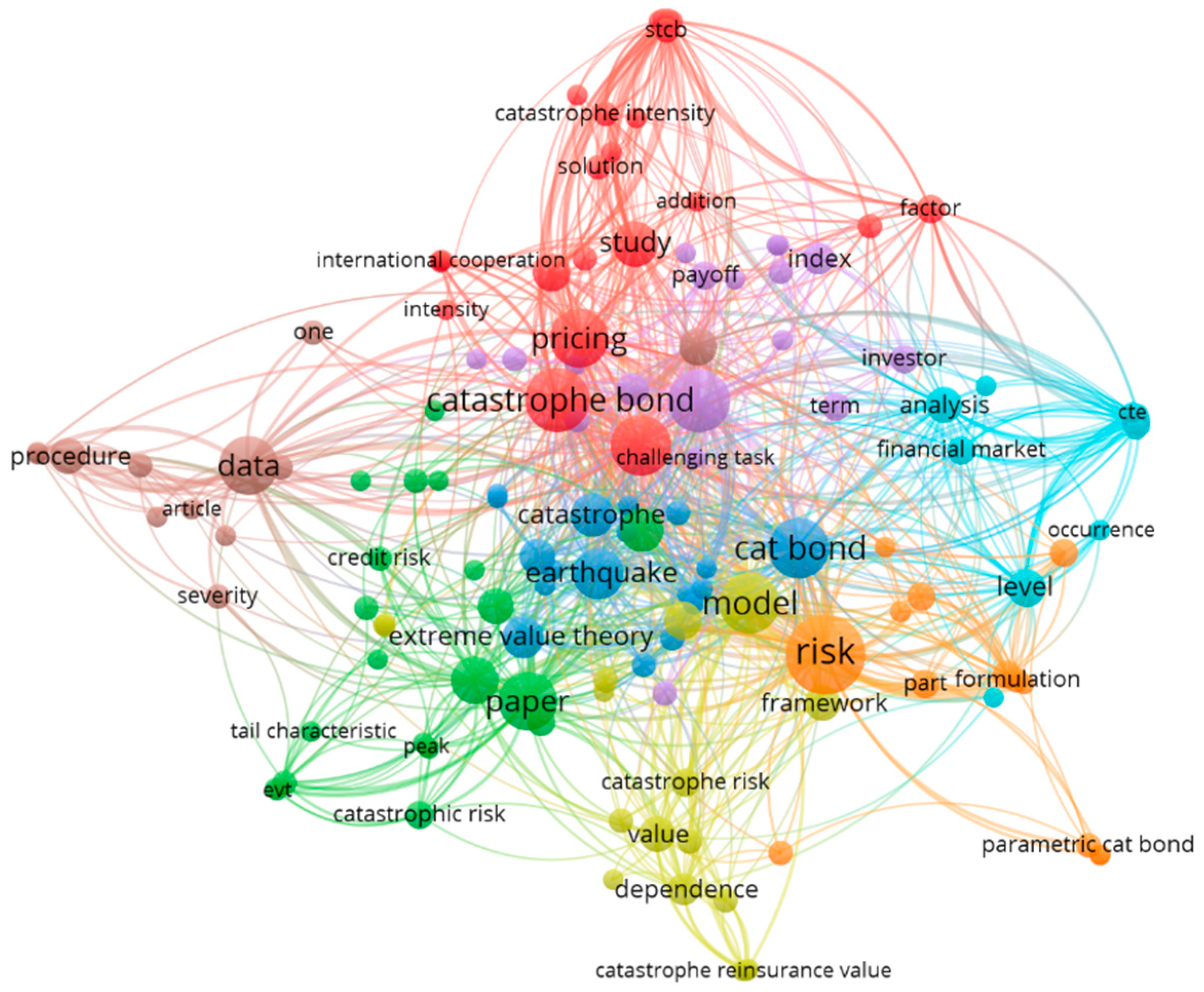
4.4. Bibliometric Analysis
5. Discussion
- (a)
- An earthquake depth parameter is required [43], since the usage of earthquake magnitude triggers [23,44] has not represented the severity of earthquake disasters [57]. However, using the approaches described in [25,27,29,42] necessitates the development of a model of the dependence of earthquake magnitude distribution and depth using copulas.
- (b)
- Analysis of the characteristics of earthquakes based on seismic parameters is required, since the earthquake’s severity depends on its location, magnitude, and depth [57,63]. The method discussed could group the area’s characteristics based on the earthquake parameters. Calvet et al. [18] reviewed eight techniques for classifying the triggering events of earthquake catastrophes. Goda et al. [64] presented a bat-in-a-box grid based on the earthquake’s location and magnitude to categorize a region’s seismic conditions. Hofer et al. [65] proposed the design of earthquake bonds based on the spatial distribution of the portfolio, taking into account the combined asset portfolio consisting of residences in Italy to simplify the analysis by considering the PGA value for each particular municipality. Mistry et al. [66] proposed the design of an earthquake disaster bond based on an earthquake hazard model by considering the source area model and peak ground acceleration (PGA). The Earthquake Disaster Risk Index (EDRI) can be used to categorize places because earthquake risk has economic, social, and environmental impacts [67]. Therefore, it is possible to develop regional groupings using earthquake parameters, EDRI, and PGA. The purpose of grouping areas is to obtain a more accurate calculation of the probability of an earthquake event so as to produce a calculation of disaster bonds that can minimize moral hazard [26,68].
- (c)
- The earthquake magnitude distribution was modeled using GEV [23]. This method was used along with BMM to select extreme values; however, it could eliminate extreme values in a period [29]. This would require GPD to fix the problem by selecting trigger data that exceed the threshold using the POT method [41,42,44].
- (d)
- The main challenge in the POT model is selecting the optimal threshold to fit the model. The threshold value could be determined using a trigger value that causes economic losses or fatalities [29] due to earthquake disasters.
- (e)
- Vasicek’s [44] modeling of interest rates and coupons permits negative values [69,70]. Bond prices are also unrealistic because the volatility of interest rate fluctuations should be constant [58]. In comparison to Vasicek’s model [59], the coupon rate modeled using CIR is superior. However, it has limitations, including continual volatility and no surge caused by monetary policy [58]. The model could be built utilizing an extended Cox–Ingersoll–Ross (ECIR) approach to solve the current shortcomings [71].
- (f)
- Modeling interest rates and inflation using ARIMA [43] requires a data requirement test, and allows negative values. Another method for predicting time-series data without a data requirement test [72] and guaranteeing positive values is fuzzy time series, as long as the data are positive. This method can be used for predicting interest rates and inflation.
- (g)
- (h)
- The payoff function is modeled using a binary function in [41,42,44], while [23,43] use a linear piecewise function. Linear piecewise modeling is better than a binary function because it can describe the level of losses due to earthquakes. Therefore, it is recommended to use a linear piecewise function for modeling the payoff function.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shin, J.Y.; Chen, S.; Kim, T.W. Application of Bayesian Markov Chain Monte Carlo Method with Mixed Gumbel Distribution to Estimate Extreme Magnitude of Tsunamigenic Earthquake. KSCE J. Civ. Eng. 2015, 19, 366–375. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Z.; Wang, W.; Feng, X. Rapid Estimation of Earthquake Fatalities in Mainland China Based on Physical Simulation and Empirical Statistics—A Case Study of the 2021 Yangbi Earthquake. Int. J. Environ Res Public Health. 2022, 19, 6820. [Google Scholar] [CrossRef]
- Nichols, J.M.; Beavers, J.E. Development and Calibration of an Earthquake Fatality Function. Earthq. Spectra. 2003, 19, 605–633. [Google Scholar] [CrossRef]
- Long, L.; Zheng, S.; Zhang, Y.; Sun, L.; Zhou, Y.; Dong, L. CEDLES: A framework for plugin-based applications for earthquake risk prediction and loss assessment. Nat Hazards 2020, 103, 531–556. [Google Scholar] [CrossRef]
- Rashid, M.; Ahmad, N. Economic losses due to earthquake—induced structural damages in RC SMRF structures. Cogent. Eng. 2017, 4, 1296529. [Google Scholar] [CrossRef]
- Chávez-García, G.J.; Jaramillo, H.M.; Cano, M.G.; Vila Ortega, J.J. Vulnerability and site effects in earthquake disasters in Armenia (Colombia). I—Site effects. Geosciences 2018, 8, 254. [Google Scholar] [CrossRef] [Green Version]
- UNDRR. Global Natural Disaster Assessment Report 2019. 2020. Available online: https://www.preventionweb.net/files/73363_2019globalnaturaldisasterassessment.pdf (accessed on 4 May 2022).
- Dominguez, E.A.G.; Golunga, A.T.; Rocha, L.E.P.; Aranda, H.I.A.; Bernal, A.G.; Torres, R.P.R.; Cruz, J.L.E. The 7 September 2017 Tehuantepec, Mexico, earthquake: Damage assessment in masonry structures for housing. Int. J. Disaster Risk Reduct. 2021, 56, 102123. [Google Scholar] [CrossRef]
- EERI. Learning from Earthquakes: The Pisco, Peru, Earthquake of 15 August 2007; EERI Special Earthquake Report; Earthquake Engineering Research Institute (EERI): San Francisco, CA, USA, 2007. [Google Scholar]
- EERI. 8.8 Chile Earthquake of 27 February 2010; EERI Special Earthquake Report; Earthquake Engineering Research Institute (EERI): San Francisco, CA, USA, 2010. [Google Scholar]
- Dollet, C.; Guéguen, P. Global occurrence models for human and economic losses due to earthquakes (1967–2018) considering exposed GDP and population. Nat Hazards 2022, 110, 349–372. [Google Scholar] [CrossRef]
- Ye, S.; Zhai, G.; Hu, J. Damages and Lessons from the Wenchuan Earthquake in CHINA. Hum. Ecol. Risk Assess. 2011, 17, 598–612. [Google Scholar] [CrossRef]
- Kiohos, A.; Paspati, M. Alternative to Insurance Risk Transfer: Creating a catastrophe bond for Romanian earthquakes. Bull. Appl. Econ. 2021, 8, 1–17. [Google Scholar] [CrossRef]
- Shao, J.; Papaioannou, A.D.; Pantelous, A.A. Pricing and simulating catastrophe risk bonds in a Markov-dependent environment. Appl. Math. Comput. 2017, 309, 68–84. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Lee, J.P.; Yu, M.T. Catastrophe risk, reinsurance and securitized risk-transfer solutions: A review. China Financ. Rev. Int. 2021, 11, 449–473. [Google Scholar] [CrossRef]
- Gürtler, M.; Hibbeln, M.; Winkelvos, C. The Impact of the Financial Crisis and Natural Catastrophes on CAT Bonds. J. Risk Insur. 2016, 83, 579–612. [Google Scholar] [CrossRef] [Green Version]
- Pizzutilo, F.; Venezia, E. Are catastrophe bonds effective financial instruments in the transport and infrastructure industries? Evidence and review from international financial markets. Bus. Econ. Horizons 2018, 14, 256–267. [Google Scholar] [CrossRef] [Green Version]
- Calvet, L.; Lopeman, M.; De Armas, J.; Franco, G.; Juan, A.A. Statistical and machine learning approaches for the minimization of trigger errors in parametric earthquake catastrophe bonds. SORT-Stat. Oper. Res. Trans. 2017, 41, 373–391. [Google Scholar] [CrossRef]
- Wu, D.; Zhou, Y. Catastrophe bond and risk modeling: A review and calibration using Chinese earthquake loss data. Hum. Ecol. Risk Assess. 2010, 16, 510–523. [Google Scholar] [CrossRef]
- Sukono; Juahir, H.; Ibrahim, R.A.; Saputra, M.P.A.; Hidayat, Y.; Prihanto, I.G. Application of Compound Poisson Process in Pricing Catastrophe Bonds: A Systematic Literature Review. Mathematics 2022, 10, 2668. [Google Scholar] [CrossRef]
- Morana, C.; Sbrana, G. Climate Change Implications for the Catastrophe Bonds Market: An Empirical Analysis. Econ. Model. 2018, 81, 274–294. [Google Scholar] [CrossRef]
- Cummins, J.D. CAT bonds and other risk-linked securities: State of the market and recent developments. Risk Manag. Insur. 2008, 11, 23–47. [Google Scholar] [CrossRef]
- Zimbidis, A.A.; Frangos, N.E.; Pantelous, A.A. Modeling Earthquake Risk via Extreme Value Theory and Pricing the Respective Catastrophe Bonds. ASTIN Bull. 2007, 37, 163–183. [Google Scholar] [CrossRef]
- Liu, Z.; Wei, W.; Wang, L. An Extreme Value Theory-Based Catastrophe Bond Design for Cyber Risk Management of Power Systems. IEEE Trans. Smart Grid. 2022, 13, 1516–1528. [Google Scholar] [CrossRef]
- Ibrahim, R.A.; Sukono; Napitupulu, H. Multiple-Trigger Catastrophe Bond Pricing Model and Its Simulation Using Numerical Methods. Mathematics 2022, 10, 1363. [Google Scholar] [CrossRef]
- Marvi, M.T.; Linders, D. Decomposition of Natural Catastrophe Risks: Insurability using parametric cat bonds. Risks 2021, 9, 215. [Google Scholar] [CrossRef]
- Chao, W. Valuing Multirisk Catastrophe Reinsurance Based on the Cox-Ingersoll-Ross (CIR) Model. Discret. Dyn. Nat. Soc. 2021, 2021, 8818486. [Google Scholar] [CrossRef]
- Deng, G.; Liu, S.; Li, L.; Deng, C.; Yu, W. Research on the Pricing of Global Drought Catastrophe Bonds. Math. Probl. Eng. 2020, 2020, 3898191. [Google Scholar] [CrossRef]
- Chao, W.; Zou, H.; Cordero, A. Multiple-Event Catastrophe Bond Pricing Based on CIR-Copula-POT Model. Discret. Dyn. Nat. Soc. 2018, 2018, 9. [Google Scholar] [CrossRef]
- Hagedorn, D.; Heigl, C.; Müllera, A.; Seidler, G. Choice of Triggers. In The Handbook of Insurance-Linked Securities; John Wiley & Sons: Hoboken, NJ, USA, 2015; pp. 37–48. [Google Scholar] [CrossRef]
- Zhang, N.; Huang, H. Assessment of World Disaster Severity Processed by Gaussian Blur Based on Large Historical Data: Casualties as an Evaluating Indicator. Nat. Hazards 2018, 92, 173–187. [Google Scholar] [CrossRef]
- Wahono, R.S. A Systematic Literature Review of Software Defect Prediction: Research Trends, Datasets, Methods and Frameworks. J. Softw. Eng. 2015, 1, 1–16. [Google Scholar]
- Griffiths, P. Evidence informing practice: Introducing the mini-review. Br. J. Community Nurs. 2002, 7, 38–39. [Google Scholar] [CrossRef]
- Amelia, R.; Anggriani, N.; Supriatna, A.K.; Istifadah, N. Mathematical Model for Analyzing the Dynamics of Tungro Virus Disease in Rice: A Systematic Literature Review. Mathematics 2022, 10, 2944. [Google Scholar] [CrossRef]
- Mengist, W.; Soromessa, T.; Legese, G. Method for Conducting Systematic Literature Review and Meta-Analysis for Environmental Science Research. MethodsX 2020, 7, 100777. [Google Scholar] [CrossRef]
- Carvalho, F.M.V.; Teles, E.O.; Vieira de Melo, S.A.B.; Mendonça, F.F.G. Supply chain risk management modelling: A systematic literature network analysis review. IMA J. Manag. Math. 2020, 31, 387–416. [Google Scholar] [CrossRef]
- Hezam, I.M.; Nayeem, M.K. A Systematic Literature Review on Mathematical Models of Humanitarian Logistics. Symmetry 2021, 13, 11. [Google Scholar] [CrossRef]
- Moher, D.; Liberati, A.; Tetzlaff, J.; Altman, D.G. Academia and Clinic Annals of Internal Medicine Preferred Reporting Items for Systematic Reviews and Meta-Analyses. Ann. Intern. Med. 2009, 151, 264–269. [Google Scholar] [CrossRef] [Green Version]
- Tresna, S.T.; Subiyanto; Supian, S. Mathematical Models for Typhoid Disease Transmission: A Systematic Literature Review. Mathematics 2022, 10, 2506. [Google Scholar] [CrossRef]
- Donthu, N.; Kumar, S.; Mukherjee, D.; Pandey, N.; Lim, W.M. How to conduct a bibliometric analysis: An overview and guidelines. J. Bus. Res. 2021, 133, 285–296. [Google Scholar] [CrossRef]
- Härdle, W.K.; Cabrera, B.L. Calibrating CAT bonds for Mexican earthquakes. J. Risk Insur. 2010, 77, 625–650. [Google Scholar] [CrossRef] [Green Version]
- Wei, L.; Liu, L.; Hou, J. Pricing Hybrid-Triggered Catastrophe Bonds Based on Copula-EVT Model. Quant. Financ. Econ. 2022, 6, 223–243. [Google Scholar] [CrossRef]
- Shao, J.; Pantelous, A.; Papaioannou, A.D. Catastrophe Risk Bonds with Applications to Earthquakes. Eur. Actuar. J. 2015, 5, 113–138. [Google Scholar] [CrossRef]
- Tang, Q.; Yuan, Z. Cat Bond Pricing Under a Product Probability Measure with Pot Risk Characterization. ASTIN Bull. 2019, 49, 457–490. [Google Scholar] [CrossRef]
- Vakili, W.; Ghaffari, H.A. CAT Bond Pricing in Uncertain Environment. Iran J. Manag. Stud. 2022, 15, 347–364. [Google Scholar] [CrossRef]
- Liu, J.; Xiao, J.; Yan, L.; Wen, F. Valuing catastrophe bonds involving credit risks. Math. Probl. Eng. 2014, 2014, 563086. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Cummins, J.D. Longevity bond premiums: The Extreme Value Approach and Risk Cubic Pricing. Insur. Math. Econ. 2010, 46, 150–161. [Google Scholar] [CrossRef]
- Ma, Z.G.; Ma, C.Q. Pricing Catastrophe Risk Bonds: A Mixed Approximation Method. Insur. Math. Econ. 2013, 52, 243–254. [Google Scholar] [CrossRef]
- Bahl, R.K.; Sabanis, S. Model-Independent Price Bounds for CATASTROPHIC Mortality Bonds. Insur. Math. Econ. 2021, 96, 276–291. [Google Scholar] [CrossRef]
- Xu, M.; Zhang, Y. Data Breach CAT Bonds: Modeling and Pricing. North. Am. Actuar. J. 2021, 25, 543–561. [Google Scholar] [CrossRef]
- Hofer, L.; Gardoni, P.; Zanini, M.A. Risk-Based CAT Bond Pricing Considering Parameter Uncertainties. Sustain. Resilient Infrastruct. 2021, 6, 315–329. [Google Scholar] [CrossRef]
- Stupfler, G.; Yang, F. Analyzing and Predicting CAT Bond Premiums: A Financial Loss Premium Principle and Extreme Value Modeling. ASTIN Bull. 2018, 48, 375–411. [Google Scholar] [CrossRef] [Green Version]
- Ma, Z.; Ma, C.; Xiao, S. Pricing Zero-Coupon Catastrophe Bonds Using EVT with Doubly Stochastic Poisson Arrivals. Discret. Dyn. Nat. Soc. 2017, 2017, 3279647. [Google Scholar] [CrossRef] [Green Version]
- Karagiannis, N.; Assa, H.; Pantelous, A.A.; Turvey, C.G. Modelling and pricing of catastrophe risk bonds with a temperature-based agricultural application. Quant Financ. 2016, 16, 1949–1959. [Google Scholar] [CrossRef]
- Cox, S.H.; Pedersen, H.W. Catastrophe risk bonds. N. Am. Actuar. J. 2000, 4, 56–82. [Google Scholar] [CrossRef]
- Giuricich, M.N.; Burnecki, K. Modelling of Left-Truncated Heavy-Tailed Data with Application to Catastrophe Bond Pricing. Phys. A Stat. Mech. Its Appl. 2019, 525, 498–513. [Google Scholar] [CrossRef]
- Ansari, K.; Bae, T.S. Clustering Analysis of Seismicity in the Space–Time–Depth–Magnitude Domain Preceding the 2016 Kumamoto Earthquake, Southwestern Japan. Int. J. Earth Sci. 2021, 110, 253–261. [Google Scholar] [CrossRef]
- Orlando, G.; Mininni, R.M.; Bufalo, M. Interest rates calibration with a CIR model. J. Risk. Financ. 2019, 20, 370–387. [Google Scholar] [CrossRef]
- Majumder, M.M.R.; Hossain, M.I. Limitation of ARIMA in Extremely Collapsed Market: A Proposed Method. In Proceedings of the 2nd International Conference on Electrical, Computer and Communication Engineering, ECCE 2019, Cox’s Bazar, Bangladesh, 7–9 February 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Braun, A.; Kousky, C. Catastrophe Bond; Wharton Risk Centre Primer; Wharton University of Pensylvania: Risk Management and Decision Processes Center: Philadelphia, PA, USA, 2021; pp. 1–10. [Google Scholar]
- Cummins, J.D.; Lalonde, D.; Phillips, R.D. The Basis Risk of Catastrophic-Loss Index Securities. J. Financ. Econ. 2004, 71, 77–111. [Google Scholar] [CrossRef] [Green Version]
- Finken, S.; Laux, C. Catastrophe Bonds and Reinsurance: The Competitive Effect of Information-Insensitive Triggers. J. Risk Insur. 2009, 76, 579–605. [Google Scholar] [CrossRef]
- Ansari, E.M.; Caldera, H.J.; Heshami, S.; Moshahedi, N.; Wirasinghe, S.C. The Severity of Earthquake Events—Statistical Analysis and Classification. Int. J. Urban Sci. 2016, 20, 4–24. [Google Scholar] [CrossRef]
- Goda, K.; Franco, G.; Song, J.; Radu, A. Parametric Catastrophe Bonds for Tsunamis: Cat-in-a-Box Trigger and Intensity-Based Index Trigger Methods. Earthq. Spectra 2019, 55, 113–136. [Google Scholar] [CrossRef]
- Hofer, L.; Zanini, M.A.; Gardoni, P. Risk-Based Catastrophe Bond Design for a Spatially Distributed Portfolio. Struct. Saf. 2020, 83, 101908. [Google Scholar] [CrossRef]
- Mistry, H.K.; Lombardi, D. Pricing Risk-Based Catastrophe Bonds for Earthquakes at an Urban Scale. Struct. Saf. 2022, 12, 1–13. [Google Scholar] [CrossRef]
- Erdik, M. Earthquake Risk Assessment. Bull. Earthq. Eng. 2017, 15, 5055–5092. [Google Scholar] [CrossRef]
- Franco, G. Minimization of Trigger Error in Cat-in-a-Box Parametric Earthquake Catastrophe Bonds with an Application to Costa Rica. Earthq. Spectra 2010, 26, 983–998. [Google Scholar] [CrossRef]
- Mamon, R. Three Ways to Solve for Bond Prices in the Vasicek Model. J. Appl. Math. Decis. Sci. 2004, 8, 1–14. [Google Scholar] [CrossRef]
- Samimia, O.; Mehrdoust, F. Vasicek interest rate model under Lévy process and pricing bond option. Commun. Stat. Simul. Comput. 2022, 51, 1–17. [Google Scholar] [CrossRef]
- Peng, Q.; Schellhorn, H. On the distribution of extended CIR model. Stat. Probab. Lett. 2018, 142, 23–29. [Google Scholar] [CrossRef]
- Selim, K.S.; Elanany, G.A. A new method for short multivariate fuzzy time series based on genetic algorithm and fuzzy clustering. Adv. Fuzzy Syst. 2013, 2013, 10. [Google Scholar] [CrossRef]
| Date of Issues | Sponsor | SPV | Value | Peril | Trigger Type |
|---|---|---|---|---|---|
| May 2006 | FONDEN | Cat-Mex Ltd. | USD 160 million | Earthquake in Mexico | Parametric |
| October 2009 | FONDEN | Multicat Mexico Ltd. | USD 290 million | Tornado and earthquake in Mexico | Parametric |
| August 2017 | FONDEN | IBRBD CAR 113–115 | The US $360 Million | Tornado and earthquake in Mexico | Parametric |
| February 2018 | Republic of Chile | IBRD CAR 116 | USD 500 million | Earthquake in Chile | Parametric |
| February 2018 | Republic of Colombia | IBRD CAR 117 | USD 400 million | Earthquake in Colombia | Parametric |
| February 2018 | FONDEN | IRBD CAR 118–119 | USD 260 million | Earthquake in Mexico | Parametric |
| February 2018 | Republic of Peru | IBRD CAR 120 | USD 200 million | Earthquake in Peru | Parametric |
| November 2019 | Republic of the Philippines | World Bank IBRD 123–124 | USD 225 million | Earthquake and tropical cyclone in the Philippines | Modeled loss |
| Stage | Keywords | Number of Articles | ||
|---|---|---|---|---|
| Scopus | Science Direct | ProQuest | ||
| 1 | (“catastrophe bond” OR “CAT bond” OR “pricing cat bond” OR “valuation CAT bond”) | 194 | 372 | 317 |
| 2 | (“catastrophe bond” OR “cat bond” OR “pricing cat bond” OR “valuation CAT bond”) AND (“earthquake” OR “tsunamis”) | 73 | 71 | 154 |
| 3 | (“catastrophe bond” OR “CAT bond” OR “pricing CAT bond” OR “valuation CAT bond”) AND (“earthquake” OR “tsunamis”) AND (“extreme value theory”) | 19 | 11 | 14 |
| Inclusion criteria | I1 | Articles discussing the pricing of catastrophe bonds |
| I2 | The developed model relates to earthquake disasters | |
| I3 | Trigger modeling using extreme value theory | |
| I4 | Articles in English | |
| I5 | Articles published in a Scopus-indexed journal | |
| Exclusion criteria | E1 | Duplicate articles |
| E2 | Inaccessible articles |
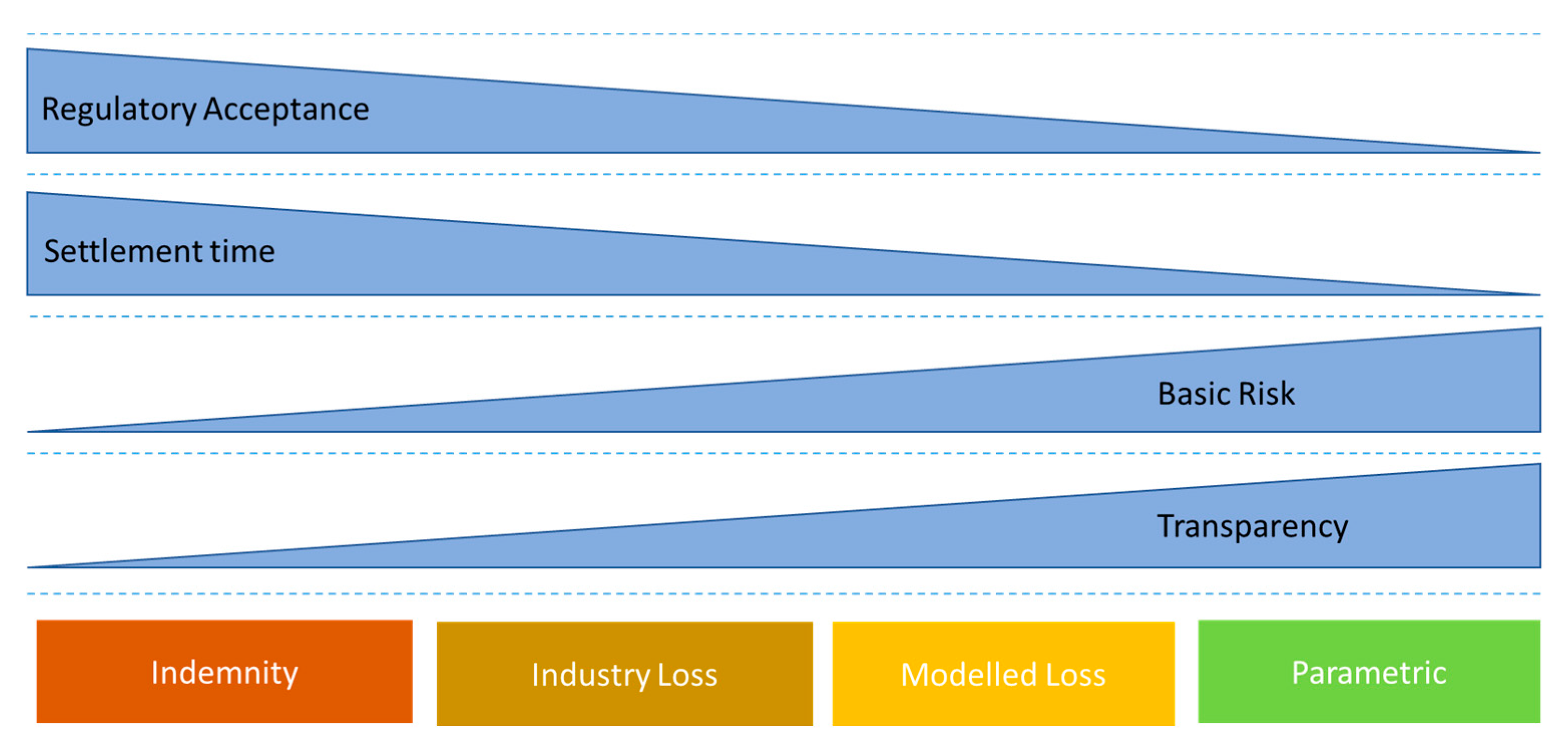
| No | QR1 | QR2 | QR3 | QR4 | Description | Ref. |
|---|---|---|---|---|---|---|
| 1 | Developing a multi-period CAT bond pricing under uncertain conditions | Linear membership function, renewal process, ruin index, optimization model, and binary payoff function. | Indemnity | - | Not suitable | [45] |
| 2 | Creating a multi-period multiple-trigger CAT bond pricing model for coupon and zero-coupon bonds | ARIMA, Burr, generalized extreme value (GEV), Weibull, generalized Pareto (GPD), Log logistic, maximum likelihood estimation (MLE), nonhomogeneous Poisson process (NHPP), binary cash value function, Nuel recursive method (NRM), and Kolmogorov–Smirnoff | Modeled loss | Storm catastrophe in the United States | Not suitable | [25] |
| 3 | Developing a multi-hazard and multiregional CAT bond pricing | GEV, hydraulic flow model, and Monte Carlo simulation | Parametric | Flood in Oregon, US | Not suitable | [26] |
| 4 | Introducing a CAT bond pricing for a single period with coupon payments in Romania | Linear piecewise payoff function, GEV, block maxima method (BMM), and maximum likelihood estimation (MLE) | Parametric | Earthquake in Romania | Not suitable | [13] |
| 5 | Developing a framework for valuing multi-period multi-risk reinsurance contract | Poisson, CIR, GPD, MLE, copula, Kolmogorov–Smirnov, sensitivity analysis, and Monte Carlo simulation | Modeled loss | Simulation data of flood reinsurance | Not suitable | [27] |
| 6 | Studying the pricing of multi-period drought CAT bonds by the POT model and high quantile estimation | Kurtosis method, the static term structure of interest rates, the binary payoff function, the Poisson process, GPD, Lagrangian, and MLE | Modeled loss | Drought catastrophe for 21 countries | Not suitable | [28] |
| 7 | Developing multi-period CAT bond pricing for multiple event catastrophe bonds based on CIR, copula, and POT models | Poisson process, binary payoff function, CIR, peaks over threshold, GPD, copula, Monte Carlo simulation, sensitivity analysis to determine the impact of catastrophe intensity, maturity date, and the dependence on catastrophe bond prices | Modeled loss | - | Not suitable | [29] |
| 8 | Developing multi-period CAT bond pricing considering risk credit | Linear piecewise payoff function, probability of default, GEV, and MLE | Industry loss | USA catastrophe | Not suitable | [46] |
| 9 | Developing explicit multi-period CAT bond prices in terms of four different payoff functions | CIR, compound Poisson, semi-Markovian dependence structure in continuous time, binary and piecewise payoff function, GEV | Industry loss | USA catastrophe | Not suitable | [14] |
| 10 | Analyzing the securitization of longevity risk, with an emphasis on longevity risk modeling and longevity bond premium pricing | Option payoff function, mortality index model, the classic Lee–Carter model, singular value decomposition, random walk model with drift, normal distribution, EVT to model tail distribution, premium spread model, conditional expected loss, Cobb–Douglass function to capture the tradeoff between CEL and PFL, and the Lane Financial Corporation (LFC) cubic model | Mortality index | - | Not suitable | [47] |
| 11 | Developing multi-period CAT bond pricing with and without coupons | CIR, Poisson process, compound Poisson process, binary payoff function, nonhomogeneous Poisson process, fast Fourier transform, inversion method, approximation method, recursive method, gamma, skewness, GEV | Industry loss | US catastrophe | Not suitable | [48] |
| 12 | Valuation of a CAT mortality bonds model | Mortality index model, linear piecewise payoff function, binary payoff function t, the proportion of the principal returned model, and a discounted cash flow model | Mortality index | - | Not suitable | [49] |
| 13 | Developing a framework for multi-period pricing of data breach CAT bonds | Linear piecewise payoff function, equilibrium pricing theory, GEV, MLE, Akaike information criterion (AIC), and negative likelihood | Industry loss | - | Not suitable | [50] |
| 14 | Developing multi-period CAT bond pricing with coupons to propose a mathematical formulation for the probability that the incurred losses exceed a certain threshold D before the bonds’ expiration | Compound Poisson process and CIR | Modeled loss | - | Not suitable | [51] |
| 15 | Developing multi-period CAT bond pricing based on a product pricing measure combined with a distorted probability function | GEV, GPD, MLE, and R function, Vasicek, sensitivity analysis, and Wang transformation | Parametric | Californian earthquake | Referencepaper | [44] |
| 16 | Developing a pricing model for multi-period CAT bond premiums | Linear piecewise payoff function, expected loss model, correlation test, value at risk (VaR), conditional tail expectation, EVT, asymptotic analysis, MLE, GEV, and GPD | Modeled loss | Wildfire Fort McMurray, Canada | Not suitable | [52] |
| 17 | Modeling multi-period CAT bond pricing | Hull–White, NHPP, compound Poisson process, doubly stochastic process, GPD, maximum likelihood, and numerical optimization | Industry loss | US catastrophe | Not suitable | [53] |
| 18 | Modeling CAT bond pricing with a temperature based on agriculture | Utility without catastrophe risk bond model, utility with and without catastrophe risk bond model, and ask-and-bid price model | Parametric | Agriculture in Iran | Not suitable | [54] |
| 19 | Developing Cox and Pederson [55] single- and multi-period CAT bond pricing models with multiple catastrophes and risks | Linear piecewise payoff function, ARIMA (1, 1, 1), CIR, block maxima, GEV, and gamma | Parametric | Californian earthquake | Referencepaper | [43] |
| 20 | Creating single- and multi-period CAT bond pricing for the earthquakes in the Greek border area | Log-normality, CIR, linear piecewise payoff function, GEV, MLE, and the FORTRAN subroutine MLEGEV | Parametric | Greek earthquakes | Referencepaper | [23] |
| 21 | Modeling of left-truncated heavy-tailed data for application to catastrophe bond pricing | Compound Poisson process, NHPP, naïve approach, shifting approach, conditional complete data (CCD), MLE, maximum product of spacing (MPS), goodness-of-fit test, Moran’s log spacing statistic, Burr, GPD, and GEV | Industry loss | - | Not suitable | [56] |
| 22 | Analyzing multi-period CAT bonds with and without coupons | Homogeneous Poisson process (HPP), NHPP, continuous compound interest, binary payoff function, regression analysis, mean excess function, mean absolute difference (MAD), mean absolute values’ relative differences (MAVRD), Log-normal, Pareto, Burr, exponential, gamma, and Weibull | Hybrid trigger (modeled index losses) | Mexican earthquake | Reference paper | [41] |
| 23 | Developing multi-period hybrid CAT bonds with coupons | Poisson distribution, Poisson process, binary payoff function, POT, GPD, Archimedean copula, CIR, and continuous compound interest | Hybrid trigger (modeled losses and parametric) | Losses and their magnitude in China | Reference paper | [42] |
| Model 1 [44] | |
| Model 2 [43] | Single-Period Model Multi-Period Model |
| Model 3 [23] | Single-Period Multi-Period |
| Model 4 [41] | Zero-Coupon Bond Coupon Bond |
| Model 5 [42] |
| Author | Trigger Parameter | |||
|---|---|---|---|---|
| Magnitude | Depth | Losses | Aggregate Losses | |
| Tang and Yuan [44] | √ | - | - | - |
| Shao et al. [43] | √ | √ | - | - |
| Zimbidis et al. [23] | √ | - | - | - |
| Hardle and Carbera [41] | - | - | - | √ |
| Wei et al. [42] | √ | - | √ | - |
| Author | Trigger Distribution | ||||||
|---|---|---|---|---|---|---|---|
| GEV | GPD | Gamma | AC | NHPP | Burr | Log-Normal | |
| Tang and Yuan [44] | √ | √ | - | - | - | - | - |
| Shao et al. [43] | √ | - | √ | - | - | - | - |
| Zimbidis et al. [23] | √ | - | - | - | - | - | - |
| Hardle and Carbera [41] | - | √ | - | - | √ | √ | √ |
| Wei et al. [42] | - | √ | - | √ | - | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anggraeni, W.; Supian, S.; Sukono; Halim, N.B.A. Earthquake Catastrophe Bond Pricing Using Extreme Value Theory: A Mini-Review Approach. Mathematics 2022, 10, 4196. https://doi.org/10.3390/math10224196
Anggraeni W, Supian S, Sukono, Halim NBA. Earthquake Catastrophe Bond Pricing Using Extreme Value Theory: A Mini-Review Approach. Mathematics. 2022; 10(22):4196. https://doi.org/10.3390/math10224196
Chicago/Turabian StyleAnggraeni, Wulan, Sudradjat Supian, Sukono, and Nurfadhlina Binti Abdul Halim. 2022. "Earthquake Catastrophe Bond Pricing Using Extreme Value Theory: A Mini-Review Approach" Mathematics 10, no. 22: 4196. https://doi.org/10.3390/math10224196





