Infection Eradication Criterion in a General Epidemic Model with Logistic Growth, Quarantine Strategy, Media Intrusion, and Quadratic Perturbation
Abstract
:1. Introduction
- •
- Deterministic Part:The first part contains the transfer rates between the classes, with the positive parameters defined in Table 2.If we only consider this part without adding random fluctuations, we obtain a deterministic model that simulates the spread of a given disease under an isolation strategy and media intrusion. To classify and sort the long-term behavior of this disease, we can use the basic reproductive ratio [58]. According to the calculus presented in Section 3 of [59], is expressed as follows:where
- •
- Stochastic Part:This part characterizes and describes the effects of complex environmental fluctuations, whereWe consider a probability triple and an increasing right-continuous filtration along with the fact that includes all -null sets. The six Wiener processes are all mutually independent and defined on ; are the intensities of white noises in the linear part, while are the intensities of white noises in the quadratic part.
2. Theoretical Results
3. Numerical Application: Herpes Simplex Virus (HSV)
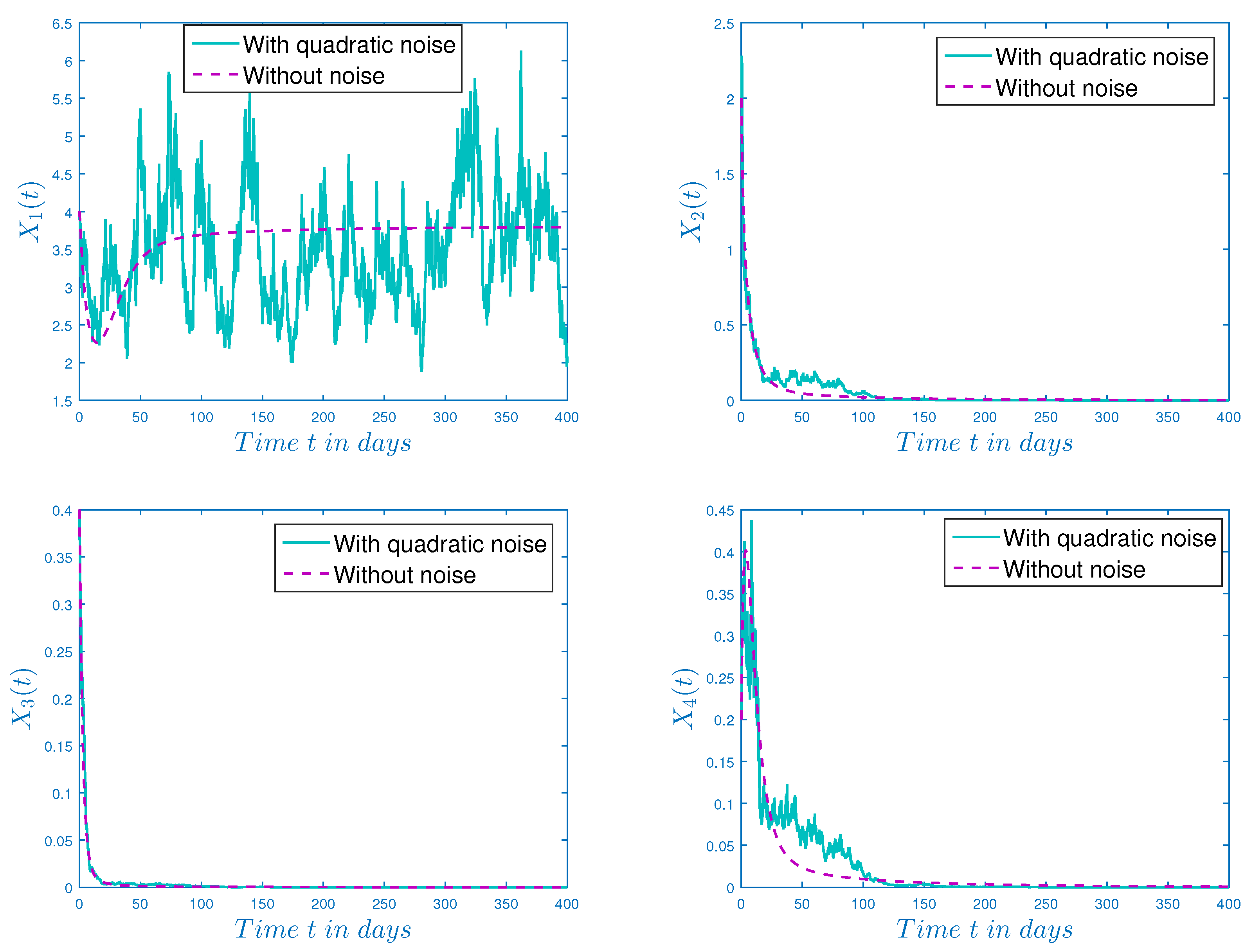
3.1. Case 1: When
3.2. Case 2: When
3.3. Impact of Quadratic Noise on Eradication Time of HSV
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- May, R.M. Stability and Complexity in Model Ecosystems; Princeton Landmarks in Biology; Princeton University Press: Princeton, NJ, USA, 2001. [Google Scholar]
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. A Math. Phys. Eng. Sci. 1927, 115, 700–721. [Google Scholar]
- Neufeld, Z.; Khataee, H.; Czirok, A. Targeted adaptive isolation strategy for COVID-19 pandemic. Infect. Dis. Model. 2020, 5, 357–361. [Google Scholar] [CrossRef] [PubMed]
- Buonomo, B. Effects of information-dependent vaccination behavior on coronavirus outbreak: Insights from a SIRI model. Ric. Di Mat. 2020, 69, 483–499. [Google Scholar] [CrossRef] [Green Version]
- Hossain, M. The effect of the Covid-19 on sharing economy activities. J. Clean. Prod. 2021, 280, 124782. [Google Scholar] [CrossRef] [PubMed]
- Sabbar, Y.; Kiouach, D.; Rajasekar, S.; El-idrissi, S.E.A. The influence of quadratic Lévy noise on the dynamic of an SIC contagious illness model: New framework, critical comparison and an application to COVID-19 (SARS-CoV-2) case. Chaos Solitons Fractals 2022, 2022, 112110. [Google Scholar] [CrossRef] [PubMed]
- Anderson, R.M.; May, R.M. Population biology of infectious diseases: Part I. Nature 1979, 280, 361–367. [Google Scholar] [CrossRef]
- Kiouach, D.; Sabbar, Y.; El-idrissi, S.E.A. New results on the asymptotic behavior of an SIS epidemiological model with quarantine strategy, stochastic transmission, and Levy disturbance. Math. Methods Appl. Sci. 2021, 44, 13468–13492. [Google Scholar] [CrossRef]
- Shaikhet, L. Improving Stability Conditions for Equilibria of SIR Epidemic Model with Delay under Stochastic Perturbations. Mathematics 2020, 8, 1302. [Google Scholar] [CrossRef]
- Bunimovich-Mendrazitsky, S.; Shaikhet, L. Stability Analysis of Delayed Tumor-Antigen-Activated Immune Response in Combined BCG and IL-2 Immunotherapy of Bladder Cancer. Processes 2020, 8, 1564. [Google Scholar] [CrossRef]
- Goel, N.S.; Dyn, N.R. Stochastic Models in Biology; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Winkelmann, S.; Schutte, C. Stochastic Dynamics in Computational Biology; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Wilkinso, D.J. Stochastic Modelling for Systems Biology; Chapman and Hall-CRC: London, UK, 2006. [Google Scholar]
- Matis, J.H.; Zheng, Q.; Kiffe, T.R. Describing the spread of biological populations using stochastic compartmental models with births. Math. Biosci. 1995, 126, 215–247. [Google Scholar] [CrossRef]
- Faddy, M.J. Nonlinear stochastic compartmental models. Math. Med. Biol. A J. IMA 1985, 2, 287–297. [Google Scholar] [CrossRef] [PubMed]
- Kiouach, D.; Sabbar, Y. Modeling the impact of media intervention on controlling the diseases with stochastic perturbations. AIP Conf. Proc. 2019, 2074, 020026. [Google Scholar]
- Kiouach, D.; Sabbar, Y. Developing new techniques for obtaining the threshold of a stochastic SIR epidemic model with 3-dimensional Levy process. arXiv 2020, arXiv:2002.09022. [Google Scholar] [CrossRef]
- Ditlevsen, S.; Samson, A. Introduction to stochastic models in biology. Stoch. Biomath. Model. 2013, 2013, 3–35. [Google Scholar]
- Ji, C.; Jiang, D.; Shi, N. The behavior of an SIR epidemic model with stochastic perturbation. Stoch. Anal. Appl. 2012, 30, 755–773. [Google Scholar] [CrossRef]
- Zhang, X.B.; Huo, H.F.; Xiang, H.; Shi, Q.; Li, D. The threshold of a stochastic SIQS epidemic model. Phys. A Stat. Mech. Its Appl. 2017, 482, 362–374. [Google Scholar] [CrossRef]
- Zhao, Y.; Jiang, D. The threshold of a stochastic SIS epidemic model with vaccination. Appl. Math. Comput. 2014, 243, 718–727. [Google Scholar] [CrossRef]
- Liu, X.Q.; Zhong, S.M.; Tian, B.D.; Zheng, F.X. Asymptotic properties of a stochastic predator-prey model with Crowley-Martin functional response. J. Appl. Math. Comput. 2013, 43, 479–490. [Google Scholar] [CrossRef]
- Belabbas, M.; Ouahab, A.; Souna, F. Rich dynamics in a stochastic predator-prey model with protection zone for the prey and multiplicative noise applied on both species. Nonlinear Dyn. 2021, 106, 2761–2780. [Google Scholar] [CrossRef]
- Naim, M.; Sabbar, Y.; Zeb, A. Stability characterization of a fractional-order viral system with the non-cytolytic immune assumption. Math. Model. Numer. Simul. Appl. 2022, 2, 164–176. [Google Scholar] [CrossRef]
- Kar, T.; Nandi, S.; Jana, S.; Mandal, M. Stability and bifurcation analysis of an epidemic model with the effect of media. Chaos Solitons Fractals 2019, 120, 188–199. [Google Scholar] [CrossRef]
- Özköse, F.; Yavuz, M.; Şenel, M.T.; Habbireeh, R. Fractional order modelling of omicron SARS-CoV-2 variant containing heart attack effect using real data from the United Kingdom. Chaos Solitons Fractals 2022, 157, 111954. [Google Scholar] [CrossRef] [PubMed]
- Özköse, F.; Yavuz, M. Investigation of interactions between COVID-19 and diabetes with hereditary traits using real data: A case study in Turkey. Comput. Biol. Med. 2022, 141, 105044. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Jiang, D.; ORegan, D. The extinction and persistence of the stochastic SIS epidemic model with vaccination. Phys. A Stat. Mech. Its Appl. 2013, 392, 4916–4927. [Google Scholar] [CrossRef]
- Naik, P.A.; Eskandari, Z.; Yavuz, M.; Zu, J. Complex dynamics of a discrete-time Bazykin–Berezovskaya prey-predator model with a strong Allee effect. J. Comput. Appl. Math. 2022, 413, 114401. [Google Scholar] [CrossRef]
- Chéagé Chamgoué, A.; Yamapi, R.; Woafo, P. Bifurcations in a birhythmic biological system with time-delayed noise. Nonlinear Dyn. 2013, 73, 2157–2173. [Google Scholar] [CrossRef]
- Liu, Q.; Jiang, D.; Shi, N.; Hayat, T.; Alsaedi, A. Stationarity and periodicity of positive solutions to stochastic SEIR epidemic models with distributed delay. Discret. Contin. Dyn. Syst.-B 2017, 22, 2479. [Google Scholar] [CrossRef]
- Hammouch, Z.; Yavuz, M.; Özdemir, N. Numerical solutions and synchronization of a variable-order fractional chaotic system. Math. Model. Numer. Simul. Appl. 2021, 1, 11–23. [Google Scholar] [CrossRef]
- Sene, N. Theory and applications of new fractional-order chaotic system under Caputo operator. Int. J. Optim. Control 2022, 12, 20–38. [Google Scholar] [CrossRef]
- Liu, Q.; Jiang, D.; Hayat, T.; Alsaedi, A. Dynamics of a stochastic predator–prey model with stage structure for predator and Holling type II functional response. J. Nonlinear Sci. 2018, 28, 1151–1187. [Google Scholar] [CrossRef]
- Liu, Q.; Jiang, D. Influence of the fear factor on the dynamics of a stochastic predator-prey model. Appl. Math. Lett. 2021, 112, 106756. [Google Scholar] [CrossRef]
- Mineeja, K.; Ignatius, R.P. Lévy noise-induced near-death spikes and phase transitions of a biological neural network. Nonlinear Dyn. 2020, 99, 3265–3283. [Google Scholar] [CrossRef]
- Pak, S. Solitary wave solutions for the RLW equation by He’s semi inverse method. Int. J. Nonlinear Sci. Numer. Simul. 2009, 10, 505–508. [Google Scholar] [CrossRef]
- Uçar, E.; Özdemir, N.; Altun, E. Qualitative analysis and numerical simulations of new model describing cancer. J. Comput. Appl. Math. 2022, 422, 114899. [Google Scholar] [CrossRef]
- Uçar, E.; Uçar, S.; Evirgen, F.; Özdemir, N. A fractional SAIDR model in the frame of Atangana–Baleanu derivative. Fractal Fract. 2021, 5, 32. [Google Scholar] [CrossRef]
- Hristov, J. On a new approach to distributions with variable transmuting parameter: The concept and examples with emerging problems. Math. Model. Numer. Simul. Appl. 2022, 2, 73–87. [Google Scholar] [CrossRef]
- Liu, Q.; Jiang, D. Stationary distribution and extinction of a stochastic SIR modelwith nonlinear perturbation. Appl. Math. Lett. 2017, 73, 8–15. [Google Scholar] [CrossRef]
- Lu, C.; Sun, G.; Zhang, Y. Stationary distribution and extinction of a multi stage HIV model with nonlinear stochastic perturbation. J. Appl. Math. Comput. 2021, 68, 885–907. [Google Scholar] [CrossRef]
- Liu, Q. Dynamics of a stochastic SICA epidemic model for HIVtransmission with higher order perturbation. Stoch. Anal. Appl. 2021, 40, 209–235. [Google Scholar] [CrossRef]
- Rajasekar, S.P.; Pitchaimani, M.; Zhu, Q. Higher order stochastically perturbed SIRS epidemic model with relapse and media impact. Math. Methods Appl. Sci. 2021, 2021, 843–863. [Google Scholar]
- Weiwei, Z.; Xinzhu, M.; Yulin, D. Periodic Solution and Ergodic Stationary Distribution of Stochastic SIRI Epidemic Systems with Nonlinear Perturbations. J. Syst. Sci. Complex. 2019, 32, 1104–1124. [Google Scholar]
- Liu, Q.; Jiang, D. Dynamical behavior of a higher order stochastically perturbed HIV-AIDS model with differential infectivity and amelioration. Chaos Solitons Fractals 2020, 141, 110333. [Google Scholar] [CrossRef]
- Han, B.; Jiang, D.; Hayat, T.; Alsaedi, A.; Ahmed, B. Stationary distribution and extinction of a stochastic staged progression AIDS model with staged treatment and second-order perturbation. Chaos Solitons Fractals 2020, 140, 110238. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Jiang, D.; Hayat, T.; Alsaedi, A.; Ahmed, B. Dynamical behavior of a higher order stochastically perturbed SIRI epidemic model with relapse and media coverage. Chaos Solitons Fractals 2020, 139, 110013. [Google Scholar] [CrossRef]
- Lv, X.; Meng, X.; Wang, X. Extinction and stationary distribution of an impulsive stochastic chemostat model with nonlinear perturbation. Chaos Solitons Fractals 2018, 110, 273–279. [Google Scholar] [CrossRef]
- Liu, Q.; Jiang, D.; Hayat, T.; Alsaedi, A. Stationary distribution of a regime switching predator prey model with anti predator behaviour and higher order perturbations. Physica A 2019, 515, 199–210. [Google Scholar] [CrossRef]
- Liu, Q.; Jiang, D.; Hayat, T.; Alsaedi, A. Long-time behavior of a stochastic logistic equation with distributed delay and nonlinear perturbation. Physica A 2018, 508, 289–304. [Google Scholar] [CrossRef]
- Liu, Q.; Jiang, D.; Hayat, T.; Ahmed, B. Periodic solution and stationary distribution of stochastic SIR epidemic models with higher order perturbation. Physica A 2017, 482, 209–217. [Google Scholar] [CrossRef]
- Zu, L.; Jiang, D.; ORegan, D.; Hayat, T.; Ahmed, B. Ergodic property of a Lotka Volterra predator prey model with white noise higher order perturbation under regime switching. Appl. Math. Comput. 2018, 330, 93–102. [Google Scholar] [CrossRef]
- Liu, Q.; Jiang, D.; Hayat, T.; Ahmed, B. Stationary distribution and extinction of a stochastic predator prey model with additional food and nonlinear perturbation. Appl. Math. Comput. 2018, 320, 226–239. [Google Scholar] [CrossRef]
- Liu, Q.; Jiang, D. Dynamical behavior of a stochastic multigroup staged-progression HIV model with saturated incidence rate and higher-order perturbations. Int. J. Biomath. 2021, 17, 2150051. [Google Scholar] [CrossRef]
- Zhou, B.; Han, B.; Jiang, D.; Hayat, T. Ergodic stationary distribution and extinction of a hybrid stochastic SEQIHR epidemic model with media coverage, quarantine strategies and pre existing immunity under discrete Markov switching. Appl. Math. Comput. 2021, 410, 126388. [Google Scholar] [CrossRef]
- Ikram, R.; Khan, A.; Zahri, M.; Saeed, A.; Yavuz, M.; Kumam, P. Extinction and stationary distribution of a stochastic COVID-19 epidemic model with time-delay. Comput. Biol. Med. 2022, 141, 105115. [Google Scholar] [CrossRef] [PubMed]
- Heffernan, J.M.; Smith, R.J.; Wahl, L.M. Perspectives on the basic reproductive ratio. J. R. Soc. Interface 2005, 2, 281–293. [Google Scholar] [CrossRef] [PubMed]
- Sahu, G.P.; Dhar, J. Dynamics of an SEQIHRS epidemic model with media coverage, quarantine and isolation in a community with pre-existing immunity. J. Math. Anal. Appl. 2015, 421, 1651–1672. [Google Scholar] [CrossRef] [PubMed]
- Kutoyants, Y.A. Statistical Inference for Ergodic Diffusion Processes; Springer: London, UK, 2004. [Google Scholar]
- Peng, S.; Zhu, X. Necessary and sufficient condition for comparison theorem of 1-dimensional stochastic differential equations. Stoch. Process. Their Appl. 2006, 116, 370–380. [Google Scholar] [CrossRef]
- Mao, X. Stochastic Differential Equations and Applications; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Blower, S. Modelling the genital herpes epidemic. Herpes-Cambridge 2004, 11, 138A–146A. [Google Scholar]






| Symbol | Epidemiological Classification |
|---|---|
| Susceptible persons | |
| Exposed persons | |
| Isolated persons | |
| Infected persons | |
| Hospitalized persons | |
| Recovered persons |
| Parameter | Epidemiological Meaning | Unit |
|---|---|---|
| The natural intrinsic growing rate of | days | |
| The carrying amplitude of | 1 million | |
| The propagation ratio between and | days | |
| The maximal efficient contact rate between and | days | |
| The maximal efficient contact rate between and | days | |
| The reduced active contact rate due to media intrusion associated with , () | – | |
| The reduced active contact rate due to media intrusion associated with , () | – | |
| The isolation rate of | days | |
| The transition rate from to | days | |
| The normal death rate of , | days | |
| The cure rate of | days | |
| The cure rate of | days | |
| The cure rate of | days | |
| The cure rate of | days | |
| The disease-related mortality rate of | days | |
| The disease-related mortality rate of | days | |
| The coefficient of media intrusion associated with | – | |
| The coefficient of media intrusion associated with | – | |
| The hospitalization ratio of | days | |
| The hospitalization ratio of | days |
| Parameter | Case 1 | Case 2 | Source |
|---|---|---|---|
| 0.1 | 0.1 | Estimated | |
| 3.8 | 4.4 | [63] | |
| 0.02 | 0.02 | Estimated | |
| 0.2 | 0.2 | Estimated | |
| 0.02 | 0.02 | Estimated | |
| 0.13 | 0.13 | Estimated | |
| 0.16 | 0.16 | Estimated | |
| 0.01 | 0.01 | [63] | |
| 0.1 | 0.1 | [63] | |
| 0.05 | 0.05 | Estimated | |
| 0.2857 | 0.2857 | Estimated | |
| 0.3 | 0.3 | Estimated | |
| 0.08 | 0.08 | Estimated | |
| 0.1 | 0.1 | Estimated | |
| 0.042 | 0.042 | [63] | |
| 0.028 | 0.028 | [63] | |
| 1 | 1 | Supposed | |
| 1.5 | 1.5 | Supposed | |
| 0.057 | 0.057 | [63] | |
| 0.051 | 0.051 | [63] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sabbar, Y.; Yavuz, M.; Özköse, F. Infection Eradication Criterion in a General Epidemic Model with Logistic Growth, Quarantine Strategy, Media Intrusion, and Quadratic Perturbation. Mathematics 2022, 10, 4213. https://doi.org/10.3390/math10224213
Sabbar Y, Yavuz M, Özköse F. Infection Eradication Criterion in a General Epidemic Model with Logistic Growth, Quarantine Strategy, Media Intrusion, and Quadratic Perturbation. Mathematics. 2022; 10(22):4213. https://doi.org/10.3390/math10224213
Chicago/Turabian StyleSabbar, Yassine, Mehmet Yavuz, and Fatma Özköse. 2022. "Infection Eradication Criterion in a General Epidemic Model with Logistic Growth, Quarantine Strategy, Media Intrusion, and Quadratic Perturbation" Mathematics 10, no. 22: 4213. https://doi.org/10.3390/math10224213








