Study of Fractional Differential Equations Emerging in the Theory of Chemical Graphs: A Robust Approach

Abstract

The study of the interconnections between chemical systems is known as chemical graph theory. Through the use of star graphs, a limited group of researchers has examined the space of possible solutions for boundary-value problems. They recognized that for their strategy to function, they needed a core node related to other nodes but not to itself; as a result, they opted to use star graphs. In this sense, the graphs of neopentane will be helpful in extending the scope of our technique. It has the CAS number 463-82-1 and the chemical formula $C_5{H}_{12}$, and it is a component of a petrochemical precursor. In order to determine whether or not the suggested boundary-value problems on these graphs have any known solutions, we use the theorems developed by Schaefer and Krasnoselskii on fixed points. In addition, we illustrate our preliminary results with the help of an example that we present.

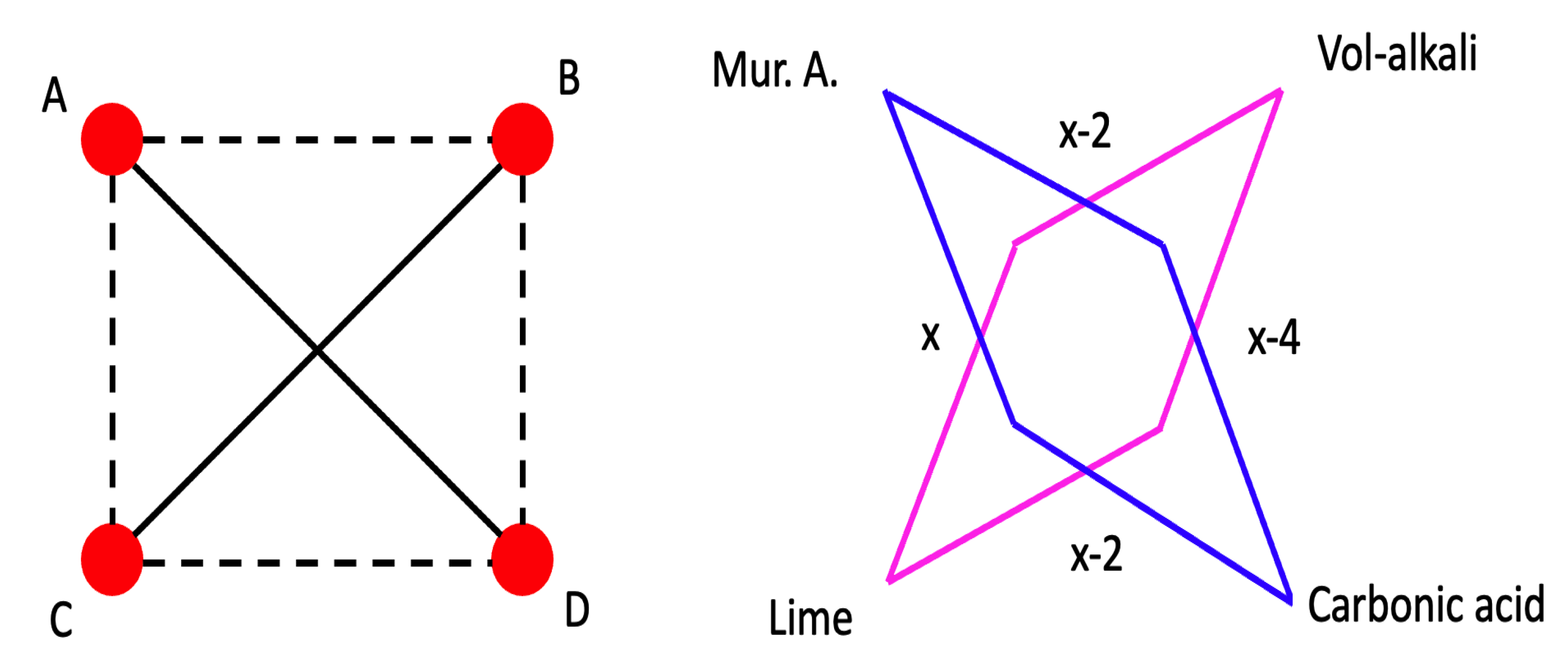
1. Introduction

Mathematical applications have proliferated in the twenty-first century. When quantum chemistry emerged in the 1920s, it left a trail of several mathematical specialties chemists felt compelled to understand. These included calculus and various branches of linear algebra, including matrix and group theories. Group theory is often used in fields such as crystallography and molecular structure analysis since it has gained widespread acceptance among chemists. However, graph theory is being used in a number of fields, including categorizing, systematization, enumeration, and construction of chemical interest systems.

We have reached a stage where we believe that it is appropriate to say that, due to the applications of mathematics that have been developed in the chemical world, mathematics plays an essential role in contemporary chemistry. We believe that the era of the 1990s represents a precious time to present excessive applications of the varied directions of mathematics to chemistry. In order to distinguish the subject that is concerned with the unique and challenging application of mathematics to chemistry, the phrase “mathematical chemistry” was first used in the early 1980s. As is customary in this field, we can broadly define chemistry to cover the classic areas of inorganic, organic, and physical chemistry and its hybrid descendants, including chemical physics and biochemistry.

The contemporary landscape of chemical theory is primarily built around fundamentally graph-theoretical premises. Today, all of the main fields of chemistry employ chemical graphs for various reasons. The history of the first implicit use of the graph theory is of significant relevance given the current extensive use of the chemical graph. The second part of the eighteenth century saw the invention of chemical diagrams. It will be essential to discuss the dominant viewpoints in nineteenth-century chemistry to comprehend their necessity at the time and the conditions of their entrance into the chemical literature.

The Scottish scientist William Cullen designed the first chemical graphs that were easily identifiable as such. To illustrate the alleged forces that exist between pairs of molecules undergoing different chemical reactions, Cullen began using so-called “affinity diagrams” in his lectures in 1758. Sadly, none of these diagrams were ever published and they were instead just used to illustrate his chemistry lecture notes (see [1]). Similar images to Cullen’s were subsequently posted by Black, who claimed erroneously to have originated them (see [2]); by the end of the eighteenth century, similar diagrams were prevalent in British chemistry textbooks. Figure 1 displays copies of two Cullen-attributed surviving schematics.

The goal of using graph theory in chemical graph theory is to characterize molecules in order to investigate their many different physical properties. A set $\Theta$ of vertices (or nodes) and a set $\Xi$ of unordered pairings of various components of $\Theta$ that create the edges make up the components of a graph denoted by the equation $\mathbb{G}=(\Theta ,\Xi )$. In chemistry, the atoms that make up a molecule are represented by the vertices of the structure, while the edges show the chemical bonds.

On the other hand, recently, there has been significant theoretical and practical progress in the area of differential equations (see, [3,4,5,6,7,8,9]). In the context of special functions, publications on fractional calculus focus mainly on the solution of differential equations (for detail, see [10,11,12,13,14,15,16,17]). Recently, many new articles on nonlinear fractional differential equations and their solutions employing approaches such as the Leray–Schauder theorem, stability analysis, variational iteration methods, and fixed-point theory methods have been publicly released (see [18,19,20,21,22,23,24] and references therein).

Lumer was the first to apply the principles of differential equation theory to graphs (for details, see [25]). He studied extended evolution equations by altering stated operators on implications spaces. In 1989, Zavgorodnij explored differential equations using a geometric net (see [26]), with the recommended solutions to boundary value problems placed at the inner vertices of the system. However, in [27], the authors used the double-sweep technique, which they discovered to be more effective on graphs, to obtain numerical solutions for differential equations.

Although only a tiny amount of work has been dedicated to the topic, using fixed point theory approaches (see [28,29]), it has been proven that solutions exist for boundary value issues involving star graphs (see Figure 2). One can see the most up-to-date research in this area in which the authors use different types of graphs (i.e., ethane [30,31], glucose [32], methylpropane [33], hexasilinane [34], cyclohexane [35], octane [36], etc.) and defined the differential equations on their edges.

Neopentane graphs, which are more pliable than star graphs, were used here to broaden this problem by utilizing the notion of neopentane graphs (see Figure 3).

Furthermore, the methods used in [28,29] are insufficient since, as compared to the star graph, neopentane graphs have several junction points. As a robust approach, we use an alternative method in which we assign integer values (0 or 1) to the vertices and edge lengths $|{\tilde{b}}_{\tau }|=1$ of the last graph (see Figure 4).

By utilizing the above idea, here, we consider the following system, which is stated for each $\tau =1,2,\dots ,25$ by

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\mathfrak{D}}^r{z}_{\tau }\left(s\right)& ={\mathcal{W}}_{\tau }(s,z_{\tau }\left(s\right),{\mathfrak{D}}^q{z}_{\tau }\left(s\right),z_{\tau }^{\prime }\left(s\right))(s\in [0,1]),\hfill \\ \hfill z_{\tau }\left(0\right)& ={\mathfrak{D}}^{r-1}{z}_{\tau }\left(1\right),{\ell }_1{z}_{\tau }^{\prime }\left(0\right)+{\ell }_2{z}_{\tau }^{\prime }\left(1\right)={\ell }_3{\int }_0^a{\mathfrak{D}}^{r-1}{z}_{\tau }\left(\theta \right)d\theta ,\hfill \end{array}\right.\end{array}$$

(1)

where $z_{\tau }:[0,1]\to \infty$ is an unknown function, ${\ell }_k(k=1,2,3)\in \mathbb{R}$ with ${\ell }_k\ne 0,$ $a\in (0,1),$ ${\mathfrak{D}}^r$ and ${\mathfrak{D}}^q$ are the Caputo fractional derivative of orders $1<r\le 2$ and $q\in (0,1),$ respectively. Moreover, ${\mathcal{W}}_{\tau }:[0,1]\times \mathbb{R}\times \mathbb{R}\times \mathbb{R}\to \mathbb{R}$ is a given continuously differentiable function, where $\tau =16$ is the neopentane graph’s vertex count with $|{\tilde{b}}_{\tau }|=1.$

We want to apply relevant fixed point theorems to establish the existence of workable solutions to the Problem (1) at hand. Finally, we show how our findings fit into the larger body of literature by providing a concrete example.

2. Preliminaries

We shall need the following results in the next sections.

Definition 1

([37]). Let $\hslash >0$. The fractional derivative of Caputo for $\mathcal{W}\in C^{\chi }[0,+\infty )$ can be defined as

$${\mathfrak{D}}^{\hslash }\mathcal{W}\left(s\right)=\frac{1}{\Gamma (\chi -\hslash )}{\int }_0^s{(s-\theta )}^{\chi -\hslash -1}{\mathcal{W}}^{\left(\chi \right)}\left(\theta \right)d\theta (\chi -1<\hslash <\chi ),$$

where $\chi =[\hslash ]+1$ and $\Gamma (·)$ is a gamma function.

For $\hslash >0,$ the general solution of ${\mathfrak{D}}^{\hslash }\mathcal{W}\left(\nu \right)=0$ is given as

$$\mathcal{W}\left(\nu \right)={\varrho }_0+{\varrho }_1\nu +{\varrho }_2{\nu }^2+\dots +{\varrho }_{n-1}{\nu }^{n-1}.$$

Additionally,

$${\mathbb{I}}^{\hslash }{\mathfrak{D}}^{\hslash }\mathcal{W}\left(\nu \right)=z\left(\nu \right)+{\varrho }_0+{\varrho }_1\nu +{\varrho }_2{\nu }^2+\dots +{\varrho }_{n-1}{\nu }^{n-1},$$

where ${\varrho }_k\in \mathbb{R},k=0,1,\dots ,n-1$ $(n-1<\hslash <n)$.

Now, we will show the proof of the following lemma, which will be used in the latter portion of the study.

Lemma 1.

Suppose that $\varphi \in C\left(\right[0,1],\mathbb{R})$. Then, $z^{★}:[0,1]\to \mathbb{R}$ is a solution of the subsequent system

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\mathfrak{D}}^{r}z\left(s\right)& =\varphi \left(s\right)(s\in [0,1\left]\right),\hfill \\ \hfill z\left(0\right)& ={\mathfrak{D}}^{r-1}z\left(1\right),{\ell }_1{z}^{\prime }\left(0\right)+{\ell }_2{z}^{\prime }\left(1\right)={\ell }_3{\int }_0^a{\mathfrak{D}}^{r-1}z\left(\theta \right)d\theta ,\hfill \end{array}\right.\end{array}$$

(2)

iff $z^{★}$ is a solution for the equation stated below

$$\begin{array}{ccc}\hfill z\left(s\right)& =& {\int }_0^s\frac{{(s-\theta )}^{r-1}}{\Gamma \left(r\right)}\varphi \left(\theta \right)d\theta +{\int }_0^1\varphi \left(\theta \right)d\theta \hfill \\ & & +\left(\frac{1}{\Gamma (3-r)}+s\right)\left[\frac{{\ell }_3}{A_0}{\int }_0^a{\int }_0^{\theta }\varphi \left(\zeta \right)d\zeta d\theta -\frac{{\ell }_2}{A_0}{\int }_0^1\frac{{(1-\theta )}^{r-2}}{\Gamma (r-1)}\varphi \left(\theta \right)d\theta \right],\hfill \\ \hfill \end{array}$$

(3)

where

$$A_0=\left[{\ell }_1+{\ell }_2-\frac{a^{3-r}}{\Gamma (4-r)}\right].$$

Proof. 

Assume that $z^{★}:[0,1]\to \mathbb{R}$ is a solution of (2). Thus, there are constants $d_0,d_1\in \mathbb{R}$ such that

$$z^{★}\left(s\right)={\int }_0^s\frac{{(s-\theta )}^{r-1}}{\Gamma \left(r\right)}\varphi \left(\theta \right)d\theta +d_0+d_{1}s.$$

(4)

We use the boundary conditions from (2) to achieve this goal. Therefore,

$$\begin{array}{ccc}\hfill d_1& =& \frac{1}{A_0}\left[{\ell }_3{\int }_0^a{\int }_0^{\theta }\varphi \left(\zeta \right)d\zeta d\theta -{\ell }_2{\int }_0^1\frac{{(1-\theta )}^{r-2}}{\Gamma (r-1)}\varphi \left(\theta \right)d\theta \right],\hfill \\ \hfill d_0& =& {\int }_0^1\varphi \left(\theta \right)d\theta +\frac{1}{A_0\Gamma (3-r)}\left[{\ell }_3{\int }_0^a{\int }_0^{\theta }\varphi \left(\zeta \right)d\zeta d\theta -{\ell }_2{\int }_0^1\frac{{(1-\theta )}^{r-2}}{\Gamma (r-1)}\varphi \left(\theta \right)d\theta \right].\hfill \end{array}$$

A solution (3) is obtained by substituting the values of $d_0,d_1$ into (4). If $z^{★}$ is a solution of (3), then it follows that it is also a solution of (2). □

The Schaefer and Krasnoselskii fixed point theorems are now provided.

Theorem 1

([38]). Let $\mathcal{Y}$ be a Banach space. If $\mathcal{A}$ is completely continuous, then either $\mathcal{A}$ has at least one fixed point or $\left\{z\in \mathcal{Y}:z=b\mathcal{A}z \mathit{for} \mathit{some} 0<b<1\right\}$ is unbounded.

Theorem 2

([38]). Let $\mathcal{V}$ be a nonempty, bounded, closed, and convex subset of Banach space $\mathcal{Y}$ and the operators ${\mathcal{A}}_1,{\mathcal{A}}_2:\mathcal{V}\to \mathcal{Y}$ with ${\mathcal{A}}_{1}k+{\mathcal{A}}_2{k}^{\prime }\in \mathcal{V},$ $\forall k,k^{\prime }\in \mathcal{V}$, ${\mathcal{A}}_1$ is compact and continuous and ${\mathcal{A}}_2$ is a contraction map. Then, ${\mathcal{A}}_1+{\mathcal{A}}_2$ has a fixed point.

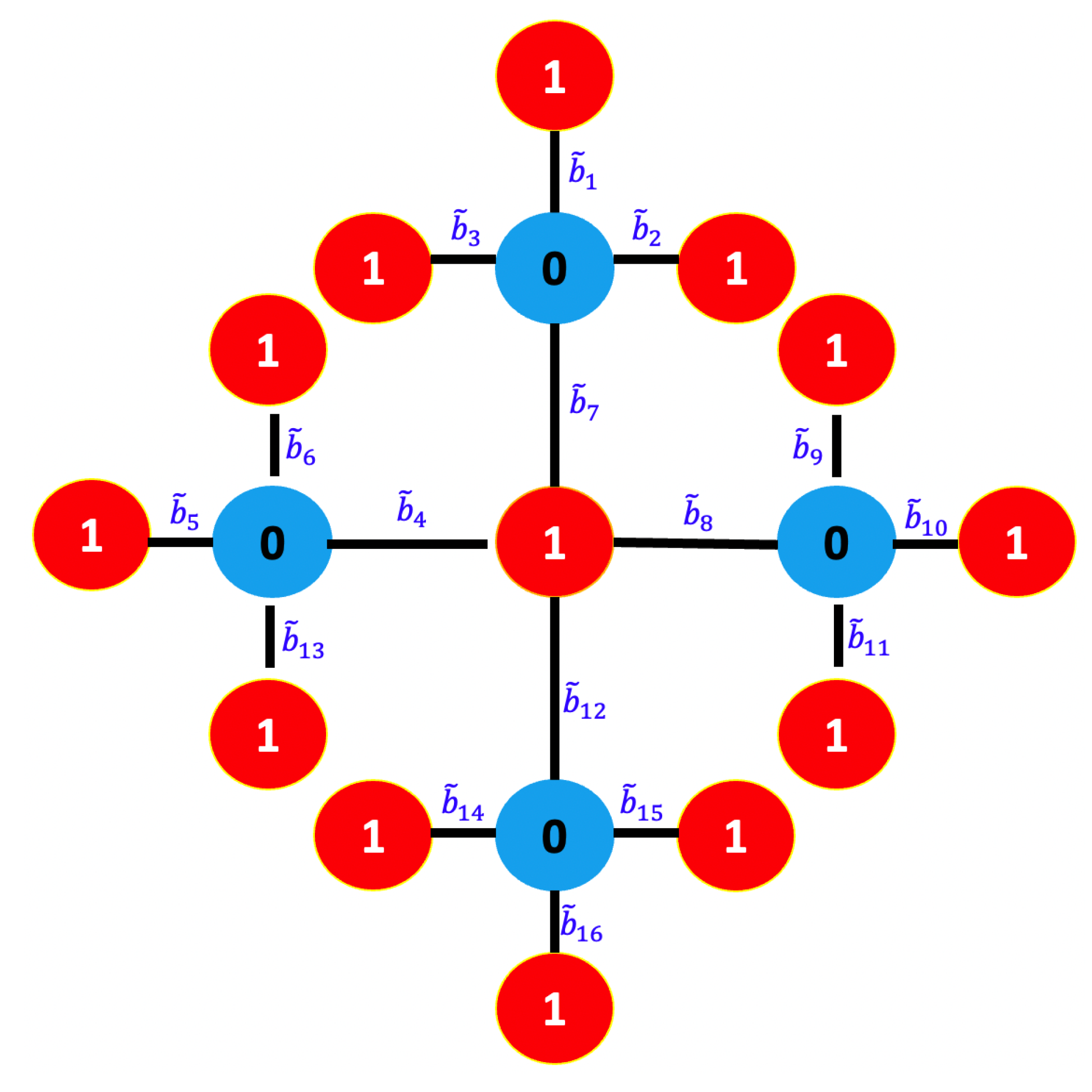
3. Main Results

Define $\tilde{\mathcal{Y}}=\{z:[0,1]\to \mathbb{R}:z,{\mathfrak{D}}^{q}z,z^{\prime }\in C([0,1],\mathbb{R})\}$ as a Banach space with

$${∥z∥}_{\tilde{\mathcal{Y}}}=\underset{s\in [0,1]}{sup}\left|z\left(s\right)\right|+\underset{s\in [0,1]}{sup}\left|{\mathfrak{D}}^{q}z\left(s\right)\right|+\underset{s\in [0,1]}{sup}\left|z^{\prime }\left(s\right)\right|.$$

Hence, it can be clearly seen that $\mathcal{Y}={\tilde{\mathcal{Y}}}_{16}$ is a Banach space with

$${∥z=(z_1,z_2,\dots ,z_{16})∥}_{\mathcal{Y}}=\sum _{\tau =1}^{16}{∥z_{\tau }∥}_{\tilde{\mathcal{Y}}}.$$

As addressing Lemma 1, for each $(z_1,z_2,\dots ,z_{16})\in \mathcal{Y}$, we introduce $\mathcal{A}:\mathcal{Y}\to \mathcal{Y}$ by

$$\mathcal{A}(z_1,z_2,\dots ,z_{16}):=\left({\mathcal{A}}_1(z_1,z_2,\dots ,z_{16}),{\mathcal{A}}_2(z_1,z_2,\dots ,z_{16}),\dots ,{\mathcal{A}}_{16}(z_1,z_2,\dots ,z_{16})\right),$$

(5)

for each $\tau =1,2,\dots ,16$ and $(z_1,z_2,\dots ,z_{16})\in \mathcal{Y}$, we define ${\mathcal{A}}_{\tau }:\mathcal{Y}\to \tilde{\mathcal{Y}}$ by

$$\begin{array}{ccc}\hfill {\mathcal{A}}_{\tau }(z_1,z_2,\dots ,z_{16})\left(s\right)& =& {\int }_0^s\frac{{(s-\theta )}^{r-1}}{\Gamma \left(r\right)}{\mathcal{W}}_{\tau }(\theta ,z_{\tau }\left(\theta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right),z_{\tau }^{\prime }\left(\theta \right))d\theta \hfill \\ & & +{\int }_0^1{\mathcal{W}}_{\tau }(\theta ,z_{\tau }\left(\theta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right),z_{\tau }^{\prime }\left(\theta \right))d\theta +\left(\frac{1}{\Gamma (3-r)}+s\right)\times \hfill \\ & & \left[\frac{{\ell }_3}{A_0}{\int }_0^a{\int }_0^{\theta }{\mathcal{W}}_{\tau }(\zeta ,z_{\tau }\left(\zeta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\zeta \right),z_{\tau }^{\prime }\left(\zeta \right))d\zeta d\theta \right.\hfill \\ & & \left.-\frac{{\ell }_2}{A_0}{\int }_0^1\frac{{(1-\theta )}^{r-2}}{\Gamma (r-1)}{\mathcal{W}}_{\tau }(\theta ,z_{\tau }\left(\theta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right),z_{\tau }^{\prime }\left(\theta \right))d\theta \right],\hfill \end{array}$$

(6)

for all $s\in [0,1].$

For the purpose of clarity, we will be performing all computations using the following notation:

$$\begin{array}{ccc}\hfill A_0& =& \left[{\ell }_1+{\ell }_2-\frac{a^{3-r}}{\Gamma (4-r)}\right]\ne 0\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill A_1& =& \left[|{\ell }_1|+|{\ell }_2|+\frac{1}{\Gamma (4-r)}\right]\ne 0\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill {\mathcal{Y}}_0^{\ast }& =& \frac{1}{\Gamma (r+1)}+1+\frac{1}{A_1}\left(\frac{1}{\Gamma (3-r)}+1\right)\left(\frac{|{\ell }_3|}{2}+\frac{|{\ell }_2|}{\Gamma \left(r\right)}\right)\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill {\mathcal{Y}}_1^{\ast }& =& \frac{1}{\Gamma (r-q+1)}+\left(\frac{1}{A_1\Gamma (2-q)}\right)\left(\frac{|{\ell }_3|}{2}+\frac{|{\ell }_2|}{\Gamma \left(r\right)}\right)\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill {\mathcal{Y}}_2^{\ast }& =& \frac{1}{\Gamma \left(r\right)}+\frac{1}{A_1}\left(\frac{|{\ell }_3|}{2}+\frac{|{\ell }_2|}{\Gamma \left(r\right)}\right)\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill {\mathcal{V}}_0^{\ast }& =& 1+\frac{1}{A_1}\left(\frac{1}{\Gamma (3-r)}+1\right)\left(\frac{|{\ell }_3|}{2}+\frac{|{\ell }_2|}{\Gamma \left(r\right)}\right)\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill {\mathcal{V}}_1^{\ast }& =& \frac{1}{A_1\Gamma (2-q)}\left(\frac{|{\ell }_3|}{2}+\frac{|{\ell }_2|}{\Gamma \left(r\right)}\right)\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill {\mathcal{V}}_2^{\ast }& =& \frac{1}{A_1}\left(\frac{|{\ell }_3|}{2}+\frac{|{\ell }_2|}{\Gamma \left(r\right)}\right).\hfill \end{array}$$

(14)

Now, we will discuss the most important findings from this section.

Theorem 3.

Consider the proposed Problem (1). Assume that ${\mathcal{W}}_1,{\mathcal{W}}_2,\dots ,{\mathcal{W}}_{16}:[0,1]\times \mathbb{R}\times \mathbb{R}\times \mathbb{R}\to \mathbb{R}$ are continuous functions and there is ${\mathsf{{\rm Y}}}_{\tau }>0,$ $\forall \tau =1,2,\dots ,16$ with $\left|{\mathcal{W}}_{\tau }(s,z,\tilde{z},\tilde{\tilde{z}})\right|\le {\mathsf{{\rm Y}}}_{\tau },$ $\forall z,\tilde{z},\tilde{\tilde{z}}\in \mathbb{R}$ and $s\in [0,1]$. Then, there exists a solution to Problem (1).

Proof. 

The existence of the fixed points of $\mathcal{A}$ specified by (5) is a foregone conclusion if and only if (1) has a solution, as implied by (6). Here, the complete continuity of operator $\mathcal{A}$′ is established first.

As ${\mathcal{W}}_1,{\mathcal{W}}_2,\dots ,{\mathcal{W}}_{16}$ are continuous, so $\mathcal{A}:\mathcal{Y}\to \mathcal{Y}$ is also continuous. Consider a bounded set $\mathcal{O}\in \mathcal{Y}$ and $z=(z_1,z_2,\dots ,z_{16})\in \mathcal{Y}$, so, for each $s\in [0,1],$ we have

$$\begin{array}{ccc}\hfill \left|\left({\mathcal{A}}_{\tau }z\right)\left(s\right)\right|& \le & {\int }_0^s\frac{{(s-\theta )}^{r-1}}{\Gamma \left(r\right)}\left|{\mathcal{W}}_{\tau }(\theta ,z_{\tau }\left(\theta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right),z_{\tau }^{\prime }\left(\theta \right))\right|d\theta \hfill \\ & & +{\int }_0^1\left|{\mathcal{W}}_{\tau }(\theta ,z_{\tau }\left(\theta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right),z_{\tau }^{\prime }\left(\theta \right))\right|d\theta \hfill \\ & & +\frac{1}{|A_0|}\left(\frac{1}{\Gamma (3-r)}+s\right)\times \left[|{\ell }_3|{\int }_0^a{\int }_0^{\theta }|{\mathcal{W}}_{\tau }(\zeta ,z_{\tau }\left(\zeta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\zeta \right),z_{\tau }^{\prime }\left(\zeta \right))|d\zeta d\theta \right.\hfill \\ & & \left.+|{\ell }_2|{\int }_0^1\frac{{(1-\theta )}^{r-2}}{\Gamma (r-1)}|{\mathcal{W}}_{\tau }(\theta ,z_{\tau }\left(\theta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right),z_{\tau }^{\prime }\left(\theta \right))|d\theta \right]\hfill \\ & \le & {\mathsf{{\rm Y}}}_{\tau }{\mathcal{Y}}_0^{\ast },\hfill \end{array}$$

where ${\mathcal{Y}}_0^{\ast }$ is given in (9). Additionally,

$$\begin{array}{ccc}\hfill \left|\left({\mathfrak{D}}^q{\mathcal{A}}_{\tau }z\right)\left(s\right)\right|& \le & {\int }_0^s\frac{{(s-\theta )}^{r-q-1}}{\Gamma (r-q)}|{\mathcal{W}}_{\tau }(\theta ,z_{\tau }\left(\theta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right),z_{\tau }^{\prime }\left(\theta \right))|d\theta \hfill \\ & & +\left(\frac{s^{1-q}}{|A_0|\Gamma (2-q)}\right)\times \left[|{\ell }_3|{\int }_0^a{\int }_0^{\theta }\left|{\mathcal{W}}_{\tau }(\zeta ,z_{\tau }\left(\zeta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\zeta \right),z_{\tau }^{\prime }\left(\zeta \right))\right|d\zeta d\theta \right.\hfill \\ & & +\left.|{\ell }_2|{\int }_0^1\frac{{(1-\theta )}^{r-2}}{\Gamma (r-1)}\left|{\mathcal{W}}_{\tau }(\theta ,z_{\tau }\left(\theta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right),z_{\tau }^{\prime }\left(\theta \right))\right|d\theta \right]\hfill \\ & \le & {\mathsf{{\rm Y}}}_{\tau }{\mathcal{Y}}_1^{\ast }\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill \left|\left({\mathcal{A}}_{\tau }^{\prime }z\right)\left(s\right)\right|& \le & {\int }_0^s\frac{{(s-\theta )}^{r-2}}{\Gamma (r-1)}|{\mathcal{W}}_{\tau }(\theta ,z_{\tau }\left(\theta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right),z_{\tau }^{\prime }\left(\theta \right))|d\theta \hfill \\ & & +\left(\frac{1}{|A_0|}\right)\times \left[|{\ell }_3|{\int }_0^a{\int }_0^{\theta }\left|{\mathcal{W}}_{\tau }(\zeta ,z_{\tau }\left(\zeta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\zeta \right),z_{\tau }^{\prime }\left(\zeta \right))\right|d\zeta d\theta \right.\hfill \\ & & \left.+|{\ell }_2|{\int }_0^1\frac{{(1-\theta )}^{r-2}}{\Gamma (r-1)}\left|{\mathcal{W}}_{\tau }(\theta ,z_{\tau }\left(\theta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right),z_{\tau }^{\prime }\left(\theta \right))\right|d\theta \right]\hfill \\ & \le & {\mathsf{{\rm Y}}}_{\tau }{\mathcal{Y}}_2^{\ast },\hfill \end{array}$$

for all $s\in [0,1],$ where ${\mathcal{Y}}_1^{\ast },{\mathcal{Y}}_2^{\ast }$ are given in (10) and (11), respectively. Therefore,

$${∥\left({\mathcal{A}}_{\tau }z\right)\left(s\right)∥}_{\tilde{\mathcal{Y}}}\le {\mathsf{{\rm Y}}}_{\tau }\left({\mathcal{Y}}_0^{\ast }+{\mathcal{Y}}_1^{\ast }+{\mathcal{Y}}_2^{\ast }\right).$$

Hence,

$$\begin{array}{ccc}\hfill {∥\left(\mathcal{A}z\right)\left(s\right)∥}_{\mathcal{Y}}& =& \sum _{\tau =1}^{16}{∥\left({\mathcal{A}}_{\tau }z\right)\left(s\right)∥}_{\tilde{\mathcal{Y}}}\hfill \\ & \le & \sum _{\tau =1}^{16}{\mathsf{{\rm Y}}}_{\tau }\left({\mathcal{Y}}_0^{\ast }+{\mathcal{Y}}_1^{\ast }+{\mathcal{Y}}_2^{\ast }\right)\hfill \\ & <& \infty .\hfill \end{array}$$

This proves that there exists a uniform bound on $\mathcal{A}$.

The next step is to demonstrate the equicontinuity of $\mathcal{A}$. For this purpose, let $z=(z_1,z_2,\dots ,z_{16})\in \mathcal{O}$ and $s_1,s_2\in [0,1]$ with $s_1<s_2.$ Then, we have

$$\begin{array}{ccc}\hfill \left|\left({\mathcal{A}}_{\tau }z\right)\left(s_2\right)-\left({\mathcal{A}}_{\tau }z\right)\left(s_1\right)\right|& \le & {\int }_0^{s_1}\frac{{(s_2-\theta )}^{r-1}-{(s_1-\theta )}^{r-1}}{\Gamma \left(r\right)}\times \hfill \\ & & |{\mathcal{W}}_{\tau }(\theta ,z_{\tau }\left(\theta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right),z_{\tau }^{\prime }\left(\theta \right))|d\theta \hfill \\ & & +{\int }_{s_1}^{s_2}\frac{{(s_2-\theta )}^{r-1}}{\Gamma \left(r\right)}|{\mathcal{W}}_{\tau }(\theta ,z_{\tau }\left(\theta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right),z_{\tau }^{\prime }\left(\theta \right))|d\theta \hfill \\ & & +\left(\frac{s_2-s_1}{|A_0|}\right)\times [|{\ell }_3|\hfill \\ & & {\int }_0^a{\int }_0^{\theta }\left|{\mathcal{W}}_{\tau }(\zeta ,z_{\tau }\left(\zeta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\zeta \right),z_{\tau }^{\prime }\left(\zeta \right))\right|d\zeta d\theta \hfill \\ & & \left.+|{\ell }_2|{\int }_0^1\frac{{(1-\theta )}^{r-2}}{\Gamma (r-1)}\left|{\mathcal{W}}_{\tau }(\theta ,z_{\tau }\left(\theta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right),z_{\tau }^{\prime }\left(\theta \right))\right|d\theta \right].\hfill \end{array}$$

It is clear that if $s_1\to s_2$ then, independently, the RHS of the above expression converges to zero. Moreover,

$$\underset{s_1\to s_2}{lim}\left|\left({\mathfrak{D}}^q{\mathcal{A}}_{\tau }z\right)\left(s_2\right)-\left({\mathfrak{D}}^q{\mathcal{A}}_{\tau }z\right)\left(s_1\right)\right|=0,\underset{s_1\to s_2}{lim}\left|\left({\mathcal{A}}_{\tau }^{\prime }z\right)\left(s_2\right)-\left({\mathcal{A}}_{\tau }^{\prime }z\right)\left(s_1\right)\right|=0.$$

For this reason, ${∥\left(\mathcal{A}z\right)\left(s_2\right)-\left(\mathcal{A}z\right)\left(s_1\right)∥}_{\mathcal{Y}}\to 0$ as $s_1\to s_2.$ This shows that $\mathcal{A}$ is an equicontinuous on $\mathcal{Y}={\mathcal{Y}}_1\times {\mathcal{Y}}_2\times \dots \times {\mathcal{Y}}_{16}$. For this reason, we know that the operator is completely continuous because of the Arzela–Ascoli theorem.

Further, we define

$$\Theta :=\left\{(z_1,z_2,\dots ,z_{16})\in \mathcal{Y}:(z_1,z_2,\dots ,z_{16})=b\mathcal{A}(z_1,z_2,\dots ,z_{16}),b\in (0,1)\right\}$$

of $\mathcal{Y}$. We will demonstrate the boundedness property of $\Theta$ here. To this end, let $(z_1,z_2,\dots ,z_{16})\in \Theta .$ Then, we can write

$$(z_1,z_2,\dots ,z_{16})=b\mathcal{A}(z_1,z_2,\dots ,z_{16}),$$

and so

$$z_{\tau }\left(s\right)=b{\mathcal{A}}_{\tau }(z_1,z_2,\dots ,z_{16}),\forall s\in [0,1],and\tau =1,2,\dots ,16.$$

Thus,

$$\begin{array}{ccc}\hfill \left|z_{\tau }\left(s\right)\right|& \le & b\left[{\int }_0^s\frac{{(s-\theta )}^{r-1}}{\Gamma \left(r\right)}\left|{\mathcal{W}}_{\tau }(\theta ,z_{\tau }\left(\theta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right),z_{\tau }^{\prime }\left(\theta \right))\right|d\theta \right.\hfill \\ & & +{\int }_0^1\left|{\mathcal{W}}_{\tau }(\theta ,z_{\tau }\left(\theta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right),z_{\tau }^{\prime }\left(\theta \right))\right|d\theta \hfill \\ & & +\frac{1}{|A_0|}\left(\frac{1}{\Gamma (3-r)}+s\right)\times \left\{|{\ell }_3|{\int }_0^a{\int }_0^{\theta }\left|{\mathcal{W}}_{\tau }(\zeta ,z_{\tau }\left(\zeta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\zeta \right),z_{\tau }^{\prime }\left(\zeta \right))\right|d\zeta d\theta \right.\hfill \\ & & \left.\left.+|{\ell }_2|{\int }_0^1\frac{{(1-\theta )}^{r-2}}{\Gamma (r-1)}\left|{\mathcal{W}}_{\tau }(\theta ,z_{\tau }\left(\theta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right),z_{\tau }^{\prime }\left(\theta \right))\right|d\theta \right\}\right]\hfill \\ & \le & b{\mathsf{{\rm Y}}}_{\tau }{\mathcal{Y}}_0^{\ast },\hfill \end{array}$$

and by similar computations, we obtain

$$\begin{array}{ccc}\hfill \left|{\mathfrak{D}}^q{z}_{\tau }\left(s\right)\right|& \le & b{\mathsf{{\rm Y}}}_{\tau }{\mathcal{Y}}_1^{\ast },\hfill \\ \hfill \left|z_{\tau }^{\prime }\left(s\right)\right|& \le & b{\mathsf{{\rm Y}}}_{\tau }{\mathcal{Y}}_2^{\ast },\hfill \end{array}$$

where ${\mathcal{Y}}_0^{\ast }-{\mathcal{Y}}_2^{\ast }$ are given in (9)–(11). Hence,

$$\begin{array}{ccc}\hfill {∥z∥}_{\mathcal{Y}}& =& \sum _{\tau =1}^{16}{∥z_{\tau }∥}_{\tilde{\mathcal{Y}}}\hfill \\ & \le & b\sum _{\tau =1}^{16}{\mathsf{{\rm Y}}}_{\tau }\left({\mathcal{Y}}_0^{\ast }+{\mathcal{Y}}_1^{\ast }+{\mathcal{Y}}_2^{\ast }\right)\hfill \\ & <& \infty .\hfill \end{array}$$

It demonstrates that $\Theta$ is bounded. We now know that the operator $\mathcal{A}$ has a fixed point in $\mathcal{Y}$ by applying Theorem 1 and Lemma 1. This demonstrates that the problem described in (1) has a solution. □

We will now consider the solution to the Problem (1) under a variety of assumptions.

Theorem 4.

Consider the proposed Problem (1). Suppose that ${\mathcal{W}}_1,{\mathcal{W}}_2,\dots ,{\mathcal{W}}_{16}:[0,1]\times \mathbb{R}\times \mathbb{R}\times \mathbb{R}\to \mathbb{R}$ are continuous functions and there are bounded continuous functions ${\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_{16}:[0,1]\to \mathbb{R},$ ${\mathcal{F}}_1,{\mathcal{F}}_2,\dots ,{\mathcal{F}}_{16}:[0,1]\to [0,\infty )$ and nondecreasing continuous functions ${\mathcal{M}}_1,{\mathcal{M}}_2,\dots ,{\mathcal{M}}_{16}:[0,1]\to [0,\infty )$ with the properties

$$\left|{\mathcal{W}}_{\tau }(s,z,\tilde{z},\tilde{\tilde{z}})\right|\le {\mathcal{F}}_{\tau }\left(s\right){\mathcal{M}}_{\tau }(\left|z\right|+\left|\tilde{z}\right|+\left|\tilde{\tilde{z}}\right|)$$

and

$$\left|{\mathcal{W}}_{\tau }(s,z_1,z_2,z_3)-{\mathcal{W}}_{\tau }(s,{\tilde{z}}_1,{\tilde{z}}_2,{\tilde{z}}_3)\right|\le {\mathcal{G}}_{\tau }\left(s\right)(\left|z_1-{\tilde{z}}_1\right|+\left|z_2-{\tilde{z}}_2\right|+\left|z_3-{\tilde{z}}_3\right|)$$

$\forall s\in [0,1],$$z_1,z_2,z_3,{\tilde{z}}_1,{\tilde{z}}_2,{\tilde{z}}_3\in \mathbb{R}$ and $\tau =1,2,\dots ,16.$ If

$$\mathrm{\Lambda }:=\left({\mathcal{V}}_0^{\ast }+{\mathcal{V}}_1^{\ast }+{\mathcal{V}}_2^{\ast }\right)\sum _{\tau =1}^{16}∥{\mathcal{G}}_{\tau }∥<1,$$

then (1) has a solution, where $∥{\mathcal{G}}_{\tau }∥={sup}_{s\in [0,1]}\left|{\mathcal{G}}_{\tau }\left(s\right)\right|$ and the constants ${\mathcal{V}}_0^{\ast }$–${\mathcal{V}}_2^{\ast }$ are defined in (12)–(14), respectively.

Proof. 

Let $∥{\mathcal{F}}_{\tau }∥={sup}_{s\in [0,1]}\left|{\mathcal{F}}_{\tau }\left(s\right)\right|$ and for appropriate constants ${\epsilon }_{\tau }$, we have

$${\epsilon }_{\tau }\ge \sum _{\tau =1}^{16}{\mathcal{M}}_{\tau }\left({∥z_{\tau }∥}_{{\mathcal{Y}}_{\tau }}\right)∥{\mathcal{F}}_{\tau }∥\left\{{\mathcal{Y}}_0^{\ast }+{\mathcal{Y}}_1^{\ast }+{\mathcal{Y}}_2^{\ast }\right\},$$

(15)

where ${\mathcal{Y}}_0^{\ast }-{\mathcal{Y}}_2^{\ast }$ are defined in (9)–(11). Here, we introduce a set

$${\mathcal{O}}_{{\epsilon }_{\tau }}:=\left\{z=(z_1,z_2,\dots ,z_{16})\in \mathcal{Y}:{∥z∥}_{\mathcal{Y}}\le {\epsilon }_{\tau }\right\},$$

where ${\epsilon }_{\tau }$ can be seen in (15). Here, ${\mathcal{O}}_{{\epsilon }_{\tau }}$ is obviously a closed, bounded, nonempty, and convex subset of $\mathcal{Y}={\mathcal{Y}}_1\times {\mathcal{Y}}_2\times \dots \times {\mathcal{Y}}_{16}$. Now, we define ${\mathcal{A}}_1$ and ${\mathcal{A}}_2$ on ${\mathcal{O}}_{{\epsilon }_{\tau }}$ by

$$\begin{array}{ccc}\hfill {\mathcal{A}}_1(z_1,z_2,\dots ,z_{16})\left(s\right)& :=& \left({\mathcal{A}}_1^{\left(1\right)}(z_1,z_2,\dots ,z_{16})\left(s\right),\dots ,{\mathcal{A}}_1^{\left(16\right)}(z_1,z_2,\dots ,z_{16})\left(s\right)\right),\hfill \\ \hfill {\mathcal{A}}_2(z_1,z_2,\dots ,z_{16})\left(s\right)& :=& \left({\mathcal{A}}_2^{\left(1\right)}(z_1,z_2,\dots ,z_{16})\left(s\right),\dots ,{\mathcal{A}}_2^{\left(16\right)}(z_1,z_2,\dots ,z_{16})\left(s\right)\right),\hfill \end{array}$$

where

$$\left({\mathcal{A}}_1^{\left(\tau \right)}z\right)\left(s\right)={\int }_0^s\frac{{(s-\theta )}^{r-1}}{\Gamma \left(r\right)}{\mathcal{W}}_{\tau }(\theta ,z_{\tau }\left(\theta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right),z_{\tau }^{\prime }\left(\theta \right))d\theta$$

(16)

and

$$\begin{array}{ccc}\hfill \left({\mathcal{A}}_2^{\left(\tau \right)}z\right)\left(s\right)& =& {\int }_0^1{\mathcal{W}}_{\tau }(\theta ,z_{\tau }\left(\theta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right),z_{\tau }^{\prime }\left(\theta \right))d\theta \hfill \\ & & +\frac{1}{A_0}\left(\frac{1}{\Gamma (3-r)}+s\right)\left[{\ell }_3{\int }_0^a{\int }_0^{\theta }{\mathcal{W}}_{\tau }(\zeta ,z_{\tau }\left(\zeta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\zeta \right),z_{\tau }^{\prime }\left(\zeta \right))d\zeta d\theta \right.\hfill \\ & & \left.-{\ell }_2{\int }_0^1\frac{{(1-\theta )}^{r-2}}{\Gamma (r-1)}{\mathcal{W}}_{\tau }(\theta ,z_{\tau }\left(\theta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right),z_{\tau }^{\prime }\left(\theta \right))d\theta \right]\hfill \end{array}$$

(17)

for all $s\in [0,1]$ and $z=(z_1,z_2,\dots ,z_{16})\in {\mathcal{O}}_{{\epsilon }_{\tau }}.$

Let ${\tilde{\mathcal{M}}}_{\tau }={sup}_{z_{\tau }\in {\mathcal{Y}}_{\tau }}{\mathcal{M}}_{\tau }\left({∥z_{\tau }∥}_{{\mathcal{Y}}_{\tau }}\right).$ Now, for every $\tilde{z}=({\tilde{z}}_1,{\tilde{z}}_2,\dots ,{\tilde{z}}_{16}),$ $z=(z_1,z_2,\dots ,z_{16})\in {\mathcal{O}}_{{\epsilon }_{\tau }},$ we have

$$\begin{array}{ccc}\hfill \left|\left({\mathcal{A}}_1^{\left(\tau \right)}\tilde{z}+{\mathcal{A}}_2^{\left(\tau \right)}z\right)\left(s\right)\right|& \le & {\int }_0^s\frac{{(s-\theta )}^{r-1}}{\Gamma \left(r\right)}|{\mathcal{W}}_{\tau }(\theta ,{\tilde{z}}_{\tau }\left(\theta \right),{\mathfrak{D}}^q{\tilde{z}}_{\tau }\left(\theta \right),{\tilde{z}}_{\tau }^{\prime }\left(\theta \right))|d\theta \hfill \\ & & +{\int }_0^1\left|{\mathcal{W}}_{\tau }(\theta ,z_{\tau }\left(\theta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right),z_{\tau }^{\prime }\left(\theta \right))\right|d\theta \hfill \\ & & +\frac{1}{|A_0|}\left(\frac{1}{\Gamma (3-r)}+s\right)\times \left[|{\ell }_3|\right.\hfill \\ & & {\int }_0^a{\int }_0^{\theta }\left|{\mathcal{W}}_{\tau }(\zeta ,z_{\tau }\left(\zeta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\zeta \right),z_{\tau }^{\prime }\left(\zeta \right))\right|d\zeta d\theta \hfill \\ & & \left.+|{\ell }_2|{\int }_0^1\frac{{(1-\theta )}^{r-2}}{\Gamma (r-1)}\left|{\mathcal{W}}_{\tau }(\theta ,z_{\tau }\left(\theta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right),z_{\tau }^{\prime }\left(\theta \right))\right|d\theta \right]\hfill \\ & \le & {\int }_0^s\frac{{(s-\theta )}^{r-1}}{\Gamma \left(r\right)}{\mathcal{F}}_{\tau }\left(\theta \right){\mathcal{M}}_{\tau }\left(\left|{\tilde{z}}_{\tau }\left(\theta \right)\right|+\left|{\mathfrak{D}}^q{\tilde{z}}_{\tau }\left(\theta \right)\right|+\left|{\tilde{z}}_{\tau }^{\prime }\left(\theta \right)\right|\right)d\theta \hfill \\ & & +{\int }_0^1{\mathcal{F}}_{\tau }\left(\theta \right){\mathcal{M}}_{\tau }\left(\left|z_{\tau }\left(\theta \right)\right|+\left|{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right)\right|+\left|z_{\tau }^{\prime }\left(\theta \right)\right|\right)d\theta \hfill \\ & & +\frac{1}{|A_0|}\left(\frac{1}{\Gamma (3-r)}+s\right)\times \hfill \\ & & \left[|{\ell }_3|{\int }_0^a{\int }_0^{\theta }{\mathcal{F}}_{\tau }\left(\zeta \right){\mathcal{M}}_{\tau }\left(\left|z_{\tau }\left(\zeta \right)\right|+\left|{\mathfrak{D}}^q{z}_{\tau }\left(\zeta \right)\right|+\left|z_{\tau }^{\prime }\left(\zeta \right)\right|\right)d\zeta d\theta \right.\hfill \\ & & +|{\ell }_2|{\int }_0^1\frac{{(1-\theta )}^{r-2}}{\Gamma (r-1)}\times \hfill \end{array}$$

$$\begin{array}{ccc}& & \left.{\mathcal{F}}_{\tau }\left(\theta \right){\mathcal{M}}_{\tau }\left(\left|z_{\tau }\left(\theta \right)\right|+\left|{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right)\right|+\left|z_{\tau }^{\prime }\left(\theta \right)\right|\right)d\theta \right]\hfill \\ & \le & ∥{\mathcal{F}}_{\tau }∥{\tilde{\mathcal{M}}}_{\tau }{\mathcal{Y}}_0^{\ast }.\hfill \end{array}$$

By using similar computations, we obtain

$$\begin{array}{ccc}\hfill \left|\left({\mathfrak{D}}^q{\mathcal{A}}_1^{\left(\tau \right)}\tilde{z}\right)\left(s\right)+\left({\mathfrak{D}}^q{\mathcal{A}}_2^{\left(\tau \right)}z\right)\left(s\right)\right|& \le & ∥{\mathcal{F}}_{\tau }∥{\tilde{\mathcal{M}}}_{\tau }{\mathcal{Y}}_1^{\ast },\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill \left|{\left({\mathcal{A}}_1^{\left(\tau \right)}\tilde{z}\right)}^{\prime }\left(s\right)+{\left({\mathcal{A}}_2^{\left(\tau \right)}z\right)}^{\prime }\left(s\right)\right|& \le & ∥{\mathcal{F}}_{\tau }∥{\tilde{\mathcal{M}}}_{\tau }{\mathcal{Y}}_2^{\ast }.\hfill \end{array}$$

This yields that

$$\begin{array}{ccc}\hfill {∥{\mathcal{A}}_1\tilde{z}+{\mathcal{A}}_{2}z∥}_{\mathcal{Y}}& =& \sum _{\tau =1}^{16}{∥{\mathcal{A}}_1^{\left(\tau \right)}\tilde{z}+{\mathcal{A}}_2^{\left(k\right)}z∥}_{\tilde{\mathcal{Y}}}\hfill \\ & \le & ∥{\mathcal{F}}_{\tau }∥{\tilde{\mathcal{M}}}_{\tau }\left({\mathcal{Y}}_0^{\ast }+{\mathcal{Y}}_1^{\ast }+{\mathcal{Y}}_2^{\ast }\right)\hfill \\ & \le & {\epsilon }_{\tau },\hfill \end{array}$$

and so ${\mathcal{A}}_1\tilde{z}+{\mathcal{A}}_{2}z\in {\mathcal{O}}_{{\epsilon }_{\tau }}.$ Furthermore, the continuity of ${\mathcal{W}}_{\tau }$ refers ${\mathcal{A}}_1$’s continuity.

We will now prove that there exists a uniform bound on the expression ${\mathcal{A}}_1$. To this end, we have

$$\begin{array}{ccc}\hfill \left|\left({\mathcal{A}}_1^{\left(\tau \right)}z\right)\left(s\right)\right|& \le & {\int }_0^s\frac{{(s-\theta )}^{r-1}}{\Gamma \left(r\right)}|{\mathcal{W}}_{\tau }(\theta ,z_{\tau }\left(\theta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right),z_{\tau }^{\prime }\left(\theta \right))|d\theta \hfill \\ & \le & \frac{1}{\Gamma (r+1)}∥{\mathcal{F}}_{\tau }∥{\mathcal{M}}_{\tau }\left(\left|z_{\tau }\left(\theta \right)\right|+\left|{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right)\right|+\left|z_{\tau }^{\prime }\left(\theta \right)\right|\right).\hfill \end{array}$$

for all $z\in {\mathcal{O}}_{{\epsilon }_{\tau }}.$ Additionally,

$$\begin{array}{ccc}\hfill \left|\left({\mathfrak{D}}^q{\mathcal{A}}_1^{\left(\tau \right)}z\right)\left(s\right)\right|& \le & {\int }_0^s\frac{{(s-\theta )}^{r-q-1}}{\Gamma (r-q)}|{\mathcal{W}}_{\tau }(\theta ,z_{\tau }\left(\theta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right),z_{\tau }^{\prime }\left(\theta \right))|d\theta \hfill \\ & \le & \frac{1}{\Gamma (r-q+1)}∥{\mathcal{F}}_{\tau }∥{\mathcal{M}}_{\tau }\left(\left|z_{\tau }\left(\theta \right)\right|+\left|{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right)\right|+\left|z_{\tau }^{\prime }\left(\theta \right)\right|\right),\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill \left|{\left({\mathcal{A}}_1^{\left(\tau \right)}z\right)}^{\prime }\left(s\right)\right|& \le & \frac{1}{\Gamma \left(r\right)}∥{\mathcal{F}}_{\tau }∥{\mathcal{M}}_{\tau }\left(\left|z_{\tau }\left(\theta \right)\right|+\left|{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right)\right|+\left|z_{\tau }^{\prime }\left(\theta \right)\right|\right),\hfill \end{array}$$

for all $z\in {\mathcal{O}}_{{\epsilon }_{\tau }}.$ Thus,

$$\begin{array}{ccc}\hfill {∥{\mathcal{A}}_{1}z∥}_{\mathcal{Y}}& =& \sum _{\tau =1}^{16}{∥{\mathcal{A}}_1^{\left(\tau \right)}z∥}_{\tilde{\mathcal{Y}}}\hfill \\ & \le & \left\{\frac{r+1}{\Gamma (r+1)}+\frac{1}{\Gamma (r-q+1)}\right\}\sum _{\tau =1}^{16}∥{\mathcal{F}}_{\tau }∥{\mathcal{M}}_{\tau }\left({∥z_{\tau }∥}_{{\mathcal{Y}}_{\tau }}\right),\hfill \end{array}$$

which demonstrates the uniformly boundedness property of the operator ${\mathcal{A}}_1$ on ${\mathcal{O}}_{{\epsilon }_{\tau }}$.

Here, it remains for us to show the compactness of the operator ${\mathcal{A}}_1$ on ${\mathcal{O}}_{{\epsilon }_{\tau }}$. To this end, let $s_1,s_2\in [0,1]$ with $s_1<s_2.$ Then, we have

$$\begin{array}{ccc}\hfill \left|\left({\mathcal{A}}_1^{\left(\tau \right)}z\right)\left(s_2\right)-\left({\mathcal{A}}_1^{\left(\tau \right)}z\right)\left(s_1\right)\right|& \le & \left|{\int }_0^{s_2}\frac{{(s_2-\theta )}^{r-1}}{\Gamma \left(r\right)}{\mathcal{W}}_{\tau }\left(\theta ,z_{\tau }\left(\theta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right),z_{\tau }^{\prime }\left(\theta \right)\right)d\theta \right.\hfill \\ & & \left.-{\int }_0^{s_1}\frac{{(s_1-\theta )}^{r-1}}{\Gamma \left(r\right)}{\mathcal{W}}_{\tau }\left(\theta ,z_{\tau }\left(\theta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right),z_{\tau }^{\prime }\left(\theta \right)\right)d\theta \right|\hfill \end{array}$$

$$\begin{array}{ccc}& \le & \left|{\int }_0^{s_1}\frac{{(s_2-\theta )}^{r-1}-{(s_1-\theta )}^{r-1}}{\Gamma \left(r\right)}\times \right.\hfill \\ & & \left.{\mathcal{W}}_{\tau }\left(\theta ,z_{\tau }\left(\theta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right),z_{\tau }^{\prime }\left(\theta \right)\right)d\theta \right|\hfill \\ & & +\left|{\int }_{s_1}^{s_2}\frac{{(s_2-\theta )}^{r-1}}{\Gamma \left(r\right)}{\mathcal{W}}_{\tau }\left(\theta ,z_{\tau }\left(\theta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right),z_{\tau }^{\prime }\left(\theta \right)\right)d\theta \right|\hfill \\ & \le & {\int }_0^{s_1}\frac{{(s_2-\theta )}^{r-1}-{(s_1-\theta )}^{r-1}}{\Gamma \left(r\right)}\times \hfill \\ & & \left|{\mathcal{W}}_{\tau }\left(\theta ,z_{\tau }\left(\theta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right),z_{\tau }^{\prime }\left(\theta \right)\right)\right|d\theta \hfill \\ & & +{\int }_{s_1}^{s_2}\frac{{(s_2-\theta )}^{r-1}}{\Gamma \left(r\right)}\left|{\mathcal{W}}_{\tau }\left(\theta ,z_{\tau }\left(\theta \right),{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right),z_{\tau }^{\prime }\left(\theta \right)\right)\right|d\theta \hfill \\ & \le & \left\{\frac{s_2^r-s_1^r-{\left(s_2-s_1\right)}^r}{\Gamma (r+1)}+\frac{{\left(s_2-s_1\right)}^r}{\Gamma (r+1)}\right\}\times \hfill \\ & & ∥{\mathcal{F}}_{\tau }∥{\mathcal{M}}_{\tau }\left({∥z_{\tau }∥}_{{\mathcal{Y}}_{\tau }}\right).\hfill \end{array}$$

Hence, $\left|\left({\mathcal{A}}_1^{\left(\tau \right)}z\right)\left(s_2\right)-\left({\mathcal{A}}_1^{\left(\tau \right)}z\right)\left(s_1\right)\right|\to 0$ as $s_1\to s_2.$ Additionally, we have

$$\begin{array}{c}\hfill \underset{s_1\to s_2}{lim}\left|\left({\mathfrak{D}}^q{\mathcal{A}}_1^{\left(\tau \right)}z\right)\left(s_2\right)-\left({\mathfrak{D}}^q{\mathcal{A}}_1^{\left(\tau \right)}z\right)\left(s_1\right)\right|=0,\\ \hfill \underset{s_1\to s_2}{lim}\left|{\left({\mathcal{A}}_1^{\left(\tau \right)}z\right)}^{\prime }\left(s_2\right)-{\left({\mathcal{A}}_1^{\left(\tau \right)}z\right)}^{\prime }\left(s_1\right)\right|=0.\end{array}$$

Hence, ${∥\left({\mathcal{A}}_{1}z\right)\left(s_2\right)-\left({\mathcal{A}}_{1}z\right)\left(s_1\right)∥}_{\mathcal{Y}}$ tends to zero as $s_1\to s_2$. As a result, the operator ${\mathcal{A}}_1$ defined on ${\mathcal{O}}_{{\epsilon }_{\tau }}$ is relatively compact since it is equicontinuous. By utilizing the results proven by Arzela–Ascoli, we claim that the operator ${\mathcal{A}}_1$ is compact on ${\mathcal{O}}_{{\epsilon }_{\tau }}$.

In end, it still needs to be shown that ${\mathcal{A}}_2$ is a contraction mapping. As evidence, we let $\tilde{z},z\in {\mathcal{O}}_{{\epsilon }_{\tau }},$

$$\begin{array}{ccc}\hfill \left|\left({\mathcal{A}}_2^{\left(\tau \right)}\tilde{z}\right)\left(s\right)-\left({\mathcal{A}}_2^{\left(\tau \right)}z\right)\left(s\right)\right|& \le & {\int }_0^1{\mathcal{G}}_{\tau }\left(\theta \right)\left(\left|{\tilde{z}}_{\tau }\left(\theta \right)-z_{\tau }\left(\theta \right)\right|+\left|{\mathfrak{D}}^q{\tilde{z}}_{\tau }\left(\theta \right)-{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right)\right|\right.\hfill \\ & & \left.+\left|{\tilde{z}}_{\tau }^{\prime }\left(\theta \right)-z_{\tau }^{\prime }\left(\theta \right)\right|\right)d\theta \hfill \\ & & +\frac{1}{|A_0|}\left(\frac{1}{\Gamma (3-r)}+s\right)\left[|{\ell }_3|\times \right.\hfill \\ & & {\int }_0^a{\int }_0^{\theta }{\mathcal{G}}_{\tau }\left(\zeta \right)\left(\left|{\tilde{z}}_{\tau }\left(\zeta \right)-z_{\tau }\left(\zeta \right)\right|\right.\hfill \\ & & \left.+\left|{\mathfrak{D}}^q{\tilde{z}}_{\tau }\left(\zeta \right)-{\mathfrak{D}}^q{z}_{\tau }\left(\zeta \right)\right|+\left|{\tilde{z}}_{\tau }^{\prime }\left(\zeta \right)-z_{\tau }^{\prime }\left(\zeta \right)\right|\right)d\zeta d\theta \hfill \\ & & +|{\ell }_2|{\int }_0^1\frac{{(1-\theta )}^{r-2}}{\Gamma (r-1)}{\mathcal{G}}_{\tau }\left(\theta \right)\left(\left|{\tilde{z}}_{\tau }\left(\theta \right)-z_{\tau }\left(\theta \right)\right|\right.\hfill \\ & & \left.+\left|{\mathfrak{D}}^q{\tilde{z}}_{\tau }\left(\theta \right)-{\mathfrak{D}}^q{z}_{\tau }\left(\theta \right)\right|+\left|{\tilde{z}}_{\tau }^{\prime }\left(\theta \right)-z_{\tau }^{\prime }\left(\theta \right)\right|\right)d\theta ]\hfill \\ & \le & ∥{\mathcal{G}}_{\tau }∥{\mathcal{V}}_0^{\ast }{∥{\tilde{z}}_{\tau }-z_{\tau }∥}_{{\mathcal{Y}}_{\tau }}\hfill \end{array}$$

for each $\tau =1,2,\dots ,16,$ where ${\mathcal{V}}_0^{\ast }$ is given in (12). According to the same kind of calculations, we also have

$$\underset{s\in [0,1]}{sup}\left|\left({\mathfrak{D}}^q{\mathcal{A}}_2^{\left(\tau \right)}\tilde{z}\right)\left(s\right)-\left({\mathfrak{D}}^q{\mathcal{A}}_2^{\left(\tau \right)}z\right)\left(s\right)\right|\le ∥{\mathcal{G}}_{\tau }∥{\mathcal{V}}_1^{\ast }{∥{\tilde{z}}_{\tau }-z_{\tau }∥}_{{\mathcal{Y}}_{\tau }}.$$

$$\underset{s\in [0,1]}{sup}\left|{\left({\mathcal{A}}_2^{\left(\tau \right)}\tilde{z}\right)}^{\prime }\left(s\right)-{\left({\mathcal{A}}_2^{\left(\tau \right)}z\right)}^{\prime }\left(s\right)\right|\le ∥{\mathcal{G}}_{\tau }∥{\mathcal{V}}_2^{\ast }{∥{\tilde{z}}_{\tau }-z_{\tau }∥}_{{\mathcal{Y}}_{\tau }},$$

where ${\mathcal{V}}_1^{\ast }$ and ${\mathcal{V}}_2^{\ast }$ are given in (13) and (14), respectively. Thus, we have

$$\begin{array}{ccc}\hfill {∥{\mathcal{A}}_2\tilde{z}-{\mathcal{A}}_{2}z∥}_{\mathcal{Y}}& =& \sum _{\tau =1}^{16}{∥{\mathcal{A}}_2^{\left(\tau \right)}\tilde{z}-{\mathcal{A}}_2^{\left(\tau \right)}z∥}_{\tilde{\mathcal{Y}}}\hfill \\ & \le & \left({\mathcal{V}}_0^{\ast }+{\mathcal{V}}_1^{\ast }+{\mathcal{V}}_2^{\ast }\right)\sum _{\tau =1}^{16}∥{\mathcal{G}}_{\tau }∥{∥{\tilde{z}}_{\tau }-z_{\tau }∥}_{{\mathcal{Y}}_{\tau }},\hfill \end{array}$$

and so

$${∥{\mathcal{A}}_2\tilde{z}-{\mathcal{A}}_{2}z∥}_{\mathcal{Y}}\le \mathrm{\Lambda }{∥\tilde{z}-z∥}_{\mathcal{Y}}.$$

As $\mathrm{\Lambda }<1,$ which means that ${\mathcal{A}}_2$ is a contraction on ${\mathcal{O}}_{{\epsilon }_{\tau }}.$ In this demonstration, we use Theorem 2, to show that there exists a fixed point of $\mathcal{A}$ such that the problem has a solution (1). □

4. An Example

The following illustration demonstrates the relevance of our findings.

Example 1.

Consider the problem stated below:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\mathfrak{D}}^{1.5}{z}_1\left(s\right)& =\frac{36e^s{\left[z_1\left(s\right)\right]}^2}{\mathrm{40,000}(1+{\left[z_1\left(s\right)\right]}^2)}+0.0009e^{s}sin\left({\mathfrak{D}}^{0.08}{z}_1\left(s\right)\right)+\frac{180e^{s}arctan{z}_1^{\prime }\left(s\right)}{\mathrm{200,000}},\hfill \\ \hfill {\mathfrak{D}}^{1.5}{z}_2\left(s\right)& =\frac{s\left(arctan{z}_2\left(s\right)\right)}{\mathrm{25,000}}+0.00004s\left(sin\left({\mathfrak{D}}^{0.08}{z}_2\left(s\right)\right)\right)+\frac{4s{\left[z_2^{\prime }\left(s\right)\right]}^2}{\mathrm{100,000}\left(1+{\left[z_2^{\prime }\left(s\right)\right]}^2\right)},\hfill \\ \hfill {\mathfrak{D}}^{1.5}{z}_3\left(s\right)& =0.0001s\left({sinh}^{-1}{z}_3\left(s\right)\right)+\frac{60s{\left[{\mathfrak{D}}^{0.08}{z}_3\left(s\right)\right]}^2}{\mathrm{600,000}+\mathrm{600,000}{\left[{\mathfrak{D}}^{0.08}{z}_3\left(s\right)\right]}^2}+\frac{3s\left(arctan{z}_3^{\prime }\left(s\right)\right)}{\mathrm{30,000}},\hfill \end{array}\right.\end{array}$$

(18)

associated with the following boundary conditions:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill z_1\left(0\right)& ={\mathfrak{D}}^{0.5}{z}_1\left(1\right)\hfill \\ \hfill \frac{13}{17}{z}_1^{\prime }\left(0\right)+\frac{6}{29}{z}_1^{\prime }\left(1\right)& =\frac{15}{43}{\int }_0^1{\mathfrak{D}}^{0.5}{z}_1\left(\theta \right)d\theta \hfill \\ \hfill z_2\left(0\right)& ={\mathfrak{D}}^{0.5}{z}_2\left(1\right)\hfill \\ \hfill \frac{13}{17}{z}_2^{\prime }\left(0\right)+\frac{6}{29}{z}_2^{\prime }\left(1\right)& =\frac{15}{43}{\int }_0^1{\mathfrak{D}}^{0.5}{z}_2\left(\theta \right)d\theta \hfill \\ \hfill z_3\left(0\right)& ={\mathfrak{D}}^{0.5}{z}_3\left(1\right)\hfill \\ \hfill \frac{13}{17}{z}_3^{\prime }\left(0\right)+\frac{6}{29}{z}_3^{\prime }\left(1\right)& =\frac{15}{43}{\int }_0^1{\mathfrak{D}}^{0.5}{z}_3\left(\theta \right)d\theta \hfill \end{array}\right.\end{array}$$

(19)

where $r=1.5,q=0.08,{\ell }_1=\frac{13}{17},{\ell }_2=\frac{6}{29},{\ell }_3=\frac{15}{43}$ and ${\mathfrak{D}}^r$, ${\mathfrak{D}}^q$ serve as the Caputo derivative of order r and $q,$ respectively. Let ${\mathcal{W}}_1,{\mathcal{W}}_2,{\mathcal{W}}_3:[0,1]\times \mathbb{R}\times \mathbb{R}\times \mathbb{R}\to \mathbb{R}$ be continuous functions given by

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\mathcal{W}}_1\left(s,z,\tilde{z},\tilde{\tilde{z}}\right)& =\frac{36e^s{\left[z\right]}^2}{\mathrm{40,000}(1+{\left[z\right]}^2)}+0.0009e^s\left(sin\left({\mathfrak{D}}^{0.08}\tilde{z}\right)\right)+\frac{180e^s\left(arctan\tilde{\tilde{z}}\right)}{\mathrm{200,000}},\hfill \\ \hfill {\mathcal{W}}_2\left(s,z,\tilde{z},\tilde{\tilde{z}}\right)& =\frac{s\left(arctanz\right)}{\mathrm{25,000}}+0.00004s\left(sin\left({\mathfrak{D}}^{0.08}\tilde{z}\right)\right)+\frac{4s{\left[\tilde{\tilde{z}}\right]}^2}{\mathrm{100,000}\left(1+{\left[\tilde{\tilde{z}}\right]}^2\right)},\hfill \\ \hfill {\mathcal{W}}_3\left(s,z,\tilde{z},\tilde{\tilde{z}}\right)& =0.0001s\left({sinh}^{-1}z\right)+\frac{60s{\left[{\mathfrak{D}}^{0.08}\tilde{z}\right]}^2}{\mathrm{600,000}+\mathrm{600,000}{\left[{\mathfrak{D}}^{0.08}\tilde{z}\right]}^2}+\frac{3s\left(arctan\tilde{\tilde{z}}\right)}{\mathrm{30,000}},\hfill \end{array}\right.\end{array}$$

for all $z,\tilde{z},\tilde{\tilde{z}}\in \mathbb{R}$, $s\in [0,1],$ and ${\mathcal{W}}_4,{\mathcal{W}}_5,\dots ,{\mathcal{W}}_{16}:[0,1]\times \mathbb{R}\times \mathbb{R}\times \mathbb{R}\to \mathbb{R}$ are zero functions. Let $z_1,z_2,{\tilde{z}}_1,{\tilde{z}}_2,{\tilde{\tilde{z}}}_1,{\tilde{\tilde{z}}}_2\in \mathbb{R}$ and $s\in [0,1]$. Then, we have

$$\begin{array}{c}\hfill \left|{\mathcal{W}}_1\left(s,z_1,{\tilde{z}}_1,{\tilde{\tilde{z}}}_1\right)-{\mathcal{W}}_1\left(s,z_2,{\tilde{z}}_2,{\tilde{\tilde{z}}}_2\right)\right|\le \frac{9e^s}{\mathrm{10,000}}\left(\left|z_1-z_2\right|+\left|{\tilde{z}}_1-{\tilde{z}}_2\right|+\left|{\tilde{\tilde{z}}}_1-{\tilde{\tilde{z}}}_2\right|\right),\\ \hfill \left|{\mathcal{W}}_2\left(s,z_1,{\tilde{z}}_1,{\tilde{\tilde{z}}}_1\right)-{\mathcal{W}}_2\left(s,z_2,{\tilde{z}}_2,{\tilde{\tilde{z}}}_2\right)\right|\le \frac{s}{\mathrm{25,000}}\left(\left|z_1-z_2\right|+\left|{\tilde{z}}_1-{\tilde{z}}_2\right|+\left|{\tilde{\tilde{z}}}_1-{\tilde{\tilde{z}}}_2\right|\right),\\ \hfill \left|{\mathcal{W}}_3\left(s,z_1,{\tilde{z}}_1,{\tilde{\tilde{z}}}_1\right)-{\mathcal{W}}_3\left(s,z_2,{\tilde{z}}_2,{\tilde{\tilde{z}}}_2\right)\right|\le \frac{s}{\mathrm{10,000}}\left(\left|z_1-z_2\right|+\left|{\tilde{z}}_1-{\tilde{z}}_2\right|+\left|{\tilde{\tilde{z}}}_1-{\tilde{\tilde{z}}}_2\right|\right).\end{array}$$

Here, ${\mathcal{G}}_1\left(s\right)=\frac{9e^s}{\mathrm{10,000}},{\mathcal{G}}_2\left(s\right)=\frac{s}{\mathrm{25,000}},{\mathcal{G}}_3\left(s\right)=\frac{s}{\mathrm{10,000}}$, and ${\mathcal{G}}_4\left(s\right)={\mathcal{G}}_5\left(s\right)=\dots ={\mathcal{G}}_{16}\left(s\right)=0$, where $∥{\mathcal{G}}_1∥=\frac{9}{\mathrm{10,000}},∥{\mathcal{G}}_2∥=\frac{1}{\mathrm{25,000}},∥{\mathcal{G}}_3∥=\frac{1}{\mathrm{10,000}},and∥{\mathcal{G}}_4∥=∥{\mathcal{G}}_5∥=\dots =∥{\mathcal{G}}_{16}∥=0.$ Let ${\mathcal{M}}_1,{\mathcal{M}}_2,\dots ,{\mathcal{M}}_{16}:[0,\infty )\to \mathbb{R}$ be identity functions. Thus, we obtain

$$\begin{array}{ccc}\hfill \left|{\mathcal{W}}_1\left(s,z,\tilde{z},\tilde{\tilde{z}}\right)\right|& \le & \frac{9e^s}{\mathrm{10,000}}\left(\left|z\right|+\left|\tilde{z}\right|+\left|\tilde{\tilde{z}}\right|\right),\hfill \\ \hfill \left|{\mathcal{W}}_2\left(s,z,\tilde{z},\tilde{\tilde{z}}\right)\right|& \le & \frac{s}{\mathrm{25,000}}\left(\left|z\right|+\left|\tilde{z}\right|+\left|\tilde{\tilde{z}}\right|\right),\hfill \\ \hfill \left|{\mathcal{W}}_3\left(s,z,\tilde{z},\tilde{\tilde{z}}\right)\right|& \le & \frac{s}{\mathrm{10,000}}\left(\left|z\right|+\left|\tilde{z}\right|+\left|\tilde{\tilde{z}}\right|\right),\hfill \end{array}$$

for all $z,\tilde{z},\tilde{\tilde{z}}$ and $s\in [0,1]$, where the continuous function ${\mathcal{F}}_1,{\mathcal{F}}_2,\dots ,{\mathcal{F}}_{16}:[0,1]\to \mathbb{R}$ are defined by

$${\mathcal{F}}_1\left(s\right)=\frac{9e^s}{\mathrm{10,000}},{\mathcal{F}}_2\left(s\right)=\frac{s}{\mathrm{25,000}},{\mathcal{F}}_3\left(s\right)=\frac{s}{\mathrm{10,000}},{\mathcal{F}}_4\left(s\right)={\mathcal{F}}_5\left(s\right)=\dots ={\mathcal{F}}_{16}\left(s\right)=0.$$

Additionally,

$${\mathcal{V}}_0^{\ast }\simeq 1.3773,{\mathcal{V}}_1^{\ast }\simeq 0.1779\mathit{and}{\mathcal{V}}_2^{\ast }\simeq 0.1773,$$

and so

$${\mathcal{V}}_0^{\ast }+{\mathcal{V}}_1^{\ast }+{\mathcal{V}}_2^{\ast }\simeq 1.7325.$$

Furthermore,

$$\mathrm{\Lambda }:=\left({\mathcal{V}}_0^{\ast }+{\mathcal{V}}_1^{\ast }+{\mathcal{V}}_2^{\ast }\right)\left(∥{\mathcal{G}}_1∥+∥{\mathcal{G}}_2∥+∥{\mathcal{G}}_3∥+∥{\mathcal{G}}_4∥\right)\simeq 0.0018<1.$$

According to Theorem 4, there exists a solution to Problems (18) and (19).

5. Discussion and Conclusions

The scope of the study on chemical graph theory encompasses all aspects of the applications of graph theory to the field of chemistry. The word “chemical” is used to distinguish chemical graph theory from traditional graph theory, where rigorous mathematical proofs are often preferred to the intuitive grasp of key ideas and theorems. However, graph theory is used to represent the structural features of chemical substances. The tremendous growth of this discipline over the last several decades has resulted in the development of a plethora of cutting-edge concepts and methods for conducting this kind of study.

Using the idea of star graphs, several scholars have studied the solutions of fractional differential equations. They chose to utilize star graphs since their method required a central node connected to nearby vertices through interconnections, but there are no edges between the nodes.

The purpose of this study was to extend the technique’s applicability by introducing the concept of a neopentane graph, a fundamental molecule in chemistry with the formula $C_5{H}_{12}$. In this manner, we explored a network in which the vertices were either labeled with 0 or 1, and the structure of the chemical molecule neopentane was shown to have an effect on this network. To study whether or not there were solutions to the offered boundary value problems within the context of the Caputo fractional derivative, we used the fixed point theorems developed by Schaefer and Krasnoselskii. In conclusion, an example was given to illustrate the significance of the findings obtained from this research line.

Our method can be used for various graphs, such as digraphs, which are necessary for protein networks in biomedical engineering. The following open problems are presented for the consideration of readers interested in this topic:

• Is there another approach that leads to the same conclusion as we proposed?
• Can this concept be applied to graphs with a circular ring structure?
• We also present the suggested fractional differential Equation (1)’s stability as an unsolved problem.