Efficient Implementation of SPEEDY Block Cipher on Cortex-M3 and RISC-V Microcontrollers ^†

Abstract

The SPEEDY block cipher family announced at the CHES 2021 shows excellent performance on hardware architectures. Due to the nature of the hardware-friendly design of SPEEDY, the algorithm has low performance for software implementations. In particular, 6-bit S-box and bit permutation operations of SPEEDY are inefficient in software implementations, where it performs word-wise computations. We implemented the SPEEDY block cipher on a 32-bit microcontroller for the first time by applying the bit-slicing techniques. The optimized encryption performance results on ARM Cortex-M3 for SPEEDY-5-192, SPEEDY-6-192, and SPEEDY-7-192 are 65.7, 75.25, and 85.16 clock cycles per byte (i.e., cpb), respectively. It showed better performance than AES-128 constant-time implementation and GIFT constant-time implementation in the same platform. In RISC-V, the performance showed 81.9, 95.5, and 109.2 clock cycles per byte, which outperformed the previous works. Finally, we conclude that SPEEDY can show efficient software implementation on low-end embedded environments.

1. Introduction

SPEEDY [1] is a very low-latency block cipher designed with high performance as the highest priority for high-end CPU security. It shows higher performance than competing block ciphers [2,3,4,5]. The software implementation of SPEEDY, designed to be hardware-friendly, is relatively inefficient. In general, ciphers designed with hardware performance in mind are relatively inefficient for implementation in software. Some researchers applied the bit-slicing technique and implemented it efficiently in the software environment. Bao [6] improved software performance by using bit-slicing technology instead of LUT for PRINCE and LED in 8-bit microcontroller. Papagiannopoulos et al. [7] presented a high-throughput assembly implementation of the PRESENT, PRINCE and KATAN64 ciphers for the ATtiny family of AVR microcontrollers. A method of applying ‘bit-slicing’ technology to a lightweight encryption implementation is provided. Reis et al. [8] showed that a bit-slicing implementation of PRESENT can be efficiently implemented on 32-bit ARM. Using bit-slicing on the Cortex-M3, we improved the speed by 8× compared to our previous work. Adomnicai et al. [9] demonstrated a highly efficient software implementation of GIFT with a new technique called fix-slicing. The Cortex-M3 microcontroller performed faster than the then-best AES [10] constant-time implementation microcontrollers. Based on these studies, we explored bit-slicing implementation with the goal of efficient implementation on SPEEDY’s software. A cipher with high performance in both hardware and software is considered competitive over other ciphers. SPEEDY’s high-performance software implementation will increase SPEEDY’s competitiveness.

Ref. [1] provided two software-implemented reference implementations and a 6 × 32-bit implementation. From this, we could observe the parts that caused performance degradation in the SPEEDY software implementation. In the case of the reference implementation, the state of the 192 bits of SPEEDY is expressed by 248 bits. That expression causes an additional operation. In the reference implementation, SubBox uses a method of retrieving the value of the 6-bit S-box from the dictionary table. For this, the state represented by 248 bits is decomposed into 6 bits before input to the S-box. The output 6-bit result is then recombined to convert it back to a representation of an 8-bit 24 array. This process is also included in the ShiftColumns MixColumns step. The conversion process is inefficient, as it consumes additional time and memory. The 6 × 32-bit implementation stores 6 bits in 8-bit storage to solve this problem. The conversion process can be eliminated, but it is wasted by using 256 bits of storage space. A bit-slicing implementation can overcome these shortcomings. The conversion process is unnecessary by using 832-bit storage spaces. It also eliminates wasted space in a 6 × 32-bit implementation. As shown in

Table 1. Comparison of reference and bit-slicing C implementation results. Performance is evaluated in cpb (clock cycles per byte).

Intel 8th Core i7-8850H	Speed (cpb)
SPEEDY-7-192 encryption reference [9]	2983
6 × 32 reference [9]	1278
bitslice(our)	852

, the bit-slicing implementation is faster than previous software results. These results motivated the implementation of SPEEDY in an embedded environment that requires fewer resources. We implemented optimally in Cortex-m3 and Risc-V environments to analyze whether SPEEDY’s bit-slicing implementation works efficiently in an embedded environment.

1.1. Extended Version of ICISC’21

The previous work in ICISC’21 is extended in this paper [11]. In [11], efficient software implementations of SPEEDY on low-end ARM Cortex-M4 microcontrollers were investigated. This work presents optimized implementations of SPEEDY on modern 32-bit RISC-V microcontrollers as well. We fully utilized features (i.e., registers and instructions) of RISC-V to improve the performance, significantly.

1.2. Contributions

We achieved higher speed performance than the prior software implementation of SPEEDY. SPEEDY is designed to be hardware-friendly and shows relatively low performance in the software reference implementation of [1]. We observed that SPEEDY’s 6-bit S-box, ShiftColumns, and MixColumns are naturally optimized in the bit-slicing implementation. In addition, the implementation of bit-slicing naturally achieves a constant time implementation, preventing timing attacks [12,13,14]. We also show an implementation that effectively turns SPEEDY’s 192-bit blocks into representations of bit slicing. It was first implemented on 32-bit ARM processors and RISC-V [15] processors to achieve outstanding performance. Especially when implemented in Cortex-M3, higher performance can be achieved using the barrel shifter module. On ARM Cortex-M3, SPEEDY-5-192, SPEEDY-6-192 and SPEEDY-7-192 achieved 65.7, 75.25 and 85.16 clock cycles per byte, respectively, faster than previous constant-time implementations of GIFT-128 and AES-128. In RISC-V (i.e., RV32I), SPEEDY-5-192, SPEEDY-6-192, and SPEEDY-7-192 achieved 81.9, 95.5, and 109.2 clock cycles per byte, respectively. The implementation results of this paper will be available in https://github.com/amdjd0704/speedy_bitslice (accessed on 10 November 2022).

2. SPEEDY Algorithm

SPEEDY is a high-speed, high-security priority block cipher with very low latency, designed for hardware security solutions built into high-end CPUs that require high performance in terms of latency and throughput. The block length and key length use 192 bits, which is the least common multiple of 6 and 64 considering a 64-bit CPU, and use a 6-bit S-box. The 192 bits can be expressed in 32 rows of 6 bits each. The SPEEDY family is divided into SPEEDY-5-192, SPEEDY-6-192, SPEEDY-7-192 according to the number of rounds. As for the security level provided by each algorithm, SPEEDY-6-192 provides a security level of 128 bits, and SPEEDY-7-192 provides a security level of 192 bits. SPEEDY-5-192 provides a sufficient level of security for use in real applications. The block length of SPEEDY-r-6ℓ is 6$\times \ell$) and the number of rounds is r. The 6$\times \ell$ can be seen as a rectangular array.

2.1. The Round Function of SPEEDY

The 6-bit S-box used by SPEEDY is based on the NAND gate. It is designed to run fast on CMOS hardware while providing excellent cryptographic properties. Our implementation follows the disjunctive normal form (DNF) operation, and S-box is implemented with the AND operation and OR operation. The S-box is applied to each status row, and the DNF of the S-box is as follows:

$$\begin{array}{cc}\hfill & y_0=(x_3\wedge \neg x_5)\vee (x_3\wedge x_4\wedge x_2)\vee (\neg x_3\wedge x_1\wedge x_0)\vee (x_5\wedge x_4\wedge x_1)\hfill \\ \hfill & y_1=(x_5\wedge x_3\wedge \neg x_2)\vee (\neg x_5\wedge x_3\wedge \neg x_4)\vee (x_5\wedge x_2\wedge x_0)\vee (\neg x_3\wedge \neg x_0\wedge x_1)\hfill \\ \hfill & y_2=(\neg x_3\wedge x_0\wedge x_4)\vee (x_3\wedge x_0\wedge x_1)\vee (\neg x_3\wedge \neg x_4\wedge x_2)\vee (\neg x_0\wedge \neg x_2\wedge \neg x_5)\hfill \\ \hfill & y_3=(\neg x_0\wedge x_2\wedge \neg x_3)\vee (x_0\wedge x_2\wedge x_4)\vee (x_0\wedge \neg x_2\wedge x_5)\vee (\neg x_0\wedge x_3\wedge x_1)\hfill \\ \hfill & y_4=(x_0\wedge \neg x_3)\vee (x_0\wedge \neg x_4\wedge \neg x_2)\vee (\neg x_0\wedge x_4\wedge x_5)\vee (\neg x_4\wedge \neg x_2\wedge x_1)\hfill \\ \hfill & y_5=(x_2\wedge x_5)\vee (\neg x_2\wedge \neg x_1\wedge x_4)\vee (x_2\wedge x_1\wedge x_0)\vee (\neg x_1\wedge x_0\wedge x_3)\hfill \end{array}$$

2.1.1. ShiftColumns

In ShiftColumns, the j-th column of the state is rotated in reverse by j bits. When implementing hardware, it can be implemented for free with simple wiring. However, software implementation requires additional work.

$$y_{[i,j]}=x_{[i+j,j]}$$

2.1.2. Mixcolumns

Mixcolumns allows for a simple implementation using only XOR gates in hardware implementations. However, additional calculations are required when implementing the software. In Mixcolumns, a cyclic binary matrix is multiplied by each column of states. The implementation is as follows, where n = (n1, ..., n6) is the version-specific parameter value.

$$y_{[i,j]}=x_{i,j}\oplus x_{[i+n_1,j]}\oplus x_{[i+n_2,j]}\oplus x_{[i+n_3,j]}\oplus x_{[i+n_4,j]}\oplus x_{[i+n_5,j]}\oplus x_{[i+n_6,j]}$$

2.1.3. AddRoundKey

Addroundkey performs an XOR operation on the state value and the 6ℓ-bit round key $R{K}_r$:

$$y_{[i,j]}=x_{[i,j]}\oplus R{K}_{r[i,j]}$$

2.1.4. AddRoundConstant

AddRoundConstant performs an XOR operation of the state value and the round constant value 6ℓ-bit $c_r$.

The 6ℓ-bit constant $c_r$ is XORed to the whole of the state. Round constants $c_r$ is chosen as the binary digits of the number $\pi -3=0.141....$:

$$y_{[i,j]}=x_{[i,j]}\oplus c_{r[i,j]}$$

One round of encryption works in the following order: AddRoundkey → SubBytes → ShiftColumns → SubBytes → ShiftColumns → MixColumns → AddRoundConstant. Last round of encryption works in the following order: AddRoundkey → SubBytes → ShiftColumns → SubBytes → AddRoundkey. In decryption, inversed SubBytes, ShiftColumns and MixColumns work in reverse.

3. Proposed Technique

We aimed for an efficient implementation of SPEEDY on a 32-bit microcontroller. In SPEEDY, the 192-bit state is expressed in 32 lines of 6 bits each. However, 6-bit does not fit into the 8-bit, 32-bit, and 64-bit used in typical processor architectures. This results in wasted space and additional computations in SPEEDY’s software implementation. In particular, ShiftColumns require bit exchange between blocks, which is difficult in software operation. In a bit-slicing implementation, these characteristics are reversed. In the bit-slicing representation, the 192-bit state is expressed in 6 rows of 32 bits each. Therefore, in software implementation, the state can be stored without waste with 6 storage spaces of 32 bits. We observed that SPEEDY’s round function in the bit-slicing representation is very suitable for software implementations. Six blocks can be processed in parallel with 32-bit logic operation in the S-box layer. ShiftColumns are easily handled as exchanges between registers. MixColumns can be processed with several rotations and XOR operations. First, we implemented SPEEDY in C language by applying bit-slicing. Table 1 is a comparison to the previous reference implementation. The clock cycles per byte of the encryption process including the key schedule were measured on a commercial computer. The bit-slicing implementation shows a 250% 50% speedup over the respective reference implementations. You can see that SPEEDY’s implementation of bit-slicing is more efficient in software. Based on this, we show the application of bit-slicing to a resource-limited 32-bit microcontroller.

3.1. SPEEDY on ARM Cortex–M3

The Cortex-M3 is ARM’s family of 32-bit processors. It is designed to be inexpensive and energy efficient for use in embedded microcontrollers, making it very effective for IoT services. It features a barrel shifter support. A barrel shifter is a hardware device that can shift or rotate multiple bits within a data word in one operation. In arithmetic or logical operations, rotation or translation can be performed simultaneously with a single instruction. This microprocessor has 16 32-bit registers. Of these, 14 registers are available for the developer (e.g., $R_0\sim R_{12}$, $R_{14}$). Arithmetic and logical operations use only one clock cycle, but branches, loads, and stores can take many more. Therefore, minimizing access to memory and using registers can improve computational performance. For the SPEEDY implementation on our Cortex-M3, all 14 registers are used for efficient operation. It uses 6 fixed registers to store the intermediate value of the operation. Then, the address value of the round key used periodically is stored in one register and called during the operation of the AddRoundKey function. In order to improve computational performance, functions except for AddRoundKey function are implemented not to access memory. For this, the SubBox function requires 7 temporary storage, and ShiftColumns and MixColumns each requires 6 temporary storage. Since all registers are used during the operation, the value containing the ciphertext address is stored on the stack at the start of the operation and loaded last.

3.2. SPEEDY on RISC-V(RV32I)

RISC-V is a computer CPU architecture that has been under development at UC Berkeley since 2010. The main feature of the RISC-V processor is that RISC-V ISA is provided under an open-source license. In this paper, the 32-bit RV32I basic instruction set is used to support small microcontrollers [16]. The RV32I contains 47 unique instructions and has 32 general purpose registers (i.e., $x_0\sim x_{31}$). Registers are used similarly for the Cortex-M3 processor. The address value of the round key that is used periodically is stored in one register and used repeatedly, and the intermediate value of the operation is stored by fixing 6 registers. The SubBox function requires 7 temporary storage spaces, and the ShiftColumns and MixColumns functions each requires 6 temporary storage spaces. Since more registers than Cortex-M3 can be used, the value including the ciphertext address is stored in the register and used.

3.3. Bit-Slicing SPEEDY

Bit-slicing was first used instead of lookup tables by Biham [17] to speed up the software implementation of DES. Bit-slicing represents the data of the n bit block as 1 bit and stores it in the n register. This representation allows multiple blocks to be processed in parallel using bitwise operation instructions. The bit-slicing technique, which computes multiple instances in parallel, is widely used because it can save a lot of computation with high parallelism. However, in the case of a microcontroller, it is difficult to apply because it does not provide enough registers. Additionally, it can be used only when parallel operation is possible, such as in CTR mode. Bit-slicing for a single block can be used regardless of the implementation mode. Since our target is a 32-bit microcontroller, bit-slicing is performed for a single block. For bit-slicing, a function must be expressed as a logical operation. Packing to change the block to the bit-slicing representation and the unpacking process to return to the original representation are required. For a bit-slicing implementation, SPEEDY’s 192-bit plaintext is represented by six 32-bit registers.

Table 2. Bit-slicing representation from using 6 32-bit registers $R_0$, ..., $R_5$ to process 8 blocks $b^0,...,b^7$ in parallel where $b_j^i$ refers to the j-th bit of the i-th block.

	$Block0$	$Block1$	$Block2$	$Block3$	⋯	⋯	$Block28$	$Block29$	$Block30$	$Block31$
$R_0$	$b_0^0$	$b_0^1$	$b_0^2$	$b_0^3$	⋯	⋯	$b_0^{28}$	$b_0^{29}$	$b_0^{30}$	$b_0^{31}$
$R_1$	$b_1^0$	$b_1^1$	$b_1^2$	$b_1^3$	⋯	⋯	$b_1^{28}$	$b_1^{29}$	$b_1^{30}$	$b_1^{31}$
$R_2$	$b_2^0$	$b_2^1$	$b_2^2$	$b_2^3$	⋯	⋯	$b_2^{28}$	$b_2^{29}$	$b_2^{30}$	$b_2^{31}$
$R_3$	$b_3^0$	$b_3^1$	$b_3^2$	$b_3^3$	⋯	⋯	$b_3^{28}$	$b_3^{29}$	$b_3^{30}$	$b_3^{31}$
$R_4$	$b_4^0$	$b_4^1$	$b_4^2$	$b_4^3$	⋯	⋯	$b_4^{28}$	$b_4^{29}$	$b_4^{30}$	$b_4^{31}$
$R_5$	$b_5^0$	$b_5^1$	$b_5^2$	$b_5^3$	⋯	⋯	$b_5^{28}$	$b_5^{29}$	$b_5^{30}$	$b_5^{31}$

is a bit-slicing representation used for implementation. Using this representation, blocks of SPEEDY operate in parallel across all functions and can be efficiently implemented with fewer instructions. The SWAPMOVE technique [18] is a common technique used to efficiently change the bit-slicing representation. It is simply changed with a few SWAPMOVE operations.

$$SWAPMOVE(A,B,M,n):T=(B\oplus (A\ll n\left)\right)\wedge MB=B\oplus TA=A\oplus (T\gg n)$$

(1)

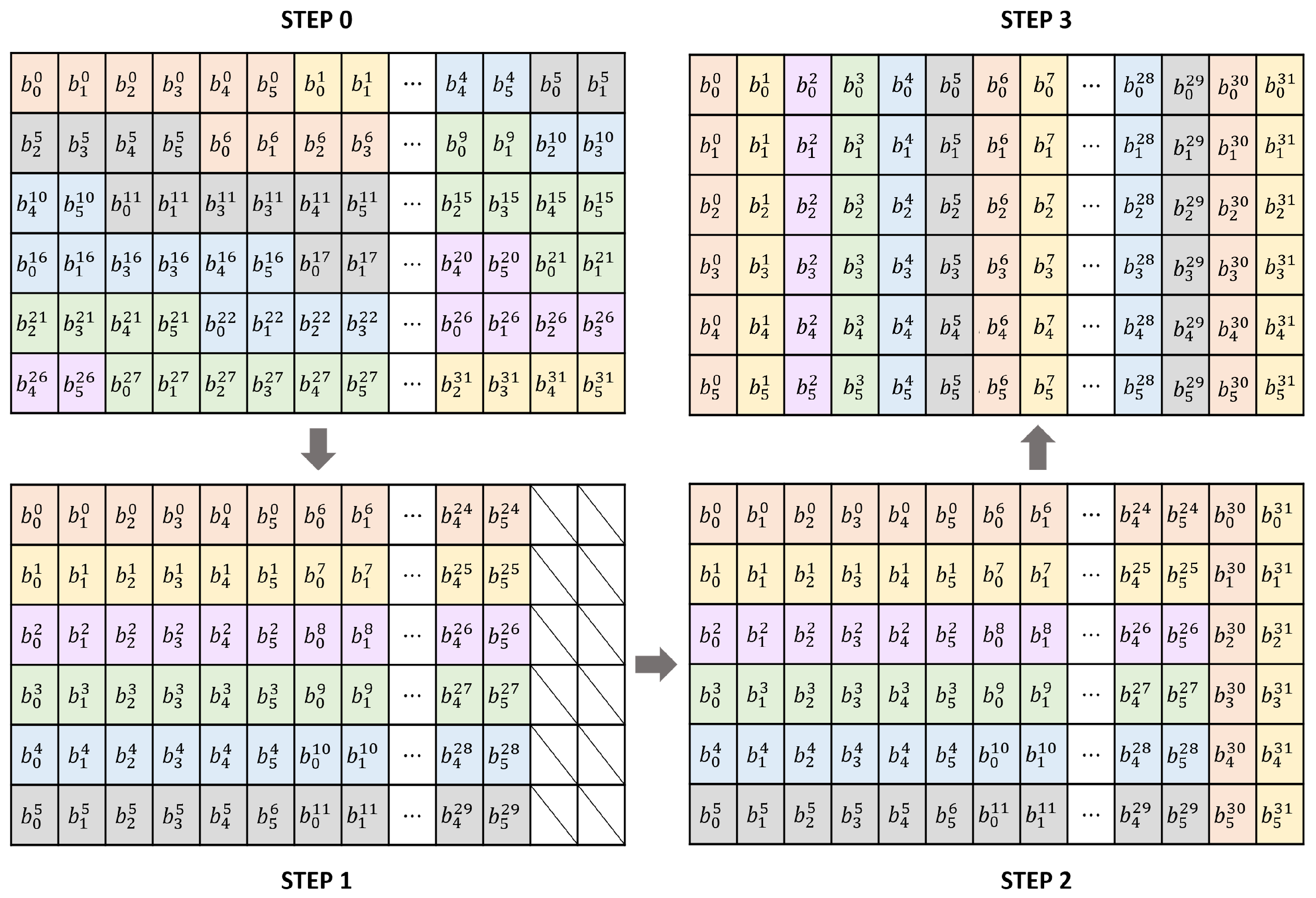
On a 32-bit processor, 192 bits of plain text are stored in six segments without waste. At this time, 6-bit blocks are stored in different spaces. Due to truncated blocks, SPEEDY cannot create a bit-slicing representation using only SWAPMOVE. Taking this into account, we implemented a three-step process with the goal of using fewer instructions. One 32-bit register can completely store five 6-bit blocks. SWAPMOVE technology is applied to blocks of index 0 to 29, and the rest are implemented by moving 1 bit at a time. This method can be effectively implemented by maximizing the known SWAPMOVE technology. Step 1 places five 6-bit blocks in a 32-bit register. Step 2 rearranges indices 30 and 31 into bit-slicing representations. It is shifted one bit at a time. Finally, in step 3, the block is rearranged from the 0th to the 29th index by the SWAPMOVE operation.

Step 0 of the Figure 1 is the initial state in which input 192 bits are stored in 6 registers. SPEEDY is divided into 32 6-bit blocks and operated. Since it does not match the register size, it can be seen that some blocks are divided and stored. In step 1, the block is sorted using only 30 bits of the register, excluding 2 bits from 32 bits. A total of 180 bits of input are stored in the registers, leaving 12 bits. The remaining 12 bits correspond to the last two blocks of 32 blocks. We implemented it efficiently by using UBFX, BFI, LSL, and LSR instructions in Cortex-M3 processor and SRLI, SLLI, and AND instructions in RV32I. In Step 2, the remaining 12 bits are filled in the 2 unfilled bits. The last block, the 32-nd block, is stored in the least significant bit of each register, and the 31-st block is stored in the second least significant bit. These values do not change until the last step.

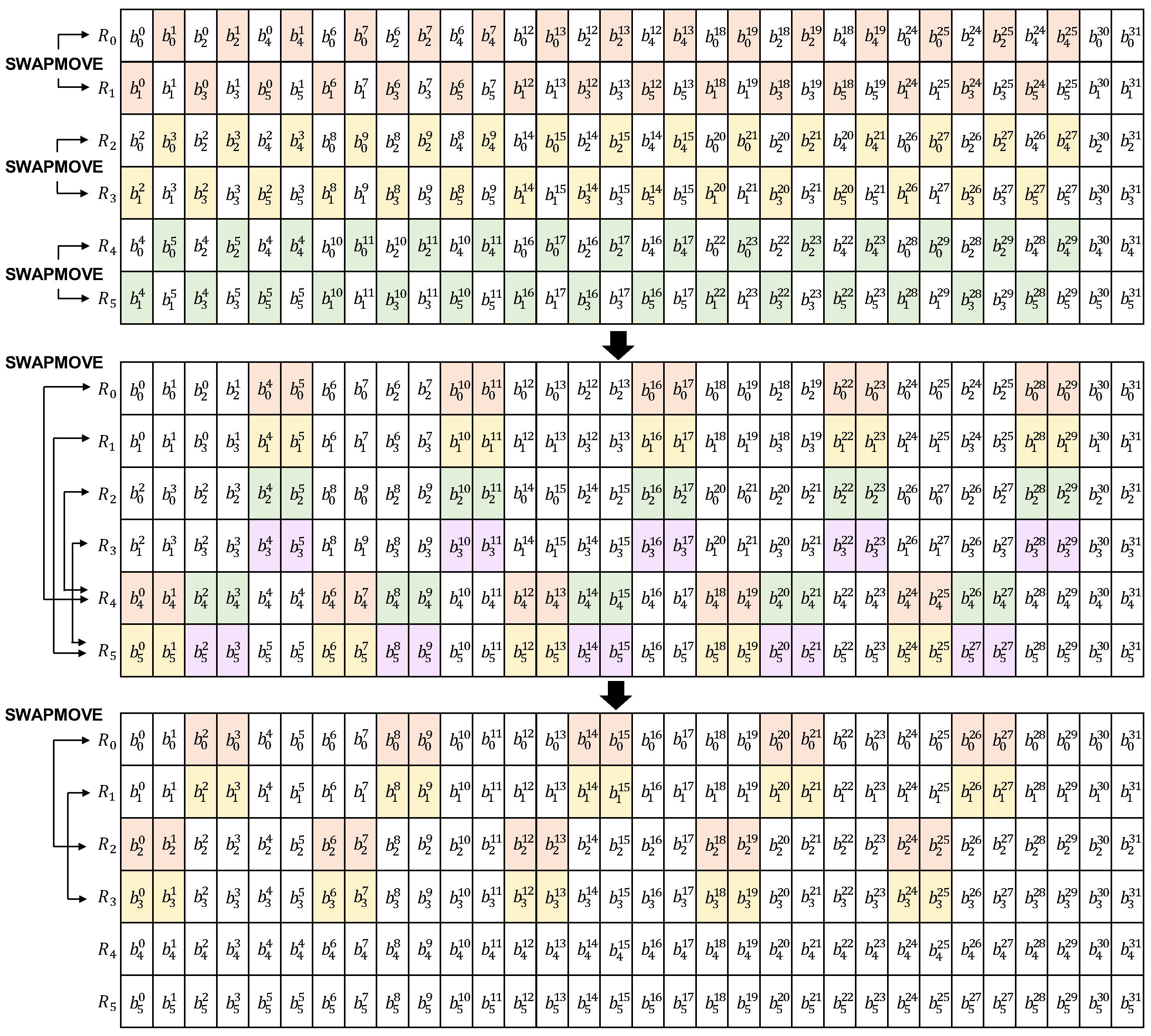
Finally, in Step 3, we use SWAPMOVE to sort by bit-slicing representation as shown in Figure 2. Initially, 15 bit exchanges are made at (R0, R1), (R2, R3), and (R4, R5). Next, 10 bit exchanges are made in the following order: (R0, R4), (R1, R5), (R2, R4), and (R3, R5). The last 10 bit exchange is done at (R0, R2) and (R1, R3).

3.4. SubBox

To implement bit-slicing, SubBox layer operations are performed by combining logical operators rather than lookup table methods. By combining logical operators, 32 blocks of 6 bits can be operated in parallel. The logical operator provided in [1] was used. We reduce the number of logical operations by using the rules of logical operators as shown in the following formula for efficient implementation. This saves 8 instructions in the SubBox layer.

$$\begin{array}{cc}\hfill & y_0=(x_3\wedge (\neg x_5\vee (x_4\wedge x_2))\vee (x_1\wedge ((\neg x_3\wedge x_0)\vee (x_5\wedge x_4))\hfill \\ \hfill & y_1=(x_5\wedge ((x_3\wedge \neg x_2)\vee (x_2\wedge x_0)))\vee (\neg x_5\wedge x_3\vee \neg x_4)\vee (\neg x_3\wedge \neg x_0\wedge x_1)\hfill \\ \hfill & y_2=(x_0\wedge ((\neg x_3\wedge x_4)\vee (x_3\wedge x_1)))\vee (\neg x_3\wedge \neg x_4\wedge x_2)\vee (\neg x_0\wedge \neg x_2\wedge x_5)\hfill \\ \hfill & y_3=(x_2\wedge ((\neg x_0\wedge \neg x_3)\vee (x_0\wedge x_4)))\vee (x_0\wedge \neg x_2\wedge x_5)\vee (\neg x_0\wedge x_3\wedge x_1)\hfill \\ \hfill & y_4=(x_0\wedge \neg x_3)\vee (\neg x_0\wedge x_4\wedge x_5)\vee ((\neg x_4\wedge \neg x_2)\wedge (x_0\vee x_1))\hfill \\ \hfill & y_5=(x_2\wedge (x_5\vee (x_1\wedge x_0)))\vee (\neg x_1\wedge ((\neg x_2\wedge x_4)\vee (x_0\wedge x_3)))\hfill \end{array}$$

For an efficient implementation, as in Algorithm 1, the ¬ operation and the $a\wedge \neg b$ operation are performed using the ORN instruction. For example, for $(x_3\wedge x_4\wedge x_2)\vee$ $(\neg x_3\wedge x_1\wedge x_0)$, we use the logical operator convention to use $(x_3\wedge x_4\wedge x_2)\vee$ $\neg \left(\right(x_3\vee$$\neg x_1)\vee$$\neg x_0)$

Algorithm 1 Bit-slicing implementations of S-box in ARMv6 assembly.
Input:X0-X5 (r4-r9),  temporal register T (r14)	28: ORN Y2, Y3, Y4
Output:Y0-Y5 (r1-r3, r10-r12)	29: AND Y3, X0, X4
	30: ORR Y4, X0, X3
1: AND Y3, X2, X4 2: ORN Y3, Y3, X5 3: AND Y3, Y3, X3 4: AND Y4, X5, X4 5: ORN Y5, X3, X0 6: ORN Y4, Y4, Y5 7: AND Y4, X1, Y4 8: ORR Y0, Y4, Y3	31: ORN Y3, Y3, Y4 32: AND Y3, Y3, X2 33: AND Y4, X0, X5 34: ORN Y4, X2, Y4 35: ORN Y3, Y3, Y4 36: AND Y4, X1, X3 37: ORN Y4, X0, Y4 38: ORN Y3, Y3, Y4
9: AND Y3, X0, X2 10: ORN Y4, X2, X3 11: ORN Y3, Y3, Y4 12: AND Y3, Y3, X5 13: ORR Y4, X5, X4 14: ORN Y4, Y4, X3 15: ORN Y3, Y3, Y4 16: ORR Y4, X0, X3 17: ORN Y4, Y4, X1 18: ORN Y1, Y3, Y4	39: MOV T, $\#s0$ 40: ORR Y4, X4, X2 41: ORR Y5, X0, X1 42: ORN Y4, Y4, Y5 43: ORN Y4, T, Y4 44: ORN Y5, X3, X0 45: ORN Y4, Y4, Y5 46: AND Y5, X4, X5 47: ORN Y5, X0, Y5 48: ORN Y4, Y4, Y5
19: AND Y3, X1, X3 20: ORN Y4, X3, X4 21: ORN Y3, Y3, Y4 22: AND Y3, X0, Y3 23: ORR Y4, X3, X4 24: ORN Y4, Y4, X2 25: ORN Y3, Y3, Y4 26: ORR Y4, X0, X2 27: ORR Y4, Y4, X5	49: AND T, X0, X3 50: ORN Y5, X2, X4 51: ORN T, T, Y5 52: ORN T, X1, T 53: AND Y5, X1, X0 54: ORR Y5, Y5, X5 55: AND Y5, Y5, X2 56: ORN Y5, Y5, T

3.5. ShiftColumns

In ShiftColumns, the bits in the block are shifted columnwise. A large-scale exchange of bits is performed between blocks. Since the software implementation is word-wise, it is expensive to handle the bit exchange in the classic representation. In the bit-slicing representation, the bits are converted into row-wise transposes because rows and columns are switched. This means that ShiftColumns can be changed from bit swapping to word rotation operations. So it can be implemented with a few rotation instructions. It can be implemented as Algorithm 2. Cortex-M3 can further optimize the operation. Using the Barrel Shifter of Cortex-M3, it can be implemented with 6 MOV instructions, like the assembly code of Algorithm 3. The value shifted after rotation to combine with the MC operation is stored in another register. Values stored in existing registers are reused in MC operations. The RV32I does not support barrel shifters, so a combination of SRLI, SLLI, and XOR instructions implements a rotation operation. Therefore, in RV32I, it is implemented using 6 rotation operations after one MOV instruction. Therefore, 19 commands are used.

Algorithm 2 Bit-slicing implementations of ShiftColumns.

Input:state[0-5] Output:state[0-5]   1:state[1] = (state[1] << 1) | (state[1] >> 31)   2:state[2] = (state[2] << 2) | (state[2] >> 30)   3:state[3] = (state[3] << 3) | (state[3] >> 29)   4:state[4] = (state[4] << 4) | (state[4] >> 28)   5:state[5] = (state[5] << 5) | (state[5] >> 27)

Algorithm 3 Bit-slicing implementations of ShiftColumns in ARMv6 assembly.
Input:X0-X5 (r1-r3, r10-r12)	3: MOV Y2, X2, ROR $\#30$
Output:Y0-Y5 (r4-r9)	4: MOV Y3, X3, ROR $\#29$
1: MOV Y0, X0	5: MOV Y4, X4, ROR $\#28$
2: MOV Y1, X1, ROR $\#31$	6: MOV Y5, X5, ROR $\#27$

3.6. MixColumns

In a bit-slicing implementation, MixColumns swaps rows and columns, so we rotate each row by $alpha(1,5,9,15,21,26)$ and do an XOR as shown below.

$$\begin{array}{cc}\hfill & y\left[i\right]=x\left[i\right]\oplus (x\left[i\right]<<<a_0)\oplus (x\left[i\right]<<<a_1)\oplus (x\left[i\right]<<<a_2)\hfill \\ \hfill & \oplus (x\left[i\right]<<<a_3)\oplus (x\left[i\right]<<<a_4)\oplus (x\left[i\right]<<<a_5)\hfill \end{array}$$

The classic implementation is more efficient because it requires 6 × 32 XOR operations, while the bit-slicing implementation requires 6 × 6 XOR operations. In particular, Cortex-M3 can process rotation and XOR operations together like Algorithm 4 if a barrel-shifter is used. Each row rotates by $alpha(1,5,9,15,21,26)$ and XORs the result of the previous SC process with the stored register. The operation of MixColumns can be processed with 36 XOR instructions. Since RV32I does not support barrel shift, a total of 144 instructions are used, a rotation operation that combines SRLI, SLLI operation, and XOR operation.

Algorithm 4 Bit-slicing implementations MixColumns in ARMv6 assembly.
Input:X0-X5 (r1-r3, r10-r12),	18: EOR Y2, Y2, X2, ROR $\#4$
Y0-Y5 (r4-r9)
Output:Y0-Y5 (r4-r9)	19: EOR Y3, Y3, X3, ROR $\#28$
	20: EOR Y3, Y3, X3, ROR $\#24$
1: EOR Y0, Y0, X0, ROR $\#31$ 2:EOR Y0, Y0, X0, ROR $\#27$ 3:EOR Y0, Y0, X0, ROR $\#23$ 4:EOR Y0, Y0, X0, ROR $\#17$	21: EOR Y3, Y3, X3, ROR $\#20$ 22: EOR Y3, Y3, X3, ROR $\#14$ 23:EOR Y3, Y3, X3, ROR $\#8$ 24: EOR Y3, Y3, X3, ROR $\#3$
5: EOR Y0, Y0, X0, ROR $\#11$
6: EOR Y0, Y0, X0, ROR $\#6$	25: EOR Y4, Y4, X4, ROR $\#27$
	26: EOR Y4, Y4, X4, ROR $\#23$
7: EOR Y1, Y1, X1, ROR $\#30$ 8: EOR Y1, Y1, X1, ROR $\#26$ 9: EOR Y1, Y1, X1, ROR $\#22$ 10: EOR Y1, Y1, X1, ROR $\#16$	27: EOR Y4, Y4, X4, ROR $\#19$ 28:EOR Y4, Y4, X4, ROR $\#13$ 29: EOR Y4, Y4, X4, ROR $\#7$ 30: EOR Y4, Y4, X4, ROR $\#2$
11: EOR Y1, Y1, X1, ROR $\#10$
12: EOR Y1, Y1, X1, ROR $\#5$	31: EOR Y5, Y5, X5, ROR $\#26$
	32: EOR Y5, Y5, X5, ROR $\#22$
13: EOR Y2, Y2, X2, ROR $\#29$ 14: EOR Y2, Y2, X2, ROR $\#25$ 15: EOR Y2, Y2, X2, ROR $\#21$ 16: EOR Y2, Y2, X2, ROR $\#15$ 17: EOR Y2, Y2, X2, ROR $\#9$	33: EOR Y5, Y5, X5, ROR $\#18$ 34: EOR Y5, Y5, X5, ROR $\#12$ 35: EOR Y5, Y5, X5, ROR $\#6$ 36: EOR Y5, Y5, X5, ROR $\#1$

3.7. AddRoundKey and AddRoundConstant

AddRoundConstant can be preprocessed by XORing AddRoundKey and key schedule. AddRoundKey and AddRoundConstant are XORed, packed into a bit-slicing representation, and XORed in the AR layer. Both Cortex-m3 and RV31I are implemented using load and XOR 6, respectively.

4. Evaluation

In this section, we compare the results for our implementation. Implementation on ARM Cortex-M3 processor is developed with Arduino IDE on ArduinoDUE (AT91SAM3X8E) development board. The operating clock is 84 MHz, and it has 512 KB of flash memory and 96 KB of RAM. Performance comparisons are measured through average cycles in encryption in ECB mode. Key scheduling is not taken into account, as round keys are assumed to be precomputed and stored in RAM. To confirm that our bit-slicing implementation has higher performance in the 32-bit embedded environment, we compare it with the reference code of the previous implementation [1]. In addition, the bit-slicing implementation of SPEEDY is compared with other constant-time implementation ciphers to check its competitiveness compared to other ciphers.

Comparison with GIFT, which achieved high performance on 32-bit ARM with the fastest constant implementation of the most popular block cipher AES and Fixslicing technique. Both ciphers could be compared in the same environment because the source code of the fastest implementation was released. Since SPEEDY encrypts 192-bit blocks, the performance difference was compared based on cycle per byte (cpb) for fair comparison. We implemented SPEEDY-5-192, SPEEDY-6-192 and SPEEDY-7-192. Reference implementation and AES-128 and GIFT-128 were compared in the same environment. The result is shown in

Table 3. Comparison of SPEEDY implementation results and various constant-time implementation results on ARM Cortex-M3 and RISC-V. The performance is evaluated in clock cycles per byte (cpb).

ARM Cortex-M3	Speed (cpb)	Block Size	Parallel Blocks
GIFT-128 encryption [9]	104.1	128	1
AES-128 encryption [19]	120.4	128	2
SPEEDY-7-192 encryption (reference)	15,407	192	1
SPEEDY-5-192 encryption (ours)	65.7	192	1
SPEEDY-6-192 encryption (ours)	75.2	192	1
SPEEDY-7-192 encryption (ours)	85.1	192	1
RISC-V	Speed (cpb)	Block Size	Parallel Blocks
AES-128 encryption [19]	78.9	128	8
SPEEDY-7-192 encryption (reference)	18,096	192	1
SPEEDY-5-192 encryption (ours)	81.9	192	1
SPEEDY-6-192 encryption (ours)	95.5	192	1
SPEEDY-7-192 encryption (ours)	109.2	192	1

. Comparing the SPEEDY-7-192 with our implementation and the reference C implementation, there was a huge speed difference of about 180×. In addition, when comparing our implemented SPEEDY-6-192 with the same security level AES-128 and GIFT-128, the result of 75.2 cpb was 1.6× faster than 120.4 cpb of AES-128 and 1.3× faster than 104.1 cpb of GIFT-128. Considering that SPEEDY is designed to be hardware-friendly, this is a remarkable result.

Implementation on RV32I RISC-V processor was developed with SiFive Freedom Studio RISC-V IDE on HiFive1 Rev B (FE310-G002) development board. The operating clock is 320 MHz, and it has 16 MB of flash memory and 16 KB of RAM. Performance comparison measured the average cycle when encrypting. Key scheduling is not taken into account, as it is assumed that round keys are pre-computed and stored in RAM. We implemented SPEEDY-5-192, SPEEDY-6-192, and SPEEDY-7-192. AES-128 implemented in constant time in the same environment were compared. Similar to the ARM Cortex-M3, it showed a noticeable performance improvement. As shown in Table 3, compared to the reference C implementation of SPEEDY-7-192, the speed difference was about 165×. Similar to the ARM Cortex-M3, it showed a noticeable performance improvement. However, when comparing the implemented SPEEDY-6-192 with the same security level AES-128, it is 1.2× slower than the result of 78.9 cpb for AES-128. It can be seen that our SPEEDY bit-slicing implementation is very efficient on a 32-bit microcontroller.

5. Conclusions

By applying bit-slicing implementation technology, we implemented SPEEDY on a low-cost microcontroller. For performance comparison, we measure the speed of encryption on ARM Cortex-M3 and RISC-V (RV32I). On ARM Cortex-M3, SPEEDY-5-192, SPEEDY-6-192 and SPEEDY-7-192 achieved 65.7 cpb, 75.25 cpb and 85.16 cpb, respectively. In the same environment, it showed better performance with 120.4 cpb for GIFT-128 and 104.1 cpb for AES-128 in on-time implementation. In RISC-V (RV32I), SPEEDY-5-192, SPEEDY-6-192, and SPEEDY-7-192 achieved 81.9 cpb, 95.5 cpb, and 109.2 cpb, respectively. This showed that SPEEDY can be run very efficiently in software and can be applied specifically to microcontrollers. The proposed implementation works with constant timing, which is advantageous for timing attacks. Our first proposed implementation of bit-slicing SPEEDY can be used as a reference for other processor implementations. In future research, we plan to apply an efficient masking technique for additional side-channel security.