Formation Control with Connectivity Assurance for Missile Swarms by a Natural Co-Evolutionary Strategy
Abstract
:1. Introduction
2. Preliminaries and Problem Formulation
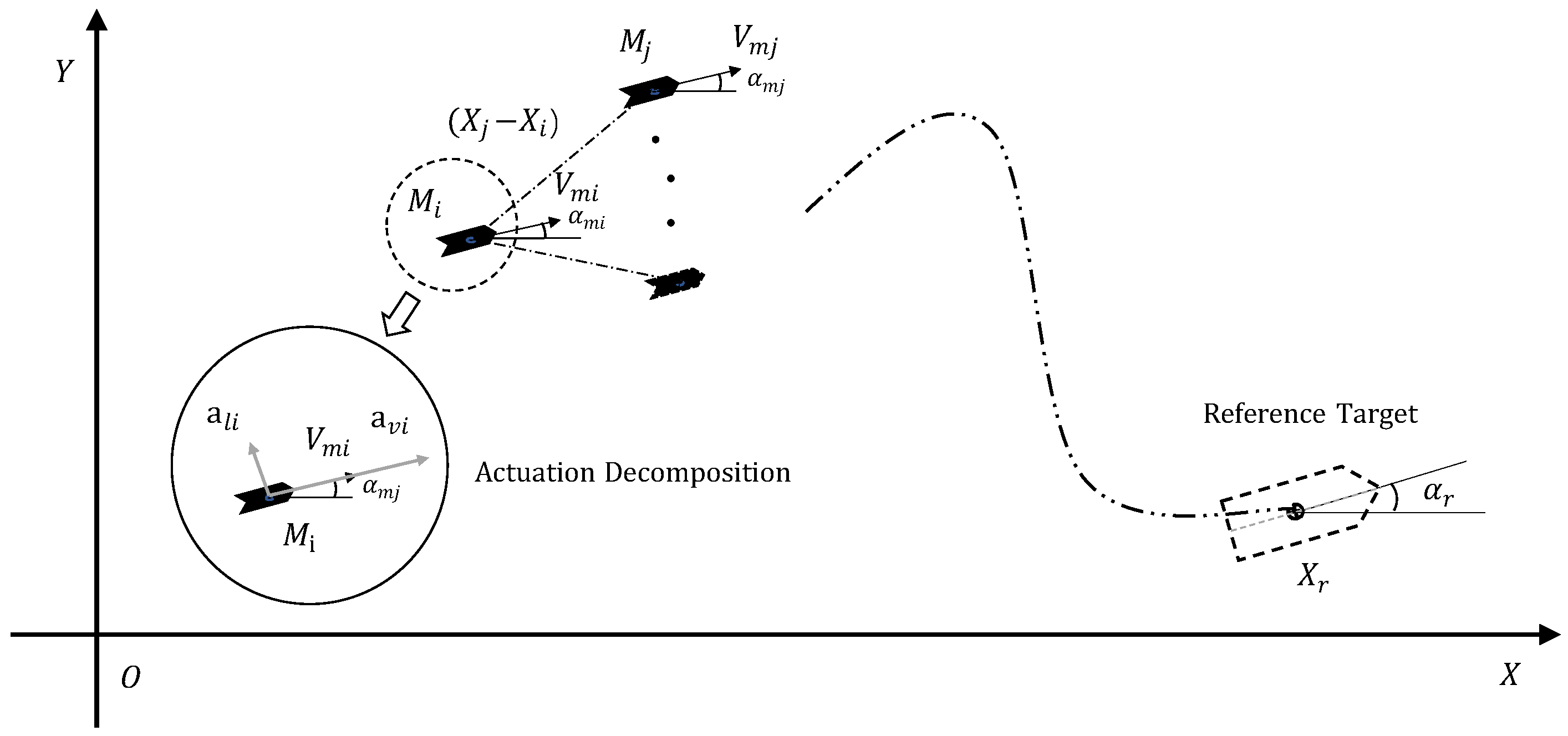
2.1. System Modeling of a Swarm of Cruise Missiles
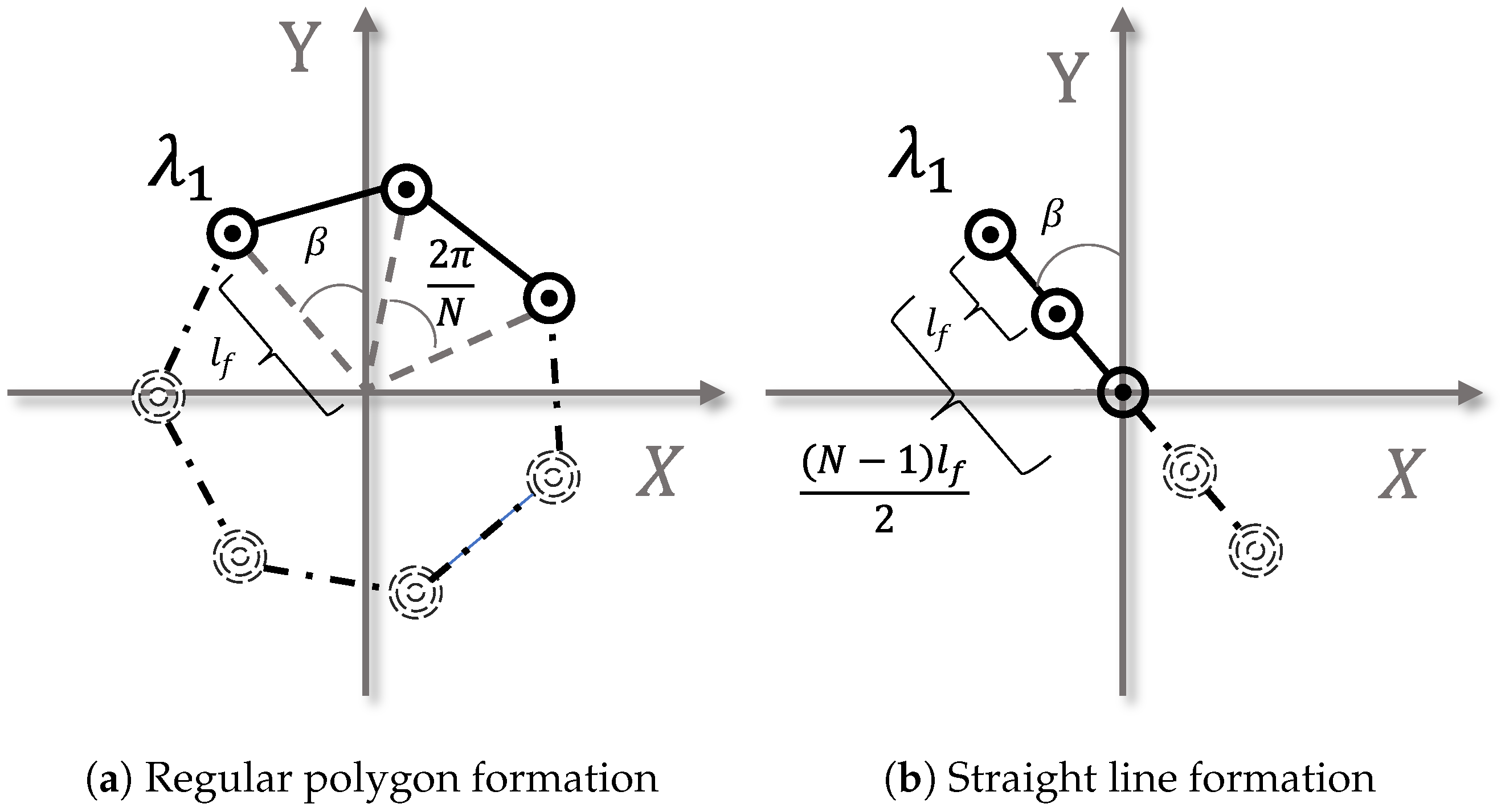
2.2. Formation Control under Displacement-Based Framework
3. Applying Natural Co-Evolutionary Strategy to Formation Control via Neural Networks
3.1. Natural Co-Evolutionary Strategy for MASs
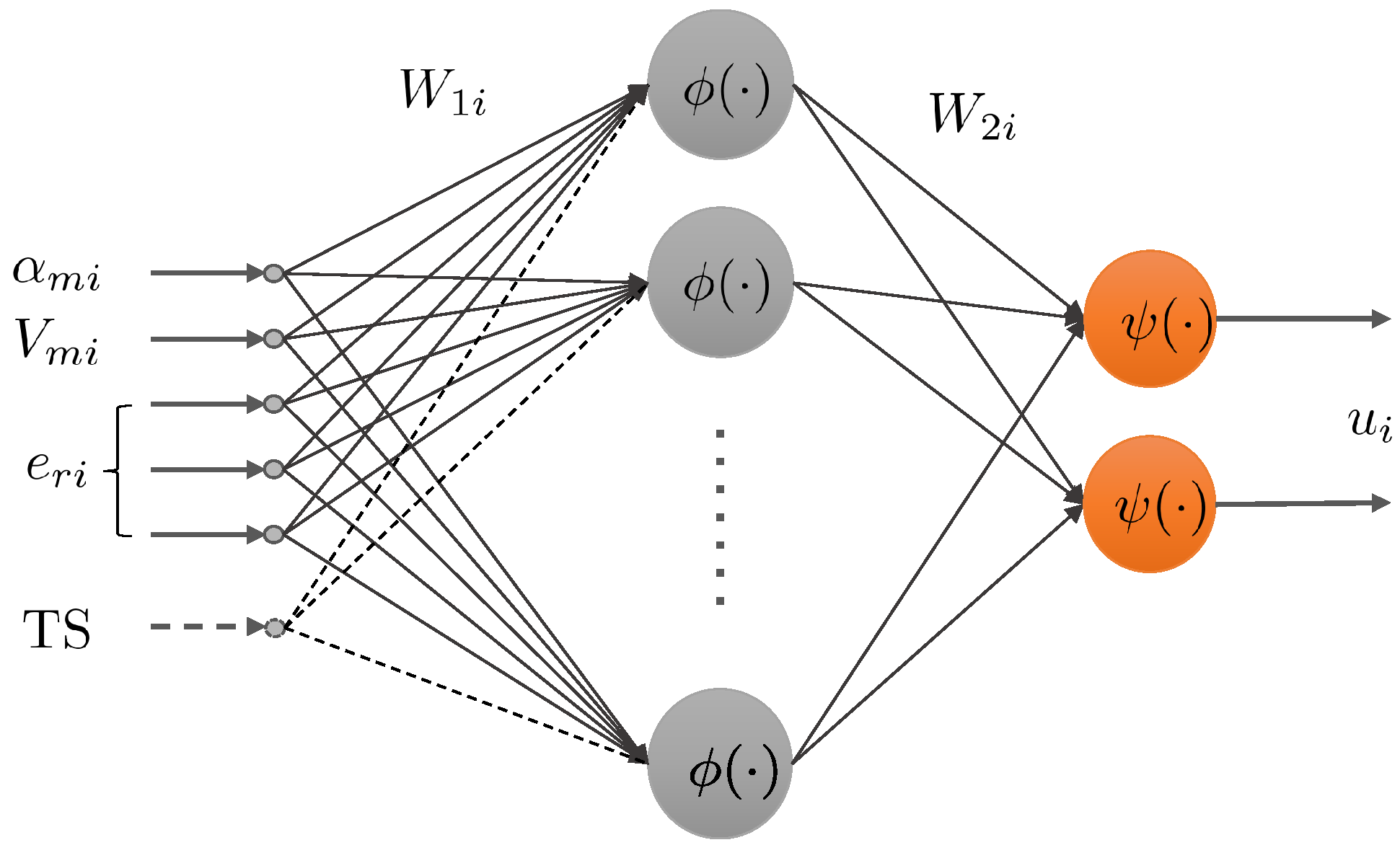
3.2. Distributed Co-Evolutionary Strategy Optimizing a Neural Network Controller
3.3. Population Adaptation Technique
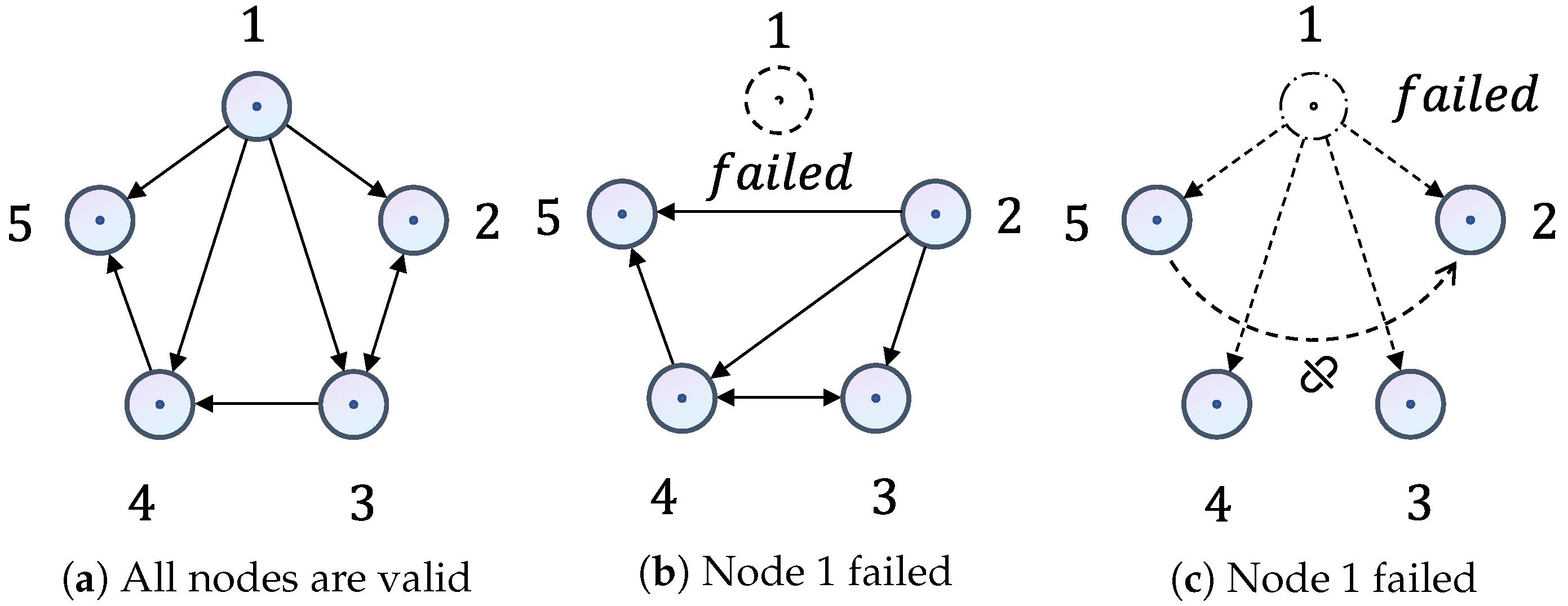
3.4. Cluster-Based Adaptive Topology
3.5. Model-Based Constrained Policy
| Algorithm 1 The distributed NCES based formation control algorithm. |
| Input: agent number N, population size , standard deviation , rotation angle , evolution path , number of parameters m, iteration t |
|
| Algorithm 2 Adapt population size (). |
|
4. Simulation and Result Analysis
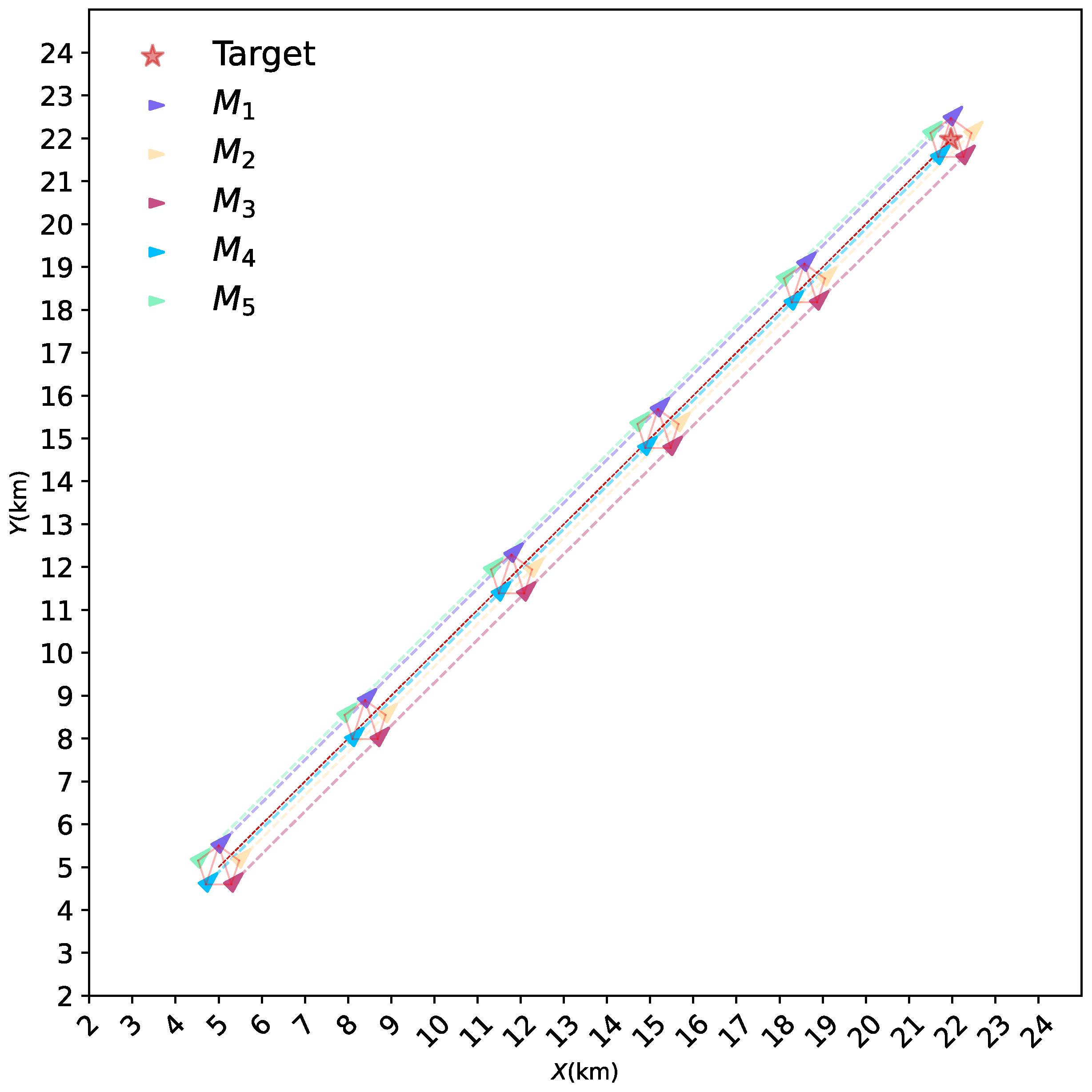
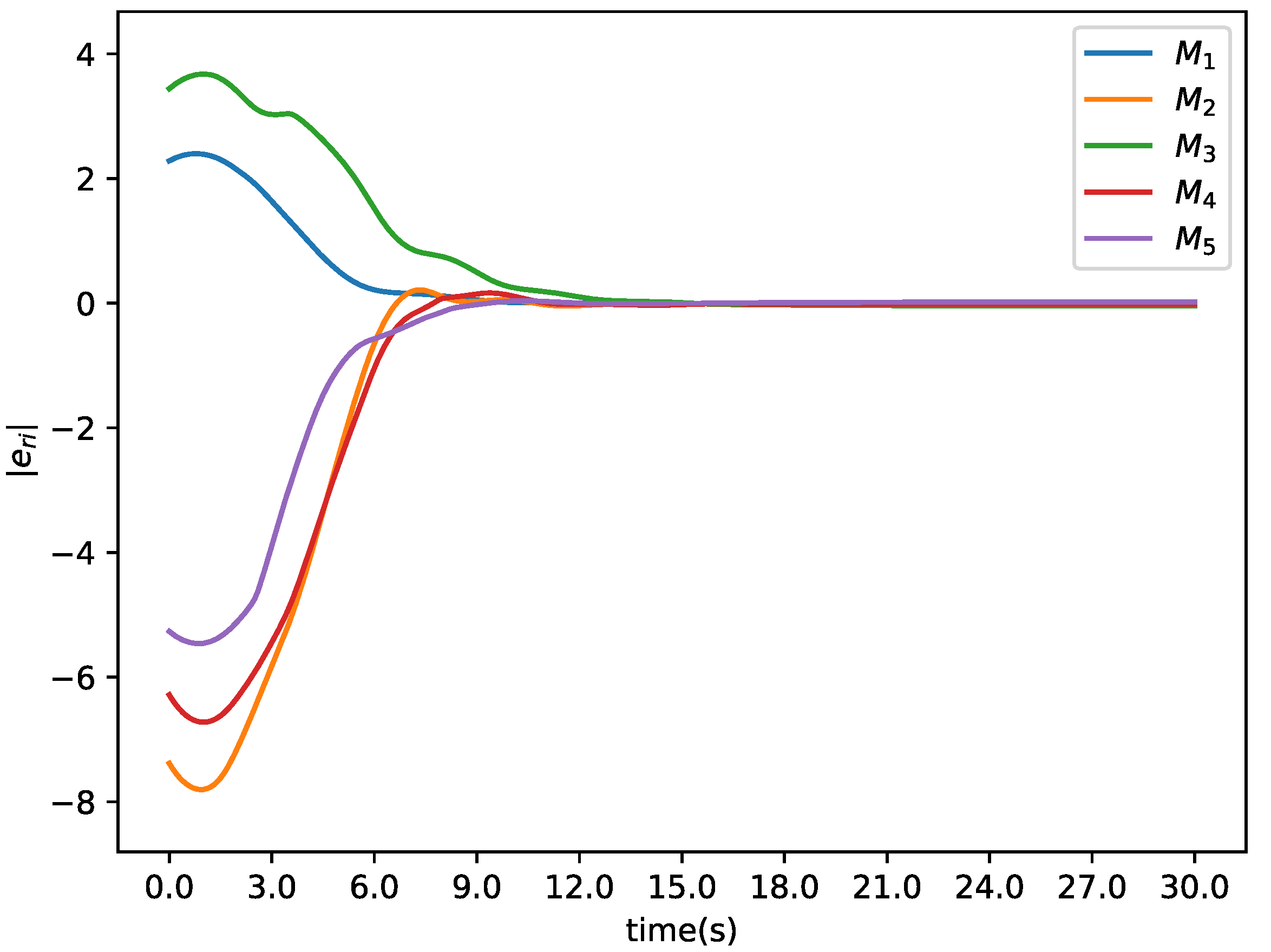
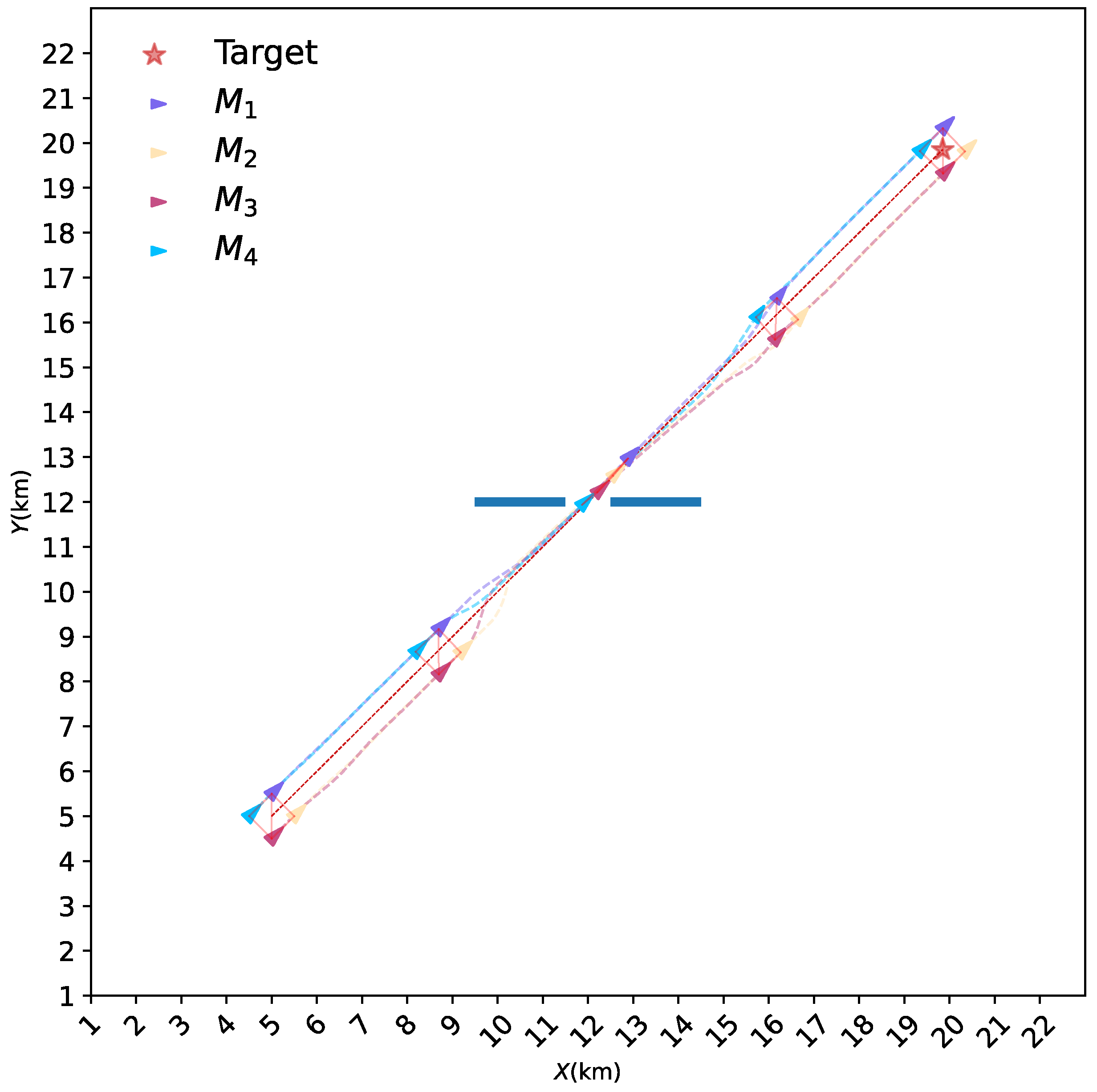
4.1. Basic Formation Control
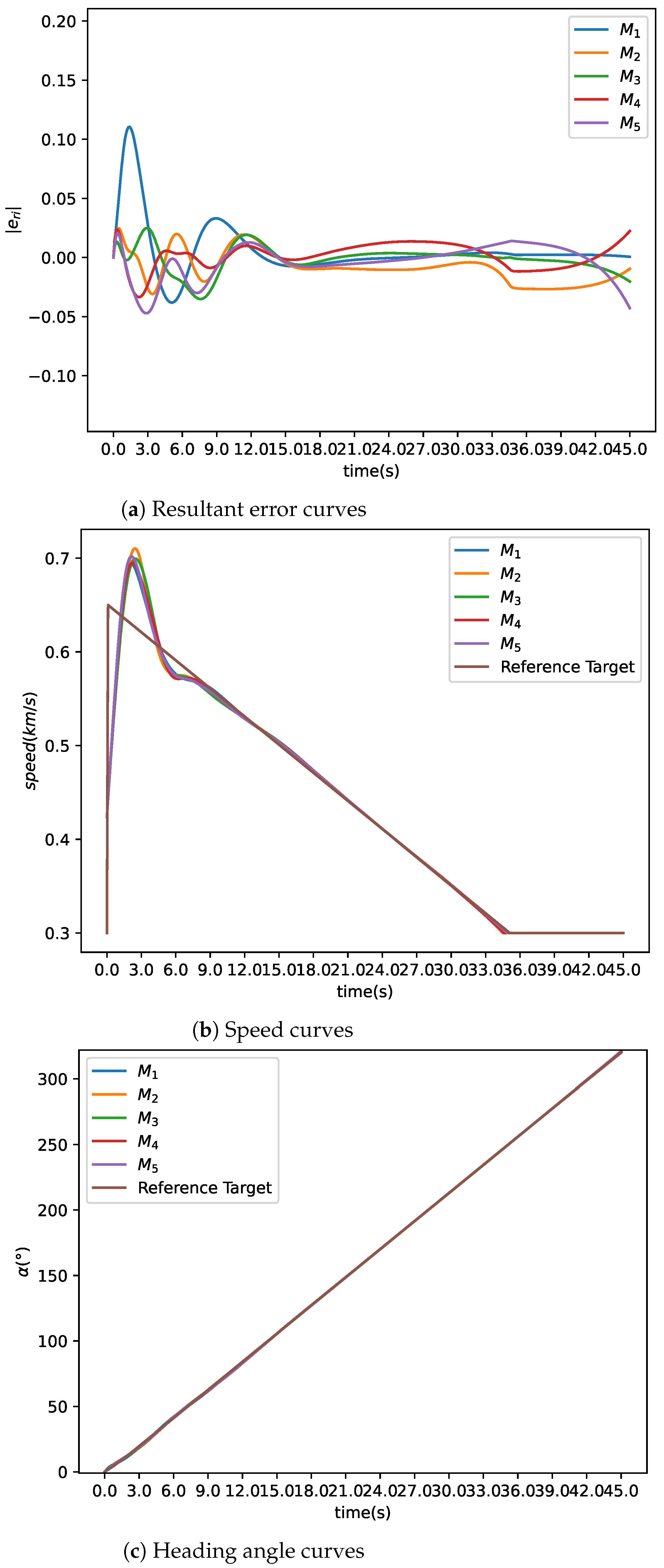
4.2. Moving into Formation
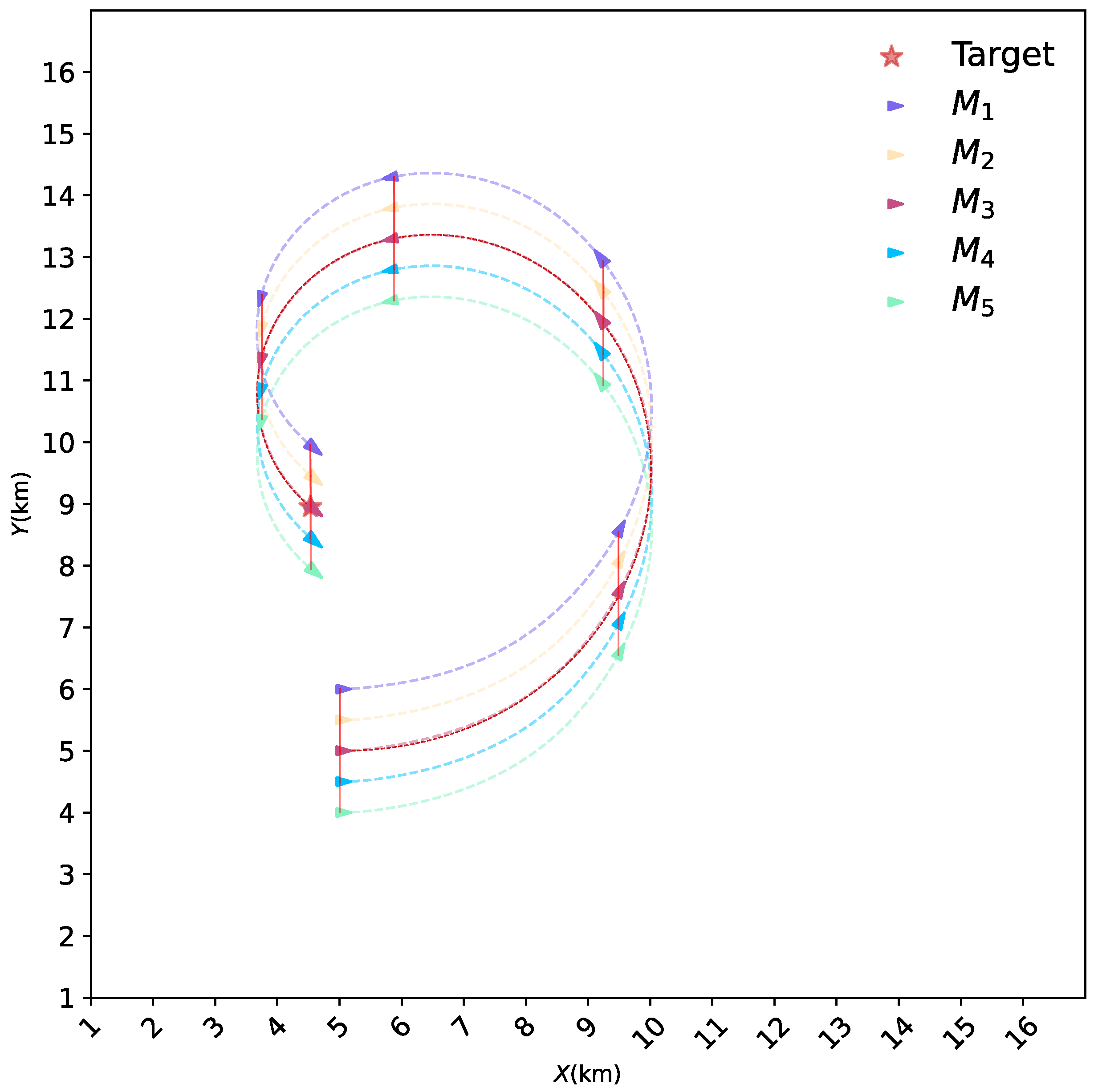
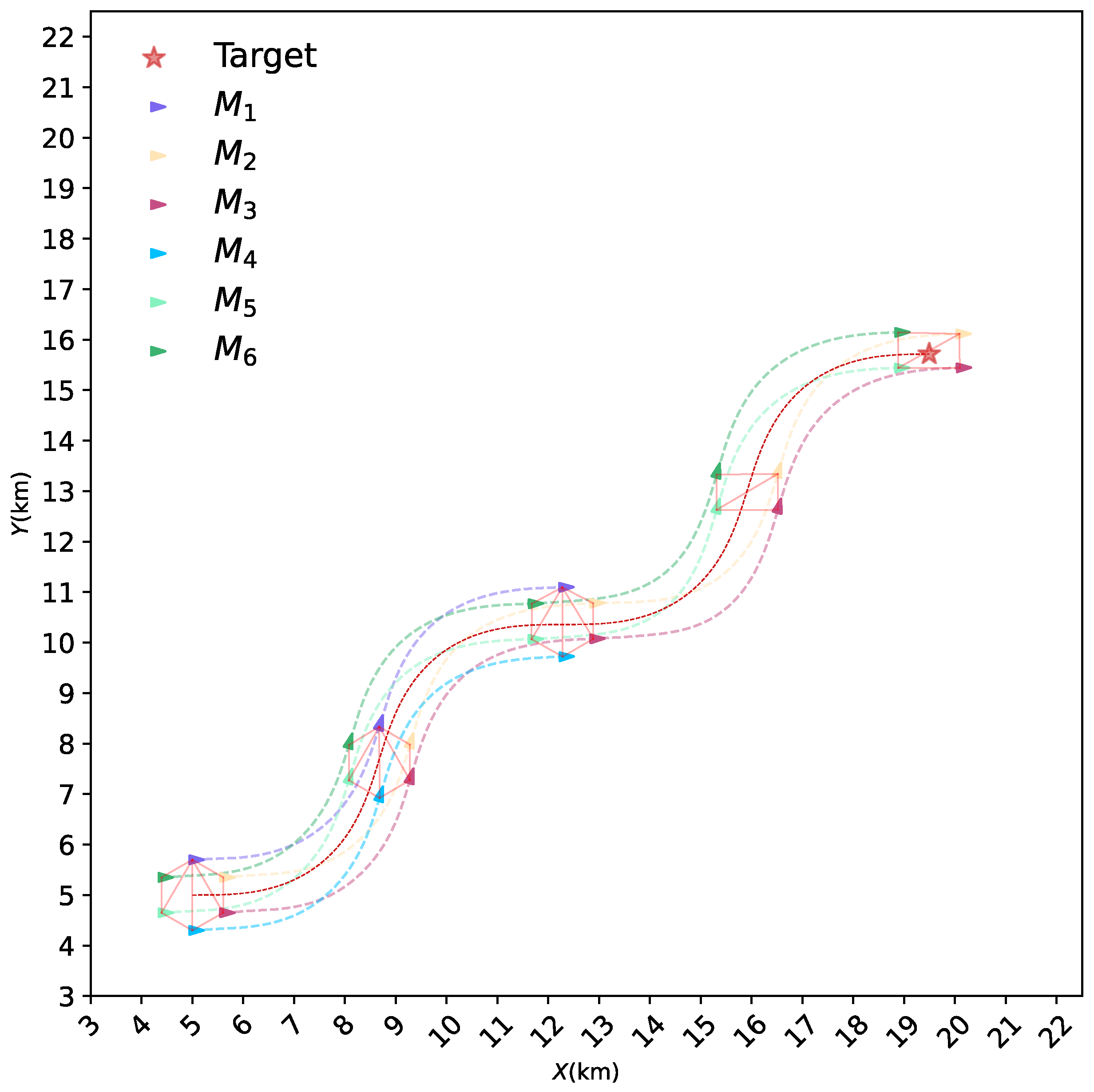
4.3. Switching Formations
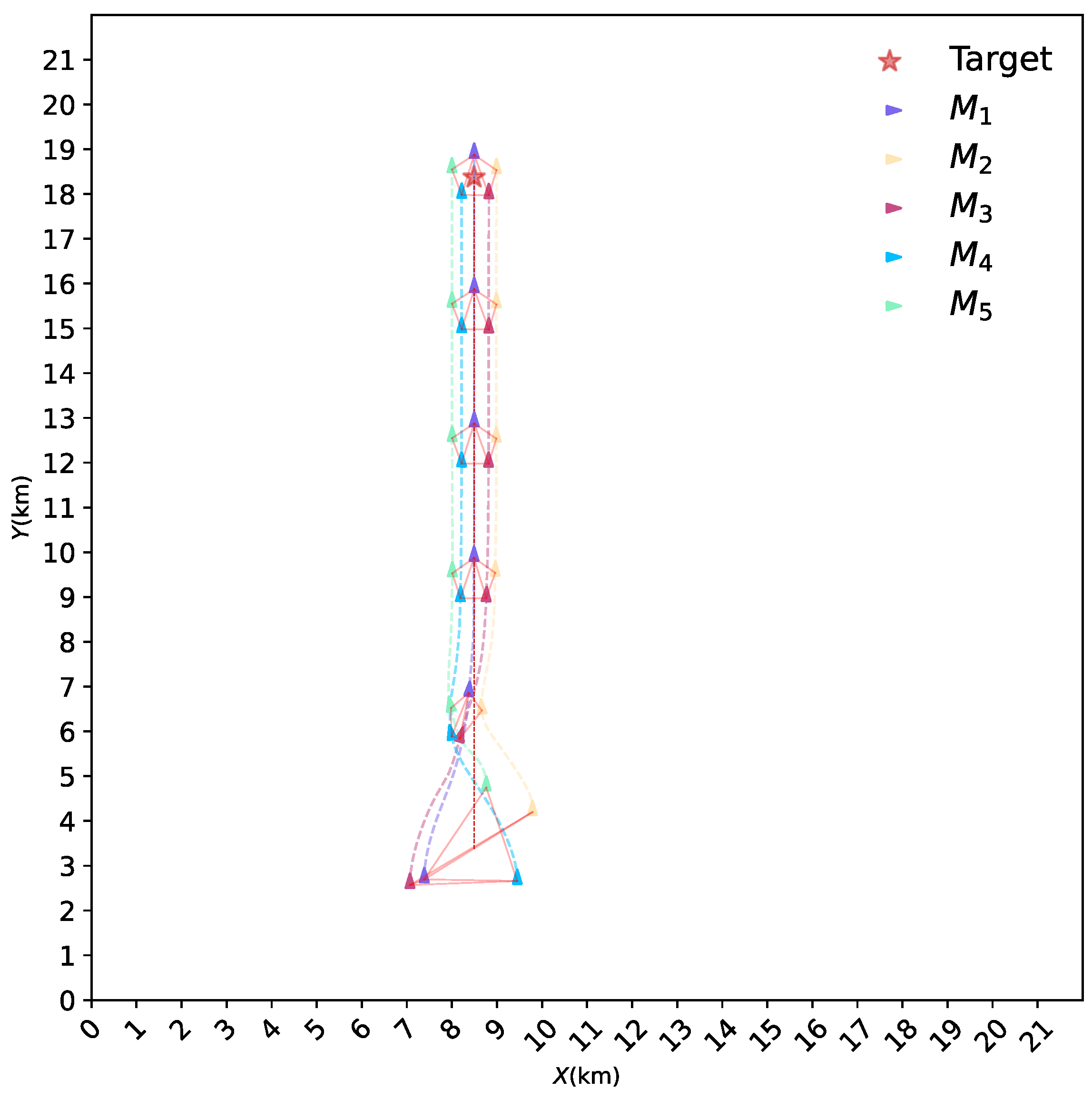
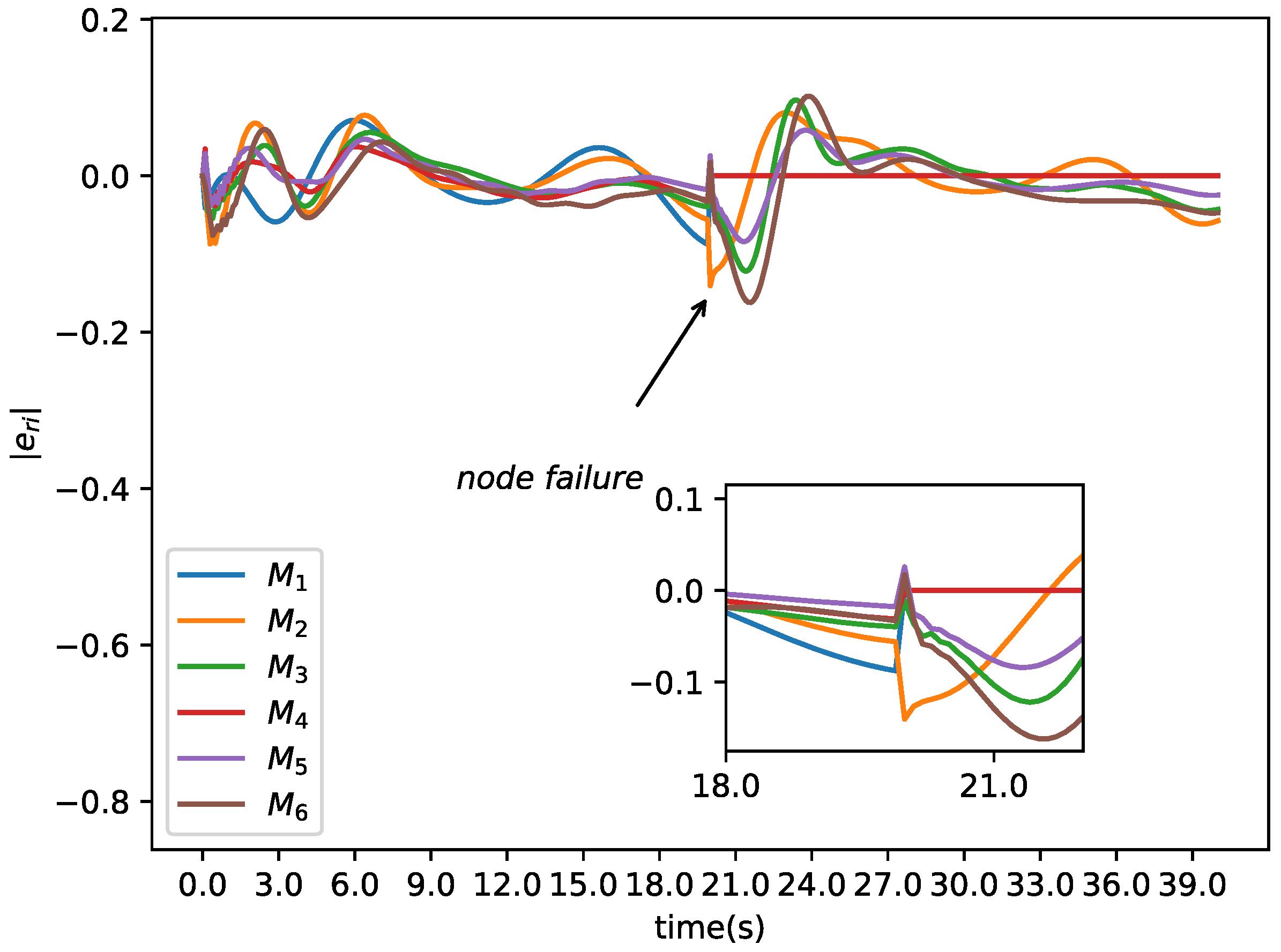
4.4. Formation Control under Node Failure
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lim, H.; Yeonsik, K.; Kim, J.; Kim, C. Formation Control of Leader Following Unmanned Ground Vehicles Using Nonlinear Model Predictive Control. In Proceedings of the 2009 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Singapore, 14–17 July 2009; pp. 945–950. [Google Scholar] [CrossRef]
- Shi, P.; Yan, B. A Survey on Intelligent Control for Multiagent Systems. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 161–175. [Google Scholar] [CrossRef]
- Reynolds, C.W. Flocks, Herds, and Schools: A Distributed Behavioral Model. In SIGGRAPH ’87: Proceedings of the 14th Annual Conference on Computer Graphics and Interactive Techniques; Association for Computing Machinery: New York, NY, USA, 1987; p. 10. [Google Scholar]
- Cui, N.; Wei, C.; Guo, J.; Zhao, B. Research on Missile Formation Control System. In Proceedings of the 2009 International Conference on Mechatronics and Automation, Changchun, China, 9–12 August 2009; pp. 4197–4202. [Google Scholar] [CrossRef]
- Ren, W.; Cao, Y. Distributed Coordination of Multi-Agent Networks; Communications and Control Engineering; Springer: London, UK, 2011. [Google Scholar] [CrossRef]
- Oh, K.K.; Park, M.C.; Ahn, H.S. A Survey of Multi-Agent Formation Control. Automatica 2015, 53, 424–440. [Google Scholar] [CrossRef]
- Marshall, J.; Broucke, M.; Francis, B. Formations of Vehicles in Cyclic Pursuit. IEEE Trans. Autom. Control 2004, 49, 1963–1974. [Google Scholar] [CrossRef]
- Asaamoning, G.; Mendes, P.; Rosário, D.; Cerqueira, E. Drone Swarms as Networked Control Systems by Integration of Networking and Computing. Sensors 2021, 21, 2642. [Google Scholar] [CrossRef]
- Shrit, O.; Martin, S.; Alagha, K.; Pujolle, G. A New Approach to Realize Drone Swarm Using Ad-Hoc Network. In Proceedings of the 2017 16th Annual Mediterranean Ad Hoc Networking Workshop (Med-Hoc-Net), Budva, Montenegro, 28–30 June 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Chen, W.; Liu, J.; Guo, H.; Kato, N. Toward Robust and Intelligent Drone Swarm: Challenges and Future Directions. IEEE Netw. 2020, 34, 278–283. [Google Scholar] [CrossRef]
- Slotine, J.J.E.; Li, W. Applied Nonlinear Control; Prentice Hall: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]
- Wu, Y. A Survey on Population-Based Meta-Heuristic Algorithms for Motion Planning of Aircraft. Swarm Evol. Comput. 2021, 62, 100844. [Google Scholar] [CrossRef]
- Liu, S.; Huang, F.; Yan, B.; Zhang, T.; Liu, R.; Liu, W. Optimal Design of Multimissile Formation Based on an Adaptive SA-PSO Algorithm. Aerospace 2021, 9, 21. [Google Scholar] [CrossRef]
- Lee, S.M.; Kim, H.; Myung, H.; Yao, X. Cooperative Coevolutionary Algorithm-Based Model Predictive Control Guaranteeing Stability of Multirobot Formation. IEEE Trans. Control Syst. Technol. 2015, 23, 37–51. [Google Scholar] [CrossRef]
- Pessin, G.; Osório, F.; Hata, A.Y.; Wolf, D.F. Intelligent Control and Evolutionary Strategies Applied to Multirobotic Systems. In Proceedings of the 2010 IEEE International Conference on Industrial Technology, Via del Mar, Chile, 14–17 March 2010; pp. 1427–1432. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Nguyen, N.D.; Nahavandi, S. Deep Reinforcement Learning for Multiagent Systems: A Review of Challenges, Solutions, and Applications. IEEE Trans. Cybern. 2020, 50, 3826–3839. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Zhu, D. An Adaptive SOM Neural Network Method for Distributed Formation Control of a Group of AUVs. IEEE Trans. Ind. Electron. 2018, 65, 8260–8270. [Google Scholar] [CrossRef]
- Barreto, G.; Araujo, A. Identification and Control of Dynamical Systems Using the Self-Organizing Map. IEEE Trans. Neural Networks 2004, 15, 1244–1259. [Google Scholar] [CrossRef]
- Zhang, H.; Jiang, H.; Luo, Y.; Xiao, G. Data-Driven Optimal Consensus Control for Discrete-Time Multi-Agent Systems With Unknown Dynamics Using Reinforcement Learning Method. IEEE Trans. Ind. Electron. 2017, 64, 4091–4100. [Google Scholar] [CrossRef]
- Tanaka, T.; Moriya, T.; Shinozaki, T.; Watanabe, S.; Hori, T.; Duh, K. Automated Structure Discovery and Parameter Tuning of Neural Network Language Model Based on Evolution Strategy. In Proceedings of the 2016 IEEE Spoken Language Technology Workshop (SLT), San Diego, CA, USA, 13–16 December 2016; pp. 665–671. [Google Scholar] [CrossRef]
- Vidnerová, P.; Neruda, R. Evolution Strategies for Deep Neural Network Models Design. Ceur Workshop Proc. 2017, 1885, 159–166. [Google Scholar]
- Wang, X.; Yadav, V.; Balakrishnan, S.N. Cooperative UAV Formation Flying With Obstacle/Collision Avoidance. IEEE Trans. Control Syst. Technol. 2007, 15, 672–679. [Google Scholar] [CrossRef]
- Vasile, M.; Minisci, E.; Locatelli, M. Analysis of Some Global Optimization Algorithms for Space Trajectory Design. J. Spacecr. Rocket. 2010, 47, 334–344. [Google Scholar] [CrossRef]
- Hughes, E. Multi-Objective Evolutionary Guidance for Swarms. In Proceedings of the 2002 Congress on Evolutionary Computation, CEC’02 (Cat. No.02TH8600). Honolulu, HI, USA, 12–17 May 2002; Volume 2, pp. 1127–1132. [Google Scholar] [CrossRef]
- Lan, X.; Wu, Z.; Xu, W.; Liu, G. Adaptive-Neural-Network-Based Shape Control for a Swarm of Robots. Complexity 2018, 2018, 8382702. [Google Scholar] [CrossRef]
- Fei, Y.; Shi, P.; Lim, C.C. Neural Network Adaptive Dynamic Sliding Mode Formation Control of Multi-Agent Systems. Int. J. Syst. Sci. 2020, 51, 2025–2040. [Google Scholar] [CrossRef]
- Ni, J.; Shi, P. Adaptive Neural Network Fixed-Time Leader–Follower Consensus for Multiagent Systems With Constraints and Disturbances. IEEE Trans. Cybern. 2021, 51, 1835–1848. [Google Scholar] [CrossRef]
- Yang, S.; Bai, W.; Li, T.; Shi, Q.; Yang, Y.; Wu, Y.; Chen, C.L.P. Neural-Network-Based Formation Control with Collision, Obstacle Avoidance and Connectivity Maintenance for a Class of Second-Order Nonlinear Multi-Agent Systems. Neurocomputing 2021, 439, 243–255. [Google Scholar] [CrossRef]
- Lan, X.; Liu, Y.; Zhao, Z. Cooperative Control for Swarming Systems Based on Reinforcement Learning in Unknown Dynamic Environment. Neurocomputing 2020, 410, 410–418. [Google Scholar] [CrossRef]
- Chen, J.; Lan, X.; Zhao, Z.; Zou, T. Cooperative Guidance of Multiple Missiles: A Hybrid Co-Evolutionary Approach. arXiv 2022, arXiv:2208.07156. [Google Scholar]
- Xingguang, X.; Zhenyan, W.; Zhang, R.; Shusheng, L. Time-Varying Fault-Tolerant Formation Tracking Based Cooperative Control and Guidance for Multiple Cruise Missile Systems under Actuator Failures and Directed Topologies. J. Syst. Eng. Electron. 2019, 30, 587–600. [Google Scholar] [CrossRef]
- Wei, C.; Shen, Y.; Ma, X.; Guo, J.; Cui, N. Optimal Formation Keeping Control in Missile Cooperative Engagement. Aircr. Eng. Aerosp. Technol. 2012, 84, 376–389. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, K.; Han, Z. A Novel Cooperative Control System of Multi-Missile Formation Under Uncontrollable Speed. IEEE Access 2021, 9, 9753–9770. [Google Scholar] [CrossRef]
- Aicardi, M.; Casalino, G.; Bicchi, A.; Balestrino, A. Closed Loop Steering of Unicycle like Vehicles via Lyapunov Techniques. IEEE Robot. Autom. Mag. 1995, 2, 27–35. [Google Scholar] [CrossRef]
- Dinesh, K.; Vijaychandra, J.; SeshaSai, B.; Vedaprakash, K.; Srinivasa, R.K. A Review on Cascaded Linear Quadratic Regulator Control of Roll Autopilot Missile. 2021. Available online: https://doi.org/10.2139/ssrn.3768344 (accessed on 1 January 2020).
- Ren, W. Consensus Strategies for Cooperative Control of Vehicle Formations. IET Control Theory Appl. 2007, 1, 505–512. [Google Scholar] [CrossRef]
- Das, A.; Fierro, R.; Kumar, V.; Ostrowski, J.; Spletzer, J.; Taylor, C. A Vision-Based Formation Control Framework. IEEE Trans. Robot. Autom. 2002, 18, 813–825. [Google Scholar] [CrossRef] [Green Version]
- Lewis, M.A.; Tan, K.H. High Precision Formation Control of Mobile Robots Using Virtual Structures. Auton. Robot. 1997, 4, 387–403. [Google Scholar] [CrossRef]
- Sefrioui, M.; Perlaux, J. Nash Genetic Algorithms: Examples and Applications. In Proceedings of the 2000 Congress on Evolutionary Computation. CEC00 (Cat. No.00TH8512), La Jolla, CA, USA, 16–19 July 2000; Volume 1, pp. 509–516. [Google Scholar] [CrossRef]
- Nishida, K.; Akimoto, Y. PSA-CMA-ES: CMA-ES with Population Size Adaptation. In Proceedings of the Genetic and Evolutionary Computation Conference, Kyoto, Japan, 15–19 July 2018; pp. 865–872. [Google Scholar] [CrossRef]
- Nomura, M.; Ono, I. Towards a Principled Learning Rate Adaptation for Natural Evolution Strategies. In Applications of Evolutionary Computation, Proceedings of the 25th European Conference, EvoApplications 2022, Held as Part of EvoStar 2022, Madrid, Spain, 20–22 April 2022; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Glasmachers, T.; Schaul, T.; Yi, S.; Wierstra, D.; Schmidhuber, J. Exponential Natural Evolution Strategies. In Proceedings of the 12th Annual Conference on Genetic and Evolutionary Computation (GECCO ’10), Portland, OR, USA, 7–11 July 2010; p. 393. [Google Scholar] [CrossRef] [Green Version]
- Desai, J.; Ostrowski, J.; Kumar, V. Controlling Formations of Multiple Mobile Robots. In Proceedings of the 1998 IEEE International Conference on Robotics and Automation (Cat. No.98CH36146), Leuven, Belgium, 20 May 1998; Volume 4, pp. 2864–2869. [Google Scholar] [CrossRef]
- Barabási, A.L. Network Science Network Robustness. p. 54. Available online: http://networksciencebook.com/chapter/8 (accessed on 1 January 2020).
- Lin, Z.; Francis, B.; Maggiore, M. State Agreement for Continuous-Time Coupled Nonlinear Systems. SIAM J. Control Optim. 2007, 46, 288–307. [Google Scholar] [CrossRef]
- Achiam, J.; Held, D.; Tamar, A.; Abbeel, P. Constrained Policy Optimization. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 22–31. [Google Scholar]
- Ray, A.; Achiam, J.; Amodei, D. Benchmarking Safe Exploration in Deep Reinforcement Learning. arXiv 2019, arXiv:1910.01708. [Google Scholar]
- Coumans, E.; Bai, Y. Pybullet, a Python Module for Physics Simulation for Games, Robotics and Machine Learning. 2016–2019. Available online: http://pybullet.org (accessed on 1 January 2020).
- Mason, K.; Duggan, J.; Howley, E. Forecasting Energy Demand, Wind Generation and Carbon Dioxide Emissions in Ireland Using Evolutionary Neural Networks. Energy 2018, 155, 705–720. [Google Scholar] [CrossRef]
- Concepcion II, R.; Lauguico, S.; Almero, V.J.; Dadios, E.; Bandala, A.; Sybingco, E. Lettuce Leaf Water Stress Estimation Based on Thermo-Visible Signatures Using Recurrent Neural Network Optimized by Evolutionary Strategy. In Proceedings of the 2020 IEEE 8th R10 Humanitarian Technology Conference (R10-HTC), Kuching, Malaysia, 1–3 December 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Chen, A.; Choo, K.; Astrakhantsev, N.; Neupert, T. Neural Network Evolution Strategy for Solving Quantum Sign Structures. Phys. Rev. Res. 2022, 4, L022026. [Google Scholar] [CrossRef]


| Symbol | Description | Value |
|---|---|---|
| Learning rate | 0.02 | |
| Time step | 0.1 | |
| Standard deviation | 0.2 | |
| Population size adaptation factor | 0.84 | |
| Cost weight matrix |
| Symbol | Description | Value |
|---|---|---|
| Maximum speed of both missile and reference target | 0.8 km/s | |
| Minimum speed of both missile and reference target | 0.3 km/s | |
| Maximum lateral acceleration | 40 g | |
| Maximum speed acceleration | 30 g |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Lan, X.; Zhou, Y.; Liang, J. Formation Control with Connectivity Assurance for Missile Swarms by a Natural Co-Evolutionary Strategy. Mathematics 2022, 10, 4244. https://doi.org/10.3390/math10224244
Chen J, Lan X, Zhou Y, Liang J. Formation Control with Connectivity Assurance for Missile Swarms by a Natural Co-Evolutionary Strategy. Mathematics. 2022; 10(22):4244. https://doi.org/10.3390/math10224244
Chicago/Turabian StyleChen, Junda, Xuejing Lan, Ye Zhou, and Jiaqiao Liang. 2022. "Formation Control with Connectivity Assurance for Missile Swarms by a Natural Co-Evolutionary Strategy" Mathematics 10, no. 22: 4244. https://doi.org/10.3390/math10224244
APA StyleChen, J., Lan, X., Zhou, Y., & Liang, J. (2022). Formation Control with Connectivity Assurance for Missile Swarms by a Natural Co-Evolutionary Strategy. Mathematics, 10(22), 4244. https://doi.org/10.3390/math10224244







