Wolbachia Invasion Dynamics by Integrodifference Equations

Abstract

Releasing mosquitoes infected with the endosymbiotic bacterium Wolbachia to invade and replace the wild populations can effectively interrupt dengue transmission. Recently, a reasonable discrete competitive non-spatial model was developed and the conditions for the successful invasion of Wolbachia were given. However, Wolbachia propagation is a matter of spatial dynamics. In this paper, we introduce a dispersal kernel and establish integrodifference equations, a class of discrete-time spatial diffusion systems that have recently gained much attention as an important tool for spatial ecology. We analyzed the spatial model by average dispersal success approximation to find the criteria for the successful spread of Wolbachia, and then compared it with the non-spatial model to discuss the effect of spatial parameters.

1. Introduction

A huge public health threat caused by mosquitoes, which spread quickly and can transmit the dreaded dengue fever, has been widely publicized, but there is no efficient and sustainable countermeasure [1,2]. In recent years, a promising method has been found that uses the endosymbiotic bacterium Wolbachia for mosquito control. Wolbachia reduces the ability of mosquitoes to spread dengue by infecting them and gives infected females a reproductive advantage due to its maternal transmission and cytoplasmic incompatibility (CI) [3,4]. Therefore, releasing mosquitoes stably carrying specific Wolbachia bacteria into the wild can successfully invade the wild populations under certain conditions, reducing the number of mosquitoes and blocking dengue spread.

Mathematical modeling is of significance in Wolbachia invasion dynamics, and a great many authors have, since the pioneer work of Caspari and Watson [5], incorporated Wolbachia into their models [6,7,8,9,10]. The study of rational mathematical models can help us to correctly perceive the population or disease invasion [11] and provide reliable theoretical support for relevant researchers. For example, in 2014, Zheng et al. established a model of delay differential equations and found an infection threshold above which Wolbachia is guaranteed to invade the entire wild population [8]. However, the discrete time model is richer in properties and can better describe changes in mosquito populations based on discrete observations data. Thus, recently, we established a discrete model from the perspective of competition between the released Wolbachia-infected mosquitos and uninfected wild mosquitoes [12], which is as follows:

$$\left\{\begin{array}{c}{x}_{t+1}=\frac{b_1{x}_t}{1+\alpha (x_t+y_t)}+(1-d_1)x_t,\hfill \\ y_{t+1}=\frac{b_2{y}_t}{1+\beta (x_t+y_t)}\frac{y_t}{x_t+y_t}+(1-d_2)y_t,\hfill \end{array}\right.$$

(1)

where $x_t$ represents the infected mosquito population density at time t and $y_t$ is the uninfected competitor, $b_i$ are the birth rates, $\alpha$ and $\beta$ are the competition coefficients, $d_i$ are the mortality rates, and $i=1,2$ for $x_t$ and $y_t$, respectively. Because Wolbachia often induces a fitness cost [8], we assume that $0<d_2<d_1<1$; the fraction $y_t/(x_t+y_t)$ indicates the CI mechanism of the Wolbachia-infected population [13].

When we define an auxiliary function as follows,

$$f(x,y)=\left\{\begin{array}{cc}\frac{b_{2}y}{1+\beta (x+y)}\frac{y}{x+y}+(1-d_2)y,\hfill & (x,y)\ne (0,0),\hfill \\ 0,\hfill & (x,y)=(0,0),\hfill \end{array}\right.$$

the right part of the second equation in (1) is well-defined in ${\mathbf{R}}^2$, and thus system $\left(1\right)$ has a trivial state $E_0(0,0)$. In addition, system $\left(1\right)$ has two semi-trivial states $E_1\left(\frac{1}{\alpha }(\frac{b_1}{d_1}-1),0\right)$ and $E_2\left(0,\frac{1}{\beta }(\frac{b_2}{d_2}-1)\right)$ provided that $b_1>d_1$ and $b_2>d_2$, respectively, and the coexistence state

$$E_3\left(\frac{1}{\alpha }(\frac{b_1}{d_1}-1)(1-\frac{d_2}{b_2}[1+\frac{\beta }{\alpha }(\frac{b_1}{d_1}-1)]),\frac{d_2}{\alpha b_2}(\frac{b_1}{d_1}-1)[1+\frac{\beta }{\alpha }(\frac{b_1}{d_1}-1)]\right)$$

provided that $b_1>d_1,b_2>d_2$ and $\frac{1}{\beta }(\frac{b_2}{d_2}-1)>\frac{1}{\alpha }(\frac{b_1}{d_1}-1)$. The following lemma, extracted from [12], gives the stability results for each steady state, and their stability diagram in $(b_1,b_2)$-space is displayed in Figure 1.

 Lemma 1. 

Assume that all coefficients of system $\left(1\right)$ are positive. Then, the following statements hold:

(1) 

If $b_1\le d_1,b_2\le d_2,$ then the only steady state $E_0$ is globally asymptotically stable. Otherwise, it is unstable.

(2) 

If $b_1>d_1,$ then there exists a stable semi-trivial steady state $E_1$. Moreover, if $\frac{1}{\beta }(\frac{b_2}{d_2}-1)<\frac{1}{\alpha }(\frac{b_1}{d_1}-1)$, then $E_1$ is globally asymptotically stable.

(3) 

If $b_2>d_2$, then there exists a semi-trivial steady state $E_2$, and it is stable if $\frac{1}{\beta }(\frac{b_2}{d_2}-1)>\frac{1}{\alpha }(\frac{b_1}{d_1}-1)$. Moreover, if $b_1\le d_1$, then $E_2$ is globally asymptotically stable.

(4) 

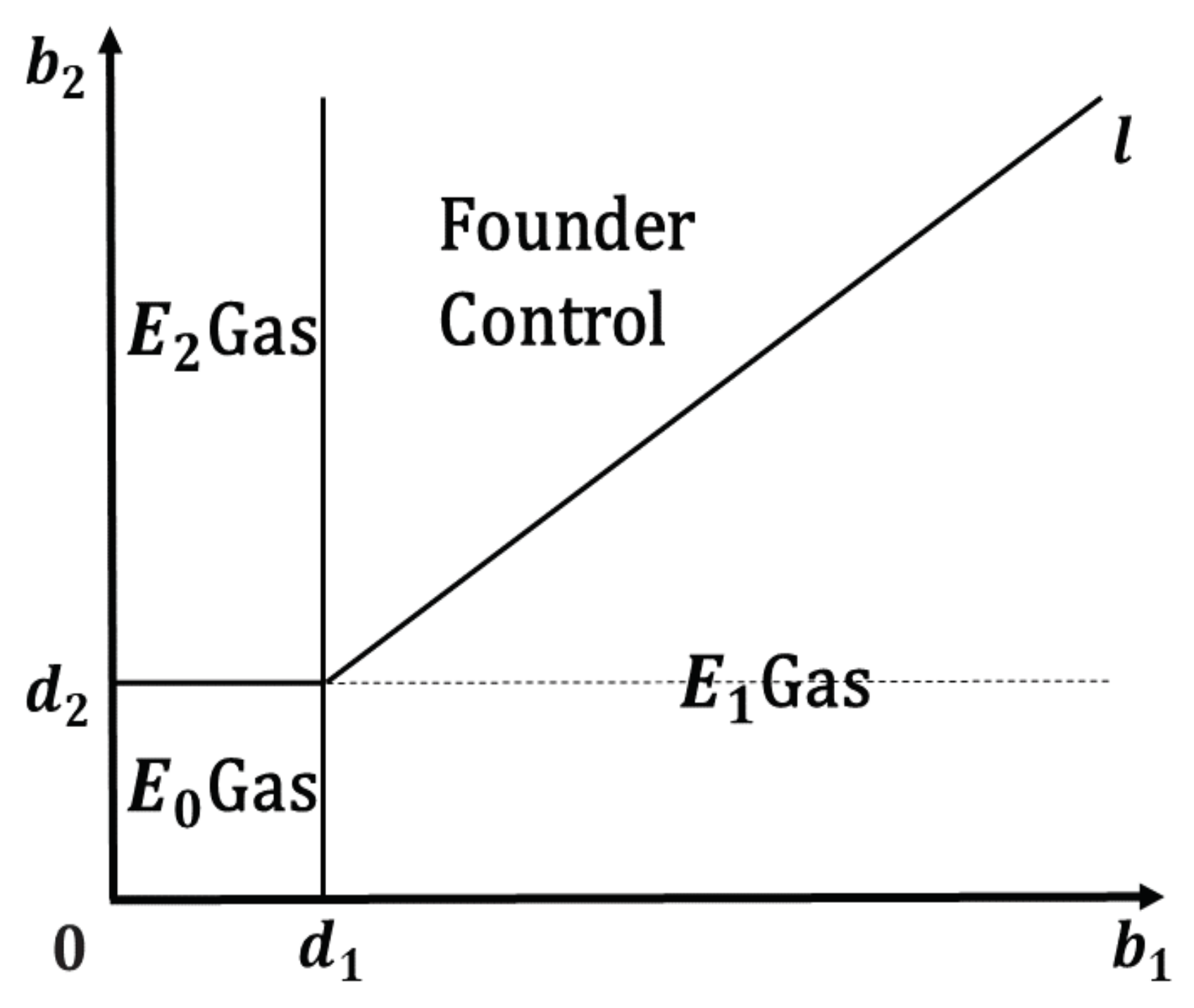
If $b_1>d_1,b_2>d_2$ and $\frac{1}{\beta }(\frac{b_2}{d_2}-1)>\frac{1}{\alpha }(\frac{b_1}{d_1}-1)$, then the coexistence steady state $E_3$ exists and is a saddle, and the case where both semi-trivial states are locally stable and coexistence state is unstable is called founder control.

The stability conditions of the steady states in Lemma 1 can be explained biologically as follows. When $b_1\le d_1,b_2\le d_2$, the birth rates of both populations are too low to ensure the population’s survival. The stability of $E_1$ when $b_1>d_1$ means that Wolbachia-infected population $x_t$ obtains a sufficient birth rate to persist, and, further, when $\frac{1}{\beta }(\frac{b_2}{d_2}-1)<\frac{1}{\alpha }(\frac{b_1}{d_1}-1)$, we claim that Wolbachia infection has a fitness benefit [8], which results in population $x_t$ winning the competition, i.e., Wolbachia invasion is successful. However, when $b_2>d_2$, $E_2$ exists but is not necessarily stable due to the CI mechanism that imposes a reproductive disadvantage on the uninfected population $y_t$. Only if $\frac{1}{\beta }(\frac{b_2}{d_2}-1)>\frac{1}{\alpha }(\frac{b_1}{d_1}-1)$, where the infection has a fitness cost, can $y_t$ persist. Further, $y_t$ can win the competition only when the competitor $x_t$ does not last, i.e., $b_1\le d_1$, which fully illustrates the important role of CI in Wolbachia diffusion. $E_3$ is always unstable, implying that two populations cannot coexist, in accordance with the principle of competitive exclusion, and thus the successful invasion of populations in this paper is equivalent to replacement. In fact, $E_3$ undergoes a transcritical bifurcation at $\frac{1}{\beta }(\frac{b_2}{d_2}-1)=\frac{1}{\alpha }(\frac{b_1}{d_1}-1)$, and we will discuss it in the next section.

Wolbachia invasion dynamics essentially belongs to the domain of spatial ecology. The spatial dispersal of species may be a response to climate variation and local environmental degradation [14], and mosquitoes are strongly reliant on their environment for breeding and dispersal [2]. Therefore, spatial considerations must be taken into account when modeling the evolution of released infected Wolbachia mosquitoes competing with wild ones over a specific area.

In modeling dispersal, the reaction–diffusion equations, continuous-time growth models with within-habitat dispersal, provide insight into spatial patterns in ecology and the mathematical structure of infinite-dimensional dynamical systems, and there are many related works [15,16,17,18]. However, as mentioned above, when considering a spatial model with the support of discrete observation data, the discrete-time model can more accurately reflect the actual evolutionary pattern of the species and is typically easier to simulate. After the precursor work of Weinberger [19], the integrodifference equations rise to fame, and a number of scholars [20,21,22,23,24,25,26,27] made remarkable contributions to the study of such infinite dimensional recursions. Overall, this relatively new discrete-time spatial diffusion system can well-characterize the spatial diffusion of individuals and the interactions between populations, and is an essential tool for spatial ecology research.

In this paper, we establish an integrodifference equation model corresponding to the non-spatial model $\left(1\right)$, give the conditions for successful Wolbachia propagation, and discuss the influence of spatial factors. The rest of this paper is organized as follows. In Section 2, we discuss the bifurcation of system $\left(1\right)$, where results based on normal forms and the center manifold theorem show that the coexistence state of the system undergoes a transcritical bifurcation. In Section 3, we first equip the non-spatial model $\left(1\right)$ with a Laplace kernel to obtain an integrodifference competition model and give its standing assumptions. Then, we obtain the invasion conditions of Wolbachia using stability analysis. In particular, the non-trivial state of the spatial model cannot be calculated explicitly; for explicit but approximate calculations, we apply the average dispersal success approximation method and obtain a tractable, spatially implicit model. Further, we compare spatial and non-spatial models and analyze the effect of spatial parameters on Wolbachia diffusion. A brief conclusion is given in Section 4.

2. Bifurcation of Non-Spatial Model

In this section, we focus on the transcritical bifurcation of the coexistence state $E_3$ of system $\left(1\right)$. Normal forms and the center manifold theorem were adopted to study the existence and direction of such a type of bifurcation. It is shown that, if the competition coefficient $\beta$ is used as a bifurcation parameter, there is a threshold ${\beta }^{*}$ for the survival of the population $y_t$.

 Theorem 1. 

System $\left(1\right)$ undergoes a transcritical bifurcation at $E_3$ if $b_1>d_1,b_2>d_2$ and $\beta =\alpha \frac{d_1(b_2-d_2)}{d_2(b_1-d_1)}$.

Proof of Theorem 1.

For notational simplicity, let $E_3(x^{*},y^{*})$ be the coexistence state of system $\left(1\right)$, i.e.,

$$E_3(x^{*},y^{*})=E_3\left(\frac{1}{\alpha }(\frac{b_1}{d_1}-1)(1-\frac{d_2}{b_2}[1+\frac{\beta }{\alpha }(\frac{b_1}{d_1}-1)]),\frac{d_2}{\alpha b_2}(\frac{b_1}{d_1}-1)[1+\frac{\beta }{\alpha }(\frac{b_1}{d_1}-1)]\right).$$

If $b_1>d_1,b_2>d_2$ and $\frac{1}{\beta }(\frac{b_2}{d_2}-1)=\frac{1}{\alpha }(\frac{b_1}{d_1}-1)$, or, equivalently, $\beta =\alpha \frac{d_1(b_2-d_2)}{d_2(b_1-d_1)}$, then the eigenvalues of the linearization of (1) at $E_3(x^{*},y^{*})$ are ${\lambda }_1=1$ and ${\lambda }_2=d_2(\frac{d_2}{b_2}-1)+1$, where $0<{\lambda }_2<1$. In fact, let ${\beta }^{*}=\alpha \frac{d_1(b_2-d_2)}{d_2(b_1-d_1)}$; then, it is the critical value that causes the first Jury condition $1-trJ+detJ>0$ at $E_3$ to be broken. The Jury conditions can not only determine the stability of the steady state, but can also be useful in judging the type of bifurcation. If the above mentioned Jury condition is violated at a bifurcation point, it usually results in a transcritical bifurcation [24,28], as we prove below.

Let $u=x-x^{*},v=y-y^{*}$ and $\overline{\beta }=\beta -{\beta }^{*}$. We now consider the bifurcation of the point $(0,0)$ at $\overline{\beta }=0$ for the following map:

$$\left(\begin{array}{c}u\\ \overline{\beta }\\ v\end{array}\right)\mapsto \left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ d_2(\frac{d_2}{b_2}-2)& -\frac{d_2^2{(b_1-d_1)}^2}{{\alpha }^2{d}_1^2{b}_2}& d_2(\frac{d_2}{b_2}-1)+1\end{array}\right)\left(\begin{array}{c}u\\ \overline{\beta }\\ v\end{array}\right)+\left(\begin{array}{c}{f}_1(u,\overline{\beta },v)\\ 0\\ f_2(u,\overline{\beta },v)\end{array}\right),$$

(2)

where

$$\begin{array}{cc}\hfill & f_1(u,\overline{\beta },v)=-\frac{\alpha d_1^2}{b_1}{u}^2-\frac{\alpha d_1^2}{b_1}uv+O\left(\right(\left|u\right|+\left|v\right|+|\overline{\beta }{\left|\right)}^3),\hfill \end{array}$$

$$\begin{array}{cc}\hfill & f_2(u,\overline{\beta },v)=\frac{\alpha d_1{d}_2[d_2^2+3b_2(b_2-d_2)]}{b_2^2(b_1-d_1)}{u}^2-\frac{\alpha d_1{d}_2^2(b_2-d_2)}{b_2^2(b_1-d_1)}{v}^2+\frac{d_2^3{(b_1-d_1)}^3}{{\alpha }^3{d}_1^3{b}_2^2}{\overline{\beta }}^2\hfill \\ \hfill & +\frac{2\alpha d_1{d}_2{(b_2-d_2)}^2}{b_2^2(b_1-d_1)}uv+\frac{2d_2^2(b_1-d_1)(b_2-d_2)}{\alpha d_1{b}_2^2}u\overline{\beta }\hfill \\ \hfill & -\frac{2d_2^3(b_1-d_1)}{\alpha d_1{b}_2^2}v\overline{\beta }+O\left(\right(\left|u\right|+\left|v\right|+|\overline{\beta }{\left|\right)}^3).\hfill \end{array}$$

We then consider the following similarity transformation:

$$\left(\begin{array}{c}u\\ \overline{\beta }\\ v\end{array}\right)=\left(\begin{array}{ccc}\frac{b_2-d_2}{d_2-2b_2}& \frac{d_2{(b_1-d_1)}^2}{{\alpha }^2{d}_1^2(d_2-2b_2)}& 0\\ 0& 1& 0\\ 1& 0& 1\end{array}\right)\left(\begin{array}{c}X\\ \mu \\ Y\end{array}\right),$$

(3)

and the map $\left(2\right)$ can be turned into the following normal form:

$$\left(\begin{array}{c}X\\ \mu \\ Y\end{array}\right)\mapsto \left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& d_2(\frac{d_2}{b_2}-1)+1\end{array}\right)\left(\begin{array}{c}X\\ \mu \\ Y\end{array}\right)+\left(\begin{array}{c}{F}_1(X,\mu ,Y)\\ 0\\ F_2(X,\mu ,Y)\end{array}\right),$$

(4)

where

$$\begin{array}{cc}\hfill & F_1(X,\mu ,Y)=c_1{X}^2+c_{2}XY+c_3\mu X+c_4\mu Y+c_5{\mu }^2+O\left(\right(\left|X\right|+\left|Y\right|+{\left|\mu \right|)}^3),\hfill \end{array}$$

$$\begin{array}{cc}\hfill & F_2(X,\mu ,Y)=c_6{X}^2+c_{7}XY+c_8{Y}^2+c_9\mu X+c_{10}\mu Y+c_{11}{\mu }^2+O\left(\right(\left|X\right|+\left|Y\right|+{\left|\mu \right|)}^3),\hfill \end{array}$$

and their coefficients are listed in detail below:

$$\begin{array}{cc}\hfill & c_1=\frac{\alpha d_1^2{b}_2}{b_1(d_2-2b_2)},c_2=-\frac{\alpha d_1^2}{b_1},c_3=\frac{d_2^2{(b_1-d_1)}^2}{\alpha b_1(b_2-d_2)(d_2-2b_2)},\hfill \\ \hfill & c_4=-\frac{d_2{(b_1-d_1)}^2}{\alpha b_1(b_2-d_2)},c_5=-\frac{d_2^2{(b_1-d_1)}^4}{{\alpha }^3{d}_1^2{b}_1(b_2-d_2)(d_2-2b_2)},\hfill \\ \hfill & c_6=-\frac{\alpha d_1{b}_2[b_1{d}_2(b_2-d_2)+d_1(b_1-d_1)(d_2-2b_2)]}{b_1(b_1-d_1){(d_2-2b_2)}^2},\hfill \\ \hfill & c_7=\frac{\alpha d_1[2b_1{d}_2(b_2-d_2)+d_1(b_1-d_1)(d_2-2b_2)]}{b_1(b_1-d_1)(d_2-2b_2)},c_8=-\frac{\alpha d_1{d}_2^2(b_2-d_2)}{b_2^2(b_1-d_1)},\hfill \\ \hfill & c_9=-\frac{d_2^2(b_1-d_1)[2b_1{b}_2(b_2-d_2)+d_1(b_1-d_1)(d_2-2b_2)]}{\alpha d_1{b}_1(b_2-d_2){(d_2-2b_2)}^2},\hfill \\ \hfill & c_{10}=\frac{d_2(b_1-d_1)[2b_1{d}_2(b_2-d_2)+d_1(b_1-d_1)(d_2-2b_2)]}{\alpha b_1{d}_1(b_2-d_2)(d_2-2b_2)},\hfill \\ \hfill & c_{11}=\frac{d_2^2{(b_1-d_1)}^3[b_1{d}_2(b_2-d_2)(3b_2-d_2)+d_1{b}_2(b_1-d_1)(d_2-2b_2)]}{{\alpha }^3{d}_1^3{b}_1{b}_2(b_2-d_2){(d_2-2b_2)}^2}.\hfill \end{array}$$

For the implementation of the center manifold theorem, we assume that $W^c(0,0,0)$ is the center manifold of $\left(4\right)$ evaluated at $(0,0)$ in a small neighborhood of $\mu =0$. Then, $W^c(0,0,0)$ is approximated as follows:

$$W^c(0,0,0)=\{(X,\mu ,Y)\in {\mathbb{R}}^3\mid Y=h_1{X}^2+h_2\mu X+h_3{\mu }^2+O\left(\right(\left|X\right|+{\left|\mu \right|)}^3\left)\right\},$$

where

$$\begin{array}{cc}\hfill & h_1=\frac{\alpha d_1{b}_2^2[b_1{d}_2(b_2-d_2)+d_1(b_1-d_1)(d_2-2b_2)]}{b_1{d}_2(b_1-d_1)(d_2-b_2){(d_2-2b_2)}^2},\hfill \\ \hfill & h_2=-\frac{b_2{d}_2^2(b_1-d_1)[2b_1{b}_2(b_2-d_2)+d_1(b_1-d_1)(d_2-2b_2)]}{\alpha d_1{d}_2{b}_1{(b_2-d_2)}^2{(d_2-2b_2)}^2},\hfill \\ \hfill & h_3=\frac{d_2{(b_1-d_1)}^3[b_1{d}_2(b_2-d_2)(3b_2-d_2)+d_1{b}_2(b_1-d_1)(d_2-2b_2)]}{{\alpha }^3{d}_1^3{b}_1{(b_2-d_2)}^2{(d_2-2b_2)}^2}.\hfill \end{array}$$

The map $\left(4\right)$ restricted to the center manifold $W^c(0,0,0)$ [29] is given by

$$\begin{array}{cc}\hfill & F:X\to X+\frac{\alpha d_1^2{b}_2}{b_1(d_2-2b_2)}{X}^2+\frac{d_2^2{(b_1-d_1)}^2}{\alpha b_1(b_2-d_2)(d_2-2b_2)}\mu X\hfill \\ \hfill & -\frac{d_2^2{(b_1-d_1)}^4}{{\alpha }^3{d}_1^2{b}_1(b_2-d_2)(d_2-2b_2)}{\mu }^2+O\left(\right(\left|X\right|+{\left|\mu \right|)}^3).\hfill \end{array}$$

(5)

If the map $\left(4\right)$ undergoes a transcritical bifurcation, then it must satisfy the following conditions:

$${\gamma }_1=\frac{{\partial }^{2}F(0,0)}{\partial X\partial \mu }\ne 0,{\gamma }_2=\frac{{\partial }^{2}F(0,0)}{\partial X^2}\ne 0,$$

Due to $b_2>d_2$, a simple calculation shows that

$${\gamma }_1=\frac{d_2^2{(b_1-d_1)}^2}{\alpha b_1(b_2-d_2)(d_2-2b_2)}<0,{\gamma }_2=\frac{2\alpha d_1^2{b}_2}{b_1(d_2-2b_2)}<0.$$

From the above analysis and the bifurcation theory, we conclude that this is a transcritical bifurcation and that the associated steady states are $E_2$ and $E_3$. In a small neighborhood of the critical parameter ${\beta }^{*}$, $E_2$ is stable and $E_3$ is unstable when $\beta <{\beta }^{*}$, whereas $E_2$ is unstable and the biologically meaningless state $E_3$ is stable when $\beta >{\beta }^{*}$. We have completed the proof. □

The chosen bifurcation parameter $\beta$ is the competition coefficient of uninfected population $y_t$, whereas ${\beta }^{*}$ can be considered as a threshold for the possible survival of $y_t$. Since CI causes a reproductive inferiority for $y_t$, it may persist under a specific initial values only if its competition coefficient is less than a threshold, i.e., $\beta <{\beta }^{*}$ and $E_2$ is stable for the case of founder control. Otherwise, when $\beta >{\beta }^{*}$, $E_2$ is unstable and $y_t$ becomes extinct, which means that Wolbachia invasion is successful.

3. Spatial Model

Effective experiments of Wolbachia propagation, such as [4,30], usually manifest as the release of the infected populations into specific areas, followed by the invasion and replacement of local uninfected populations. Based on the previous non-spatial model $\left(1\right)$, in this section, we introduce a dispersal kernel to build and analyze an integrodifference competition model over a one-dimensional bounded domain.

3.1. Model

If the location prior to dispersal was y, a dispersal kernel, denoted by $K(x,y)$, describes the probability density of the location of the individual after dispersal. A well-proven kernel that is frequently used in calculations is the Laplace kernel [20,24]:

$$K(x,y)=\frac{a}{2}exp(-a|x-y\left|\right),$$

(6)

where $1/a$ has units of length and denotes the mean dispersal distance. Furthermore, it is non-negative, symmetric, continuous, and satisfies ${\int }_{\Omega }K(x,y)dx\le 1$ for all $y\in \Omega$, where $\Omega =[-L/2,L/2]$ is the one-dimensional domain of interest of length L. We now introduce dispersal into the non-spatial model $\left(1\right)$ and denote by $K_1$ and $K_2$ the Laplace kernels of the two competitive populations, respectively. Then, we have the following growth-dispersal model:

$$\left\{\begin{array}{c}{u}_{t+1}\left(x\right)={\int }_{\Omega }{K}_1(x,y)[\frac{b_1{u}_t\left(y\right)}{1+\alpha (u_t\left(y\right)+v_t\left(y\right))}+(1-d_1)u_t\left(y\right)]dy,x\in \Omega ,\hfill \\ v_{t+1}\left(x\right)={\int }_{\Omega }{K}_2(x,y)[\frac{b_2{v}_t\left(y\right)}{1+\beta (u_t\left(y\right)+v_t\left(y\right))}\frac{v_t\left(y\right)}{u_t\left(y\right)+v_t\left(y\right)}+(1-d_2)v_t\left(y\right)]dy,x\in \Omega ,\hfill \\ u_0\left(x\right)=u\left(x\right),v_0\left(x\right)=v\left(x\right),x\in \Omega ,\hfill \end{array}\right.$$

(7)

where $u_t\left(x\right)$ and $v_t\left(x\right)$ denote the population densities of the Wolbachia-infected and uninfected mosquitoes at time t and location x, respectively; the non-negative functions $u\left(x\right)$ and $v\left(x\right)$ are their initial distribution, respectively; the kernel $K_i$ contains the coefficients $a_i,i=1,2$, respectively. The remaining coefficients can be referred to in the previous system $\left(1\right)$. Further, we assume that all coefficients are positive; then, it is easy to prove that the integral operator of system $\left(7\right)$ is compact in the space of continuous functions together with the system being monotone bounded and satisfying the Krein–Rutman theorem.

3.2. Analysis

We focus on analyzing the stabilities of steady states and bifurcations of the spatial model $\left(7\right)$ and give its corresponding ecological interpretations. Let

$$F(u_t\left(x\right),v_t\left(x\right))=\frac{b_1{u}_t\left(x\right)}{1+\alpha (u_t\left(x\right)+v_t\left(x\right))}+(1-d_1)u_t\left(x\right),$$

and

$$G(u_t\left(x\right),v_t\left(x\right))=\frac{b_2{v}_t\left(x\right)}{1+\beta (u_t\left(x\right)+v_t\left(x\right))}\frac{v_t\left(x\right)}{u_t\left(x\right)+v_t\left(x\right)}+(1-d_2)v_t\left(x\right),$$

$x\in \Omega$; then, system $\left(7\right)$ can be extended continuously to $(0,0)$ by defining

$$G(0,0)=0.$$

We will maintain this assumption without specifications in the following discussions. Clearly, system $\left(7\right)$ has a trivial state $E_0^{*}(0,0)$, where, below, we analyze its stability. Since the system is not differentiable at $(0,0)$, we could discuss the perturbations to the two components of $E_0^{*}$ separately, thus transforming into the study of the stability problem for a single species. In particular, the stability of the trivial state of a single equation is judged by the critical patch-size [20,24], which is the size of the suitable habitat, above which, the population gain through reproduction exceeds the population loss through dispersal, and thus the population can grow. Conversely, the population goes extinct, implying that the trivial state is stable.

Specifically, for system $\left(7\right)$, let $v_t\left(x\right)=0$; then, we can study stability conditions with respect to perturbations in $u_t\left(x\right)$ only, leading to a single equation:

$$u_{t+1}\left(x\right)={\int }_{\Omega }{K}_1(x,y)F(u_t\left(y\right),0)dy,$$

(8)

which has a steady state $u=0$. In the following, we give its stability conditions by critical patch-size. Assume that $b_1>d_1$—otherwise, the population cannot grow because its birth rate is too low—and then let $R_u=F_u(0,0)=b_1-d_1+1>0$. It is easy to prove that Equation $\left(8\right)$ satisfies the Krein–Rutman theorem, and its eigenvalue problem reads as

$$\lambda \varphi \left(x\right)=R_u{\int }_{\Omega }{K}_1(x,y)\varphi \left(y\right)dy.$$

A typical calculation (see e.g., Proposition 3.1 in [24]), which we omit, shows that the critical patch-size for $u_t\left(x\right)$ survival under the Laplace kernel is

$$L_u^{*}=\frac{2}{a_1\sqrt{b_1-d_1}}arctan\left(\frac{1}{\sqrt{b_1-d_1}}\right).$$

When $L<L_u^{*}$, then $u=0$ is stable, which indicates that the dispersal loss of the population $u_t\left(x\right)$ exceeds the reproductive gain and thus $u_t\left(x\right)$ fails to persist. Conversely, when $L>L_u^{*}$, then $u=0$ is unstable, and $u_t\left(x\right)$ survives, which means that $E_0^{*}$ is unstable. Further, the monotonic boundedness of Equation $\left(8\right)$ guarantees the existence of a unique positive steady state $u^{*}$. This implies that system $\left(7\right)$ possesses a semi-trivial state $E_1^{*}(u^{*}\left(x\right),0)$, and we will discuss its stability below.

Similarly, let $u_t\left(x\right)=0$; then, the reduced equation is

$$v_{t+1}\left(x\right)={\int }_{\Omega }{K}_2(x,y)G(0,v_t\left(y\right))dy.$$

(9)

Assume that $b_2>d_2$, and let $R_v=G_v(0,0)=b_2-d_2+1>0$; then, the critical patch-size, which determines the stability of steady state $v=0$ of Equation $\left(9\right)$, is given by

$$L_v^{*}=\frac{2}{a_2\sqrt{b_2-d_2}}arctan\left(\frac{1}{\sqrt{b_2-d_2}}\right).$$

When $L<L_v^{*}$, then $v=0$ is stable, and $v_t\left(x\right)$ extinct. When $L>L_v^{*}$, then $v=0$ is unstable, which also implies that $E_0^{*}$ is unstable. Similar properties indicate that there is a unique positive steady state $v^{*}$ for Equation $\left(9\right)$, i.e., system $\left(7\right)$ possesses a semi-trivial state $E_2^{*}(0,v^{*}\left(x\right))$.

In summary, let $L^{*}=min\{L_u^{*},L_v^{*}\}$, and, when $L<L^{*}$, the only steady state $E_0^{*}$ of system $\left(7\right)$ is stable and, therefore, it is globally asymptotically stable. Otherwise, it is unstable. In addition, the system has two semi-trivial states $E_1^{*}(u^{*}\left(x\right),0)$ and $E_2^{*}(0,v^{*}\left(x\right))$ provided that $L>L_u^{*}$ and $L>L_v^{*}$, respectively, where $u^{*}\left(x\right)$ and $v^{*}\left(x\right)$ cannot be explicitly expressed.

The stability of $E_1^{*}(u^{*}\left(x\right),0)$ is proved as follows. The linearization at this state leads to the eigenvalue problem

$$\left\{\begin{array}{c}\lambda \varphi \left(x\right)={\int }_{\Omega }{K}_1(x,y)[(\frac{b_1}{{(1+\alpha u^{*}\left(y\right))}^2}+1-d_1)\varphi \left(y\right)-\frac{\alpha b_1{u}^{*}\left(y\right)}{{(1+\alpha u^{*}\left(y\right))}^2}\psi \left(y\right)]dy,\hfill \\ \lambda \psi \left(x\right)={\int }_{\Omega }{K}_2(x,y)(1-d_2)\psi \left(y\right)dy.\hfill \end{array}\right.$$

(10)

Since the system decouples, we are allowed to study the two equations of $\left(10\right)$ separately. On the one hand, the perturbation of the state $E_1^{*}$ with respect to the first component leads to a single species with positive steady state stability considerations. Due to the monotonic boundedness and concavity of F—see Lemma 4.2 and 4.3 in [24]—it is guaranteed that the state $E_1^{*}$ is stable with respect to perturbations in $u_t\left(x\right)$ only, even though the function $u^{*}\left(x\right)$ is unknown. On the other hand, the perturbation of the state $E_1^{*}$ with respect to the second component is the stability problem of a single equation with a trivial state. It is easy to see that the dominant eigenvalue $\lambda$ of the second equation of $\left(10\right)$ satisfies $\lambda <1-d_2<1$, and thus the state $E_1^{*}$ is stable against perturbations in $v^{*}\left(x\right)$ only. We have completed the proof. So far, for system $\left(7\right)$, we could only obtain the following valuable conclusions.

 Theorem 2. 

For system $\left(7\right)$, assume that $b_1>d_1$ and $b_2>d_2$. Then, the following statements hold:

(i) 

If $L<L^{*}$, then the only steady state $E_0^{*}(0,0)$ is globally asymptotically stable. Otherwise, it is unstable.

(ii) 

If $L>L_u^{*}$, then there exists a stable semi-trivial steady state $E_1^{*}(u^{*}\left(x\right),0)$.

The global stability of the state $E_0^{*}$ at $L<L^{*}$ indicates that the habitat in which the two populations are located is too small for them to survive due to severe dispersal loss. When $L>L_u^{*}$, the existence and stability of $E_1^{*}$ suggest that when the Wolbachia-infected population $u_t\left(x\right)$ acquires a habitat size sufficient for its own survival, it can successfully invade, at least for a specific initial value. Even in an environment of fitness benefit, the infected population $u_t\left(x\right)$ can certainly exclude the uninfected population $v_t\left(x\right)$ by competition.

We would like to further analyze the remaining stability conclusions for System $\left(7\right)$; however, the non-trivial steady state cannot be calculated exactly, causing the analysis to become challenging. For an exact and complete discussion, we employed the average dispersal success to obtain an approximation system that is manageable and effectively reflects the dynamics of system $\left(7\right)$. The average dispersal success [26],

$$\overline{S}=\frac{1}{|\Omega |}{\int }_{\Omega }{\int }_{\Omega }K(x,y)dxdy,$$

can be interpreted as the spatially averaged probability that an individual remains in the bounded area $\Omega$ after a dispersal process under the dispersal behavior determined by the kernel $K(x,y)$, where $|\Omega |={\int }_{\Omega }{d}_x$ is the volume of $\Omega$. It can be calculated explicitly under the Laplace kernel as

$$\overline{S}=1-\frac{1-exp(-aL)}{aL},\overline{S}<1.$$

Therefore, if we take the spatial average of both sides of the equation in system $\left(7\right)$ and then extract the lowest-order approximation from the Taylor series expansion of the right-hand function, we obtain the so-called spatially implicit model [23]:

$$\left\{\begin{array}{c}{u}_{t+1}={\overline{S}}_u[\frac{b_1{u}_t}{1+\alpha (u_t+v_t)}+(1-d_1)u_t],\hfill \\ v_{t+1}={\overline{S}}_v[\frac{b_2{v}_t}{1+\beta (u_t+v_t)}\frac{v_t}{u_t+v_t}+(1-d_2)v_t],\hfill \end{array}\right.$$

(11)

where $u_t$ and $v_t$ are the spatially averaged densities of the two populations at time t, respectively; ${\overline{S}}_u$ and ${\overline{S}}_v$ are the average dispersal successes of the two populations and are computed from $K_1$ and $K_2$, respectively. Compared to system $\left(1\right)$, ${\overline{S}}_u,{\overline{S}}_v<1$ implies a reduction in the growth of both populations over the bounded domain due to diffusion loss. The numerical results show that the approximation is quite accurate when applying the average dispersal success to the IDE system with a symmetric kernel [24]. Thus, by discussing the approximation system $\left(11\right)$, some explicit but approximate results of the spatial model $\left(7\right)$ can be obtained. Similarly, system $\left(11\right)$ has a trivial state $E_0^{*}(0,0)$. In addition, there are two semi-trivial states

$$E_1^{*}\left(\frac{1}{\alpha }(\frac{b_1}{d_1^{*}}-1),0\right),E_2^{*}\left(0,\frac{1}{\beta }(\frac{b_2}{d_2^{*}}-1)\right),$$

provided $b_1>d_1^{*}$ and $b_2>d_2^{*}$, respectively. The quantities $d_1^{*}=\frac{1}{{\overline{S}}_u}-1+d_1,d_2^{*}=\frac{1}{{\overline{S}}_v}-1+d_2$, and, thus, $d_1^{*}>d_1,d_2^{*}>d_2$. Finally, the coexistence state

$$E_3^{*}\left(\frac{1}{\alpha }(\frac{b_1}{d_1^{*}}-1)(1-\frac{d_2^{*}}{b_2}[1+\frac{\beta }{\alpha }(\frac{b_1}{d_1^{*}}-1)]),\frac{d_2^{*}}{\alpha b_2}(\frac{b_1}{d_1^{*}}-1)[1+\frac{\beta }{\alpha }(\frac{b_1}{d_1^{*}}-1)]\right)$$

exists provided that $b_1>d_1^{*},b_2>d_2^{*}$ and $\frac{1}{\beta }(\frac{b_2}{d_2^{*}}-1)>\frac{1}{\alpha }(\frac{b_1}{d_1^{*}}-1)$. The following theorem summarizes the stability and bifurcation conclusions of system $\left(11\right)$.

 Theorem 3. 

For the approximation system $\left(11\right)$, the following statements hold:

(i) 

If $b_1\le d_1^{*},b_2\le d_2^{*}$, then the only steady state $E_0^{*}$ is globally asymptotically stable. Otherwise, it is unstable.

(ii) 

If $b_1>d_1^{*}$, then there exists a stable semi-trivial steady state $E_1^{*}$. Moreover, if $\frac{1}{\beta }(\frac{b_2}{d_2^{*}}-1)<\frac{1}{\alpha }(\frac{b_1}{d_1^{*}}-1)$, then $E_1^{*}$ is globally asymptotically stable.

(iii) 

If $b_2>d_2^{*}$, then there exists a semi-trivial steady state $E_2^{*}$, and it is stable if $\frac{1}{\beta }(\frac{b_2}{d_2^{*}}-1)>\frac{1}{\alpha }(\frac{b_1}{d_1^{*}}-1)$. Moreover, if $b_1\le d_1^{*}$, then $E_2^{*}$ is globally asymptotically stable.

(iv) 

If $b_1>d_1^{*},b_2>d_2^{*}$ and $\frac{1}{\beta }(\frac{b_2}{d_2^{*}}-1)>\frac{1}{\alpha }(\frac{b_1}{d_1^{*}}-1)$, then the coexistence steady state $E_3^{*}$ exists and is a saddle.

(v) 

If $b_1>d_1^{*},b_2>d_2^{*}$ and $\beta =\alpha \frac{d_1^{*}(b_2-d_2^{*})}{d_2^{*}(b_1-d_1^{*})}$, then the system undergoes a transcritical bifurcation at $E_3^{*}$.

Proof of Theorem 3.

The discussion of the stability of $E_0^{*}$ can be summarized as its stability with respect to perturbations in the two components separately. Then, the stability of the non-trivial steady states is discussed using the eigenvalues, and the Jacobian of system $\left(11\right)$ is

$${\mathbf{J}}^{*}={\left(\begin{array}{cc}{\overline{S}}_u(\frac{b_1(1+\alpha v)}{{[1+\alpha (u+v)]}^2}+1-d_1)& {\overline{S}}_u(\frac{-\alpha b_{1}u}{{[1+\alpha (u+v)]}^2})\\ \\ {\overline{S}}_v(\frac{-b_2{v}^2[1+2\beta (u+v)]}{{[1+\beta (u+v)]}^2{(u+v)}^2})& {\overline{S}}_v(\frac{b_{2}v(2u+v)+2b_2\beta uv(u+v)}{{[1+\beta (u+v)]}^2{(u+v)}^2}+1-d_2)\end{array}\right)}_{,}$$

(12)

evaluated at $E_1^{*}$, and $E_2^{*}$ and $E_3^{*}$ read as

$${\mathbf{J}}_{\mathbf{1}}^{*}={\left(\begin{array}{cc}{\overline{S}}_u(\frac{{d_1^{*}}^2}{b_1}+1-d_1)& {\overline{S}}_u(\frac{{d_1^{*}}^2}{b_1}-d_1^{*})\\ \\ 0& {\overline{S}}_v(1-d_2)\end{array}\right)}_{,}$$

$${\mathbf{J}}_{\mathbf{2}}^{*}={\left(\begin{array}{cc}{\overline{S}}_u(\frac{b_1}{1+\frac{\alpha }{\beta }(\frac{b_2}{d_2^{*}}-1)}+1-d_1)& 0\\ \\ {\overline{S}}_v(\frac{{d_2^{*}}^2}{b_2}-2d_2^{*})& {\overline{S}}_v(\frac{{d_2^{*}}^2}{b_2}+1-d_2)\end{array}\right)}_{,}$$

and

$${\mathbf{J}}_{\mathbf{3}}^{*}={\left(\begin{array}{cc}{\overline{S}}_u(\frac{{d_1^{*}}^2(1+\frac{d_2^{*}}{b_2}(\frac{b_1}{d_1^{*}}-1)[1+\frac{\beta }{\alpha }(\frac{b_1}{d_1^{*}}-1)])}{b_1}+1-d_1)& {\overline{S}}_u(\frac{{d_1^{*}}^2}{b_1}-d_1^{*})(1-\frac{d_2^{*}}{b_2}[1+\frac{\beta }{\alpha }(\frac{b_1}{d_1^{*}}-1)])\\ \\ {\overline{S}}_v(\frac{-{d_2^{*}}^2[1+\frac{2\beta }{\alpha }(\frac{b_1}{d_1^{*}}-1)]}{b_2})& {\overline{S}}_v(\frac{-{d_2^{*}}^2[1+\frac{2\beta }{\alpha }(\frac{b_1}{d_1^{*}}-1)]}{b_2}+1+d_2)\end{array}\right)}_{,}$$

respectively. Analyses similar to [12], which we omit, show that the conclusions in $\left(i\right),\left(ii\right),\left(iii\right),\left(iv\right)$ are correct.

Finally, we prove that $\left(v\right)$. Through a simple calculation found when $b_1>d_1^{*},b_2>d_2^{*}$ and $\frac{1}{\beta }(\frac{b_2}{d_2^{*}}-1)=\frac{1}{\alpha }(\frac{b_1}{d_1^{*}}-1)$, the first jury condition $1-trJ+detJ>0$ is broken. A similar analysis to Section 2 shows that system $\left(11\right)$ undergoes a transcritical bifurcation at $E_3^{*}$. If $\beta$ is taken as the bifurcation parameter, ${\beta }^{*}=\alpha \frac{d_1^{*}(b_2-d_2^{*})}{d_2^{*}(b_1-d_1^{*})}$ is actually the threshold that determines the survival of the population $v_t$, above which, $v_t$ will go extinct and the Wolbachia invasion will be successful. Below the threshold, the population $v_t$ is likely to survive. We have completed the proof. □

Although the original integrodifference equation model $\left(7\right)$ cannot be fully analyzed, we applied the average dispersal success approximation method to give a spatial approximation system $\left(11\right)$ that can be computed exactly and analyzed completely, thus establishing a correspondence with the non-spatial model $\left(1\right)$. In the next section, we will discuss the impact of the spatial parameters by comparing the spatial model with the non-spatial model.

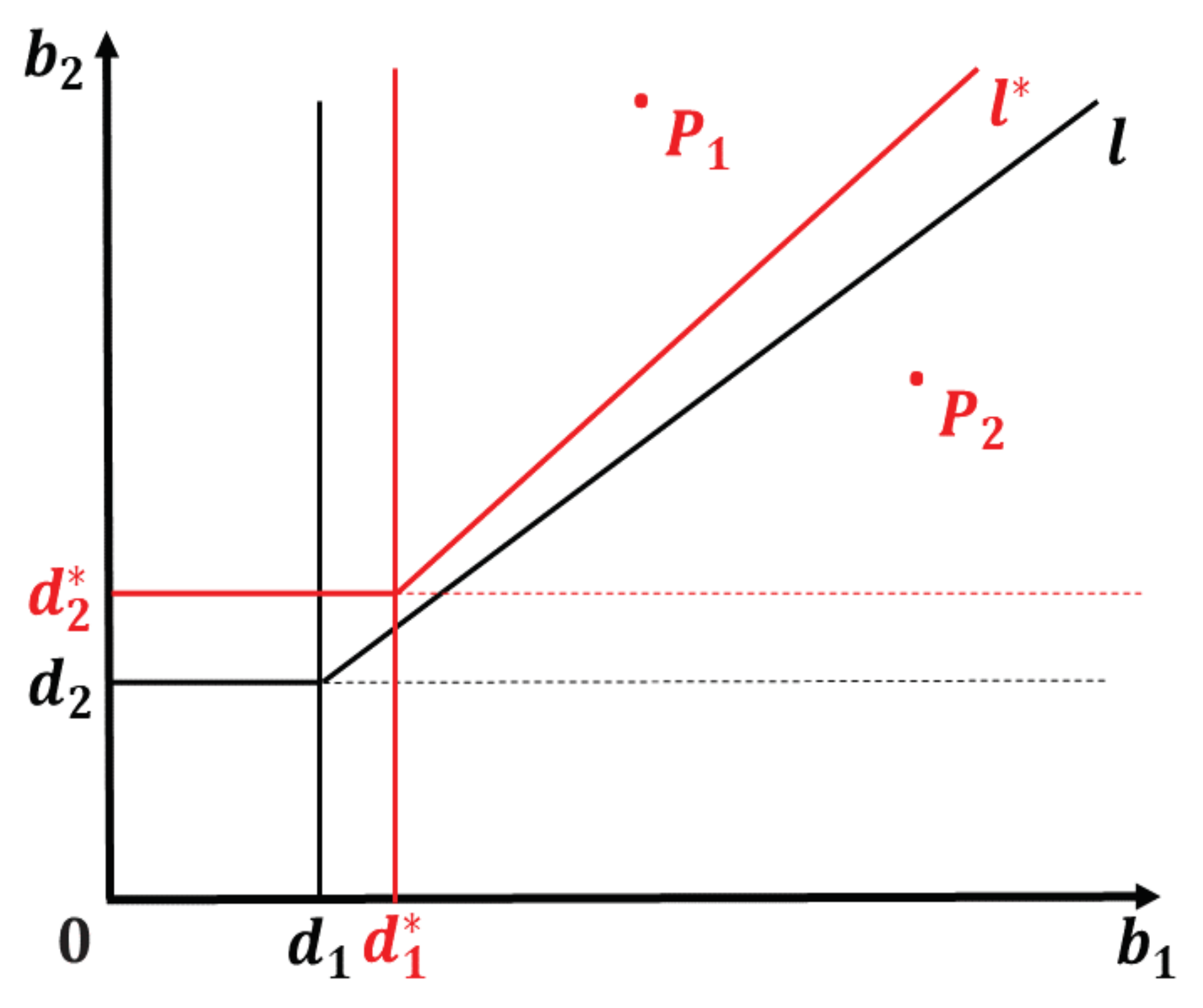
3.3. Comparison

In this section, we illustrate how the spatially implicit model $\left(11\right)$ with dispersal loss from the domain differs from the non-spatial model $\left(1\right)$ and the interesting patterns that result from the variation in the spatial parameters. The Figure 2 summarizes the stability regions of the two models on the $(b_1,b_2)$-space.

Obviously, we see that $d_1^{*}>d_1$ and $d_2^{*}>d_2$; this is because dispersal loss requires higher birth rates to ensure the persistence of both populations. The quantity $1/a_i,i=1,2$ denotes the mean dispersal distance of $u_t\left(x\right)$ and $v_t\left(x\right)$, respectively. Fixing the other parameters and increasing $a_i$, this means that the dispersal ability of both populations is weakened; then, it is noticed that $d_i^{*}$ will become smaller, which indicates that the weaker the dispersal ability of the population, the easier it is to survive in the domain. Increasing L also causes $d_i^{*}$ to decrease, i.e., it has the same effect, because the expansion of the habitat makes it more likely that the population will remain after dispersal. In the extreme case, when $a_{i}L\to \infty$, then $d_i^{*}\to d_i$, and we say that the spatial factor can be almost ignored. However, the approximation is more accurate for smaller values of L, so we will not expand on this case.

A surprising modification of the stability pattern arises from the introduction of and variation in spatial parameters. Because infection with Wolbachia causes a fitness cost, the dispersal ability of infected populations $u_t\left(x\right)$ is generally weaker than that of uninfected populations $v_t\left(x\right)$, so we discuss the effects of an increase in the ratio $a_1/a_2$ below. In the founder control case of the non-spatial model, i.e., when $b_1>d_1,b_2>d_2$ and $\frac{1}{\beta }(\frac{b_2}{d_2}-1)>\frac{1}{\alpha }(\frac{b_1}{d_1}-1)$, Wolbachia may not succeed in invading. However, at the same parameter values, introducing the spatial parameters $a_i$ and L, we consider the founder control case of the spatial implicit model, i.e., when $b_1>d_1^{*},b_2>d_2^{*}$ and $\frac{1}{\beta }(\frac{b_2}{d_2^{*}}-1)>\frac{1}{\alpha }(\frac{b_1}{d_1^{*}}-1)$. Fixing the other parameters and increasing $a_1/a_2$ implies that the dispersal ability of $u_t\left(x\right)$ becomes increasingly weaker with respect to $v_t\left(x\right)$; then, $d_1^{*}/d_2^{*}$ decreases, which can change the stability pattern to some extent so that $\frac{1}{\beta }(\frac{b_2}{d_2^{*}}-1)<\frac{1}{\alpha }(\frac{b_1}{d_1^{*}}-1)$. In this case, $E_1^{*}$ is globally asymptotically stable, implying that Wolbachia can certainly succeed in invading.

In addition, from the spatial implicit model itself, fixing other parameters and increasing $a_1/a_2$, $d_1^{*}/d_2^{*}$ becomes smaller and the slope of $l^{*}$ becomes larger, leading to a smaller stable region of $E_2^{*}$. This implies that the relative dispersal ability of population $v_t\left(x\right)$ becomes greater, but is not advantageous for its survival in the domain.

The numerical Figure 3 verify the stability of the spatially implicit model $\left(11\right)$ at the parameter values used for the two points $P_1$ and $P_2$ in Figure 2 by choosing the appropriate initial values.

4. Conclusions

This paper focuses on developing feasible integrodifference equations to explore the Wolbachia invasion dynamics. If the Wolbachia-infected mosquitoes win the competition with the uninfected ones, they contribute to the successful propagation of Wolbachia and interrupt the transmission of dengue. This promising topic has been preliminarily discussed by a non-spatial model in which we investigated its steady-state stability, as well as the type and direction of bifurcation. The results are summarized in Figure 1, where the parameter conditions within the region of $E_1$ global asymptotic stability guarantee the success of the Wolbachia invasion, whereas the other parameter conditions are not so favorable.

Spatial factors have an essential influence on Wolbachia propagation; therefore, we established an integrodifference model by introducing a Laplace kernel, and investigated the evolutionary patterns of two competing populations over a one-dimensional bounded domain. Similar analytical results are presented in Figure 2; however, some interesting observations caused by the variation in spatial parameters occur. We found that habitat expansion is beneficial for population persistence, but the expansion of the population dispersal ability has the opposite effect. Since infection with Wolbachia causes a fitness cost, we consider a reasonable parameter variation that fixes the other parameters and increases the ratio $a_1/a_2$, implying that the relative dispersal ability of the infected population becomes weaker. By comparison, our results show that, under the parameter condition where the non-spatial model cannot guarantee the success of Wolbachia dispersal, introducing the spatial factor and increasing $a_1/a_2$ can lead to the success of the Wolbachia invasion.

The following advanced work can be considered based on this paper. In the present analysis, we applied a monotone Beverton–Holt growth function. However, if we consider the non-monotone cases, such as applying the Ricker function, the dynamical behavior will be richer, with period-doubling bifurcation or even chaos. In addition, we only gave an analysis on the bounded domain. In fact, the present work can be extended to an unbounded domain and the traveling wave problem was considered. In particular, the analysis of bistable traveling waves may exhibit attractive results.