Forecasting Day-Ahead Traffic Flow Using Functional Time Series Approach
Abstract
:1. Introduction
2. Literature Review
3. Methods and Models
3.1. Functional Data Analysis
3.2. Functional Autoregressive Model
3.3. Autoegressive Integrated Moving Average (ARIMA) Model
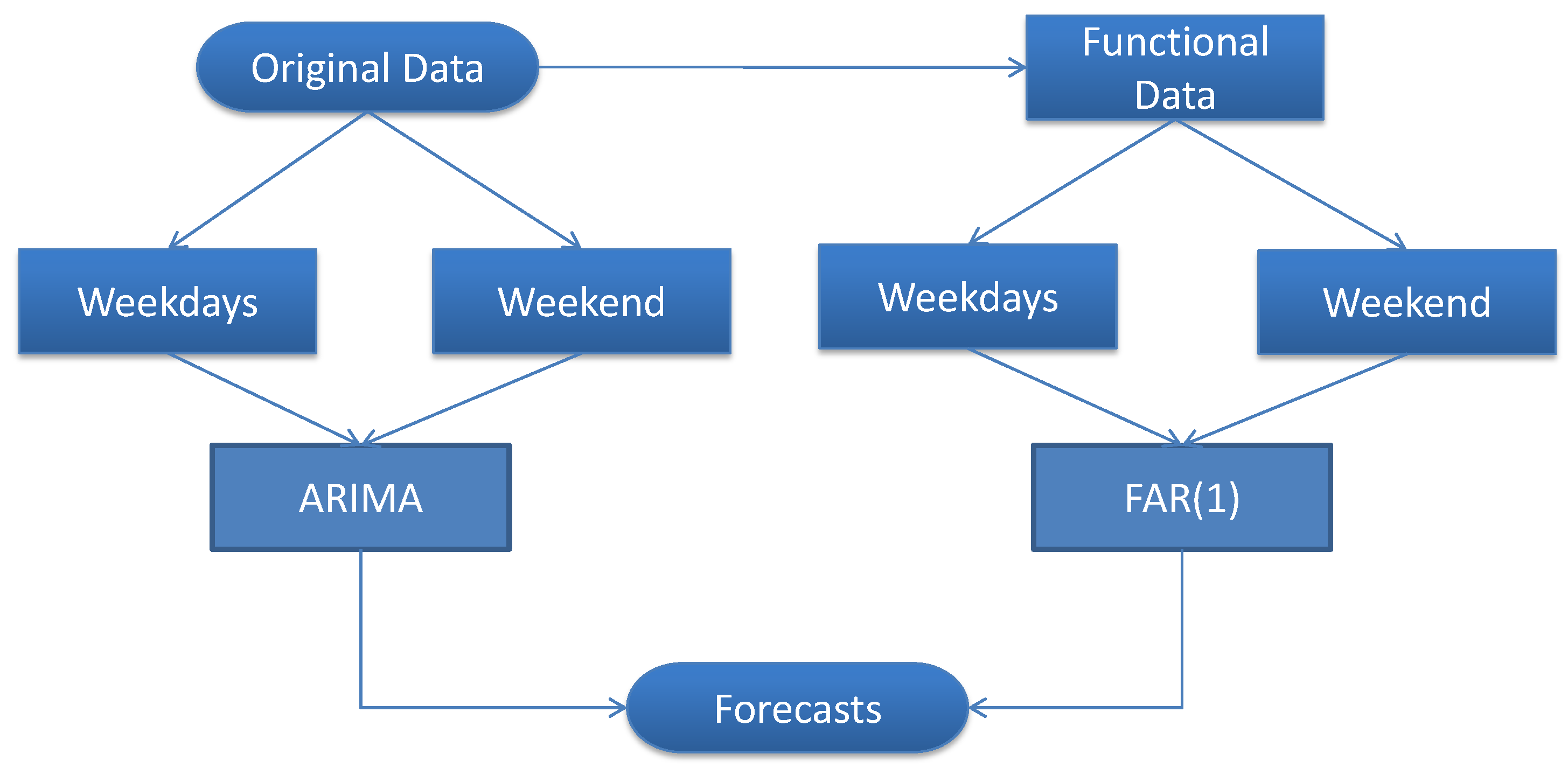
4. Analysis and Results
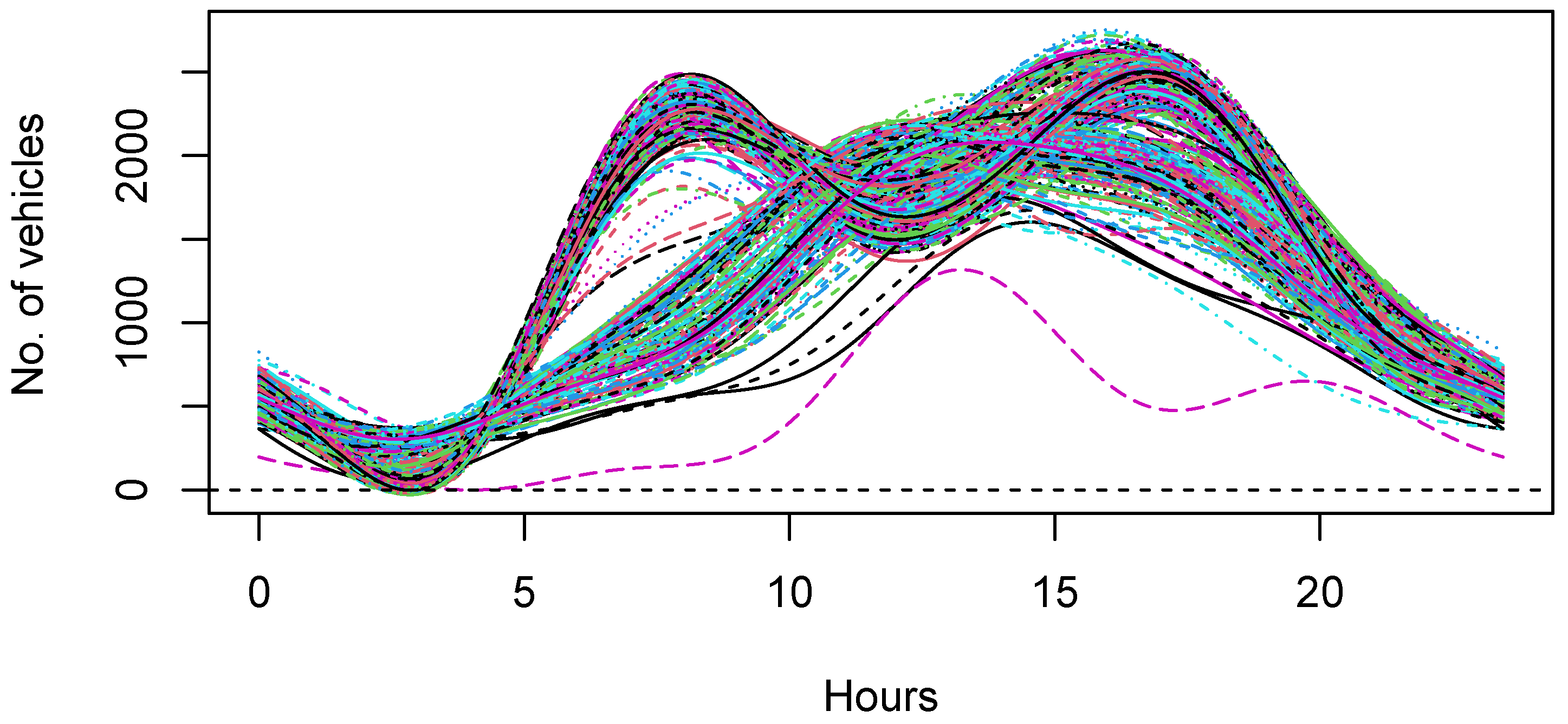
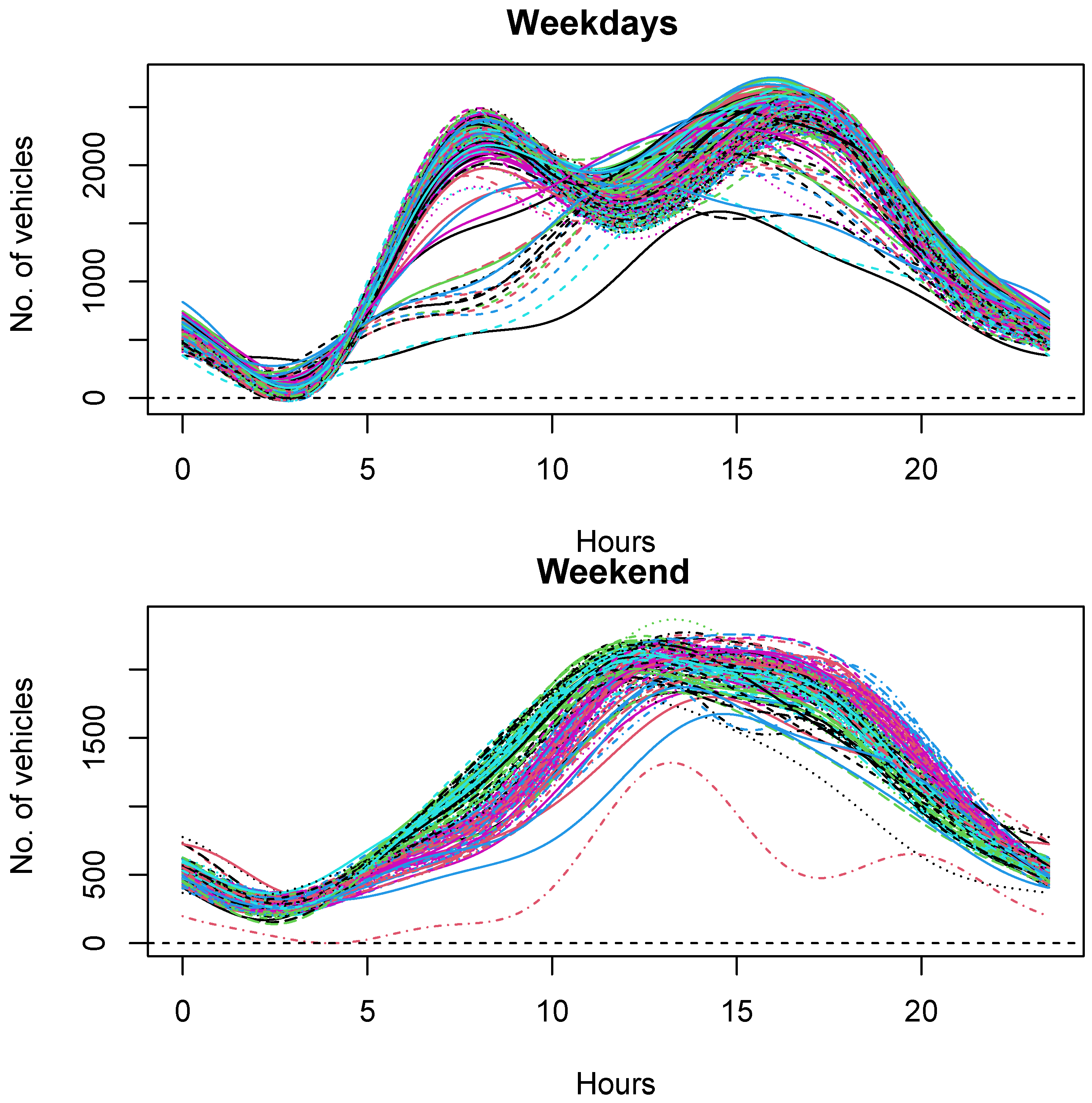
4.1. Data Description
4.2. Discrete Noisy Data Conversion to Functional Data
4.3. Models Estimation
4.4. Out-of-Sample Forecasting
5. Conclusions and Recommendations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vlahogianni, E.I.; Karlaftis, M.G.; Golias, J.C. Short-term traffic forecasting: Where we are and where we’re going. Transp. Res. Part C Emerg. Technol. 2014, 43, 3–19. [Google Scholar] [CrossRef]
- Zhou, T.; Han, G.; Xu, X.; Lin, Z.; Han, C.; Huang, Y.; Qin, J. δ-agree AdaBoost stacked autoencoder for short-term traffic flow forecasting. Neurocomputing 2017, 247, 31–38. [Google Scholar] [CrossRef]
- Fang, W.; Cai, W.; Fan, B.; Yan, J.; Zhou, T. Kalman-LSTM model for short-term traffic flow forecasting. In Proceedings of the 2021 IEEE 5th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 12–14 March 2021; Volume 5, pp. 1604–1608. [Google Scholar]
- Hou, Y.; Deng, Z.; Cui, H. Short-term traffic flow prediction with weather conditions: Based on deep learning algorithms and data fusion. Complexity 2021, 2021, 6662959. [Google Scholar] [CrossRef]
- Guo, J.; Huang, W.; Williams, B.M. Adaptive Kalman filter approach for stochastic short-term traffic flow rate prediction and uncertainty quantification. Transp. Res. Part C Emerg. Technol. 2014, 43, 50–64. [Google Scholar] [CrossRef]
- Vlahogianni, E.I.; Golias, J.C.; Karlaftis, M.G. Short-term traffic forecasting: Overview of objectives and methods. Transp. Rev. 2004, 24, 533–557. [Google Scholar] [CrossRef]
- Wang, K.; Ma, C.; Qiao, Y.; Lu, X.; Hao, W.; Dong, S. A hybrid deep learning model with 1DCNN-LSTM-Attention networks for short-term traffic flow prediction. Phys. A Stat. Mech. Appl. 2021, 583, 126293. [Google Scholar] [CrossRef]
- Cheng, Z.; Pang, M.S.; Pavlou, P.A. Mitigating traffic congestion: The role of intelligent transportation systems. Inf. Syst. Res. 2020, 31, 653–674. [Google Scholar] [CrossRef]
- Cui, Z.; Huang, B.; Dou, H.; Cheng, Y.; Guan, J.; Zhou, T. A Two-Stage Hybrid Extreme Learning Model for Short-Term Traffic Flow Forecasting. Mathematics 2022, 10, 2087. [Google Scholar] [CrossRef]
- Wu, Y.; Tan, H.; Qin, L.; Ran, B.; Jiang, Z. A hybrid deep learning based traffic flow prediction method and its understanding. Transp. Res. Part C Emerg. Technol. 2018, 90, 166–180. [Google Scholar] [CrossRef]
- Olayode, I.O.; Severino, A.; Tartibu, L.K.; Arena, F.; Cakici, Z. Performance Evaluation of a Hybrid PSO Enhanced ANFIS Model in Prediction of Traffic Flow of Vehicles on Freeways: Traffic Data Evidence from South Africa. Infrastructures 2021, 7, 2. [Google Scholar] [CrossRef]
- Lv, Y.; Duan, Y.; Kang, W.; Li, Z.; Wang, F.Y. Traffic flow prediction with big data: A deep learning approach. IEEE Trans. Intell. Transp. Syst. 2014, 16, 865–873. [Google Scholar] [CrossRef]
- Yang, S.; Li, H.; Luo, Y.; Li, J.; Song, Y.; Zhou, T. Spatiotemporal Adaptive Fusion Graph Network for Short-Term Traffic Flow Forecasting. Mathematics 2022, 10, 1594. [Google Scholar] [CrossRef]
- Ghosh, B.; Basu, B.; O’Mahony, M. Time-series modelling for forecasting vehicular traffic flow in Dublin. In Proceedings of the 84th Annual Meeting of the Transportation Research Board, Washington, DC, USA, 9–13 January 2005; pp. 1–22. [Google Scholar]
- Theodorou, T.I.; Salamanis, A.; Kehagias, D.D.; Tzovaras, D.; Tjortjis, C. Short-term traffic prediction under both typical and atypical traffic conditions using a pattern transition model. In Proceedings of the International Conference on Vehicle Technology and Intelligent Transport Systems, Porto, Portugal, 22–24 April 2017; Volume 2, pp. 79–89. [Google Scholar]
- Yao, S.N.; Shen, Y.C. Functional data analysis of daily curves in traffic: Transportation forecasting in the real-time. In Proceedings of the Computing Conference, London, UK, 18–20 July 2017; pp. 1394–1397. [Google Scholar]
- Chiou, J.M. Dynamical functional prediction and classification, with application to traffic flow prediction. Ann. Appl. Stat. 2012, 6, 1588–1614. [Google Scholar] [CrossRef] [Green Version]
- Su, F.; Dong, H.; Jia, L.; Qin, Y.; Tian, Z. Long-term forecasting oriented to urban expressway traffic situation. Adv. Mech. Eng. 2016, 8, 1687814016628397. [Google Scholar] [CrossRef]
- Liu, W. Traffic Flow Prediction Based on Local Mean Decomposition and Big Data Analysis. Ing. Syst. Inf. 2019, 24, 547–552. [Google Scholar] [CrossRef] [Green Version]
- Feng, S.; Wang, X.; Sun, H.; Zhang, Y.; Li, L. A better understanding of long-range temporal dependence of traffic flow time series. Phys. A Stat. Mech. Appl. 2018, 492, 639–650. [Google Scholar] [CrossRef]
- Chi, Z.; Shi, L. Short-term traffic flow forecasting using ARIMA-SVM algorithm and R. In Proceedings of the 5th International Conference on Information Science and Control Engineering (ICISCE), Zhengzhou, China, 20–22 July 2018; pp. 517–522. [Google Scholar]
- Min, X.; Hu, J.; Chen, Q.; Zhang, T.; Zhang, Y. Short-term traffic flow forecasting of urban network based on dynamic STARIMA model. In Proceedings of the 12th International IEEE Conference on Intelligent Transportation Systems, St. Louis, MO, USA, 4–7 October 2009; pp. 1–6. [Google Scholar]
- Doğan, E. Analysis of the relationship between LSTM network traffic flow prediction performance and statistical characteristics of standard and nonstandard data. J. Forecast. 2020, 39, 1213–1228. [Google Scholar] [CrossRef]
- Sabry, M.; Abd-El-Latif, H.; Badra, N. Comparison between regression and ARIMA models in forecasting traffic volume. Aust. J. Basic Appl. Sci. 2007, 1, 126–136. [Google Scholar]
- Kim, T.; Kim, H.; Lovell, D.J. Traffic flow forecasting: Overcoming memoryless property in nearest neighbor non-parametric regression. In Proceedings of the IEEE Intelligent Transportation Systems, Vienna, Austria, 16 September 2005; pp. 965–969. [Google Scholar]
- Alam, I.; Farid, D.M.; Rossetti, R.J. The prediction of traffic flow with regression analysis. In Emerging Technologies in Data Mining and Information Security; Springer Nature Singapore Pte Ltd.: Singapore, 2019; pp. 661–671. [Google Scholar]
- Polson, N.G.; Sokolov, V.O. Deep learning for short-term traffic flow prediction. Transp. Res. Part C Emerg. Technol. 2017, 79, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Kong, F.; Li, J.; Jiang, B.; Zhang, T.; Song, H. Big data-driven machine learning-enabled traffic flow prediction. Trans. Emerg. Telecommun. Technol. 2019, 30, e3482. [Google Scholar] [CrossRef]
- Hou, Q.; Leng, J.; Ma, G.; Liu, W.; Cheng, Y. An adaptive hybrid model for short-term urban traffic flow prediction. Phys. A Stat. Mech. Appl. 2019, 527, 121065. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, N.; Luo, X.; Yang, M. Traffic Flow Forecasting Analysis based on Two Methods. J. Phys. Conf. Ser. 2021, 1861, 012042. [Google Scholar] [CrossRef]
- Ren, C.; Chai, C.; Yin, C.; Ji, H.; Cheng, X.; Gao, G.; Zhang, H. Short-Term Traffic Flow Prediction: A Method of Combined Deep Learnings. J. Adv. Transp. 2021, 2021, 15. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Haghani, A. A hybrid short-term traffic flow forecasting method based on spectral analysis and statistical volatility model. Transp. Res. Part C Emerg. Technol. 2014, 43, 65–78. [Google Scholar] [CrossRef]
- Hu, W.; Yan, L.; Liu, K.; Wang, H. A short-term traffic flow forecasting method based on the hybrid PSO-SVR. Neural Process. Lett. 2016, 43, 155–172. [Google Scholar] [CrossRef]
- Cai, W.; Yang, J.; Yu, Y.; Song, Y.; Zhou, T.; Qin, J. PSO-ELM: A hybrid learning model for short-term traffic flow forecasting. IEEE Access 2020, 8, 6505–6514. [Google Scholar] [CrossRef]
- Zhang, T.; Hu, L.; Liu, Z.; Zhang, Y. Nonparametric regression for the short-term traffic flow forecasting. In Proceedings of the International Conference on Mechanic Automation and Control Engineering (IEEE), Wuhan, China, 26–28 June 2010; pp. 2850–2853. [Google Scholar]
- Wang, W.; Zhang, H.; Li, T.; Guo, J.; Huang, W.; Wei, Y.; Cao, J. An interpretable model for short term traffic flow prediction. Math. Comput. Simul. 2020, 171, 264–278. [Google Scholar] [CrossRef]
- Rong, Y.; Zhang, X.; Feng, X.; Ho, T.K.; Wei, W.; Xu, D. Comparative analysis for traffic flow forecasting models with real-life data in Beijing. Adv. Mech. Eng. 2015, 7, 1687814015620324. [Google Scholar] [CrossRef] [Green Version]
- Chang, G.; Zhang, Y.; Yao, D.; Yue, Y. A summary of short-term traffic flow forecasting methods. In ICCTP: Towards Sustainable Transportation Systems, Proceedings of the 11th International Conference of Chinese Transportation Professionals, Nanjing, China, 14–17 August 2011; American Society of Civil Engineers: Reston, VA, USA; pp. 1696–1707.
- Lippi, M.; Bertini, M.; Frasconi, P. Short-term traffic flow forecasting: An experimental comparison of time-series analysis and supervised learning. IEEE Trans. Intell. Transp. Syst. 2013, 14, 871–882. [Google Scholar] [CrossRef]
- Smith, B.L.; Demetsky, M.J. Traffic flow forecasting: Comparison of modeling approaches. J. Transp. Eng. 1997, 123, 261–266. [Google Scholar] [CrossRef]
- Peng, H.; Bobade, S.U.; Cotterell, M.E.; Miller, J.A. Forecasting traffic flow: Short term, long term, and when it rains. In Proceedings of the International Conference on Big Data, Seattle, WA, USA, 25–30 June 2018; pp. 57–71. [Google Scholar]
- Ramsay, J.O.; Dalzell, C. Some tools for functional data analysis. J. R. Stat. Soc. Ser. (Methodol.) 1991, 53, 539–561. [Google Scholar] [CrossRef]
- Ferraty, F.; Vieu, P. Nonparametric Functional Data Analysis: Theory and Practice; Springer: New York, NY, USA, 2006. [Google Scholar]
- Ramsay, J.; Hooker, A.G.; Graves, S. Functional Data Analysis with R and MATLAB; Springer: New York, NY, USA, 2009. [Google Scholar]
- Elezovic, S.; de Luna, X. A Note on the Estimation of Functional Autoregressive Models. 2009, pp. 1–12. Available online: https://www.diva-portal.org/smash/record.jsf?dswid=8261&pid=diva2%3A174705 (accessed on 17 January 2022).
- Horváth, L.; Kokoszka, P. Inference for Functional Data with Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 200, pp. 1–426. [Google Scholar]


| Date | 1/1/2016 | 2/1/2016 | 3/1/2016 | 4/1/2016 | 5/1/2016 | 6/1/2016 | 7/1/2016 |
|---|---|---|---|---|---|---|---|
| 9:30 | 544 | 1141 | 918 | 1510 | 1642 | 1733 | 1784 |
| 11:30 | 986 | 1688 | 1437 | 1582 | 1624 | 1533 | 1585 |
| 13:30 | 1432 | 1697 | 1935 | 1861 | 1775 | 1739 | 1654 |
| 15:30 | 1543 | 1833 | 2083 | 2002 | 1838 | 1896 | 1993 |
| 17:30 | 1323 | 1621 | 1862 | 2565 | 2264 | 2527 | 2479 |
| 19:30 | 917 | 1209 | 1361 | 1344 | 1360 | 1294 | 1474 |
| 21:30 | 622 | 621 | 788 | 712 | 777 | 763 | 915 |
| 23:30 | 373 | 545 | 473 | 497 | 445 | 399 | 481 |
| Days | Model | MSE | MAE | MAPE | MSPE |
|---|---|---|---|---|---|
| Full data | FAR(1) | 24,762.96 | 102.01 | 9.94 | 2.75 |
| ARIMA(7,1,0) | 38,871.68 | 118.13 | 11.80 | 3.90 | |
| Working-days only | FAR(1) | 21,445.71 | 86.94 | 8.24 | 2.19 |
| ARIMA(5,1,0) | 28,791.97 | 99.20 | 9.41 | 2.58 | |
| Weekend days only | FAR(1) | 12,228.96 | 80.73 | 9.36 | 2.170 |
| ARIMA(2,1,0) | 19,632.88 | 97.40 | 10.30 | 2.48 |
| Days | Models | MAPE for Each Day of the Week | ||||||
|---|---|---|---|---|---|---|---|---|
| M | T | W | T | F | S | S | ||
| Working-days and | FAR(1) | 13.09 | 7.66 | 7.13 | 7.80 | 8.63 | 11.40 | 13.66 |
| weekend combine | ARIMA(7,1,0) | 14.65 | 11.47 | 8.37 | 7.09 | 12.13 | 16.33 | 12.54 |
| Working-days | FAR(1) | 11.51 | 7.33 | 6.70 | 6.20 | 9.45 | ||
| ARIMA(5,1,0) | 11.87 | 9.38 | 7.74 | 6.85 | 11.21 | |||
| Weekend | FAR(1) | 9.27 | 9.44 | |||||
| ARIMA(2,1,0) | 10.08 | 10.52 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shah, I.; Muhammad, I.; Ali, S.; Ahmed, S.; Almazah, M.M.A.; Al-Rezami, A.Y. Forecasting Day-Ahead Traffic Flow Using Functional Time Series Approach. Mathematics 2022, 10, 4279. https://doi.org/10.3390/math10224279
Shah I, Muhammad I, Ali S, Ahmed S, Almazah MMA, Al-Rezami AY. Forecasting Day-Ahead Traffic Flow Using Functional Time Series Approach. Mathematics. 2022; 10(22):4279. https://doi.org/10.3390/math10224279
Chicago/Turabian StyleShah, Ismail, Izhar Muhammad, Sajid Ali, Saira Ahmed, Mohammed M. A. Almazah, and A. Y. Al-Rezami. 2022. "Forecasting Day-Ahead Traffic Flow Using Functional Time Series Approach" Mathematics 10, no. 22: 4279. https://doi.org/10.3390/math10224279
APA StyleShah, I., Muhammad, I., Ali, S., Ahmed, S., Almazah, M. M. A., & Al-Rezami, A. Y. (2022). Forecasting Day-Ahead Traffic Flow Using Functional Time Series Approach. Mathematics, 10(22), 4279. https://doi.org/10.3390/math10224279








