Modern Physical-Mathematical Models and Methods for Design Surface Acoustic Wave Devices: COM Based P-Matrices and FEM in COMSOL

Abstract

Comparative results of calculation and measurement of the frequency responses of the surface acoustic waves filter on a piezoelectric substrate of 64°YX-cut lithium niobate and delay line on a piezoelectric substrate of 128°YX-cut lithium niobate is presented. The calculation was performed on the basis of two approaches—the finite element method in the COMSOL Multiphysics software and using the model of coupling of modes based on P-matrices. A brief overview and features of each approach are presented. The calculation results based on the two approaches are in good agreement with each other and with the experimental results of measurements of the characteristics of the bandpass filter. The delay line operating with the use of the third harmonic frequency is calculated by FEM. The results showed a good match between numerical simulation and experiment. The considered approaches for designing SAW devices allow us to relatively quickly and accurately predict the frequency responses at the simulation stage, thereby reducing the number of experimental iterations and increasing the efficiency of development.

1. Introduction

In recent decades, devices based on surface acoustic waves (SAW) have become an integral part of modern radio electronics [1,2]. They are massively used both in household electronic equipment and in communication systems, military and special equipment with special operating conditions. SAW devices carve out a niche in the frequency range from tens of megahertz to 2.5…3 GHz due to the advantages of mass-dimensional indicators, high reliability, low cost and excellent electrical characteristics [1,2]. Research and development of new SAW devices are relevant due to the increasing need for such components for modernization and the creation of new equipment for telecommunication systems.

One of the important stages in the design of SAW filters is mathematical modeling. The reduction in design time and simultaneous reduction in filter development costs is an urgent task, which can be solved both by applying modern computational soft and by improving and developing already-known modeling tools. The modeling stage allows you to reduce the time of the device’s entry into the market and increase the efficiency of development, both by increasing accuracy and by minimizing experimental iterations.

A comparison of the simulation and measurements for SAW devices shows good agreement for different approaches [3,4,5,6,7]. Analytical [3,4,5] and numerical [6,7] approaches are equally popular with developers. The priority is determined by the specific task. For example, analytical methods are required for the initial synthesis and optimization of SAW device topology; numerical methods are suitable for the SAW parameter extraction [8]. Finally, the numerical approach is suitable for verification of development at the final stage, because the real experiment can be replaced by a very accurate multiphysics simulation.

Therefore, the topic of developing SAW devices is relevant today.

The presence of periodic multi-element topological structures (electrodes) is one of the features of SAW devices. The principle of operation is based on the effects of multiple reflections and transformations of SAW in such structures. The SAW filter (Figure 1a) and SAW delay line (DL) (Figure 1b) consist of a piezoelectric substrate with input and output inter-digital transducers (IDT) applied to it for the excitation and reception of acoustic waves. The operating frequency is determined by the velocity of the SAW and the step of the arrangement of the electrodes of the IDT (f = V/λ, where V is the velocity of the wave, λ is the wavelength).

The aim of the work is to demonstrate the capabilities of modern approaches for modeling SAW devices by the example of calculating a bandpass filter on a piezoelectric substrate of 64°YX-cut lithium niobate and a test SAW DL on 128°YX-cut lithium niobate. The calculation is based on two approaches—the finite element method (FEM) in the COMSOL Multiphysics software and the model of the coupling of modes (COM-model) based on P-matrices.

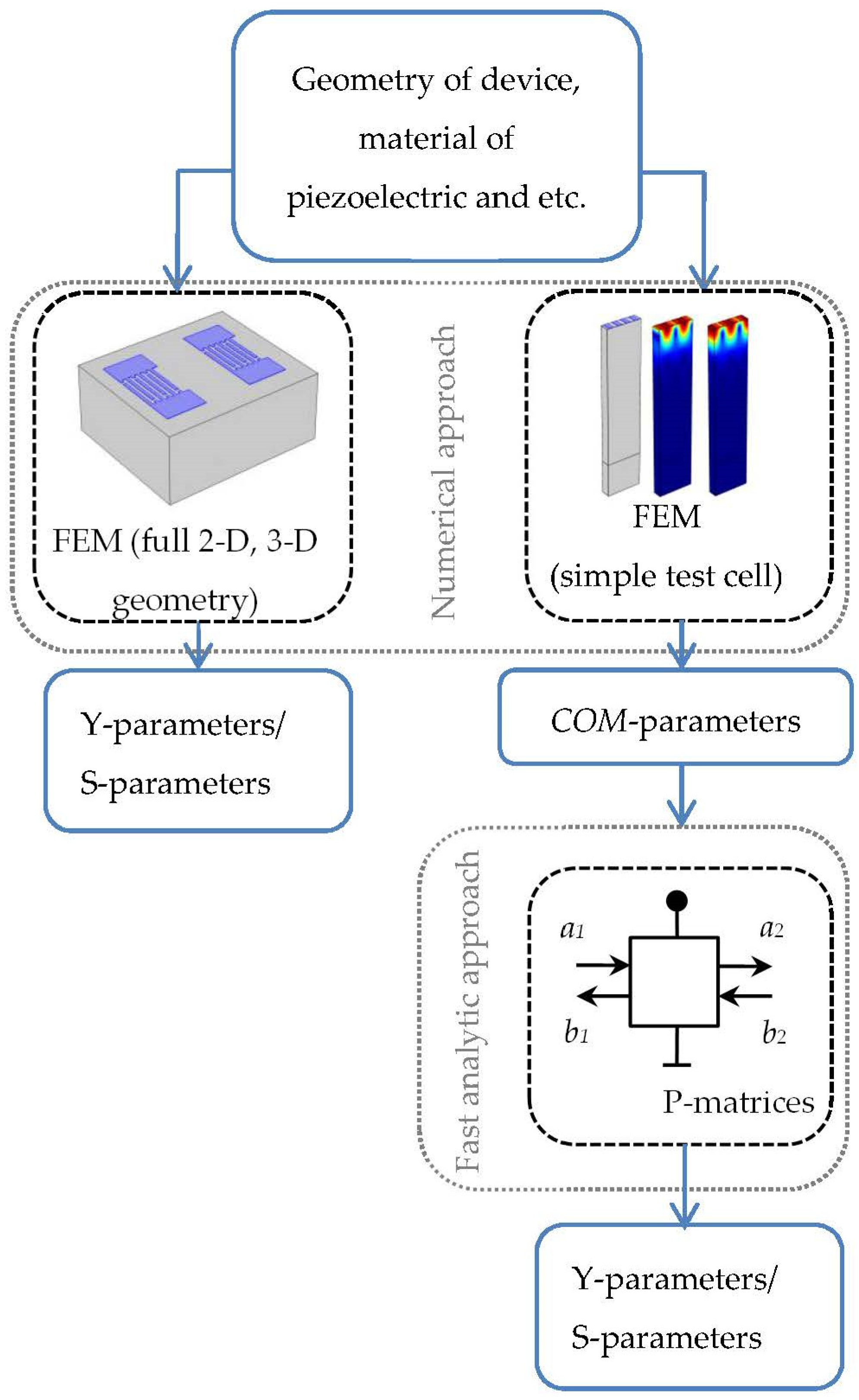
2. Physical-Mathematical Models

Today, there are various models [9,10,11,12,13] and methods for modeling SAW devices that allow predicting the frequency responses of devices with varying degrees of accuracy. These are the delta sources method, the method of equivalent circuits [11], the COM model [9,10], P-matrices [9,10], Green’s functions, some discrete analysis approaches [12,13], hierarchical cascading based on B-matrices [14] and the finite element method (FEM) [15].

The analytical approach based on the COM model and its formalization based on the P-matrices is most widely used among developers for designing SAW devices. The COM model requires a small number of key COM parameters and a relatively short calculation time, which allows the synthesis and optimization of parameters of the topology of a SAW device.

The rapid progress of computing technologies and the development of software have made it possible to solve many problems with multiphysical communication. Recently, numerical methods of analysis involving standard computer packages, such as COMSOL and ANSYS, have become widespread [16,17,18,19,20,21,22,23]. The main advantage of numerical approaches based on FEM is that their use requires only knowledge of the constants of the material and the geometry of the device. Therefore, it is possible to calculate devices entirely in 3-D and 2-D dimensions. In addition, these methods allow, based on the analysis of simple test cells, to determine the values of key COM parameters for fast analytical approaches based on COM and P-matrices. However, it should be understood that taking into account many parameters in 3-D modeling of real full-aperture devices leads to a very large increase in the requirements for computing resources and an increase in the analysis time.

Figure 2 shows schematically two modern approaches to modeling SAW devices. The first approach is to calculate the device as a whole using FEM. The second is a preliminary analysis of simple test cells using FEM in order to obtain key COM parameters [24,25,26], and then based on these parameters, calculations are performed using a fast P-matrix approach. The purpose of each approach is to calculate a complete set of Y-parameters, from which they are converted to S-parameters by recalculation.

2.1. COM-Model

The model [27] is based on the consideration of two homogeneous plane waves propagating in opposite directions in the structure of the device:

$$R\left(x,k\right)=R\left(k\right)\exp \left(-jkx\right);S\left(x,k\right)=S\left(k\right)\exp \left(+jkx\right),$$

(1)

where R(k), S(k)—the amplitudes of the corresponding waves,

j—imaginary unit,

x—coordinate along which the wave propagates,

k = ω/V—the wave number,

ω = 2πf—the circular frequency,

f—the frequency,

V—the velocity in the structure.

Processes of reflection and transformation of SAW take place when the wave propagates in the periodic electrode structure. The presence of electrodes on the surface changes the velocity of wave propagation and causes mutual communication between the waves. Note, two reasons: the first is the partial reflection of SAW from the electrodes and the second is the excitation of SAW by current flowing in metal electrodes. For example, you can write equations linking the complex amplitudes of waves at the input R₁(x,k), S₁(x,k) and the output R₂(x,k), S₂(x,k) of the input IDT and the equation for the current through the input IDT I (Figure 3a). To formalize the calculation process, it is convenient to present the coupled wave equations in matrix form in the form of P-matrices elements connecting the amplitudes of acoustic waves at the input and output of acoustic ports, as well as the current and applied potential at the electrical port.

$$\left[\begin{array}{c}{b}_1^{}\\ a_2\\ I\end{array}\right]=\left[\begin{array}{ccc}{P}_{11}& P_{12}& P_{13}\\ P_{21}& P_{22}& P_{23}\\ P_{31}& P_{32}& P_{33}\end{array}\right]\left[\begin{array}{c}{a}_1\\ b_2\\ U\end{array}\right],$$

(2)

where b₁, b₂, a₁, a₂ are the amplitudes of the waves at the input and output of the acoustic ports of a single IDT,

I and U—the current and voltage at the electrical port.

Consider the topology of the SAW DL from the positions of the COM model (Figure 3a). Each IDT is considered an element with two acoustic inputs and one electric. Following the ideology of the P-matrix method, the topology of the DL can be formally represented in the form of three elements of P-matrices, shown in Figure 3b. The first element displays the input IDT and is connected to the input port. The second element is the free surface of the piezoelectric material or the gap between the transducers. The third element is the output IDT connected to the output port. The acoustic ports of the units are connected in series with each other in accordance with the topological description. The potential U₁ is applied to the input port, U₂ is applied to the output port, and currents I₁ and I₂ flow through them, respectively.

The sequence of actions when using the P-matrices method is as follows:

• an equivalent acoustoelectric circuit is drawn up (Figure 3b);
• the P-matrices of all elements of the device are calculated;
• the total P-matrix (P^∑) is calculated (Figure 3c), which determines the relationship of complex wave amplitudes at the input and output of the device as a whole.

The components of the total P-matrix of the acoustic channel (P^∑) can be calculated by multiplying the corresponding components. Conditionally write down:

P^∑ = P^IDT−1 × P^gap × P^IDT−2.

(3)

The total matrix determines the relationship of the complex amplitudes of the waves at the input and output of the SAW device. It can be used to form a matrix of admittances. Moreover, it is necessary to calculate the total matrices relative to the input and output ports from the following physical considerations:

$$\left[\begin{array}{c}{b}_1\\ a_4\\ I_i\end{array}\right]=\left[\begin{array}{ccc}{P}_{11}^{\Sigma }& P_{12}^{\Sigma }& P_{13}^{\Sigma }\\ P_{21}^{\Sigma }& P_{22}^{\Sigma }& P_{23}^{\Sigma }\\ P_{31}^{\Sigma }& P_{32}^{\Sigma }& {\left(P_{33}^{\Sigma }\right)}_{ik}\end{array}\right]{\left[\begin{array}{c}{a}_1\\ b_4\\ U_k\end{array}\right]}_{U_j=0},$$

(4)

where b₁, b₄, a₁, a₄—the amplitudes of the waves at the input and output of the acoustic ports of the DL,

I_i, U_k, i, k, j = 1, 2 (k ≠ j)—the currents and voltages at the input and output electrical ports,

(P^∑₃₃)_ik—an element of the total matrix is the admittance Y_ik, depending on the state of the electrical ports.

In matrices form, the SAW DL under consideration, as a two-port device, shown in Figure 3d, can be described using the admittance matrix of interest to us:

$$\left[\begin{array}{c}{I}_1\\ I_2\end{array}\right]=\left[\begin{array}{cc}{Y}_{11}& Y_{12}\\ Y_{21}& Y_{22}\end{array}\right]\left[\begin{array}{c}{U}_1\\ U_2\end{array}\right],$$

(5)

where I_i и U_i, i = 1, 2 currents and voltages at the input and output electrical ports, respectively, elements Y₁₁, Y₁₂, Y₂₁, Y₂₂—Y-parameters, must be determined.

For the successful implementation of COM based on P-matrices, it is necessary to know:

1.

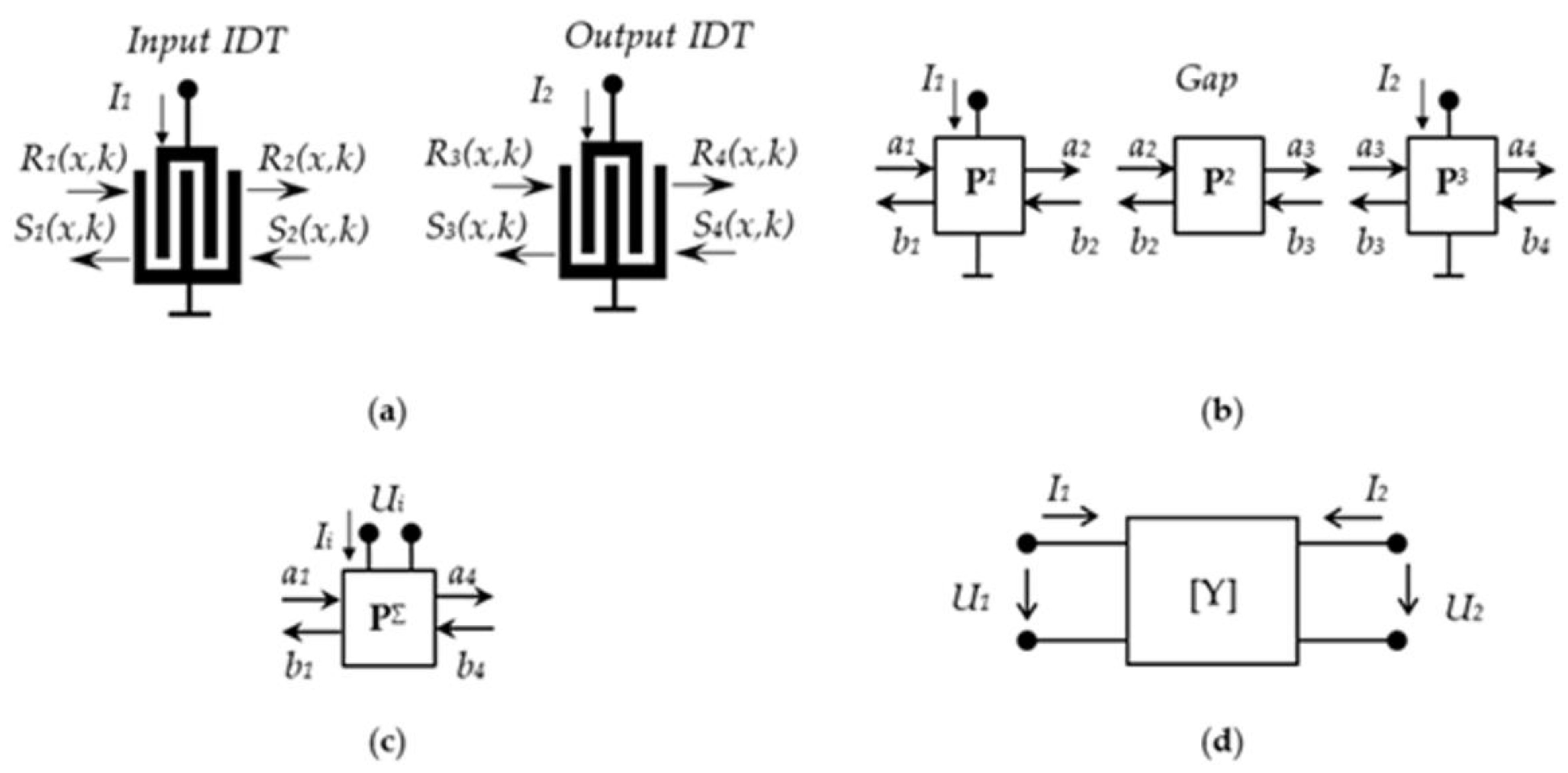
The physical interpretation of all components of the P-matrices [9,10]. Acoustic components P₁₁, P₁₂, P₂₁, and P₂₂ describe the transmission and reflection coefficients over the acoustic ports. The components P₁₃ and P₂₃ show the efficiency of excitation of surface acoustic waves by applying voltage U to the bus bars of the IDT. The components P₃₁ and P₃₂ characterize the efficiency of conversion of SAW into the electric current I in the IDT. P₁₃, P₂₃, P₃₁, and P₃₂ are directly proportional to the effective value of the electromechanical coupling coefficient. The element P₃₃ of the total matrix determines the desired admittance of the device. To analyze the devices, it is necessary to determine all the components of the P-matrices;

2.

Rules for cascading P-matrices [9]. So, for example, the element P₃₃ of the total P-matrix of two “neighboring” blocks is calculated by the formula:

$$P_{33}^{\Sigma }=P_{33}^1+P_{33}^2+P_{32}^1\frac{P_{13}^2+P_{11}^2{P}_{23}^1}{1-P_{11}^2{P}_{22}^1}+P_{31}^2\frac{P_{23}^1+P_{22}^1{P}_{13}^2}{1-P_{22}^1{P}_{11}^2};$$

(6)

3.

The transition from a set of Y-parameters to S-parameters. Example of recalculation for the transmission coefficient:

$$S_{21}=\frac{-2Y_{21}{Y}_0}{\left(Y_0+Y_{11}\right)\left(Y_0+Y_{22}\right)-Y_{12}{Y}_{21}}$$

(7)

Most often, the S-parameters are determined with a characteristic impedance value equal to Z₀ = 50 ohms. The physical meaning of S₁₁ is the reflection coefficient at the input, and S₂₁ is the complex transmission coefficient. Y₀ = 1/Z₀.

4.

A method for determining COM parameters [8,24,25,26]. A set of key COM parameters is necessary to find all the components of the P-matrices. The most common ways to obtain COM parameters are the following:

• Analytical solutions;
• Extraction of parameters from experimental data with subsequent construction of empirical dependencies;
• Numerical solutions based on FEM.

It should be noted that analytical solutions, as a rule, are limited to either simple geometries and the case of isotropic materials, or to special cases for which these solutions are valid. In general, a large number of corrections and empirical coefficients are needed, taking into account the features of the topology and manufacturing technology, as well as the materials used. Thus, the method of obtaining the necessary coefficients based on numerical modeling is seen by the author as a good alternative to additional experimental studies. In the approach described here (FEM + COM), the author adheres to the technique of extracting key COM parameters based on the numerical approach in the COMSOL.

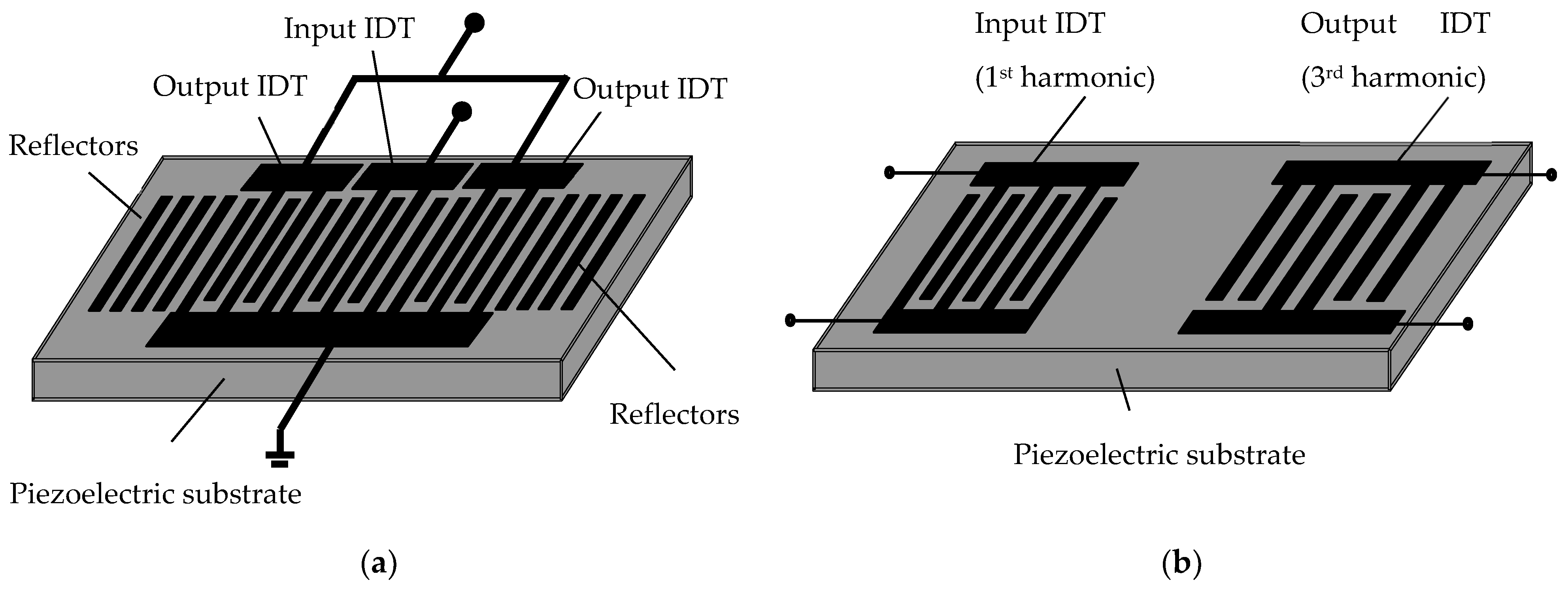
2.2. FEM in COMSOL

The COMSOL Multiphysics software based on the finite element method allows the modeling of SAW devices. The problem of SAW propagation is determined by differential equations and solved considering the complex geometry of the device, the properties of materials (substrate, electrodes, reflectors) and boundary conditions.

It is known that the presence of a wave of mechanical displacements and an associated wave of electric potential propagating at the same phase velocity is a feature of the propagation of SAW in piezoelectric substrates. Moreover, in the general case of acoustic waves (Rayleigh and leaky SAW), three orthogonal components of mechanical displacement (two shear and one longitudinal) must be taken into account. Taking into account all these physical features, it is possible by analyzing the propagation of SAW only by numerical method.

Piezoelectric equations in tensor form have the following form:

$$\begin{array}{l}T=C\cdot S-e\cdot E\\ D=\epsilon \cdot E+e\cdot S\end{array}$$

(8)

where T, S—stress and strain tensors;

E, D—electric field intensity and induction vectors;

C, e, ε—tensors of elastic modulus, piezomodules and permittivity, respectively. These tensors and the density of the material are constants that fully describe the piezoelectric substrate.

The FEM-based approach makes it possible to obtain the necessary parameters and characteristics in 3-D dimension, including estimating the leaky of a useful acoustic mode into the depth of the substrate and obtaining information about all acoustic modes excited in a particular topology, in contrast to the one-dimensional consideration of the problem using COM-model. At its core, such 3-D modeling will be the most accurate, since it more adequately takes into account wave processes in real devices. However, at the same time, this calculation requires large computational and time resources.

Reducing and optimizing the model, consider several assumptions:

(1)

The transducer must have no apodization by amplitude weighting;

(2)

The transducer aperture must not be less than 15 wavelengths; otherwise, the waveguide effect must be taken into account [28];

(3)

The distance between neighboring transducers should be small, then it is possible not to take diffraction into account;

(4)

The solution for a small aperture extends to the full transducer aperture with the accuracy of the aperture coefficient;

(5)

We do not consider the influence of contact bus bars.

It is clear that these assumptions significantly narrow the range of analyzed SAW devices, but at the same time, this approach is applicable to the Double Mode SAW filter (DMS) [29] and the DL.

Figure 4 shows the principle of design (DMS-filter) optimization for FEM in COMSOL. For example, a topology with a small number of IDT electrodes and reflectors is considered.

As can be seen from Figure 4, a full 3D design, together with bus bars, requires a fairly large number of finite elements or mesh elements for a discretized model. Figure 4 presents an approach to reduce and simplify the design in question. It should be understood that each node will have four unknowns (three components of mechanical displacement and potential), which depend on the physics of the problem to be solved (in our case-piezoelectric), then the number of degrees of freedom (DOF) for the entire structure will also be large. Therefore, by reducing (“narrowing”) the geometry and optimizing the mesh, the number of DOF can also be reduced quite significantly. In the real design of the considered filter, the total number of electrodes of IDT and reflectors is more than 150 pieces.

COMSOL allows performing analysis of SAW devices in the Eigenfrequency domain, time analysis (Time Dependent), and calculation of the frequency domain and stationary. In our case, it is necessary to calculate the admittance of the SAW device, that is, to find the real and imaginary parts of the admittances Y₁₁, Y₂₁, Y₁₂, and Y₂₂ in the frequency domain. The calculation sequence in COMSOL is as follows:

• Defining the workspace and setting the geometry;
• The input of initial data (material, aperture, etc.);
• Setting the initial and boundary conditions (potentials on the electrodes, a perfectly matched layer (PML), etc.);
• Building a mesh;
• Determination of the parameters of the solver and calculation.

Finally, we obtain a large set of decisions on the number of DOF. We can go to the necessary characteristics of the device, in our case it is a set of Y-parameters from the built-in COMSOL tools. Then, to determine the transfer coefficient, go from the Y-parameters to the S-parameters.

3. Results

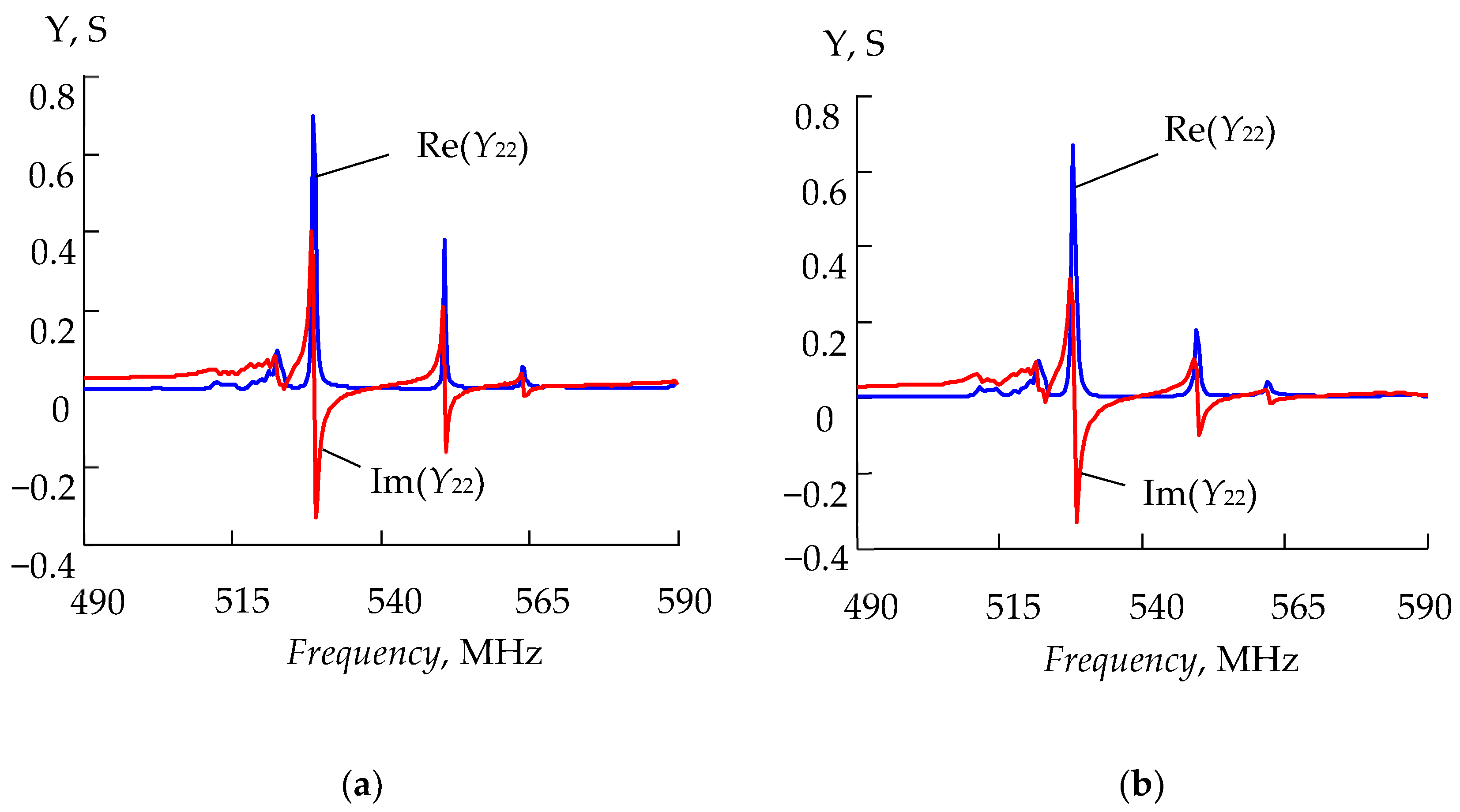
3.1. DMS Filter

Let us present the results of the calculation of the output admittance and frequency response of one section of the DMS filter, performed on the basis of two presented approaches: analytical-COM and numerical-FEM.

Figure 1a shows the topology of the resonator filter on longitudinal resonant modes or DMS filter, for which the responses are calculated. In the simulation, the frequency dependencies of admittances (Y₁₁, Y₁₂, Y₂₁, Y₂₂) are calculated, and then the S-parameters can be determined.

Figure 5 shows an example of the display of the constructed mesh and the solution in the form of a mechanical displacement for a model based on the FEM.

In the responses to the output admittance (Figure 6), calculated by two methods, there is a small discrepancy in the area of the rightmost resonant mode, which seems to be associated with a greater value of acoustic energy leakage at the upper frequencies, inherent in the leaky SAW. Despite this, the results of the bandwidth analysis on the frequency response (Figure 7a) show that this discrepancy is not so significant. In the process of simulation of one section of DMS using the FEM, the following effects were not taken into account: resistive losses in IDT electrodes, acoustic wave diffraction, and losses due to the viscous properties of the material. This is conducted for the following reasons. Firstly, it is possible to fully take into account diffraction and resistive losses, but then it will be necessary to draw a complete 3D model, which will require a large number of mesh elements and DOF, and, as a result, large computational resources and calculation times. Secondly, taking into account propagation losses is associated with the need to introduce appropriate coefficients into the model, the erroneous values of which will lead to additional errors in the calculations.

Then let us compare the calculation results with the available experimental results for the filter obtained on the basis of the cascade inclusion of two sections of DMS. Such inclusion is quite typical for this class of DMS filters and is popular among manufacturers of acoustoelectric SAW products. In the basis of calculation let us take COM but connect to the calculation some types of sources of losses, namely resistive losses, propagation losses, losses on the leakage of the main acoustic mode into the substrate depth and taking into account the excitation of SAW after a certain cutoff frequency.

Figure 7a shows the calculated frequency response of one section of the DMS-filter without losses on a 64°YX cut lithium niobate substrate. Figure 7b shows a comparison of the frequency response of the filter based on the simulation by COM and experiment results for cascade inclusion of two section DMS.

The main results and peculiarities of calculation are summarized in the

Table 1. Comparison of the result of calculating one section DMS filter based on two approaches: FEM in COMSOL and COM based P-matrices.

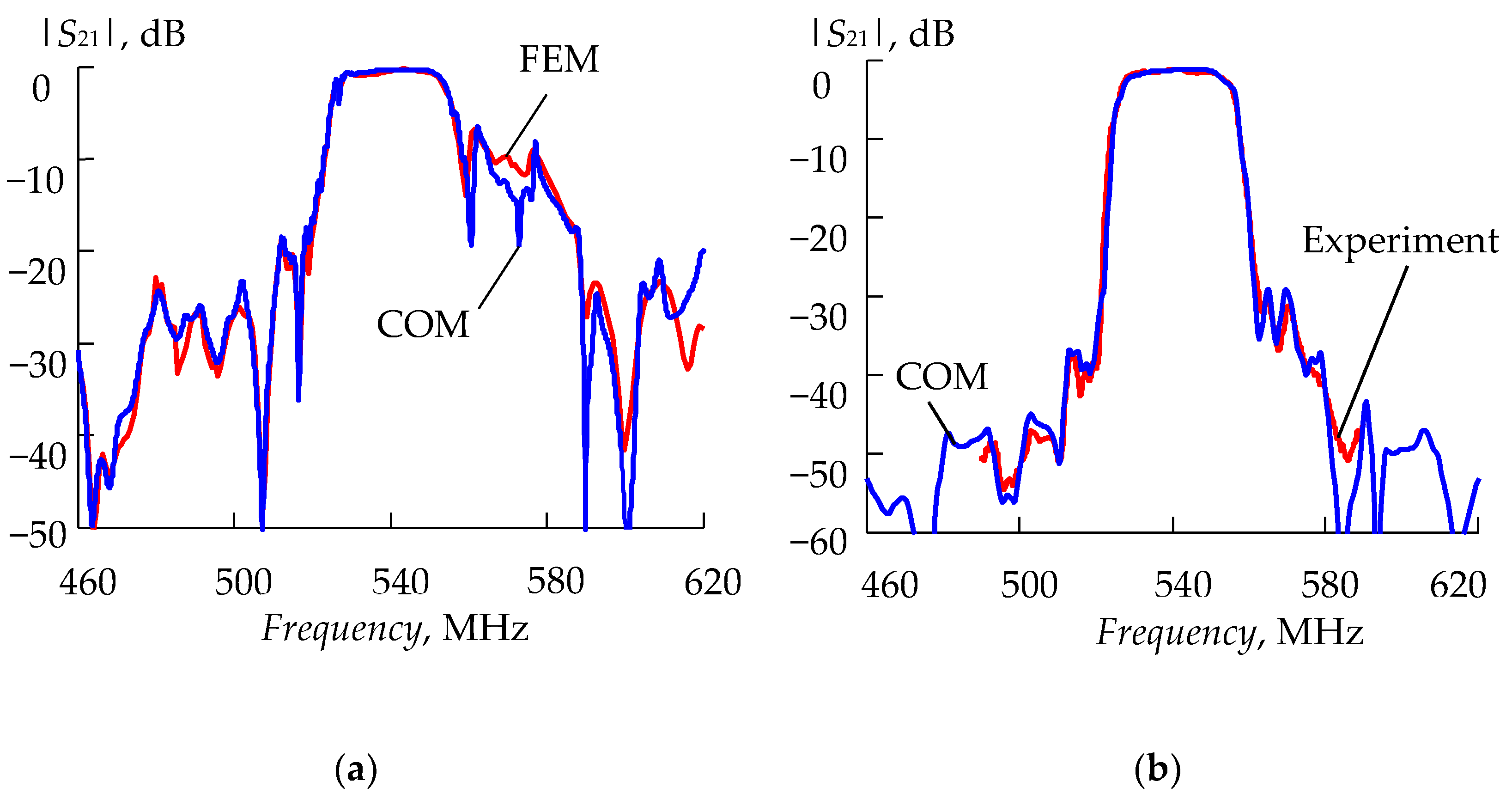
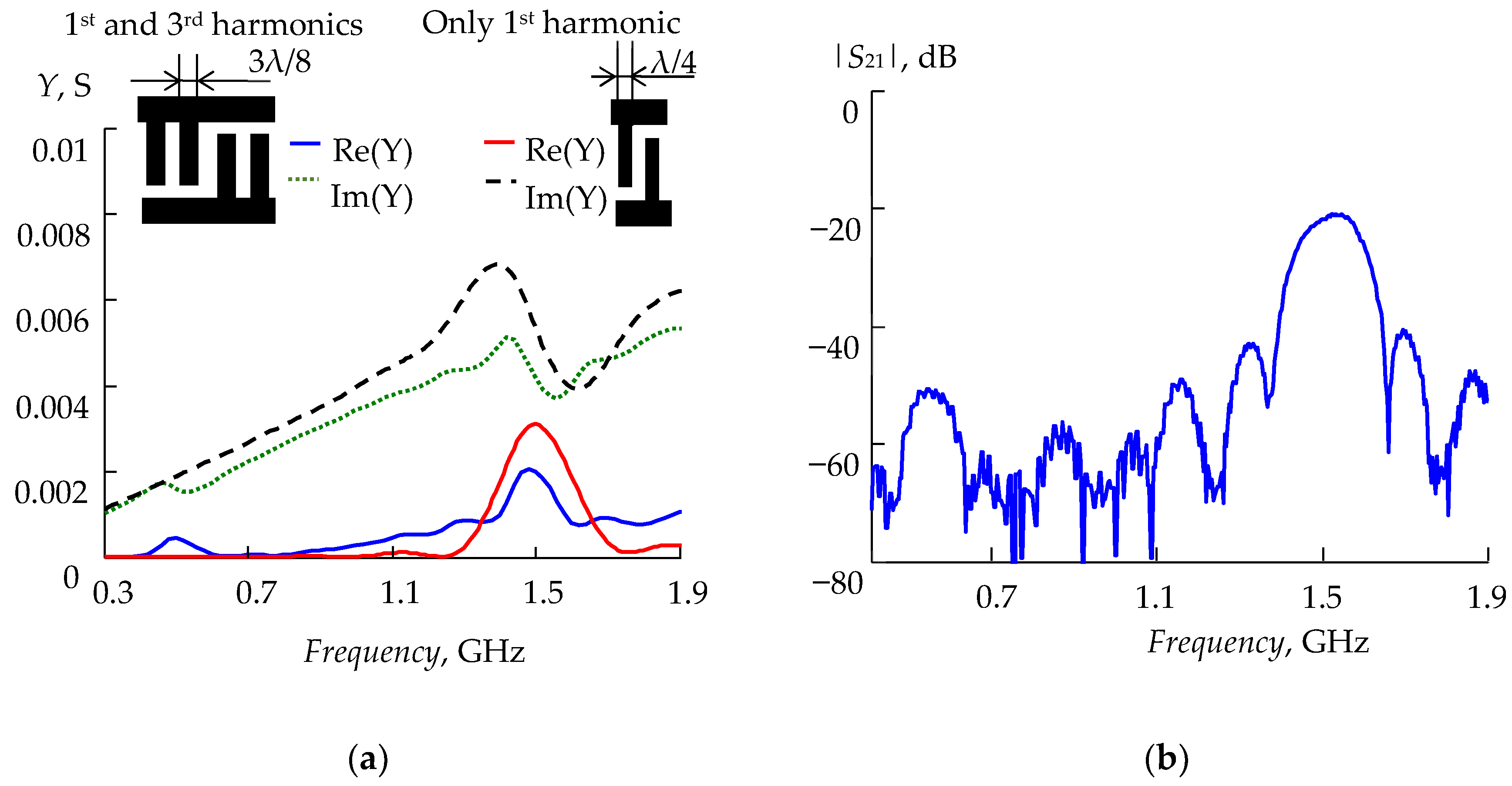
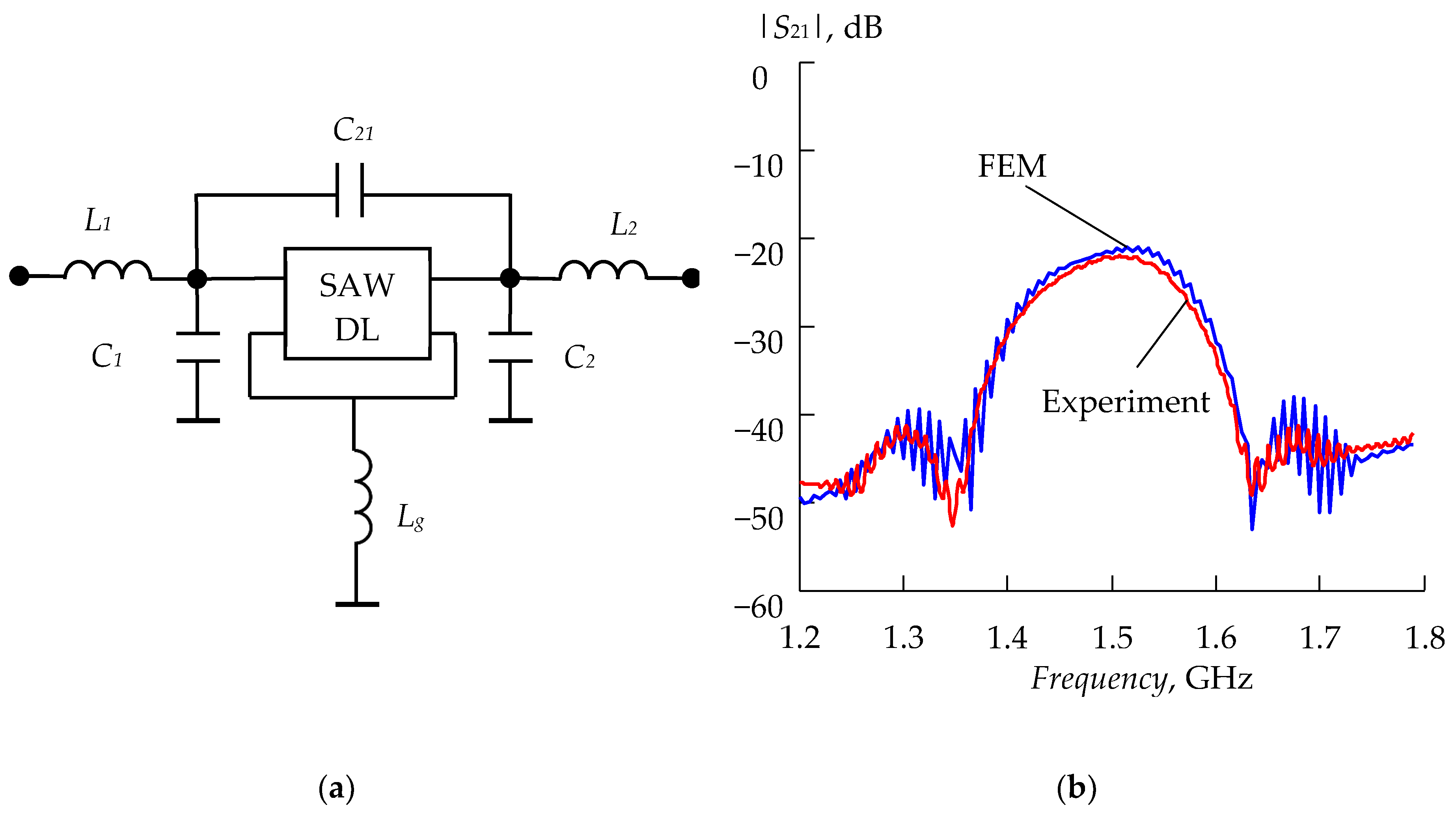
Parameter	FEM	COM
Mesh discretization, wavelengths	1/12	-
Number of elements (mesh statistics)	157,738	-
Required RAM, GB	29.23	-
Number of degrees of freedom (DOF)	3,105,240	-
Number of frequency points	201	201
Computation time	~16 h 30 min	2 s
Bandpass at level of –1 dB, MHz	24.4	24.6
Insertion loss, dB	–0.29	–0.32
Passband ripple, dB	0.6	0.45
Central frequency, MHz	540.25	540.45

.

The FEM calculations did not have the task of optimizing the calculation time, so a direct solver was used, the number of mesh elements was about 157,738, and the density of the mesh was 12 elements per wavelength. In general, both calculations showed approximately the same result, which is a good indicator for a preliminary evaluation of the output characteristics. The greatest discrepancy in the response is observed in the high-frequency region, where “parasitic” bulk acoustic waves (BAW) predominate, where, although it is possible to take them into account in the COM, is still approximate. However, and most importantly, the difference is that the FEM-based calculation took about 16 h, while the COM-based calculation took about 2 s.

A comparison of the results of calculating the transmission coefficient obtained on the basis of the COM with the experimental data for the two-section DMS filter is shown in Figure 7b. The filter has a center frequency of 540 MHz and a bandpass (at a level of –1 dB) of 24.3 MHz or 4.5%. Insertion loss—1.3 dB. Differences in the frequency responses in the passband do not exceed 0.15 dB, in the stopband −5 dB. The greatest calculation accuracy is found in the passband of the filter. The accuracy in the stopband is less due to the presence of the parasitic LC elements and “secondary effects” in the real devices.

3.2. Delay Line

Despite the fact that FEM is inferior in calculation speed, it is a very effective tool for calculation devices with a small number of electrodes, because of many secondary effects, such as leakage of the wave into the substrate volume, the presence of parasitic BAW modes and harmonic frequencies, are automatically taken into account.

Transducers can operate not only at main, but at harmonic frequencies [30,31]. The intensity of excitation high harmonics depends on different parameters: the metallization coefficient, the thickness of the metallization, the shape of the electrode and the type of transducer.

Figure 8a shows the principle of operation of the transducers at harmonics. It can be seen that the IDT with λ/4 operates only in fundamental mode to a frequency of 1.5 GHz, while for the IDT with split electrodes: 1.5 GHz—the third harmonic, the main mode is at a frequency of 0.5 GHz. The combination of IDTs as the input and output IDTs—is the base of our SAW DL, we calculate the admittance parameters for the DL.

The DL topology consists of two bidirectional transducers. The input of the transducer is IDT with λ/4 electrodes operating in the main mode, the output is a split-electrode transducer with a 3λ/8 electrode width. The center frequency of the delay line is 1.5 GHz. The substrate is 128° YX cut lithium niobate. The input IDT is six pairs. The output is four. The relative value of the metallization thickness is H_m/λ = 2.9%, the absolute value is H_m = 75 nm.

Figure 9a shows a schematic with “parasitic” LC elements. Taking into account the LC elements allows us to compare the simulation and measurement results shown in Figure 9b. The center frequency of the DL is 1.5 GHz and the bandpass (at a level of –3 dB) is 112 MHz or 7.46%. The insertion loss is 22.2 dB. The results showed good agreement between the numerical simulation and experiment.

4. Discussion

The accumulated experience in the use of different approaches to the modeling of SAW devices allows us to draw conclusions.

The COM-based analytical approach and the numerical approach (FEM in COMSOL) are in demand in the design of SAW devices. Both approaches are comparable in accuracy in bandpass calculations. In the stopband, FEM is more accurate because it automatically takes into account several secondary effects, such as wave leakage into the substrate depth. The main disadvantages of FEM are high computational resource requirements and long computation time. Therefore, FEM is more suitable for analysis at the final stage of development where we can replace the real experiment with a qualitative multiphysics simulation. In addition, FEM is well suited for preliminary analysis of acoustic wave parameters based on simple test cells.

The COM-based analytical approach allows us to obtain results significantly faster. It is reasonable to use COM for preliminary characterization during the synthesis and topology optimization stage. Optimization is also one of the important stages of development. We can proceed to it when the adequacy of the model is proved. Since one iteration for COM takes a couple of seconds, it is very convenient to do topology optimization based on the analytical approach. The issue of optimization of SAW devices should be considered separately.

One of the features of COM is the need to find the model parameters beforehand. The parameters can be extracted from simple test cells [24] using FEM. Such a combined approach (FEM + COM) includes all the advantages of a fast analytical model with the accuracy provided by FEM only.

The full calculation algorithm using FEM in COMSOL is presented in [31]. The experiment was carried out in accordance with the manufacturing process of SAW devices. More details about the manufacturing process can be found, for example, in [32].

5. Conclusions

A comparative analysis of the results of numerical simulation and calculations based on the COM model is carried out. The calculation results are in good agreement with each other and with the experimental results of measurements of the characteristics of a bandpass filter. It shows the adequacy of both approaches, which are based on fundamentally different provisions. Practical recommendations for reducing the calculation time of SAW devices in modeling based on the FEM in COMSOL have been proposed. The use of different approaches allows us to approach the experiment with a high probability of successful results. Finally, analytical models still for fast and effective synthesis and optimization of filter parameters are necessary.