Phase Analysis of Event-Related Potentials Based on Dynamic Mode Decomposition
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Acquisition and Preprocessing
2.2. Computation of the Dynamic Mode Decomposition
2.3. Analysis for Phase Information of DMD Modes
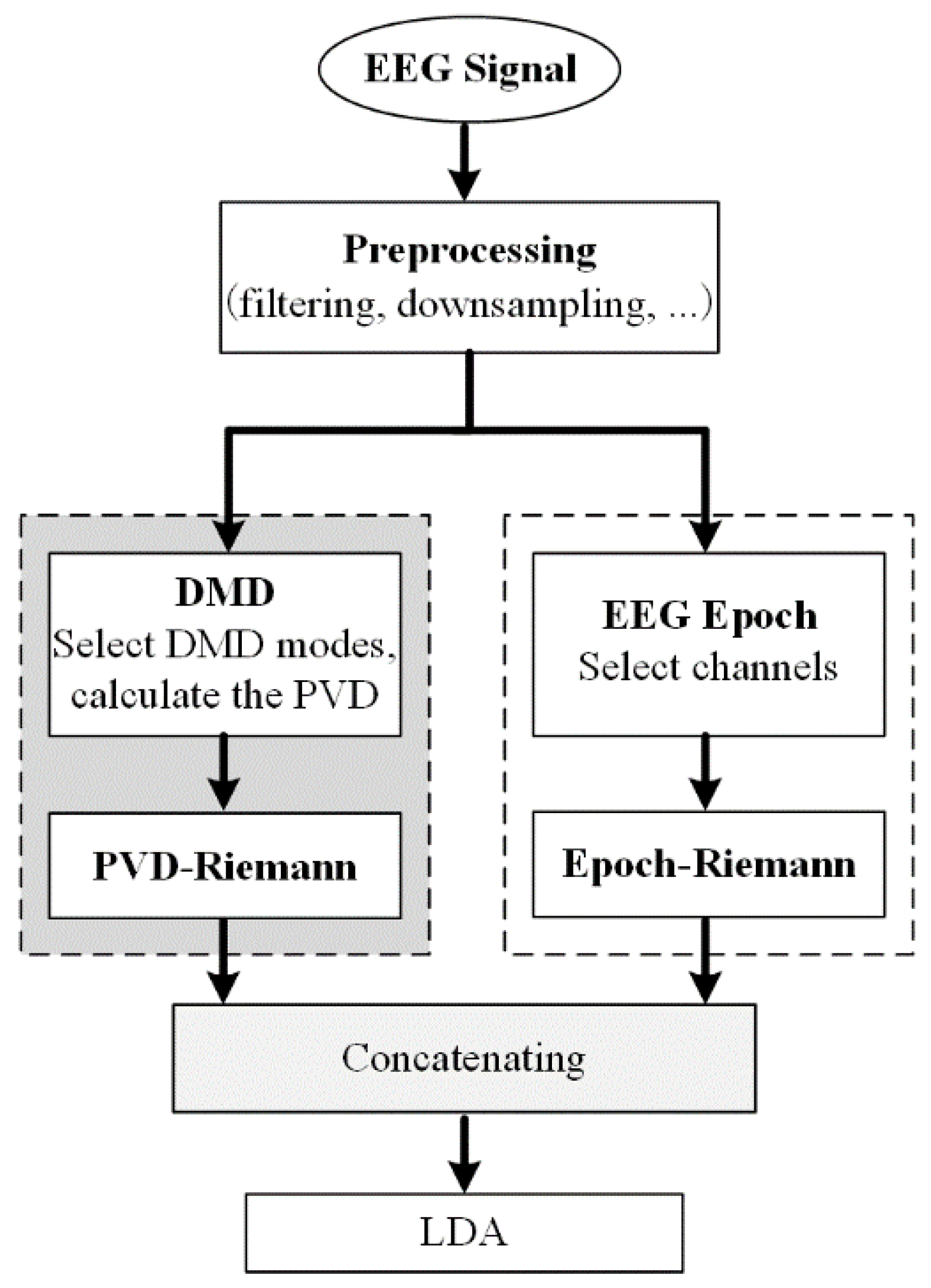
2.4. Classification Based on DMD Phase Information and Riemann Approach
3. Results
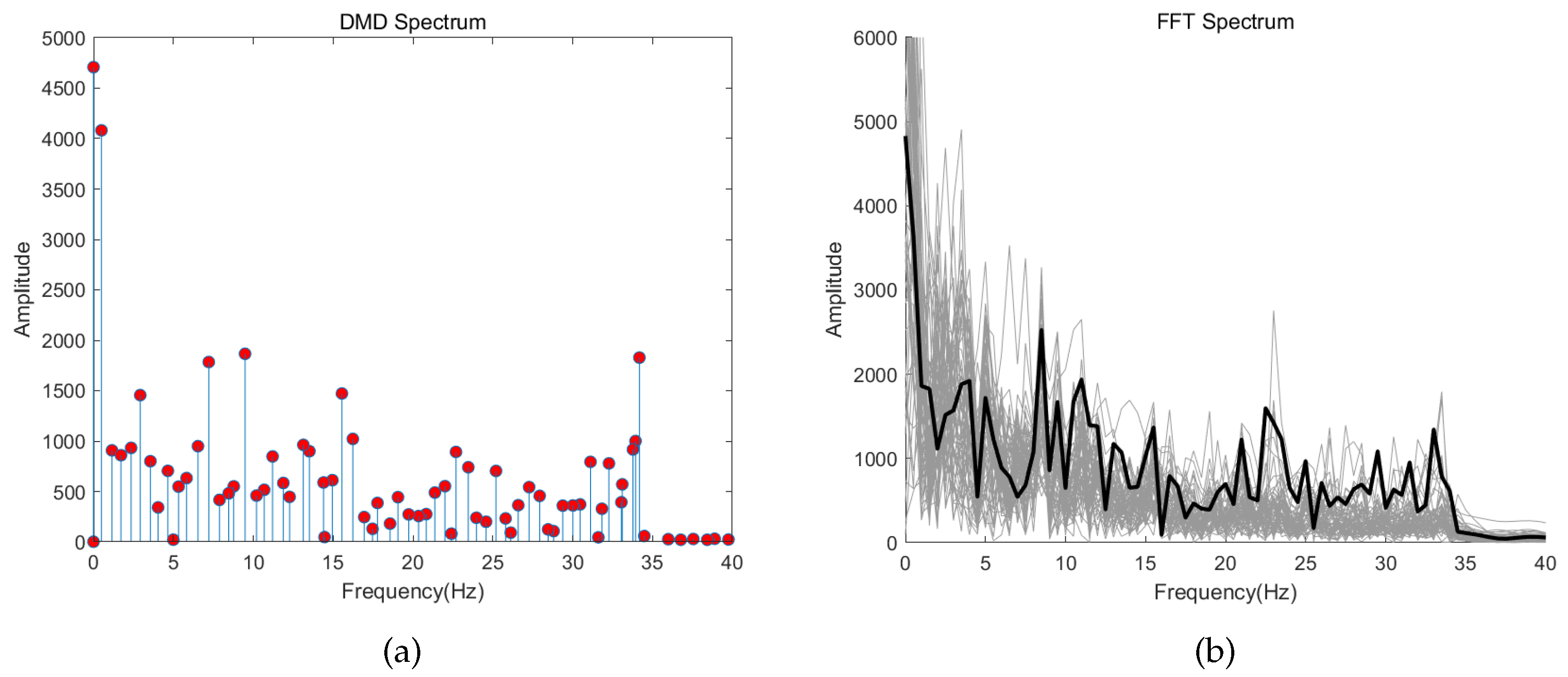
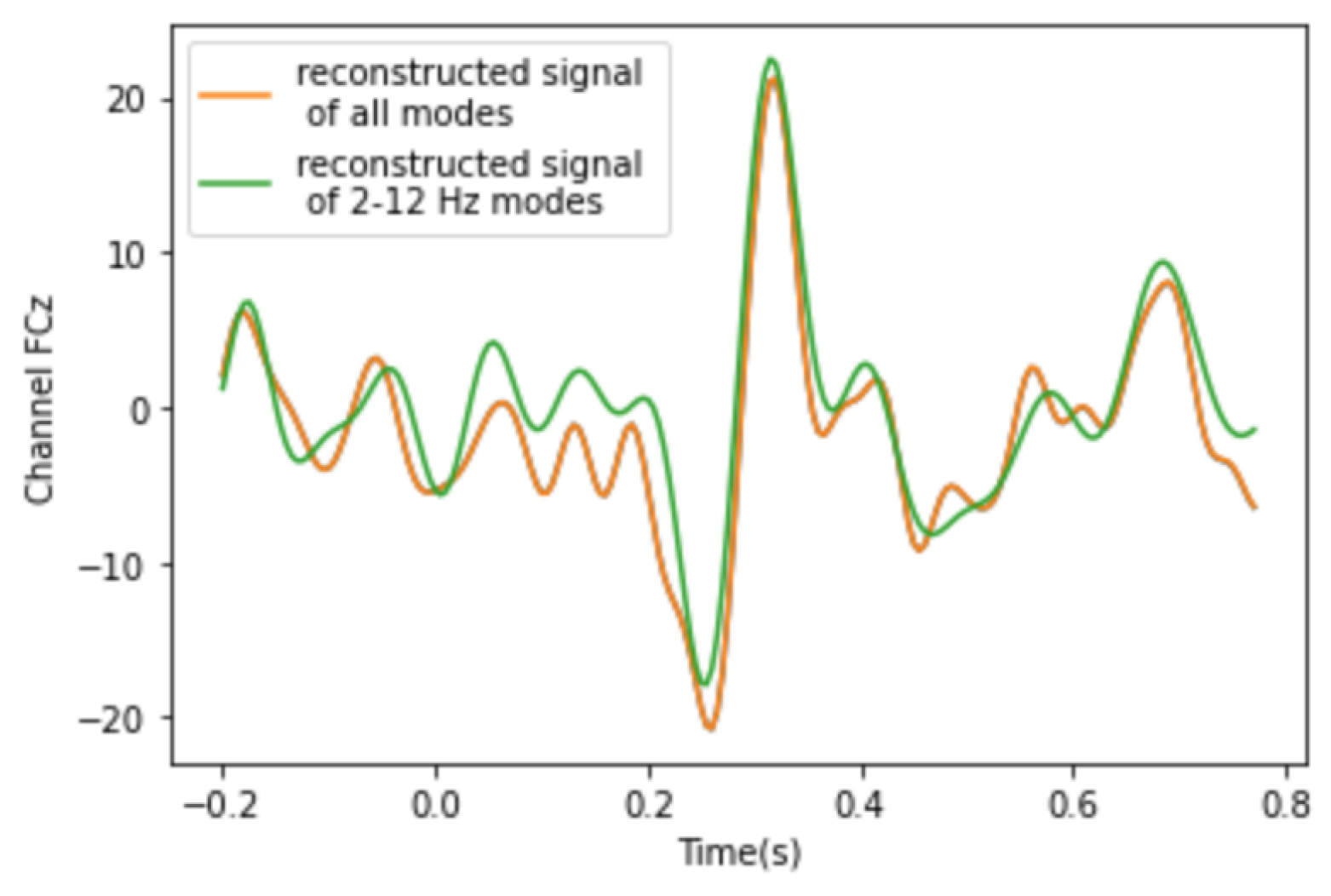
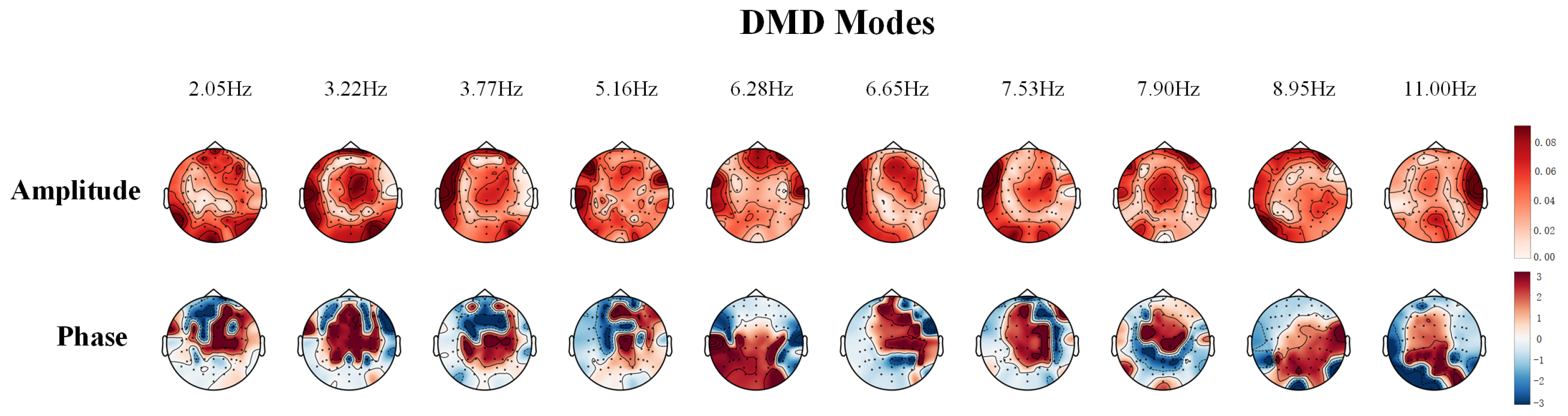
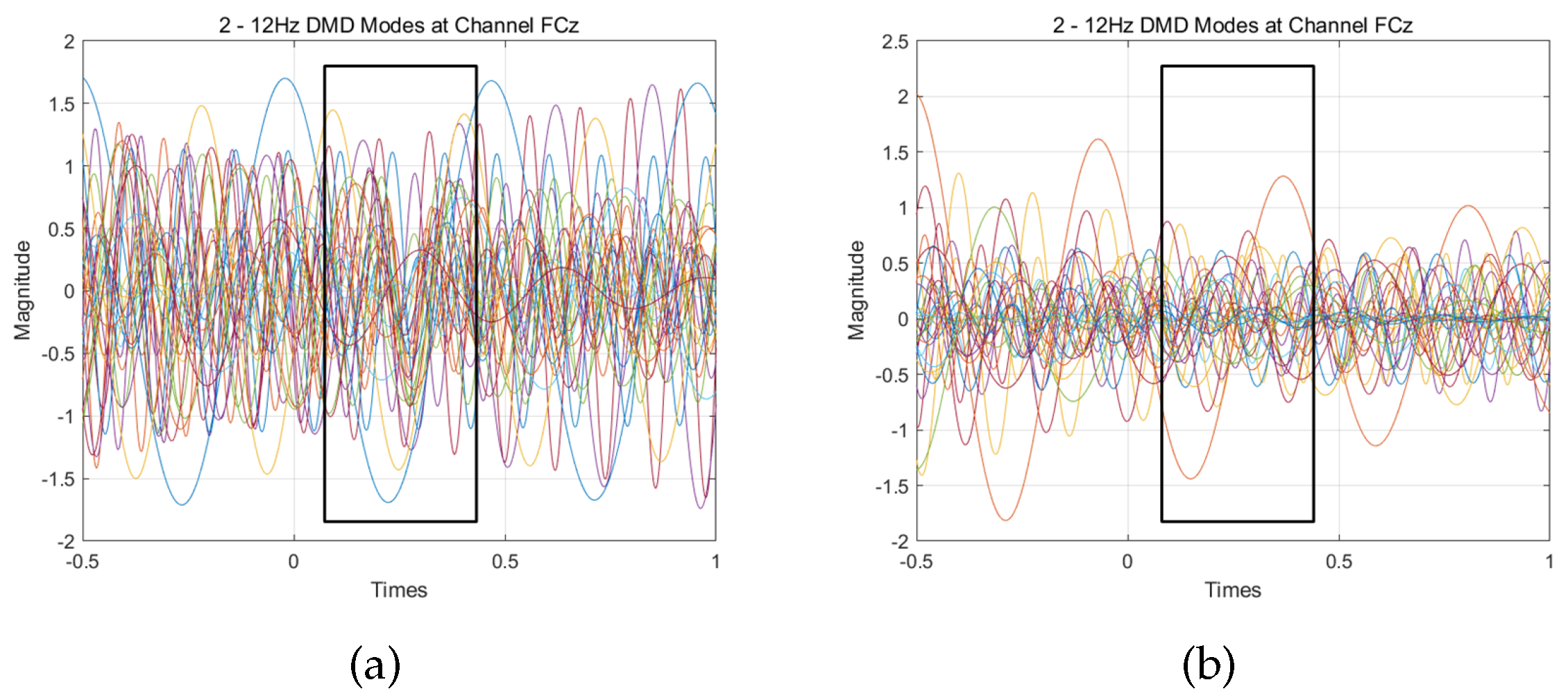
3.1. Analysis of DMD Modes
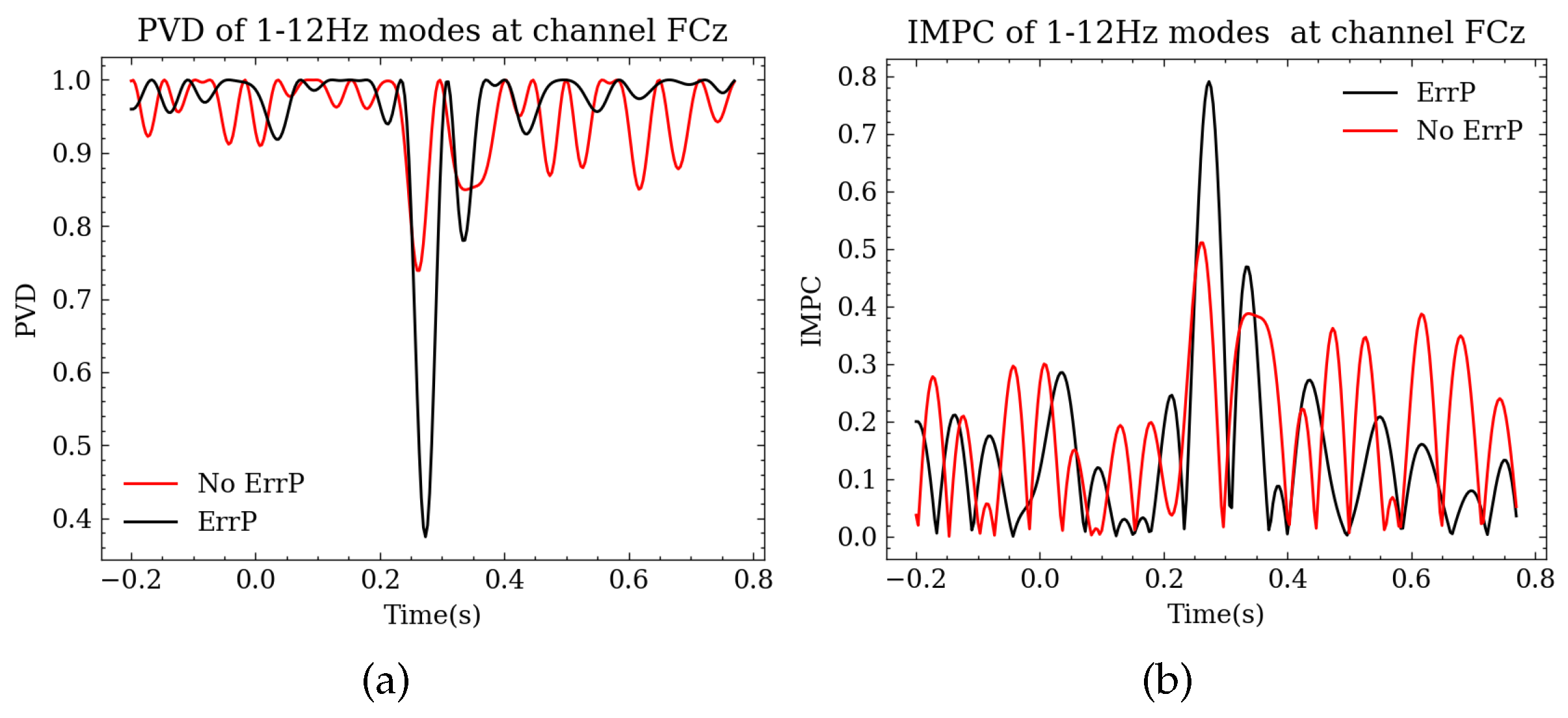
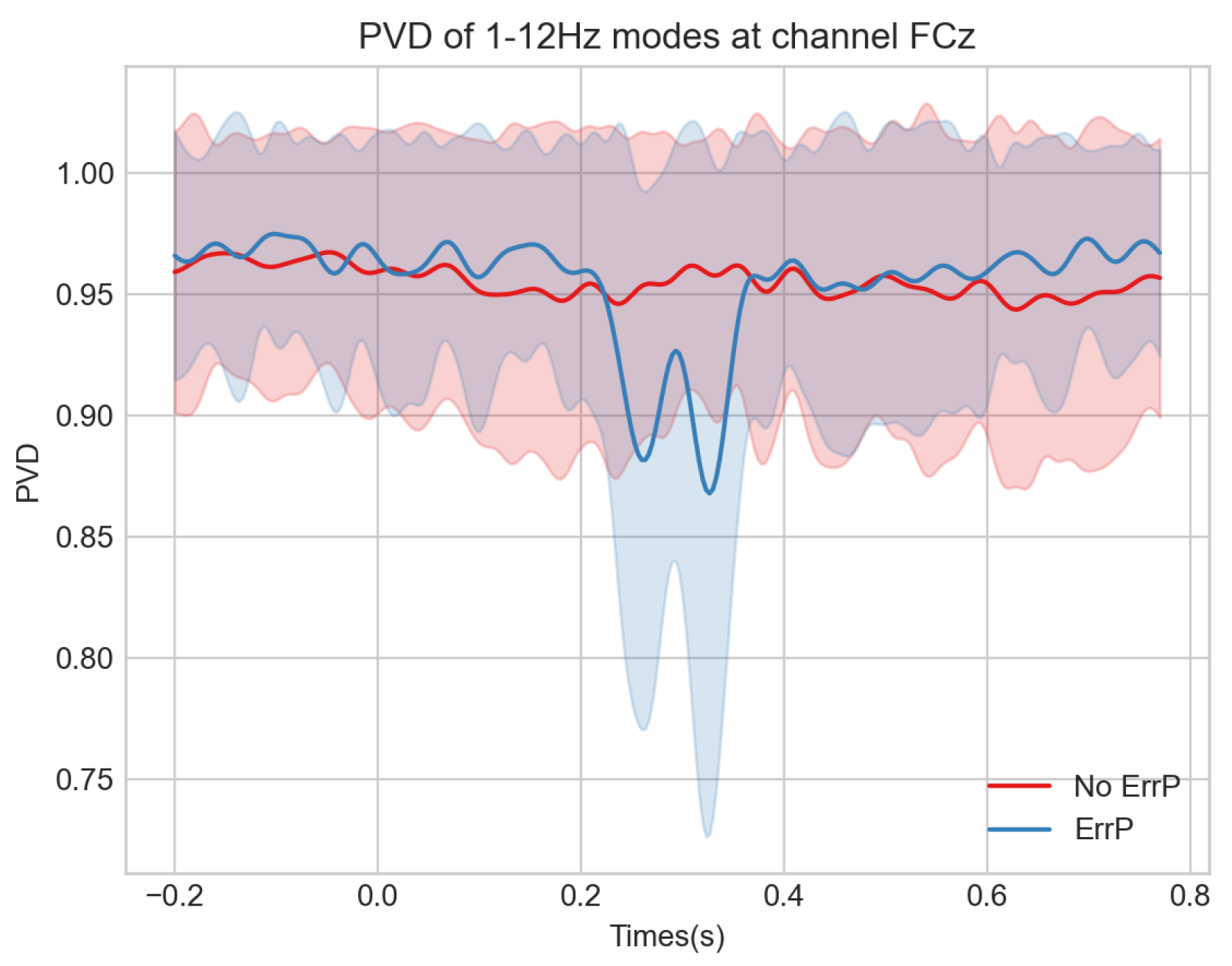
3.2. Analysis of PVD
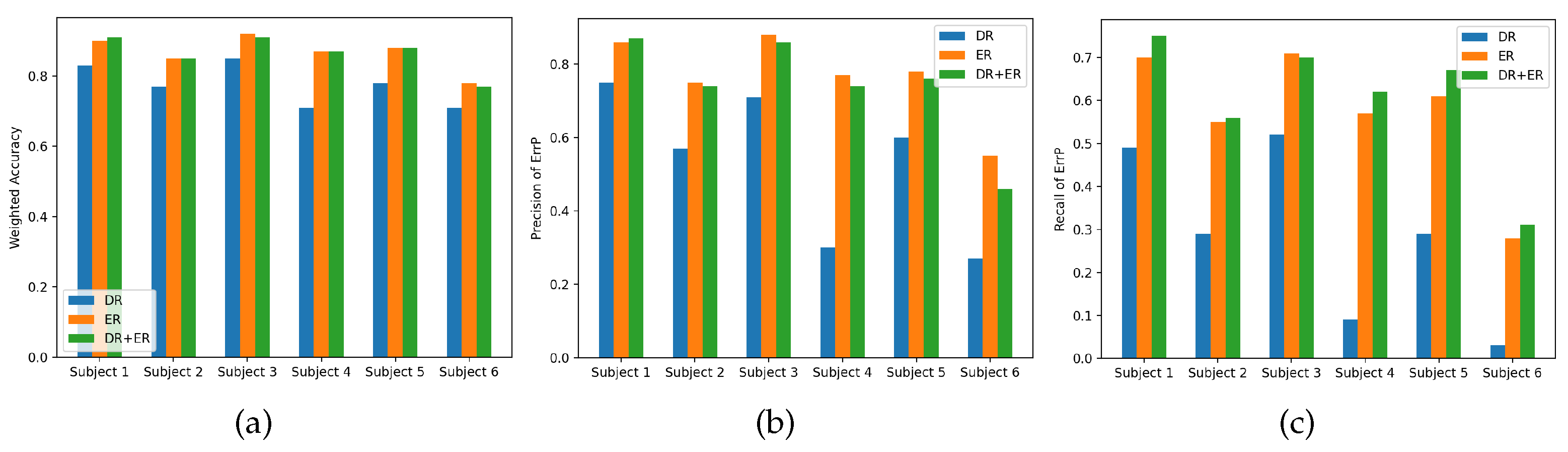
3.3. Performance of ErrP Classification Based on PVD
4. Discussion and Limitation
4.1. Discussion
4.2. Limitation and Future Works
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bansal, D.; Mahajan, R. EEG-based brain-computer interfacing (BCI). In EEG-Based Brain-Computer Interfaces; Elsevier: Amsterdam, The Netherlands, 2019; pp. 21–71. [Google Scholar]
- Woodman, G.F. A brief introduction to the use of event-related potentials in studies of perception and attention. Atten. Percept. Psychophys. 2010, 72, 2031–2046. [Google Scholar] [CrossRef] [PubMed]
- Buzsaki, G.; Draguhn, A. Neuronal oscillations in cortical networks. Science 2004, 304, 1926–1929. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fries, P. A mechanism for cognitive dynamics: Neuronal communication through neuronal coherence. Trends Cogn. Sci. 2005, 9, 474–480. [Google Scholar] [CrossRef] [PubMed]
- Raghavachari, S.; Kahana, M.J.; Rizzuto, D.S.; Caplan, J.B.; Kirschen, M.P.; Bourgeois, B.; Madsen, J.R.; Lisman, J.E. Gating of human theta oscillations by a working memory task. J. Neurosci. 2001, 21, 3175–3183. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Uhlhaas, P.J.; Roux, F.; Rodriguez, E.; Rotarska-Jagiela, A.; Singer, W. Neural synchrony and the development of cortical networks. Trends Cogn. Sci. 2010, 14, 72–80. [Google Scholar] [CrossRef]
- Cole, S.R.; Voytek, B. Brain oscillations and the importance of waveform shape. Trends Cogn. Sci. 2017, 21, 137–149. [Google Scholar] [CrossRef]
- Bastiaansen, M.; Mazaheri, A.; Jensen, O. Beyond erps: Oscillatory neuronal. In The Oxford Handbook of Event-Related Potential Components; Oxford University Press: Oxford, UK, 2011; pp. 31–50. [Google Scholar]
- Klimesch, W.; Sauseng, P.; Hanslmayr, S.; Gruber, W.; Freunberger, R. Event-related phase reorganization may explain evoked neural dynamics. Neurosci. Biobehav. Rev. 2007, 31, 1003–1016. [Google Scholar] [CrossRef]
- Sauseng, P.; Klimesch, W.; Gruber, W.R.; Hanslmayr, S.; Freunberger, R.; Doppelmayr, M. Are event-related potential components generated by phase resetting of brain oscillations? A critical discussion. Neuroscience 2007, 146, 1435–1444. [Google Scholar] [CrossRef]
- Min, B.K.; Busch, N.A.; Debener, S.; Kranczioch, C.; Hanslmayr, S.; Engel, A.K.; Herrmann, C.S. The best of both worlds: Phase-reset of human EEG alpha activity and additive power contribute to ERP generation. Int. J. Psychophysiol. 2007, 65, 58–68. [Google Scholar] [CrossRef]
- Aviyente, S.; Tootell, A.; Bernat, E.M. Time-frequency phase-synchrony approaches with ERPs. Int. J. Psychophysiol. 2017, 111, 88–97. [Google Scholar] [CrossRef]
- Roach, B.J.; Mathalon, D.H. Event-related EEG time-frequency analysis: An overview of measures and an analysis of early gamma band phase locking in schizophrenia. Schizophr. Bull. 2008, 34, 907–926. [Google Scholar] [CrossRef] [Green Version]
- Sauseng, P.; Klimesch, W. What does phase information of oscillatory brain activity tell us about cognitive processes? Neurosci. Biobehav. Rev. 2008, 32, 1001–1013. [Google Scholar] [CrossRef]
- Thatcher, R.W.; North, D.; Biver, C. EEG and intelligence: Relations between EEG coherence, EEG phase delay and power. Clin. Neurophysiol. 2005, 116, 2129–2141. [Google Scholar] [CrossRef]
- Tallon-Baudry, C.; Bertrand, O.; Delpuech, C.; Pernier, J. Stimulus specificity of phase-locked and non-phase-locked 40 Hz visual responses in human. J. Neurosci. 1996, 16, 4240–4249. [Google Scholar] [CrossRef] [Green Version]
- Bajaj, V.; Pachori, R.B. Classification of seizure and nonseizure EEG signals using empirical mode decomposition. IEEE Trans. Inf. Technol. Biomed. 2011, 16, 1135–1142. [Google Scholar] [CrossRef]
- Sweeney-Reed, C.M.; Nasuto, S.J. A novel approach to the detection of synchronisation in EEG based on empirical mode decomposition. J. Comput. Neurosci. 2007, 23, 79–111. [Google Scholar] [CrossRef]
- Liang, H.; Bressler, S.L.; Desimone, R.; Fries, P. Empirical mode decomposition: A method for analyzing neural data. Neurocomputing 2005, 65, 801–807. [Google Scholar] [CrossRef]
- Rowley, C.W.; Mezić, I.; Bagheri, S.; Schlatter, P.; Henningson, D.S. Spectral analysis of nonlinear flows. J. Fluid Mech. 2009, 641, 115–127. [Google Scholar] [CrossRef] [Green Version]
- Schmid, P.J. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef] [Green Version]
- Budišić, M.; Mohr, R.; Mezić, I. Applied koopmanism. Chaos: Interdiscip. J. Nonlinear Sci. 2012, 22, 047510. [Google Scholar] [CrossRef]
- Alfatlawi, M.; Srivastava, V. An incremental approach to online dynamic mode decomposition for time-varying systems with applications to EEG data modeling. arXiv 2019, arXiv:1908.01047. [Google Scholar] [CrossRef]
- Brunton, B.W.; Johnson, L.A.; Ojemann, J.G.; Kutz, J.N. Extracting spatial–Temporal coherent patterns in large-scale neural recordings using dynamic mode decomposition. J. Neurosci. Methods 2016, 258, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Shiraishi, Y.; Kawahara, Y.; Yamashita, O.; Fukuma, R.; Yamamoto, S.; Saitoh, Y.; Kishima, H.; Yanagisawa, T. Neural decoding of electrocorticographic signals using dynamic mode decomposition. J. Neural Eng. 2020, 17, 036009. [Google Scholar] [CrossRef]
- Tu, J.H. Dynamic Mode Decomposition: Theory and Applications. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 2013. [Google Scholar]
- Chavarriaga, R.; Millán, J.D.R. Learning from EEG error-related potentials in noninvasive brain-computer interfaces. IEEE Trans. Neural Syst. Rehabil. Eng. 2010, 18, 381–388. [Google Scholar] [CrossRef] [Green Version]
- Chavarriaga, R.; Sobolewski, A.; Millán, J.D.R. Errare machinale est: The use of error-related potentials in brain-machine interfaces. Front. Neurosci. 2014, 208. [Google Scholar] [CrossRef]
- Spüler, M.; Niethammer, C. Error-related potentials during continuous feedback: Using EEG to detect errors of different type and severity. Front. Hum. Neurosci. 2015, 9, 155. [Google Scholar] [PubMed] [Green Version]
- Abu-Alqumsan, M.; Kapeller, C.; Hintermüller, C.; Guger, C.; Peer, A. Invariance and variability in interaction error-related potentials and their consequences for classification. J. Neural Eng. 2017, 14, 066015. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ludwig, K.A.; Miriani, R.M.; Langhals, N.B.; Joseph, M.D.; Anderson, D.J.; Kipke, D.R. Using a common average reference to improve cortical neuron recordings from microelectrode arrays. J. Neurophysiol. 2009, 101, 1679–1689. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gramfort, A.; Luessi, M.; Larson, E.; Engemann, D.A.; Strohmeier, D.; Brodbeck, C.; Goj, R.; Jas, M.; Brooks, T.; Parkkonen, L.; et al. MEG and EEG data analysis with MNE-Python. Front. Neurosci. 2013, 7, 267. [Google Scholar] [CrossRef] [Green Version]
- Kutz, J.N.; Brunton, S.L.; Brunton, B.W.; Proctor, J.L. Dynamic Mode Decomposition: Data-Driven Modeling of Complex Systems; SIAM: Bangkok, Thailand, 2016. [Google Scholar]
- Aydarkhanov, R.; Ušćumlić, M.; Chavarriaga, R.; Gheorghe, L.; del R Millan, J. Spatial covariance improves BCI performance for late ERPs components with high temporal variability. J. Neural Eng. 2020, 17, 036030. [Google Scholar] [CrossRef]
- Congedo, M.; Barachant, A.; Andreev, A. A new generation of brain-computer interface based on riemannian geometry. arXiv 2013, arXiv:1310.8115. [Google Scholar]
- Congedo, M.; Barachant, A.; Bhatia, R. Riemannian geometry for EEG-based brain-computer interfaces; a primer and a review. Brain-Comput. Interfaces 2017, 4, 155–174. [Google Scholar] [CrossRef]
- Yger, F.; Berar, M.; Lotte, F. Riemannian approaches in brain-computer interfaces: A review. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 25, 1753–1762. [Google Scholar] [CrossRef] [Green Version]
- Siuly, S.; Li, Y.; Zhang, Y. EEG signal analysis and classification. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 11, 141–144. [Google Scholar]
- Barachant, A.; Bonnet, S.; Congedo, M.; Jutten, C. Multiclass brain–computer interface classification by Riemannian geometry. IEEE Trans. Biomed. Eng. 2011, 59, 920–928. [Google Scholar] [CrossRef] [Green Version]
- Izenman, A.J. Linear discriminant analysis. In Modern Multivariate Statistical Techniques; Springer: Berlin/Heidelberg, Germany, 2013; pp. 237–280. [Google Scholar]
- Kalaganis, F.; Chatzilari, E.; Georgiadis, K.; Nikolopoulos, S.; Laskaris, N.; Kompatsiaris, Y. An error aware SSVEP-based BCI. In Proceedings of the 2017 IEEE 30th International Symposium on Computer-Based Medical Systems (CBMS), Thessaloniki, Greece, 22–24 June 2017; pp. 775–780. [Google Scholar]
- Gholampour, S.; Fatouraee, N. Boundary conditions investigation to improve computer simulation of cerebrospinal fluid dynamics in hydrocephalus patients. Commun. Biol. 2021, 4, 394. [Google Scholar] [CrossRef]
- Gholampour, S.; Yamini, B.; Droessler, J.; Frim, D. A New Definition for Intracranial Compliance to Evaluate Adult Hydrocephalus After Shunting. Front. Bioeng. Biotechnol. 2022, 10, 900644. [Google Scholar] [CrossRef]

| Subject | Session | CSP+LDA | Waveform+LDA | DMD+Riemann | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| wAcc | Precision | Recall | wAcc | Precision | Recall | wAcc | Precision | Recall | ||
| 1 | 1 | 0.70 | 0.22 | 0.09 | 0.88 | 0.77 | 0.74 | 0.91 | 0.87 | 0.75 |
| 2 | 0.77 | 0.38 | 0.14 | 0.91 | 0.85 | 0.73 | 0.93 | 0.88 | 0.78 | |
| 2 | 1 | 0.73 | 0.38 | 0.35 | 0.79 | 0.54 | 0.48 | 0.85 | 0.74 | 0.56 |
| 2 | 0.70 | 0.33 | 0.34 | 0.78 | 0.52 | 0.51 | 0.82 | 0.71 | 0.47 | |
| 3 | 1 | 0.77 | 0.23 | 0.07 | 0.87 | 0.70 | 0.62 | 0.91 | 0.86 | 0.70 |
| 2 | 0.78 | 0.12 | 0.06 | 0.91 | 0.79 | 0.66 | 0.92 | 0.86 | 0.67 | |
| 4 | 1 | 0.80 | 0.59 | 0.18 | 0.83 | 0.58 | 0.58 | 0.87 | 0.74 | 0.62 |
| 2 | 0.77 | 0.17 | 0.05 | 0.77 | 0.42 | 0.35 | 0.82 | 0.62 | 0.40 | |
| 5 | 1 | 0.74 | 0.15 | 0.05 | 0.83 | 0.62 | 0.55 | 0.88 | 0.76 | 0.67 |
| 2 | 0.76 | 0.39 | 0.15 | 0.77 | 0.49 | 0.43 | 0.85 | 0.74 | 0.54 | |
| 6 | 1 | 0.78 | 0.33 | 0.10 | 0.74 | 0.36 | 0.29 | 0.77 | 0.46 | 0.31 |
| 2 | 0.80 | 0.18 | 0.05 | 0.77 | 0.32 | 0.27 | 0.80 | 0.44 | 0.24 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Luo, J.; Li, Y.; Zhang, L.; Guo, Y. Phase Analysis of Event-Related Potentials Based on Dynamic Mode Decomposition. Mathematics 2022, 10, 4406. https://doi.org/10.3390/math10234406
Li L, Luo J, Li Y, Zhang L, Guo Y. Phase Analysis of Event-Related Potentials Based on Dynamic Mode Decomposition. Mathematics. 2022; 10(23):4406. https://doi.org/10.3390/math10234406
Chicago/Turabian StyleLi, Li, Jingjing Luo, Yang Li, Lei Zhang, and Yuzhu Guo. 2022. "Phase Analysis of Event-Related Potentials Based on Dynamic Mode Decomposition" Mathematics 10, no. 23: 4406. https://doi.org/10.3390/math10234406
APA StyleLi, L., Luo, J., Li, Y., Zhang, L., & Guo, Y. (2022). Phase Analysis of Event-Related Potentials Based on Dynamic Mode Decomposition. Mathematics, 10(23), 4406. https://doi.org/10.3390/math10234406








