Improved Fractional-Order Extended State Observer-Based Hypersonic Vehicle Active Disturbance Rejection Control
Abstract
:1. Introduction
2. Dynamic Model of Hypersonic Vehicle
3. FOESO-Based ADRC
3.1. Stability Analysis of FOESO-ADRC
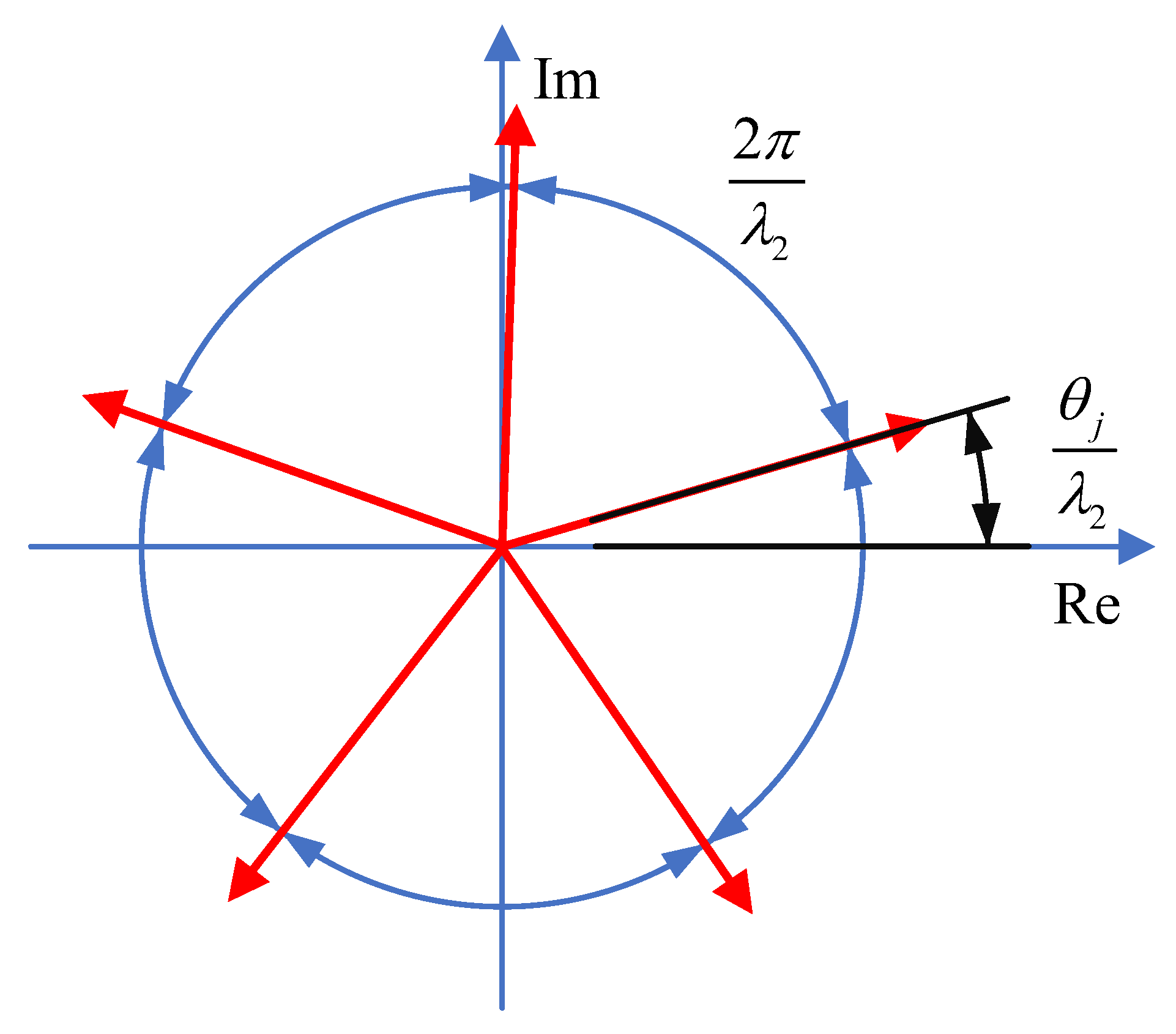
3.2. Parameter Tuning
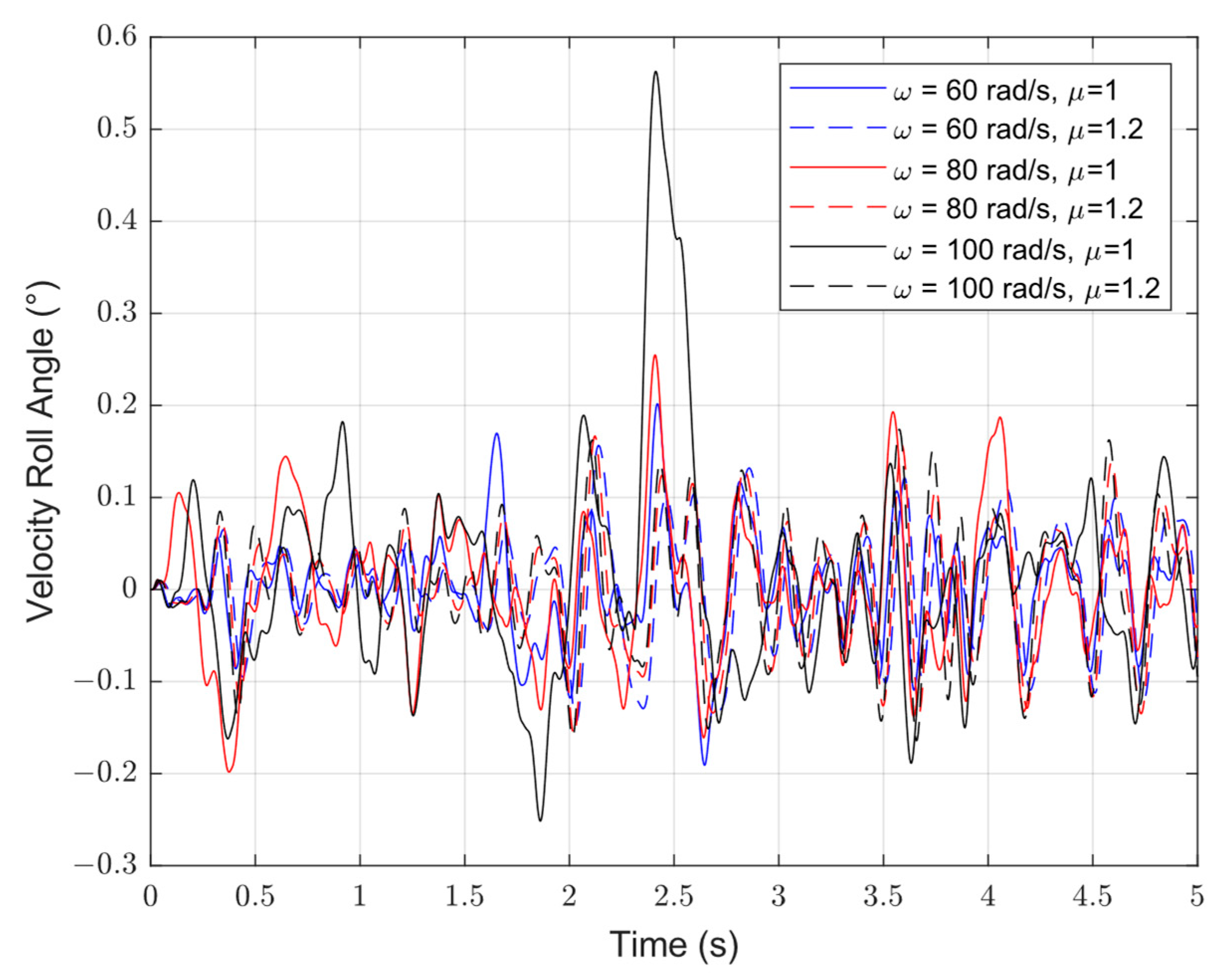
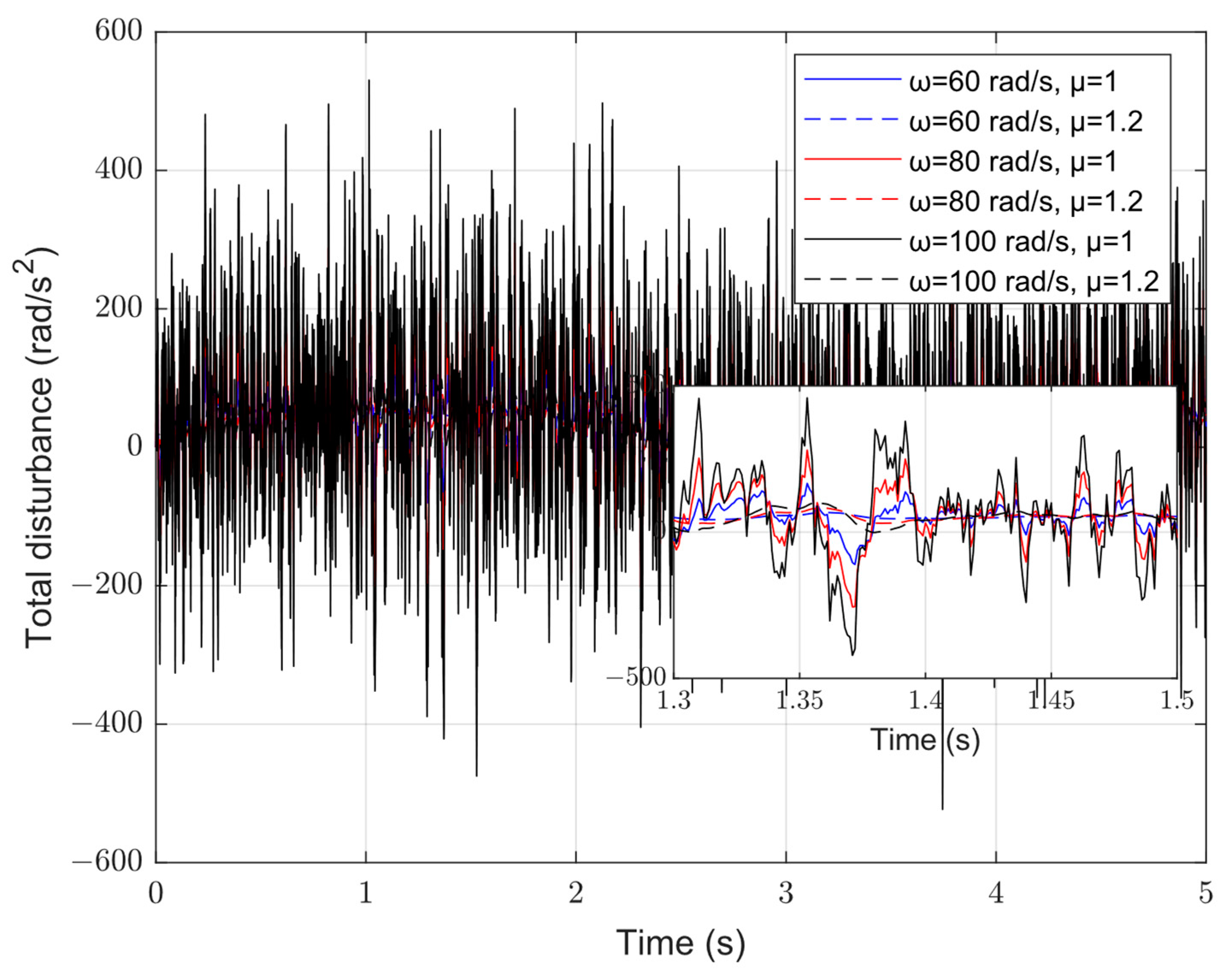
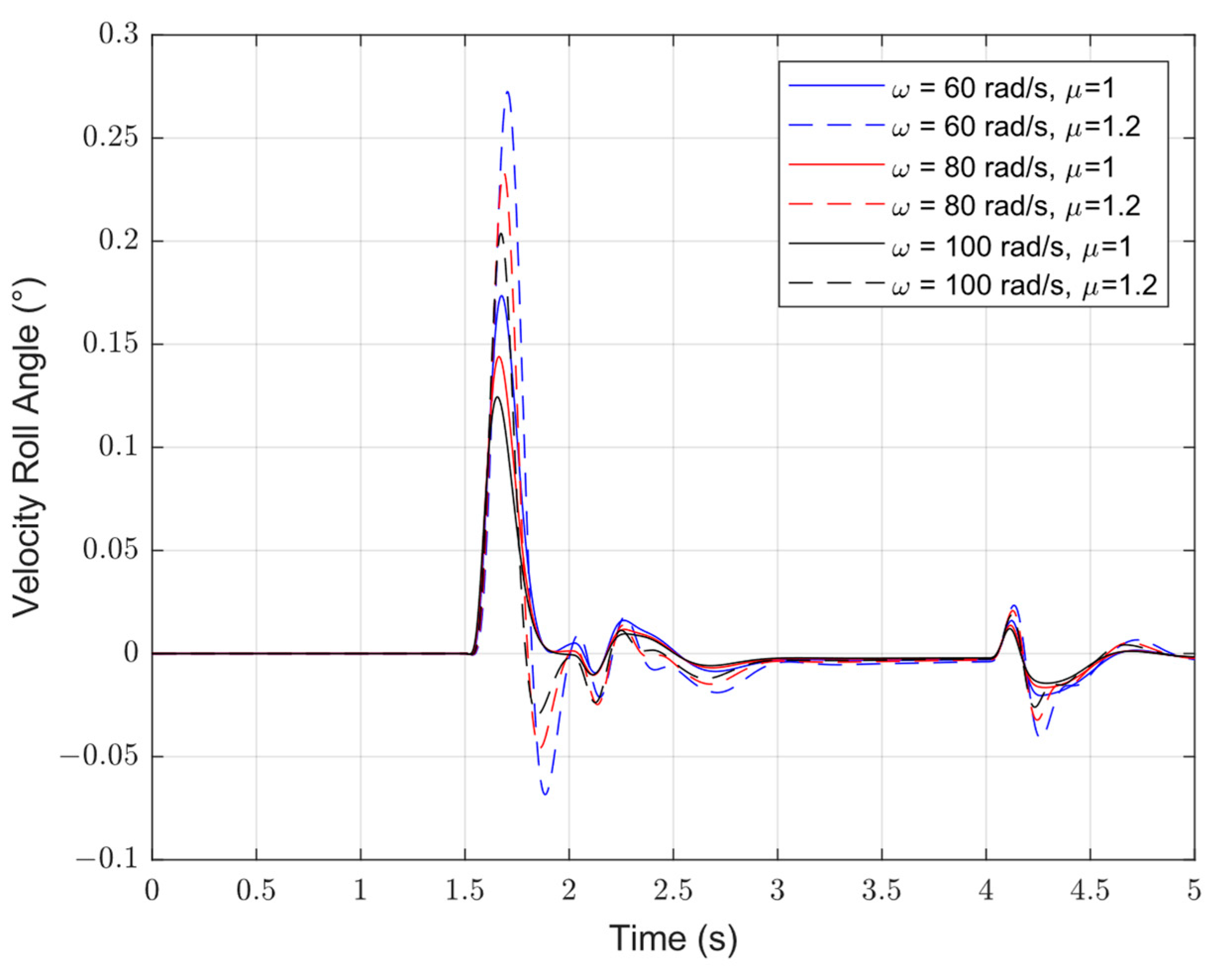
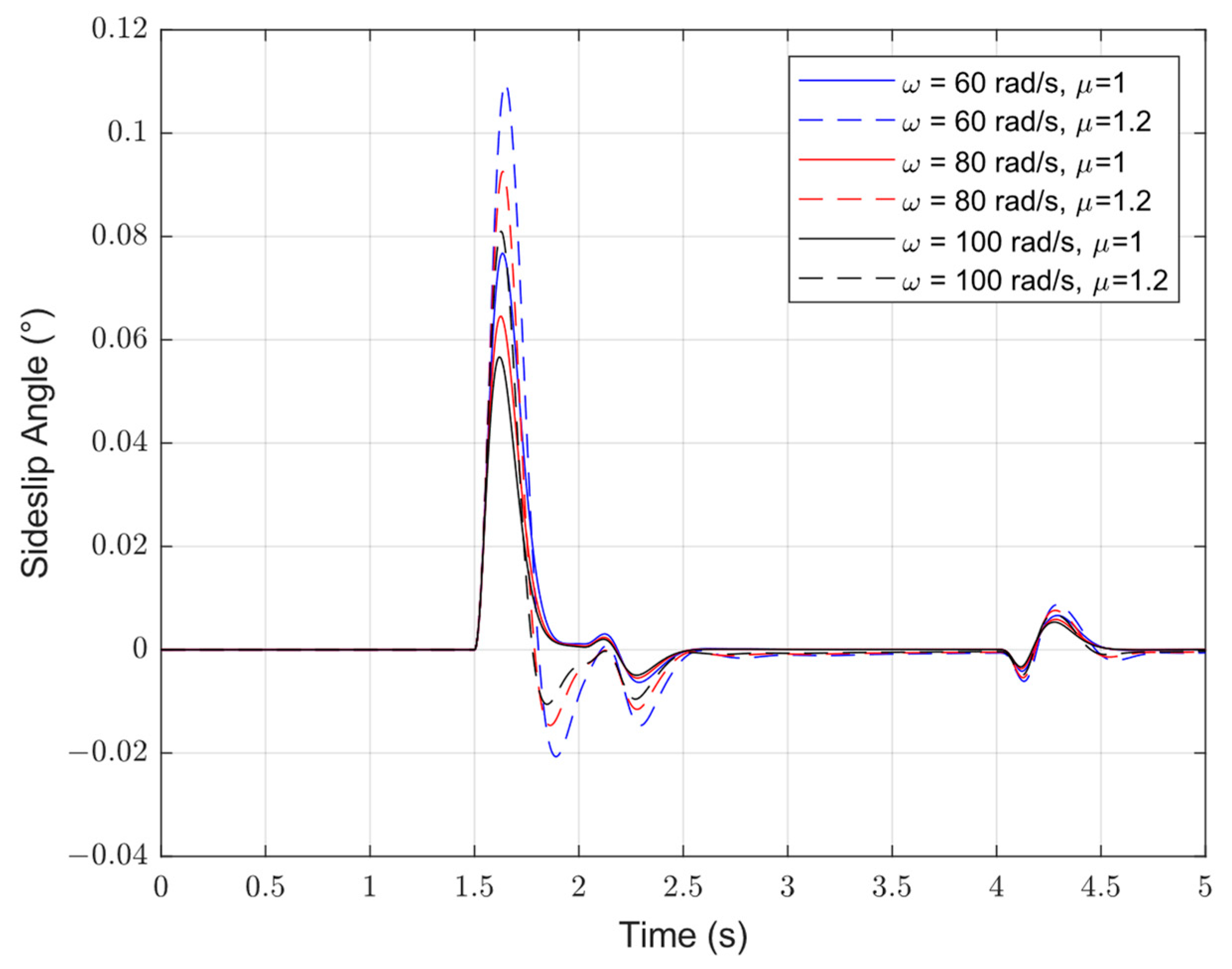
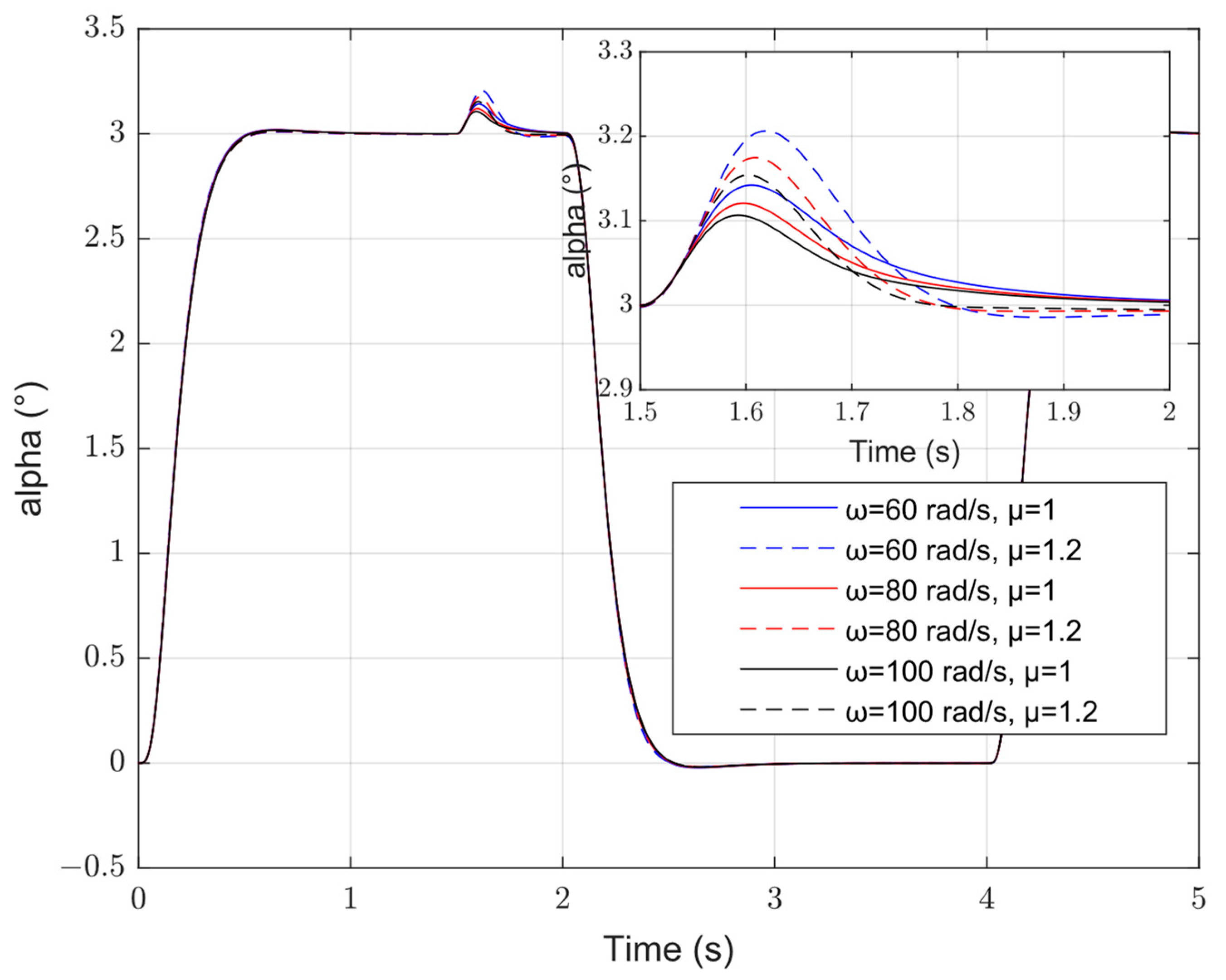
4. Simulation Analysis
4.1. FOESO Versus ESO: Nominal Situation
4.2. FOESO Versus ESO: Measurement Noise Situation
4.3. FOESO Versus ESO: Total Disturbance Situation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Song, J.; Luo, Y.; Zhao, M.; Hu, Y.; Zhang, Y. Fault-Tolerant Integrated Guidance and Control Design for Hypersonic Vehicle Based on PPO. Mathematics 2022, 10, 3401. [Google Scholar] [CrossRef]
- Qin, W.; Liu, J.; Liu, G.; He, B.; Wang, L. Robust parameter dependent receding horizon H∞ control of flexible air-breathing hypersonic vehicles with input constraints. Asian J. Control. 2015, 17, 508–522. [Google Scholar] [CrossRef]
- Hu, X.; Wu, L.; Hu, C.; Wang, Z.; Gao, H. Dynamic output feedback control of a flexible air-breathing hypersonic vehicle via T–S fuzzy approach. Int. J. Syst. Sci. 2014, 45, 1740–1756. [Google Scholar] [CrossRef]
- Bao, C.; Wang, P.; Tang, G. Integrated method of guidance, control and morphing for hypersonic morphing vehicle in glide phase. Chin. J. Aeronaut. 2021, 34, 535–553. [Google Scholar] [CrossRef]
- Zhao, H.; Yang, L. Global adaptive neural backstepping control of a flexible hypersonic vehicle with disturbance estimation. Aircr. Eng. Aerosp. Technol. 2021, 94, 492–504. [Google Scholar] [CrossRef]
- Song, J.; Wang, L.; Cai, G.; Qi, X. Nonlinear fractional order proportion-integral-derivative active disturbance rejection control method design for hypersonic vehicle attitude control. Acta Astronaut. 2015, 111, 160–169. [Google Scholar] [CrossRef]
- Guo, F.; Lu, P. Improved adaptive integral-sliding-mode fault-tolerant control for hypersonic vehicle with actuator fault. IEEE Access 2021, 9, 143–151. [Google Scholar] [CrossRef]
- Sun, H.; Li, S.; Sun, C. Finite time integral sliding mode control of hypersonic vehicles. Nonlinear Dyn. 2013, 73, 229–244. [Google Scholar] [CrossRef]
- Han, J. From PID to Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Yoo, D.; Yau, S.; Gao, Z. Optimal fast tracking observer bandwidth of the linear extended state observer. Int. J. Control 2007, 80, 102–111. [Google Scholar] [CrossRef]
- Razmjooei, H.; Palli, G.; Abdi, E. Continuous finite-time extended state observer design for electro-hydraulic systems. J. Frankl. Inst. 2022, 10, 5036–5055. [Google Scholar] [CrossRef]
- Razmjooei, H.; Palli, G.; Nazari, M. Disturbance observer-based nonlinear feedback control for position tracking of electro-hydraulic systems in a finite time. Eur. J. Control. 2022, 67, 100659. [Google Scholar] [CrossRef]
- Razmjooei, H.; Palli, G.; Abdi, E.; Strano, S.; Terzo, M. Finite-time continuous extended state observers: Design and experimental validation on electro-hydraulic systems. Mechatronics 2022, 85, 102812. [Google Scholar] [CrossRef]
- Zhao, J.; Feng, D.; Cui, J.; Wang, X. Finite-Time Extended State Observer-Based Fixed-Time Attitude Control for Hypersonic Vehicles. Mathematics 2022, 10, 3162. [Google Scholar] [CrossRef]
- Gao, K.; Song, J.; Wang, X.; Li, H. Fractional-order proportional-integral-derivative linear active disturbance rejection control design and parameter optimization for hypersonic vehicles with actuator faults. Tsinghua Sci. Technol. 2020, 26, 9–23. [Google Scholar] [CrossRef]
- Sun, J.; Pu, Z.; Yi, J. Conditional disturbance negation based active disturbance rejection control for hypersonic vehicles. Control. Eng. Pract. 2019, 84, 159–171. [Google Scholar] [CrossRef]
- Wei, W.; Zhang, Z.; Zuo, M. Phase leading active disturbance rejection control for a nanopositioning stage. ISA Trans. 2021, 116, 218–231. [Google Scholar] [CrossRef]
- Doye, I.; Salama, K.; Laleg-Kirati, T. Robust fractional-order proportional-integral observer for synchronization of chaotic fractional-order systems. IEEE/CAA J. Autom. Sin. 2018, 6, 268–277. [Google Scholar] [CrossRef]
- Doostdar, F.; Mojallali, H. An ADRC-based backstepping control design for a class of fractional-order systems. ISA Trans. 2022, 121, 140–146. [Google Scholar] [CrossRef]
- Doostdar, F.; Mojallali, H. A novel algorithm on adaptive backstepping control for a class of uncertain fractional-order systems: An ADRC approach. In Proceedings of the 2021 7th International Conference on Control, Instrumentation and Automation (ICCIA), IEEE, Tabriz, Iran, 23–24 February 2021; pp. 1–5. [Google Scholar]
- Zheng, W.; Chen, Y.; Wang, X.; Chen, Y.; Lin, M. Enhanced fractional order sliding mode control for a class of fractional order uncertain systems with multiple mismatched disturbances. ISA Trans. 2022, 2, 1879–2022. [Google Scholar] [CrossRef]
- Piao, M.; Sun, M.; Huang, J.; Wang, Z.; Chen, Z. Attitude Control of Hypersonic Vehicle Based on Optimized ADRC. In Proceedings of the 2019 IEEE 8th Data Driven Control and Learning Systems Conference (DDCLS), Dali, China, 24–27 May 2019; pp. 740–747. [Google Scholar]
- Tian, J.; Zhang, S.; Zhang, Y.; Li, T. Active disturbance rejection control based robust output feedback autopilot design for airbreathing hypersonic vehicles. ISA Trans. 2018, 74, 45–59. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Pu, Z.; Yi, J.; Liu, Z. Fixed-time control with uncertainty and measurement noise suppression for hypersonic vehicles via augmented sliding mode observers. IEEE Trans. Ind. Inform. 2019, 16, 1192–1203. [Google Scholar] [CrossRef]
- Liang, S.; Xu, B.; Ren, J. Kalman-filter-based robust control for hypersonic flight vehicle with measurement noises. Aerosp. Sci. Technol. 2021, 112, 106566. [Google Scholar] [CrossRef]
- Shi, S.; Zeng, Z.; Zhao, C.; Guo, L.; Chen, P. Improved Active Disturbance Rejection Control (ADRC) with Extended State Filters. Energies 2022, 15, 5799. [Google Scholar] [CrossRef]
- J Humaidi, A.; Kasim Ibraheem, I. Speed control of permanent magnet DC motor with friction and measurement noise using novel nonlinear extended state observer-based anti-disturbance control. Energies 2019, 12, 1651. [Google Scholar] [CrossRef] [Green Version]
- Shaughnessy, J.D.; Pinckney, S.Z.; McMinn, J.D.; Cruz, C.I.; Kelley, M.L. Hypersonic Vehicle Simulation Model: Winged-Cone Configuration. In An Overview of an Experimental Demonstration Aerotow Program; NASA Langley Research Center Hampton: Hampton, VA, USA, 1990. [Google Scholar]
- Chen, P.; Luo, Y.; Zheng, W.; Gao, Z.; Chen, Y. Fractional order active disturbance rejection control with the idea of cascaded fractional order integrator equivalence. ISA Trans. 2021, 114, 359–369. [Google Scholar] [CrossRef]





| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Mass | 1250 kg | Reference area | 3.35 m2 |
| Vehicle length | 6.1 m | Rolling moment | 156 kg·m2 |
| Lateral-directional reference length | 1.83 m | Yawing moment | 1162 kg·m2 |
| Longitudinal reference length | 2.44 m | Pitching moment | 1267 kg·m2 |
| Distance from nose to the center of gravity | 3.78 m |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Altitude | 33.5 km | Attack angle | 0° |
| Velocity | 15 Ma | Sideslip angle | 0° |
| Path angle | 0° | Velocity roll angle | 0° |
| Path azimuth angle | 0° |
| Parameters | Roll | Yaw | Pitch |
|---|---|---|---|
| Kp | 119.5 | 74.9 | 198.7 |
| Ki | 10.1 | 0 | 1.65 |
| Kd | 20.1 | 17.4 | 19.4 |
| Integrated Order | Error | Fractional Order | Error | |
|---|---|---|---|---|
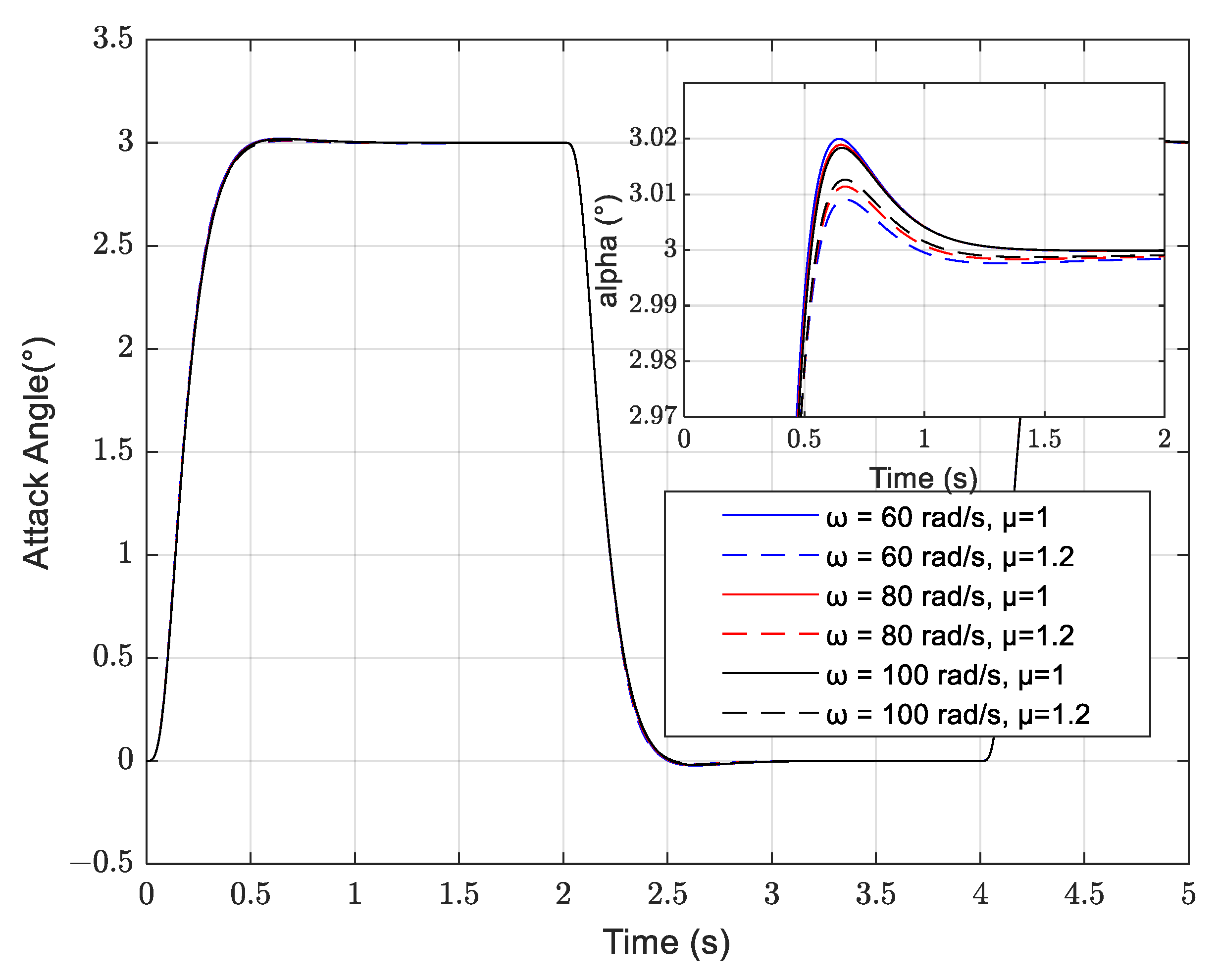
| Attack Angle | ω = 60 rad/s | 0.17° | ω = 60 rad/s | 0.03° |
| ω = 80 rad/s | 0.3° | ω = 80 rad/s | 0.05° | |
| ω = 100 rad/s | 0.5° | ω = 100 rad/s | 0.1° | |
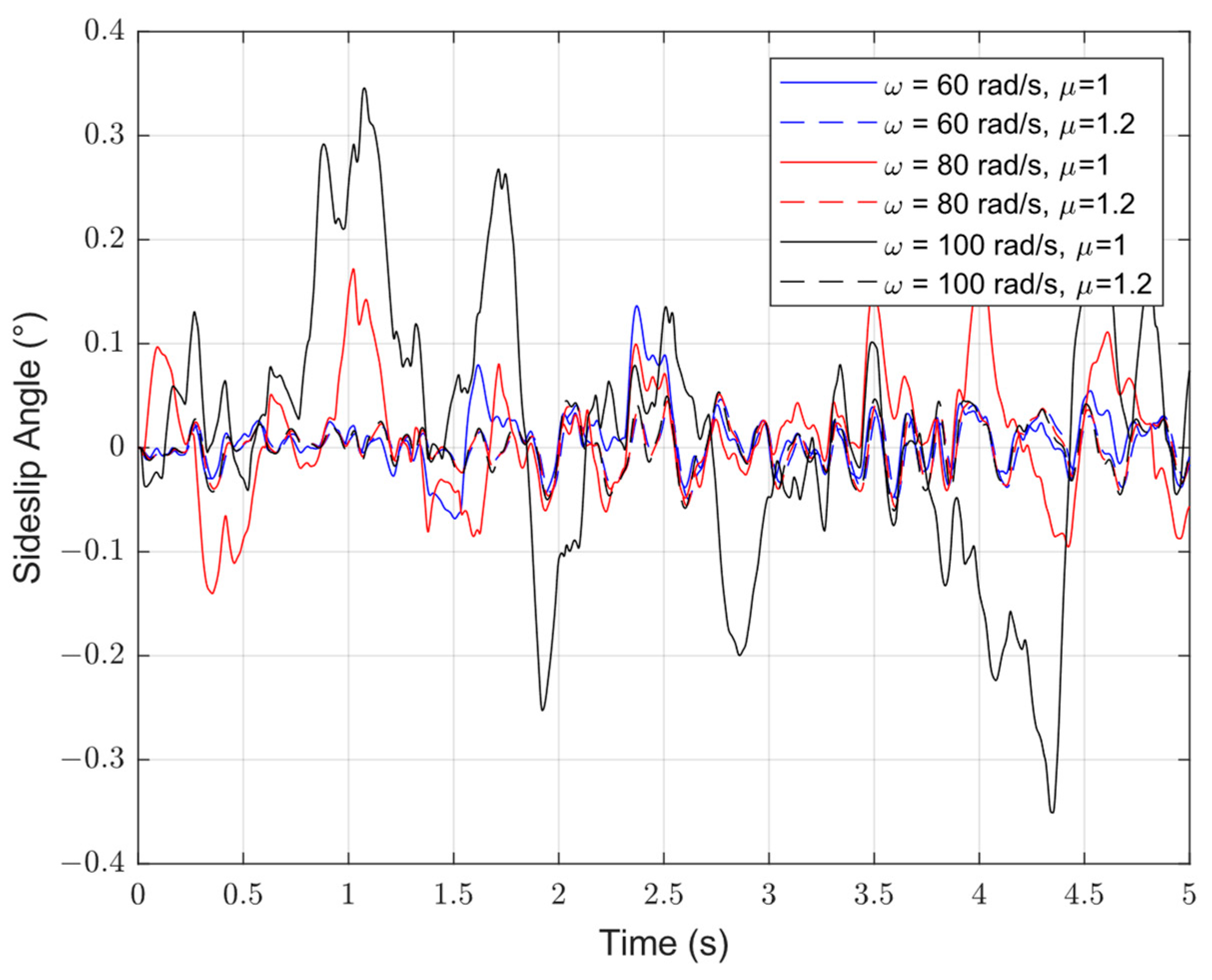
| Sideslip Angle | ω = 60 rad/s | 0.13° | ω = 60 rad/s | 0.06° |
| ω = 80 rad/s | 0.17° | ω = 80 rad/s | 0.06° | |
| ω = 100 rad/s | 0.34° | ω = 100 rad/s | 0.06° | |
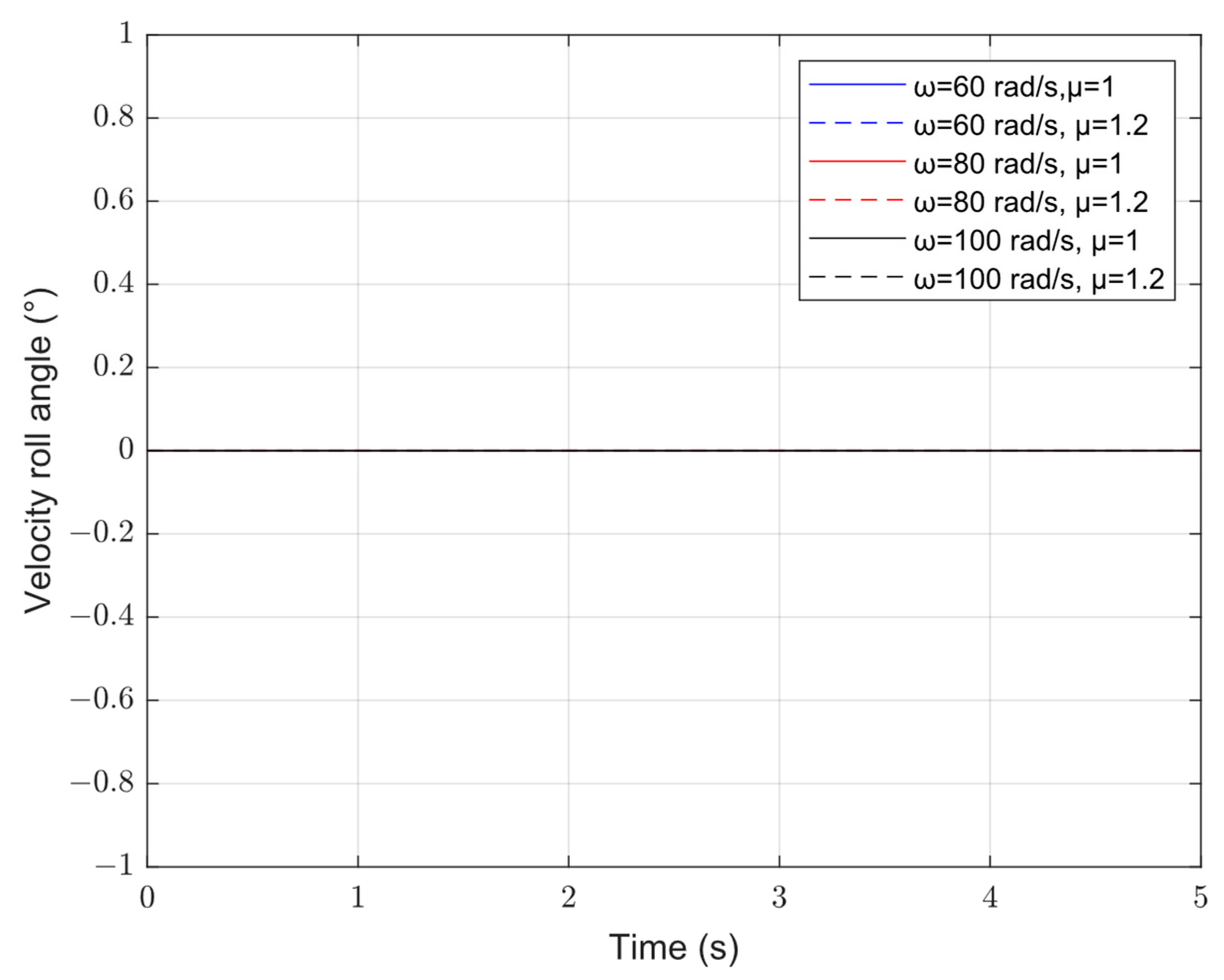
| Velocity Roll Angle | ω = 60 rad/s | 0.2° | ω = 60 rad/s | 0.14° |
| ω = 80 rad/s | 0.25° | ω = 80 rad/s | 0.13° | |
| ω = 100 rad/s | 0.56° | ω = 100 rad/s | 0.1° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, M.; Hu, Y.; Song, J. Improved Fractional-Order Extended State Observer-Based Hypersonic Vehicle Active Disturbance Rejection Control. Mathematics 2022, 10, 4414. https://doi.org/10.3390/math10234414
Zhao M, Hu Y, Song J. Improved Fractional-Order Extended State Observer-Based Hypersonic Vehicle Active Disturbance Rejection Control. Mathematics. 2022; 10(23):4414. https://doi.org/10.3390/math10234414
Chicago/Turabian StyleZhao, Mingfei, Yunlong Hu, and Jia Song. 2022. "Improved Fractional-Order Extended State Observer-Based Hypersonic Vehicle Active Disturbance Rejection Control" Mathematics 10, no. 23: 4414. https://doi.org/10.3390/math10234414






