Generalized Thermoelastic Interactions in an Infinite Viscothermoelastic Medium under the Nonlocal Thermoelastic Model

Abstract

The wave propagation in viscothermoelastic materials is discussed in the present work using the nonlocal thermoelasticity model. This model was created using the Lord and Shulman generalized thermoelastic model due to the consequences of delay times in the formulations of heat conduction and the motion equations. This model was created using Eringen’s theory of the nonlocal continuum. The linear Kelvin–Voigt viscoelasticity model explains the viscoelastic properties of isotropic material. The analytical solutions for the displacement, temperature, and thermal stress distributions are obtained by the eigenvalues approach with the integral transforms in the Laplace transform techniques. The field functions, namely displacement, temperature, and stress, have been graphically depicted for local and nonlocal viscothermoelastic materials to assess the quality of wave propagation in various outcomes of interest. The results are displayed graphically to illustrate the effects of nonlocal thermoelasticity and viscoelasticity. Comparisons are made with and without thermal relaxation time. The outcomes show that Eringen’s nonlocal viscothemoelasticity theory is a promising criterion for analyzing nanostructures, considering the small size effects.

1. Introduction

The nonlocal elastic model was first advocated by Eringen [1]. After a two-year term, the nonlocal of the thermoelastic model was explored by Eringen [2]. Under the nonlocal elastic model, he examined constitutive relations, basic equations, displacement equations, laws of temperature, and equilibrium and continuum mechanics. According to the nonlocal elastic model, in the case of translational motion, strain is the applied stress of the continuous body at point x that relies on the strain point and is also impacted by the body’s stresses at every other area close to this point x. Due to their effects on a nanoscale size, authors have given matching nonlocal beam theories a lot of attention. Traditionally, both the strain state and stress condition are described at the same time. In contrast, the nonlocal continuum model sees the stress states at a location as functions of the strain levels at all body points.

According to local elasticity (classical elastic) experts, material particles circulate continuously and interact with short-range force. The reference strain tensor is used to define the stresses tensor via the algebraic connections of the Hookes models. In contrast, in nonlocal elasticity, long-range force interacts with the particle of the materials, and the algebraic constitutive equations are substituted by an integral or gradient-generalized constitutive equations. Small-scale impacts are additionally accounted for by the addition of a parameter with an internal length scale that emphasizes the effect of the above integrals or differential constitutive operators on the responses of the local materials with respect to a distinct macroscopic dimension of the considered specimen.

Eringen [3] studied nonlocal electromagnetic solids and super-conductivity under the elastic theorem. Eringen and Wegner [4] have elaborated on nonlocal theories of field elasticity concerning continuum mechanics. Povstenko [5] preferred the nonlocal elastic theorem to take into account the forces of actions between atoms. Abouelregal and Zenkour [6] studied the vibrations of thermal conductivity subjected to harmonically varying heating sources using the nonlocal thermoelasticity theory. Yu and Liu [7] discussed Eringen’s nonlocal of thermoelastic with a size-dependent model. In the framework of the nonlocal model of elasticity with nanodigms, Ref. [8] investigated the implications of ultrasonic wave properties. When the law of Fourier heat conductions inspired Biot [9], the coupled thermoelastic theory (CD theory) was developed. This theory is very useful for high-temperature applications in current engineering. Thermoelastic models, however, are physically unacceptable in the situation of low temperatures and are unable to achieve an equilibrium state. To resolve this conflict, Lord et al. [10] (LS) added a one-delay time to Fourier’s rule of heat conduction equation. In their studies of the Lord–Shulman theory for photothermal wave propagation in semiconductor nonlocal elastic media, Sarkar et al. [11] and Saeed [12] applied the hybrid finite element method to study the effects of the fractional time derivative model in piezothermoelastic materials. Sarkar [13] studied the responses of thermoelasticity with the nonlocal model in an elastic rod. The model of nonlocal thermoelasticity with fractional derivative heating transmissions in thermoelastic material was explored by Bachher and Sarkar [14]. Bayones et al. [15] evaluated the impact of changing heat sources on magnetothermo-elastic rods under Eringen’s nonlocal models with TPL with memory-dependent derivatives. Numerous studies were conducted using the thermoelastic hypothesis, including [16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44].

This article attempts to obtain the analytical solution of the nonlocal viscothermoelastic problem using the Laplace transform and eigenvalues approach. The eigenvalue technique provides an accurate solution in the Laplace domain without any imposed constraints on the actual physical parameters. Numerical outcomes for the variation of displacement, the increment of temperature and the distributions of stress are presented graphically. The analytical solutions for the temperature, displacement, and distribution of thermal stress are obtained by the eigenvalues approach with integral transforms in the Laplace transform techniques. The effects of nonlocal parameters and the thermal and viscoelastic delay times on the distributions of wave propagations of physical fields for mediums are shown graphically and discussed.

2. The Nonlocal Viscothermoelasticity Models

Following Eringen [45] and Lord–Shulman [10], the basic formulations for nonlocal viscothermoelastic medium in the absence of thermal sources and of body force are taken by:

$$\rho \left(1-{\beta }^2{\nabla }^2\right)\frac{{\partial }^2{u}_i}{\partial t^2}=\mu u_{i,jj}+\left(\lambda +\mu \right)u_{j,ij}-\gamma T_{,i},$$

(1)

$$K{\nabla }^{2}T=\left(1-{\beta }^2{\nabla }^2\right)\left(\frac{\partial }{\partial t}+{\tau }_o\frac{{\partial }^2}{\partial t^2}\right)\left(\rho c_{e}T+\gamma T_o{u}_{i,i}\right),$$

(2)

$$\left(1-{\beta }^2{\nabla }^2\right){\sigma }_{ij}=\left(\lambda u_{k,k}-\gamma T\right){\delta }_{ij}+\mu \left(u_{i,j}+u_{j,i}\right).$$

(3)

As the medium is viscoelastic, the parameters $\lambda ={\lambda }_e\left(1+{\alpha }_1\frac{\partial }{\partial t}\right)$, $\mu ={\mu }_e\left(1+{\alpha }_2\frac{\partial }{\partial t}\right)$, $\gamma ={\gamma }_e\left(1+{\gamma }_1\frac{\partial }{\partial t}\right)$, ${\gamma }_e=\left(3{\lambda }_e+2{\mu }_e\right){\alpha }_t$, ${\gamma }_1=\frac{\left(3{\lambda }_e{\alpha }_1+2{\mu }_e{\alpha }_2\right){\alpha }_t}{{\gamma }_e}$; where $\gamma$ and ${\gamma }_e$ are the thermoelastic and viscothermoelastic coupling constants; $\beta$ is the nonlocal parameter; $\rho$ is the material density; ${\alpha }_1, {\alpha }_2$ are the viscoelastic relaxation times; $T_o$ is the reference temperature; $T=T^{*}-T_o$, $T^{*}$ are the temperature variations; ${\sigma }_{ij}$ are the stress components; ${\lambda }_e, {\mu }_e$ are the Lame’s constants; $\lambda , \mu$ are the viscoelastic Lame’s constants; $u_i$ is the displacements; $c_e$ is the specific heat at constant strain; ${\alpha }_t$ is the coefficient of linear thermal expansions; ${\tau }_o$ is the thermal relaxation time; $t$ is the time; $K$ is the thermal conductivity. Consider now a half-space ($x\ge 0$) in which the x-axis points into the mediums. The analysis is simplified when the one-dimensional problem is considered. The displacement components for one-dimensional media, as shown in Figure 1, are as follows:

$$u_x=u\left(x,t\right),\hspace{1em}\hspace{1em} u_y=0,\hspace{1em}\hspace{1em} u_z=0.$$

(4)

The relation between the components of strain and the component of displacement are given by

$$e_{xx}=\frac{\partial u}{\partial x}$$

(5)

From Equations (4) and (5), in the basic equations, (1)–(3) can be given as

$$\rho \left(1-{\beta }^2\frac{{\partial }^2}{\partial x^2}\right)\frac{{\partial }^{2}u}{\partial t^2}=\left({\lambda }_e\left(1+{\alpha }_1\frac{\partial }{\partial t}\right)+2{\mu }_e\left(1+{\alpha }_2\frac{\partial }{\partial t}\right)\right)\frac{{\partial }^{2}u}{\partial x^2}-{\gamma }_e\left(1+{\gamma }_1\frac{\partial }{\partial t}\right)\frac{\partial T}{\partial x},$$

(6)

$$K\frac{{\partial }^{2}T}{\partial x^2}=\left(1-{\beta }^2\frac{{\partial }^2}{\partial x^2}\right)\left(\frac{\partial }{\partial t}+{\tau }_o\frac{{\partial }^2}{\partial t^2}\right)\left(\rho c_{e}T+T_o{\gamma }_e\left(1+{\gamma }_1\frac{\partial }{\partial t}\right)\frac{\partial u}{\partial x}\right),$$

(7)

$$\left(1-{\beta }^2\frac{{\partial }^2}{\partial x^2}\right){\sigma }_{xx}=\left(\left(1+{\alpha }_1\frac{\partial }{\partial t}\right){\lambda }_e+2\left(1+{\alpha }_2\frac{\partial }{\partial t}\right){\mu }_e\right)\frac{\partial u}{\partial x}-{\gamma }_e\left(1+{\gamma }_1\frac{\partial }{\partial t}\right)T=\sigma .$$

(8)

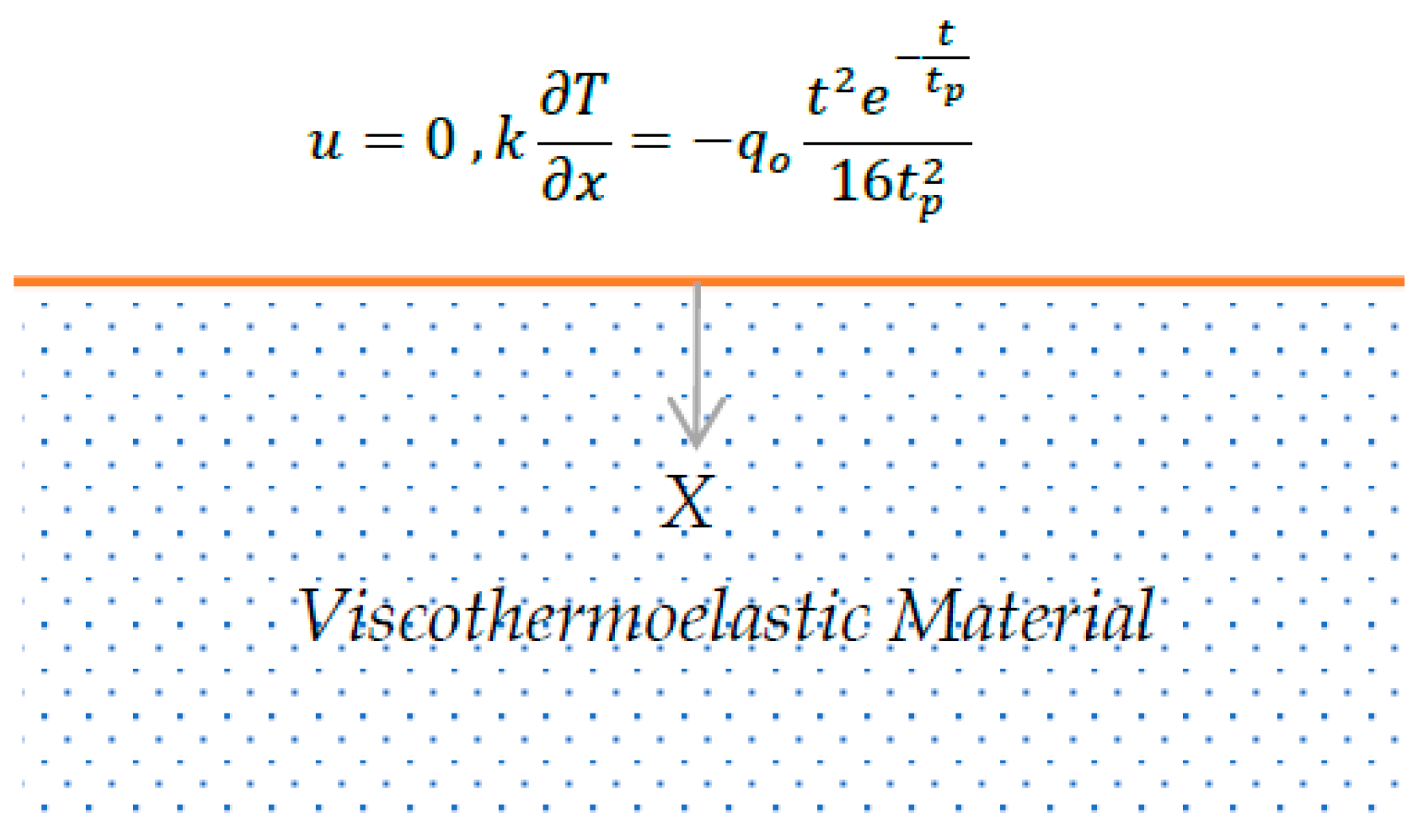
3. Application

Mechanically and thermally, the medium is assumed to be at rest, i.e.,

$$T\left(x,0\right)=0,\frac{\partial T\left(x,0\right)}{\partial t}=0,u\left(x,0\right)=0,\frac{\partial u\left(x,0\right)}{\partial t}=0$$

(9)

The thermal and mechanical boundary conditions can be expressed as in [46].

$$u\left(0,t\right)=0,K{\frac{\partial T\left(x,t\right)}{\partial x}|}_{x=0}=-q_o\frac{t^2{e}^{-\frac{t}{t_p}}}{16t_p^2}$$

(10)

where $t_p$ is the pulse heatflux characteristic time and $q_o$ is a constant. The following dimensionless variables may be utilised to obtain the main fields in a non-dimensional form:

$$\begin{gathered} \left(x^{\prime },u^{\prime },{\beta }^{\prime }\right)=\eta c\left(x,u,\beta \right), T^{\prime }=\frac{{\gamma }_{e}T}{\rho c^2}, {\sigma }^{\prime }=\frac{\sigma }{\rho c^2}, \\ \left(t^{\prime },t_p^{\prime },{\tau }_o^{\prime },{\alpha }_1^{\prime },{\alpha }_2^{\prime },{\gamma }_1^{\prime }\right)=\eta c^2\left(t,t_p,{\tau }_o,{\alpha }_1,{\alpha }_2,{\gamma }_1\right) \end{gathered}$$

(11)

where $c^2=\frac{{\lambda }_e+2{\mu }_e}{\mathsf{\rho }}$, $\eta =\frac{\rho c_e}{K}$. By using the variables of dimensionless forms (11), the fundamental relationships with the omission of dashes may be expressed by:

$$\left(1-{\beta }^2\frac{{\partial }^2}{\partial x^2}\right)\frac{{\partial }^{2}u}{\partial t^2}=\left(1+ϵ\frac{\partial }{\partial t}\right)\frac{{\partial }^{2}u}{\partial x^2}-\left(1+{\gamma }_1\frac{\partial }{\partial t}\right)\frac{\partial T}{\partial x}$$

(12)

$$\frac{{\partial }^{2}T}{\partial x^2}=\left(1-{\beta }^2\frac{{\partial }^2}{\partial x^2}\right)\left(\frac{\partial }{\partial t}+{\tau }_o\frac{{\partial }^2}{\partial t^2}\right)\left(T+\vartheta \left(1+{\gamma }_1\frac{\partial }{\partial t}\right)\frac{\partial u}{\partial x}\right),$$

(13)

$$\left(1-{\beta }^2\frac{{\partial }^2}{\partial x^2}\right){\sigma }_{xx}=\sigma =\left(1+ϵ\frac{\partial }{\partial t}\right)\frac{\partial u}{\partial x}-\left(1+{\gamma }_1\frac{\partial }{\partial t}\right)T,$$

(14)

$$\frac{\partial T\left(x,0\right)}{\partial t}=0,u\left(x,0\right)=0,\frac{\partial u\left(x,0\right)}{\partial t}=0,$$

(15)

$$u=0 , \frac{\partial T}{\partial x}=-q_o\frac{t^2{e}^{-\frac{t}{t_p}}}{16t_p^2},$$

(16)

where $ϵ=\frac{\left({\lambda }_e{\alpha }_1+2{\mu }_e{\alpha }_2\right)}{\left({\lambda }_e+2{\mu }_e\right)}$ and $\vartheta =\frac{{\gamma }_e^2{T}_o}{\left({\lambda }_e+2{\mu }_e\right)\rho c_e}$.

4. Analytical Method

The Laplace transforms for the relations (12)–(16) are defined by

$$\overline{f}\left(x,p\right)=L\left[f\left(x,t\right)\right]={\int }_0^{\infty }f\left(x,t\right)e^{-pt}dt.$$

(17)

Hence, the following system is obtained:

$$\left(1-{\beta }^2\frac{d^2}{d{x}^2}\right)p^2\overline{u}=\left(1+ϵp\right)\frac{d^2\overline{u}}{d{x}^2}-\left(1+{\gamma }_{1}p\right)\frac{d\overline{T}}{dx},$$

(18)

$$\frac{d^2\overline{T}}{d{x}^2}=\left(1-{\beta }^2\frac{d^2}{d{x}^2}\right)\left(p+{\tau }_o{p}^2\right)\left(\overline{T}+\vartheta \left(1+{\gamma }_{1}p\right)\frac{d\overline{u}}{dx}\right),$$

(19)

$$\overline{\sigma }=\left(1+ϵp\right)\frac{d\overline{u}}{dx}-\left(1+{\gamma }_{1}s\right)\overline{T},$$

(20)

$$\overline{u}=0,\frac{d\overline{T}}{dx}=\frac{-q_o{t}_p}{8{\left(p{t}_p+1\right)}^3}.$$

(21)

Equations (18) and (19) can be rewritten by the following forms:

$$\frac{d^2\overline{u}}{d{x}^2}=a_{31}\overline{u}+a_{34}\frac{d\overline{T}}{dx},$$

(22)

$$\frac{d^2\overline{T}}{d{x}^2}=a_{42}\overline{T}+a_{43}\frac{d\overline{u}}{dx},$$

(23)

where

$$a_{31}=\frac{p^2}{\left(\left(1+ϵp\right)+{\beta }^2{p}^2\right)}, a_{34}=\frac{\left(1+{\gamma }_{1}p\right)}{\left(\left(1+ϵp\right)+{\beta }^2{p}^2\right)},$$

$$a_{42}=\frac{\left(p+{\tau }_o{p}^2\right)}{\left(1+{\beta }^2\left(p+{\tau }_o{p}^2\right)+{\beta }^2\vartheta \left(1+{\gamma }_{1}p\right)\left(p+{\tau }_o{p}^2\right)a_{12}\right)},$$

$$a_{43}=\frac{\left(p+{\tau }_o{p}^2\right) \vartheta \left(1+{\gamma }_{1}p\right)\left[1-{\beta }^2{a}_{11}\right]}{\left(1+{\beta }^2\left(p+{\tau }_o{p}^2\right)+{\beta }^2\vartheta \left(1+{\gamma }_{1}p\right)\left(p+{\tau }_o{p}^2\right)a_{12}\right)},$$

Now, the coupled differential Equations (22) and (23) may be solved by the eigenvalue’s approaches proposed [47,48,49]:

$$\frac{dV}{dx}=AV,$$

(24)

where V $={\left[\begin{array}{cccc}\overline{u}& \overline{T}& \frac{d\overline{u}}{dx}& \frac{d\overline{T}}{dx}\end{array}\right]}^T$ and $A=\left[\begin{array}{cccc}0& 0& 1& 0\\ 0& 0& 0& 1\\ a_{31}& 0& 0& a_{34}\\ 0& a_{42}& a_{43}& 0\end{array}\right]$.

Consequently, the matrix characteristic relations of $A$ are assumed to be

$${\zeta }^4-{\zeta }^2\left(a_{31}+a_{42}+a_{34}{a}_{43}\right)+a_{31}{a}_{42}=0.$$

(25)

The eigenvalues of matrix $A$ are the four roots of relation (25), denoted by the symbols $\pm {\zeta }_1, \pm {\zeta }_2.$ Therefore, the equivalent eigenvectors $Y_i$ can be calculated as:

$$Y_i=\left[\begin{array}{c}\zeta a_{34}\\ {\zeta }^2-a_{31}\\ {\zeta }^2{a}_{34}\\ \zeta \left({\zeta }^2-a_{31}\right)\end{array}\right].$$

(26)

Thus, the analytical solution of Equation (24) can be given by:

$$\mathrm{V}\left(x,p\right)={\sum }_{i=1}^4{B}_i{Y}_i{e}^{{\zeta }_{i}x},$$

(27)

Thus, the field variables can be written for $x$ and $p$ as:

$$\overline{u}\left(x,p\right)={\zeta }_1{a}_{34}{B}_1{e}^{{\zeta }_{1}x}+{\zeta }_2{a}_{34}{B}_2{e}^{{\zeta }_{2}x}+{\zeta }_3{a}_{34}{B}_3{e}^{{\zeta }_{3}x}+{\zeta }_4{a}_{34}{B}_4{e}^{{\zeta }_{4}x},$$

(28)

$$\overline{T}\left(x,p\right)=\left({\zeta }_1^2-a_{31}\right)B_1{e}^{{\zeta }_{1}x}+\left({\zeta }_2^2-a_{31}\right)B_2{e}^{{\zeta }_{2}x}+\left({\zeta }_3^2-a_{31}\right)B_3{e}^{{\zeta }_{3}x}+\left({\zeta }_4^2-a_{31}\right)B_4{e}^{{\zeta }_{4}x},$$

(29)

where $B_1, B_2, B_3$, and $B_4$ are evaluated by the problem’s boundary conditions. The numerical inversion methodology utilizes the temperature, displacement, and stress distribution of the final solutions. The Stehfest algorithm [50] may be described as follows: we use a numerical inversion approach based on the Stehfest [50] for the final solution of temperature, displacement, and stress distributions in the time domain. The relation approximates the inverse of the Laplace transform in this approach.

$$f\left(x,t\right)=\frac{ln\left(2\right)}{t}{\sum }_{n=1}^G{V}_n\overline{f}\left(x,n\frac{ln\left(2\right)}{t}\right),$$

(30)

with

$$V_n={\left(-1\right)}^{\left(\frac{G}{2}+1\right)}{\sum }_{k=\left[\frac{n+1}{2}\right]}^{min\left(n,\frac{G}{2}\right)}\frac{\left(2k\right)!k^{\left(\frac{G}{2}+1\right)}}{k!\left(n-k\right)!\left(\frac{G}{2}-k\right)!\left(2n-1\right)!},$$

The parameter $G$ is the number of terms that should be evenly used in the summation in Equation (30) and should be optimized by trial and error. Increasing $G$ increases the accuracy of the result up to a point, and then the accuracy declines because of increasing round-off errors. An optimal choice of 10 ≤ G ≤ 14 has been reported by Lee et al. for some problems in their interest [51].

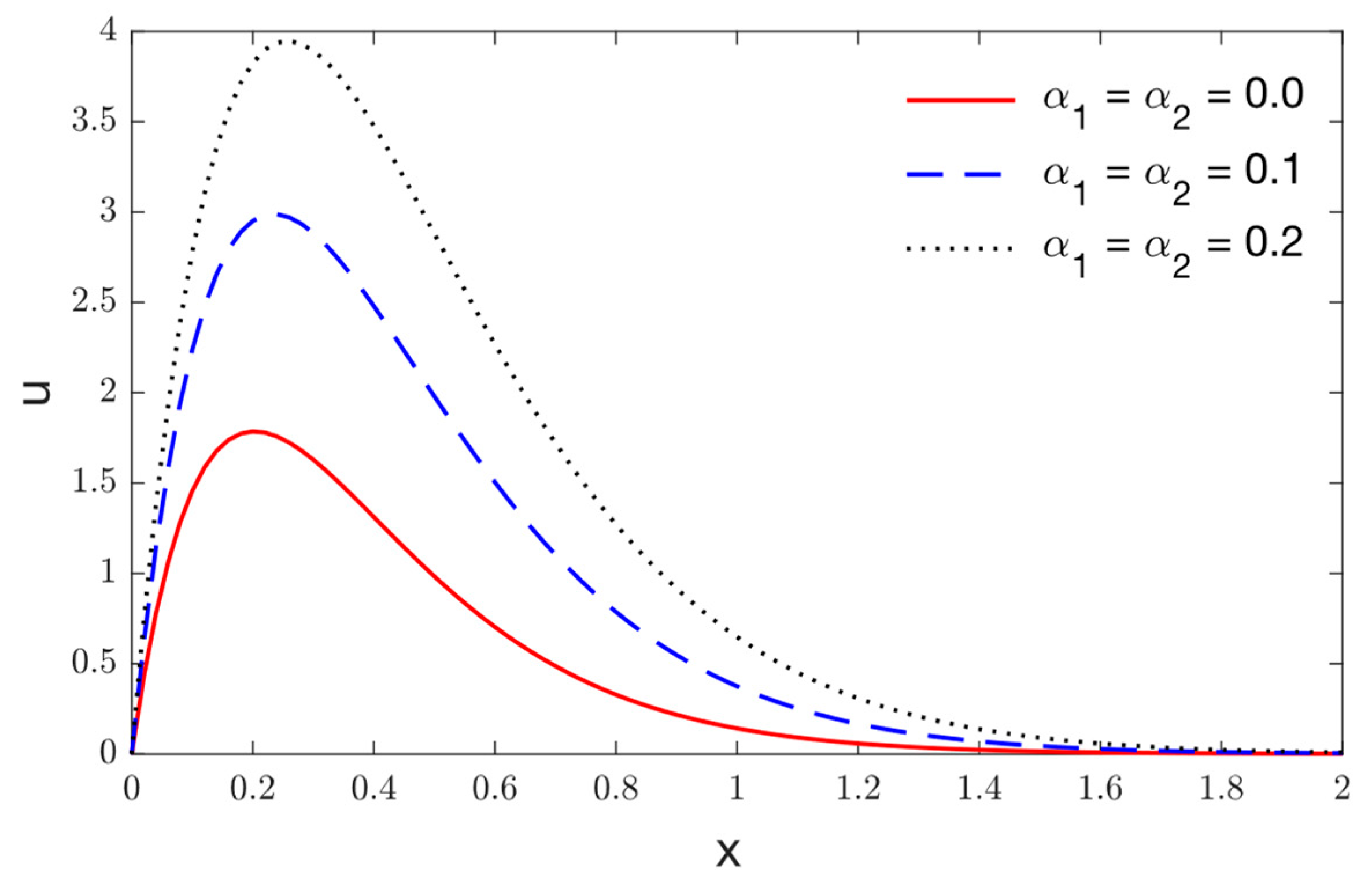
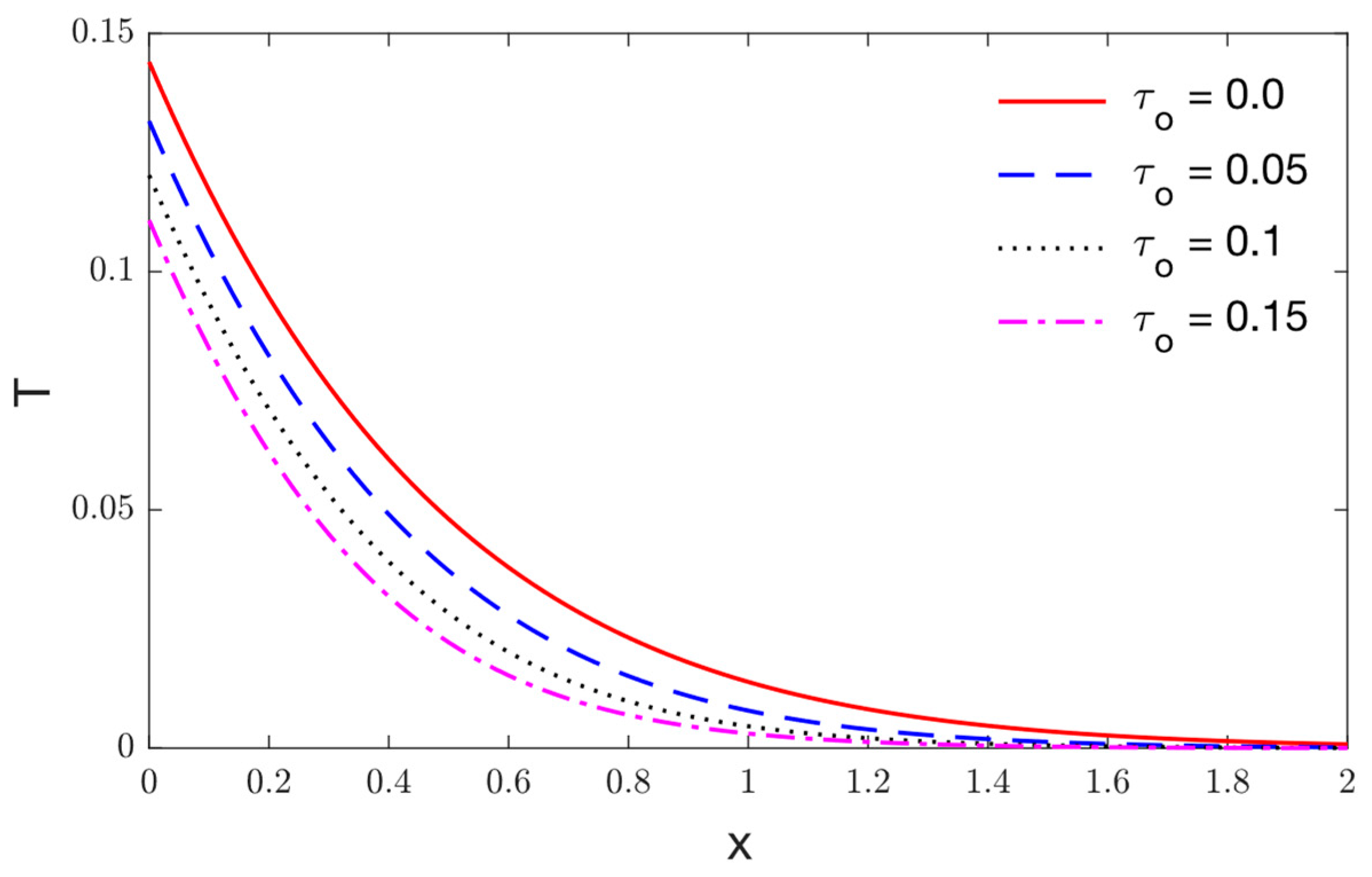
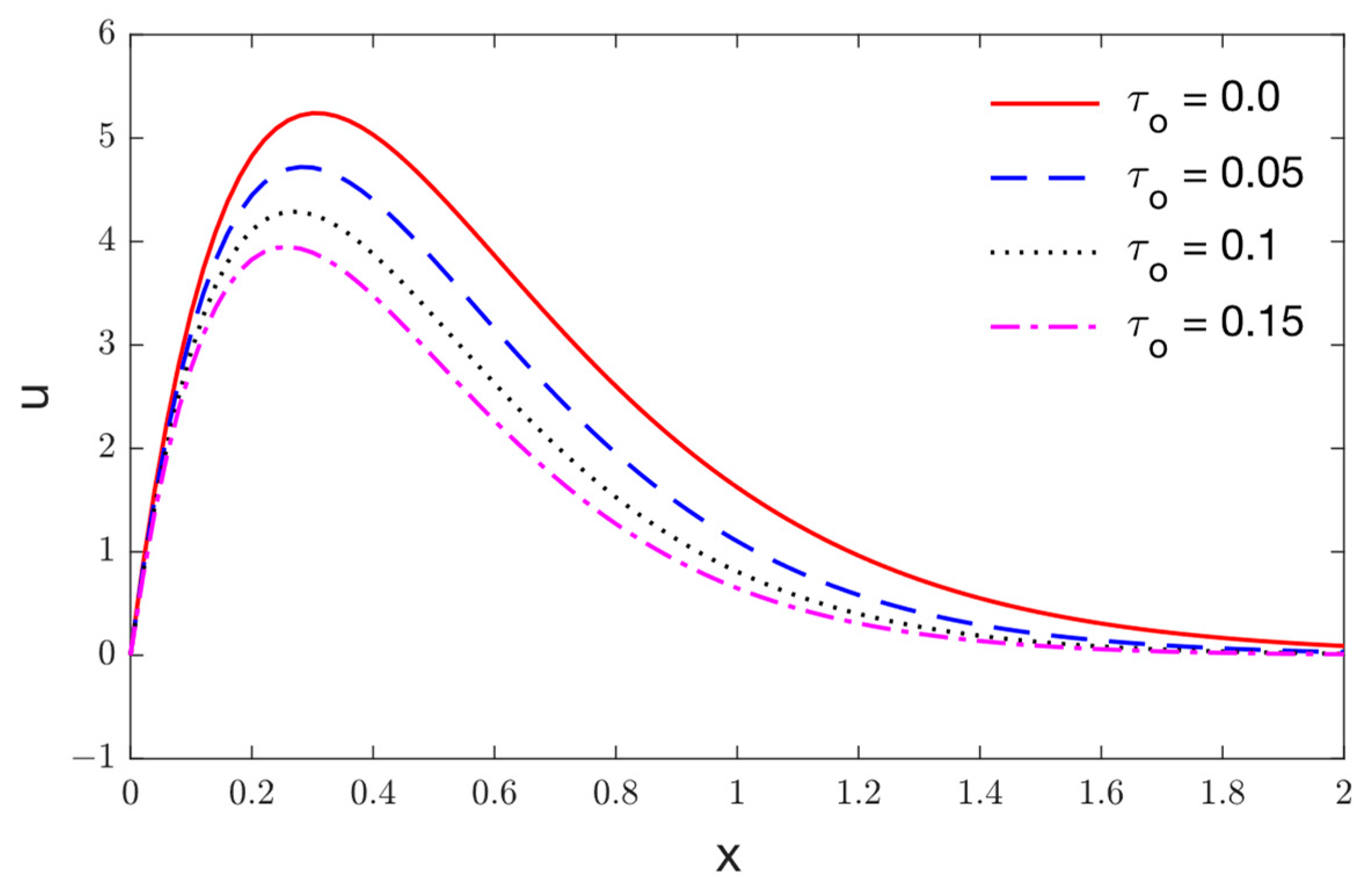
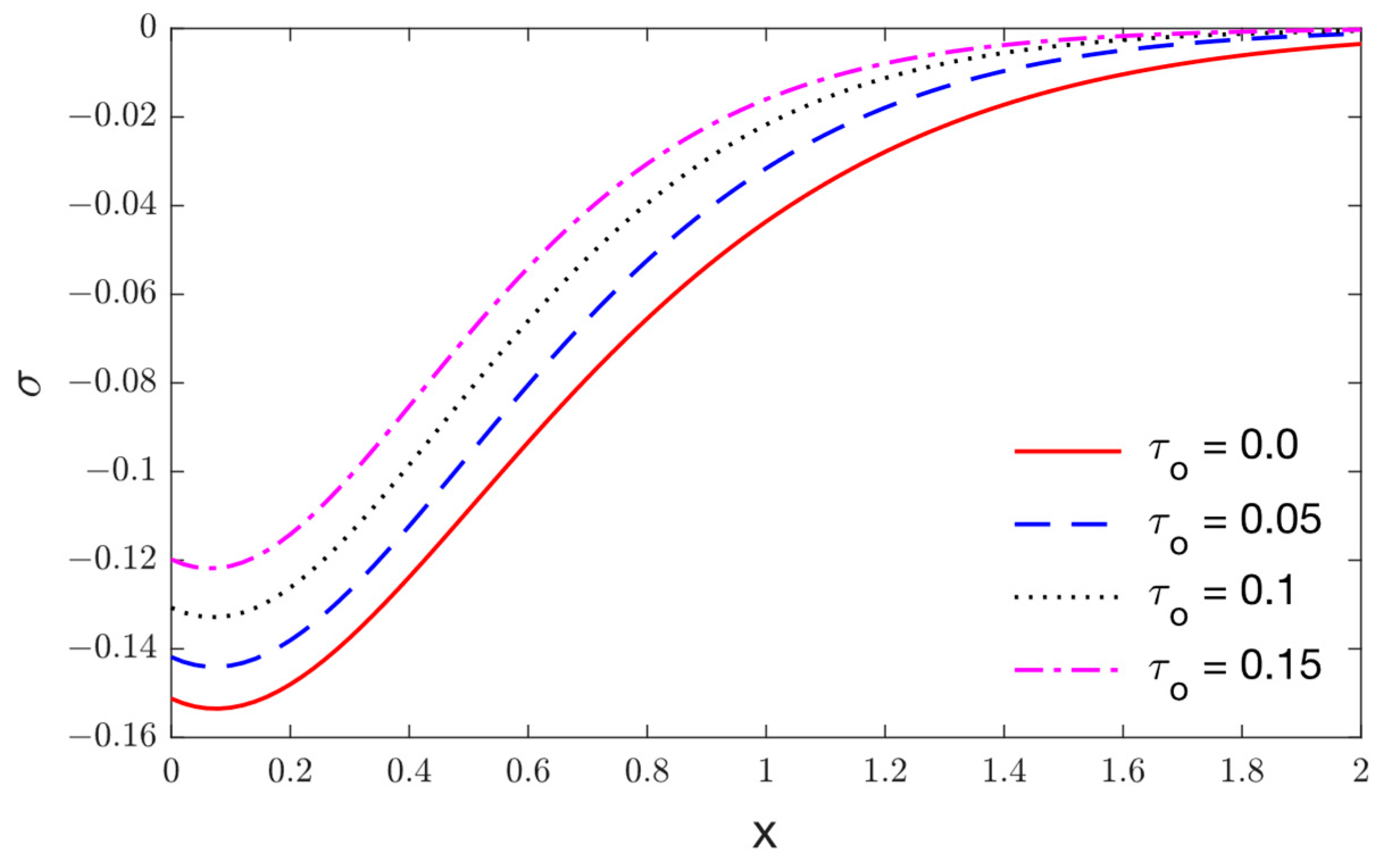
5. Results and Discussions

To demonstrate the problem and compare the theoretical results under the nonlocal viscothermoelastic theory, we shall plot several numerical outcomes and graphs. The authors discuss the material characteristics of the copper material, whose physical properties are outlined in the list below [15].

$$\lambda =7.76\times {10}^{10} \mathrm{N}/{\mathrm{m}}^2, {\alpha }_t=1.78\times {10}^{-5}{ \mathrm{k}}^{-1}, \rho =8954 \mathrm{kg}/{\mathrm{m}}^3,\mu =3.86\times {10}^{10} \mathrm{N}/{\mathrm{m}}^2,$$

$$c_e=383.1 {\mathrm{m}}^2/\mathrm{k}, T_o=293 \mathrm{k}, t=0.4, \beta =0.15,{\tau }_o=0.15,t_p=0.3,K=386 \mathrm{N}/\left(\mathrm{ks}\right).$$

Calculations are performed numerically for three distinct cases: the impacts of nonlocal parameters, the viscoelastic relaxation times, and the thermal relaxation times. In the first one, a comparison is made between the local viscothermoelastic model $\left(\beta =0.0\right)$ and the nonlocal viscothermoelastic model $\left(\beta =0.15\right)$ when $\left({\alpha }_1={\alpha }_2=0.2 ,{\tau }_o=0.15\right)$, as shown in Figure 2, Figure 3 and Figure 4. In the second case, the impacts of viscothermoelastic relaxation times on the displacement, temperature, and stress variations when $\left(\beta =0.15 ,{\tau }_o=0.15\right)$ are presented in Figure 5, Figure 6 and Figure 7. In the third case, the effect of thermal relaxation times on the variations of displacement, temperature, and stress when $\left(\beta =0.15 ,{\alpha }_1={\alpha }_2=0.2\right)$ are shown in Figure 8, Figure 9 and Figure 10.

Figure 2, Figure 5 and Figure 8 show the temperature variation along the distance x. It is observed that the temperature starts from the maximum values at the boundary and then decreases with the increase in the distance $x$ to close to zero. Figure 3, Figure 6 and Figure 9 display the displacement variations concerning the distance x. It is observed that the displacement starts from the zero value at the boundary, which satisfies the problem boundary conditions; then, the displacement increases gradually with the increase in distance until height values and then decreases with the increase in the distance $x$ to close to zero. Figure 4, Figure 7 and Figure 10 show the variations of stress via the distance. It observed that the magnitudes of stress start from the maximum values, then the magnitudes of stress increase with the increase in $x$ to reach the zero values.

From Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10, one concludes that the local generalized thermoelastic model and the generalized thermoelastic model with nonlocal thermal conduction and elastic are compared in Figure 2, Figure 3 and Figure 4. Figure 5, Figure 6 and Figure 7 depict the impacts of viscoelastic relaxation times under the generalized nonlocal viscothermoelastic model. Figure 8, Figure 9 and Figure 10 show the impacts of thermal relaxation times under the thermoelastic theory under nonlocal elastic and thermal conduction. A comparison of the data leads to the conclusion that the nonlocal viscothermoelasticity hypothesis is a significant phenomenon and has a significant impact on the distributions of physical variables.

6. Conclusions

The problem of investigating the temperature, displacement, and stress in an isotropic, homogeneous, unbounded, extended Kelvin–Voigt-type visco-thermoelasticity continuum has been studied under the generalized themoelasticity model. The problem has been described using the Cartesian coordinate system, and the solutions are found in the transformed domain of Laplace. Stehfest’s approach was used to conduct the numerical inversion of the Laplace transform. The following are some conclusions that we may derive from the theoretical and numerical discussion:

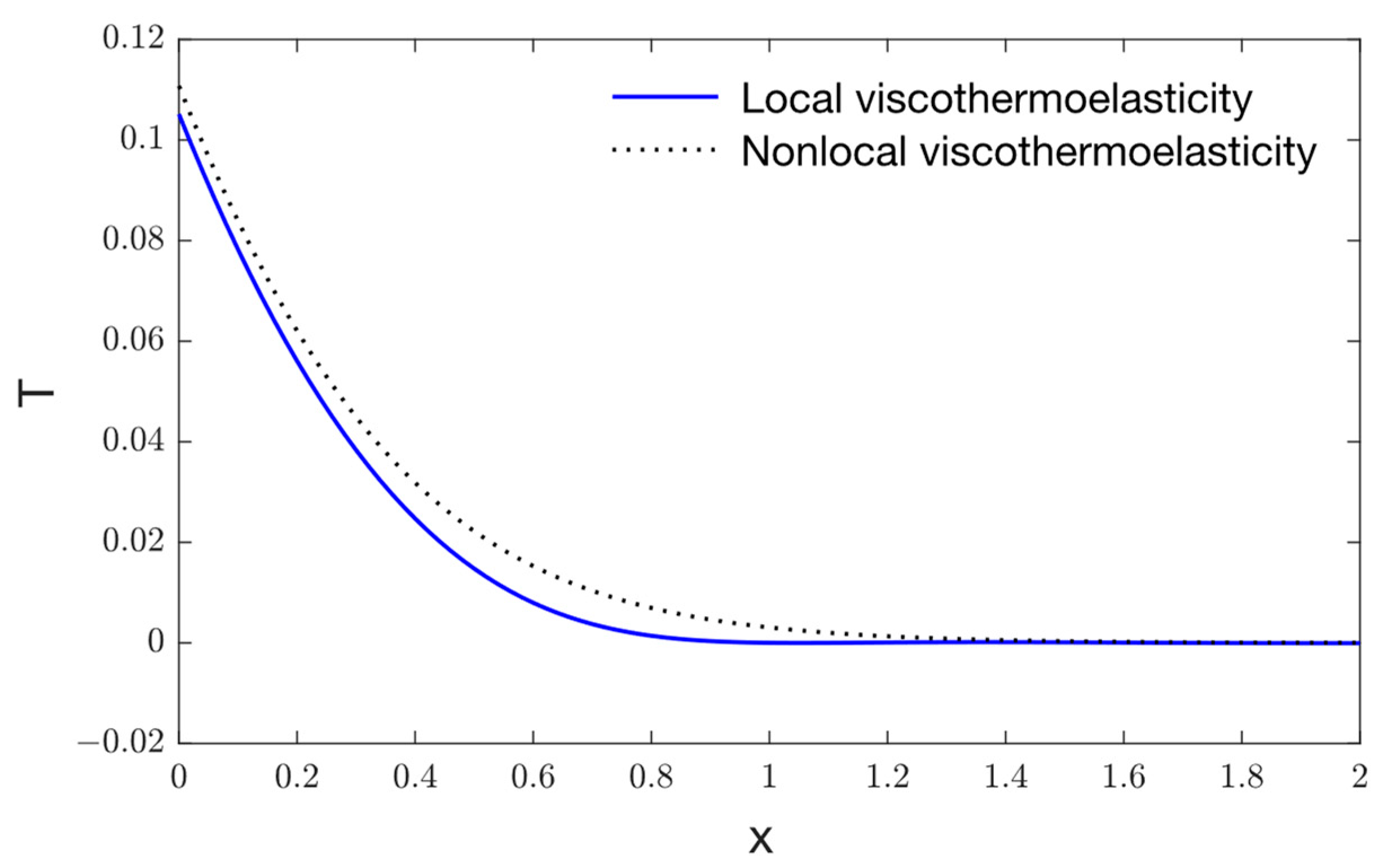
• According to the extended theory of thermoelasticity, all thermophysical values disappear beyond a certain distance.
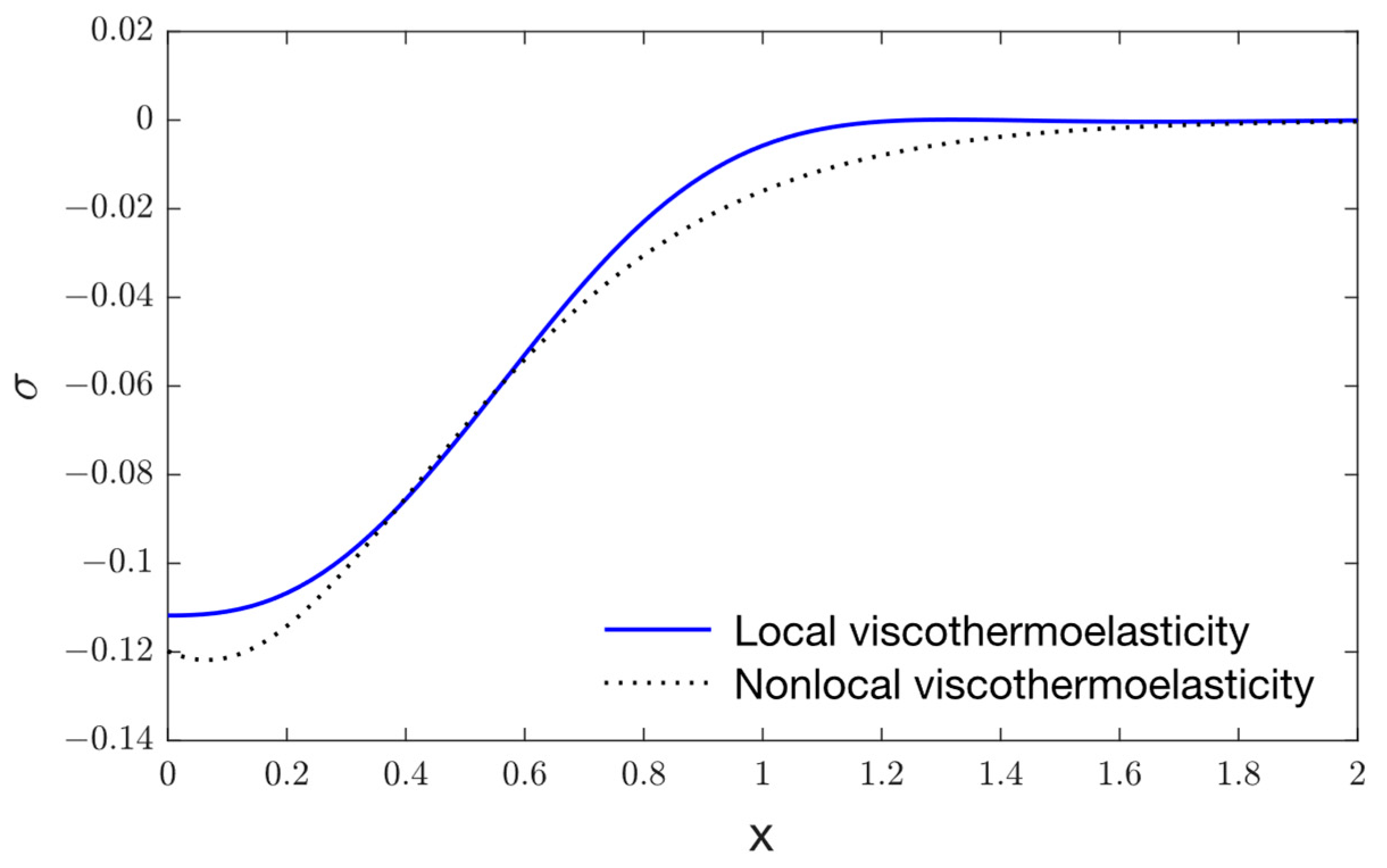
• Magnitudes of temperature, displacement, and stress, corresponding to the nonlocal thermoelastic model, are larger than the local thermoelastic model in the viscothermoelastic medium.
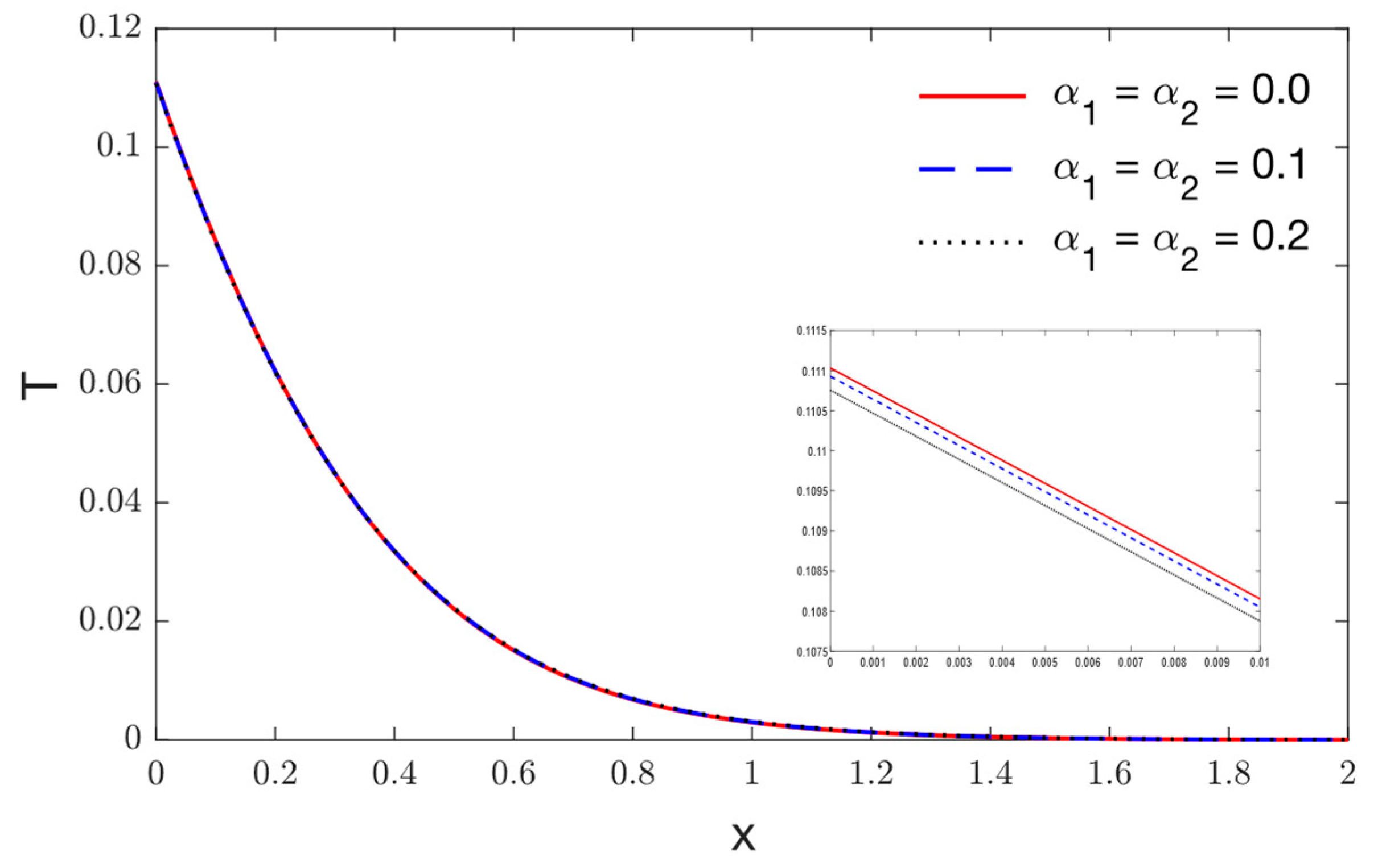
• Significant effects of viscothermoelastic relaxation parameters on the distributions of thermophysical quantities are observed.
• As the viscothermoelastic relaxation parameter rises, the maximum magnitude of the displacement and the stress grow and move further away from the surface before disappearing.