Special Fractional-Order Map and Its Realization

Abstract

Recent works have focused the analysis of chaotic phenomena in fractional discrete memristor. However, most of the papers have been related to simulated results on the system dynamics rather than on their hardware implementations. This work reports the implementation of a new chaotic fractional memristor map with “hidden attractors”. The fractional memristor map is developed based on a memristive map by using the Grunwald–Letnikov difference operator. The fractional memristor map has flexible fixed points depending on a system’s parameters. We study system dynamics for different values of the fractional orders by using bifurcation diagrams, phase portraits, Lyapunov exponents, and the 0–1 test. We see that the fractional map generates rich dynamical behavior, including coexisting hidden dynamics and initial offset boosting.

1. Introduction

While the concept of non-integer order derivative dates back to 1695, discrete fractional calculus was introduced about fifty years ago [1]. Namely, fractional difference equations were derived for the first time in 1974 via the discretization of continuous-time operators [2]. By virtue of the great attention recently received by discrete fractional calculus, several difference operators have been proposed in the literature, including the Grunwald–Letnikov difference operator [3].

Since the discovery of chaos, various works have been made to deeply analyze the dynamics of classical systems and fractional systems [4,5]. Referring to the latter, several papers have been published on the study of chaotic behaviors in nonlinear maps described by difference equations of fractional order [6,7]. Based on the Caputo-left difference operator, Wu et al. [8] have introduced a fractional logistic map where the chaotic behavior was investigated. In [9], a simple one-dimensional fractional map with chaotic attractors and quasi-periodic behaviors is proposed. Khennaoui et al. [10] further proved the existence of chaotic attractors in three fractional maps. In the same year, Peng et al. [11] reported the dynamic behavior of a higher dimensional fractional order chaotic map, whereas in [12], the authors have investigated a fractional order higher-dimensional multicavity chaotic map. Recently, Lu et al. have investigated the dynamics of a fractional order memristor-based Rulkov neuron map [13]. On the other hand, the chaos and stability of the fractional-order discrete COVID-19 pandemic model is reported in [14]. In addition, there are many studies in the literature that investigate some special phenomena such as hidden attractors as well as coexistence attractors in fractional-order maps. Chaos on a novel fractional map with an infinite number of fixed points is investigated in [15]. In [16], the behavior of a fractional-order discrete Bonhoeffer-van der Pol oscillator is illustrated. The map highlights the coexistence of different types of attractors, including quasi-periodical and periodic attractors, as well as chaotic and hyperchaotic attractors. Moreover, Almatroud et al. [17] demonstrated the hidden extrem multistability in a novel 2D fractional-order chaotic map. In recent years, memristive maps have been proposed. In [18], the dynamic properties of a novel discrete memristive logistic map have been illustrated, while a memristive map with hyperchaotic was introduced in [19].

In this study, a new fractional memristive map with infinite fixed points and no fixed points is constructed using the Grunwald–Letnikov operator. This new fractional memristive map possess not only hidden attractors but also coexisting attractors. The hidden attractors are numerically analyzed by bifurcation diagrams, phase portraits, and the 0–1 test. Moreover, the initial boosting phenomena is investigated in the proposed map. Furthermore, a microcontroller is used to realize in hardware the proposed 2D fractional map. The experimental results clearly show the presence of chaotic hidden attractors, indicating that the approach developed herein is sound.

2. General Model

We consider the memristive map

$$\left\{\begin{array}{c}x\left(k+1\right)=a_{1}sin\left(a_{2}cos\left(y\left(k\right)\right)x\left(k\right)\right)+a_3,\hfill \\ y\left(k+1\right)=y\left(k\right)+x\left(k\right),\hfill \end{array}\right.$$

(1)

where $a_1,a_2,a_3$ are bifurcation parameters. This map has been recently introduced in [20]. Fixed points in the map (1) are calculated by:

$$\left\{\begin{array}{c}x=a_{1}sin\left(a_{2}cos\left(y\right)x\right)+a_3,\hfill \\ y=y+x.\hfill \end{array}\right.$$

(2)

By solving Equation (2), we derive the following two cases:

Cas 1.

When $a_3=0$, the fixed points of system (1) in this case are given by $S=(0,\theta )$, where $\theta$ is an arbitrary value depending on the memristor initial state. This implies that the the memristor map (1) has infinite fixed points.

The Jacobian matrix at set $S=(0,\theta )$ can be expressed as:

$$J=\left(\begin{array}{cc}{a}_1{a}_{2}cos\left(\theta \right)& 0\\ 1& 1\end{array}\right).$$

(3)

The characteristic roots of map (1) in this case are ${\lambda }_1=1$ and ${\lambda }_2=a_1{a}_{2}cos\left(\theta \right)$. The fixed points S are stable if the eigenvalues ${\lambda }_1$ and ${\lambda }_2$ satisfy $|{\lambda }_i|<1,$$\forall i=1,2$. Since there is a real root $|{\lambda }_1|=1$, we can not determine the stability of line equilibrium points S, but it can determined by the numerical results.

Cas 2.

When $a_3\ne 0$, Equation (2) has no real solution, demonstrating that the memristor map has no fixed point.

Based on the definition in [21], all strange attractors generated by a chaotic system with no fixed point or with infinite fixed points are regarded as hidden attractors since the bassin of attraction does not not intersect with small neighbourhoods of any fixed points. That is to say that all the chaotic attractors generated by the memristor map (1) are hidden attractors. On the other hand, the memristor map is invariant under the transformation $(x,y)$ to $(-x,-y)$ for $a_3=0$, i.e., if $(x,y)$ is a solution of the memristor map then $(-x,-y)$ is a solution, which indicates that the integer-order map is symmetric with respect to the origin. This exact symmetry could serve to justify the appearance of multiple coexisting hidden attractors.

3. Fractional Model

Among the difference operators that have been defined in discrete fractional calculus, this paper focus on the Grunwald–Letnikov operator [22]:

$${\Delta }^{\alpha }y\left(n\right)=\frac{1}{h^{\alpha }}\sum _{j=0}^1\left(\begin{array}{c}\alpha \\ j\end{array}\right)y(n-j),$$

(4)

where $0<\alpha \le 1$ is the fractional order; the positive number $h\in ]0,+\infty [$ is the sampling time; and $\left(\begin{array}{c}\alpha \\ j\end{array}\right)$ is the binomial coefficient, which is defined as $\frac{\alpha (\alpha -1)\dots (\alpha -j+1)}{j!}$ for $j>0$.

Considering an original discrete system

$$y(n+1)=g\left(y\right(n\left)\right),$$

(5)

where $g\left(y\right(n\left)\right)$ is the nonlinear term and $y\in {\mathbb{R}}^2$ is the two-dimensional state vector. To achieve our goal, the first-order difference equation is given first

$$\Delta y_n=g\left(y\left(n\right)\right)-y\left(n\right).$$

(6)

By applying the Grunwald–Letnikov operator, the fractional form of Equation (6) becomes

$${\Delta }^{\alpha }{y}_n=g\left(y\left(n\right)\right)-y\left(n\right).$$

(7)

Moreover, according to definition (4), Equation (7) can be rewritten as

$${\Delta }^{\alpha }{y}_n=y(n+1)-\alpha y\left(n\right)+\sum _{j=2}^{n+1}{(-1)}^j\left(\begin{array}{c}\alpha \\ j\end{array}\right)y(n-j+1).$$

(8)

For simplicity, we denote $p=j-1$, and we substitute Equation (12) into Equation (7) so that we obtain [23]:

$$y(n+1)=g\left(y\left(n\right)\right)+(\mu -1)y\left(n\right)+\sum _{p=1}^n{\beta }_{p}y(n-p),$$

(9)

where the binomial coefficient ${\beta }_p$ is calculated by the following recursive formula

$${\beta }_0=-\mu ,{\beta }_p=\left(1-\frac{1+\alpha }{p+1}\right){\beta }_{p-1}.$$

(10)

It is reported that the value of ${\beta }_p$ decreases when the iteration p increases, regardless of the value of order $\alpha$ [24]. Consequently, in order to avoid computational inefficiency and large data storage, it is possible to exploit a finite truncation to study a fractional map. By indicating with L the truncation length and by taking into account the binomial coefficients, Equation (9) becomes [23]:

$$y(n+1)=g\left(y\left(n\right)\right)+(\mu -1)y\left(n\right)+\sum _{p=1}^L{\beta }_{p}y(n-p).$$

(11)

By considering a trade-off between the computation complexity and the approximate error, herein $L=20$ is selected, as suggested in reference [24]. By applying Equation (11) to the integer-order map (1), the following fractional order version based on the Grunwald–Letnikov discrete operator (4) is obtained:

$$\left\{\begin{array}{c}x(n+1)=a_{1}sin\left(a_{2}cos\left(y\left(k\right)\right)x\left(k\right)\right)+a_3+({\alpha }_1-1)x\left(n\right)-\sum _{p=1}^L{\beta }_{p_1}x(n-p),\hfill \\ y(n+1)=y\left(n\right)+x\left(n\right)+({\alpha }_2-1)y\left(n\right)-\sum _{p=1}^L{\beta }_{p_2}y(n-p),\hfill \end{array}\right.$$

(12)

where ${\alpha }_1,{\alpha }_2$ are the fractional orders and $a_1,a_2,a_3$ are constant parameters. For $a_1=2.6$, $a_2=1.1$, $a_3=0.001$, $\left(x\right(0),y(0\left)\right)=(1,2)$, and ${\alpha }_1={\alpha }_2=0.98$, the fractional map generates strange attractors, as shown in Figure 1a. Figure 1b shows the translation components $p-q$ using the 0–1 test [25], in which a Brownian-like (unbounded) trajectory is found, indicating the occurrence of a hidden chaotic attractor. Correspondingly, the maximum Lyapunov exponents are calculated as ${\lambda }_1=0.3$, which confirm the results.

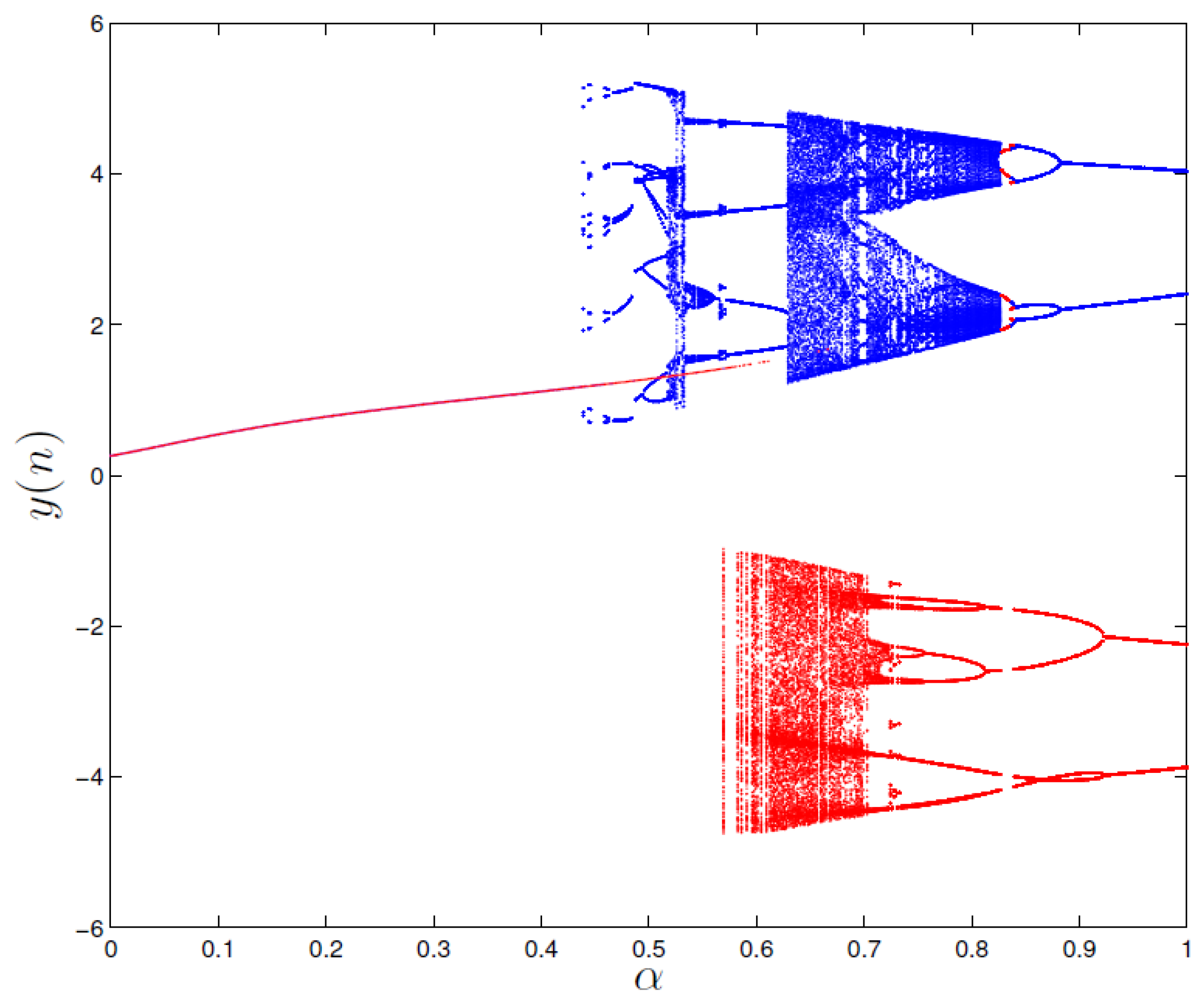
4. Dynamical Analysis of the Fractional Order Map

The effect of the fractional order and system parameters of the hidden dynamics of the proposed fractional map are discussed. In the process of numerical analysis, the system parameters are fixed where they satisfy the condition $a_3\ne 0$ or $a_3=0$ so that the attractors of these 2D fractional map are hidden.

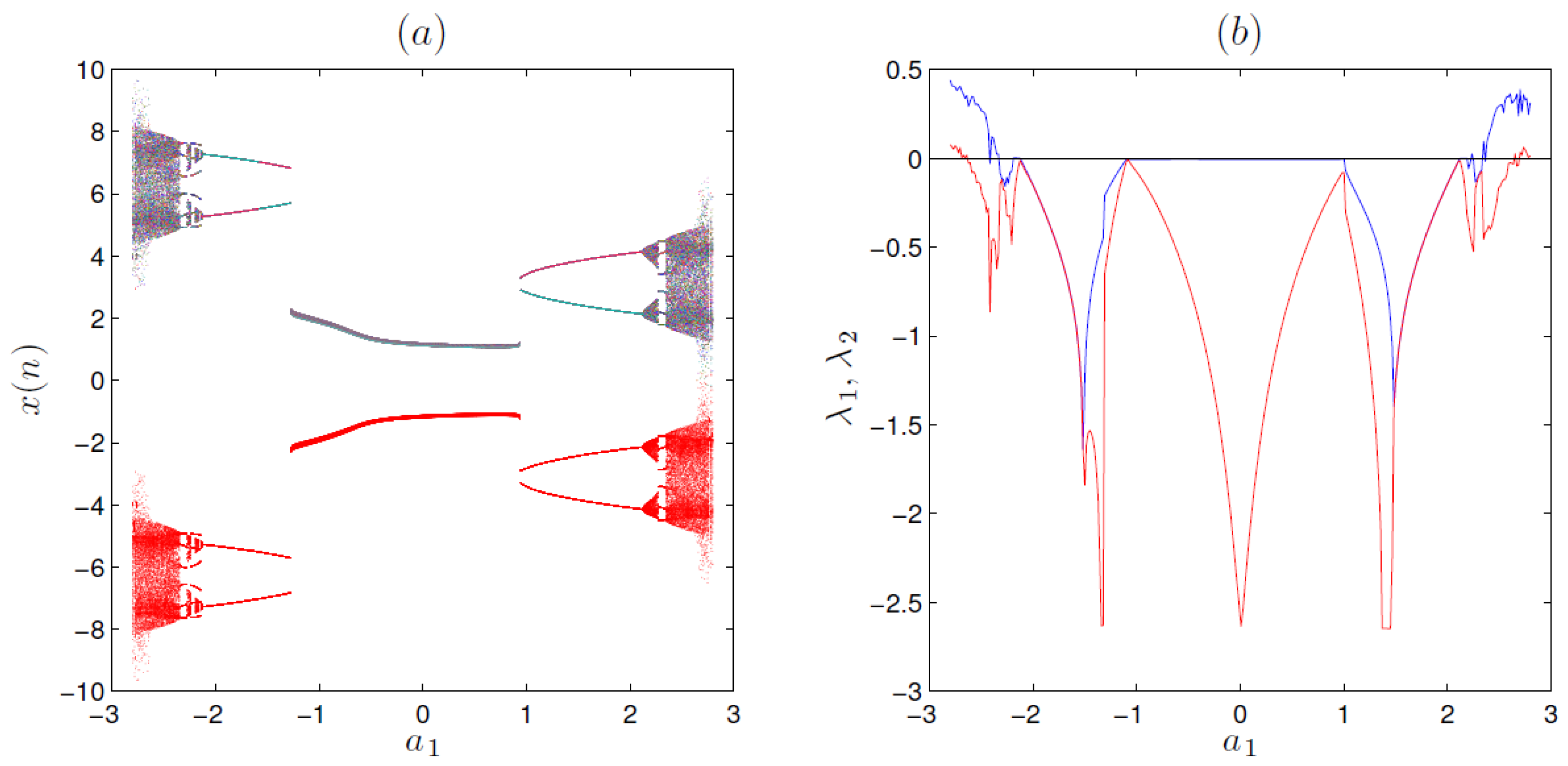
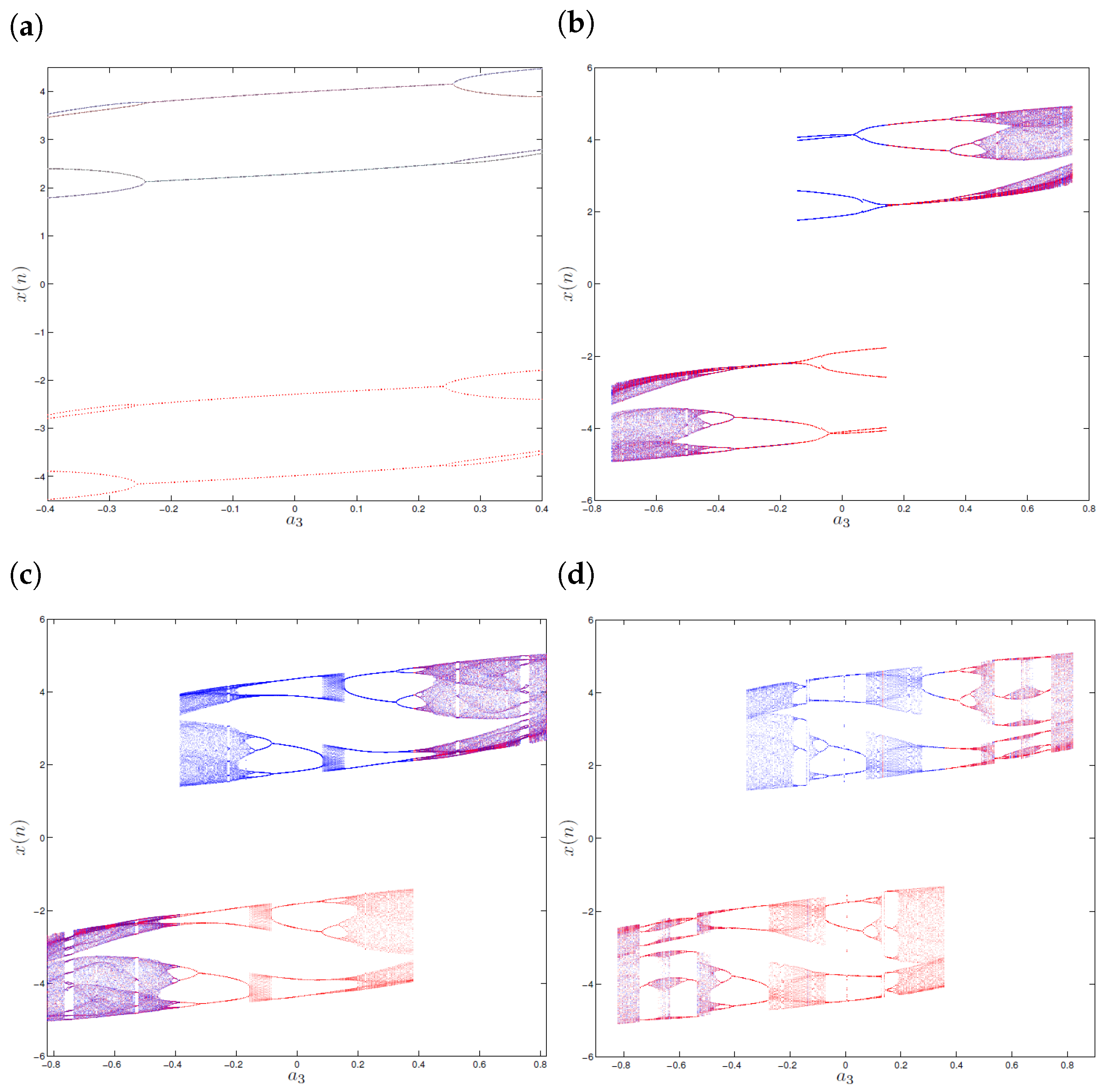
4.1. Case 1 for $a_3=0$

Firstly, we set $a_1$ as the bifurcation parameter and the system parameters are chosen as $a_2=1.1$, $a_3=0$, with fractional order $\alpha ={\alpha }_1={\alpha }_2=0.99$. The bifurcation diagram and Lyapunov exponents are derived and shown in Figure 2a,b, respectively. Note that the blue diagram is obtained for the initial condition (IC) $(1,2)$, while the red diagram is obtained for $(-1,-2)$. It can be seen that the fractional map shows the phenomena of coexistence hidden attractors in the chaotic and periodic interval. Moreover, the fractional memristor map (12) produces complex dynamical behavior under different bifurcation parameter values, where tangent bifurcation, chaos crisis, period-doubling bifurcation, and reverse-period-doubling bifurcation are included. When the bifurcation parameter $a_1$ is increased in $[-2.78,-2.35]$, it can be seen from the bifurcation diagram in Figure 2a that the states of the system start from chaos and go into periodic windows via the tangent bifurcation route. When $a_1$ is further increased, the fractional memrtistor map (12) evolves from a periodic to a chaotic state via the period-doubling route.

Without a loss of generality, the hidden attractors at several fractional orders corresponding to Figure 2 are shown in Figure 3a,c,e,g. Figure 3b,d,f,h, gives the $p-q$ chaotic dynamics in which the Brownian-like dynamics are a significant occurrence of the chaotic behaviors. The red and blue trajectories stand for the ICs $(1,2)$ and $(-1,-2)$, respectively.

4.2. Case 2 for $a_3\ne 0$

Considering that the system parameter and the initial condition of the 2D fractional memristor map are taken as $a_1=2.1,a_2=0.8,$ and IC $(1,2)$ (blue diagram), IC $(-1,-2)$ (red diagram), the coexistence of the bifurcation diagrams versus $a_3$ of the system for fractional-order values $\alpha =0.98,\alpha =0.85,\alpha =0.8,\alpha =0.75$ are plotted in Figure 4a–c, and Figure 4d, respectively. Different dynamical behaviors, including the chaos, period, and period-doubling routes, and multiple coexisting attractors, can be detected. For $\alpha =0.98$, it can be seen from Figure 4a that the fractional memristor map presents periodic behavior around $a_3\in (-0.6,0.6)$. When $\alpha =0.85$, the fractional map is in a chaotic state and eventually goes into a periodic state via reverse period-doubling bifurcation. In the interval $a_3\in [-0.126,0.142]$, a four-period attractor is observed. As $a_3$ is further increased, the motion trajectories starting from both initial conditions evolve from periodic to chaos via period-doubling bifurcation. The bifurcation diagram corresponding to the fractional order $\alpha =0.8$ is shown in in Figure 4c. Basically, when $a_3\in [-0.882,-0.4]$ the states of the fractional map goes from chaos to periodic attractors via reverse period-doubling bifurcation. However, when $a_3\in [-0.4,0.4]$ the attraction domain of the two attractors are significantly different, where two different types of coexisting attractors are obtained. For example, the state starting from IC $(-1,-2)$ (red diagram) shows the period-doubling route to chaos, and then at $a_3=0.4$ it jumps into the periodic state. However, the motion trajectories of the IC $(1,2)$ jump into the chaotic state at $a_3=-0.4$ and eventually return to the periodic state via inverse period bifurcation. For $a_3>0.4$, a period-doubling route to chaos is observed for both initial conditions. On decreasing the fractional order $\alpha$ to $0.75$, the bifurcation diagram is provided in Figure 4d. The bifurcation diagram in this case is similar to the one in Figure 4c, where more periodic behavior is observed.

In addition, the fractional order $\alpha =({\alpha }_1,{\alpha }_2)$ is considered as bifurcation parameter, and the bifurcation diagrams are derived as shown in Figure 5. Note that the blue diagrams are obtained for the IC $(1,2)$ and system parameters $a_1=2.1,a_2=0.8,a_3=0.3$, while the red diagram is obtained for IC $(-1,-2)$. It is observed that the new system produces more complex dynamics than the integer-order map (1). In particular, for the corresponding integer-order value $\alpha =1$ the fractional map is periodic; however, it becomes chaotic as the fractional-order value decreases, which indicates that the dynamic characteristic of the system is more complex. Moreover, the ICs have the same bifurcation behavior after entering the chaotic state via the inverse period bifurcation, but the red diagram lags behind the blue diagram. Finally, the fractional memristor map returns to the periodic state via the internal recovering crisis. The above numerical simulations demonstrate that the fractional memristor map with hidden attractors and under the Grunwald operator can describe the coexisting multiple phenomena [26,27,28].

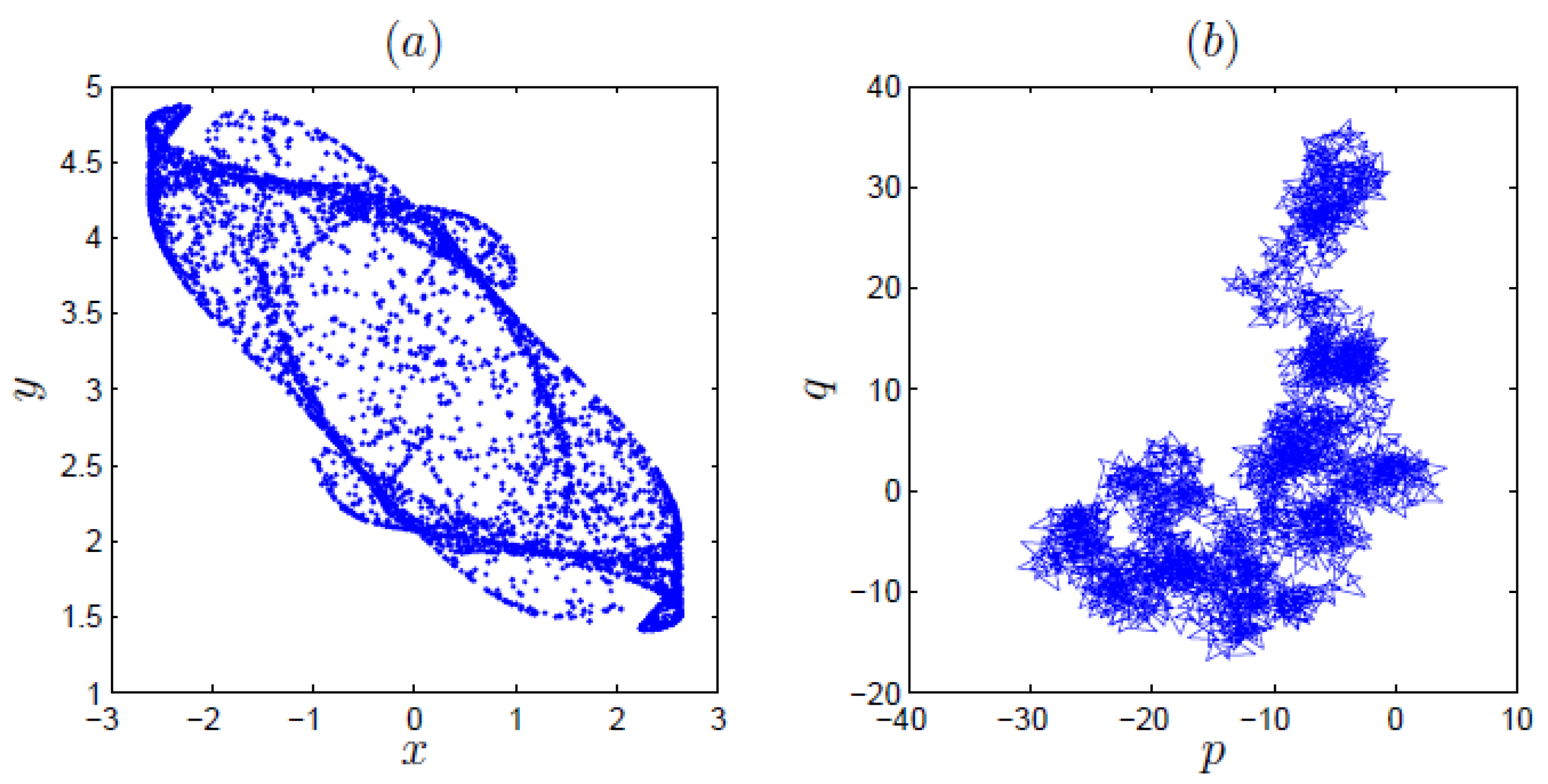
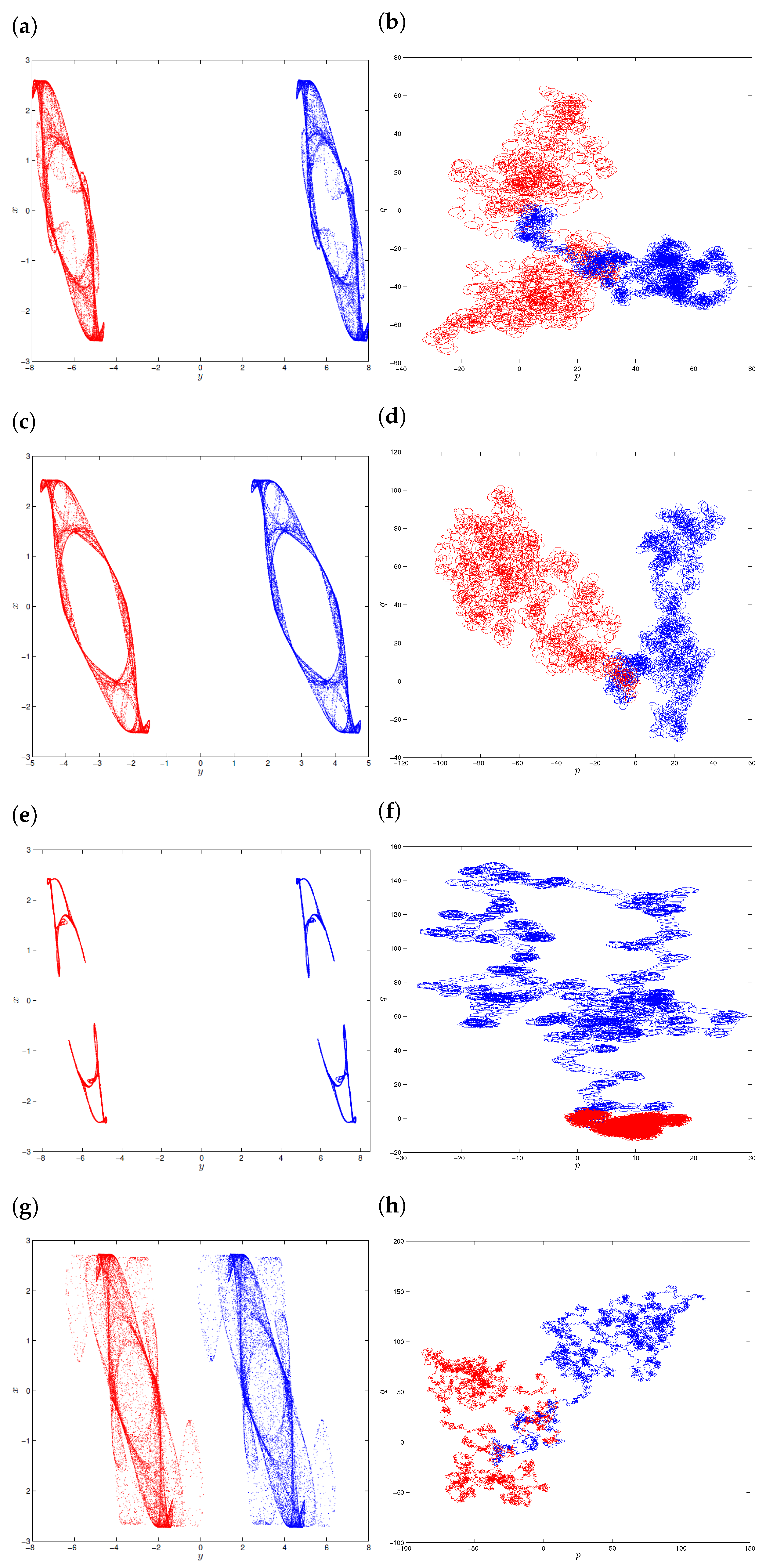
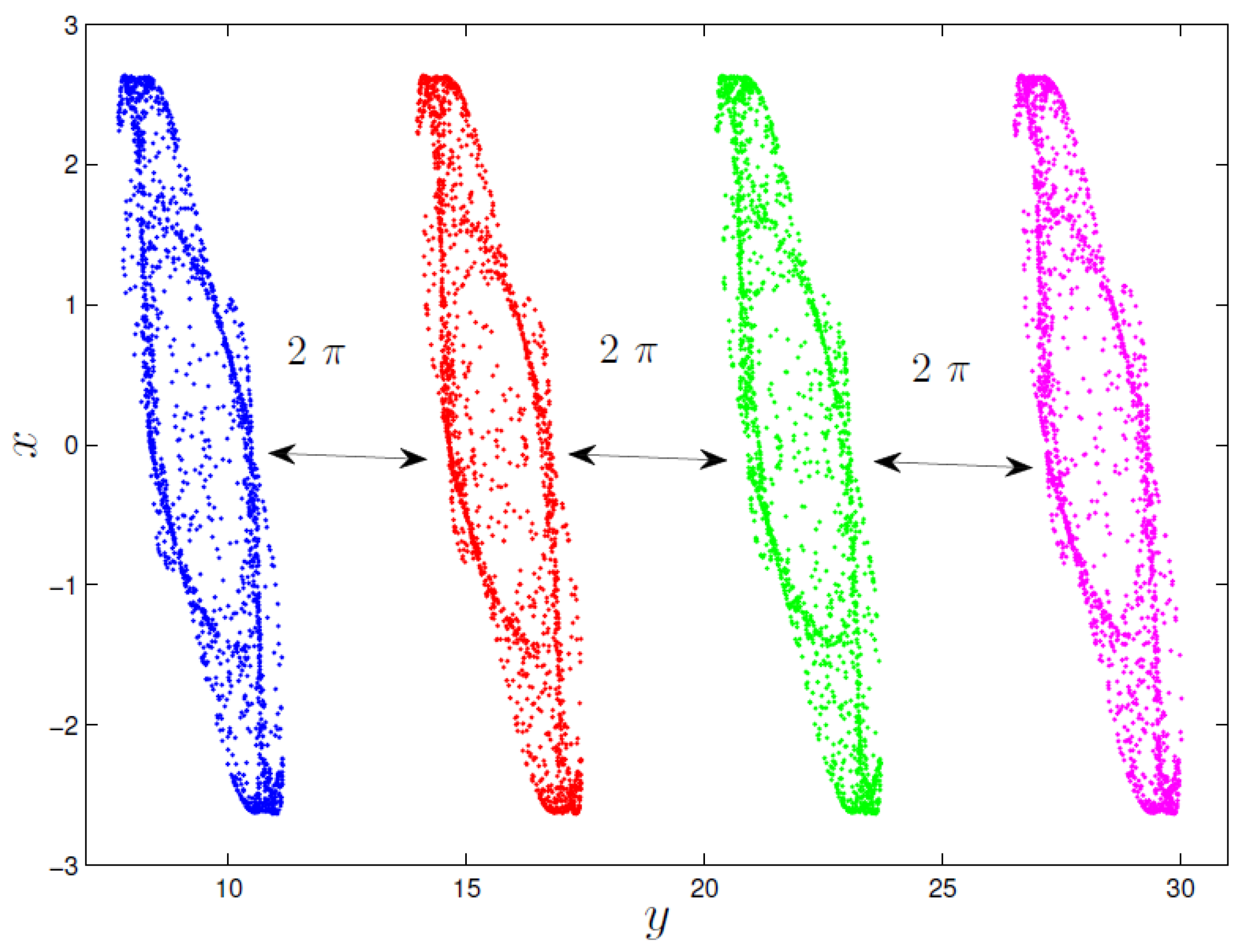
5. Initial Offset Boosting

In order to show the complex dynamics of the fractional memristor (1), the bifurcation diagrams and phase portraits are ploted by changing the IC y with $2\pi$ period $y\left(0\right)=2+2n\pi$ with fixed order $\alpha =0.99$ where $n=1,2,3,4$. Figure 6 illustrates the bifurcation diagrams of system (12) when $a_2=1.1$, $a_3=0.001$.

By fixing $a_1=2.6,a_2=1.1$, $a_3=0.001$ and varying $\alpha =0.99$, the attractors are displayed in Figure 7 for $y\left(0\right)=2+2n\pi$, where $n=1,2,3,4$. Clearly, all these hidden chaotic attractors have the same shape as the regime of homogenous multistability $2\pi$.

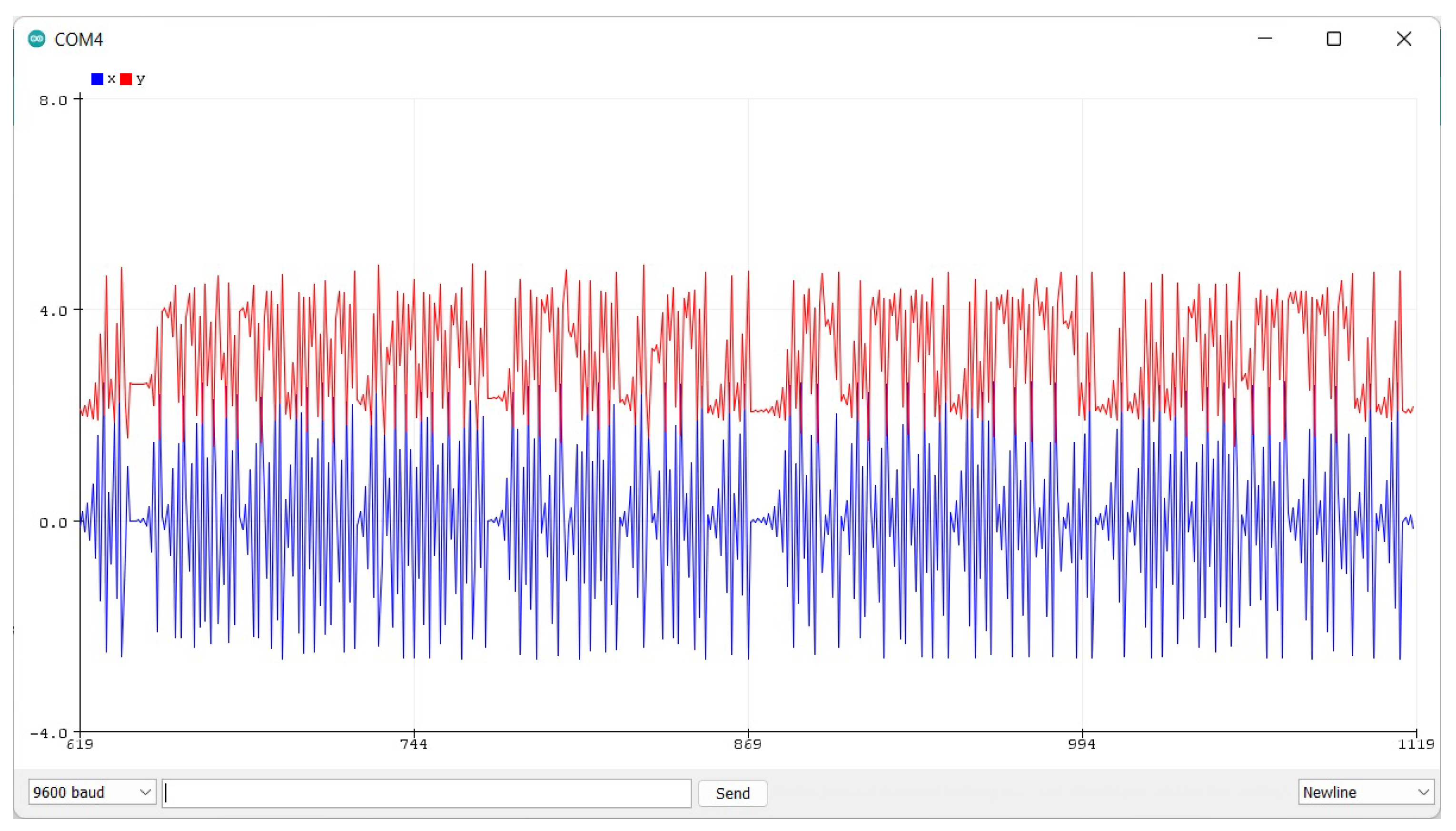
6. Realization of the Fractional Order Map

The map has been implemented by using the Equation (12). We have considered the trade-off between the computation complexity, the approximate error, and the limit resource of the hardware platform [29]. The truncation length L is 20. We have used the Arduino Uno board with an ATmega328P microcontroller. The microcontroller board is connected to a laptop via a USB cable (please see Figure 8). We realized the proposed map for the case $a_1=2.6$, $a_2=1.1$, $a_3=0.001$, $\left(x\right(0),y(0\left)\right)=(1,2)$, ${\alpha }_1={\alpha }_2=0.98$. Obtained signals are recorded and captured from the micro-controller. The experimental result in Figure 9 confirms chaos in the map. It is noted that the state y of the map has both positive and negative values based on the selected initial condition. We have implemented the map with the initial condition (1,2). Therefore, the experimental result matches with the numerical result in Figure 1a, where the value of the state y is positive.

7. Conclusions

In this paper, a fractional memristor map with hidden chaotic attractors is proposed. Under the different system parameter $a_3$, the fractional memristor map has either infinite fixed points or no fixed points. The map’s dynamic is verified by the bifurcation diagram, the Lyapunov exponents, the phase diagram, and the 0–1 test. It is found that there are many types of coexisting attractors in the fractional map. By further analysis, it is found that the fractional map generates multiple coexisting hidden attractors. Then, a microcontroller has been used to implement in hardware the conceived 2D fractional map.