A New Pre-Stretching Method to Increase Critical Flutter Dynamic Pressure of Heated Panel in Supersonic Airflow
Abstract
:1. Introduction
2. Governing Equations
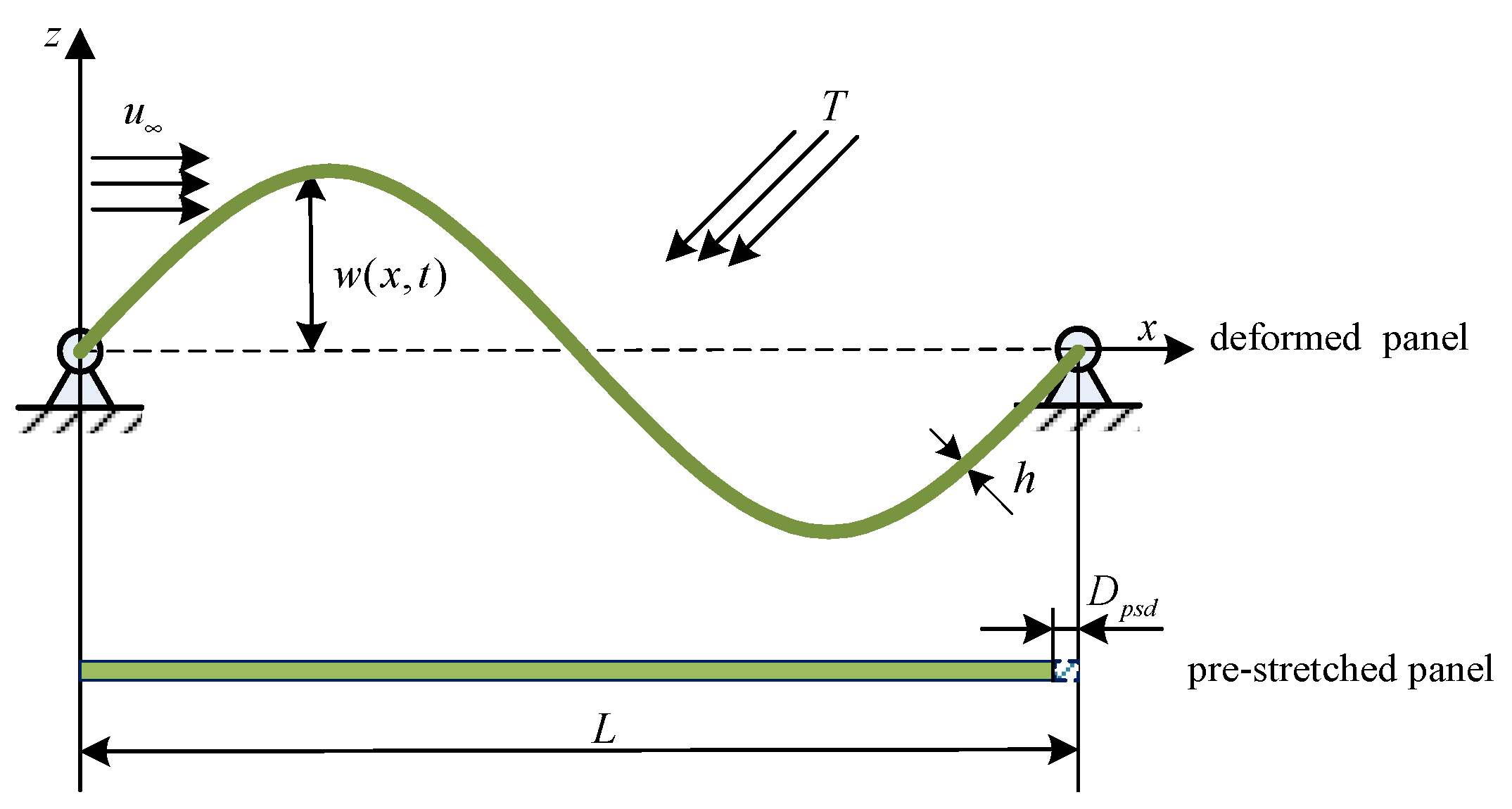
2.1. Geometrical Relationship of Deformation
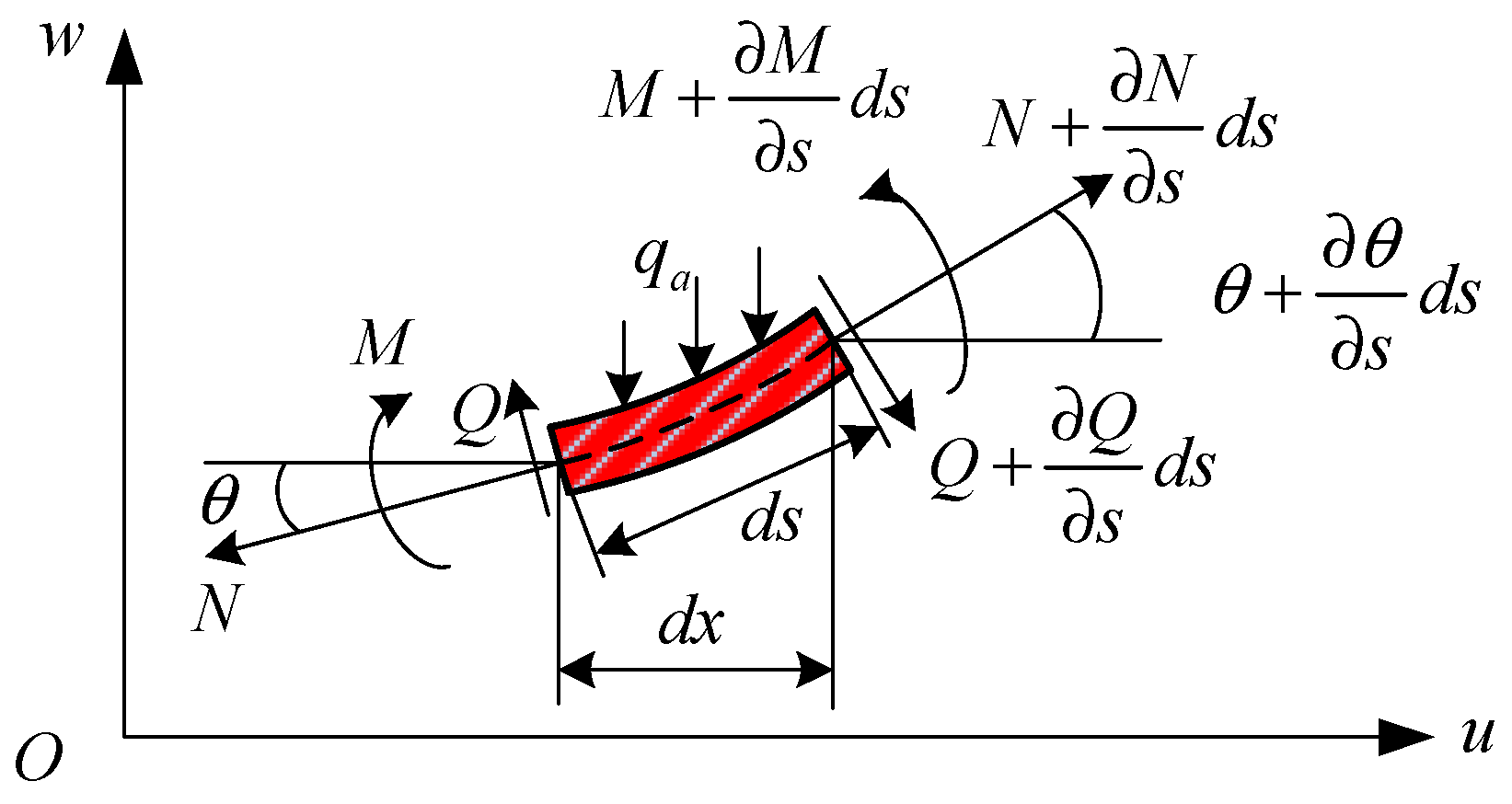
2.2. Differential Equilibrium Equation
2.3. Aerodynamic Equations
2.4. Governing Equation
3. Solution Methodology
3.1. Routh–Hurwitz Algebraic Criterion
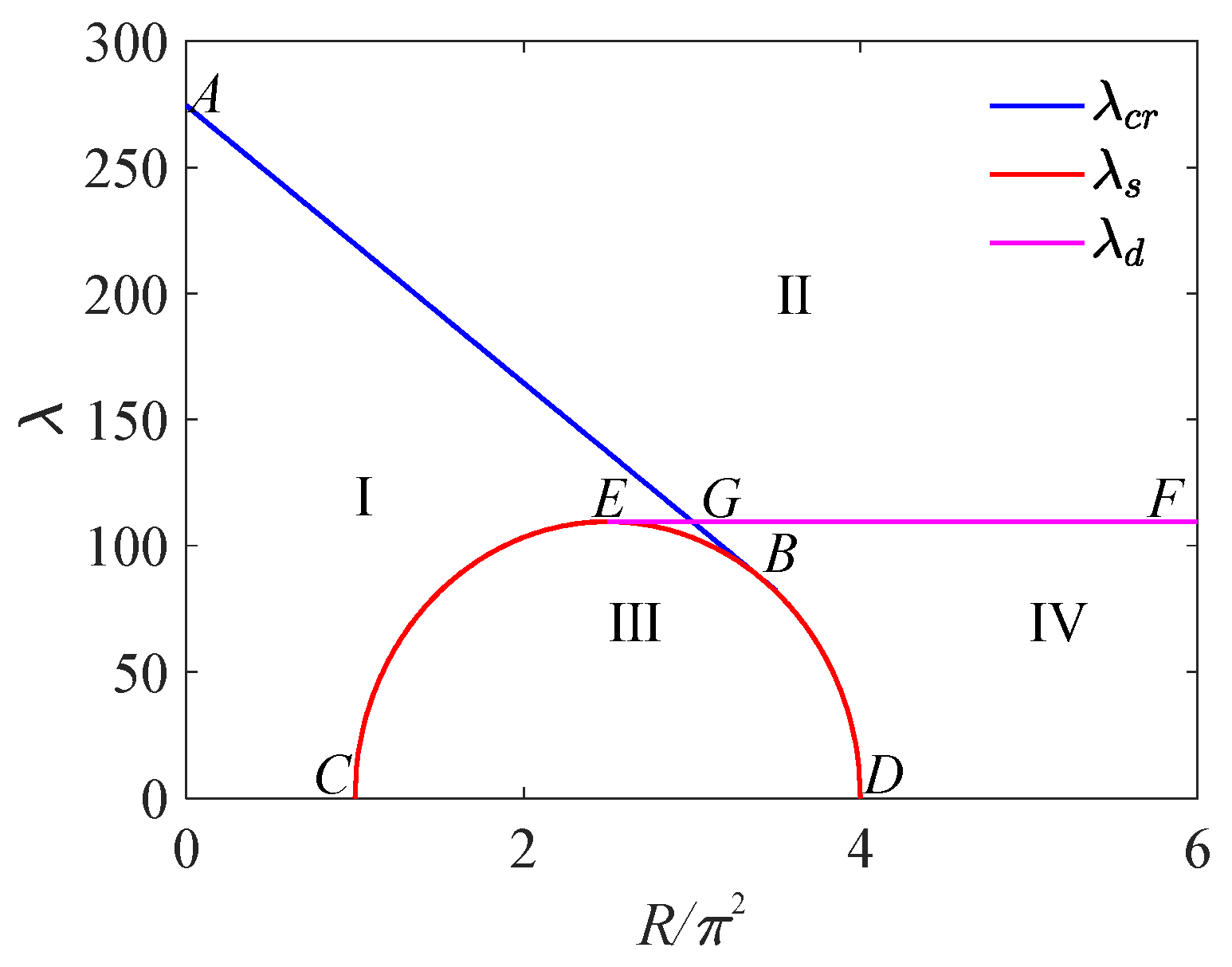
3.2. Flutter Boundary
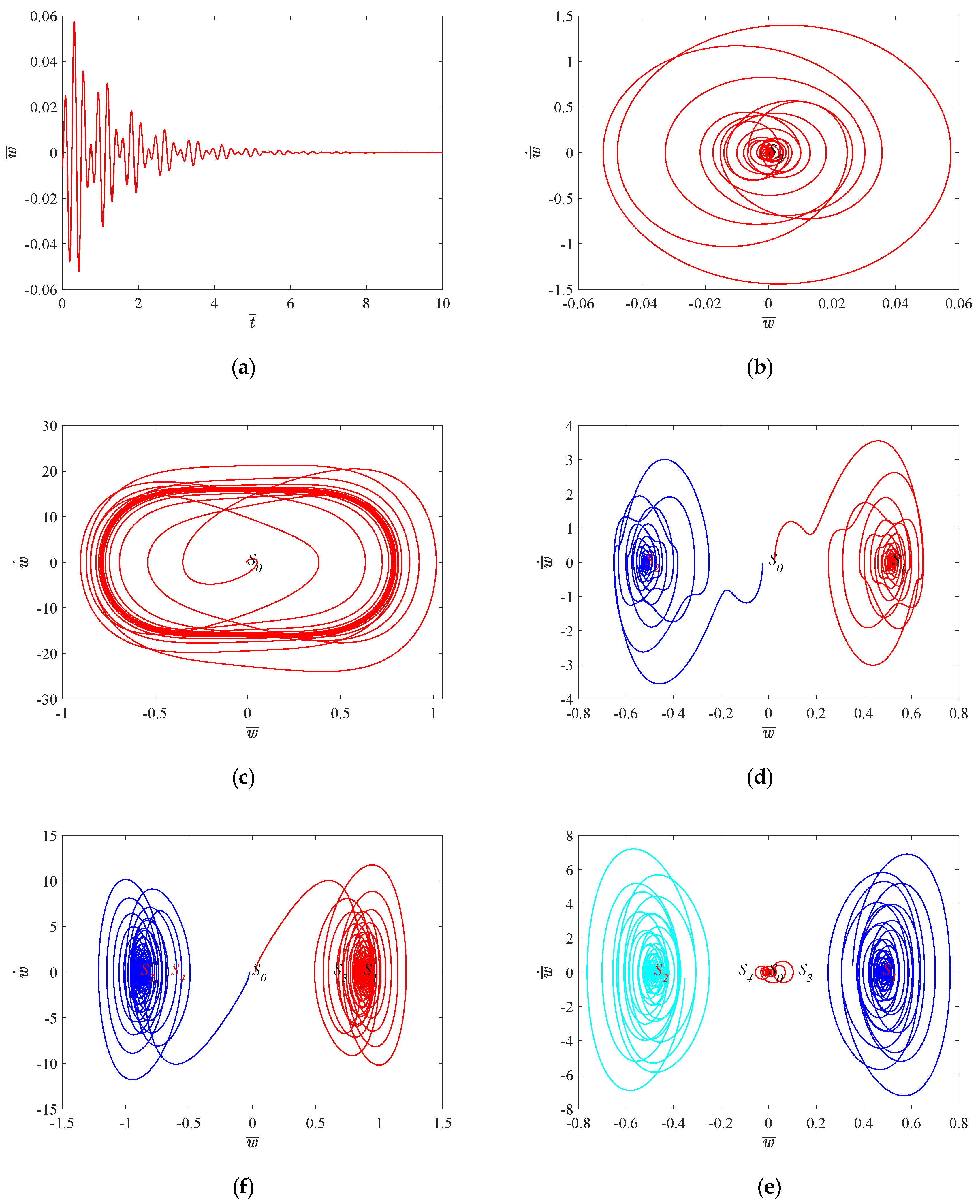
3.3. Nonlinear Post-Flutter Response
4. Results and Discussion
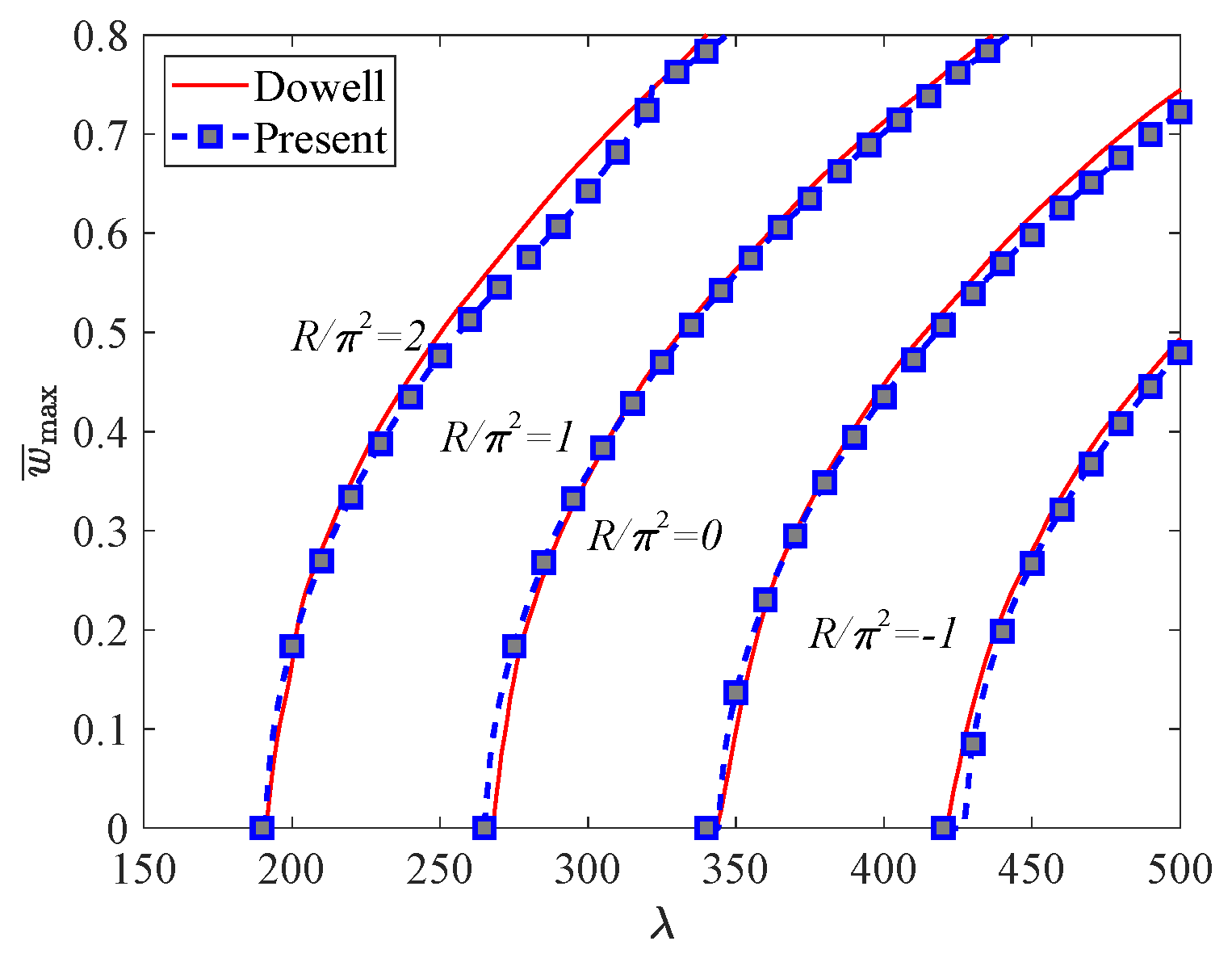
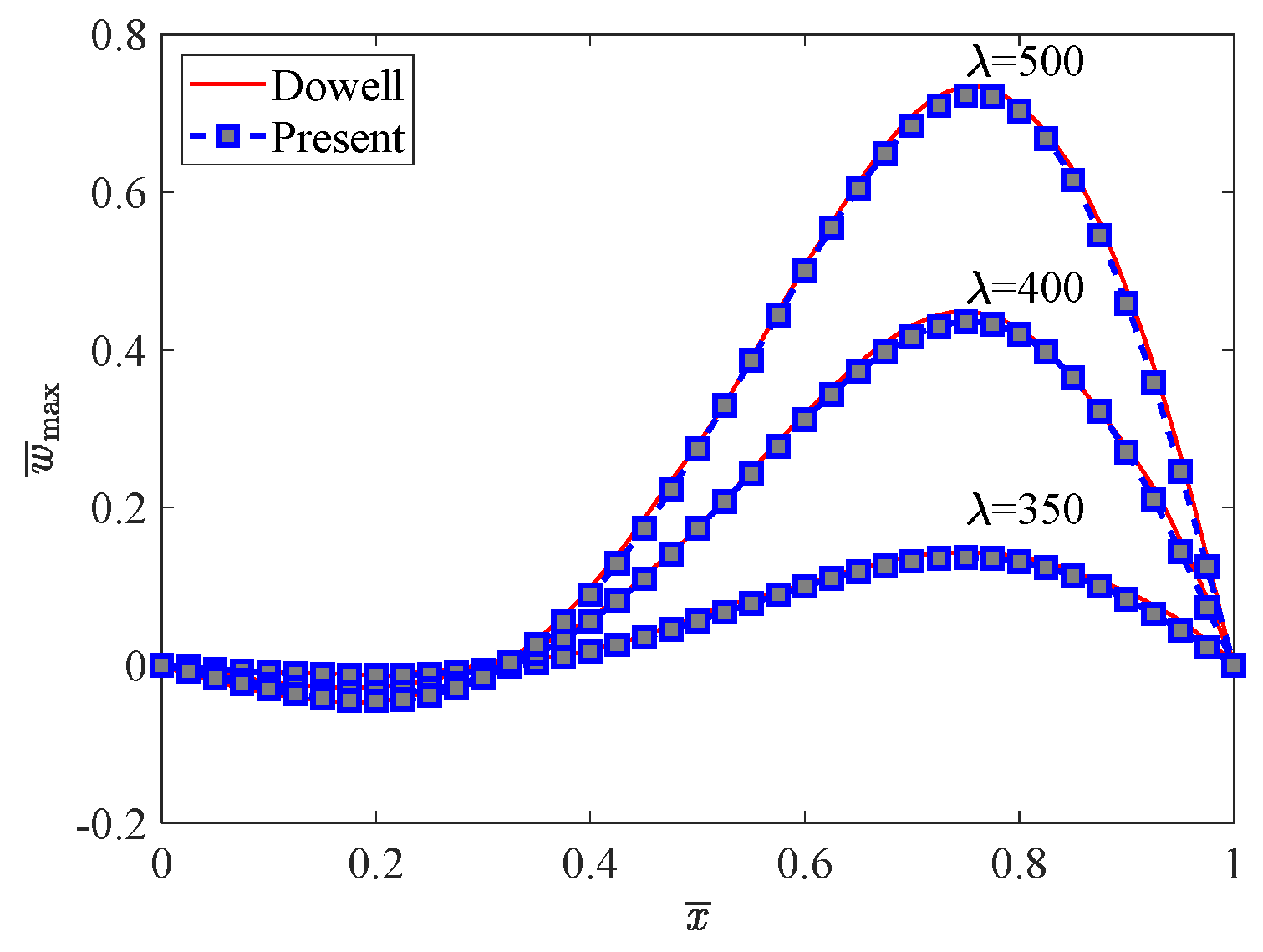
4.1. Verification
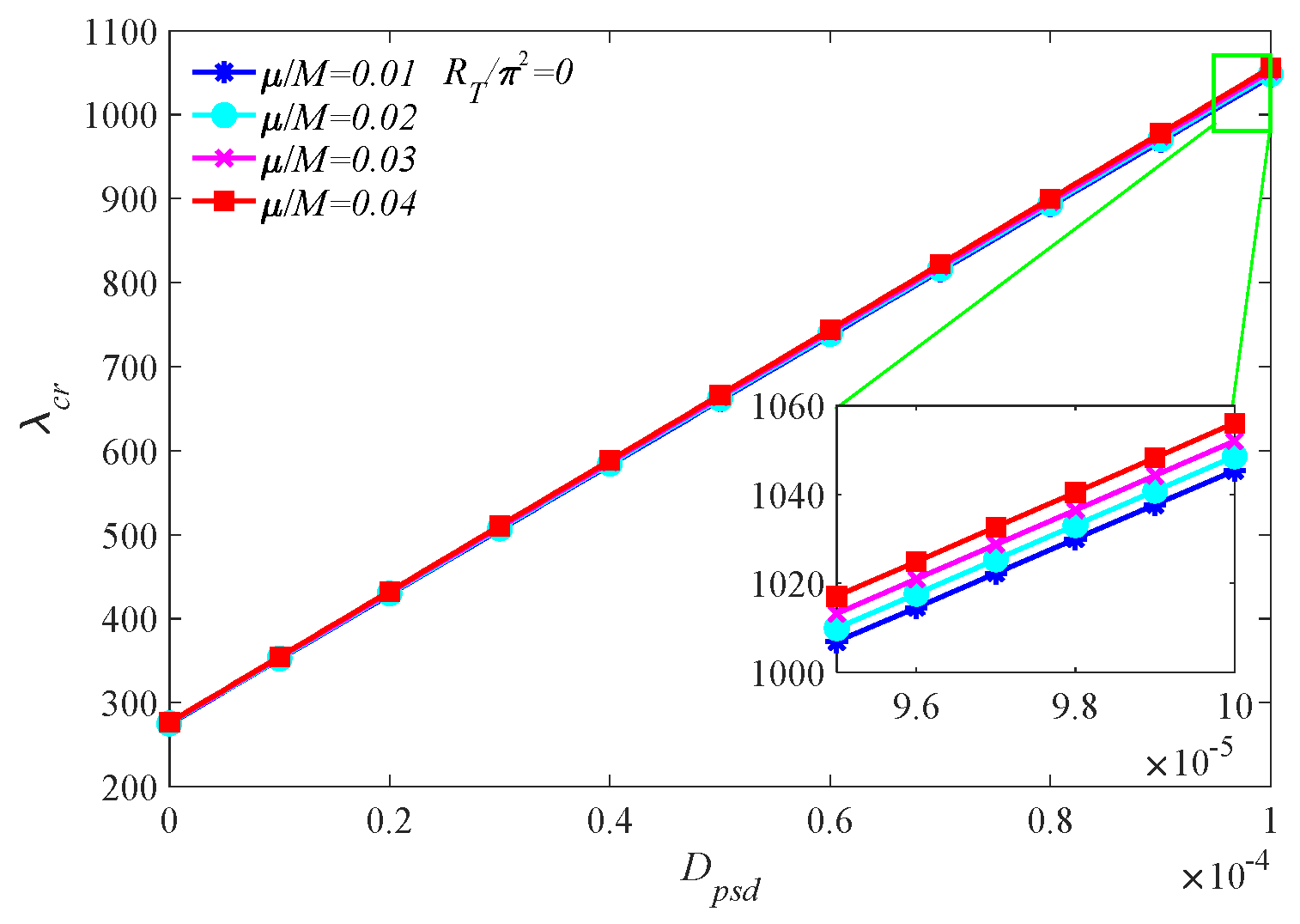
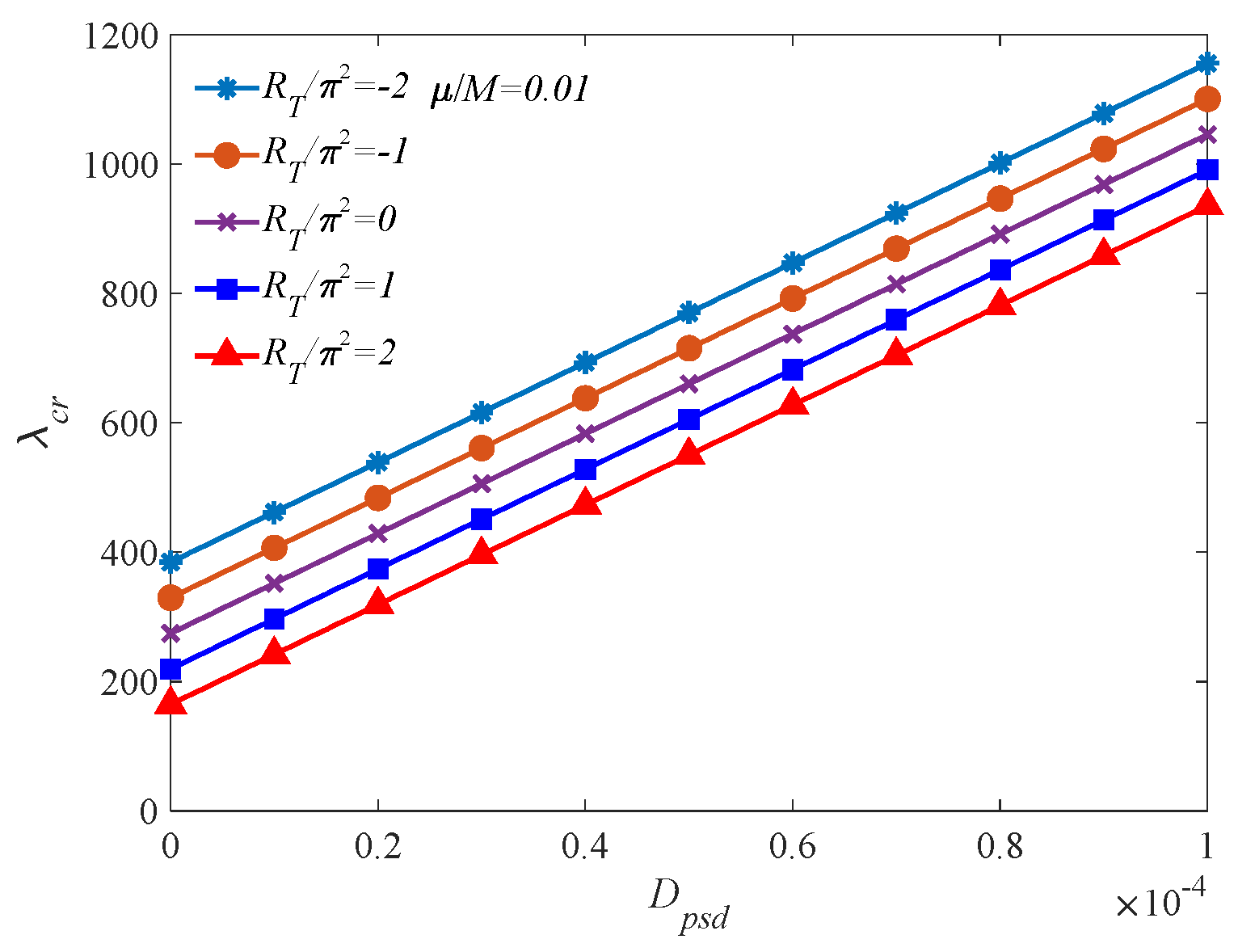
4.2. Numerical Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kehoe, M.W. A historical overview of flight flutter testing. In Proceedings of the AGARD Structures and Materials Panel Meeting, Banff, AB, Canada, 4–5 October 1995. [Google Scholar]
- Zhang, X. Local bifurcations of nonlinear viscoelastic panel in supersonic flow. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 1931–1938. [Google Scholar] [CrossRef]
- Wang, X.; Yang, Z.; Wang, W.; Tian, W. Nonlinear viscoelastic heated panel flutter with aerodynamic loading exerted on both surfaces. J. Sound Vib. 2017, 409, 306–317. [Google Scholar] [CrossRef]
- Cao, L.-N.; Yao, G. Hopf Bifurcation of Heated Panels Flutter in Supersonic Flow. Mathematics 2019, 7, 787. [Google Scholar] [CrossRef] [Green Version]
- Li, K.; Zhang, J.; Mei, G. Aerothermoelastic model of panel flutter with consideration of the history effects of aerodynamic heating. Int. J. Appl. Mech. 2012, 4, 3. [Google Scholar] [CrossRef]
- Hosseini, M.; Fazelzadeh, S.A. Aerothermoelastic Post-Critical and Vibration Analysis of Temperature-Dependent Functionally Graded Panels. J. Therm. Stress. 2010, 33, 1188–1212. [Google Scholar] [CrossRef]
- Stanford, B.; Beran, P. Aerothermoelastic topology optimization with flutter and buckling metrics. Struct. Multidiscip. Optim. 2013, 48, 149–171. [Google Scholar] [CrossRef]
- Guimarães, T.A.; Sanches, L.; Marques, F.D. Nonlinear supersonic post-flutter motion of panels with adjacent bays and thermal effects. Int. J. Non-Linear Mech. 2020, 125, 103545. [Google Scholar] [CrossRef]
- Arena, A.; Taló, M.; Snyder, M.P.; Lacarbonara, W. Enhancing flutter stability in nanocomposite thin panels by harnessing CNT/polymer dissipation. Mech. Res. Commun. 2020, 104, 103495. [Google Scholar] [CrossRef]
- Samadpour, M.; Asadi, H.; Wang, Q. Nonlinear aero-thermal flutter postponement of supersonic laminated composite beams with shape memory alloys. Eur. J. Mech. A/Solids 2016, 57, 18–28. [Google Scholar] [CrossRef]
- Kassem, M.; Yang, Z.; Gu, Y.; Wang, W.; Safwat, E. Active dynamic vibration absorber for flutter suppression. J. Sound Vib. 2019, 469, 115110. [Google Scholar] [CrossRef]
- Basta, E.; Ghommem, M.; Emam, S. Flutter control and mitigation of limit cycle oscillations in aircraft wings using distributed vibration absorbers. Nonlinear Dyn. 2021, 106, 1975–2003. [Google Scholar] [CrossRef]
- Zhao, H.; Cao, D. A study on the aero-elastic flutter of stiffened laminated composite panel in the supersonic flow. J. Sound Vib. 2013, 332, 4668–4679. [Google Scholar] [CrossRef]
- Amirzadegan, S.; Safavi, S.M.M.; Jafarzade, A. Supersonic Panel Flutter Analysis Assuming Effects of Initial Structural Stresses. J. Inst. Eng. Ser. C 2019, 100, 833–839. [Google Scholar] [CrossRef]
- Wang, T.-Q.; Wang, R.-H.; Ma, N.-J. Nonlinear Vibration of a Stiffened Plate Considering the Existence of Initial Stresses. KSCE J. Civ. Eng. 2019, 23, 2303–2312. [Google Scholar] [CrossRef]
- Rasool, M.; Singha, M.K. Aeroelastic analysis of pre-stressed variable stiffness composite panels. J. Vib. Control 2019, 26, 724–734. [Google Scholar] [CrossRef]
- Dowell, E. Nonlinear oscillations of a fluttering plate. AIAA J. 1966, 4, 1267–1275. [Google Scholar] [CrossRef]
- Xue, D.Y.; Mei, C. Finite element nonlinear flutter and fatigue life of two-dimensional panels with temperature effects. J. Aircr. 1993, 30, 993–1000. [Google Scholar] [CrossRef]

| Young’s Modulus | Poisson’s Ratio | Mass Density | Thermal Expression |
|---|---|---|---|
| E/GPa | ν | ρ/(kg·m−3) | α/(10−6K−1) |
| 70.71 | 0.3 | 2710 | 12.9 |
| Region | The Eigenvalues of the Jacobi Matrix for the Equilibrium Points | ||||
|---|---|---|---|---|---|
| I | 220 | - | - | ||
| II | 250 | - | - | ||
| III | 70 | - | |||
| IV | 100 | ||||
| EBG | 105 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.-C.; Yao, G.-F.; Wang, M.; Gao, K.-Y.; Hou, Q. A New Pre-Stretching Method to Increase Critical Flutter Dynamic Pressure of Heated Panel in Supersonic Airflow. Mathematics 2022, 10, 4506. https://doi.org/10.3390/math10234506
Zhu Y-C, Yao G-F, Wang M, Gao K-Y, Hou Q. A New Pre-Stretching Method to Increase Critical Flutter Dynamic Pressure of Heated Panel in Supersonic Airflow. Mathematics. 2022; 10(23):4506. https://doi.org/10.3390/math10234506
Chicago/Turabian StyleZhu, Yuan-Cheng, Guo-Feng Yao, Min Wang, Kui-Yang Gao, and Qi Hou. 2022. "A New Pre-Stretching Method to Increase Critical Flutter Dynamic Pressure of Heated Panel in Supersonic Airflow" Mathematics 10, no. 23: 4506. https://doi.org/10.3390/math10234506






